In this section, we propose a novel method, RMO_SODSDA, which includes two aspects: (1) satisfying separation-of-duty constraints, and (2) ensuring authorization security.
3.1. Satisfying Separation-of-Duty Constraints
Separation-of-duty constraints can be effectively enforced by mutually exclusive constraints. In order to satisfy these constraints, we constructed different variants of mutually exclusive roles to implement RSSOD based on any unconstrained role-mining algorithm for basic RMP, including algorithm design and description, computational complexity, and correctness analysis. First, we present the following definitions.
Definition 1. (static and soft mutually exclusive roles, t-m SMER) Given m roles r1,r2,…,rm, a t-m SMER states that no user is allowed to have t or more of these m roles. It is expressed as smer<{r1,r2,…,rm},t>, where each ri is a role, and m and t are integers, such that 2≤ k≤ n. A t-m SMER can be formalized as follows:
It has been shown that any
t-
m SMER can be equivalently represented using a set of
t-
t SMER [
24].
Definition 2. (static and hard mutually exclusive roles, t-t SMER) Given t roles r1,r2,…,rt, a t-t SMER states that no user is allowed to have these t roles. It is expressed as smer<{r1,r2,…,rt},t>, where each ri is a role, and t is an integer, such that t≥ 2. A t-t SMER can be formalized as follows:
Definition 3. (role-mining problem with RSSOD constraints) Given a set of users U, a set of permissions P, a user-permission assignments matrix UPA, and a set of RSSOD constraints E={e1,e2,…}, find a set of roles R, a user-role assignments matrix UA, a role–permission assignments matrix PA, and a set of SMER constraints C, such that the UA and PA are consistent with the UPA, C enforces E, and the number of mining roles |R| is minimized. It can be formalized as follows:
3.1.1. Preprocessing
Any role-mining algorithm that takes no RSSOD constraint into consideration is used for mining minimal roles in Algorithm 1.
| Algorithm 1. Preprocessing |
| Input: original matrix UPA |
| Output: decomposed matrix UA, PA, candidate set CR of roles |
| The Fast Miner method and Boolean matrix decomposition are adopted to derive CR and configure RBAC, such that |
|
3.1.2. Construction of 2–2 SMER Constraints
A 2–2 SMER constraint can be expressed as c=<{ri, rj},2>, which means that ri and rj are mutually exclusive, that is, the two roles cannot be assigned to any user. Although 2–2 SMER constraints are considered to be quite restrictive, they are sufficient to enforce any enforceable RSSOD constraint. RSSOD constraint ei is nonenforceable in one of the following cases: (1) a single role in the PA matrix owns all permissions in ei, and (2) candidate matrix UA already has user assignments violating the constraints.
| Algorithm 2. Construction of 2–2 SMER constraints |
| Input:UA, CR, set E of k-n RSSOD constraints |
| Output: set C of 2–2 SMER constraints |
| 1. C= ∅; |
| 2. for each ei in E do |
| 3. P(ei) denotes the permissions covered by ei; |
| 4. : |
| 5. if then |
| 6. ei is nonenforceable; |
| 7. continue; |
| 8. end if |
| 9. for each pair of roles (ri, rj) in S do |
| 10. if then |
| 11. if UA satisfy smer<{ri, rj},2> then |
| 12. C={smer<{ri, rj},2>} ∪ C; |
| 13. else |
| 14. ei is nonenforceable with 2–2 SMER constraints; |
| 15. end if |
| 16. end if |
| 17. end for |
| 18. end for |
In Algorithm 2, the inputs are the above UA, CR, and set E = {e1,e2,…} of k-n RSSOD constraints, and the output is set C = {c1,c2,...} of 2–2 SMER constraints, such that C enforces E. In order to construct 2–2 SMER constraints, it is necessary to find a set of roles S, such that each role in S at least has permissions in ei (line 4). Then, if any role has all the permissions in ei, we declare ei as nonenforceable (lines 5–8); otherwise, we analyze each pair of roles (ri, rj) to determine whether they are valid 2–2 SMER constraints. If ri and rj are mutually exclusive roles, each one contains at least a mutually exclusive permission that must be absent in the other (lines 9–17).
Computational complexity: constructing 2–2 SMER constraints for an RSSOD can be done in polynomial time. If the number of roles in set S for the RSSOD is m, then the time for deciding whether the RSSOD constraint is enforceable or not is O(m), and the time for constructing mutually exclusive roles is O(m2); thus, the total time complexity is (m2). The smaller m gets, the more acceptable the algorithm becomes.
3.1.3. Construction of t-t SMER Constraints
However, many RSSOD constraints might become nonenforceable in some cases because of the restrictive 2–2 SMER constraints. Next, we present an approach for implementing RSSOD with t-t SMER constraints (t > 2), which is less restrictive as compared with only using 2–2 SMER constraints. It is necessary to find a maximum t for the given RSSOD constraints in Algorithm 3.
| Algorithm 3. Construction of t-t SMER constraints |
| Input:UA, CR, set E of k-n RSSOD constraints |
| Output: set C of t-t SMER constraints |
| 1. C= ∅; |
| 2. for each ei in E do |
| 3. P(ei) denotes the permissions covered by ei; |
| 4. : |
| 5. if |S|<k then |
| 6. ei is nonenforceable; |
| 7. continue; |
| 8. else if then |
| 9. ei is nonenforceable; |
| 10. continue; |
| 11. else if then |
| 12. ei is nonenforceable; |
| 13. continue; |
| 14. else |
| 15. for t=3 to +1 do |
| 16. for any set {r1’,r2’,…rt’} in S do |
| 17. if UA satisfies smer<{r1’,r2’,…rt’},t> then |
| 18. C={smer<{r1’,r2’,…rt’},t>} ∪ C; |
| 19. else |
| 20. ei is nonenforceable with t-t SMER constraints; |
| 21. end if |
| 22. end for |
| 23. end for |
| 24. end if |
| 25. end for |
To construct t-t SMER constraints for an RSSOD ei, like in Algorithm 2, we should find set S at first. Next, we determine whether ei is enforceable or not. In Algorithm 3, line 4 determines set S from CR. Lines 5–6 indicate that if the number of roles in set S is less than k in ei, it cannot be enforced. Lines 8–9 indicate that if any role in set S has all the permissions in ei, it cannot be enforced. Lines 11–12 show that if RH relationships exist in S, ei cannot be enforced. Lines 15–23 determine whether the t-t SMER constraints are satisfied in matrix UA and insert them into set C.
Computational complexity: if the number of roles in S is m, the time for determining whether a constraint is enforceable or not is O(m). Constructing t-t SMER constraints depends on the double loops. The execution number of the first loop is –2; in the second loop, for the particular t, it is necessary to obtain any t roles from S, and the execution time is O(). Thus, the total time complexity is ()+()= O(). If m is small, the efficiency of the algorithm is acceptable.
3.1.4. Construction of t-m SMER Constraints
Compared with t-t SMER constraints, although t-m SMER constraints (2 < t < m) are less restrictive, they are more flexible for applications. The differences between t-m SMER and t-t SMER are presented in Algorithm 4.
| Algorithm 4. Construction of t-m SMER constraints |
| Input:UA, CR, set E of k-n RSSOD constraints |
| Output: set C of t-m SMER constraints |
| …… |
| 1. for t=3 to +1 do |
| 2. m=(k-1)×(t-1)+1; |
| 3. for any set {r1’,r2’,…rm’} in CR do |
| 4. if UA satisfy smer<{r1’,r2’,…rm’},t> then |
| 5. C={smer<{r1’,r2’,…rm’},t>} ∪ C; |
| 6. else |
| 7. ei is nonenforceable with t-m SMER constraints; |
| 8. end if |
| 9. end for |
| 10. end for |
| …… |
Computational complexity: constructing t-m SMER constraints depends on the double loops. The execution number in the first loop is ; in the second loop, for the particular m, it is necessary to obtain any m roles from CR. Thus, the execution time of the double loops is O(2n). The efficiency of the algorithm decreases obviously as the number of CR increases.
3.1.5. Correctness Analysis
Statement 1. Given an m-m RSSOD constraint e1, t-m SMER constraint c1 can precisely enforce e1 if and only if t = 2.
Proof. We analyze the statement from the two sides of sufficiency and necessity.
Sufficiency. When constraint c1=smer<{r1,r2,…,rm},2> holds, that is,, this indicates that at least m users are required together to have all roles of set {r1,r2,…,rm}. Any set of (m-1) users should not be able to have all m roles, that is, . According to RSSOD, c1 can enforce e1.
Necessity. It is proved by contradiction. Assume that there exist (m – 1) users who can cover all the m roles, that is,. In other words, there exists some user who has two of the n roles, that is,, which is contradictory to constraint smer<{r1,r2,…,rm},2>. Thus, the assumption is false. □
Statement 2. Given a 2–m RSSOD constraint e2, t-m SMER constraint c2 can precisely enforce e2 if and only if t = m.
Proof. We also analyze the statement from the two sides of sufficiency and necessity.
Sufficiency. When constraint c2=smer<{r1,r2,…,rm},m> holds, that is, , this indicates that no user has all roles of the set {r1,r2,…,rm}. In other words, at least two users are required together to have all the m roles. According to RSSOD, c2 can enforce e2.
Necessity. It is proved by contradiction. Assume that there exists some user who has all the m roles, that is,, which is contradictory to the constraint smer<{r1,r2,…,rm},m>. Thus, the assumption is false. □
Theorem 1. Given a k-n RSSOD constraint (k > 2) and a candidate role set CR, where k≤ n≤ |CR|, t-m SMER constraints constructed by our algorithms can precisely enforce k-n RSSOD if t ≤.
Proof. According to Definition 1, any user has (t – 1) roles at most, and any (k – 1) users have (k – 1) ×(t – 1) roles at most. It is also proved by contradiction. Without loss of generality, t=, we assume that the RSSOD constraint holds, that is, the number of roles assigned to (k – 1) users is , which breaches the k-n RSSOD. Thus, the assumption is false and the theorem is proved. □
Example 1. Constructing t-m SMER constraints based on our method can enforce rssod<{r1,r2,r3,r4,r5},k> with different k in Table 2, where 2≤ k≤ 5. 3.2. Ensuring Authorization Security
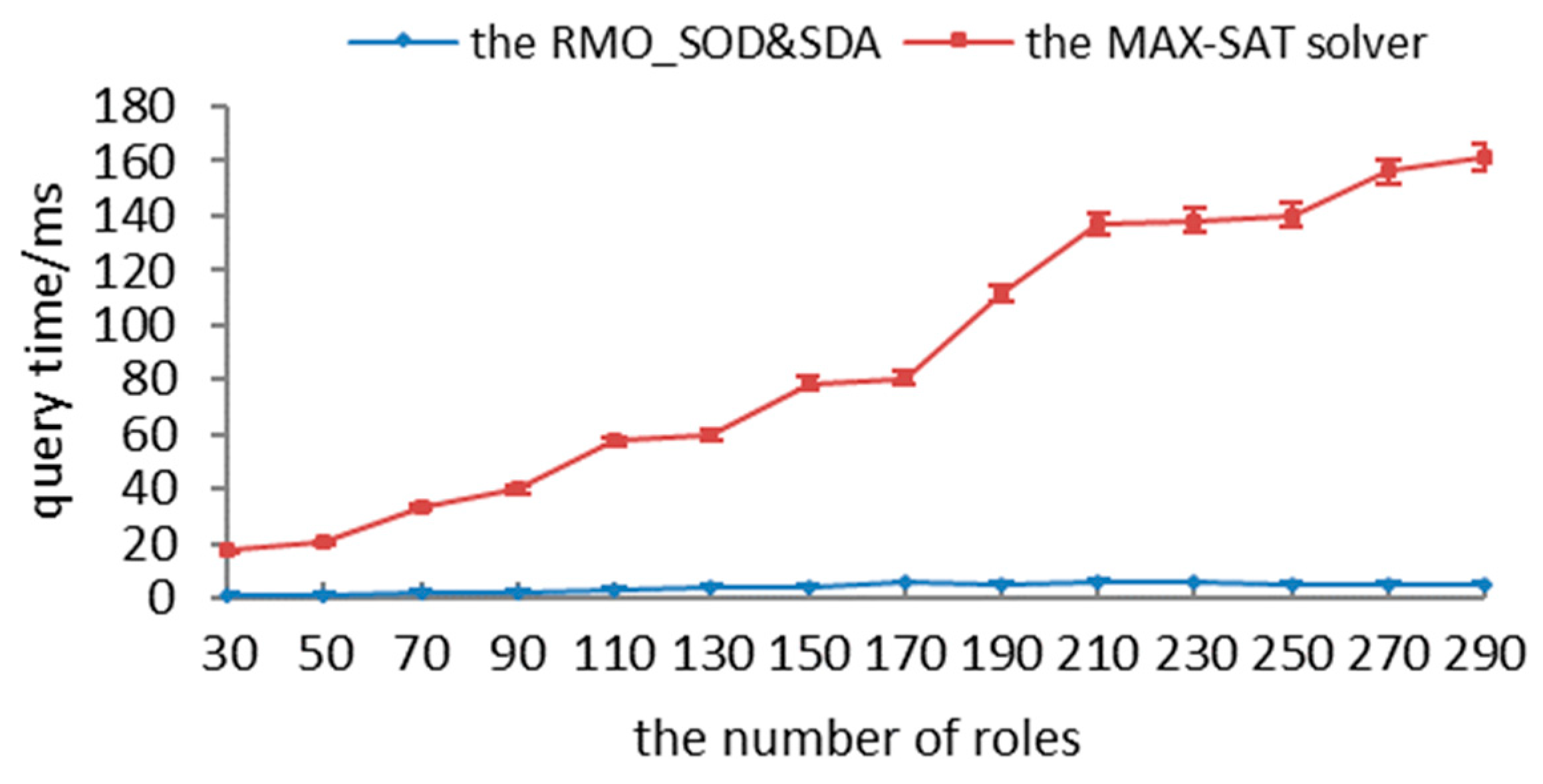
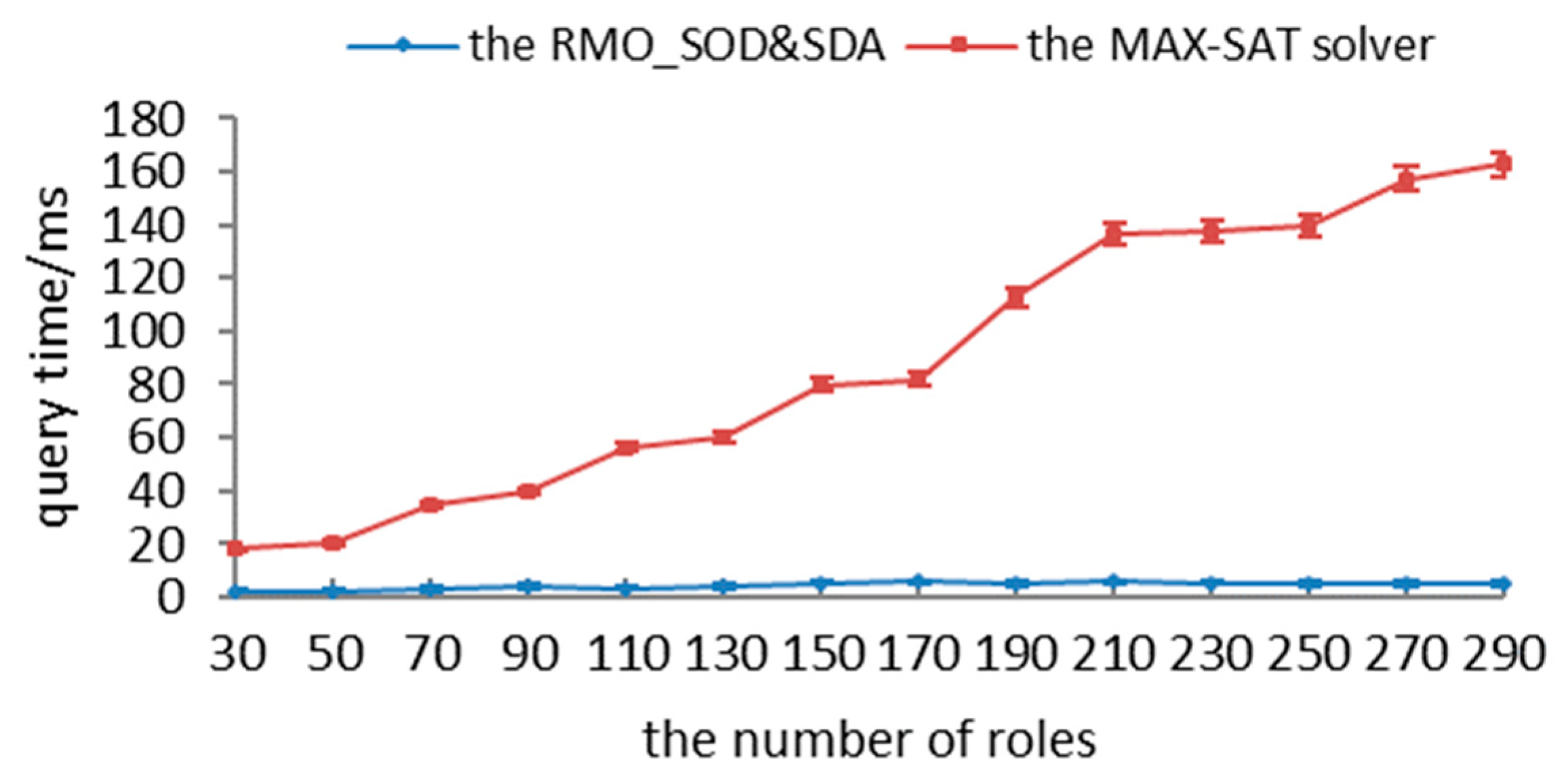
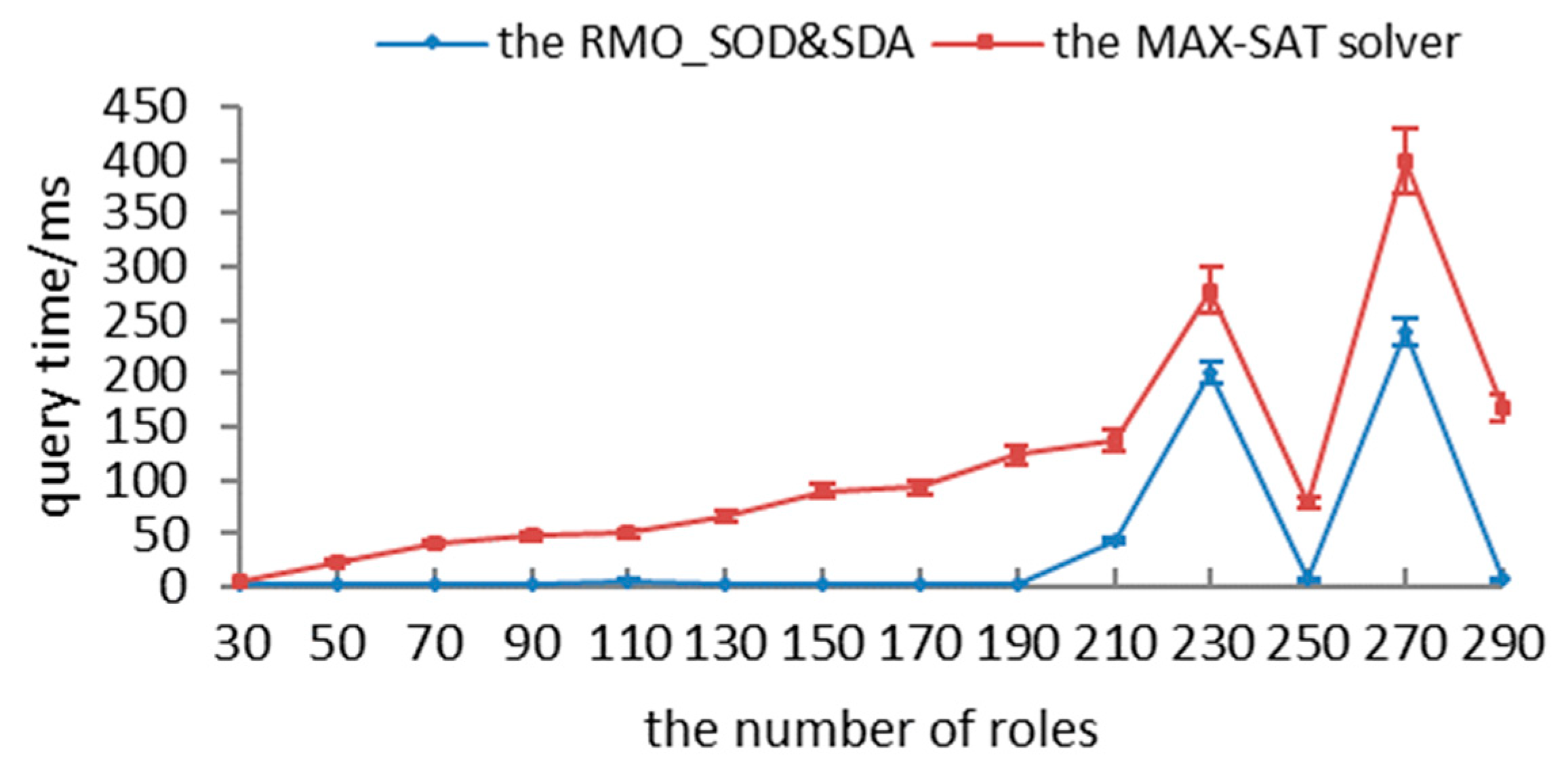
In order to ensure the security of authorizations, we converted the authorization-query problem into partial MAX-SAT as follows: (1) authorization logics and constraints are transformed into hard clauses; (2) the updating algorithm is adopted to transform the requested permissions with different matches into soft clauses; and (3) recursive and encoding algorithms are utilized to satisfy all hard clauses and as many soft clauses as possible. First, we present the definition with respect to the partial MAX-SAT.
Definition 4. (Boolean logical descriptions of partial MAX-SAT):
- (1)
Basic elements: some elements are presented using Boolean variables x1,x2,…,xi,…, xi, or ¬xi(the negation of xi), which is called a literal logic; the instance formalized as x1∨x2∨…∨xn using n literals xi is called a clause; and sentence c1∧c2∧…∧cm using m clauses ci is called the conjunctive normal form, which is expressed as cnf(c1,c2,…,cm);
- (2)
Hard clause: c1, c2,…, cm are hard clauses and satisfiable, if and only if there exist truth assignments such that the value of cnf(c1,c2,…,cm) is 1. All hard clauses are set as HC;
- (3)
Soft clause: the sentences that do not satisfy hard clauses are soft clauses. All soft clauses are set as SC.
To transform the authorization-query request into the partial MAX-SAT, we represent permission p and role r with literal and respectively, and we describe them and their logical negations as follows:
- (1)
: ;
- (2)
:;
- (3)
:;
- (4)
: .
3.2.1. Preprocessing
To transform static-authorization logics and dynamic mutual role constraints into hard clauses, we describe the transforming rules as follows:
- (1)
;
- (2)
;
- (3)
;
- (4)
;
- (5)
.
3.2.2. Updating Clauses
To reflect the least-privileges principle, we say that permissions in
Plb must be satisfied and available in a single session, which can be formalized as follows:
Similarly, permissions not in
Pub must not be satisfied or available in a single session, which can be formalized as follows:
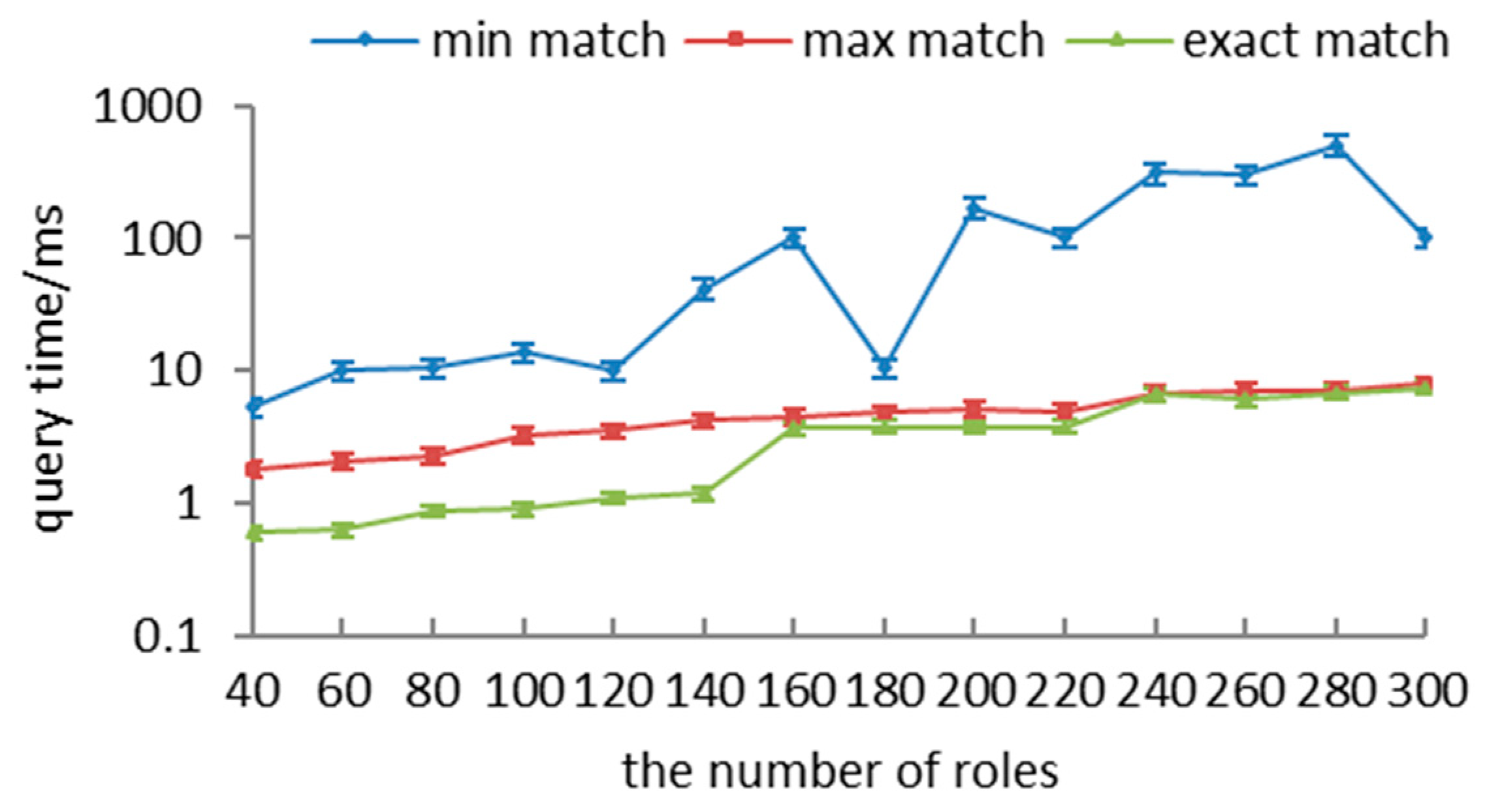
Different cases can be easily transformed into the partial MAX-SAT. Essentially, the partial MAX-SAT problem is a special extension of the MAX-SAT problem, whereby some clauses are relaxable and others are hard clauses. It aims to satisfy all hard clauses as well as a maximum number of soft ones. To translate the authorization-query problem to a partial MAX-SAT instance, all permissions in Plb should be inserted into HC, and all permissions in (Pub\Plb) should be inserted into SC. Next, to satisfy the max match, any permission in (Pub\Plb) is initially set to be true, as only permission variables can be used in the permissions request and the partial MAX-SAT is to satisfy the largest number of soft clauses; to satisfy the min match, on the other hand, any permission in (Pub\Plb) is initially set to be false. Thus, hard and soft clauses are updated in Algorithm 5.
| Algorithm 5. Updating clauses. |
| Input: the UAQ <s, Plb, Pub, match>, preprocessed results HC, SC |
| Output: updated results HC, SC |
| 1. for each p in Plb do |
| 2. HC=HC ∪ {}; |
| 3. end for |
| 4. for each p in P\Pub do |
| 5. HC=HC ∪ {¬}; |
| 6. end for |
| 7. for each p in Pub\Plb do |
| 8. if match = min then |
| 9. SC=SC ∪ {¬}; |
| 10. else if match = max then |
| 11. SC=SC ∪ {}; |
| 12. else |
| 13. SC=SC ∪ Φ; |
| 14. end if |
| 15. end for |
In Algorithm 5, the two cases are reflected in lines 1–6. If permission p is in Plb, we represent p with literal and insert it into HC. If permission p is not in Pub, we insert literal ¬ into HC. If the requested permissions are not in Plb, but in Pub, lines 7–15 transform them into soft clauses according to the different matches. We insert literal ¬ or into SC when the match objective equals to min or max, and we do not update SC when the match objective equals to exact.
3.2.3. Assigning Truth for Clauses
To satisfy all hard clauses in HC, it is necessary to search for truth assignments and make sure all clauses are true. The recursive process is described in Algorithm 6.
| Algorithm 6. Assigning truth for hard clauses. |
| Input:len(c) |
| Output: true or false |
| 1. Randomly choose clause c from HC and use len(c) as the length of c; |
| 2. if len(c) = 1 then |
| 3. c=1; |
| 4. HC=HC\{c}; |
| 5. for each clause, including c’∨c in HC, do |
| 6. HC=HC\{c’∨c}; |
| 7. end for |
| 8. for each clause, including c’’∨¬c in HC, do |
| 9. HC=(HC\{c’’∨¬c})∪{c’’}; |
| 10. end for |
| 11. return true; |
| 12. else |
| 13. Assigning truth for hard clauses (len (c)-1); |
| 14. return false; |
| 15. end if |
In Algorithm 6, lines 2–11 indicate that if chosen clause c consists of only one literal logic, we simplify HC according to the two different cases in each iteration: when a clause including c’∨c exists, we remove it from HC; when a clause including c’’∨¬c exists, we remove it from HC and insert c’’ into HC. Next, if len(c)>1, line 13 recursively calls Algorithm 6.
Theorem 2. For each given clause c, there is a truth assignment for c using Algorithm 6.
Proof. On the basis of
Section 3.2.1 and
Section 3.2.2, we can search for the truth assignment from line 2 of the algorithm using the method of mathematical induction, and detailed descriptions are omitted owing to limited space. □
3.2.4. Encoding and Querying Clauses
To satisfy as many clauses as possible, soft clauses are encoded and queried in the following steps:
Step 1. For given set of soft clauses SC = {sc1,sc2,…,scn}, introduce n new blocking variables bi(1 ≤ i ≤ n);
Step 2. Construct new clause set SCb = {sc1∨b1,sc2∨b2,…,scn∨bn}, where clause sci∨bi is considered as bi copies of sci;
Step 3. Search for minimal integer k, such that SCb is true and ;
Step 4. Consider
HC ∪
SCb as parameters, take them into the QMaxSAT [
39], and output all true clauses from
SC.
Example 2. Given set P of permissions, set R of roles, role–hierarchy relationships RH, role–permission assignment relationships PA, and set C of constraints, where P = {p0,p1,p2,p3,p4,p5,p6,p7}, R = {r0,r1,r2}, RH = {r0≥r2}, PA = {(r0,p0),(r0,p1),(r0,p2),(r0,p4),(r0,p5),(r0,p6),(r1,p3),(r1,p7),(r2,p2),(r2,p6)}, and C = {dmer<{r0,r1},2,s>}. In the preprocessing stage, hard clauses are constructed by the transforming rules, and results are listed in Table 3. Suppose there are three authorization requests: (1)
Plb = Φ,
Pub = {
p2,
p3,
p6},
match =
max; (2)
Plb = {
p2,
p3,
p6},
Pub =
P,
match =
min; (3)
Plb = {
p2,
p3,
p6},
Pub={
p2,
p3,
p6},
match=
exact. Then,
HC and
SC are, respectively, updated in Algorithms 5 and 6; the results are listed in
Table 4, and different sets of activated roles are listed in
Table 5.