Role-Mining Optimization with Separation-of-Duty Constraints and Security Detections for Authorizations

Abstract

Role-based access control (RBAC), which has been regarded as one of the most popular access-control mechanisms, is featured by the separation-of-duty constraints, mutually exclusive constraints, and the least-privileges principle. Role mining, a bottom-up role-engineering technology, is an effective method to migrate from a non-RBAC system to an RBAC system. However, conventional role-mining approaches not only do not consider the separation of duty constraints, but also cannot ensure the security of a constructed RBAC system when the corresponding mined results violate the separation of a duty constraint and/or the least-privileges principle. To solve these problems, this paper proposes a novel method called role-mining optimization with separation-of-duty constraints and security detections for authorizations (RMO_SODSDA), which mainly includes two aspects. First, we present a role-mining-optimization approach for satisfying the separation of duty constraints, and we constructed different variants of mutually exclusive constraints to correctly implement the given separation of duty constraints based on unconstrained role mining. Second, to ensure the security of the constructed system and evaluate authorization performance, we reduced the authorization-query problem to a maximal-satisfiability problem. The experiments validate the effectiveness and efficiency of the proposed method.

1. Introduction

With the rapid development of network-information technology and the comprehensive application of cloud computing and big data techniques, there is much storage and there are many exchanges in large-scale and complex information-management systems [1]. The mechanism to ensure the security of system data and user information has attracted much attention. An increasing number of enterprises and organizations have adopted role-based access control (RBAC) as their main access-control mechanism, as it makes security administration more flexible and manageable [2,3,4,5,6,7]. With the successful implementations of RBAC systems, designing an effective, complete set of roles and constructing a good RBAC system have become critical tasks. As a solution to facilitate the process of migrating from a non-RBAC system to an RBAC system, role-engineering technology [8,9] has been proposed. There are two main approaches: top-down [10] and bottom-up [11,12,13,14,15,16]. In the former approach, roles are derived by carefully analyzing particular organization functions. While this approach can reflect the functional requirements of the organization well, it is time-consuming and labor-intensive. In the latter approach, roles are aggregated by applying data-mining techniques from existing user-permission assignments, and the architectural structure of RBAC can be automatically constructed. The bottom-up approach, also known as role mining, has gained considerable interest and popularity in recent years.

Vaidya et al. [17] converted role mining into a matrix-decomposition problem and presented the definition of a basic role mining problem (basic RMP), which attempts to find a minimal set of roles from bottom-user permission assignments and completely cover the original assignments. However, it is difficult to derive an optimal role set in practical applications. Afterward, a variant of basic RMP called δ-approx RMP was proposed in the work of [17], which attempts to find a minimal set of roles by allowing a limited number of mismatches. As a result, it is easy to derive a suboptimal role set. Meanwhile, in min-noise RMP [17], the number of roles is bounded, and the number of mismatches between original assignments and assignments in the constructed system is minimized. According to different optimization objectives for role mining, many other approaches have been proposed, such as edge RMP [18], usage RMP [19], and user-oriented exact RMP [20].

A key characteristic of RBAC is that it allows the specification and enforcement of various constraint policies [21,22,23], such as cardinality constraints and separation-of-duty constraints (also called separation-of-duty policies), which can reflect security policies of different enterprises and organizations and ensure system security. The cardinality constraint limits the maximum number of roles related to users or to permissions, the maximum number of permissions a role can have, or the maximum number of users to which a role can be assigned [14]. Another significant constraint discussed in this paper is the separation-of-duty constraint, which is widely recognized to be a fundamental principle in computer security [14]. Typically, the constraint states that at least k users are required to complete a special task that requires n number of permissions. One approach requires that no (k – 1) users together have all the permissions needed to complete the task [24]. It has been widely used in the banking industry and military systems. In the approach to migrate from a non-RBAC system to an RBAC system, however, an inadequately addressed key challenge is that none of the conventional role-mining methods consider the separation-of-duty constraint.

Furthermore, both the mutually-exclusive-role constraint and the least-privileges principle play important roles [25,26] in evaluating system security and authorization performance in a constructed RBAC system. Because of free and random requests of accessing resources and fuzzy system configurations, it is impossible to find an optimal set of roles that cover all permissions for a given access request. The authorization-query problem [27] proved to be satisfiable, strictly complies with the separation-of-duty constraint, and attempts to derive a role set that can cover as many permissions as possible. Maximal satisfiability (MAX-SAT) is a core research problem of theoretical computer science that has had successful applications in various fields, such as artificial intelligence and model detection [28]. Nevertheless, conventional role-mining methods lack security detections for authorizations in the constructed RBAC system. The following problems exist: on the one hand, different results may conflict with each other and violate the mutually exclusive constraint; on the other hand, different results may include permissions outside the permission request and violate the least-privileges principle.

To address the above problems, this paper proposes a novel method called role-mining optimization with separation-of-duty constraints and security detections for authorizations (RMO_SODSDA). The main contributions of this paper are as follows:

(1)

The separation-of-duty constraint was proved to be effectively enforced by mutually exclusive constraints [24]. In order to satisfy these constraints, we presented a constrained-role optimization approach, we constructed several variants of mutually exclusive constraints to correctly implement the given separation of duty, and we evaluated the effectiveness of RMO_SODSDA.

(2)

As a branch of MAX-SAT, the partial MAX-SAT problem [29] aims to satisfy all hard clauses and as many soft clauses as possible. It is clearly more versatile. In order to ensure system security, based on the previously constructed RBAC system, we converted the authorization-query problem into the partial MAX-SAT and evaluated RMO_SODSDA efficiency.

The rest of the paper is organized as follows. In Section 2, we discuss related work and present preliminaries and basic problem descriptions to understand the rest of the paper. Section 3 proposes a novel method (RMO_SODSDA), including two aspects: (1) presenting role optimization with separation-of-duty constraints and demonstrating how to construct different kinds of mutually-exclusive-role constraints, and (2) reducing the authorization-query problem to partial MAX-SAT and demonstrating how to ensure system security. We show the results of the experimental evaluations in Section 4 and present discussions in Section 5. Section 6 concludes the paper and discusses future work.

2. Related Work

2.1. Role-Mining Methods

Many methods have been proposed for role mining. According to whether or not constraints are considered in the optimization process, existing efforts mainly fall into the following two categories: (1) role mining with no constraint, and (2) role mining with constraints.

2.1.1. Role Mining with No Constraint

Vaidya et al. converted role mining into a matrix-decomposition problem and presented the definition of basic RMP. Basic RMP has been proven to be NP-complete, for which several existing studies have already been done to find efficient solutions. In view of the lack of semantics in mining roles, Molloy et al. [30] introduced semantic information, represented roles’ characteristics with a formal concept lattice, and proposed an optimization algorithm to find roles based on formal semantic analysis that can reflect the requirements of the organization’s functions and enhance the interpretability of mining roles. To optimize the RBAC system, Zhang et al. [31] presented an algorithm using graph-optimization theory, which reduces the administration required for role-related assignments through minimizing the number of edges in the graph. However, it does not research the redundancy of the mining results. Ene et al. [32] used heuristics and graph theory to find as few optimized roles as possible, which can reduce graph representations and the redundancy of mining roles. Lu et al. [19] proposed a unified optimization framework for role mining and presented a number of greedy algorithms that could solve basic RMP, δ-approx RMP, min-noise RMP, and edge RMP based on methods of integer linear programming and Boolean matrix decomposition. Although constraints are essential for the RBAC model, none of the above role-mining methods took constraints into account.

2.1.2. Role Mining with Constraints

In order to avoid abuse of privileges, Kumar et al. [33] proposed the constrained role miner algorithm that limits the number of permissions assigned to a role. Hingankar et al. [34] proposed a biclique-cover method to derive a set of roles that limit the maximum number of users related to a role. For example, the managing-director role in a company must be assigned to only one person. John et al. proposed two alternative approaches for restricting the number of roles assigned to a user: the role priority-based approach (RPA) and the coverage of permissions-based approach (CPA). The RPA prioritizes roles based on their number of permissions, and assigns optimal roles to a user according to the priority order. The CPA chooses roles by iteratively picking the role with the largest number of permissions that are yet uncovered, and then ensures that no user contains more than a given number of roles [35]. In order to simultaneously limit the maximum number of roles assigned to a user and a related permission, Harika et al. [36] imposed these constraints during the process of mining roles and proposed a postprocessing framework and a concurrent processing framework.

2.2. Methods of RBAC Authorizations

In order to obtain permissions while satisfying a collection of constraints for a given authorization request, it is necessary to determine whether a set of roles can be activated in a particular system. Zhang et al. presented the user authorization query (UAQ) problem that adopts a greedy algorithm and a mutually-exclusive-role constraint to search for the objects. The UAQ is to discover a set of roles to be activated in a single session for the particular set of permissions requested by the user [27]. This set of roles must satisfy constraints and follow the least-privileges principle. However, it stops searching once the set of roles does not satisfy the requests. Wickramaarachchi et al. [37] introduced the lower and upper bounds for the requested permissions, respectively, converting the UAQ into the MAX-SAT, finding truth assignments that satisfied as many clauses as possible, and demonstrating its effectiveness using SAT solvers. Lu et al. [28] proposed a novel approach based on role–permission reassignments to support the UAQ, which assists administrators to modify system configurations in an automatic manner. Koshimura et al. [38] presented partial MAX-SAT solver QMaxSAT, which encodes soft clauses with the blocking variables and has been proven to be highly effective. Partial MAX-SAT is an extension of MAX-SAT. It sits between the classical SAT problem and the MAX-SAT problem. While the classical SAT problem requires all clauses to be satisfied, MAX-SAT seeks the maximum number of clauses that can be satisfied, and partial MAX-SAT relaxes this requirement by having certain clauses marked as relaxable and others as nonrelaxable [29].

Obviously, from the above analyses, we can see that there are two limitations in the current research on role-mining optimization. One limitation is that none of them consider the separation-of-duty constraint. If a constructed RBAC system lacks several necessary constraints, then a series of security requirements of the organization are not realized. The second limitation is that they lack security detections for role authorization in the constructed RBAC system. Different results may violate the separation-of-duty constraint and/or the least-privileges principle.

2.3. Preliminaries and Basic Problem Descriptions

2.3.1. Basic Elements of Role Engineering

Conventional role engineering contains the following basic elements [5,6,7]:

(1)

U, P, R, S, DC, UPA, UA, PA, and RH are the basic elements of the RBAC model, which represent a set of users, a set of permissions, a set of roles, a set of sessions, a set of constraints, a many-to-many mapping of user-permission assignments, a many-to-many mapping of user-role assignments, a many-to-many mapping of role–permission assignments, and a partial-order set on roles, respectively;

(2)

Roles(u), Permissions(r), and Perms(u) represent the mapping function of user u onto a set of roles, the mapping function of role r onto a set of permissions, and the mapping function of user u onto a set of permissions, respectively;

(3)

user_session(s), roles_session(s), and perms_session(r) represent the mapping function of session s onto a user, the mapping function of session s onto a set of roles, and the mapping function of role r onto a set of permissions in a session, respectively.

2.3.2. Separation-of-Duty Constraint

Role-static separation-of-duty constraint (k-n RSSOD) [22] states that, given a task consisting of n roles r₁, r₂,…,r_n, at least k users are required together to perform it and have all the n roles; any set of (k – 1) users should not be able to have all the roles. It is expressed as rssod<{r₁,r₂,…,r_n},k>, where each r_i is a role, and n and k are integers, such that 2≤k≤n. It can be formalized as follows:

$$\forall \left(u_1,u_2,\dots ,u_{k-1}\right)\in U:\left\{r_1,r_2,\dots ,r_n\right\}\not\subset \underset{i=1}{\overset{k-1}{{\displaystyle \cup }}}Roles\left(u_i\right)$$

(1)

2.3.3. Basic RMP Problem

Given a set of users U, a set of permissions P, and a user-permission assignments matrix UPA, the basic RMP [17] aims to find a set of roles R, a user-role assignments matrix UA, and a role–permission assignments matrix PA, such that the UA and PA are consistent with the UPA, and the number of mining roles |R| is minimized. It can be formalized as follows:

$$\{\begin{array}{c}\min \left|R\right|\\ UA\otimes PA=UPA\end{array}$$

(2)

2.3.4. UAQ Problem

The UAQ [27] is a four-tuple <s, P_lb, P_ub, match>, where s∈S, P_lb, and P_ub are the lower and upper bound for the set of requested permissions, respectively; P_lb⊆P_ub⊆P; and match∈{min, max, exact} indicates the optimization objective. It can be formalized as follows:

$$\begin{gathered} match= \\ \{\begin{array}{c}min. iff\forall s^{\prime }\in \left(S\backslash \left\{s\right\}\right),\exists \left(r,r^{\prime }\right)\in R,\\ {{\displaystyle \cup }}_{r\in roles\_session\left(s\right)}perms\_session\left(r\right)\subseteq {{\displaystyle \cup }}_{r^{\prime }\in roles\_session\left(r^{\prime }\right)}perms\_session\left(r^{\prime }\right)\subseteq P_{lb} \\ max. iff\forall s^{\prime }\in \left(S\backslash \left\{s\right\}\right),\exists \left(r,r^{\prime }\right)\in R, \\ P_{ub}\supseteq {{\displaystyle \cup }}_{r\in roles\_session\left(s\right)}perms\_session\left(r\right)\supseteq {{\displaystyle \cup }}_{r^{\prime }\in roles\_session\left(s^{\prime }\right)}perms\_session\left(r^{\prime }\right) \\ exact.iff{P}_{lb}={{\displaystyle \cup }}_{r\in roles\_session\left(s\right)}perms\_session\left(r\right)=P_{ub}\end{array}. \end{gathered}$$

(3)

For the readability, we summarize the main symbols used in the paper in

Table 1. Main symbols and their meanings.

Symbol	Meaning
< s, Plb, Pub, match>	The four tuple of permissions request
SSOD	Role-static separation-of-duty constraint
SMER	Static mutually exclusive roles
rssod<{r1,r2,…,rn},k>	The k-n SSOD constraint
smer<{r1,r2,…,rm},t>	The t-m SMER constraint
smer<{r1,r2,…,rt},t>	The t-t SMER constraint
E	The set of SSOD constraints
C	The set of SMER constraints
$\stackrel{-}{p}$, ¬$\stackrel{-}{p}$	The literal and its negation with respect to permission p
$\stackrel{-}{r}$, ¬$\stackrel{-}{r}$	The literal and its negation with respect to role r

.

3. Proposed Method

In this section, we propose a novel method, RMO_SODSDA, which includes two aspects: (1) satisfying separation-of-duty constraints, and (2) ensuring authorization security.

3.1. Satisfying Separation-of-Duty Constraints

Separation-of-duty constraints can be effectively enforced by mutually exclusive constraints. In order to satisfy these constraints, we constructed different variants of mutually exclusive roles to implement RSSOD based on any unconstrained role-mining algorithm for basic RMP, including algorithm design and description, computational complexity, and correctness analysis. First, we present the following definitions.

Definition 1.

(static and soft mutually exclusive roles, t-m SMER) Given m roles r₁,r₂,…,r_m, a t-m SMER states that no user is allowed to have t or more of these m roles. It is expressed as smer<{r₁,r₂,…,r_m},t>, where each r_i is a role, and m and t are integers, such that 2≤ k≤ n. A t-m SMER can be formalized as follows:

$$\forall u\in U:\left|\left\{r_1,r_2,\dots ,r_m\right\}{{\displaystyle \cap }}^{}Roles\left(u\right)\right|<t$$

(4)

It has been shown that any t-m SMER can be equivalently represented using a set of t-t SMER [24].

Definition 2.

(static and hard mutually exclusive roles, t-t SMER) Given t roles r₁,r₂,…,r_t, a t-t SMER states that no user is allowed to have these t roles. It is expressed as smer<{r₁,r₂,…,r_t},t>, where each r_i is a role, and t is an integer, such that t≥ 2. A t-t SMER can be formalized as follows:

$$\forall u\in U:\left\{r_1,r_2,\dots ,r_t\right\}\not\subset Roles\left(u\right)$$

(5)

Definition 3.

(role-mining problem with RSSOD constraints) Given a set of users U, a set of permissions P, a user-permission assignments matrix UPA, and a set of RSSOD constraints E={e₁,e₂,…}, find a set of roles R, a user-role assignments matrix UA, a role–permission assignments matrix PA, and a set of SMER constraints C, such that the UA and PA are consistent with the UPA, C enforces E, and the number of mining roles |R| is minimized. It can be formalized as follows:

$$\{\begin{array}{c}\min \left|R\right|\\ UA\otimes PA=UPA\\ C enforce\mathrm{s} E\end{array}$$

(6)

3.1.1. Preprocessing

Any role-mining algorithm that takes no RSSOD constraint into consideration is used for mining minimal roles in Algorithm 1.

Algorithm 1. Preprocessing

Input: original matrix UPA

Output: decomposed matrix UA, PA, candidate set CR of roles

The Fast Miner method and Boolean matrix decomposition are adopted to derive CR and configure RBAC, such that

$\{\begin{array}{c}\min \left|CR\right|\\ UA\otimes PA=UPA\end{array}$

3.1.2. Construction of 2–2 SMER Constraints

A 2–2 SMER constraint can be expressed as c=<{r_i, r_j},2>, which means that r_i and r_j are mutually exclusive, that is, the two roles cannot be assigned to any user. Although 2–2 SMER constraints are considered to be quite restrictive, they are sufficient to enforce any enforceable RSSOD constraint. RSSOD constraint e_i is nonenforceable in one of the following cases: (1) a single role in the PA matrix owns all permissions in e_i, and (2) candidate matrix UA already has user assignments violating the constraints.

Algorithm 2. Construction of 2–2 SMER constraints

Input:UA, CR, set E of k-n RSSOD constraints

Output: set C of 2–2 SMER constraints

1. C= ∅;

2. for each ei in E do

3. P(ei) denotes the permissions covered by ei;

4.  $\exists \left(S=\left(r_1,r_2,\dots \right)\right)\subseteq CR$:$\left(\forall r\in S:Permissions\left(r\right){{\displaystyle \cap }}^{}P\left(e_i\right)\ne \varnothing \right)$

5.  if $\exists r\in S:Permissions\left(r\right)\supseteq P\left(e_i\right)$ then

6.   ei is nonenforceable;

7.   continue;

8.  end if

9.  for each pair of roles (ri, rj) in S do

10.  if$\left(Permissions\left(r_i\right)⊉Permissions\left(r_j\right)\right)\wedge \left(Permissions\left(r_j\right)⊉Permissions\left(r_i\right)\right)$ then

11.    if UA satisfy smer<{ri, rj},2> then

12.     C={smer<{ri, rj},2>} ∪ C;

13.    else

14.     ei is nonenforceable with 2–2 SMER constraints;

15.    end if

16.   end if

17.  end for

18. end for

In Algorithm 2, the inputs are the above UA, CR, and set E = {e₁,e₂,…} of k-n RSSOD constraints, and the output is set C = {c₁,c₂,...} of 2–2 SMER constraints, such that C enforces E. In order to construct 2–2 SMER constraints, it is necessary to find a set of roles S, such that each role in S at least has permissions in e_i (line 4). Then, if any role has all the permissions in e_i, we declare e_i as nonenforceable (lines 5–8); otherwise, we analyze each pair of roles (r_i, r_j) to determine whether they are valid 2–2 SMER constraints. If r_i and r_j are mutually exclusive roles, each one contains at least a mutually exclusive permission that must be absent in the other (lines 9–17).

Computational complexity: constructing 2–2 SMER constraints for an RSSOD can be done in polynomial time. If the number of roles in set S for the RSSOD is m, then the time for deciding whether the RSSOD constraint is enforceable or not is O(m), and the time for constructing mutually exclusive roles is O(m²); thus, the total time complexity is (m²). The smaller m gets, the more acceptable the algorithm becomes.

3.1.3. Construction of t-t SMER Constraints

However, many RSSOD constraints might become nonenforceable in some cases because of the restrictive 2–2 SMER constraints. Next, we present an approach for implementing RSSOD with t-t SMER constraints (t > 2), which is less restrictive as compared with only using 2–2 SMER constraints. It is necessary to find a maximum t for the given RSSOD constraints in Algorithm 3.

Algorithm 3. Construction of t-t SMER constraints

Input:UA, CR, set E of k-n RSSOD constraints

Output: set C of t-t SMER constraints

1.  C= ∅;

2.  for each ei in E do

3.   P(ei) denotes the permissions covered by ei;

4.   $\exists \left(S=\left(r_1,r_2,\dots \right)\right)\subseteq CR$:$\left(\forall r\in S:Permissions\left(r\right){{\displaystyle \cap }}^{}P\left(e_i\right)\ne \varnothing \right)$

5.   if |S|<k then

6.     ei is nonenforceable;

7.     continue;

8.   else if$\exists r\in S:Permissions\left(r\right)\supseteq P\left(e_i\right)$ then

9.     ei is nonenforceable;

10.     continue;

11.   else if $\exists \left(r_i,r_j\right)\in S:\left(r_i,r_j\right)\in RH\mathrm{or}\left(r_j,r_i\right)\in RH$ then

12.     ei is nonenforceable;

13.     continue;

14.   else

15.    for t=3 to $\lfloor \frac{\left|S\right|-1}{k-1}\rfloor$+1 do

16.     for any set {r1’,r2’,…rt’} in S do

17.      if UA satisfies smer<{r1’,r2’,…rt’},t> then

18.       C={smer<{r1’,r2’,…rt’},t>} ∪ C;

19.      else

20.       ei is nonenforceable with t-t SMER constraints;

21.      end if

22.     end for

23.    end for

24.   end if

25. end for

To construct t-t SMER constraints for an RSSOD e_i, like in Algorithm 2, we should find set S at first. Next, we determine whether e_i is enforceable or not. In Algorithm 3, line 4 determines set S from CR. Lines 5–6 indicate that if the number of roles in set S is less than k in e_i, it cannot be enforced. Lines 8–9 indicate that if any role in set S has all the permissions in e_i, it cannot be enforced. Lines 11–12 show that if RH relationships exist in S, e_i cannot be enforced. Lines 15–23 determine whether the t-t SMER constraints are satisfied in matrix UA and insert them into set C.

Computational complexity: if the number of roles in S is m, the time for determining whether a constraint is enforceable or not is O(m). Constructing t-t SMER constraints depends on the double loops. The execution number of the first loop is $\lfloor \frac{\left|S\right|-1}{k-1}\rfloor$–2; in the second loop, for the particular t, it is necessary to obtain any t roles from S, and the execution time is O($C_m^t$). Thus, the total time complexity is $O$($m$)+$O$($m·C_m^t$)= O($m·C_m^t$). If m is small, the efficiency of the algorithm is acceptable.

3.1.4. Construction of t-m SMER Constraints

Compared with t-t SMER constraints, although t-m SMER constraints (2 < t < m) are less restrictive, they are more flexible for applications. The differences between t-m SMER and t-t SMER are presented in Algorithm 4.

Algorithm 4. Construction of t-m SMER constraints

Input:UA, CR, set E of k-n RSSOD constraints

Output: set C of t-m SMER constraints

……

1. for t=3 to $\lfloor \frac{n-1}{k-1}\rfloor$+1 do

2.  m=(k-1)×(t-1)+1;

3.  for any set {r1’,r2’,…rm’} in CR do

4.   if UA satisfy smer<{r1’,r2’,…rm’},t> then

5.    C={smer<{r1’,r2’,…rm’},t>} ∪ C;

6.   else

7.    ei is nonenforceable with t-m SMER constraints;

8.   end if

9.  end for

10. end for

……

Computational complexity: constructing t-m SMER constraints depends on the double loops. The execution number in the first loop is $\left(\lfloor \frac{n-1}{k-1}\rfloor -2\right)$; in the second loop, for the particular m, it is necessary to obtain any m roles from CR. Thus, the execution time of the double loops is O(2ⁿ). The efficiency of the algorithm decreases obviously as the number of CR increases.

3.1.5. Correctness Analysis

Statement 1.

Given an m-m RSSOD constraint e₁, t-m SMER constraint c₁ can precisely enforce e₁ if and only if t = 2.

Proof. 

We analyze the statement from the two sides of sufficiency and necessity.

Sufficiency. When constraint c₁=smer<{r₁,r₂,…,r_m},2> holds, that is,$\forall u\in U:\left|Roles\left(u\right){{\displaystyle \cap }}^{}\left\{r_1,r_2,\dots r_m\right\}\right|<2$, this indicates that at least m users are required together to have all roles of set {r₁,r₂,…,r_m}. Any set of (m-1) users should not be able to have all m roles, that is, $\forall \left(u_1,u_2,\dots u_{m-1}\right)\in U:{{\displaystyle \cup }}_{i=1}^{m-1}Roles\left(u_i\right)\not\supset \left\{r_1,r_2,\dots r_m\right\}$. According to RSSOD, c₁ can enforce e₁.

Necessity. It is proved by contradiction. Assume that there exist (m – 1) users who can cover all the m roles, that is,$\exists \left(u_1,u_2,\dots u_{m-1}\right)\in U:{{\displaystyle \cup }}_{i=1}^{m-1}Roles\left(u_i\right)\supseteq \left\{r_1,r_2,\dots r_m\right\}$. In other words, there exists some user who has two of the n roles, that is,$\exists u\in U:\left|Roles\left(u\right){{\displaystyle \cap }}^{}\left\{r_1,r_2,\dots r_m\right\}\right|=2$, which is contradictory to constraint smer<{r₁,r₂,…,r_m},2>. Thus, the assumption is false. □

Statement 2.

Given a 2–m RSSOD constraint e₂, t-m SMER constraint c₂ can precisely enforce e₂ if and only if t = m.

Proof. 

We also analyze the statement from the two sides of sufficiency and necessity.

Sufficiency. When constraint c₂=smer<{r₁,r₂,…,r_m},m> holds, that is, $\forall u\in U:\left|Roles\left(u\right){{\displaystyle \cap }}^{}\left\{r_1,r_2,\dots r_m\right\}\right|<m$, this indicates that no user has all roles of the set {r₁,r₂,…,r_m}. In other words, at least two users are required together to have all the m roles. According to RSSOD, c₂ can enforce e₂.

Necessity. It is proved by contradiction. Assume that there exists some user who has all the m roles, that is,$\exists u\in U:\left|Roles\left(u\right){{\displaystyle \cap }}^{}\left\{r_1,r_2,\dots r_m\right\}\right|=m$, which is contradictory to the constraint smer<{r₁,r₂,…,r_m},m>. Thus, the assumption is false. □

Theorem 1.

Given a k-n RSSOD constraint (k > 2) and a candidate role set CR, where k≤ n≤ |CR|, t-m SMER constraints constructed by our algorithms can precisely enforce k-n RSSOD if t ≤$\left(\lfloor \frac{n-1}{k-1}\rfloor +1\right)$.

Proof. 

According to Definition 1, any user has (t – 1) roles at most, and any (k – 1) users have (k – 1) ×(t – 1) roles at most. It is also proved by contradiction. Without loss of generality, t=$\left(\lfloor \frac{n-1}{k-1}\rfloor +1+1\right)$, we assume that the RSSOD constraint holds, that is, the number of roles assigned to (k – 1) users is $\left(k-1\right)\times \left(\lfloor \frac{n-1}{k-1}\rfloor +2-1\right)\approx n-1+k-1=n+k-2>n$, which breaches the k-n RSSOD. Thus, the assumption is false and the theorem is proved. □

Example 1.

Constructing t-m SMER constraints based on our method can enforce rssod<{r₁,r₂,r₃,r₄,r₅},k> with different k in

Table 2. Static and soft mutually exclusive roles (t-m SMERs) enforce k-n role-static separation-of-duty constraint (RSSOD).

RSSOD	SMERs
e1=rssod<{r1,r2,r3,r4,r5},2>	C1={smer<{r1,r2,r3,r4,r5},5>}
e2=rssod<{r1,r2,r3,r4,r5},3>	C2={smer<{r1,r2,r3},2>,smer<{r1,r2,r4},2>,smer<{r1,r2,r5},2>, smer<{r1,r3,r4},2>,smer<{r1,r3,r5},2>,smer<{r1,r4,r5},2>, smer<{r2,r3,r4},2>,smer<{r2,r3,r5},2>,smer<{r2,r4,r5},2>, smer<{r3,r4,r5},2>,smer<{r1,r2,r3,r4,r5},3>}
e3=rssod<{r1,r2,r3,r4,r5},4>	C3={smer<{r1,r2,r3,r4},2>,smer<{r1,r2,r3,r5},2>,smer<{r1,r2,r4,r5},2>, smer<{r1,r3,r4,r5},2>,smer<{r2,r3,r4,r5},2>}
e4=rssod<{r1,r2,r3,r4,r5},5>	C4={smer<{r1,r2,r3,r4,r5},2>}

, where 2≤ k≤ 5.

3.2. Ensuring Authorization Security

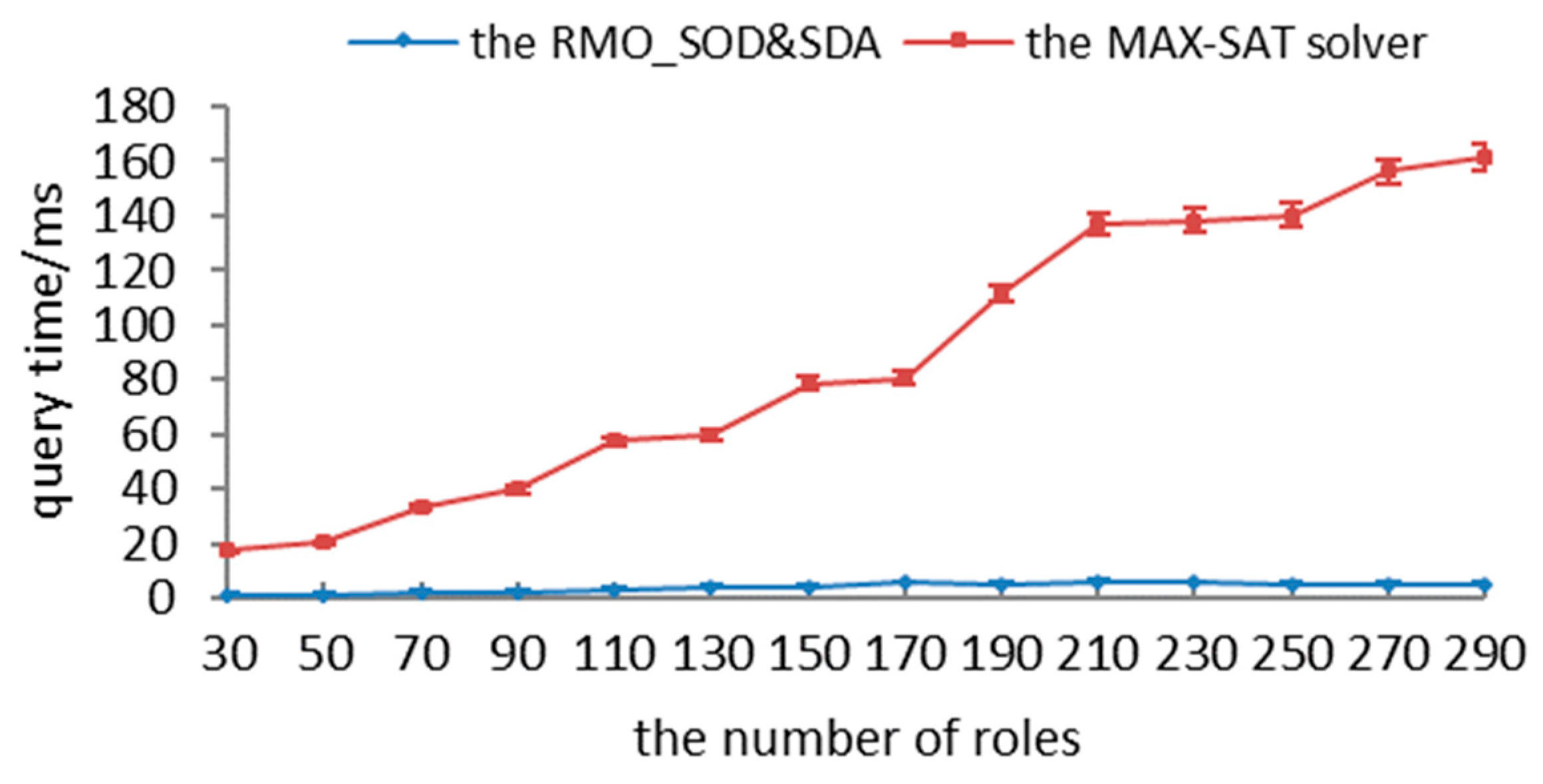
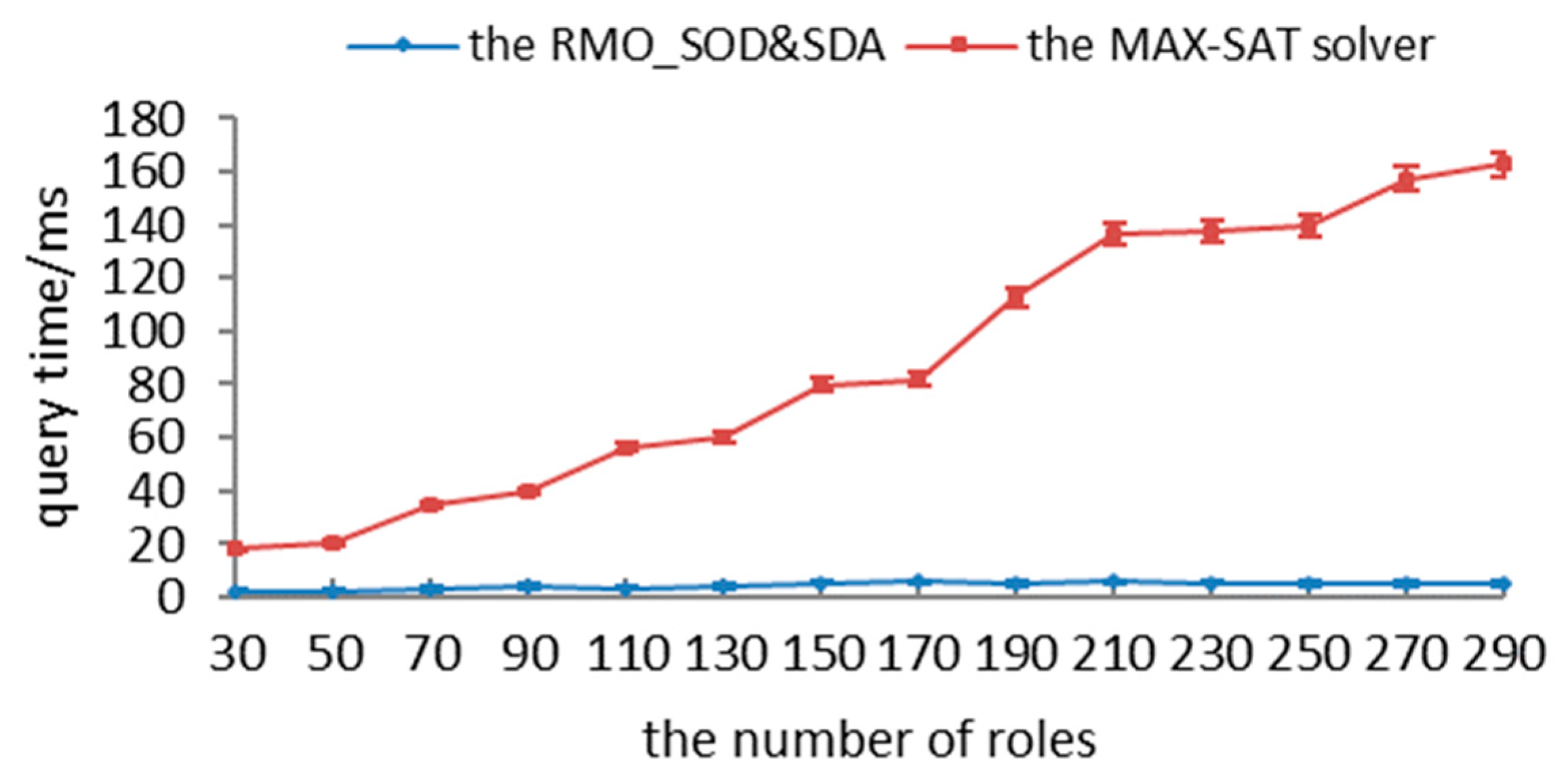
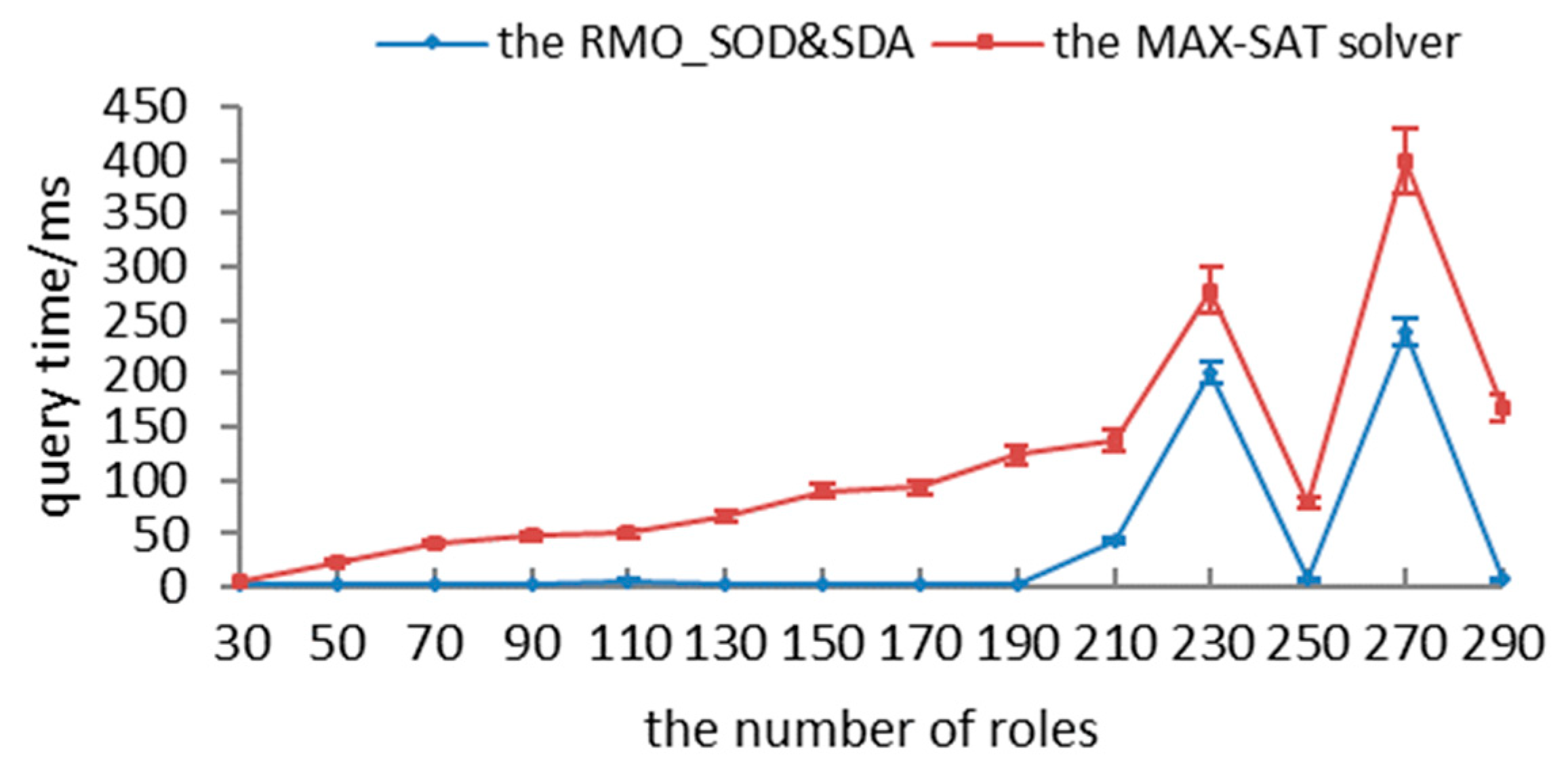
In order to ensure the security of authorizations, we converted the authorization-query problem into partial MAX-SAT as follows: (1) authorization logics and constraints are transformed into hard clauses; (2) the updating algorithm is adopted to transform the requested permissions with different matches into soft clauses; and (3) recursive and encoding algorithms are utilized to satisfy all hard clauses and as many soft clauses as possible. First, we present the definition with respect to the partial MAX-SAT.

Definition 4.

(Boolean logical descriptions of partial MAX-SAT):

(1)

Basic elements: some elements are presented using Boolean variables x₁,x₂,…,x_i,…, x_i, or ¬x_i(the negation of x_i), which is called a literal logic; the instance formalized as x₁∨x₂∨…∨x_n using n literals x_i is called a clause; and sentence c₁∧c₂∧…∧c_m using m clauses c_i is called the conjunctive normal form, which is expressed as cnf(c₁,c₂,…,c_m);

(2)

Hard clause: c₁, c₂,…, c_m are hard clauses and satisfiable, if and only if there exist truth assignments such that the value of cnf(c₁,c₂,…,c_m) is 1. All hard clauses are set as HC;

(3)

Soft clause: the sentences that do not satisfy hard clauses are soft clauses. All soft clauses are set as SC.

To transform the authorization-query request into the partial MAX-SAT, we represent permission p and role r with literal $\stackrel{-}{p}$ and $\stackrel{-}{r}$ respectively, and we describe them and their logical negations as follows:

(1)

$\stackrel{-}{p}$: $\forall p\in P,\exists r\in R,\exists s\in S,p\in {{\displaystyle \cup }}_{r\in roles\_session\left(s\right)}perms\_session\left(r\right)$;

(2)

$\neg \stackrel{-}{p}$:$\forall p\in P,\exists r\in R,\exists s\in S,p\notin {{\displaystyle \cup }}_{r\in roles\_session\left(s\right)}perms\_session\left(r\right)$;

(3)

$\stackrel{-}{r}$:$\forall r\in R,\exists s\in S,r\in roles\_session\left(s\right)$;

(4)

$\neg \stackrel{-}{r}$: $\forall r\in R,\exists s\in S,r\notin roles\_session\left(s\right)$.

3.2.1. Preprocessing

To transform static-authorization logics and dynamic mutual role constraints into hard clauses, we describe the transforming rules as follows:

(1)

$\forall p\in P,\exists \left(r,r^{\prime }\right)\in R:\left(\left(r,r^{\prime }\right)\in RH\right)\wedge \left(\left(r^{\prime },p\right)\in PA\right)$

$\Rightarrow \neg \stackrel{-}{\mathrm{r}}\vee \stackrel{-}{\mathrm{p}}$;

(2)

$\forall p\in P,\exists \left(r^{\prime },r_1,r_2,\dots \right)\in R:\left(\left(r^{\prime },p\right)\in PA\right)\wedge \left(\left(r_1,r^{\prime }\right)\in RH\right)\wedge \left(\left(r_2,r^{\prime }\right)\in RH\right)\wedge \dots$

$\Rightarrow \neg \stackrel{-}{\mathrm{p}}\vee {\stackrel{-}{\mathrm{r}}}_1\vee {\stackrel{-}{\mathrm{r}}}_2\vee \dots$;

(3)

$\forall r\in R,\exists r^{\prime }\in R,\exists \left(p_1,p_2,\dots \right)\in P:\left(\left(r,r^{\prime }\right)\in RH\right)\wedge \left(\left(r^{\prime },p_1\right)\in PA\right)\wedge \left(\left(r^{\prime },p_2\right)\in PA\right)\wedge \dots$

$\Rightarrow {\stackrel{-}{\mathrm{r}}}_1\vee \neg {\stackrel{-}{\mathrm{p}}}_1\vee \neg {\stackrel{-}{\mathrm{p}}}_2\vee \dots$;

(4)

$\forall r\in R,\exists s\in S:\left(user\_session\left(s\right),r\right)\notin UA$

$\Rightarrow \neg \stackrel{-}{\mathrm{r}}$;

(5)

$\forall {\mathrm{r}}^{\prime }\in \left\{r_1,r_2,\dots ,r_m\right\}\subseteq R,\exists s\in S,\exists t\ge 2:\left(dmer\langle \left\{r_1,r_2,\dots ,r_m\right\},t\rangle \in C\right)\wedge$

$\left(\left|\left\{{\mathrm{r}}_1,{\mathrm{r}}_2,\dots ,{\mathrm{r}}_{\mathrm{m}}\right\}{{\displaystyle \cap }}^{}{\mathrm{roles}}_{\mathrm{session}\left(\mathrm{s}\right)}\right|<\mathrm{t}\right)\Rightarrow \stackrel{-}{{\mathrm{r}}^{\prime }}$.

3.2.2. Updating Clauses

To reflect the least-privileges principle, we say that permissions in P_lb must be satisfied and available in a single session, which can be formalized as follows:

$$\forall p\in P,\exists s\in S,\forall r\in R,:p\in P_{lb}\Rightarrow p\in {{\displaystyle \cup }}_{r\in roles\_session\left(s\right)}perms\_session\left(r\right).$$

Similarly, permissions not in P_ub must not be satisfied or available in a single session, which can be formalized as follows:

$$\forall p\in P,\exists s\in S,\forall r\in R,:p\in (P\backslash P_{ub})\Rightarrow p\notin {{\displaystyle \cup }}_{r\in roles\_session\left(s\right)}perms\_session\left(r\right).$$

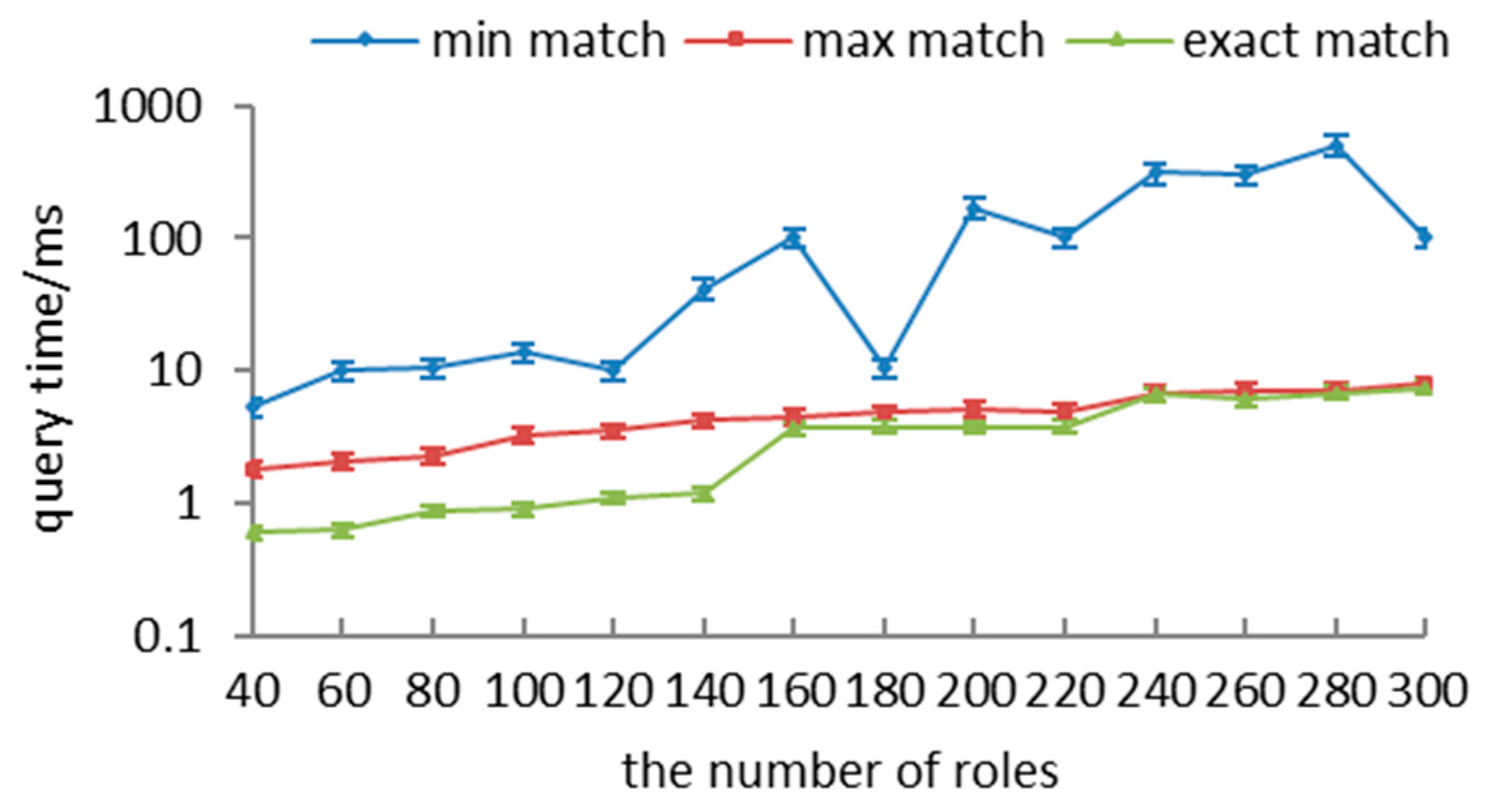
Different cases can be easily transformed into the partial MAX-SAT. Essentially, the partial MAX-SAT problem is a special extension of the MAX-SAT problem, whereby some clauses are relaxable and others are hard clauses. It aims to satisfy all hard clauses as well as a maximum number of soft ones. To translate the authorization-query problem to a partial MAX-SAT instance, all permissions in P_lb should be inserted into HC, and all permissions in (P_ub\P_lb) should be inserted into SC. Next, to satisfy the max match, any permission in (P_ub\P_lb) is initially set to be true, as only permission variables can be used in the permissions request and the partial MAX-SAT is to satisfy the largest number of soft clauses; to satisfy the min match, on the other hand, any permission in (P_ub\P_lb) is initially set to be false. Thus, hard and soft clauses are updated in Algorithm 5.

Algorithm 5. Updating clauses.

Input: the UAQ <s, Plb, Pub, match>, preprocessed results HC, SC

Output: updated results HC, SC

1. for each p in Plb do

2.   HC=HC ∪ {$\stackrel{-}{p}$};

3. end for

4. for each p in P\Pub do

5.   HC=HC ∪ {¬$\stackrel{-}{p}$};

6. end for

7. for each p in Pub\Plb do

8.   if match = min then

9.    SC=SC ∪ {¬$\stackrel{-}{p}$};

10.   else if match = max then

11.    SC=SC ∪ {$\stackrel{-}{p}$};

12.   else

13.    SC=SC ∪ Φ;

14.   end if

15. end for

In Algorithm 5, the two cases are reflected in lines 1–6. If permission p is in P_lb, we represent p with literal $\stackrel{-}{p}$ and insert it into HC. If permission p is not in P_ub, we insert literal ¬$\stackrel{-}{p}$ into HC. If the requested permissions are not in P_lb, but in P_ub, lines 7–15 transform them into soft clauses according to the different matches. We insert literal ¬$\stackrel{-}{p}$ or $\stackrel{-}{p}$ into SC when the match objective equals to min or max, and we do not update SC when the match objective equals to exact.

3.2.3. Assigning Truth for Clauses

To satisfy all hard clauses in HC, it is necessary to search for truth assignments and make sure all clauses are true. The recursive process is described in Algorithm 6.

Algorithm 6. Assigning truth for hard clauses.

Input:len(c)

Output: true or false

1. Randomly choose clause c from HC and use len(c) as the length of c;

2. if len(c) = 1 then

3.  c=1;

4.  HC=HC\{c};

5. for each clause, including c’∨c in HC, do

6.  HC=HC\{c’∨c};

7. end for

8. for each clause, including c’’∨¬c in HC, do

9.  HC=(HC\{c’’∨¬c})∪{c’’};

10. end for

11. return true;

12. else

13.  Assigning truth for hard clauses (len (c)-1);

14. return false;

15. end if

In Algorithm 6, lines 2–11 indicate that if chosen clause c consists of only one literal logic, we simplify HC according to the two different cases in each iteration: when a clause including c’∨c exists, we remove it from HC; when a clause including c’’∨¬c exists, we remove it from HC and insert c’’ into HC. Next, if len(c)>1, line 13 recursively calls Algorithm 6.

Theorem 2.

For each given clause c, there is a truth assignment for c using Algorithm 6.

Proof. 

On the basis of Section 3.2.1 and Section 3.2.2, we can search for the truth assignment from line 2 of the algorithm using the method of mathematical induction, and detailed descriptions are omitted owing to limited space. □

3.2.4. Encoding and Querying Clauses

To satisfy as many clauses as possible, soft clauses are encoded and queried in the following steps:

Step 1. For given set of soft clauses SC = {sc₁,sc₂,…,sc_n}, introduce n new blocking variables b_i(1 ≤ i ≤ n);

Step 2. Construct new clause set SC^b = {sc₁∨b₁,sc₂∨b₂,…,sc_n∨b_n}, where clause sc_i∨b_i is considered as b_i copies of sc_i;

Step 3. Search for minimal integer k, such that SC^b is true and ${\displaystyle \sum }_{i=1}^n{b}_i\le k$;

Step 4. Consider HC ∪ SC^b as parameters, take them into the QMaxSAT [39], and output all true clauses from SC.

Example 2.

Given set P of permissions, set R of roles, role–hierarchy relationships RH, role–permission assignment relationships PA, and set C of constraints, where P = {p₀,p₁,p₂,p₃,p₄,p₅,p₆,p₇}, R = {r₀,r₁,r₂}, RH = {r₀≥r₂}, PA = {(r₀,p₀),(r₀,p₁),(r₀,p₂),(r₀,p₄),(r₀,p₅),(r₀,p₆),(r₁,p₃),(r₁,p₇),(r₂,p₂),(r₂,p₆)}, and C = {dmer<{r₀,r₁},2,s>}. In the preprocessing stage, hard clauses are constructed by the transforming rules, and results are listed in

Table 3. Hard clauses.

Authorization Logics and Constraints	HC
$\forall p\in P,\exists \left(r,r^{\prime }\right)\in \mathrm{R}:$ $\left(\left(r,r^{\prime }\right)\in \mathrm{RH}\right)\wedge \left(\left(p,r^{\prime }\right)\in \mathrm{PA}\right)$	$\neg {\stackrel{-}{r}}_0\vee {\stackrel{-}{p}}_0,\neg {\stackrel{-}{r}}_0\vee {\stackrel{-}{p}}_1,\neg {\stackrel{-}{r}}_0\vee {\stackrel{-}{p}}_2,\neg {\stackrel{-}{r}}_0\vee {\stackrel{-}{p}}_4,$ $\neg {\stackrel{-}{r}}_0\vee {\stackrel{-}{p}}_5,\neg {\stackrel{-}{r}}_0\vee {\stackrel{-}{p}}_6,\neg {\stackrel{-}{r}}_1\vee {\stackrel{-}{p}}_3,\neg {\stackrel{-}{r}}_1\vee {\stackrel{-}{p}}_7,$ $\neg {\stackrel{-}{r}}_2\vee {\stackrel{-}{p}}_2,\neg {\stackrel{-}{r}}_2\vee {\stackrel{-}{p}}_6$
$\forall p\in P,\exists \left(r^{\prime },r_1,r_2,\dots \right)\in \mathrm{R}:$ $\left(\left(p,r^{\prime }\right)\in \mathrm{PA}\right)\wedge \left(\left(r_1,r^{\prime }\right)\in \mathrm{RH}\right)\wedge \left(\left(r_2,r^{\prime }\right)\in \mathrm{RH}\right)\dots$	$\neg {\stackrel{-}{p}}_0\vee {\stackrel{-}{r}}_0,\neg {\stackrel{-}{p}}_1\vee {\stackrel{-}{r}}_0,\neg {\stackrel{-}{p}}_2\vee {\stackrel{-}{r}}_0\vee {\stackrel{-}{r}}_2,\neg {\stackrel{-}{p}}_3\vee {\stackrel{-}{r}}_1,$ $\neg {\stackrel{-}{p}}_4\vee {\stackrel{-}{r}}_0,\neg {\stackrel{-}{p}}_5\vee {\stackrel{-}{r}}_0,\neg {\stackrel{-}{p}}_6\vee {\stackrel{-}{r}}_0\vee {\stackrel{-}{r}}_2,\neg {\stackrel{-}{p}}_7\vee {\stackrel{-}{r}}_1$
$\forall r\in R,\exists r^{\prime }\in \mathrm{R},\exists \left(p_1,p_2,\dots \right)\in \mathrm{P}:$ $\left(\left(r,r^{\prime }\right)\in \mathrm{RH}\right)\wedge \left(\left(p_1,r^{\prime }\right)\in \mathrm{PA}\right)\wedge \left(\left(p_2,r^{\prime }\right)\in \mathrm{PA}\right)\dots$	${\stackrel{-}{r}}_0\vee \neg {\stackrel{-}{p}}_0\vee \neg {\stackrel{-}{p}}_1\vee \neg {\stackrel{-}{p}}_2\vee \neg {\stackrel{-}{p}}_4\vee \neg {\stackrel{-}{p}}_5\vee \neg {\stackrel{-}{p}}_6,$ ${\stackrel{-}{r}}_1\vee \neg {\stackrel{-}{p}}_3\vee \neg {\stackrel{-}{p}}_7,{\stackrel{-}{r}}_2\vee \neg {\stackrel{-}{p}}_2\vee \neg {\stackrel{-}{p}}_6$
$\forall s\in S, \exists \left\{r_1,r_2,\dots \right\}\subseteq \mathrm{R}:$ $\mathrm{dmer}\langle \left\{r_1,r_2,\dots \right\},2,s\rangle \in C$	$\neg {\stackrel{-}{r}}_0\vee \neg {\stackrel{-}{r}}_1$

.

Suppose there are three authorization requests: (1) P_lb = Φ, P_ub = {p₂,p₃,p₆}, match = max; (2) P_lb = {p₂,p₃,p₆}, P_ub = P, match = min; (3) P_lb = {p₂,p₃,p₆}, P_ub={p₂,p₃,p₆}, match=exact. Then, HC and SC are, respectively, updated in Algorithms 5 and 6; the results are listed in

Table 4. Updated clauses.

Permissions Request	HC	SC
<s,Φ,{p2,p3,p6},max >	HC ∪ {¬$\stackrel{-}{p}$0,¬$\stackrel{-}{p}$1,¬$\stackrel{-}{p}$4,¬$\stackrel{-}{p}$5,¬$\stackrel{-}{p}$7}	{$\stackrel{-}{p}$2, $\stackrel{-}{p}$3, $\stackrel{-}{p}$6}
<s,{p2,p3,p6},P,min >	HC ∪ {$\stackrel{-}{p}$2, $\stackrel{-}{p}$3, $\stackrel{-}{p}$6}	{¬$\stackrel{-}{p}$0,¬$\stackrel{-}{p}$1,¬$\stackrel{-}{p}$4,¬$\stackrel{-}{p}$5,¬$\stackrel{-}{p}$7}
<s,{p2,p3,p6},{p2,p3,p6},exact >	HC ∪ {$\stackrel{-}{p}$2, $\stackrel{-}{p}$3, $\stackrel{-}{p}$6,¬$\stackrel{-}{p}$0,¬$\stackrel{-}{p}$1,¬$\stackrel{-}{p}$4,¬$\stackrel{-}{p}$5,¬$\stackrel{-}{p}$7}	Φ

, and different sets of activated roles are listed in

Table 5. Activated roles.

Permissions Request	Literal Roles	Role Set
<s,Φ,{p2,p3,p6},max>	¬$\stackrel{-}{r_0}$, ¬$\stackrel{-}{r_1}$, $\stackrel{-}{r_2}$	{r2}
<s,{p2,p3,p6},P,min>	¬$\stackrel{-}{r_0}$, $\stackrel{-}{r_1}$, $\stackrel{-}{r_2}$	{r1,r2}
<s,{p2,p3,p6},{p2,p3,p6},exact>	¬$\stackrel{-}{r_0}$, ¬$\stackrel{-}{r_1}$, ¬$\stackrel{-}{r_2}$	Φ

.

4. Experiment Evaluations

In this section, two groups of experiments were carried out. The first group of experiments was to evaluate the effectiveness of RMO_SODSDA, and the second was to evaluate its efficiency. All experiments were implemented on a standard desktop PC with an Intel i5–7400 CPU, 4 GB RAM, and 160 GB hard disks, running a 64-bit Windows 7 operating system. All simulations were compiled and executed in Eclipse IDE for a Java Developers environment.

4.1. RMO_SODSDA Effectiveness

4.1.1. Datasets and Experiment Setup

Datasets: we considered nine real-world datasets from the work of [14]. Meanwhile, in the unconstrained preprocessing stage, regular mining tool RMiner [39] was used for mining roles. The results including the number of roles and execution time are shown in

Table 6. Datasets.

Dataset	|U|	|P|	|CR|	Execution Time (s)
Americas-large	3485	10127	423	78.78
Americas-small	3477	1587	213	6.31
Apj	2044	1164	456	5.60
Customer	10961	284	276	4.66
Domino	79	231	20	0.01
Emea	35	3046	34	0.02
Firewall1	365	709	69	0.11
Firewall2	325	590	10	0.15
Healthcare	46	46	15	0.01

.

Experiment setup: constraints were constructed synthetically. According to the length of constraint enforcement, we studied four different kinds of k-n RSSOD: 2–2 RSSOD, 2–3 RSSOD, 3–5 RSSOD, and 5–10 RSSOD, where n permissions were randomly chosen from the set of all permissions. According to the amount of constraint enforcement, we chose 30 and 50 as the number of each kind of k-n RSSOD, respectively.

However, after analyzing these datasets, we found that the Domino, Firewall1, Firewall2, and Healthcare datasets could not be used to represent the performance of role-mining algorithms with RSSOD constraints. Some user sets in these datasets violate the constraints, and they have all permissions assigned to them. Thus, valid RSSOD constraints cannot be generated from them.

4.1.2. Evaluation Measures

We considered the average number of constructing SMER constraints, execution time, and percentage of RSSOD constraints that can be successfully enforced as evaluation measures.

4.1.3. Experiment Results

To evaluate the effectiveness of RMO_SODSDA, we considered preprocessing results UA, CR, and the k-n RSSOD constraints as inputs, and repeatedly implemented the experiments 20 times. The experiment results are shown in

Table 7. Results of SMER constructed from 2–2 RSSOD.

Dataset	|E22 RSSOD|= 30			|E2–2 RSSOD|= 50
	C2–2 SMER	Ct-t SMER	Ct-m SMER	C2–2 SMER	Ct-t SMER	Ct-m SMER
Americas-large	984(95%)	984(95%)	982(96%)	2461(92%)	2568(92%)	2574(93%)
Americas-small	441(80%)	439(80%)	436(80%)	1279(84%)	1272(84%)	1285(84%)
Apj	40(80%)	39(80%)	37(80%)	124(84%)	124(84%)	124(84%)
Customer	19(95%)	15(80%)	11(80%)	48(96%)	36(78%)	33(76%)
Emea	57(80%)	54(80%)	51(80%)	142(84%)	138(84%)	135(83%)

,

Table 8. Results of SMER constructed from 2–3 RSSOD.

Dataset	|E2-3 RSSOD|= 30			|E2-3 RSSOD|= 50
	C2–2 SMER	Ct-t SMER	Ct-m SMER	C2–2 SMER	Ct-t SMER	Ct-m SMER
Americas-large	3307(100%)	3306(100%)	3304(100%)	7697(98%)	7694(98%)	7692(98%)
Americas-small	995(80%)	993(80%)	991(80%)	3365(85%)	3360(85%)	3358(85%)
Apj	146(100%)	128(100%)	119(100%)	345(100%)	297(100%)	277(100%)
Customer	32(60%)	19(100%)	17(100%)	81(58%)	49(98%)	39(95%)
Emea	172(95%)	163(95%)	155(95%)	425(98%)	404(98%)	387(97%)

,

Table 9. Results of SMER constructed from 3–5 RSSOD.

Dataset	|E3–5 RSSOD|= 30			|E3–5 RSSOD|= 50
	C2–2 SMER	Ct-t SMER	Ct-m SMER	C2–2 SMER	Ct-t SMER	Ct-m SMER
Americas-large	11,335(91%)	11,335(91%)	11,335(91%)	31,155(88%)	31,155(88%)	31,147(88%)
Americas-small	2120(50%)	2120(50%)	2120(50%)	5081(48%)	5081(48%)	5078(48%)
Apj	553(95%)	574(95%)	571(95%)	1498(93%)	1556(93%)	1534(93%)
Customer	46(17%)	372(100%)	369(100%)	97(14%)	929(100%)	930(100%)
Emea	696(100%)	698(100%)	697(100%)	1819(100%)	1831(100%)	1829(100%)

and

Table 10. Results of SMER constructed from 5–10 RSSOD.

Dataset	|E5–10 RSSOD|= 30			|E5–10 RSSOD|= 50
	C2–2 SMER	Ct-t SMER	Ct-m SMER	C2–2 SMER	Ct-t SMER	Ct-m SMER
Americas-large	24,908(70%)	24,908(70%)	24,901(85%)	62,058(71%)	62,058(71%)	62,058(71%)
Americas-small	1307(15%)	1307(15%)	1307(15%)	3831(16%)	3831(16%)	3831(16%)
Apj	1459(85%)	1614(85%)	1603(85%)	3926(90%)	4258(90%)	4214(88%)
Customer	7(5%)	2180(100%)	2177(100%)	25(2%)	5461(98%)	5455(98%)
Emea	1591(100%)	1594(100%)	1594(100%)	4168(100%)	4178(100%)	4172(100%)

, where E_{k-n RSSOD} represents the set of RSSOD constraints, and C_{t-m SMER} represents the set of SMER constraints.

Firstly, by analyzing the results in Table 7, Table 8, Table 9 and Table 10, it was observed that there was a certain number of RSSOD constraints that could not be enforced when we constructed 2–2 SMER, t-t SMER, or t-m SMER constraints. The less that efficient RSSOD constraints were enforced (in other words, the less the percentage in the bracket), the fewer the constructing SMER constraints.

Second, Table 7, Table 8, Table 9 and Table 10 show that the process of constructing 2–2 SMER constraints is more difficult than the other two processes, because the 2–2 SMER was more restricted than the others. We take the Customer dataset as an example. In Table 9, percentages of successfully constructing 2–2 SMER constraints are 17% with 30 RSSOD and 14% with 50 RSSOD, while percentages of constructing the other two are both 100%. In Table 10, percentages of successfully constructing 2–2 SMER constraints are only 5% and 2%.

A further observation is that the number of constructing SMER constraints tended to increase as the number of RSSOD constraints increased in the five datasets. We take the Americas-large dataset as an example. In Table 7, when the number of RSSOD changed from 30 to 50, the number of constructing SMER increased from 984 to 2461 and 2568, respectively.

Finally, it can be observed from Table 7, Table 8, Table 9 and Table 10 that the number of constructing SMER increased as the length of RSSOD constraints increased. We take the Americas-large dataset as an example. If the number of RSSOD constraints equaled to 30, then the number of constructing SMER remarkably increased from 984 to 24,908. If the number of RSSOD constraints equaled to 50, then the number of constructing SMER changed remarkably from 2461 to 62,058.

Next, the average time for constructing SMER constraints from different kinds of RSSOD constraints is shown in

Table 11. Execution time with 2–2 RSSOD.

Dataset	|E2–2 RSSOD|= 30			|E2–2 RSSOD|= 50
	C2–2 SMER	Ct-t SMER	Ct-m SMER	C2–2 SMER	Ct-t SMER	Ct-m SMER
Americas-large	139.7 s	144.7 s	289.5 s	366.2 s	379.5 s	759.1 s
Americas-small	10.1 s	10.1 s	20.2 s	29.2 s	30.2 s	60.4 s
Apj	0.3 s	0.4 s	0.8 s	0.9 s	1.2 s	2.4 s
Customer	0.01 s	0.2 s	0.4 s	0.01 s	0.5 s	1.1 s
Emea	0.02 s	0.02 s	0.04 s	0.05 s	0.06 s	0.12 s

,

Table 12. Execution time with 2–3 RSSOD.

Dataset	|E2–3 RSSOD|= 30			|E2–3 RSSOD|= 50
	C2–2 SMER	Ct-t SMER	Ct-m SMER	C2–2 SMER	Ct-t SMER	Ct-m SMER
Americas-large	505.5 s	509.5 s	452.9 s	1203.9 s	1212.8 s	1078.1 s
Americas-small	30.5 s	31.8 s	28.3 s	89.9 s	96.3 s	85.6 s
Apj	1.5 s	1.4 s	1.2 s	3.6 s	3.1 s	2.7 s
Customer	0.5 s	0.3 s	0.3 s	1.3 s	0.7 s	0.6 s
Emea	0.07 s	0.07 s	0.06 s	0.02 s	0.1 s	0.1 s

,

Table 13. Execution time with 3–5 RSSOD.

Dataset	|E3–5 RSSOD|= 30			|E3–5 RSSOD|= 50
	C2–2 SMER	Ct-t SMER	Ct-m SMER	C2–2 SMER	Ct-t SMER	Ct-m SMER
Americas-large	2022.7 s	2054.3 s	1314.7 s	5762.9 s	5861.9 s	3751.6 s
Americas-small	117.7 s	143.6 s	91.9 s	280.9 s	337.9 s	216.2 s
Apj	6.7 s	7.1 s	4.5 s	17.9 s	19.7 s	12.6 s
Customer	1.2 s	5.0 s	3.2 s	2.7 s	12.1 s	7.7 s
Emea	0.3 s	0.3 s	0.2 s	0.8 s	0.8 s	0.5 s

and

Table 14. Execution time with 5–10 RSSOD.

Dataset	|E5–10 RSSOD|= 30			|E5–10 RSSOD|= 50
	C2–2 SMER	Ct-t SMER	Ct-m SMER	C2–2 SMER	Ct-t SMER	Ct-m SMER
Americas-large	6164.6 s	6267.3 s	7771.9 s	14,667.3 s	15,008.8 s	18,612.1 s
Americas-small	260.7 s	371.4 s	460.5 s	5.9 s	900.5 s	1116.7 s
Apj	19.7 s	23.3 s	28.9 s	47.0 s	59.4 s	73.6 s
Customer	0.9 s	28.1 s	34.8 s	2.3 s	70.5 s	87.4 s
Emea	0.7 s	0.7 s	0.8 s	1.7 s	0.7 s	0.8 s

, from which it is observed that execution time increased as the number and length of RSSOD constraints increased. Taking the Americas-large dataset as an example, the number of RSSOD changed from 30 to 50, and the length of RSSOD changed from 2 to 10. The time for constructing 2–2 SMER constraints was 139, 366, 505, 1203, 2022, 5762, 6164, and 14,667 s, respectively. Similar to analyses for the number of constructing constraints, detailed discussions of execution time were omitted in this paper owing to limited space.

4.2. RMO_SODSDA Efficiency

4.2.1. Datasets and Experiment Setup

Datasets: according to Table 6, the number of the chosen roles in the second group of experiments increased from 40 to 300 with a step of 20. In addition, the QMaxSAT solver was chosen because it performed quite well in the latest MAX-SAT evaluation and because of its efficiency on sets of encoding clauses. Clauses updated based on truth assignments were written in Java.

Experiment setup: for the given UAQ < s, P_lb, P_ub, match>, s is a session in S, Pu represents permissions assigned to user u in our constructed RBAC system, and Prequest ⊆ Pu. This can be obtained using Sat4j 2.3.4 (April 2013), an open-source satisfiability library in Java [40]. We considered three scenarios, as follows: (1) P_lb = Prequest, P_ub = Pu, match = min; (2) P_lb = Φ, P_ub = Prequest, match = max; and (3) P_lb = P_ub = Prequest, match = exact.

4.2.2. Evaluation Measures

To evaluate authorization performance of the RMO_SODSDA, we implemented the experiments and compared query time as the number of roles increased according to the three scenarios.

4.2.3. Experiment Results

We randomly selected 10 pairs of values of P_lb and P_ub for the experiments and took the median value. The results of our experiments are shown in Figure 1 with error bars, where the lateral axis represents varying values of the number of roles, and the vertical axis represents changes of query time including truth assignments for HC, encoding for SC, and execution time by using the QMaxSAT solver.

Figure 1 demonstrates that query time increased slightly as the number of roles increased in the exact and max cases. Particularly, the time was less than 10 milliseconds with up to 300 roles. In the min case, query time irregularly floated up and down with the increasing number of roles. While time taken for different match requests remained the same in the preprocessing and clause-updating stages, the time taken using the QMaxSAT solver was longer in the min case than in the other two cases. However, total query time was still below one second in any case.

In order to further validate the efficiency of the RMO_SODSDA, we considered a similar set of experiments as the ones performed in the work of [37]. More precisely, our experiments were set as follows: 30 ≤ |R|< 300, |U| = 20, |P| = 70, |C| = 5. Similar to the experiments in the previous UAQ setting section, we took the median value over 10 randomly selected pairs of values of P_lb and P_ub for the experiments. We compared the performance of our method with the results based on the MAX-SAT solver in Figure 2, Figure 3 and Figure 4 with error bars, where the lateral axis represents varying values of the number of roles, and the vertical axis represents changes of query time.

It can be observed from Figure 2 and Figure 3 that the query time of our method did not obviously vary. It was less than 20 milliseconds with up to 290 roles. In contrast, the query time in the work of [37] tended to grow linearly up to around 160 milliseconds. The total query time of our method was lower because all hard and soft clauses were completely encoded in the preprocessing stage, while in the work of [37], all clauses were encoded in the querying stage. Therefore, our method outperformed the MAX-SAT solver in the exact and max cases.

It can be observed from Figure 4 that the query time of our method did not obviously vary when |R| changed from 30 to 190. However, the query time irregularly floated up and down when |R| changed from 210 to 290, up to around 240 milliseconds in this paper and around 400 milliseconds in the work of [38]. Therefore, our method did not outperform the MAX-SAT solver in the min case.

5. Discussion

From the above analyses of the effectiveness and efficiency of RMO_SODSDA, we found the following:

(1) In the Americas-large, Apj, and Emea datasets, percentage of RSSOD constraints that can be successfully enforced exceeded 70%. However, when the length of RSSOD constraints increased to 3–5 RSSOD and 5–10 RSSOD, the percentage in the Americas-small and Customer datasets was below 50% and 17%, respectively. Thus, the Americas-large, Apj, and Emea datasets were more appropriate for the effectiveness evaluations of RMO_SODSDA.

(2) We compared the execution time of RMO_SODSDA from Table 11, Table 12, Table 13 and Table 14 with that of the unconstrained role mining from Table 6 in

Table 15. Comparison of execution time.

Dataset	RMO_SODSDA(s)	Unconstrained Role Mining(s)
Americas-large	[139.7, 18612.1]	78.78
Americas-small	[10.1, 1116.7]	6.31
Apj	[0.3, 73.6]	5.60
Customer	[0.01, 87.4]	4.66
Emea	[0.02, 0.8]	0.02

. Obviously, the time of our method was much higher than that of any unconstrained role mining method. We constructed lots of different variants of SMER constraints to correctly implement the given RSSOD constraints, although it was time-consuming.

(3) For the given cases of permissions request in this paper, the query time of RMO_SODSDA was below one second in any case. However, the method did not outperform the MAX-SAT solver in the min case.

(4) We considered a similar set of experiments as the ones from the MAX-SAT solver to evaluate the efficiency of RMO_SODSDA, and we found that the query time does not obviously vary in the exact and max cases when the number of roles exceeds 300. Thus, we did not consider and analyze further the similar results in these cases.

(5) Similar to the number of roles chosen from the MAX-SAT solver, we chose the similar set of constraints as another parameter for our method, and only the RSSOD constraint was taken into consideration. Particularly, it was observed from Table 6 that the number of mining roles from the Americas-small and Customer datasets was close to 230 and 270, respectively. However, according to the first discussion in this section, the percentages of RSSOD constraints that can be successfully enforced were very low. As the results in Figure 4, the query time irregularly floated up and down once the two datasets were chosen for the performance evaluations.

6. Conclusions

A novel method, RMO-SODSDA, was proposed in this paper. We first presented constrained role-engineering optimization with separation-of-duty constraints, and constructed several SMER variants to correctly implement the RSSOD, including algorithm design and description, and the computational complexity for constructing the different SMER constraints. Then, in order to evaluate the security of the constructed RBAC system for a given authorization-query problem, an efficient approach for ensuring system security was presented that converts the authorization-query problem into a maximal-satisfiability problem. Lastly, experiment results demonstrated the effectiveness and efficiency of the RMO_SODSDA. There are still a few interesting issues to be handled. One issue is to study the relationships between different cardinality constraints and consider how to implement multiple constraints for role-mining optimization in future work.