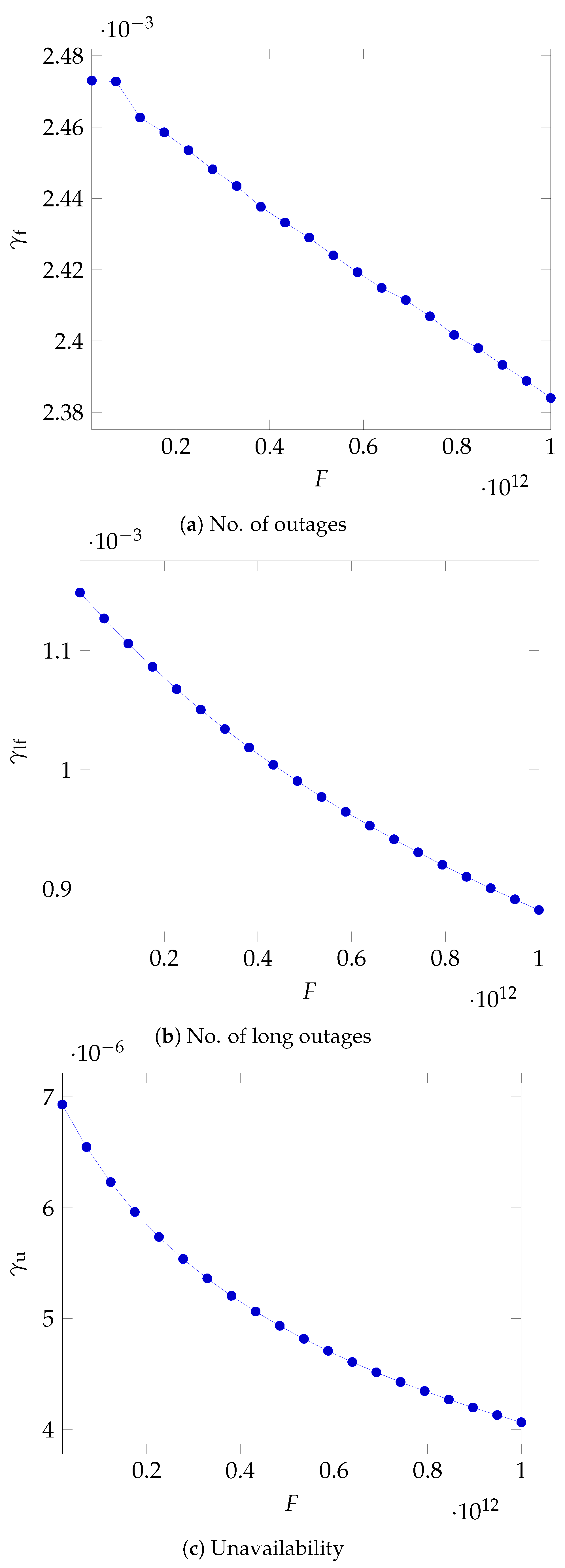1. Introduction
Service Level Agreements (SLA) are typically employed by cloud providers to provide guarantees on the quality of their services to end customers [
1,
2,
3,
4,
5,
6]. Those agreements, which form a contract or a contract-like relationship between the parties, state the obligations imposed on the cloud provider, through a set of service quality metrics and constraints to be met.
The compliance of cloud providers with those contractual or contractual-like commitments has to be monitored, and several tools have been proposed in the literature for that purpose [
7,
8,
9] or for acting on the basis of monitoring results to reach for compliance [
10]. Any tool has to measure a set of parameters related to the quality of service and compare their values against SLAs’ provisions. The foremost among them is availability [
11], defined roughly as the percentage of time that the cloud is available.
As it happens, the obligations underwritten in SLAs may not be fulfilled. In that case, the cloud provider is expected to pay penalties, if the contract so prescribes [
12], or anyway to compensate its customers for the loss incurred. If violations take place on a wide scale, penalties and compensations may endanger the economic balance of the cloud provider.
The cloud provider should therefore protect itself against such an occurrence. It can basically act in two ways:
The first countermeasure is technical in nature. Reducing the probability of occurrence and/or the amount of damages calls for investments in the infrastructure and better cloud management processes.
The second countermeasure instead relies on buying an insurance policy, whereby the insurer takes on the risk of paying all claims by customers in return for the premium to be paid by the cloud provider, which acts as the insured. The insurance approach to deal with possible excessive claims by cloud users in the framework of a Service Level Agreement has been proposed in [
13]. A major problem lies in the definition of the right premium of an insurance policy. In that paper, the correct premium has been computed for the case where the outage phenomenon is described by a Poisson process for occurrence of outages and by the generalized Pareto distribution for their duration. However, an alternative model has been recently introduced in the literature, based on an extensive measurement campaign on a private cloud [
14] belonging to a small/medium company. In that paper, the interarrival time between successive outages is modelled through a Pareto distribution, while the duration of an outage is modelled by a lognormal distribution.
In this paper, we again consider the problem of correctly determining the insurance premium against cloud outages. We adopt the expected utility paradigm as in [
13], but we consider the outage model recently proposed in [
14] in addition to the exponential-Pareto (a.k.a. Poisson–Pareto) examined in [
13]. Both outage models are here examined under three QoS metrics. Our main new results are the following:
we obtain closed formulas for the insurance premiums for all the combinations of outage model and QoS metric (rather than just for the exponential-Pareto model as in [
13];
we obtain a closed formula to set the unit compensation offered to customers so as to avoid compensations (through the resulting premium) eroding the profit margins;
we show that the maximum unit compensation is related to the service fee through an approximate inverse square law.
The paper is structured as follows.
Section 2 is devoted to describing the two models for outages. The quality of service metrics are instead described in
Section 3. The statistics of losses resulting from the models of outages are computed in
Section 4. The fair premium is derived in
Section 5. Finally, the conditions to make the refund process sustainable are derived in
Section 6.
2. Models for Outages
Our analysis relies on the use of models that describe the behaviour of the cloud. Here, we rely on a simple ON-OFF description of the service offered by the cloud, which is well suitable for cloud storage. In the ON-OFF model, the cloud alternates between two states: a fully operating period (a.k.a. uptime or ON period) and a no-service period (a.k.a. downtime or OFF period), as shown in
Figure 1. No partial performance degradation is considered in the ON-OFF model. The ON-OFF model can also serve as an approximation to more complex quality degradation processes. For example, a cloud storage provider could still be able to deliver the required files to its customers, but with a longer delivery time, i.e., with a delay with respect to normal operating conditions. In that case, a threshold could be imposed on the delivery time so that delays longer than that threshold are considered as service outages. In this section, we describe two models proposed in the literature for the statistics related to the alternance of ON and OFF states. We employ two variables to describe the duration of the two states: we use
S for the duration of the ON period and
D for that of the OFF period.
2.1. The Exponential-Pareto Model
The Exponential-Pareto model owes its name to the distributions proposed for the two alternating states of the general ON-OFF model. Namely, we have an exponential distribution for the duration of the ON period. The duration of the OFF period is instead governed by a generalized Pareto distribution (GPD). The cumulative distribution functions are therefore
where
is the scale parameter and
is the shape parameter of the GPD.
Since the duration of the ON period is the time elapsing before a new failure occurs, the MTTF (mean-time-to-failure) is simply the reciprocal of the parameter of the exponential distribution
Similarly, the duration of the OFF period is the time needed to repair the cloud, so that the MTTR (mean-time-to-repair) is the expected value of
DThe Exponential-Pareto model has first been proposed in [
15] through a best-fit procedure on a dataset of customer-reported outages for five major cloud providers (Google, Amazon, Rackspace, Salesforce, Windows Azure). The sources of data were Cloutage (
cloutage.org), founded by the Open Security Foundation in April 2010 but now discontinued, and the International Working Group on Cloud Computing Resiliency (IWGCR, a working group with a mission to monitor and analyze cloud computing resiliency.
This model has been employed in [
13] to assess the sustainability of refunds linked to insurance contracts for cloud services, as well as in [
16] to assess the contribution of the network to the overall unavailability. The values obtained for the parameters of the two distributions in that case are reported in
Table 1.
2.2. The Pareto-Lognormal Model
As the name suggests, in the Pareto-Lognormal model the distribution of operating periods is modelled as a Pareto law, while the lognormal distribution describes the duration of outages.
The model has been proposed by Dunne and Malone [
14], who analysed 300+ cloud outage events recorded for an enterprise cloud system (not better identified, but belonging to a small/medium enterprise) over an eighteen-month period. They tested seven models (Pareto, loglogistic, lognormal, gamma, exponential, logistic, and Weibull) through the Anderson–Darling test. In the end, they found the Pareto-Lognormal couple to be the best-fit solution.
The cumulative distribution function of operating periods is then
The distribution of outage duration is instead
The reliability indicators (MTTF and MTTR) are related to the parameters of the two distributions by the following formulas:
The values found by Dunne and Malone for the parameters of the two distributions are reported in
Table 2 (where the abbreviation SME—Small/Medium Enterprise—stands for the company whose cloud has been monitored during the measurement campaign, but whose name has been undisclosed); they lead to
3. Quality of Service Metrics
The assessment of damages and the ensuing compensation must be related to a metric that embodies the quality of service underwritten in the SLA. In this section, we provide three different QoS metrics with specific reference to the performance of the cloud. We adopt the same metrics already considered in [
17] to derive the correct price for an insurance policy in the case of a Markovian system, and in [
18] to assess the Value-at-Risk, again in the case of a Markovian system.
We consider the following metrics:
Number of outages;
Number of long outages;
Unavailability.
The number of outages is computed as the number of no-service intervals during the observation period
T. There are a number of technicalities involved in the detection of the actual instants of time when the cloud goes OFF and then goes back ON. We do not go into detail here and refer the reader interested to delve into the matter to [
19], where the complexity of measurements is dealt with. An advantage of this metric is that even the smallest service interruptions are accounted for; on the other hand, the severity of outages is not considered.
The number of long outages is simply the number of outages lasting more than a pre-set threshold w. The rationale for this metric is to avoid considering very short interruptions of service (glitches). Such interruptions could add considerably to the number of outages (hence, the first metric) without being significant for the user. This metric is a good choice if an outage must last some time to provoke a real damage to the company; this means that the company relies on some form of short-term resiliency against outages (this happens, e.g., with TCP where failures at the network layer can easily be recovered if they do not extend too much in space and time).
Finally, the unavailability is the percentage of time the service is OFF. According to this metric, a single long outage counts as a set of shorter outages if their cumulative duration is equal. In this case, damages simply accrue over time without any start effect.
5. Insurance Pricing
In
Section 4, we have seen how outages result in economic losses for the cloud provider. These losses have been evaluated for three quality metrics (number of outages, number of long outages, and unavailability), which account for most of the cases that may be encountered in practice. Since these losses may endanger the economic balance of the cloud provider, the latter may wish to hedge against such losses. A natural way to hedge is through an insurance policy. In this section, we derive the fair price for such a policy. We first describe the general pricing methodology based on the expected utility approach as described in [
23] and then apply that approach to the failure models described in
Section 2 and the QoS metrics described in
Section 3.
We consider a cloud provider whose assets are worth . This provider faces a possible monetary loss and wishes to buy an insurance policy. In that case, it has to pay the insurance premium P to be fully indemnified against that loss.
We assume that the cloud provider’s perception of the loss of the amount of money x is described by its utility function . The perception may be dramatically different, depending on the economic conditions of the insured cloud provider. For example, if even a modest loss changes the overall economic balance from a profit condition to a loss one, even that small amount of money leads to a large decay of the utility. On the other hand, if the cloud provider is making a large profit, it will be able to withstand larger losses without a significant reduction of its utility.
Since the loss
X is a random variable, we must consider the expected utility of the residual value of the company’s assets when the loss
X is suffered. We have to compare the provider’s utility under two conditions: incurring the uncertain loss versus paying the certain insurance premium. The maximum tolerable premium
P is the value that makes the two utilities equal. The equilibrium equation is then
The equilibrium equation may not be amenable to a closed form solution, depending on the nonlinear nature of the utility function. We can find an approximate solution by expanding both terms through a Taylor series in the neighbourhood of
:
By employing the second of these Taylor expansions, we get
Finally, by replacing those expressions in the equilibrium Equation (
42), we obtain the maximum tolerable premium
where we have introduced the risk aversion function
r, which takes into account the effect of the utility function:
Though several options are possible for the utility function (see, e.g., Section 1.3 in [
23]), a typical assumption is to consider a constant risk aversion coefficient
In that case, the utility function exhibits the Constant Absolute Risk Aversion (CARA) property [
24]; the only function that satisfies the CARA property is the exponential function
, which leads to the maximum tolerable premium
The CARA property has been assumed, e.g., in [
13,
25].
Under the CARA property, the premium formulation is therefore of the mean-variance type, where the risk-aversion coefficient is to be defined to obtain the premium: higher values of
are associated with a growing aversion for risk and then to the willingness to pay a higher premium: in [
26], the risk-aversion coefficient is assumed to take values in the [0.5,4] range. However, its assessment is rather sensitive, since it can significantly contribute to the premium. In [
27], a procedure is indicated to compute its value for a CARA utility function. Namely, it is set as
where
is the probability premium, i.e., the increase in probability above 0.5 that an individual requires to maintain a constant level of utility equal to the utility of status quo; it takes a value in the [0, 0.5] range.
In the following subsections, we derive the pricing formula for the two models described in
Section 2.
5.1. The Exponential-Pareto Model
Following the same approach adopted for the computation of the economic loss in
Section 4, we evaluate the resulting insurance premium for the three QoS metrics. In order to get a numeric feeling for the outcome, we consider the parameter values shown in
Table 4, which are fairly representative of the experiments leading to the models of
Section 2.
5.1.1. Number of Outages
Replacing the results of Equation (
10) in Equation (
48), we get the premium (actually the maximum tolerable premium) for the coverage period
T when the loss is proportional to the number of outages:
The resulting premium is proportional to the average number of outages and a quadratic function of the unit loss per outage.
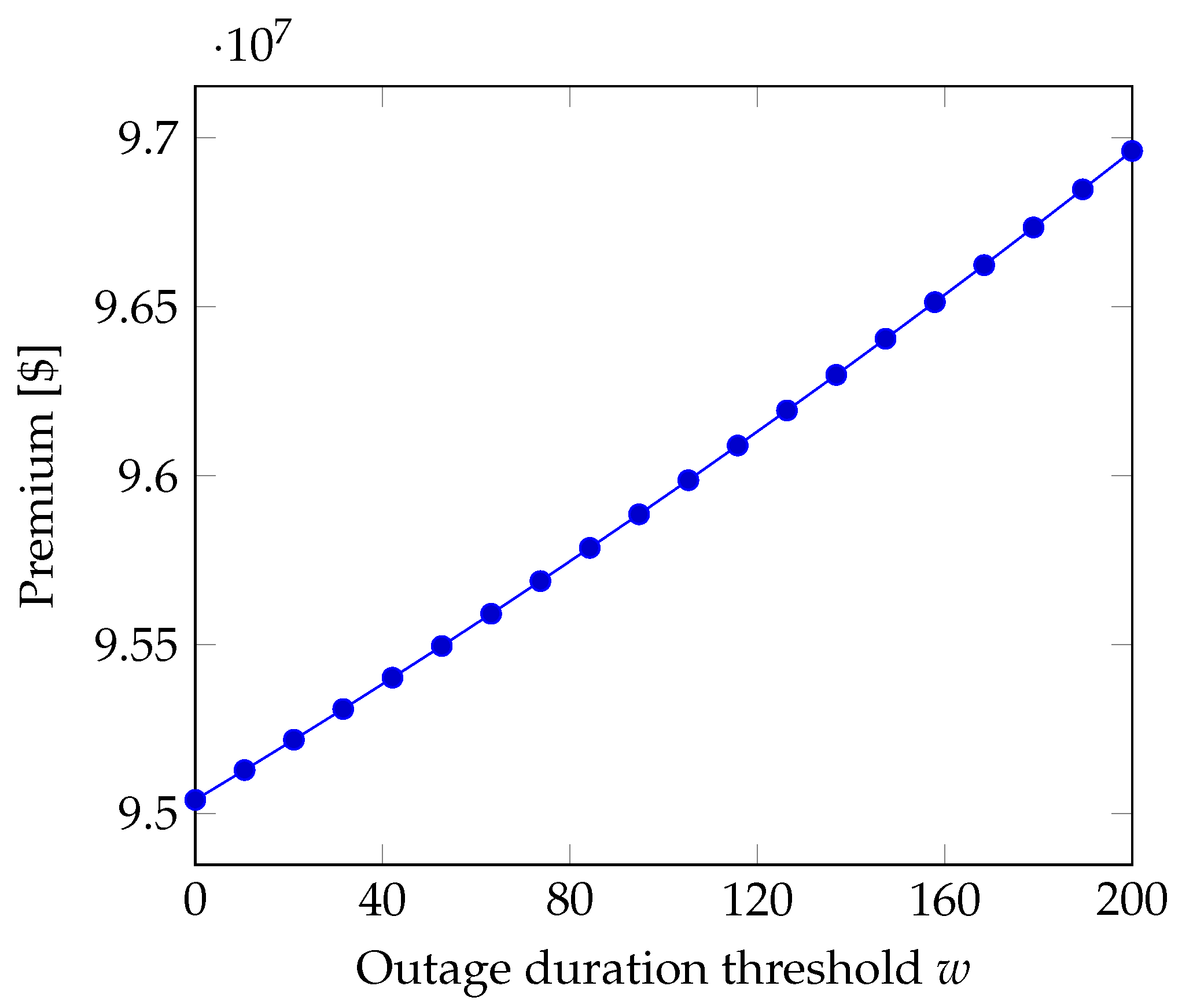
5.1.2. Number of Long Outages
If the loss is proportional to the number of outages whose duration exceeds the threshold
w, after recalling Equation (
15), we obtain the premium
Similarly to what we found for the case where the QoS metric is the number of outages, here the premium is a linear function of the average number of outages and a quadratic function of the unit loss per long outage. Instead, in
Figure 2, we see that the premium is a nearly linear function of the threshold
w that defines long outages. The picture has been obtained for the values of
Table 4 when the loss per minute is
, which lies in the low range among the values reported in
Table 3. The unit loss per long outage has been set according to the equation
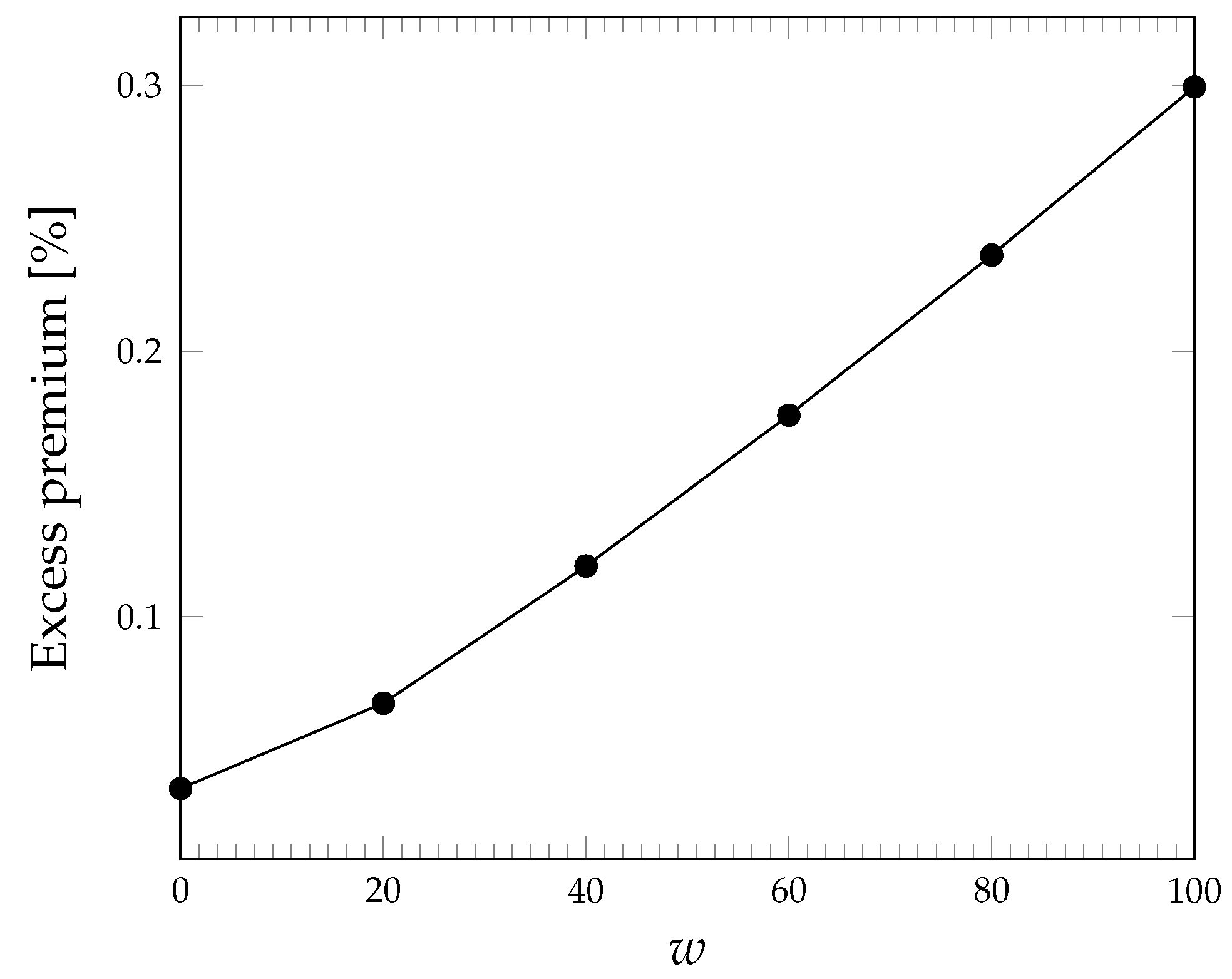
Aside from its absolute value, we can get a feeling for the size of the premium if we compare it with the expected loss, i.e., the excess premium defined as
The excess premium is shown in
Figure 3 for the same case of
Figure 2. We can see that the coverage of risk requires an excess premium of the order of some percentage points; its dependence on the outage duration threshold
w is again roughly linear.
5.1.3. Unavailability
If a loss is experienced for each minute of no service, after recalling Equations (
17) and (
18), we have the premium
The excess premium is then
For the values in
Table 4, we have the excess premium
, which represents a fairly large premium for risk.
5.2. The Pareto-Lognormal Model
Similarly to what we have done in
Section 5.1, in this section, we compute the premium when outages are described by the Pareto-Lognormal model. Again, we proceed separately for the three QoS metrics. As for the Exponential-Pareto model, we report the parameter values used for numerical examples in
Table 5.
5.2.1. Number of Outages
By recalling the general expression of the premium in Equation (
48) and the first two moments of the economic loss in Equations (
32) and (
33), we get the following premium:
5.2.2. Number of Long Outages
Here, we combine the general expression of the premium in Equation (
48) and the first two moments of the economic loss provided by Equations (
36) and (
37), which gives us the premium
The excess premium can be computed as in Equation (
54). Its behaviour as the outage duration threshold grows is however shown in
Figure 4.
5.2.3. Unavailability
Again, we employ here the general expression of the premium in Equation (
48) and the first two moments of the economic loss provided by Equations (
40) and (
41) to get
For the values in
Table 5, we have an excess premium equal to
, which is roughly half that obtained under the Exponential-Pareto model.
6. Refund Sustainability
In
Section 5, we have seen that the insurance premium is a function of the unit compensation (i.e.,
,
or
, depending on the QoS metric adopted). The relationship is typically of the quadratic kind. This means that the premium will go up with the unit compensation (and faster than that) that the cloud provider is bound to pay its customer. As a consequence, large unit compensations lead to high premiums, which may become unsustainable for the cloud provider: premiums represent a fixed (deterministic) outcome that erodes the profit margin of the cloud provider and, if large, may even turn a potential profit into a sure loss. In
Table 3, we have seen how large the unit loss per minute can be; though those values may represent a basis for setting the unit compensation (in that case for
), this way of acting may lead to an exceedingly high liability for the cloud provider. We suggest here a possible way to limit the liability of the cloud provider so as to make it sustainable. This involves setting a limit for the unit compensation that the cloud provider may pay. In this section, we derive such a limit for the two failure models and the three QoS metrics that we have considered so far. After obtaining the general expression for the maximum unit refund, we follow therefore the same approach as in
Section 3 and
Section 5, dealing separately with each subcase.
6.1. Unit Refund Limit
As hinted above, the compensation that cloud providers may pay their customers should be bounded, so that it does not pose a significant threat to the overall economic balance of the company. In many cases, the compensation is set as a percentage (well below 100%) of the service fee (the compensation is therefore a partial refund); this limit guarantees that the outflow related to refunds cannot exceed that same percentage of the revenues. In
Table 6, the percentage values set by some providers are reported for the case where the QoS metric is the availability. All providers allow for a larger refund percentage as the QoS degrades more and more. However, for three out of four providers, the refund can never be full.
In order to limit the liability of cloud providers within safe bounds, we consider here a similar approach by limiting the unit refund. We set therefore
where the asterisk is a jolly character so that the expression may be applied to any of the three performance parameters, and
defines the fraction of the fee that the cloud provider may accept to lose due to compensation for each QoS violation.
On the other hand, the cloud provider cannot be led to pay too high a premium, since the premium is a fixed periodic payment that erodes the provider’s profit. In order to guarantee that the revenues represented by the service fees are not overly reduced, we can set the premium so as not to be larger than a predefined fraction of the service fee itself:
Since the economic loss
is proportional to the QoS metric (which is either
,
or
U), as embodied by Equations (
9), (
11) and (
16), we introduce a generic variable
L to derive a general expression that may then be tailored for the case at hand by replacing
L with
,
or
U, respectively.
The general constraint on the premium can then be expressed as
This constraint leads to a quadratic inequality in the unit refund
:
Since the discriminant associated with the quadratic form is
and
, the solution of the quadratic inequality is
which gives us an upper bound for the unit refund
to be sustainable.
The premium-setting procedure therefore goes through the following steps:
Set the tolerable fraction
of the service fee as in Equation (
60);
Compute the limit unit refund as per Equation (
59);
In the following subsections, we derive the expression for
when either outage model applies and for the three QoS metrics. In order to show some numerical results, we consider the parameter values shown
Table 4 and
Table 5 for the failure models, and in
Table 7 for the refund sustainability computation. The risk aversion factor
is computed according to Equation (
49).
6.2. The Exponential-Pareto Model
6.2.1. Number of Outages
In this case, the loss statistics is the number of outages
, so that
and
and
From Equation (
64), the constraint on the refund factor then becomes
As can be seen in
Figure 5a, the maximum value for
diminishes as the fee grows with a roughly inverse square root dependence.
6.2.2. Number of Long Outages
In this case
, and
so that Equation (
64) becomes
In
Figure 5b again, we see that, as the fee grows, the cloud provider has to lower the fraction of the fee that it can return to its customers for each long outage.
6.2.3. Unavailability
In this case
, and
so that Equation (
64) becomes
The upper bound on the unit refund is now shown in
Figure 5c, where the decline as the fee grows is steeper in the lower domain of the fee values.
6.3. The Pareto-Lognormal Model
6.3.1. Number of Outages
From
Section 4.4.1, we recall that the first two moments of the number of outages are respectively
The two ratios involving those moments and employed in the computation of the maximum refund are respectively:
By replacing in the general expression (
64) the expressions just obtained and using the abbreviation
, and adopting the two shortened forms
and
, we get the final expression of the maximum unit refund when the number of outages is used as the QoS metric:
This equation shows again that the maximum unit refund has to lower according to an inverse square law as the fee grows. In
Figure 6a, we show the value of
for the parameters listed in
Table 7. The dependence here appears to be roughly linear because of the windows chosen for the fee values.
6.3.2. Number of Long Outages
Similarly to what we have done for the number of outages, we compute the ratios of the two moments for the case of long outages, by exploiting the results of
Section 4.4.2:
We can now replace those expressions into the unit refund limit general expression, adopting the abbreviation
. The maximum unit refund for the case of long outages is then
The same inverse sequare relationship appears to hold for the number of long outages as well, which is shown in
Figure 6b.
6.3.3. Unavailability
Again, for the case of unavailability, we compute the ratio of the moments of the Unavailability, employing the expressions shown in Equations (
40) and (
41):
We then replace these ratios in the general expression of the refund limit given by Equation (
64) to get the maximum unit refund for the case of unavailability:
Finally, in
Figure 6c, we show the same diminishing trend for
.
7. Conclusions
We have provided formulas for the insurance premium that cloud providers have to pay to protect themselves against the danger of excessive claims by their customers in the case of cloud outages. The formulas can be applied quite straightforwardly as a function of the parameters describing the cloud outage phenomenon. The formulas depend however on how much the cloud provider is willing to pay for each disruption unit (i.e, for each outage, or for each outage exceeding a prescribed duration, or for each minute of unavailability, depending on the QoS metric chosen). In order to keep the insurance premium within acceptable limit and avoid endangering the economic balance of the cloud provider, we have provided formulas for the maximum unit refund as well. This upper bound lowers as the service fee grows, roughly according to an inverse square law.
Our set of formulas allows cloud providers to consider insurance as an additional, non network-centric, means of protection against the consequences of poor cloud performance. A possible extension would lead us to consider a non-binary state space, where several levels of QoS degradation are possible as an approximation to the case of graceful degradation of service quality.