Assessing the Techno-Economic Benefits of Flexible Demand Resources Scheduling for Renewable Energy–Based Smart Microgrid Planning
Abstract
1. Introduction
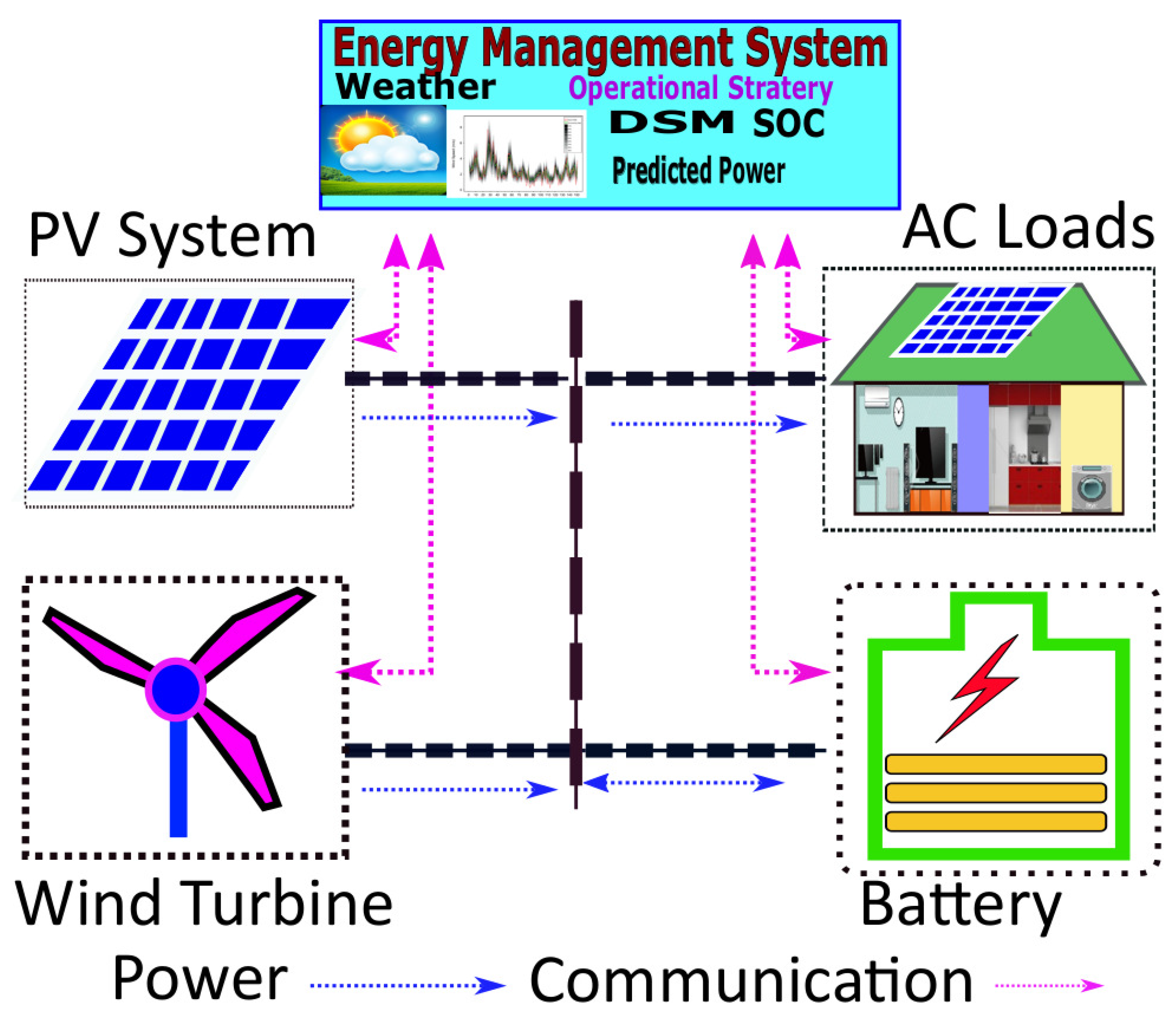
2. System Description and Modelling
2.1. Photo-Voltaic System Model (PV)
2.2. Wind Turbine Model
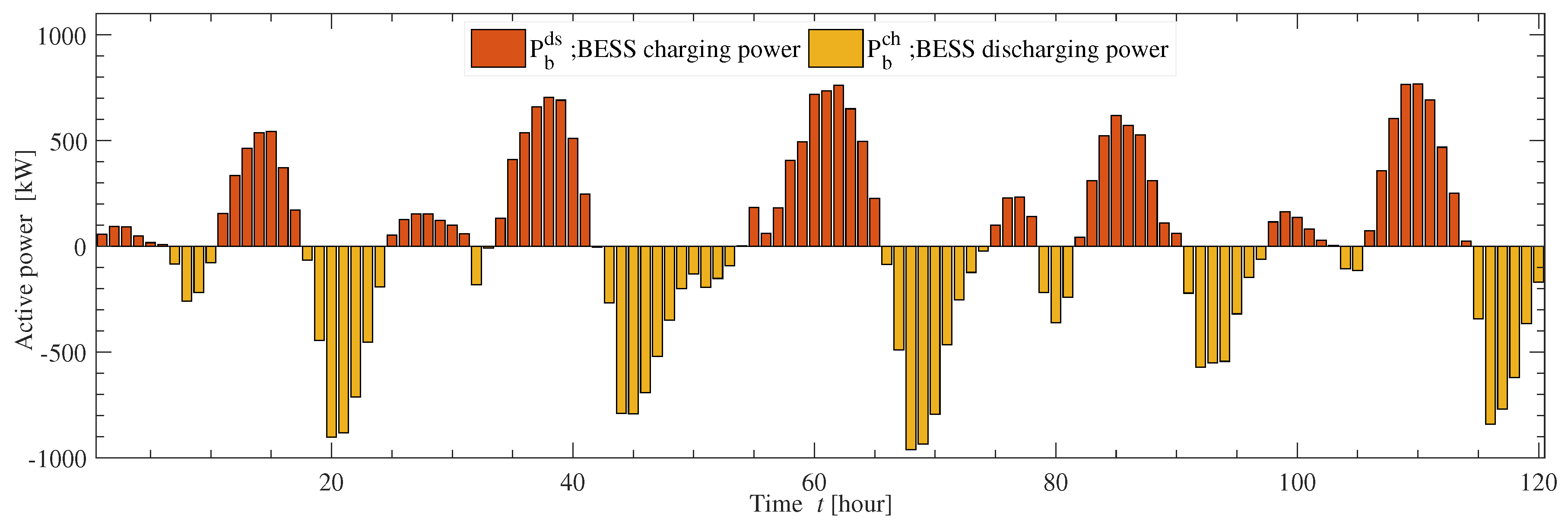
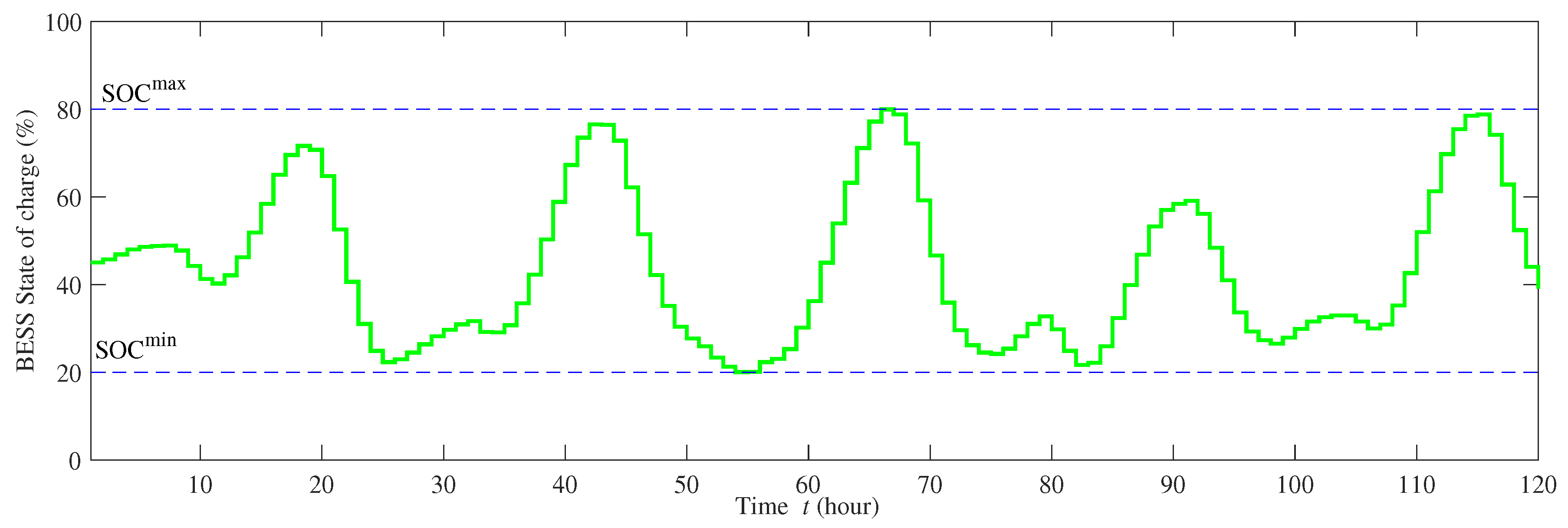
2.3. Battery Energy Storage System (BESS)
3. Demand-Side Management Strategy and Resource Forecasting
3.1. Flexible Demand Resources Modeling
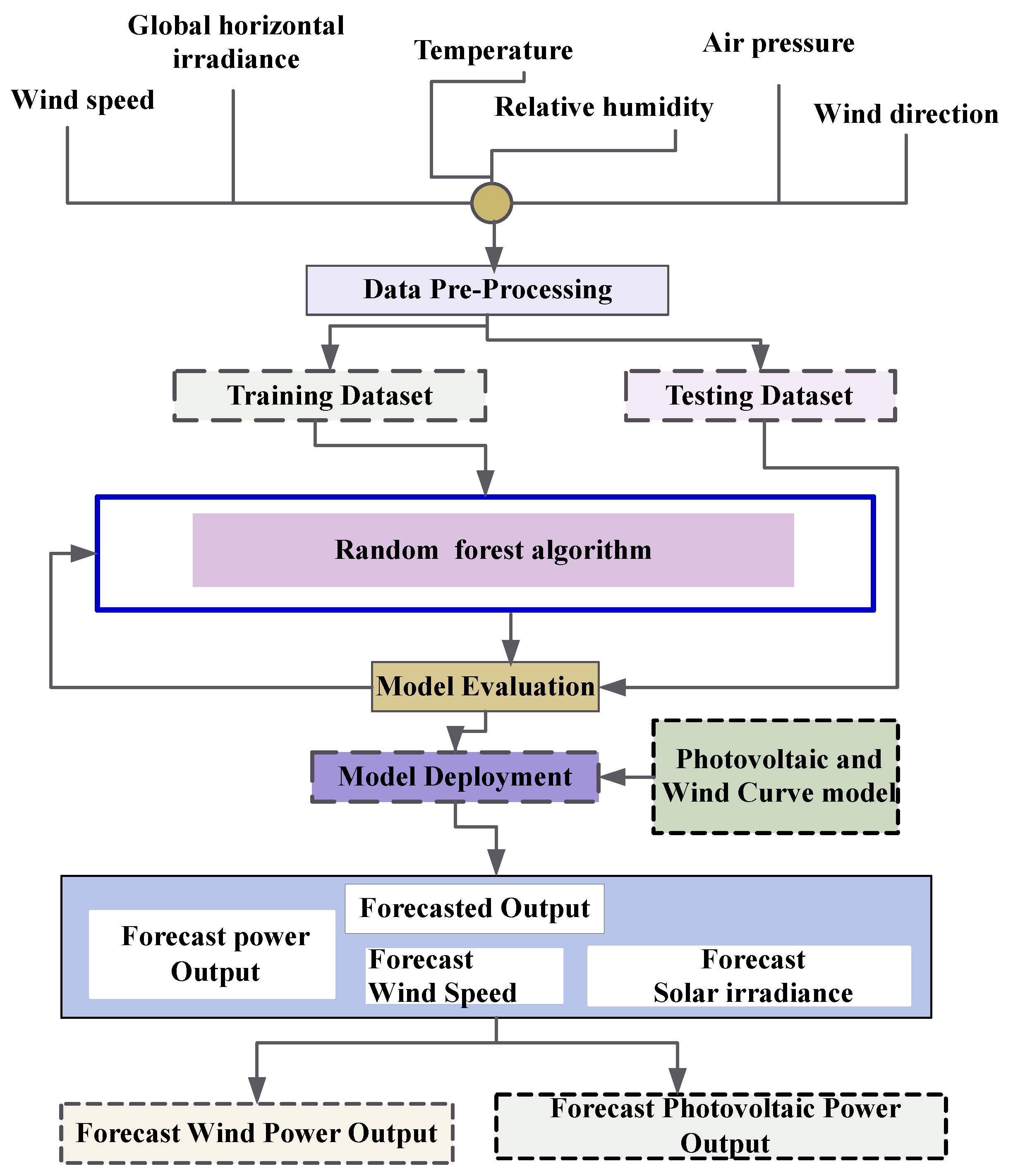
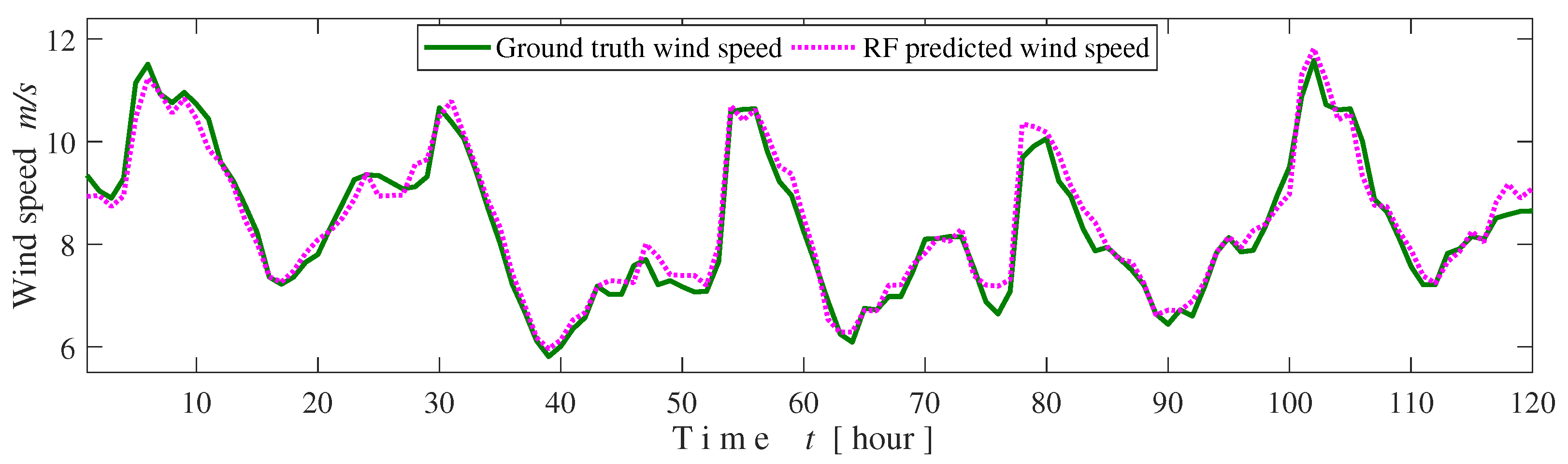
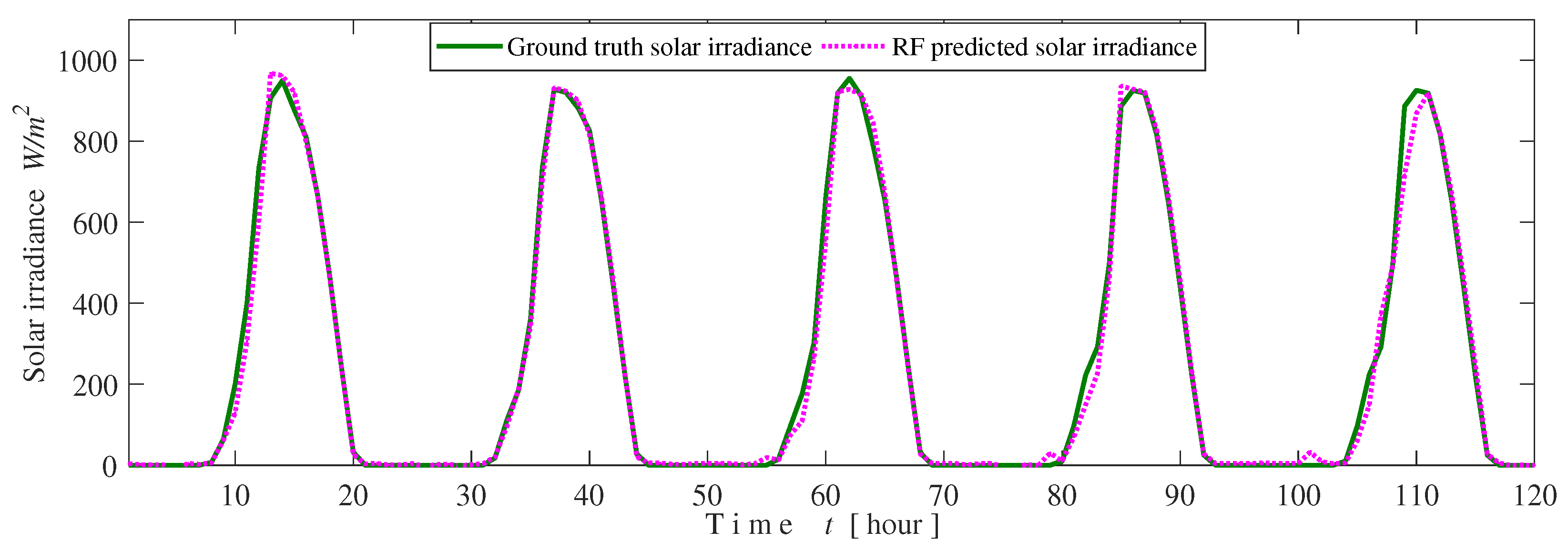
3.2. Wind and Solar Forecasting
3.2.1. Random Forest Regression
3.2.2. Random Forest Algorithm
| Algorithm 1: Random forest pseudo-code |
| Prerequisite: Training data set M, n forest trees and P traits (Temperature, wind speed, solar Irradiance, etc.) |
| 1. Growing n forest trees. |
| 2. For |
| 3. Select a random sample from training set M. |
| with replacement. |
| 4. Grow a tree without pruning. |
| 5. Split-attribute: |
| Randomly select attribute n for splitting. |
| 6. Best split: |
| Evaluate the gain of split-attribute for samples. |
| 7. End For |
| 8. Provided a new data set y: |
| 9. Predict the new data by averaging the predictions of each individual n forest trees by averaging |
| 10. End: Terminate the algorithm |
3.2.3. Forecasting Error Metrics
- MAE
- RMSE
- rwhere is the values of the predicted data, the and represent the actual and the mean of the input data respectively.
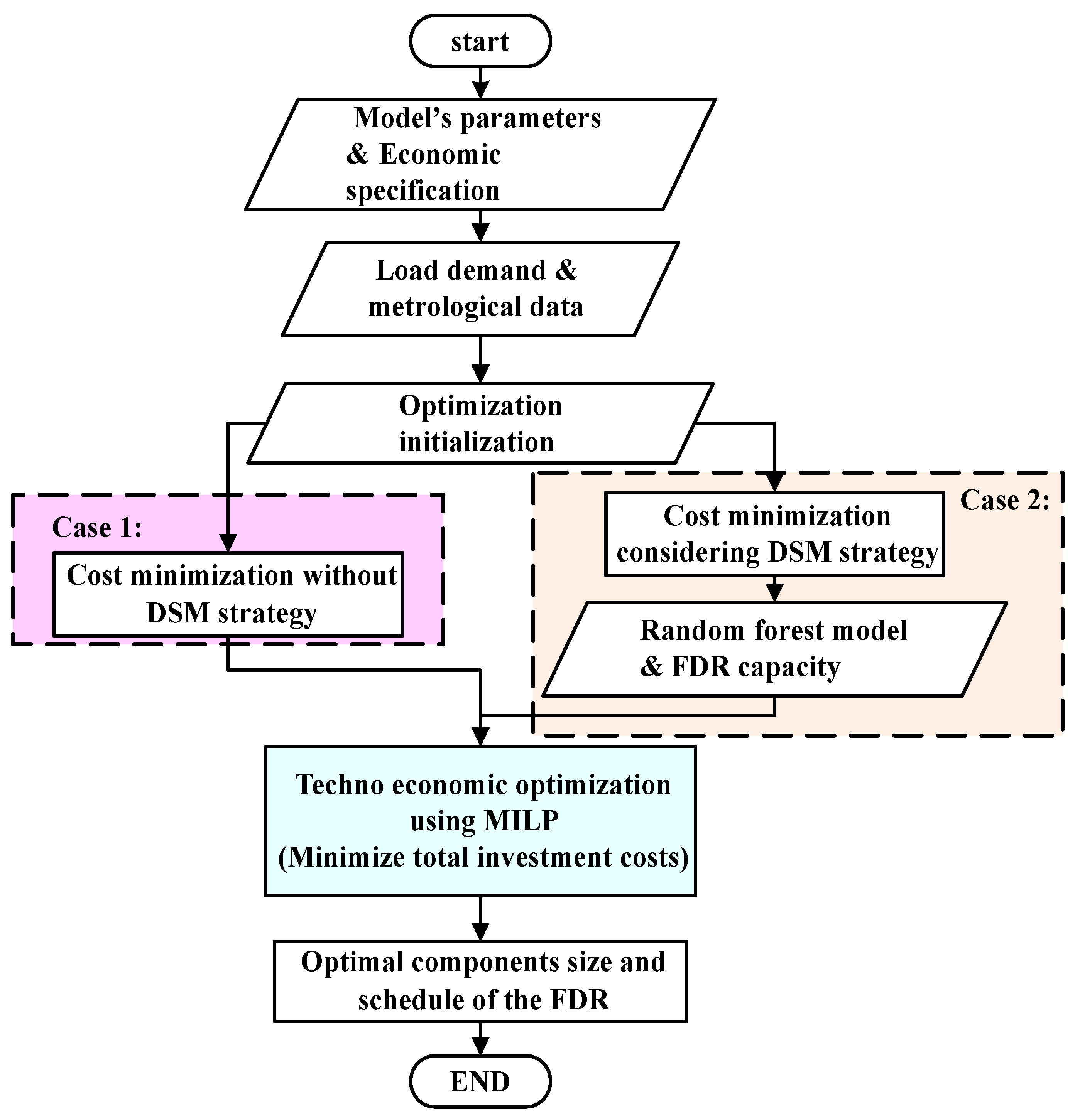
4. Sizing Optimization
4.1. Objective Function
4.2. Constraints
- Power balance constraint without FDR implementation:The total power generated should satisfy the energy demand at any given time.where is the load demand, and is the BESS discharging and charging power.
- Power balance constraint with the consideration of the FDR rescheduling program can be expressed as:
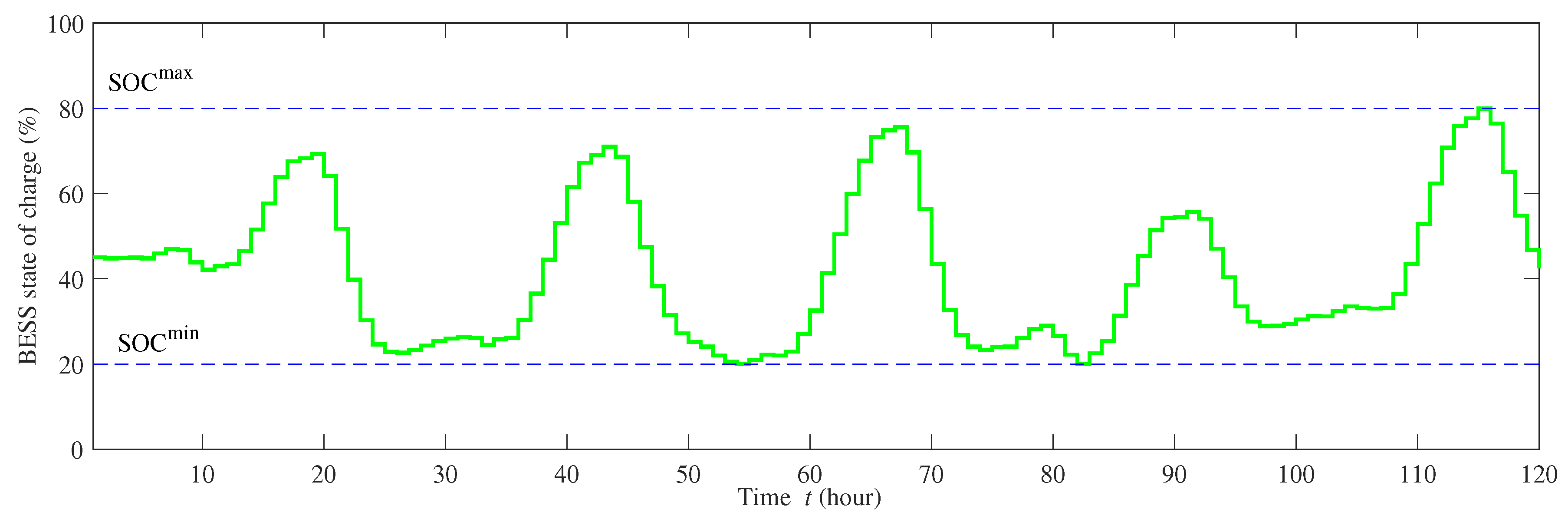
- BESS constraints: the energy stored in the BESS must be bounded within the minimum () and the maximum state of charge () limit.
- BESS maximum charging and discharging power is bounded by the maximum charging () and discharging power capacity ().
- Charging and discharging of the BESS cannot occur simultaneously.where and are the integer variables denoting the charging and discharging operation state of the BESS, respectively.
5. Simulation Parameters, Data Description and Case Study
- Case 1: Capacity optimization without DSM strategy.
- Case 2: Capacity optimization considering FDR scheduling as DSM strategy.
6. Simulation Results and Discussion
6.1. Optimum Configuration without DSM Strategy
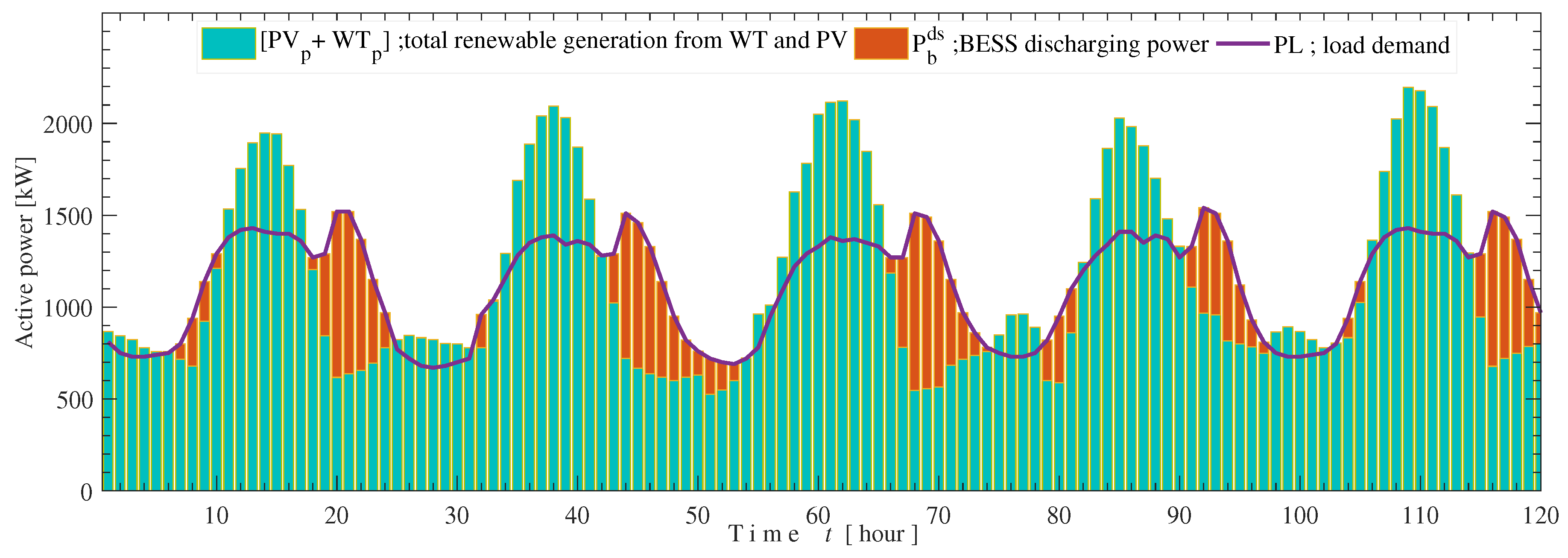
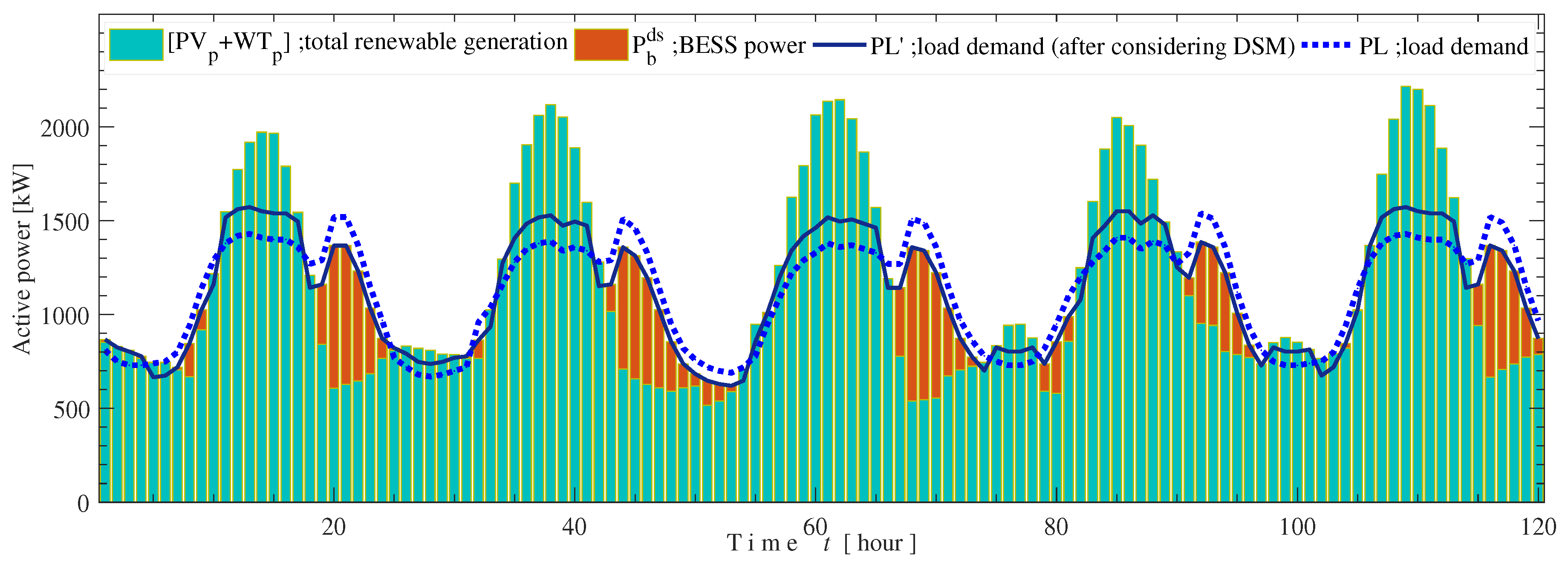
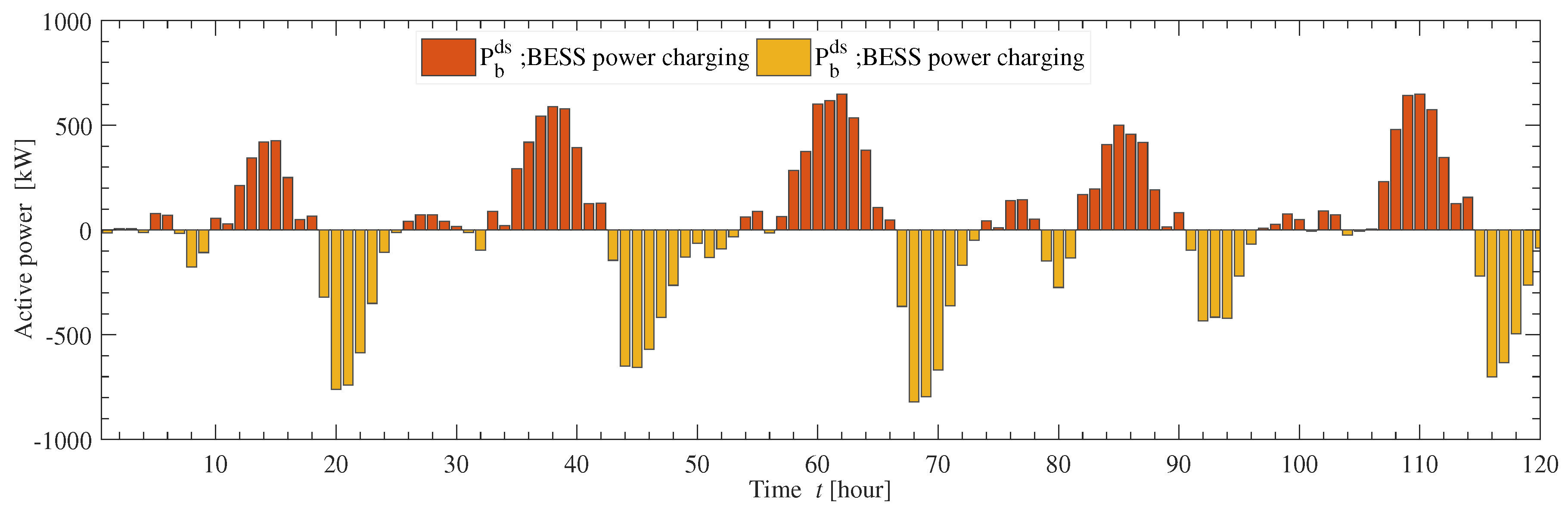
6.2. Optimum Configuration Considering DSM Strategy and Resource Forecasting
6.3. Techno-Economic Optimal System Configuration Comparison and Analysis
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| REA | Rural Electrification Authority |
| ABE | African business education |
| JICA | Japan international cooperation agency |
References
- McCollum, D.L.; Zhou, W.; Bertram, C.; De Boer, H.S.; Bosetti, V.; Busch, S.; Després, J.; Drouet, L.; Emmerling, J.; Fay, M.; et al. Energy investment needs for fulfilling the Paris Agreement and achieving the Sustainable Development Goals. Nat. Energy 2018, 3, 589. [Google Scholar] [CrossRef]
- López-González, A.; Ferrer-Martí, L.; Domenech, B. Sustainable rural electrification planning in developing countries: A proposal for electrification of isolated communities of Venezuela. Energy Policy 2019, 129, 327–338. [Google Scholar] [CrossRef]
- Kiptoo, M.K.; Adewuyi, O.B.; Lotfy, M.E.; Senjyu, T.; Mandal, P.; Abdel-Akher, M. Multi-Objective Optimal Capacity Planning for 100% Renewable Energy-Based Microgrid Incorporating Cost of Demand-Side Flexibility Management. Appl. Sci. 2019, 9, 3855. [Google Scholar] [CrossRef]
- Adewuyi, O.B.; Shigenobu, R.; Ooya, K.; Senjyu, T.; Howlader, A.M. Static voltage stability improvement with battery energy storage considering optimal control of active and reactive power injection. Electr. Pow. Syst. Res. 2019, 172, 303–312. [Google Scholar] [CrossRef]
- Kristiansen, M.; Korpås, M.; Svendsen, H.G. A generic framework for power system flexibility analysis using cooperative game theory. Appl. Energy 2018, 212, 223–232. [Google Scholar] [CrossRef]
- Alizadeh, M.I.; Moghaddam, M.P.; Amjady, N.; Siano, P.; Sheikh-El-Eslami, M.K. Flexibility in future power systems with high renewable penetration: A review. Renew. Sustain. Energy Rev. 2016, 57, 1186–1193. [Google Scholar] [CrossRef]
- Amrollahi, M.H.; Bathaee, S.M.T. Techno-economic optimization of hybrid photovoltaic/wind generation together with energy storage system in a stand-alone micro-grid subjected to demand response. Appl. Energy 2017, 202, 66–77. [Google Scholar] [CrossRef]
- Majidi, M.; Nojavan, S. Optimal sizing of energy storage system in a renewable-based microgrid under flexible demand side management considering reliability and uncertainties. J. Oper. Autom. Power Eng. 2017, 5, 205–214. [Google Scholar]
- Pietzcker, R.C.; Ueckerdt, F.; Carrara, S.; De Boer, H.S.; Després, J.; Fujimori, S.; Johnson, N.; Kitous, A.; Scholz, Y.; Sullivan, P.; et al. System integration of wind and solar power in integrated assessment models: A cross-model evaluation of new approaches. Energy Econ. 2017, 64, 583–599. [Google Scholar] [CrossRef]
- Sheth, A.; Gautam, P.; Siridevi, N.C. Intelligent Generation Scheduler for a Smart Micro Grid. In Proceedings of the 2018 2nd International Conference on Power, Energy and Environment: Towards Smart Technology (ICEPE), Shillong, India, 1–2 June 2018. [Google Scholar]
- Esfetanaj, N.N.; Nojavan, S. The Use of Hybrid Neural Networks, Wavelet Transform and Heuristic Algorithm of WIPSO in Smart Grids to Improve Short-Term Prediction of Load, Solar Power, and Wind Energy. In Operation of Distributed Energy Resources in Smart Distribution Networks; Elsevier: Amsterdam, The Netherlands, 2018; pp. 75–100. [Google Scholar]
- Notton, G.; Nivet, M.L.; Voyant, C.; Paoli, C.; Darras, C.; Motte, F.; Fouilloy, A. Intermittent and stochastic character of renewable energy sources: Consequences, cost of intermittence and benefit of forecasting. Renew. Sustain. Energy Rev. 2018, 87, 96–105. [Google Scholar] [CrossRef]
- Gürtler, M.; Paulsen, T. The effect of wind and solar power forecasts on day-ahead and intraday electricity prices in Germany. Energy Econ. 2018, 75, 150–162. [Google Scholar] [CrossRef]
- Martinez-Anido, C.B.; Botor, B.; Florita, A.R.; Draxl, C.; Lu, S.; Hamann, H.F.; Hodge, B.M. The value of day-ahead solar power forecasting improvement. Sol. Energy 2016, 129, 192–203. [Google Scholar] [CrossRef]
- Hodge, B.M.; Martinez-Anido, C.B.; Wang, Q.; Chartan, E.; Florita, A.; Kiviluoma, J. The combined value of wind and solar power forecasting improvements and electricity storage. Appl. Energy 2018, 214, 1–15. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Y.; Hu, X.; Sun, Y.; Deng, D.J.; Vinel, A.; Zhang, Y. Wireless big data computing in smart grid. IEEE Wirel. Commun. 2017, 24, 58–64. [Google Scholar] [CrossRef]
- Rana, M. Architecture of the Internet of energy network: An application to smart grid communications. IEEE Access 2017, 5, 4704–4710. [Google Scholar] [CrossRef]
- Morello, R.; De Capua, C.; Fulco, G.; Mukhopadhyay, S.C. A smart power meter to monitor energy flow in smart grids: The role of advanced sensing and IoT in the electric grid of the future. IEEE Sens. J. 2017, 17, 7828–7837. [Google Scholar] [CrossRef]
- Wu, Z.; Tazvinga, H.; Xia, X. Demand side management of photovoltaic-battery hybrid system. Appl. Energy 2015, 148, 294–304. [Google Scholar] [CrossRef]
- Hussain, M.; Gao, Y. A review of demand response in an efficient smart grid environment. Electr. J. 2018, 31, 55–63. [Google Scholar] [CrossRef]
- Ogunjuyigbe, A.; Ayodele, T.; Akinola, O. Optimal allocation and sizing of PV/Wind/Split-diesel/Battery hybrid energy system for minimizing life cycle cost, carbon emission and dump energy of remote residential building. Appl. Energy 2016, 171, 153–171. [Google Scholar] [CrossRef]
- Alhussein, M.; Haider, S.I.; Aurangzeb, K. Microgrid-Level Energy Management Approach Based on Short-Term Forecasting of Wind Speed and Solar Irradiance. Energies 2019, 12, 1487. [Google Scholar] [CrossRef]
- Wan, C.; Zhao, J.; Song, Y.; Xu, Z.; Lin, J.; Hu, Z. Photovoltaic and solar power forecasting for smart grid energy management. CSEE J. Power Energy Syst. 2015, 1, 38–46. [Google Scholar] [CrossRef]
- Persson, C.; Bacher, P.; Shiga, T.; Madsen, H. Multi-site solar power forecasting using gradient boosted regression trees. Sol. Energy 2017, 150, 423–436. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Painsky, A.; Rosset, S. Lossless Compression of Random Forests. J. Comput. Sci. Technol. 2019, 34, 494–506. [Google Scholar] [CrossRef]
- Huertas Tato, J.; Centeno Brito, M. Using smart persistence and random forests to predict photovoltaic energy production. Energies 2019, 12, 100. [Google Scholar] [CrossRef]
- Barbosa de Alencar, D.; de Mattos Affonso, C.; Limão de Oliveira, R.; Moya Rodríguez, J.; Leite, J.; Reston Filho, J. Different models for forecasting wind power generation: Case study. Energies 2017, 10, 1976. [Google Scholar] [CrossRef]
- Kim, S.G.; Jung, J.Y.; Sim, M.K. A Two-Step Approach to Solar Power Generation Prediction Based on Weather Data Using Machine Learning. Sustainability 2019, 11, 1501. [Google Scholar] [CrossRef]
- Huang, C.J.; Kuo, P.H. A short-term wind speed forecasting model by using artificial neural networks with stochastic optimization for renewable energy systems. Energies 2018, 11, 2777. [Google Scholar] [CrossRef]
- Weather History Download. Available online: https://www.meteoblue.com (accessed on 13 July 2019).
| Component and Economic Specification | ||
|---|---|---|
| Economics | ||
| Discount rate, r | 5% | |
| Inflation rate | 6% | |
| PV Module [31] | ||
| Investment cost | 1690 | US $/kW |
| Maintenance | 26 | US $/kW/yr |
| (PV) reduction factor | 84% | |
| lifetime | 25 | years |
| Wind Turbine [31] | ||
| Investment costs | 2030 | US $/kW |
| Operation and maintenance | 76 | US $/kW/year |
| lifetime | 25 | years |
| Cut-in wind speed: | 4 | m/s |
| Rated wind speed: | 14.5 | m/s |
| Cut-out wind speed: | 25 | m/s |
| Shear Coefficient | 0.14 | |
| Turbine hub height: | 50 | m |
| Lead-Acid BESS [3] | ||
| Investment cost | 300 | US $/kWh |
| Replacement costs | 300 | US $/kWh |
| Self-discharge rate | 0.01% | |
| Efficiency | 85% | |
| lifetime | 5 | years |
| Case 1 | Case 2 | |
|---|---|---|
| Demand side management | None | FDR scheduling |
| Optimal PV size, (kW) | 1196 | 1401 |
| Optimal WT size, (kW) | 2054 | 1866 |
| Optimal BESS size, (kWh) | 7150 | 5200 |
| Case 1 | Case 2 | |
|---|---|---|
| Demand side management | None | FDR scheduling |
| PV net present cost (US $) | 2,453,969.95 | 2,874,591.89 |
| WT Net present cost (US $) | 6,492,053.33 | 5,897,843.97 |
| BESS Net present cost (US $) | 6,301,300.00 | 4,582,729.8 |
| Total investment costs (US $) | 15,247,276.77 | 13,355,165.67 |
| % cost saving of TIC | - | 12.41% |
| Predictions | Error Metrics | n = 800 | n = 8 | n = 80 |
|---|---|---|---|---|
| Wind speed | MAE (m/s) | 0.24 | 0.28 | 0.26 |
| RMSE (m/s) | 0.31 | 0.38 | 0.34 | |
| 0.95 | 0.93 | 0.94 | ||
| Wind power | MAE (kW) | 37.68 | 42.91 | 39.31 |
| RMSE (kW) | 52.28 | 62.14 | 53.69 | |
| Solar irradiance | MAE (W/m) | 20.63 | 27.85 | 19.48 |
| RMSE (W/m) | 44.06 | 47.1 | 42.36 | |
| 0.98 | 0.98 | 0.98 | ||
| Solar power | MAE (kW) | 23.4 | 31.59 | 22.09 |
| RMSE (kW) | 49.97 | 53.42 | 48.05 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiptoo, M.K.; Adewuyi, O.B.; Lotfy, M.E.; Amara, T.; Konneh, K.V.; Senjyu, T. Assessing the Techno-Economic Benefits of Flexible Demand Resources Scheduling for Renewable Energy–Based Smart Microgrid Planning. Future Internet 2019, 11, 219. https://doi.org/10.3390/fi11100219
Kiptoo MK, Adewuyi OB, Lotfy ME, Amara T, Konneh KV, Senjyu T. Assessing the Techno-Economic Benefits of Flexible Demand Resources Scheduling for Renewable Energy–Based Smart Microgrid Planning. Future Internet. 2019; 11(10):219. https://doi.org/10.3390/fi11100219
Chicago/Turabian StyleKiptoo, Mark Kipngetich, Oludamilare Bode Adewuyi, Mohammed Elsayed Lotfy, Theophilus Amara, Keifa Vamba Konneh, and Tomonobu Senjyu. 2019. "Assessing the Techno-Economic Benefits of Flexible Demand Resources Scheduling for Renewable Energy–Based Smart Microgrid Planning" Future Internet 11, no. 10: 219. https://doi.org/10.3390/fi11100219
APA StyleKiptoo, M. K., Adewuyi, O. B., Lotfy, M. E., Amara, T., Konneh, K. V., & Senjyu, T. (2019). Assessing the Techno-Economic Benefits of Flexible Demand Resources Scheduling for Renewable Energy–Based Smart Microgrid Planning. Future Internet, 11(10), 219. https://doi.org/10.3390/fi11100219









