Beam Training for Millimeter-Wave Communication Based on Tabu Table Enhanced Rosenbrock Algorithm
Abstract
1. Introduction
1.1. Related Work and Motivation
1.2. Paper Contributions
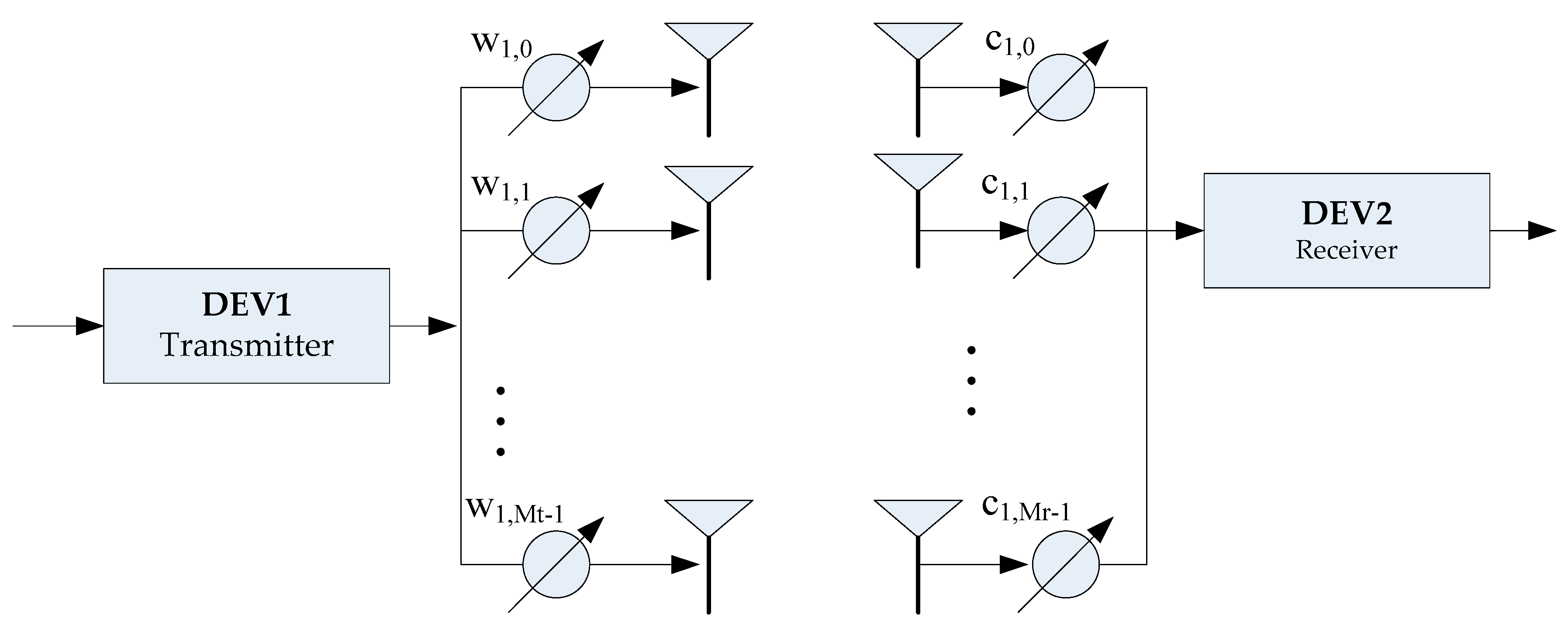
2. System Model
3. Rosenbrock-Algorithm-Based Beam Training
3.1. Problem Description
3.2. Rosenbrock Search
3.2.1. Probe Moving
3.2.2. Pattern Moving
3.2.3. Consideration of Limiting Factor
| Algorithm 1. Rosenbrock search. |
| Input: Initial solution , , and ; threshold ; initial counter . Output: .
|
4. Simulated-Annealing-Based Beam Training
4.1. Simulated Annealing
4.2. Simulated Annealing-Based Rosenbrock Search
5. Tabu-Search-Based Enhanced Rosenbrock Algorithm
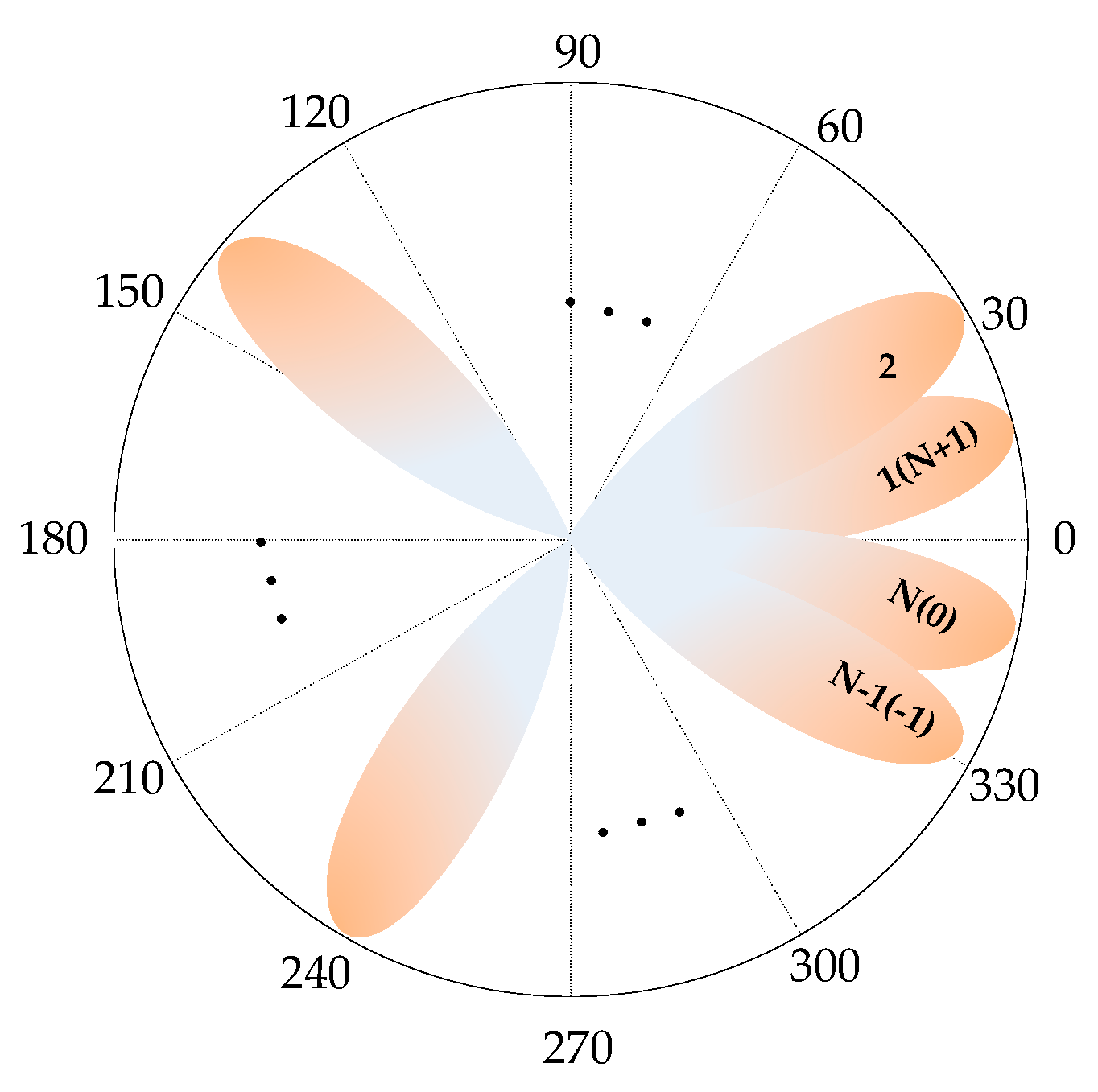
5.1. Beam Index Definition
5.2. Tabu Search
5.3. Boundary Problems
5.3.1. Neighborhood Boundary Description
5.3.2. Index Boundary Description
| Algorithm 2. The probe moving of the proposed algorithm (Subprogram of Step1 in Algorithm1). |
| Input: Initial solution ; aspiration function ; initial move steps , ; initial search directions , ; tabu table ; initial iteration counter and the maximum iterations . Output: The probed solution .
|
5.3.3. Computational Complexity and Limitation
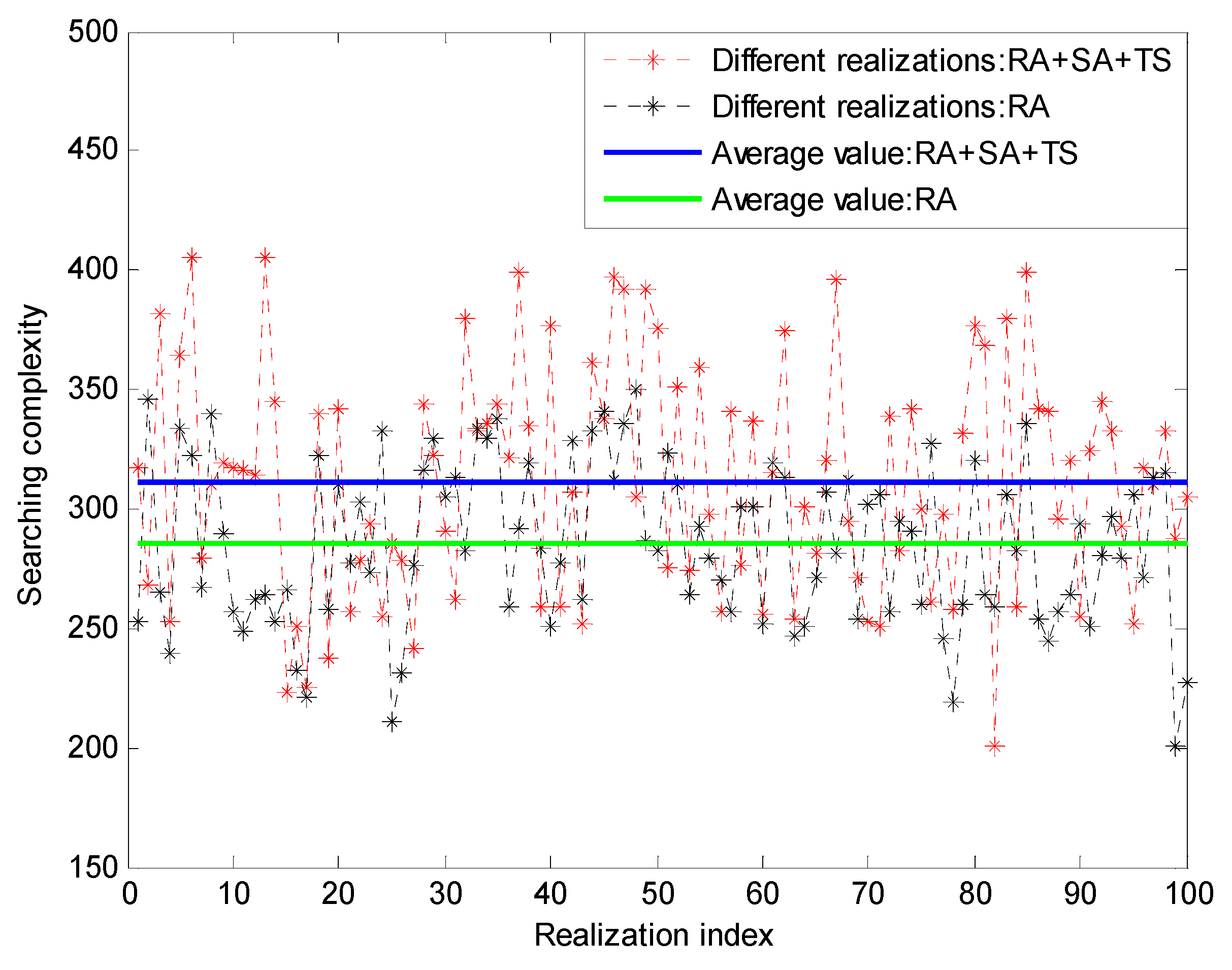
6. Experimental and Result Evaluations
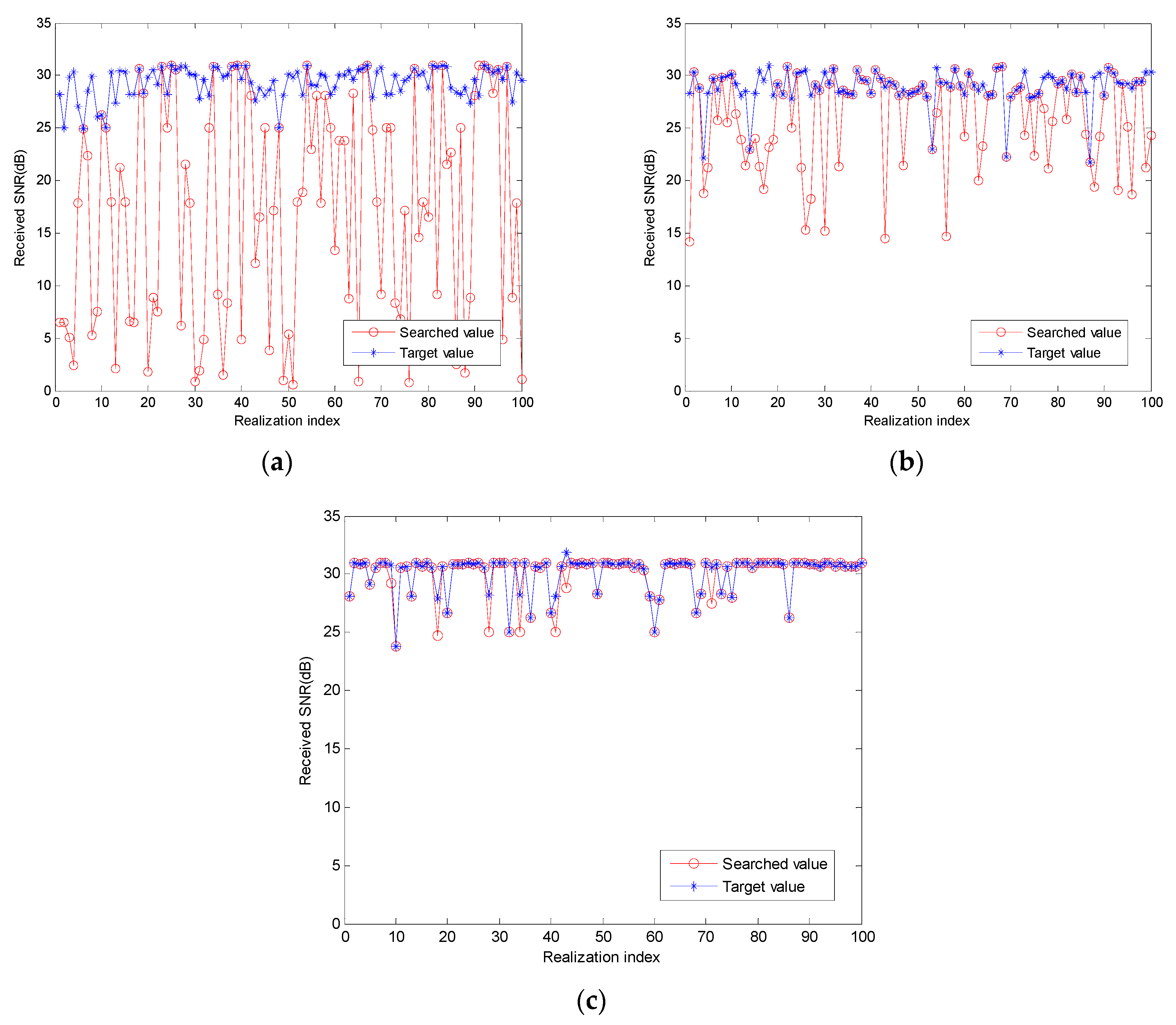
6.1. Beam Training Performance Evaluation
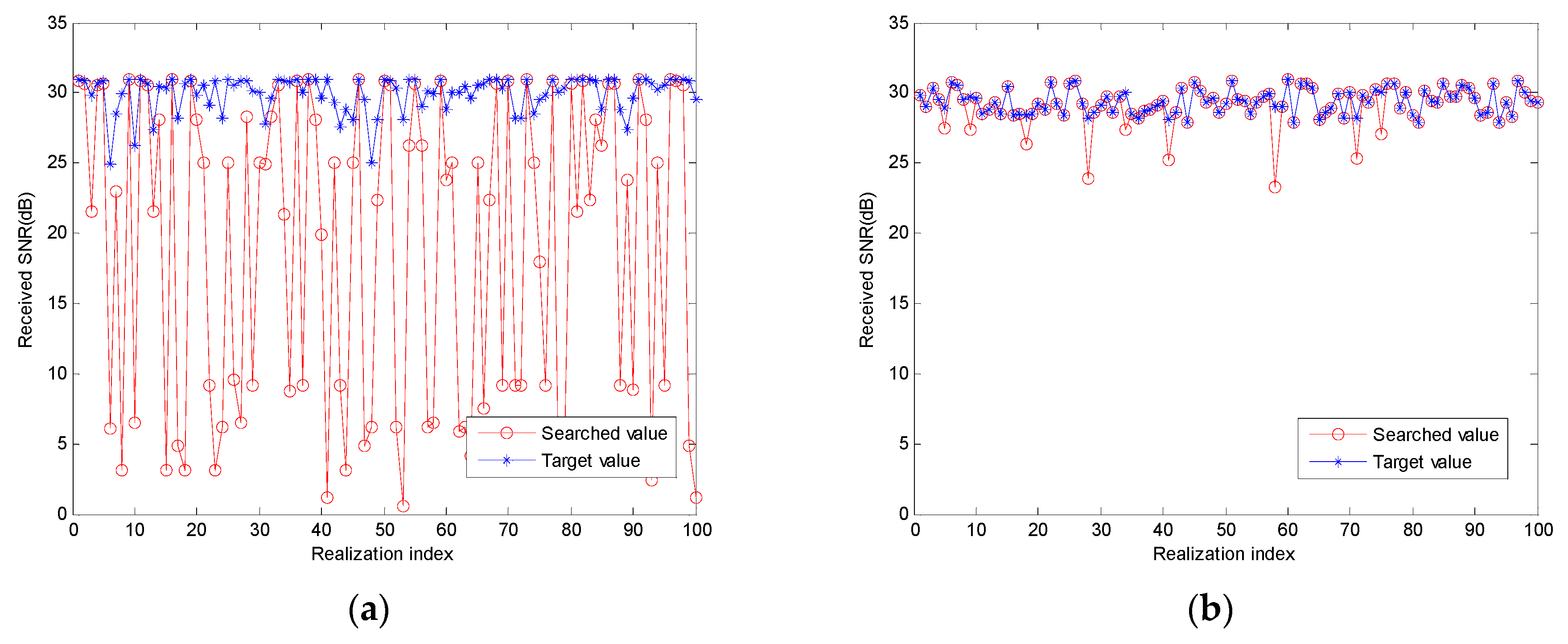
6.2. Boundary Processing
6.3. Neighborhood Structure
6.4. Complexity Analysis
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Maruhashi, K.; Kishimoto, S.; Tto, M. Wireless uncompressed-HDTV-signal transmission system utilizing compact 60-GHz-band transmitter and receiver. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, Long Beach, CA, USA, 17 June 2005; p. 4. [Google Scholar]
- Palacios, J.; De Donno, D.; Widmer, J. Tracking mm-Wave channel dynamics: Fast beam training strategies under mobility. In Proceedings of the IEEE INFOCOM 2017—IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Xia, P.; Qin, X.; Niu, H. Short Range Gigabit Wireless Communications Systems: Potentials, Challenges and Techniques. In Proceedings of the 2007 IEEE International Conference on Ultra-Wideband, Singapore, 24–26 September 2007; pp. 123–128. [Google Scholar]
- Li, B.; Zhou, Z. On the Efficient Beam-Forming Training for 60GHz Wireless Personal Area Networks. IEEE Trans. Wirel. Commun. 2013, 12, 504–515. [Google Scholar] [CrossRef]
- Wang, J.; Lan, Z.; Pyo, C.W. Beam Codebook Based Beamforming Protocol for Multi-Gbps Millimeter-Wave WPAN Systems. In Proceedings of the GLOBECOM 2009–2009 IEEE Global Telecommunications Conference, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6. [Google Scholar]
- Yin, H.; Gesbert, D. A Coordinated Approach to Channel Estimation in Large-Scale Multiple-Antenna Systems. IEEE JSAC 2013, 31, 264–273. [Google Scholar] [CrossRef]
- Rasekh, M.E.; Marzi, Z.; Zhu, Y. Noncoherent mmWave Path Tracking. In Proceedings of the ACM Press the 18th International Workshop, Sonoma, CA, USA, 21–22 February 2017; pp. 13–18. [Google Scholar]
- Chryssomallis, M. Smart antennas. IEEE Antennas. Propagat. Mag. 2000, 42, 129–136. [Google Scholar] [CrossRef]
- Okoth, P.J.; Nguyen, Q.N.; Dhakal, D.R. An Efficient Codebook-Based Beam Training Technique for Millimeter-Wave Communication Systems. In Proceedings of the 2018 Asia-Pacific Microwave Conference (APMC), Kyoto, Japan, 6–9 November 2018; pp. 666–668. [Google Scholar]
- Yuan, W.; Armour, S.M.D.; Doufexi, A. An efficient beam training technique for mmWave communication under NLoS channel conditions. In Proceedings of the 2016 IEEE Wireless Communications and Networking Conference, Doha, Qatar, 3–6 April 2016; pp. 1–6. [Google Scholar]
- Li, B.; Zhou, Z. Efficient Beamforming Training for 60-GHz Millimeter-Wave Communications: A Novel Numerical Optimization Framework. IEEE Trans. Veh. Technol. 2014, 63, 703–717. [Google Scholar] [CrossRef]
- Lim, W.L.; Alias, M.A.S.; Haron, H. A hybrid metaheuristic for the generalized quadratic assignment problem. In Proceedings of the 2015 IEEE Student Conference on Research and Development (SCOReD), Kuala Lumpur, Malaysia, 13–14 December 2015; pp. 467–471. [Google Scholar]
- Srinidhi, N.; Datta, T. Layered Tabu Search Algorithm for Large-MIMO Detection and a Lower Bound on ML Performance. IEEE Trans. Commun. 2011, 59, 2955–2963. [Google Scholar] [CrossRef]
- Jeong, J.; Jung, I.; Kim, J. A New GFDM Receiver with Tabu Search. In Proceedings of the 2019 IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 28 April–1 May 2019; pp. 1–5. [Google Scholar]
- Wang, J.; Lan, Z.; Sum, C.S. Beamforming Codebook Design and Performance Evaluation for 60GHz Wideband WPANs. In Proceedings of the 2009 IEEE 70th Vehicular Technology Conference Fall, Anchorage, AK, USA, 20–23 September 2009; pp. 1–6. [Google Scholar]
- Kojima, C.; Fujio, S.; Nishikawa, K. Novel two-step beam search method for multi user millimeter-wave communication. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017; pp. 1–6. [Google Scholar]
- Sawada, H.; Fujita, K.; Kato, S. Impulse response model for the cubicle environments at 60GHz. In Proceedings of the 2010 Asia-Pacific Microwave Conference, Yokohama, Japan, 7–10 December 2010; pp. 2131–2134. [Google Scholar]
- Sato, K.; Sawada, H.; Shoji, Y. Channel Model for Millimeter Wave WPAN. In Proceedings of the 2007 IEEE 18th International Symposium on Personal, Indoor and Mobile Radio Communications, Athens, Greece, 3–7 September 2007; pp. 1–5. [Google Scholar]
- Yoon, S.; Jeon, T. Hybrid beam-forming and beam-switching for OFDM based wireless personal area networks. IEEE J. Sel. Areas Commun. 2009, 27, 1425–1432. [Google Scholar] [CrossRef]
- Kim, T.; Chang, J.M. QoS-Aware Energy-Efficient Association and Resource Scheduling for HetNets. IEEE Trans. Veh. Technol. 2018, 67, 650–664. [Google Scholar] [CrossRef]
- Kutty, S.; Sen, D. An improved numerical optimization method for efficient beam search in 60 GHz indoor millimeter wave wireless networks. In Proceedings of the 2015 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS), Kolkata, India, 15–18 December 2015; pp. 1–6. [Google Scholar]
- Bang-Jensen, J.; Gutin, G. When the greedy algorithm fails. Discrete. Optim. 2004, 1, 121–127. [Google Scholar] [CrossRef]
- Zhong, Y.; Wu, C.; Li, L. The Study of Neighborhood Structure of Tabu Search Algorithm for Traveling Salesman Problem. In Proceedings of the 2008 Fourth International Conference on Natural Computation, Jinan, China, 18–20 October 2008; pp. 491–495. [Google Scholar]
- Gao, X.; Dai, L. Turbo-Like Beamforming Based on Tabu Search Algorithm for Millimeter-Wave Massive MIMO Systems. IEEE Trans. Veh. Technol. 2016, 65, 5731–5737. [Google Scholar] [CrossRef]
- Amuthan, A.; Thilak, K.D. Survey on Tabu Search meta-heuristic optimization. In Proceedings of the 2016 International Conference on Signal Processing, Communication, Power and Embedded System (SCOPES), Paralakhemundi, India, 3–5 October 2016; pp. 1539–1543. [Google Scholar]
- Maltsev, A.; Maslennikov, R.; Sevastyanov, A. Characteristics of indoor millimeter-wave channel at 60 GHz in application to perspective WLAN system. In Proceedings of the Antennas and Propagation (EuCAP), Barcelona, Spain, 16 May 2010. [Google Scholar]

| 1 | … | … | 32 | ||
|---|---|---|---|---|---|
| 1 | … | … | 32 | ||
| 64 | … | … | 33 | ||
| 65 | … | … | 96 | ||
| 128 | … | … | 97 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Sun, C.; Jiang, F. Beam Training for Millimeter-Wave Communication Based on Tabu Table Enhanced Rosenbrock Algorithm. Future Internet 2019, 11, 214. https://doi.org/10.3390/fi11100214
Li X, Sun C, Jiang F. Beam Training for Millimeter-Wave Communication Based on Tabu Table Enhanced Rosenbrock Algorithm. Future Internet. 2019; 11(10):214. https://doi.org/10.3390/fi11100214
Chicago/Turabian StyleLi, Xiaoyu, Changyin Sun, and Fan Jiang. 2019. "Beam Training for Millimeter-Wave Communication Based on Tabu Table Enhanced Rosenbrock Algorithm" Future Internet 11, no. 10: 214. https://doi.org/10.3390/fi11100214
APA StyleLi, X., Sun, C., & Jiang, F. (2019). Beam Training for Millimeter-Wave Communication Based on Tabu Table Enhanced Rosenbrock Algorithm. Future Internet, 11(10), 214. https://doi.org/10.3390/fi11100214




