Time and Power Allocation for Energy Efficiency Maximization in Wireless-Powered Full-Duplex Relay Systems
Abstract
1. Introduction
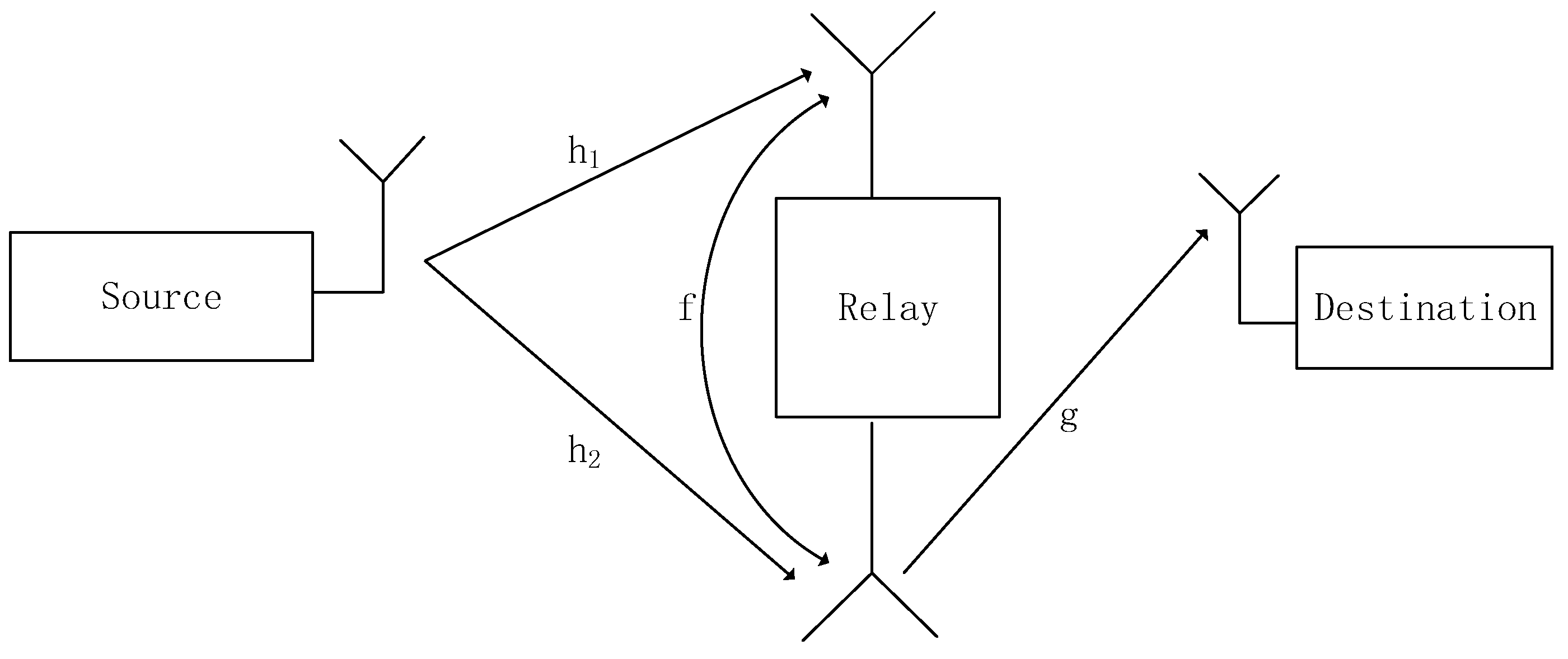
2. System Model and Problem Formulation
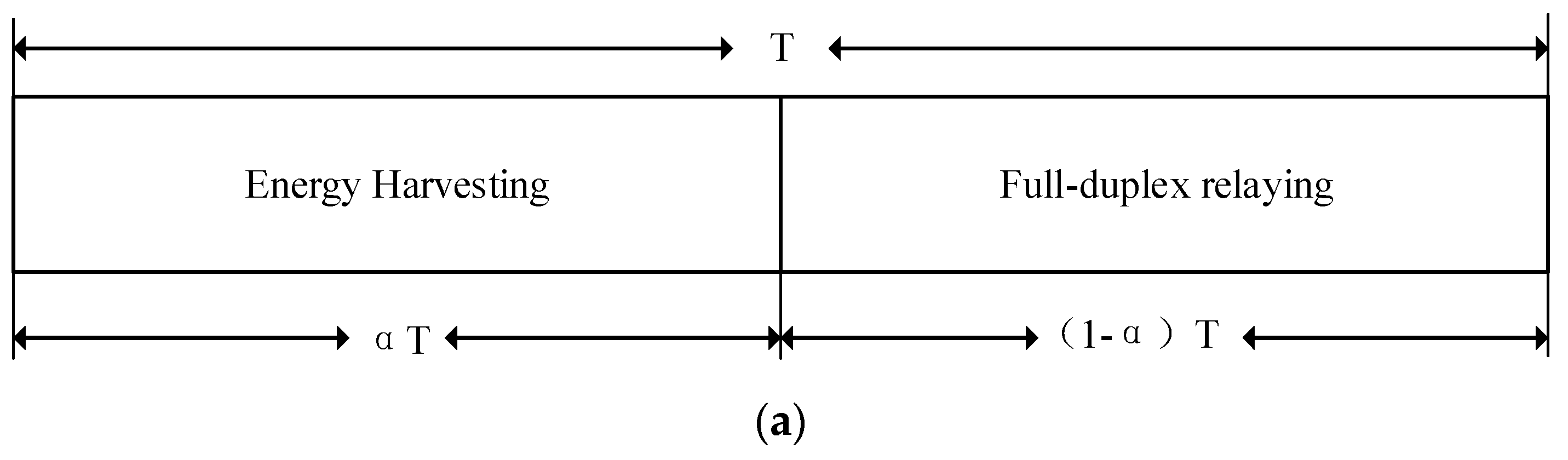
2.1. System Model
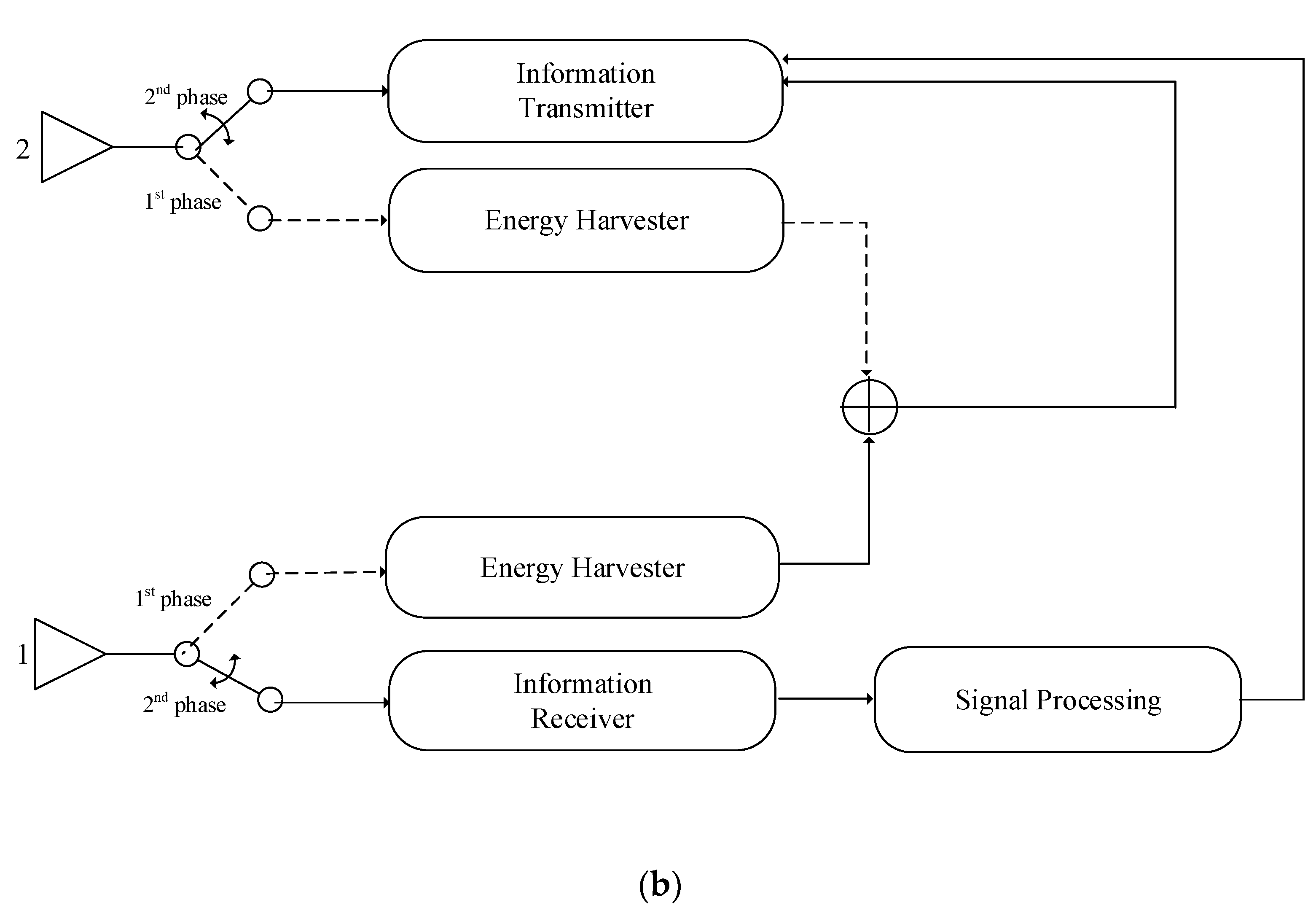
2.2. Full-Duplex Dual-Antenna Energy Harvesting
2.3. Full-Duplex Single-Antenna Energy Harvesting
3. The Full-Duplex Dual Antenna Energy Harvesting
3.1. The Optimal Time Allocation Scheme
3.2. The Optimal Power Allocation Scheme
4. Full-Duplex Single-Antenna Energy Harvesting
4.1. Optimal Time Allocation Scheme
4.2. Optimal Power Allocation Scheme
5. Half-Duplex
5.1. Optimal Time Allocation Scheme
5.2. Optimal Power Allocation Scheme
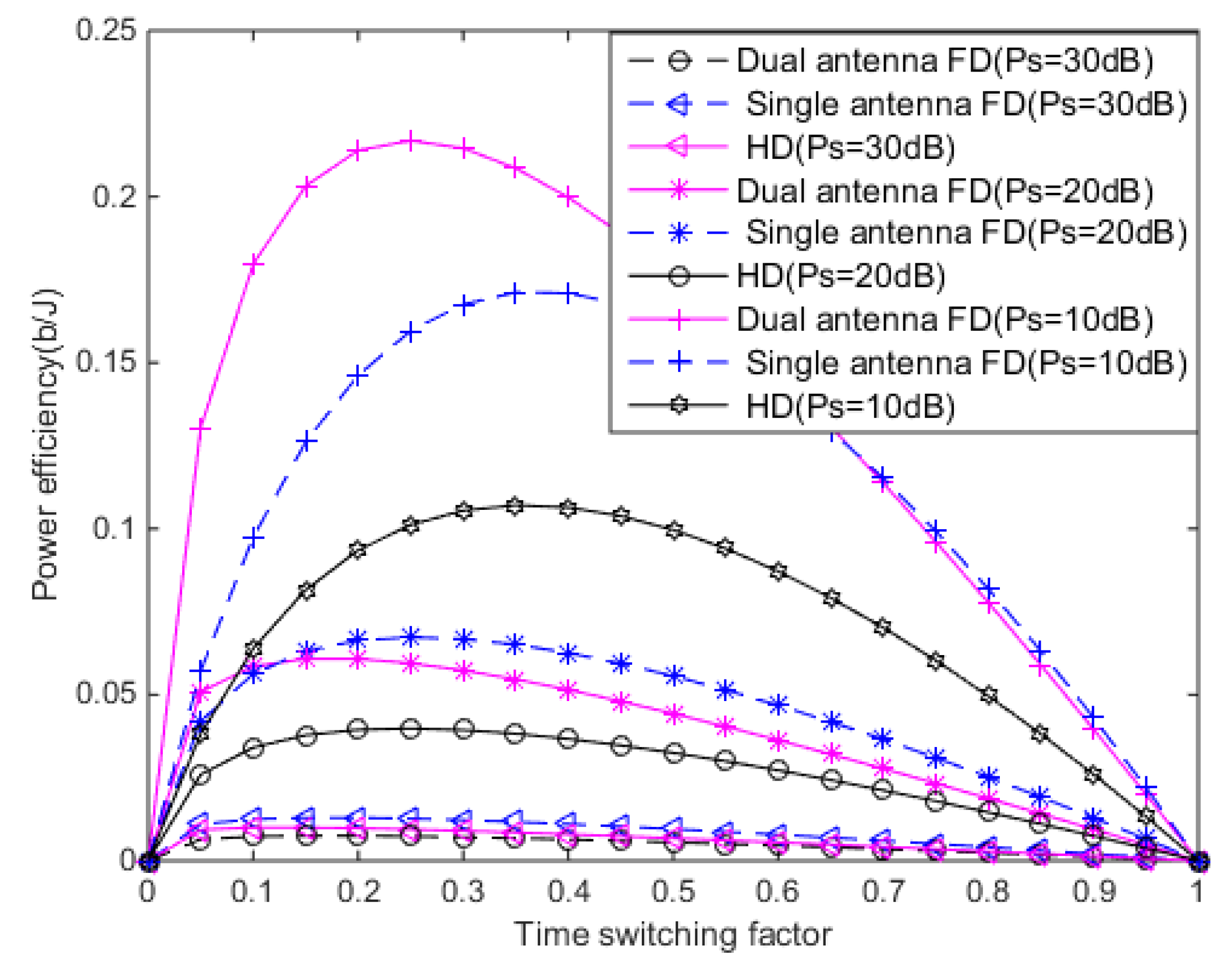
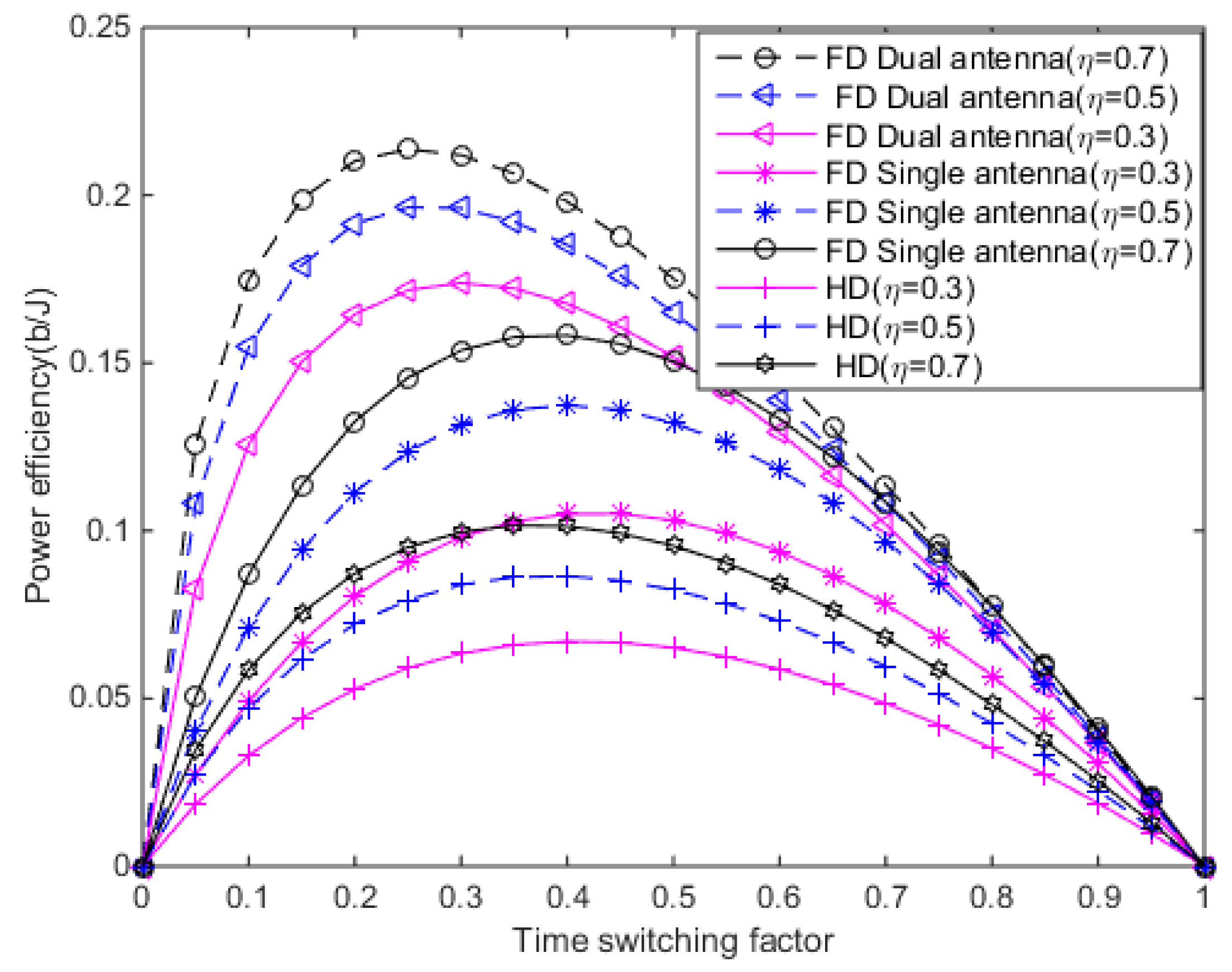
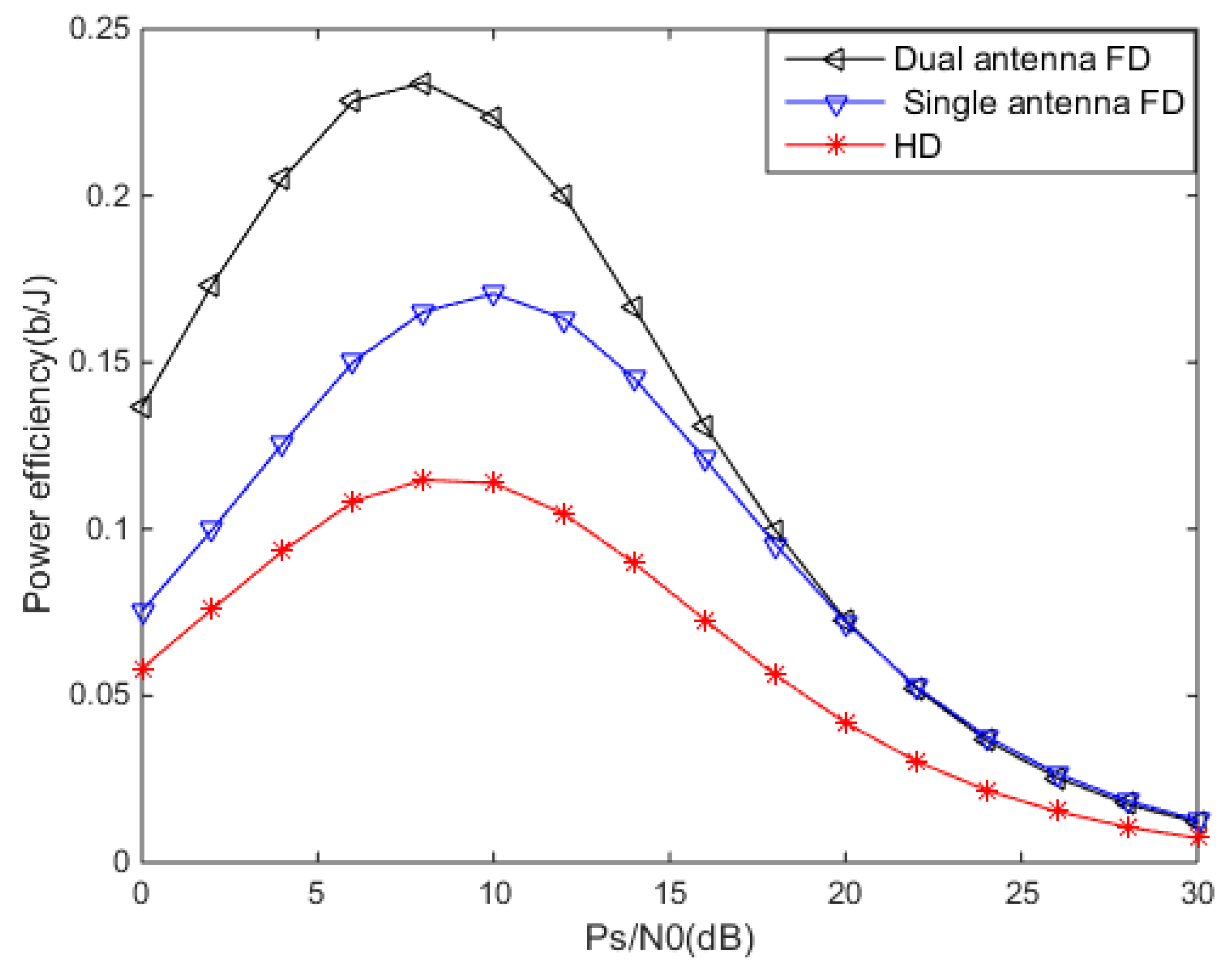
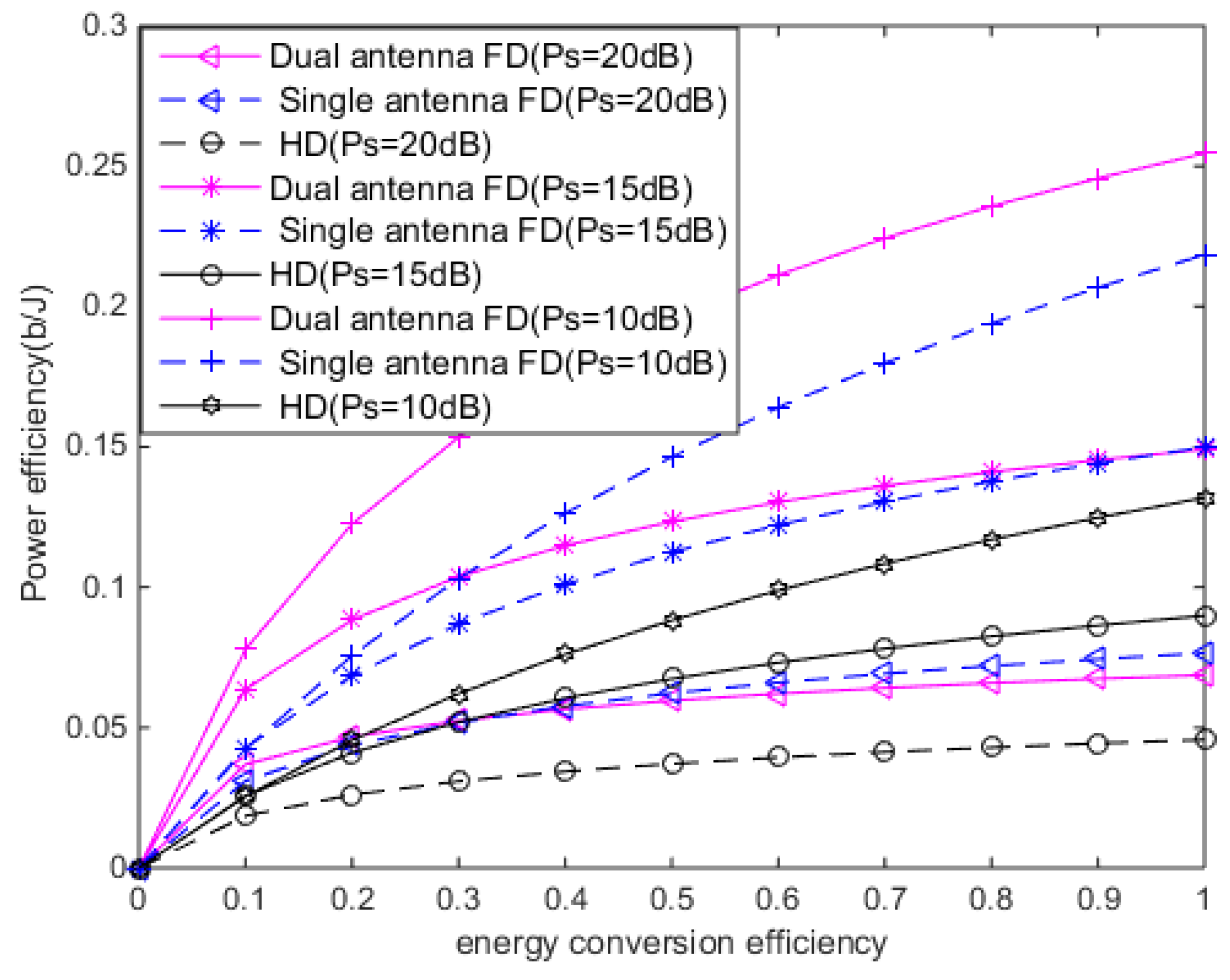
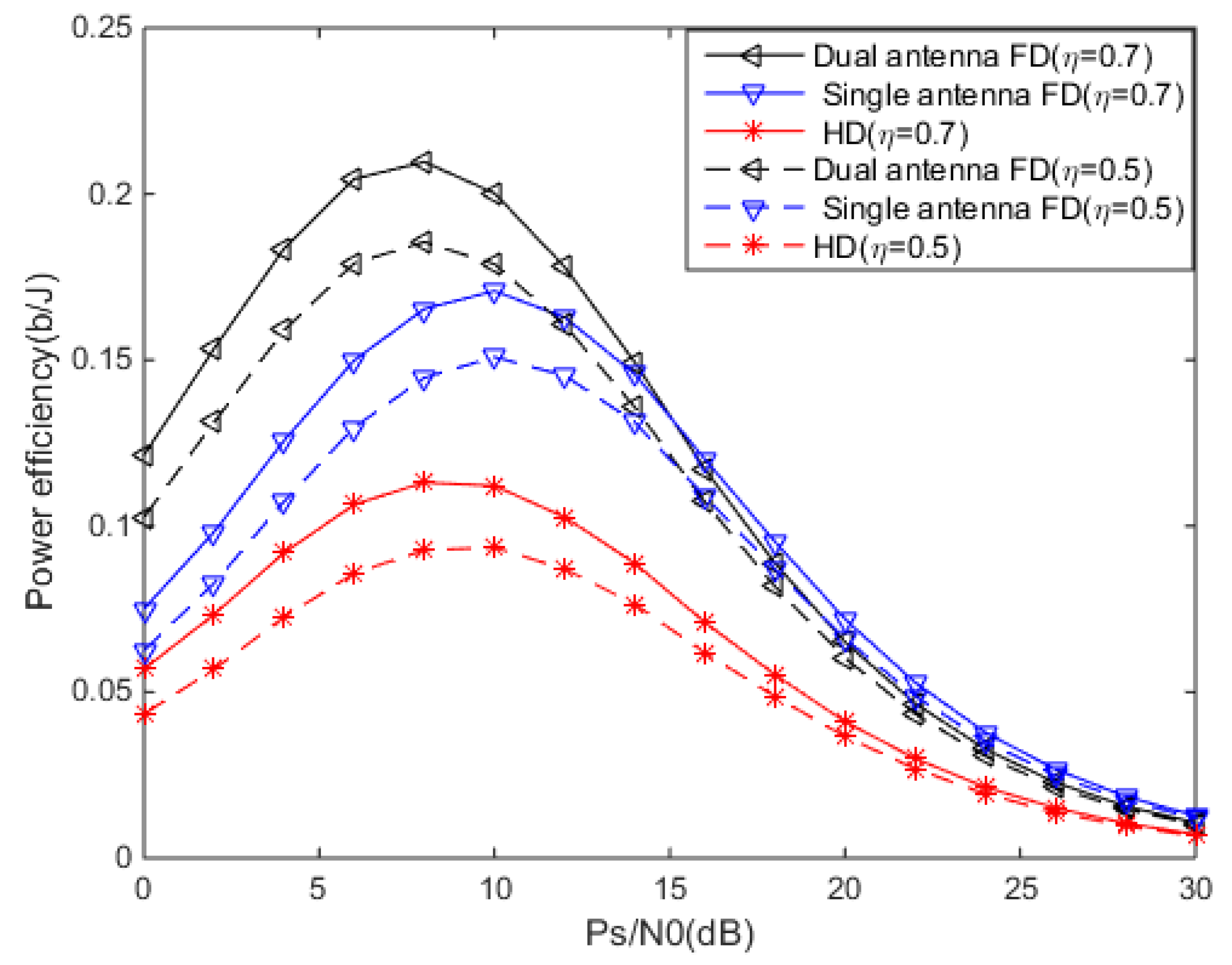
6. Simulation and Analysis
6.1. Simulation Parameters
6.2. Simulation Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Medepally, B.; Mehta, N.B. Voluntary Energy Harvesting Relays and Selection in Cooperative Wireless Networks. IEEE Trans. Wirel. Commun. 2010, 9, 3543–3553. [Google Scholar] [CrossRef]
- Venkata, P.T.; Nambi, S.A.U.; Prasad, R.V.; Niemegeers, I. Bond Graph Modeling for Energy-Harvesting Wireless Sensor Networks. Computer 2012, 45, 31–38. [Google Scholar] [CrossRef]
- Varshney, L. Transporting information and energy simultaneously. In Proceedings of the 2008 IEEE International Symposium on Information Theory, Toronto, ON, Canada, 6–11 July 2008; pp. 1612–1616. [Google Scholar]
- Grover, P.; Sahai, A. Shannon meets Tesla: Wireless information and power transfer. In Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA, 13–18 June 2010; Volume 19, pp. 2363–2367. [Google Scholar]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Wireless-powered relays in cooperative communications: Time-switching relaying protocols and throughput analysis. IEEE Trans. Commun. 2015, 63, 1607–1622. [Google Scholar] [CrossRef]
- Dong, Y.; Hossain, M.J.; Cheng, J. Joint Power Control and Time Switching for SWIPT Systems with Heterogeneous QoS Requirements. IEEE Commun. Lett. 2016, 20, 328–331. [Google Scholar] [CrossRef]
- Zhai, C.; Liu, J. Cooperative wireless energy harvesting and information transfer in stochastic networks. EURASIP J. Wirel. Commun. Netw. 2015, 2015, 44. [Google Scholar] [CrossRef][Green Version]
- Liu, L.; Zhang, R.; Chua, K.C. Wireless information and power transfer in an underlay cognitive radio network. In Proceedings of the International Conference on Signal Processing and Communication Systems (ICSPCS), Gold Coast, Australia, 16–18 December 2013; Volume 12, pp. 288–300. [Google Scholar]
- Liu, L.; Zhang, R.; Chua, K.C. Wireless Information and Power Transfer: A Dynamic Power Splitting Approach. IEEE Trans. Commun. 2013, 61, 3390–4001. [Google Scholar] [CrossRef]
- Zhong, C.J.; Himal, A.S.; Zheng, G. Improving the Throughput of Wireless Powered Dual-hop Systems with Full Duplex Relaying. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; Volume 10, pp. 4253–4258. [Google Scholar]
- Liu, Y. Wireless Information and Power Transfer for Multirelay-Assisted Cooperative Communication. IEEE Commun. Lett. 2016, 20, 784–787. [Google Scholar] [CrossRef]
- Ju, H.; Zhang, R. Throughput Maximization in Wireless Powered Communication Networks. IEEE Trans. Wirel. Commun. 2014, 13, 418–428. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Y. Wireless Power Transfer Strategies for Cooperative Relay System to Maximize Information Throughput. IEEE Access 2017, 5, 2573–2582. [Google Scholar] [CrossRef]
- Yang, Z.; Ding, Z.; Fan, P.; Karagiannidis, G.K. Outage Performance of Cognitive Relay Networks with Wireless Information and Power Transfer. IEEE Trans. Veh. Tech. 2016, 65, 3828–3833. [Google Scholar] [CrossRef]
- Ng, D.W.K.; Lo, E.S.; Schober, R. Wireless Information and Power Transfer: Energy Efficiency Optimization in OFDMA Systems. IEEE Trans. Wirel. Commun. 2013, 12, 6352–6370. [Google Scholar] [CrossRef]
- Abrol, A.; Jha, R.K. Power Optimization in 5G Networks: A Step Towards Green Communication. IEEE Access 2016, 4, 1355–1374. [Google Scholar] [CrossRef]
- Gu, Y.; Aissa, S. RF-Based Energy Harvesting in Decode-and Forward Relay Systems: Ergodic and Outage Capacities. IEEE Trans. Wirel. Commun. 2015, 14, 6425–6434. [Google Scholar] [CrossRef]
- Riihonen, T.; Werner, S.; Wichman, R. Mitigation of Loopback Self-Interference in Full-Duplex MIMO Relays. IEEE Trans. Signal Process. 2011, 59, 5983–5993. [Google Scholar] [CrossRef]
- Riihonen, T.; Werner, S.; Wichman, R. Hybrid Full-Duplex/Half-Duplex Relaying with Transmit Power Adaptation. IEEE Trans. Wirel. Commun. 2011, 10, 3074–3085. [Google Scholar] [CrossRef]
- Day, B.P.; Margetts, A.R.; Bliss, W.D.; Schniter, P. Full-Duplex MIMO Relaying: Achievable Rates Under Limited Dynamic Range. IEEE J. Sel. Areas Commun. 2012, 30, 1541–1553. [Google Scholar] [CrossRef]
- Sabharwal, A.; Schniter, P.; Guo, D.; Bliss, D.; Rangarajan, S.; Wichman, R. In-Band Full-Duplex Wireless: Challenges and Opportunities. IEEE J. Sel. Areas Commun. 2014, 32, 1637–1652. [Google Scholar] [CrossRef]
- Krikidis, I.; Suraweera, H.A.; Smith, P.J.; Yuen, C. Full-Duplex Relay Selection for Amplify-and-Forward Cooperative Networks. IEEE Trans. Wirel. Commun. 2012, 11, 4381–4393. [Google Scholar] [CrossRef]
- Mohammadi, M.; Chalise, B.K.; Suraweera, H.A.; Zhong, C.; Zheng, G.; Krikidis, I. Throughput Analysis and Optimization of Wireless-Powered Multiple Antenna Full-Duplex Relay Systems. IEEE Trans. Commun. 2016, 64, 1769–1785. [Google Scholar] [CrossRef]
- Zhang, C.; Suraweera, H.A.; Zheng, G.; Krikidis; Zhang, Z. Wireless Information and Power Transfer With Full-Duplex Relaying. IEEE Trans. Commun. 2014, 62, 3447–3461. [Google Scholar] [CrossRef]
- Lee, C.-H.; Chang, R.Y.; Lin, C.-T.; Cheng, S.-M. Sum-rate maximization for energy harvesting-aided D2D communications underlaid cellular networks. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017. [Google Scholar]
- Zhao, L.; Wang, X.; Riihonen, T. Transmission Rate Optimization of Full-Duplex Relay Systems Powered by Wireless Energy Transfer. IEEE Trans. Wirel. Commun. 2017, 16, 6348–6450. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless information and power transfer: Architecture design and rate-energy tradeoff. IEEE Commun. Lett. 2013, 61, 4754–4767. [Google Scholar] [CrossRef]
- Mou, W.; Cai, Y.; Yang, W.; Yang, W.; Xu, X.; Hu, J. Exploiting full Duplex techniques for secure communication in SWIPT system. In Proceedings of the International Conference on Wireless Communications & Signal Processing (WCSP), Nanjing, China, 15–17 October 2015; pp. 1–6. [Google Scholar]
- Chen, H.; Li, Y.; Rebelatto, J.L.; Uchoa-Filho, B.F.; Vucetic, B. Harvest-Then-Cooperate: Wireless-Powered Cooperative Communications. IEEE Trans. Signal Process. 2015, 63, 1700–1711. [Google Scholar] [CrossRef]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Relaying protocols for wireless energy harvesting and information processing. IEEE Commun. Lett. 2013, 12, 3622–3636. [Google Scholar] [CrossRef]
- Bharadia, D.; McMilin, E.; Katti, S. Full duplex radios. In Proceedings of the 2013 ACM SIGCOMM, Hong Kong, China, 12–16 August 2013; pp. 375–386. [Google Scholar]
- Chen, G.; Gong, Y.; Xiao, P.; Chambers, J.A. Physical layer network security in the full-duplex relay system. IEEE Access 2015, 10, 574–583. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Energy conversion efficiency | 0.75 |
| Noise at three nodes | 1 |
| Circuit power consumption | 6 dB |
| Power amplifier efficiency | 1 |
| Coefficient of self-interference between antennas | −80 dB |
| Source nodes transmit power | 0–30 dB |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Ni, Y.; Han, X.; Qin, L.; Dong, L. Time and Power Allocation for Energy Efficiency Maximization in Wireless-Powered Full-Duplex Relay Systems. Future Internet 2019, 11, 205. https://doi.org/10.3390/fi11100205
Song X, Ni Y, Han X, Qin L, Dong L. Time and Power Allocation for Energy Efficiency Maximization in Wireless-Powered Full-Duplex Relay Systems. Future Internet. 2019; 11(10):205. https://doi.org/10.3390/fi11100205
Chicago/Turabian StyleSong, Xin, Yue Ni, Xiuwei Han, Lei Qin, and Li Dong. 2019. "Time and Power Allocation for Energy Efficiency Maximization in Wireless-Powered Full-Duplex Relay Systems" Future Internet 11, no. 10: 205. https://doi.org/10.3390/fi11100205
APA StyleSong, X., Ni, Y., Han, X., Qin, L., & Dong, L. (2019). Time and Power Allocation for Energy Efficiency Maximization in Wireless-Powered Full-Duplex Relay Systems. Future Internet, 11(10), 205. https://doi.org/10.3390/fi11100205





