1. Introduction
Convolutional Neural Networks (CNNs) represent a class of machine learning algorithms that are able to extrapolate complex data representations from unstructured data, e.g., images, text, and audio. Starting from the astounding results obtained by Krizhevsky et al. [
1] during the 2012 ImageNet competition, CNN models have been improved substantially, achieving classification accuracies that go beyond those of a human being. Today’s CNNs are considered the state-of-the-art in several application domains, such as medical diagnosis [
2,
3,
4], personal home assistants [
5], surveillance systems [
6], and self-driving vehicles [
7]. The most important factor behind the rise of CNNs, and deep learning in general, is the availability of efficient computing platforms able to speed-up the training stages, e.g., GPUs. Nonetheless, the adoption of CNNs in pervasive applications, such as those of the Internet-of-Things, is still far from being achieved. The reason is simple: the requirements of storage capacity and computational resources do not fit into low-power embedded architectures. To better grasp these concepts, let us consider the internal structure of a CNN.
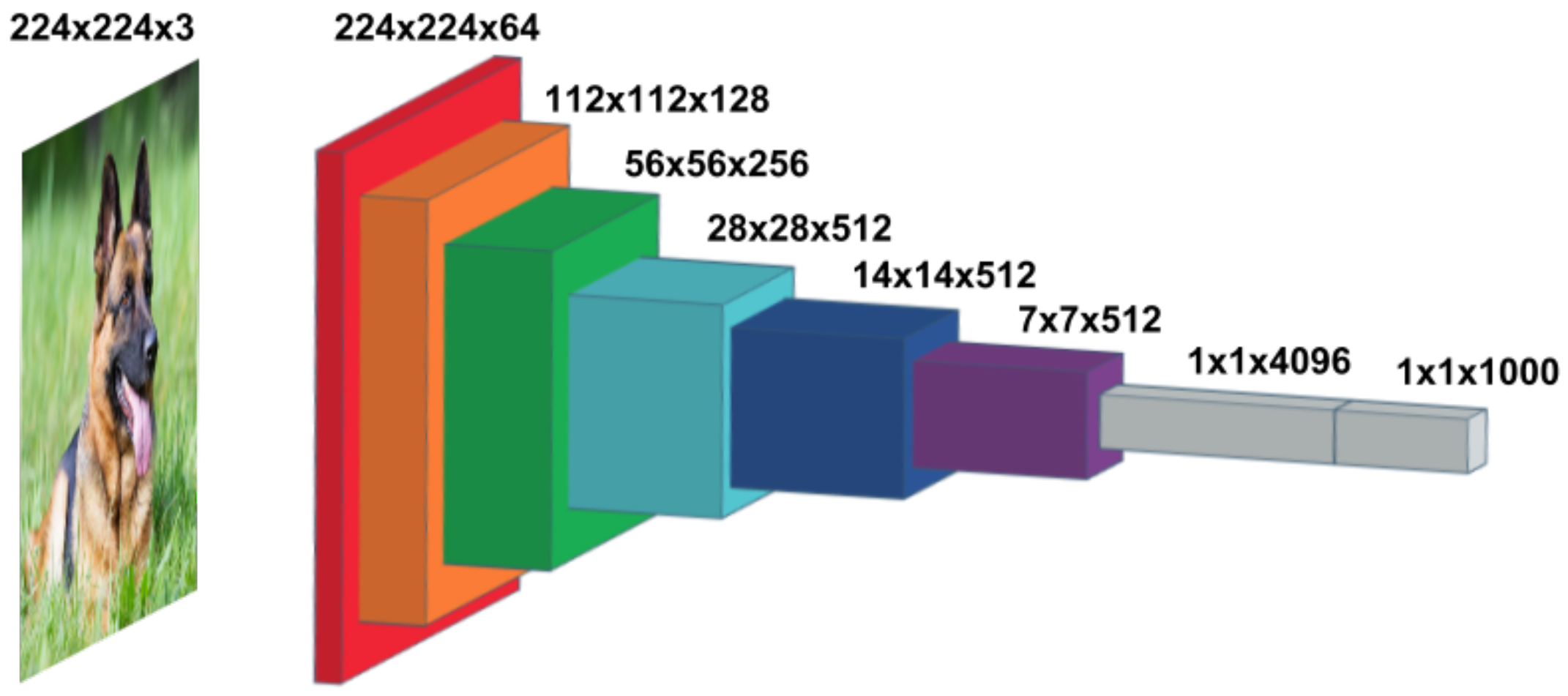
Figure 1 depicts the feature maps of the well-known VGG-16 model. It consists of several layers, each with a proper function: (
i) the
input layer (red box), which produces a first transformation of the input image to be fed to the next convolutional layers; (
) the
output layers (gray boxes), which are perceptron-based artificial neural networks in charge of producing the final answer on the classification task; and (
) the
hidden layers, where the features extraction takes place.
Figure 1 also shows the dimension of each layer; by summing up the contributions of all the layers, it results that even a small CNN model like the VGG-16 requires 138 MB of memory storage, and that is for weights alone. One should consider the feed-forward phase of a CNN asks for additional memory to store the partial results produced by each layer. It is therefore clear that CNNs have to be squeezed in order to fit into architectures with few MB of memory available.
Several strategies have been proposed to shrink pre-trained CNN models. Knowledge distillation [
8,
9] and low rank approximation [
10,
11] are representative examples of
non-destructive techniques. The original model serves as a reference point to generate a child model with a smaller structure and unchanged accuracy, or to generate linear-separable kernels that can be represented with a concise mathematical representation. By contrast,
destructive methods do apply a direct modification of the original CNN structure. Under this category, weights pruning [
12,
13,
14] and weights quantization [
15,
16] are the most widely studied techniques. Inspired by the mechanisms that control and modify neural synapses in the human brain, the pruning approach is based on the idea of removing unimportant neural connections by setting their weights to zero. Quantization, instead, is used to reduce the number of bits per weight, hence the memory footprint, and thus the precision of each weight representation. Extreme quantization techniques include the possibility to quantize weights to binary [
17,
18] or ternary [
19,
20] numbers, and thus to further reduce the complexity of multiply-and-accumulate operations (replaced with simple shift operations). However, binary and ternary networks are proved to lead to huge accuracy degradations when evaluated on large datasets [
21]. This is because most solutions apply a blind quantization, without taking into account how weights evolve during the training stages. In order to fill this gap, Ref. [
22] introduced an efficient
compressive training algorithm that accounts for weights represented in the constrained space (
). Differently from other state-of-the-art strategies, the compressive training searches for optimal
’s such that accuracy degradation is minimized. However, since the accuracy loss is unconstrained, some CNN may experience large accuracy degradation.
This work improves over the original algorithm of [
22] introducing a knob to control accuracy. The rationale is to apply the
-constrained compression only on a specific sub-set of layers. An optimal layer selection is implemented through a dedicated heuristic that quantifies the
significance of each layer, i.e., how the layer affects the classification performance. The resulting CNN is a hybrid model where less significant layers (those that contribute less to the inference process) are reduced with the compressive algorithm proposed in [
22], whereas the most significant layers remain untouched. Experimental results demonstrate that such solution is very effective and it outperforms previous techniques achieving a better compression-accuracy trade-off.
3. Compressive Training
The compressive training technique is a modified version of the SGD algorithm illustrated in
Section 2.1. The entire procedure is based on three sequential stages. Firstly, the CNN model undergoes a
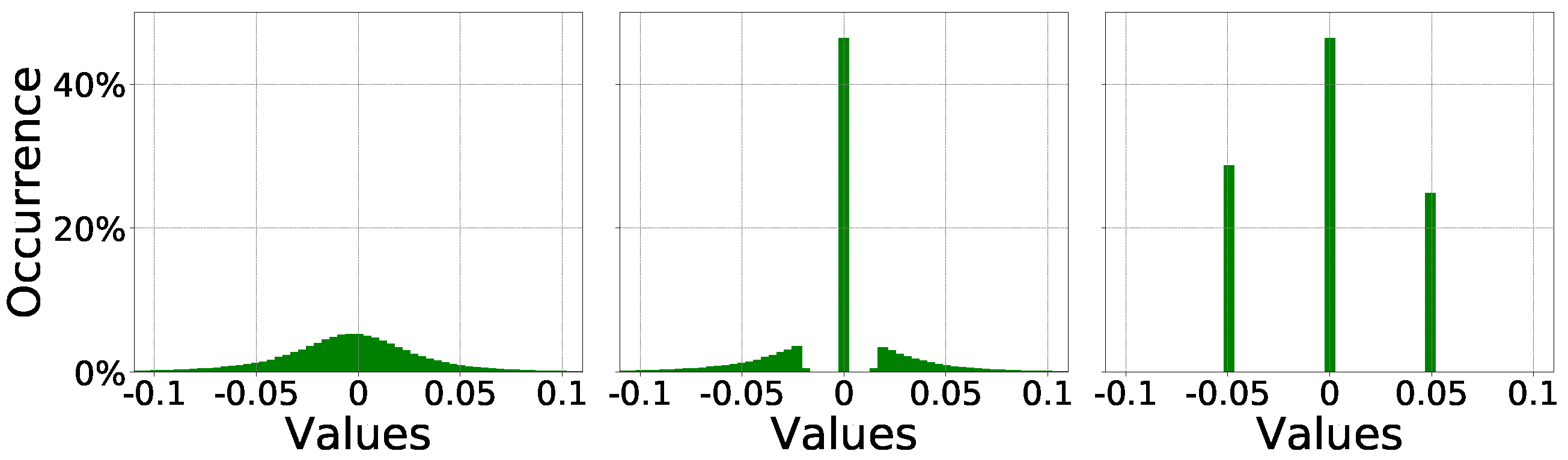
preliminary training. This is accomplished through a standard training procedure during which the weights are updated using the standard SGD algorithm. Once trained, the weights show a typical bell distribution as shown in the leftmost plot of
Figure 2. Secondly, an amplitude-based
weights pruning, as described in
Section 2.2, is applied. This stage is performed iteratively in order to gradually achieve the desired amount of sparsity, i.e., the percentage of zero-weights. Every pruning iteration is followed by a short retraining phase thus to adjust the remaining connections. The central plot in
Figure 2 illustrates a pruned weights distribution where almost half of the original weights are collapsed to zero. Thirdly, the
σ-constrained compression algorithm is applied; during this phase, weights are bounded layer-wise into the (
, 0,
) subspace; the weights distribution will then resemble the one depicted in the rightmost plot in
Figure 2. It is worth noticing that each layer may have its own optimal
.
-Constrained Stochastic Gradient Descent
During the initial stage, each layer
l is assigned to a preliminary
that is the statistical mean of the weights distribution
. The mean is calculated as reported in Equation (
11), where
is the number of weights after pruning,
are the weights, and
is the update resulting from the back-propagation of the error function:
In Equation (
11), positive and negative contributions can be split as shown in Equation (
12):
Following the description provided in
Section 2.1, where
,
is defined as in Equation (
13):
At the
-th iteration, Equation (
12) can be written as
, with
as reported in Equation (
14):
Each is updated with the weighted arithmetic mean of the gradients’ components. Hence, if a generic weight is far from its optimal value, its partial derivative would strongly affect the value of . While using the arithmetic mean for the first step represents a reasonable starting point, fine-tuning in a constrained solution space allows for carrying out an optimum search strategy.
The constrained space can be seen as a semi-bisector described as in Equation (
15), where
is a vector having components in the form
and norm
:
By expressing the non-pruned weights in their vectorized form
, all their possible values, and thus the optimal solution, can be found along the tensor
. However, some components of the direction could theoretically change because
might flip its sign. Therefore, the solution space is the set of all possible semi-bisectors, and the complete definition of
takes the form reported in Equation (
16):
Let us assume an original
matrix pruned until only two positive weights
,
and a single negative weight
are left. The solution space can be represented in three dimensions and becomes a semi-straight line, whose direction is
.
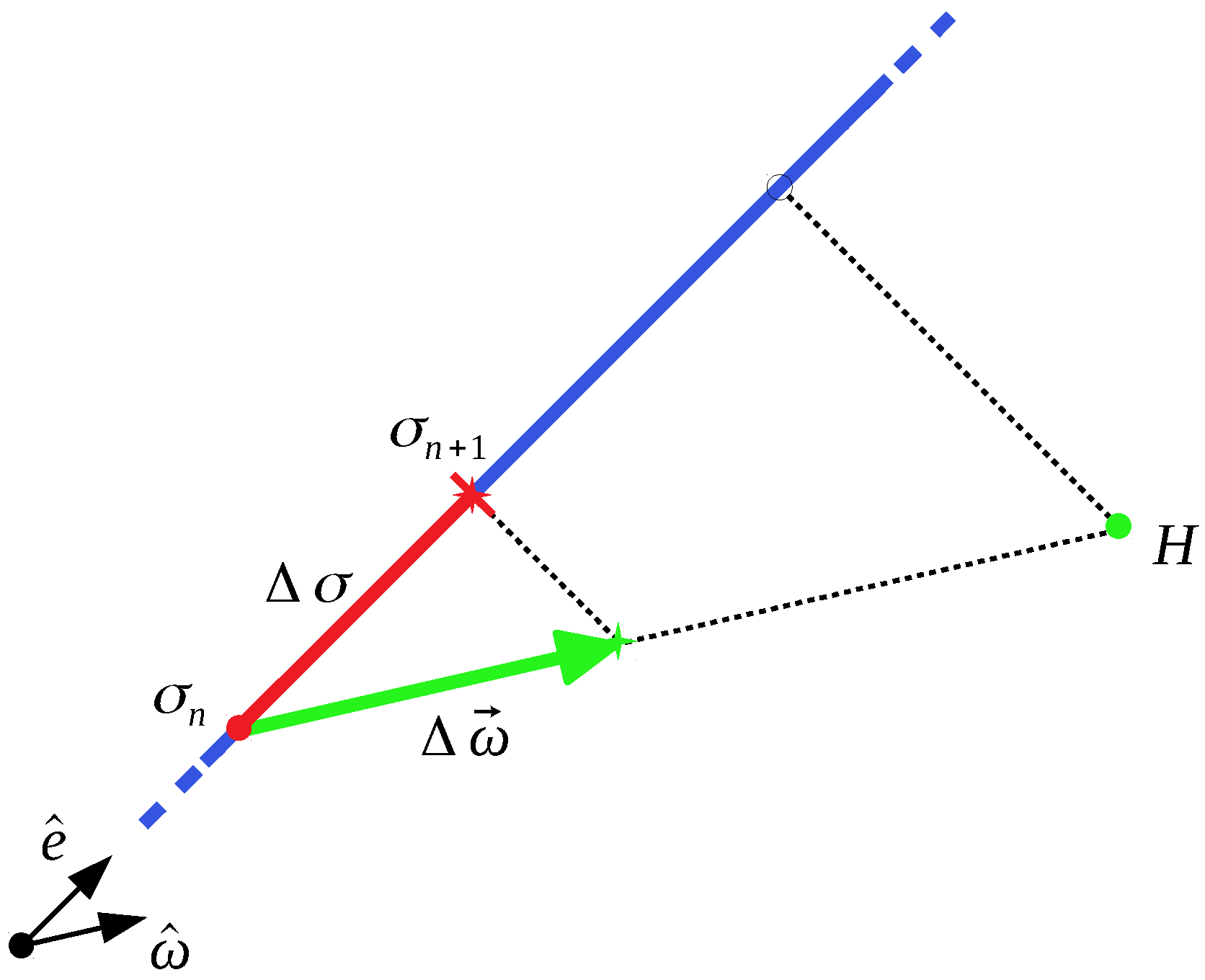
Figure 3 gives a pictorial representation of the solution space. If the actual solution
belongs to the attractive valley of a minimum point
H, then
will point towards it.
However,
can only move along
, i.e.,
. That means it is possible to find the projection of
on
to know which is the optimal
as to approach as close as possible to
H. This is the ultimate sense of this algorithm: lowering or increasing
to approach the minimum point in the best
approximated way. In fact, the scalar product Equation (
17) that projects
on
can be used to update
, obtaining a formulation which is similar to Equation (
14):
The difference between Equations (
14) and (
17) stands in the constant factor
, which works as a slowing factor of the descent in the solution space. Although very effective with several deep learning models, either convolutional or recurrent, the main drawback is the lack of control on the accuracy loss. The next section introduces an accuracy-driven compressive framework which overcomes this limitation.
4. A Greedy Approach for Compressive Training
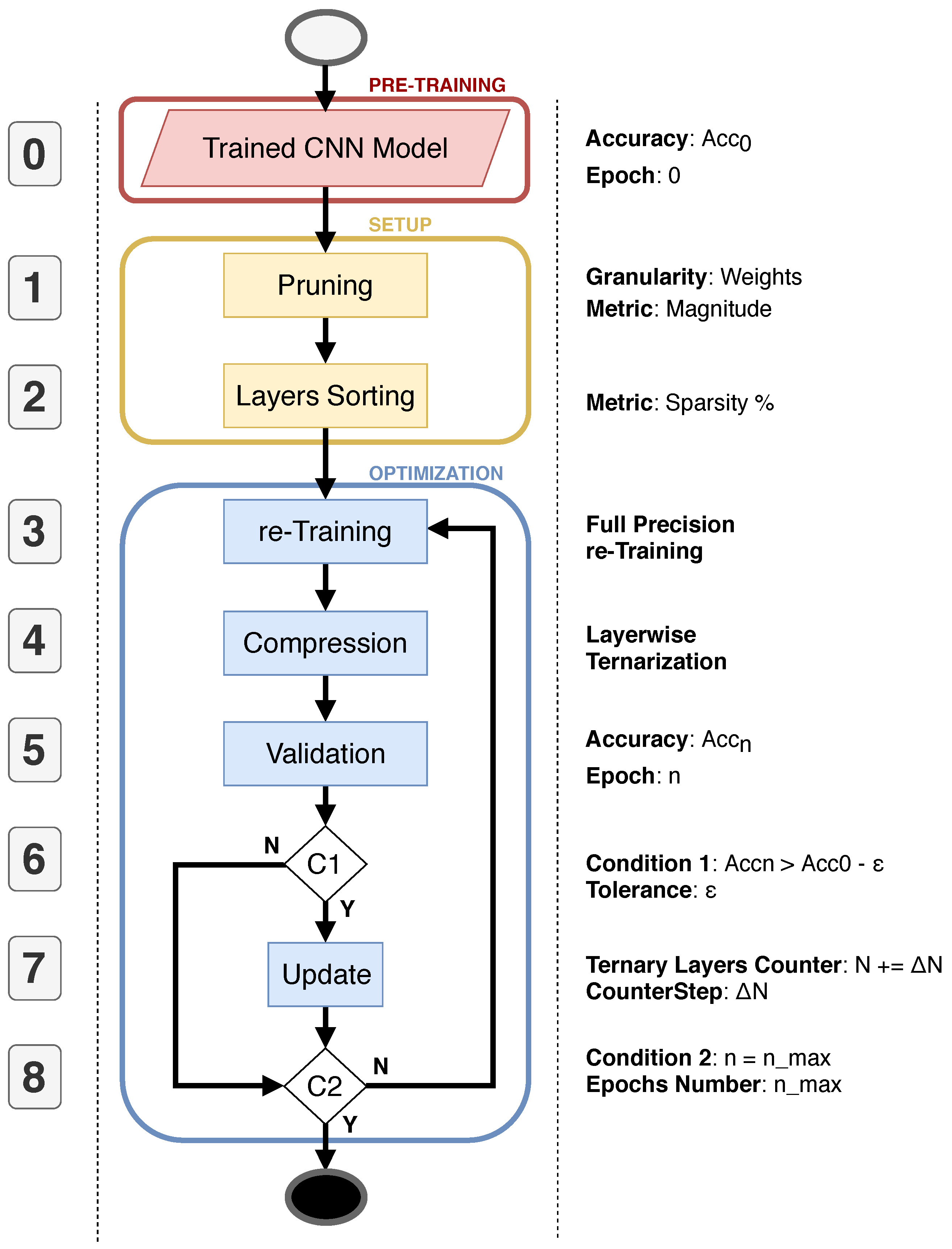
This section gives a step-by-step description of a new greedy strategy where layers are unevenly compressed using the compressive training algorithm. The flow is reported in
Figure 4. At a glance, the algorithm is composed of three main stages denoted with different colors:
pre-training (light red),
setup (yellow), and
optimization (blue). The numbered boxes serve as an index for the detailed description.
4.1. Pre-Training
Step 0—Trained CNN Model. The input of the proposed flow is represented by the trained model of the CNN that needs to be optimized. Our solution is designed to work on classical floating-point CNN models; however, it can be also applied to quantized CNNs. It can work equally on top of pre-trained floating-point CNN models, or on clean models, after a standard training process.
4.2. Setup
Step 1—Pruning. It consists of a standard magnitude-based pruning applied to both convolutional and fully-connected layers. The user specifies an a priori value for the desired percentage of sparsity of the net. Since such a value is unique for the entire CNN, each layer may show a different pruning percentage. This allows representing the CNN model with a non-homogeneous inter-layer sparsity. We decided to follow this direction under the assumption that each layer influences the knowledge of the CNN differently, i.e., each layer provides a specific contribution to the final prediction. For this reason, the layers do not all keep the same amount of information, but the knowledge is spread heterogeneously among the layers, and hence they keep different percentages of redundant parameters.
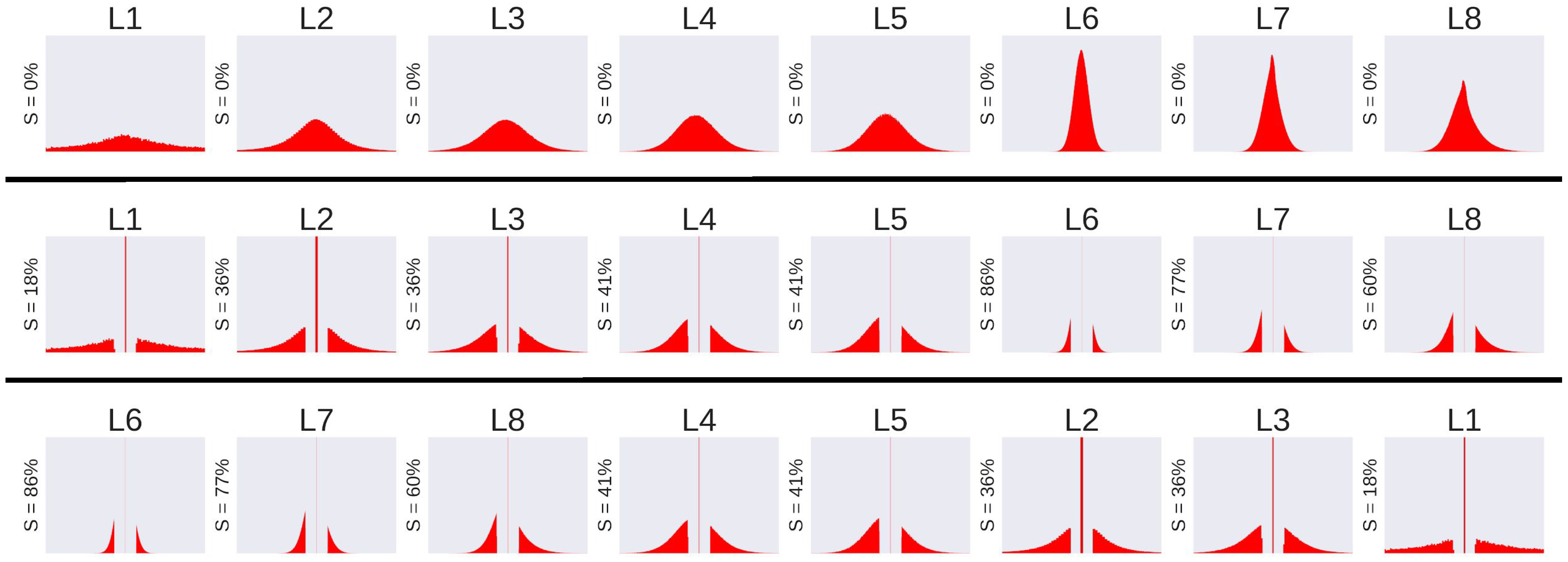
Step 2—Layers Sorting. It is known that some layers are more significant than others. That means the compression of less significant layers will marginally degrade the overall performance classification. The most significant layers, instead, should be preserved in their original form. As a rule of thumb, we selected the intra-layer sparsity as a measure of significance. More in detail, we argue that layers with lower intra-layer sparsity are those that play a major role in the classification process, whereas those with a higher intra-layer sparsity can be sacrificed to achieve a more compact CNN representation. In other words, we base our concept of significance on the number of activated neurons.
A significance-based sorted list of layers is generated at first. All layers are processed as they appear in the original model, and then pruned and sorted based on their weights distribution according to the rule
higher-sparsity first-compressed. A graphical example is reported in
Figure 5, where (
i) the top-most pictures represent the original weight distribution of each layer (numbered L1 to L8) of the AlexNet model trained on the CIFAR10 dataset; (
) the plots in the middle depicts the weight distribution after pruning; and (
) the down-most plots report the layers sorted according to their significance, namely, less important layers are those with a smaller standard deviation, which is directly correlated to their sparsity.
4.3. Optimization
Step 3—re-Training The retraining phase is applied in order to recover the accuracy loss due to pruning. The retraining is applied after pruning at first, and then after each optimization loop.
Step 4—Compression It is the compressive training described in
Section 3. The weights are projected in a sub-dimensional space composed by just three values for each layer, i.e.,
, with
defined layer-wise.
Step 5— Validation The model is validated in order to quantify the accuracy loss due to compression, and thus to decide if it is worth continuing with further compressions. Validation is a paramount step for the greedy approach as it actually enables an accuracy-driven optimization. The accuracy is evaluated and stored after each compression epoch n.
Step 6—Condition 1 (C1) The accuracy recorded during the
n-th epoch (parameter
) is used to determine if the CNN model can be further compressed, as in Equation (
18). The accuracy of the pre-trained model (
) works as baseline, whereas the parameter
represents the user-defined accuracy loss tolerance:
It is worth noticing that the higher the
, the higher the compression of the CNN model. The framework takes a larger execution time for small values of
. This is due to the increased complexity in selecting a good combination of layers that allows matching the user’s constraints. C1 can lead to two possible branches. If Equation (
18) holds true, then the algorithm goes to step 7; otherwise, the quit condition
is evaluated.
Step 7—Update This stage is applied
if Equation (
18) is verified. The counter
N indicates how many layers of the sorted list can be compressed. Each and every time
is evaluated as true, and
N is incremented by
. The latter represents another granularity knob, hence on the speed of the framework;
is mainly defined by the network size: the larger the CNN model, the larger the
.
Step 8—Condition 2 (C2) This last condition is based on the maximum number of epochs , a user-defined hyperparameter. At the n-th iteration, if more than epochs are elapsed, the algorithm stops, else the flow iterates over step 3.
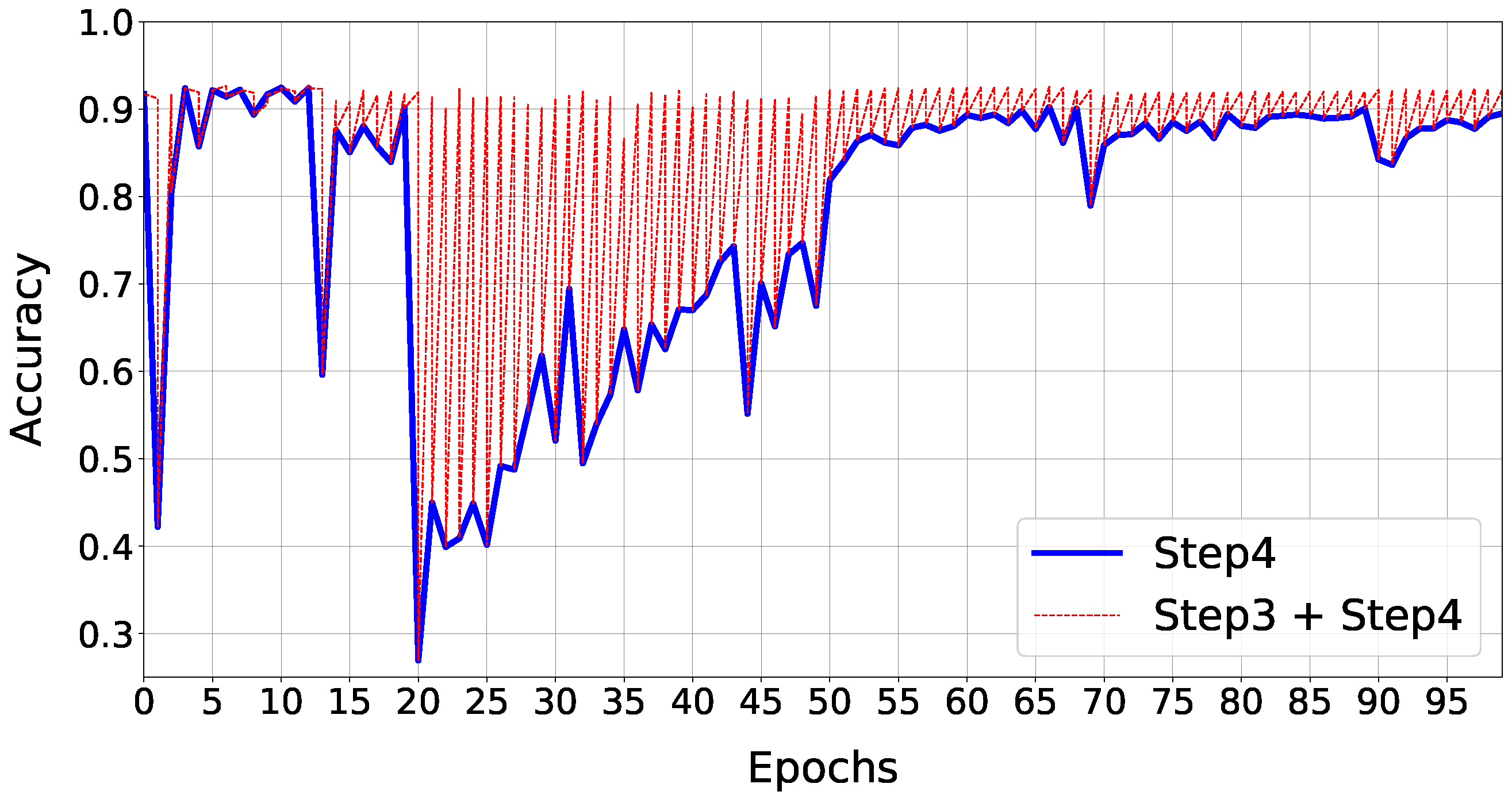
Figure 6 shows how accuracy evolves during the optimization loop: we report the validation’s trend during the algorithm’s epochs (blue-line), also reporting the accuracy values after both the re-Training and Compression phases (red-line). To better understand the behavior of the model during its compression, we recall that, for each loop, the algorithm first runs the retraining phase (based on a float32 back-propagation algorithm) and then a feature projection of the full precision model in the constrained solution space (this induces some accuracy drop). As the plot suggests, the performance loss is recovered within each retraining phase. The peak of loss reflects the addition of a new layer in the compressible subset list. There are layers that influence more the performance drop, but in general, after some epochs, the network reconstructs the information lost.
5. Results
The objective of this section is to quantify the effectiveness of our compression training w.r.t. other state-of-the-art solutions. We focus on some of the most popular CNNs models and datasets.
CNN models—The adopted CNN models are trained from scratch or retrained from the
Torchvision package of PyTorch [
24]. More specifically, we adopted the following CNNs: AlexNet [
1], VGG [
25], and several residual networks with increasing complexity [
26].
All the models are trained and tested using PyTorch [
24] (version 0.4.1). The training epochs of the compressive algorithm are fixed to 100, with a batch size of 128 and an initial learning rate of
, which is scaled every 33 epochs by a factor of 0.1.
Datasets—CIFAR10 and CIFAR100 [
27] are two large-scale image recognition benchmarks that, as their names suggest, differ for the number of available labels. Both are made up of 60,000 RGB images. The raw
data are pre-processed using a standard contrast normalization. We applied a standard data augmentation composed of a 4-pixel zero-padding with a random horizontal flip. Each dataset is equally split into 50,000 and 10,000 images for training and validation, respectively. The intersection between training-set and validation-set is void. Tested CNNs are: AlexNet [
1], VGG [
25], and residual networks [
26].
ImageNet (ILSVRC-2012 [
28]) represents a ultra-large image dataset. Being composed of about 1.2 M images for training and over 50,000 ones for validation, it accounts for a total of 1k different classes. We followed the original data augmentation reported in [
1]: the original raw images with size
are cropped into
patches with a global contrast normalization. For the training stage, the transformation is applied randomly together with a horizontal flip; during validation, a center crop manipulation is applied. AlexNet [
1] and ResNet18 [
26] are the two tested CNNs.
5.1. Performance
For the validation of the proposed technique, we consider the trade-off between the accuracy loss and the compression ratio. The two performance metrics are described in Equations (
19) and (
20). The former represents the accuracy loss and is defined as the difference in terms of accuracy percentage between the original full-precision model (
) and the compressed one (
). The latter describes the compression rate defined as the ratio between the memory storage needed to save the original model’s parameters and the storage needed for saving the compressed model after the encoding. On each compressed layer, we apply the weights encoding illustrated in [
22], using a 4-bit counter. In the original model, all the weights’ parameters (
) have to be saved in 32-bit; for the compressed model, only the different
values (one per each compressed layer) and the total number of weights of the full-precision layers
need 32 bit precision.
We first focus on the performance on CIFAR10 and CIFAR100 datasets with
,
, and
.
Table 1 and
Table 2 summarize the obtained results. In both tables, the first row reports the name of the CNN model with the baseline accuracy in parentheses; the second row reports the experimental results in terms of Top-1 accuracy and accuracy loss; the last row describes the compression rate after weights encoding for each different CNN model. Obtained numbers refer to a user-defined accuracy loss of <1%. The numbers suggest not only that the accuracy constraint is successfully met, but they also indicate that very large compression rates (e.g., 26.4× for the AlexNet model) are easily achieved. This proves the adopted rationale is sound and also applicable to very complex CNN model; it allows to preserve useful information just removing redundant, or less significant, parameters on the less significant layers.
To further understand our approach, we detail two network structures before and after the greedy compressive training.
Table 3 shows the ResNet20 architecture on CIFAR10: the two first columns show the layers ID and their input size; the next columns show the intra-layer sparsity percentage and the bit-width adopted to represent the weights, both for the full precision model (
) and the compressed model (
). The last rows report the sparsity of the resulting net, the compression rate w.r.t. the original model, and the final accuracy.
Table 4 shows the same kind of metrics for AlexNet trained on CIFAR100.
Since our framework applies automatic decisions on the number of layers to compress, for each CNN and each dataset adopted, the results may change substantially, also depending on the accuracy constraint and the number of iterations run.
5.2. Comparison with the State-of-the-Art
The analysis includes some of the most popular works on aggressive CNN compression:
Xnor-Net [
17], by Rastegari et al., where both filters and feature maps are optimized in a binary space;
Ternary Weights Network (TWN) [
20] where Li and Liu et al. overcame the binary solution space adding the zero value as third quantized instance;
Trained Ternary Quantization (TTQ) [
19], where Zhu et al. propose a new ternary quantization procedure able to use just 2-bit weights (with relative scaling factors) during CNN inference;
DoReFa-Net [
29], where Zhou el al. explored hybrid CNNs with different quantization widths for weights, gradients, and activations type with binary weights and 32-bit activations; we focus on the
1-32-32 DoReFa-Net in particular. For all the comparisons, the baseline is the accuracy obtained with full-precision models found in the PyTorch repository. In the following text, we use the accuracy loss as the main metric for comparison. Indeed, the results reported in the previous works do implement any encoding scheme and comparing the compressive rates might result in being quite unfair.
Let us first consider the results on the CIFAR10 dataset. The first row in
Table 5 describes the ResNet20 and ResNet56 baseline accuracies; each column reports the obtained results. For the first CNN model, our technique is able to outperform TTN’s solution with just 0.55% of accuracy loss, whereas, for the ResNet56, the solution is closer to the baseline. However, for both networks, we set up the accuracy tolerance
at
, reaching a considerable compression rate (6.1× and 6.9×).
Table 6 reports the experimental results obtained with the Imagenet dataset. We can see that, for AlexNet, the best solution is that achieved with TTN. In fact, they claim to be able to improve over full precision model. Their solution consists of a ternary weights CNN model (with relative scaling factors), except for the first and last layers, which are kept on float32 precision. Our solution outperforms all the other solutions, e.g., a 12.35% delta w.r.t. XNOR-Net. On the other hand, with the ResNet18 architecture, our model is able to outperform all considered state-of-the-art techniques, reaching just
of accuracy loss. For this set of experiments, considering the 1k-labels dataset complexity, we fixed the accuracy tolerance
at
, reaching compression rates of
for AlexNet and
for ResNet18.
6. Conclusions and Future Works
In this paper, we presented a layer-wise compressive training tool that is able to significantly squeeze CNN structures with minimal accuracy drops (below 1%). Our approach leverages a heuristic that identifies the most appropriate layers to be compressed. This allows for reaching a sub-optimal combination of mixed representations that obeys user-defined accuracy constraints. Experimental results show that the proposed solution overcomes the limitation of a blind pruning, thus providing a smart optimization flow for an effective deployment of CNNs on devices with low storage capacity. Despite the remarkable achievements shown in the paper, there is much room for improvement. First, the sparsity-based empirical rule used to drive the layer-by-layer compression can be expanded with additional parameters that give a more accurate estimation of the accuracy drop. That would help to improve the accuracy-compression trade-off. Second, the execution time of the compression loop can be reduced by lowering the number of retraining epochs. There exists an optimal setting of the hyper-parameters used in the flow, e.g., and , which is a function of the dataset adopted and the CNN under design. Finally, the use of quantization, e.g., fixed-point weights, represents an orthogonal knob that brings additional savings in terms of both memory storage and computational resources.