Abstract
In the social scene of opportunistic networks, message applications find suitable relay nodes or certain transmission destinations from the surrounding neighbors through specific network addresses of users. However, at the dawn of big data and 5G networks, the variational location information of nodes is difficult to be available to mobile devices all the time, and a long wait for the destination may cause severe end-to-end delay. To improve the transmission environment, this study constructs an efficient routing-delivery scheme (Predict and Forward) based on node profile for the opportunistic networks. The node profile effectively characterizes nodes by analyzing and comparing their attributes instead of network addresses, such as physical characteristics, places of residence, workplaces, occupations or hobbies. According to the optimal stopping theory, this algorithm implements the optimal transmission for Prelearn messages by dividing the complex data transmission process into two different phases (Predict and Forward). Through simulations and the comparison of routing algorithms in opportunistic networks, the proposed strategy increases the delivery ratio by 80% with the traditional methods on average, and the average end-to-end delay in this algorithm is the lowest.
1. Introduction
Opportunistic network (OppNet) [1,2] is a delay-tolerant Ad-hoc network, where the source node communicates with the destination without a complete communication route between them. Therefore, the message application uses the “opportunities” created by the movement of nodes to implement the end-to-end data transmission. In the background of big data and 5G networks, traditional face-to-face transmission methods are difficult to meet the communication requirements of large data volume, which implies it is vital for message carriers to select the proper relay nodes to forward messages. In recent years, with the rapid development of novel wireless devices, such as mobile phones, smart watches, Bluetooth earphones or other wearable sensor devices, the message applications in opportunistic social networks [3,4] may obtain more opportunities to communicate with each other. Moreover, the hot issues of opportunistic networks include routing algorithms [5,6,7], mobile models [8,9], security and cooperation [1,10], and applications [11,12].
In [8], an experiment, which anonymously tracked the movements of 700 mobile phone users in a special gathering of Boston metropolitan, shows that the delay-tolerance model is able to perform the effective emergency communication in an important subset of nodes, although the connectivity of the network is strictly dependent on the cooperation of mobile devices and the maximum permissible delay. Moreover, the experimentation on the mobile model also proves that the end-to-end connectivity in opportunistic networks can be implemented by node mobility and the store-carry-forward strategy: nodes carrying data packets use the encounter opportunities created by mobile to forward messages to the relay or destination nodes. However, destination addresses are not always available by the message applications, and this may be a big problem in the data transmission process. In particular, most traditional routing algorithms are more likely to adopt the specific addresses of nodes to implement the messages’ delivery decisions; it is difficult for them to overcome this strong limitation. Consequently, Profile-based network models [13,14] for OppNet proposed that the destination of a message can be multiple nodes or a group of nodes defined by their profiles. These profiles characterize nodes by the method of analyzing and comparing their attributes, such as physical characteristics, places of residence, workplaces or hobbies. In the profile-based network model, messages will be sent to the nodes which belong to a destination profile defined by certain attributes instead of network addresses.
Apparently, it is a complex task for the message model to obtain the attribute characteristics of nodes or the state of the network, because the complete connectivity never exists in OppNet. On the one hand, obtaining the state of the network through the broadcasting method is efficient, but it is a huge waste of storage space and computing resources. On the other hand, using the single message to study the attribute characteristics of nodes, which may raise another problem of how to choose an optimal moment between network routing and message forwarding. Fortunately, the optimal stopping theory [15] provides a strategy to select an optimal phase to stop studying the state of the network. Consequently, in the process of exploring the state of the network, messages are able to establish enough and accurate statistics about the attribute characteristics of nodes in the network, and the nodes can make precise message delivery decisions in the next phase.
However, in the proposed algorithms for opportunistic networks, the node profile defined by their attributes is rarely taken into consideration. Moreover, there is no effective strategy to identify the node profile. In other words, there are two urgent problems in opportunistic networks: how to compare the attribute characteristics of nodes and how to find the destination profile through the gathered statistics. For instance, the after-school counseling agencies need to send an advertisement to the college student with poor grades, but there is no effective method for message applications to find these students. Therefore, the message applications need a special delivery function to compare the attribute values of nodes and to optimize the data transmission process. In addition, when getting adequate information about the attribute characteristics of nodes, the message carrier begins to make the appropriate transmission decisions for messages. However, how to efficiently use the collected statistics to forward messages to the destination profile is another new issue.
To solve the above problems, we propose the Predict and Forward algorithm, which is an efficient routing-delivery scheme based on node profile in opportunistic networks. According to the optimal stopping theory, this strategy consists of two phases: studying the state of the network and making the message delivery decisions. Moreover, we propose a new message model, Prelearn, which allows messages to be sent to a destination profile identified by their attribute characteristics. We also present a specific message delivery function, which is used to compare the attribute characteristics of nodes and to find the destination profile. Meanwhile, we propose a probability prediction matrix based on the historical encounter information of nodes, which contains the probabilities of the future meeting between nodes. The message carrier in the network employs the information carried by the probability prediction matrix to select the appropriate relay node as the next hop. In conclusion, the Predict and Forward scheme is a novel routing-delivery scheme, which implements the optimal transmission for Prelearn messages through the node profile and a probability prediction matrix. The contributions of this paper are listed as follows:
- By defining a special message delivery function, the message applications implement end-to-end data communication based on node profile instead of specific network addresses. The state of the network and the attribute characteristics of nodes can be easily obtained by Prelearn message, and the destination profile can be found by the message delivery function.
- According to the strategy of updating and predicting the probability of the future meeting between nodes, we establish the relationship between historical information and future encounters. The source node can select the suitable relay nodes through the information of the future meeting, and the efficient and sustainable data transmission occurs.
- To avoid missing the optimal transition moment, the optimal stopping theory provides a way to select the best transition moment between studying the state of the network and making the message delivery decisions. Therefore, the method of exploring the network with a single message, can not only provide enough information about the state of the network but also optimize the data transmission process.
- According to the simulation results on Opportunistic Networking Environment (ONE), the Predict and Forward routing algorithm shows enhanced performances in increasing the delivery ratio and reducing the delay of end-to-end data transmission.
2. Related Works
The concept of opportunistic networks derives from early intermittent connected networks (ICNs) [16] and delay tolerant networks (DTNs) [17]. In recent years, the research on opportunity networks mainly focuses on the routing algorithm [5,6,10,12,13], and several innovative routing algorithms are proposed for different application scenarios in opportunistic networks. Consequently, in this section, we will give a brief introduction to the state-of-the-art of both two-phase and profile-based routing algorithms in opportunistic networks.
2.1. The Proposed Two-Phase Routing Algorithms
The routing algorithm attempts to divide the complex data transmission process into two phases, which is an effective method to manage the routing and forwarding of messages in opportunistic networks. Carlos Borrego et al. [18] recommended a routing-delivery scheme (Explore and Wait) for profile-casting based on PRoPHET [19] algorithm. The algorithm consists of two phases: Explore phase and Wait phase. In the Explore phase, the Relcast message routes nodes to understand the state of the network. The Relcast message will be sent to a node profile that is defined as a group of users and the node profile is identified by node attributes instead of network address. During the Wait phase, the Relcast message has already built enough statistics about the network and the message carrier forwards Relcast messages to the suitable relay nodes through the statistics shared from the Relcast message. If the destination node has not appeared in the Explore phase, the carrier does not forward the Relcast message until the destination node is found during the Wait phase.
The Spray and Wait routing algorithm is proposed by Spyropoulos et al. [20]. This algorithm also includes two different phases: Spray phase and Wait phase. In the Spray phase, the source node is trying to make enough message copies and then transmits the message copies to the nodes it encountered. During the Wait phase, if the destination has not appeared in the spray phase, the nodes which obtain a message copy do not transmit the message until they find the destination node. However, the data transmission in Spray and Wait algorithm is impossible for the Bundle Protocol to implement the status routing of messages. For another routing algorithm with two phases, Yuan et al. [21] proposed the Predict and Relay routing algorithm based on historical meeting information. In this algorithm, the message will be sent to the nodes which have a higher probability of encountering the destination than others. The Predict and Relay routing algorithm effectively improves the delivery radio and reduces the average end-to-end delay in OppNet.
2.2. The Proposed Profile-Based Routing Algorithms
The profile-based routing algorithm is more likely to adopt the contextual information to select a relay node from the neighbors. Meanwhile, the profile-based routing algorithm predicts the possibility of the future encounter between nodes through the historical meeting information, which is a major research orientation in OppNet. Lindgren et al. [19] proposed the PRoPHET algorithm, which tries to copy message groups and to estimate the probability of successful message forwarding. Moreover, the algorithm effectively reduces invalid message group copies and improves the resource utilization. Burgess et al. [22] suggested the MaxProp routing algorithm based on setting the priority for message groups. When two nodes meet, the replication order is determined through the grouping priority of the node, and the message group with a low priority cannot obtain the data transmission opportunity, which helps to avoid generating the message group with inefficient message forwarding.
Wu et al. [23] presented a routing algorithm based on information transmission probability and cache management. This algorithm proposed that each node in the network can identify its surrounding neighbors by evaluating the meeting probability between them. Additionally, the node explores the special relationships with its neighbors and makes distribution adjustment for cache data. In [24], Leguay et al. recommended the MobySpace algorithm based on the MobySpace space. The length of the axis in MobySpace space represents the possibility of two nodes meeting each other. Moreover, the message carrier selects a suitable relay node as the next hop through the length of the axis. Leguay et al. [25] suggested a routing algorithm in a mobility pattern space (MV) based on node encounters and the historical record of node visiting an area. The algorithm proposed that the source node transmits message groups to the next hop by calculating and comparing the probability of the future meeting between users.
In [26], Peng et al. proposed a contact probability and data packet freshness perception routing algorithm based on the operation rule of opportunistic networks. This algorithm uses the previous contact information to calculate the average contact interval of two nodes, which can not only update the data packet but also gain enough delay for a utility function. Finally, the node makes the forwarding decision by the utility function and Epidemic algorithm [27]. Hoang Anh Nguyen and Silvia Giordano [28] recommended a social context-based routing algorithm based on context information prediction. This algorithm tries to predict the context information related to the node through historical communication statistics of nodes. Meanwhile, by analyzing this context information, the source node can make an accurate delivery decision as to where and when to send messages to the relay node. In [29], Wang et al. presented a routing algorithm based on predicting node meeting location in OppNet. This algorithm is dedicated to predict the distance between nodes and to determine their current geographical position through the Markov model, and implements the efficient buffer management strategy.
In this paper, the Predict and Forward routing algorithm proposed for opportunistic networks is based on the research, analysis and innovation of related works.
3. Predict and Forward Scheme Based on Node Profile
At present, traditional routing algorithms of opportunistic networks select suitable relay nodes from the surrounding neighbors through their network addresses instead of a specific profile that is defined by node attributes. When the destination address is not available by message carriers, the Profile-based network model provides an effective method to identify the destination node by evaluating the attribute characteristics of nodes. Consequently, we propose Prelearn, a new profile-based message model for opportunistic networks, and Predict and Forward, an efficient routing-delivery algorithm for Prelearn messages. The proposed scheme consists of two phases: studying the state of the network to find the destination profile by collecting and comparing the attribute characteristics of nodes, and making delivery decisions for Prelearn messages through the collected statistics.
As shown in Figure 1, different users in a social scenario contain different node attributes and belong to different node profiles, which are identified by different attribute characteristics of nodes. If a source user needs to send an advertisement to the lightest user in the network, the Prelearn message collects the attribute characteristics of users, and finally, it will be sent to the users that belong to the destination profile with the minimum value of the weight attribute. In the transmission process, the message delivery function is applied to find the destination profile, the Prelearn message model is used to carry and transport information, and the node in the network can handle computing tasks. Certainly, the detailed process for data transmission will be described in the following sections. Moreover, in order to improve the understanding of the Predict and Forward scheme, we give the following important definitions strictly.
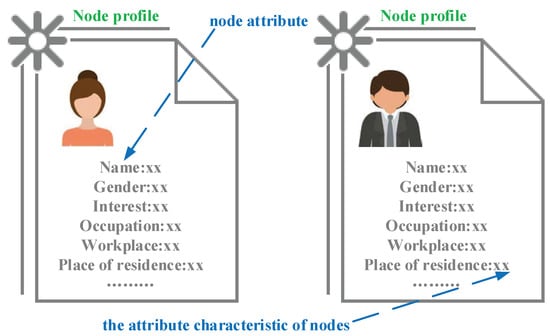
Figure 1.
The description diagram of node profile.
Definition 1 (node attributes).
The node attributes represent the social attributes of the users in an OppNet, such as their physical characteristics, places of residence, workplaces or hobbies.
Definition 2 (the attribute characteristics of nodes).
The attribute characteristics of nodes represent the attribute values of nodes in the networks, for example, the interest attribute includes the attribute characteristics of nodes (or the attribute values of nodes): movie, sport, music or reading.
Definition 3 (message delivery function).
Defined by the source node, this is a special function that is used to evaluate and compare the attribute characteristics of nodes, and to find the destination profile that meets the requirements of the source node.
Definition 4 (destination profile).
The destination profile is multiple nodes or a group of nodes. The attribute characteristics of nodes belonging to the destination profile, satisfy the message delivery function. Actually, the destination profile is a set of destinations, such as the blue eye profile; this means a set of users with blue eyes.
Definition 5 (the optimal candidate).
The optimal candidate is a node that plays an important role in the data transmission process, such as the destination node or a node that frequently encounters the destination.
3.1. Prelearn Message: Definition and Application
Opportunistic network belongs to multi-hop wireless network, where the source node communicates with the destination in the poor network state of high latency, low delivery ratio and intermittent connection. Destination addresses are not always available by the message applications in OppNet. In order to overcome this strong limitation, the profile-based network model proposed that data transmission is based on node attributes instead of destination addresses, which may emerge as another problem in the data transmission process: there is no efficient delivery strategy to characterize nodes based on their attribute characteristics. Therefore, we proposed Prelearn, a novel model that allows messages to be sent to the destination profile identified by node attributes, such as their physical characteristics, places of residence, workplaces or hobbies.
In order to find the nodes belonging to the destination profile, we firstly define S as the set of all nodes in an OppNet. Therefore, the set of all nodes S can be shown as
where the label n represents the number of nodes in the networks. Similarly, we define the destination profile R as a set of the destination users, and the destination profile R can be shown as
where the nodes ,, belonging to the destination profile R, are a group of the destination users. Obviously, the destination profile R is a subset of S, so . For a given attribute certification defined by the source node, ,, are different attribute requirements for the destination profile. Consequently, the message delivery function is a mathematical mapping from the set S to the destination profile R, and it can be shown as
For different application scenarios in opportunistic networks, various message applications may have different attribute requirements for the destination profile. Therefore, the optimal transmission process is achieved by defining different message delivery functions, such as maximum, minimum or the local optimum. Moreover, for a source node , a message delivery function , a probability prediction matrix that contains the probability of the future meeting between nodes in the network, and the data packets , we rigorously define the Prelearn message as L(,, , ), where the probability prediction matrix will be detailed in the following sections.
3.2. Predict Phase: Studying the State of the Network
During the Predict phase, Prelearn messages route from a node to another to study their attribute characteristics in the network, but the data packets are not forwarded to the nodes. Meanwhile, Prelearn message constantly builds enough and accurate statistics about the attribute characteristics of nodes. Whenever a new node is routed by Prelearn message, the statistics carried by Prelearn message are updated once in the Predict phase. Certainly, there are several different ways for a Prelearn message to build and update the statistics about the network. Figure 2 gives an example for the routing process in Predict phase. During this phase, the source sends a Prelearn message to study the state of the network. The Prelearn message routes from to in the network, finds the nodes belonging to the destination profile, and collects and updates the historical encounter information between nodes. Moreover, each node in the network adopts the information carried by Prelearn message to predict the probability of future encounters with other nodes.
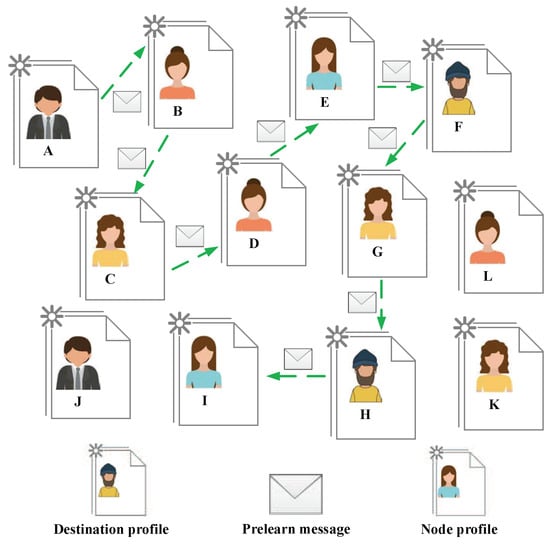
Figure 2.
The routing process diagram of Predict phase.
3.2.1. Prelearn Message Collects and Updates the Statistics about the State of the Network
For many years, the researchers have argued that the mobility of wireless devices is unpredictable in the network. However, in the literature [9], an experiment, which focuses on exploring the human mobility in a real-word scene, shows that the distributions of both contact and inter-contact times in the network presents a power law distribution. According to the theory of the experiment, the movement of delay tolerant network (DTN) nodes may be based on the predictable mobility models. If a node encounters another node frequently, they are more likely to meet each other in the future. Therefore, we adopt the function to convert the average number of historical encounters between nodes into the probability of the future meeting between them. Firstly, we define a routing metric , which represents the number of encounters between and in the past period of time t. Moreover, the forwarding metric (the possibility of the future meeting) between and can be defined as
where represents the average number of encounters between between and during the previous period of time t. After the Prelearn message obtains the attribute characteristics of a certain node, it may never route the node again, so it is important for nodes to update the forwarding metrics. Moreover, PRoPHET has provided an efficient scheme to update the forwarding metrics in opportunistic networks, so the updated forwarding metric between and can be shown as
where is defined as an initialization constant and is the meeting probability before the update. If they do not contact with each other for a long time, the forwarding metric between them is gradually getting aged, so we define as a constant, which is used to control the aging change of forwarding metrics. Additionally, the updated forwarding metric between and can be calculated as
where t is the previous period of time before the update. In opportunistic networks, the geographic location of nodes changes over time and the forwarding metrics are the important basis for a successful data transmission, so it is necessary for Prelearn messages to execute the updating operation for the meeting probability between nodes.
3.2.2. The Node in the Network Predicts the Future Meeting Probabilities with Others
In the social application scene of opportunistic networks, the movement of nodes changes the topological structure of the network, and the meeting probability between nodes will also change over time. Consequently, the prediction of the probability of a future encounter between nodes may effectively evaluate the variational transmission relationships of users. Ordinarily, the traditional SVD (snayperskaya vinyovka dragunov) method decomposes a matrix into three matrices, which will result in low computational efficiency and high cache consumption. Nevertheless, the algorithm creatively decomposes a matrix into only two matrices, so it can be applied to the mobile devices with limited memory spaces and low computing power in opportunistic networks. Firstly, we define a symmetric matrix , which includes the statistics about the forwarding metrics between nodes.
Based on the algorithm, the probability matrix can be decomposed into two different matrices and by the following Equation (8).
where each element in the probability matrix will be decomposed into two vectors and , and it corresponds to a forwarding metric value in Equation (7). The subscripts i and j represent the number of rows and columns of the element in the matrix , respectively. Additionally, this scheme considers all combinations of forwarding metrics and predictive values to minimize , and it is necessary to add a regularization term to prevent over-fitting, so the formal optimization function will be defined as follows:
where is a regularization coefficient. The stochastic gradient descent is commonly used to optimize the result of , so the derivatives of and can be computed as
Therefore, the global minimum value of is obtained by the method of the iterative calculation of the gradient descent, and the iteration formula for and can be defined as
where is an adjustable constant, and the predictive value of is the product of the derivatives of and . Consequently, the probability prediction matrix , which is a predictive value of , can be calculated by the iterative derivation and calculation of and . Consistent with PRoPHET, the Prelearn message keeps a single copy in the Predict phase, which effectively avoids the flooding mode of message routing in the network. During the Predict phase, whenever a new node is routed by Prelearn messages, the Prelearn message collects and updates the carrying information through the attribute characteristics of the node. Meanwhile, the node uses the latest statistics shared from Prelearn messages to predict the probabilities of the future meeting with others and then returns the updated information to the Prelearn message. During the Forward phase, message carriers select the suitable relay nodes through the predictive meeting probability between nodes which is stored in the probability prediction matrix .
3.3. Phase Transition: The Optimal Stopping Theory
As we defined, there are two phases in the Predict and Forward scheme: studying the state of the network and making delivery decisions for Prelearn messages. During the Predict phase, if the Prelearn message studies the state of the network for a long time, excessive statistics may cause a lack of computing resources and storage spaces of the node, and the network latency will increase dramatically, so the Prelearn message may miss the optimal candidate in the data transmission process. On the contrary, a short-lived Predict phase may imply that the Prelearn message does not obtain enough information about the attribute characteristics of nodes. Consequently, it is vital for Prelearn messages to make a precise phase transition in the data transmission process.
To solve the problem, the optimal stopping theory provides a good paradigm to find the optimal moment between studying the state of the network and making delivery decisions for Prelearn messages, it allows the Prelearn message not only to get enough information about the networks but also not to miss the optimal candidate of data transmission.
As depicted in Figure 3, we denote X, which represents the number of nodes that have routed by the Prelearn message in the Predict phase. We define K as the optimal transition moment from Predict phase to Forward phase. This means the K-th node is the last node that has been routed by the Prelearn message and the optimal candidate has appeared before the phase K. Therefore, we assume that the Prelearn message starts to study the network from the r-th node to the K-th node and each phase has an equal probability of switching to the Forward phase. If the K-th node is the optimal candidate, we define , which is the probability of switching to the forward phase at the phase K. To calculate the probability value of , we define , which represents the K-th node is the optimal candidate, and define , which represents the K-th node begins to make message delivery decisions for Prelearn messages at the phase K. Therefore, the probability value of can be computed as
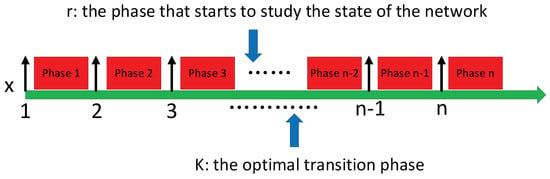
Figure 3.
The optimal transition phase between Predict and Forward.
According to the hypothesis, the K-th node is the optimal candidate in the data transmission process, so is bigger than the probabilities of switching to Forward phase at any later phase, and this can be shown as
According to the general expression of r in the above equation, the phase value r can be used to calculate the probability value , and the inference procedure is shown as follows.
Based on the calculation results, is the maximum value for . Consequently, the optimal transition phase K is , which indicates that the n/e-th node is the last node to be routed by Prelearn messages and it begins to send Prelearn messages to the destination profile.
3.4. Forward Phase: Making Delivery Decisions for Prelearn Messages
After the Predict phase, the Prelearn message has received enough and accurate statistics about the state of the network and nodes in the network have determined the probabilities of the future meeting with other nodes. Moreover, the optimal candidate carrying Prelearn messages starts to make delivery decisions based on the information stored in the Prelearn message. During the Forward phase, if the destination profile has appeared in the Predict phase, the Prelearn message will directly or indirectly be forwarded to the nodes belonging to the destination profile based on the probability prediction matrix . Specifically, Prelearn message carriers transmit data packages to the relay nodes which have a bigger probability of future meeting with the destination profile than the Prelearn message carriers. Finally, the Prelearn messages will be forwarded to the destination profile. Otherwise, when the destination profile has not appeared in the Predict phase, the message carrier does not forward Prelearn message until it finds a node that satisfies the message delivery function , which is the same as the Wait phase in Spray and Wait algorithm.
As shown in Figure 4, during the Forward phase, the , which is the last node to be routed in the Predict phase, starts to make delivery decisions for Prelean messages. The and belong to the destination profile that satisfies the message delivery function defined by the minimum weight. Moreover, according to the probability prediction matrix , the , and are the users that possess a bigger probability of future meeting with the destination profile than the . Therefore, the directly or indirectly sends Prelearn messages to the suitable relay nodes , and , and the Prelearn messages will be forwarded to the destination profile and eventually.
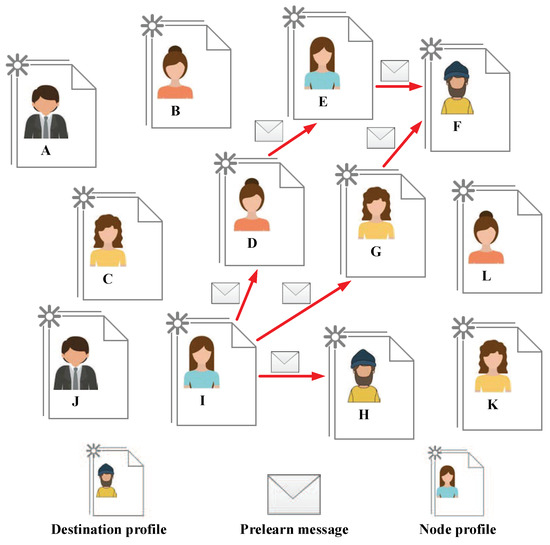
Figure 4.
The delivering process diagram of Forward phase.
3.5. Complexity Analysis of the Proposed Algorithm
In conclusion, we propose an efficient routing-delivery scheme (Predict and Forward) based on node profile in opportunistic networks, and the detailed steps of the proposed algorithm are as follows.
Step 1: The source node defines the message delivery function through its previous experience.
Step 2: The Prelearn message starts to route from a node to another in the network, gathers and updates the statistics about the attribute characteristics of nodes, and finds the destination profile by the message delivery function defined by the source node.
Step 3: When routed by the Prelearn message, the new node adopts the historical meeting information shared from the Prelearn message to predict the future encounter probabilities with others.
Step 4: Based on the optimal stopping theory, Prelearn message carriers select an optimal transition moment to forward Prelearn messages to the relay nodes which have a bigger probability of a future meeting with the destination profile than the Prelearn message carriers.
For the readability of this algorithm, we provide the pseudo-code description to introduce our proposed scheme briefly. As the pseudocode shows, the first loop represents Prelearn messages route from the source node to the n/e-th node in the Predict phase, so its time complexity is . Additionally, the second loop of the pseudo-code indicates that the message carrier compares the probability of the future meeting between nodes and makes appropriate message delivery decisions in Forward phase, so its time complexity is . On the whole, the time complexity of the proposed algorithm is . Meanwhile, we may compare the proposed algorithm with other traditional algorithms of opportunistic networks. The time complexity in Spray and Wait algorithm is , while that in the Epidemic algorithm is .
| Algorithm 1 Predict and Forward scheme |
| Input: Prelearn message L(,,,), ……., a destination node D; Output: the node set R, the probability prediction matrix ;
|
4. Performance Evaluation
The simulation adopts the Opportunistic Network Environment (ONE) to test in the Health Capability Maturity Model (HCMM) [30]. In our work, the Predict and Forward algorithm will be compared with the other three algorithms: EIMST routing algorithm (effective information transmission based on socialization nodes) [12], Epidemic routing algorithm [27] and Spray and Wait routing algorithm [20]. The EIMST routing algorithm is the latest strategy for OppNet and the other two algorithms are traditional methods in OppNet.
In this experimentation, the algorithm is trained and tested in the mathematical tool MATLAB. According to the experimental results with different simulation settings, the method shows the best performance when the regularization coefficient is 0.02 and the constant is 0.1, so the parameters and are initialized to 0.02 and 0.1 in the Predict and Forward scheme. Moreover, the other parameters are set as follows. The simulation area is 3000 m × 3000 m and there are 1000 nodes (the value of n is 1000) in the communication area. Each node in the network includes six different node attributes and the destination profile consists of 50 nodes which satisfy the message delivery function. The simulation time is set as 1–12 h, the initial value for a period of time t is 40 min and the maximum moving range of each node is 20 m. The total number of Prelearn messages is 100 and the time to create a Prelearn message is 1–10 s. Each Prelearn message occupies 100 Kb storage space. During the Predict phase, the Prelearn message always keeps a single copy to route nodes in the network. With the movement speed of 1–4 m/s, each node in the network has the cache spaces of 50 Mb and carries 10 data packets. In order to improve the readability of the simulation settings, we build Table 1 to introduce the simulation environment briefly. In the experimental results, we focus on the following parameters:

Table 1.
The simulation settings for Predict and Forward algorithm.
1. The probability of the destination profile receiving Prelearn messages (): This parameter represents the probability of the destination profile receiving Prelearn messages from the message carriers and its neighbors. The probability of the destination profile receiving Prelearn messages can be shown as , where is the total number of Prelearn messages forwarded by the node, and is the total number of Prelearn messages obtained by the destination profile.
2. Delivery ratio: This parameter represents the probability of the node receiving Prelearn messages from its neighbors. The delivery ratio can be calculated as , where is the number of Prelearn messages sent by message carriers and is the number of Prelearn messages received by the node.
3. Overhead on average: This parameter represents the network overhead of sending a Prelearn message from one node to another. Overhead on average can be calculated as , where is the total time taken for Prelearn message forwarding and is the time of a successful message forwarding.
4. Average end-to-end delay: This parameter represents the network delay of routing Prelearn messages, the delay of phase transition and the delay of forwarding Prelearn messages.
In this simulation, we first evaluate the impact of the aging variable on the probability of the destination profile receiving Prelearn messages . As shown in Figure 5, when the value of the aging variable changes, the corresponding value of always exceeds 0.7. Moreover, the reaches a maximum value of 0.85 when the aging variable is 0.3. Figure 6 shows the impact of the phase transition value on the probability of the destination profile receiving Prelearn messages . As it can be seen, when the phase transition value increases from to N, the fluctuation range of the is from 0.3 to 0.8. Particularly, when the phase transition is at , the Prelearn message has not only obtained enough statistics about the state of the network but also found the destination profile by the message delivery function. Therefore, the message carrier can make the suitable delivery decisions for Prelearn messages, the efficient data transmission performs, and the gets the maximum value of 0.8.
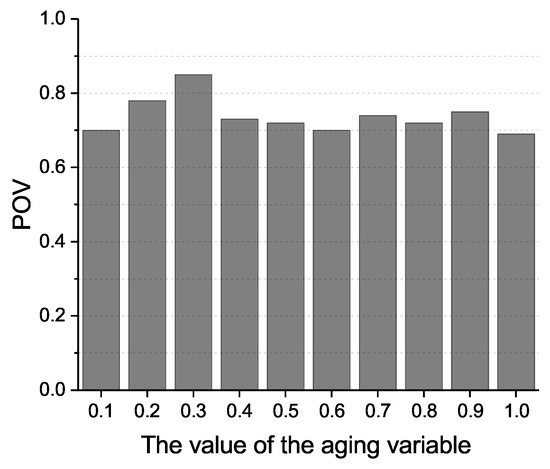
Figure 5.
The probability of the destination profile receiving Prelearn messages.

Figure 6.
The probability of the destination profile receiving Prelearn messages.
Figure 7 exhibits the impact of the phase transition value on delivery ratio. As it can be seen, the broken line first rises sharply and then falls rapidly. This means the phase transition value plays a significant role in the delivery ratio. A short Predict phase may miss the optimal candidate in the data transmission process, while a long Predict phase may imply that a large number of irrelevant nodes participate in the forwarding process of Prelearn messages. When the phase transition occurs at the optimal moment , message carriers select the suitable relay nodes based on reliable information about the state of the network, and the destination profile is more likely to have appeared in the Predict phase, so the delivery ratio reaches the maximum value of 0.95.
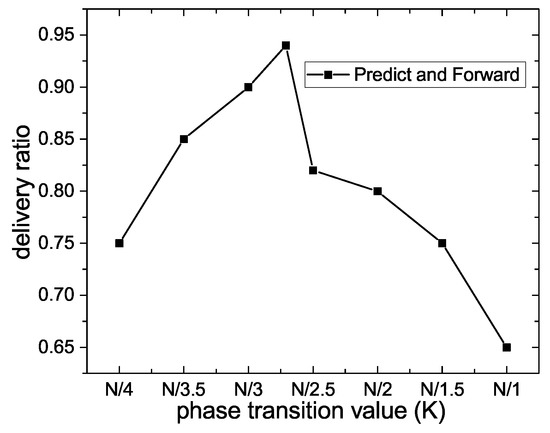
Figure 7.
Delivery ratio.
Figure 8 shows the influence of the phase transition value on network overhead. As it can be seen, the broken line first drops rapidly and then rises slowly. The later the phase transition occurs, the more the nodes take part in the forwarding process of Prelearn messages. Meanwhile, the number of nodes unrelated to the process of data transmission also increases, and more time and resources are wasted in transmitting Prelearn messages to the unrelated nodes, so the network overhead presents a rising trend. However, When the phase transition occurs at the optimal moment , the Prelearn message acquires sufficient information about the state of the network, the node obtains the exact probability of future meeting with other nodes, and the routing and delivering of the Prelearn message are at their optimal state, so the network overhead gets the minimum value of 85.
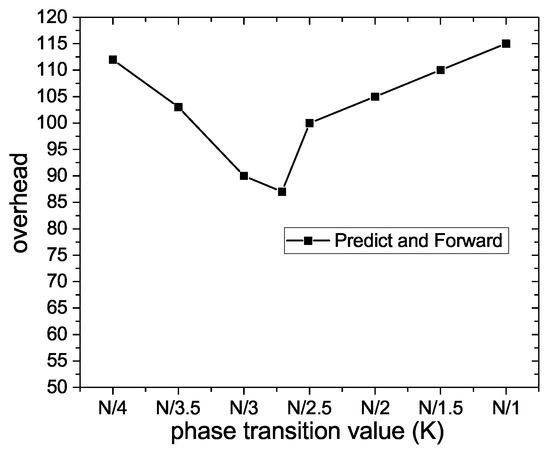
Figure 8.
Overhead.
Figure 9 exhibits the influence of the phase transition value on average end-to-end delay. As it can be seen, the broken line first declines slowly and then rises rapidly. In other words, when the number of the nodes routed by Prelearn messages increases, the number of the nodes participating in the data transmission process also goes up, so the average end-to-end delay in Predict and Forward algorithm decreases constantly. However, when the transition phase exceeds the optimal moment, more unrelated nodes participate in the routing and forwarding of Prelearn messages, the number of hops in a successful data transmission increases and a large amount of energy is consumed in mission calculations and information transportation. Consequently, the average end-to-end delay in the Predict and Forward algorithm begins to rise.
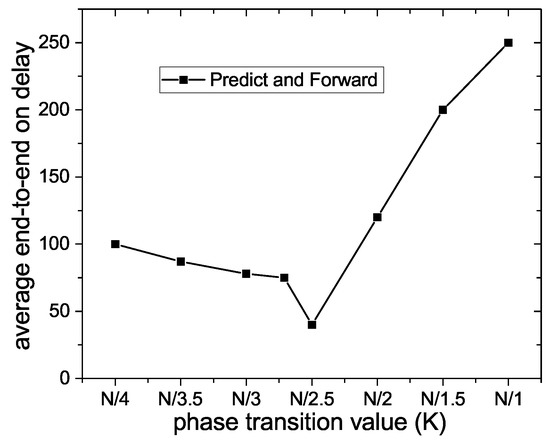
Figure 9.
Average end-to-end delay.
Figure 10 shows the comparison results between the four algorithms in terms of delivery ratio. As it can be seen, the average delivery ratio in the Predict and Forward algorithm is the highest among them. This is because the data transmission in Predict and Forward algorithm is implemented through node attributes, and Prelearn messages are transmitted to the relay nodes, which have a relatively high probability of meeting the destination profile. As the cache space continues to increase, nodes in the network can handle complex computing tasks and carry more information, so the delivery ratio is growing rapidly. In Predict and Forward scheme, the delivery ratio is over 0.9 when data cache exceeds 37.5 Mb, and it reaches the maximum value when data cache is 40 Mb. As for EIMST algorithm, it does not have an effective way to implement cache management of nodes, so the delivery ratio in this algorithm is lower than Predict and Forward. In addition, Epidemic routing algorithm and Spray and Wait algorithm produce a large number of message copies in the data transmission process, so the delivery ratio in the two algorithms is always relatively low. Overall, the delivery ratio in the Predict and Forward algorithm is 0.85 on average, which is higher than the other three algorithms.
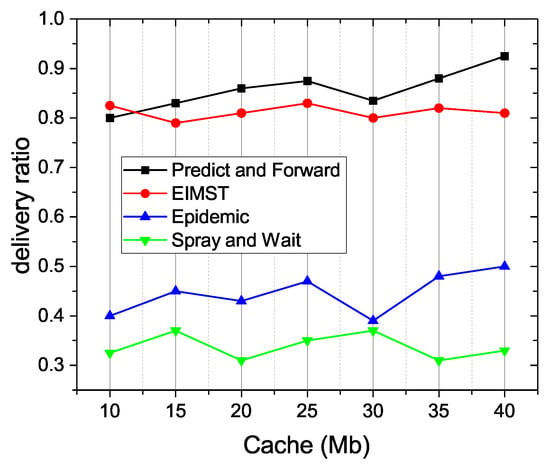
Figure 10.
Delivery ratio.
Figure 11 shows the comparison results between the four algorithms in terms of overhead on average. As it can be seen, with the increase of the cache space, the overhead on average drops dramatically. Moreover, the overhead on average in Predict and Forward scheme is the lowest among the four algorithms. When the cache space is over 20 Mb, the overhead on average in Predict and Forward algorithm always keeps the lowest, because it adopts two different phases to implement the optimal process for data transmission. When an optimal phase transition is found between Predict and Forward phases, the number of hops of a successful data transmission in Predict and Forward is less than the other algorithms, and the time spending on the routing and forwarding of Prelearn messages is also less than the other algorithms. Moreover, the increase of the cache space means there are more resources for nodes to carry information and execute computational tasks. As for the other three algorithms, the overhead on average in EIMST fluctuates between 20–150 and the overhead on average is between 80–220 in Spray and Wait or Epidemic.
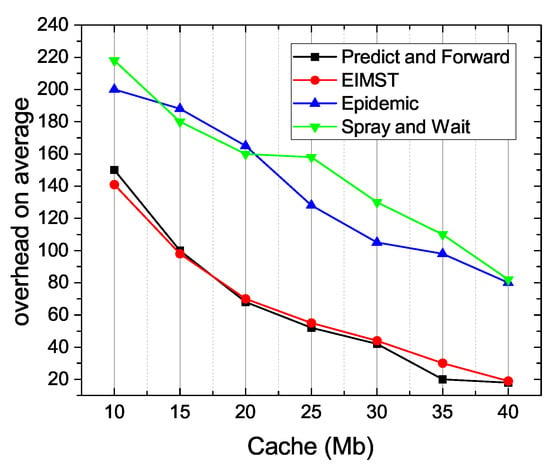
Figure 11.
Overhead on average.
Figure 12 shows the comparison results between the four algorithms in terms of average end-to-end delay. As it can be seen, the average end-to-end delay in Epidemic is always the highest among them, because the node in the network may have more computation tasks in this algorithm. However, in Spray and Wait or EIMST, the multicopy model is used to implement data transmission so that the average end-to-end delay in them is superior to the Epidemic. It is clear that the average end-to-end delay in Predict and Forward algorithm is the lowest among the four algorithms, because this scheme always selects the relay nodes which have a high probability of meeting the destination profile as the next hop. When the transition phase is at the optimal moment, this scheme keeps a balanced state between exploring the network and forwarding Prelearn messages, so the average end-to-end delay in the Predict and Forward gets a minimum value of 25. Meanwhile, when the cache space of nodes increases from 10 Mb to 40 Mb, the average end-to-end delay in Predict and Forward never exceeds 50.

Figure 12.
Average end-to-end delay.
5. Conclusions
This study proposes a routing-delivery scheme (Predict and Forward) based on node profile and the optimal stopping theory in opportunistic networks. This strategy is based on a node that will have a high probability of meeting another if it encountered another node frequently in the past. This algorithm determines the probability of the future meeting between nodes according to the historical encounter information. To avoid missing the optimal moment to make message delivery decisions, this method adopts the optimal stopping theory to select an optimal transition phase between studying the state of the network and forwarding the Prelearn messages. Meanwhile, in order to overcome the limitation that destination addresses are not always available by the message carriers, the nodes in opportunistic networks implement end-to-end communication based on their attributes instead of specific network addresses. Compared with the other three algorithms, the Predict and Forward scheme obtains improved performances in increasing delivery ratio and reducing the delay of end-to-end data transmission. In the future work, this algorithm will be used for the mobile communication in the application environment of big data and 5G networks.
Author Contributions
Conceptualization, K.L., Z.C. and J.W.; Methodology, K.L.; Software, Z.C.; Validation, K.L., Z.C. and J.W.; Formal Analysis, K.L.; Investigation, Z.C.; Resources, Z.C.; Data Curation, J.W.; Writing-Original Draft Preparation, K.L.; Writing-Review & Editing, Y.X. and H.Z.; Visualization, Z.C.; Supervision, Z.C. and J.W.; Project Administration, Z.C.; Funding Acquisition, Z.C.
Funding
This work was supported in part by the Major Program of National Natural Science Foundation of China (NO. 71633006); The National Natural Science Foundation of China (NO. 616725407); China Postdoctoral Science Foundation funded project (2017M612586); The Postdoctoral Science Foundation of Central South University (185684); the Fundamental Research Funds for the Central Universities of Central South University (No. 2018zzts615).
Acknowledgments
This work was supported partially by “Mobile Health” Ministry of Education—China Mobile Joint Laboratory.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Dede, J.; Förster, A.; Hernández-Orallo, E.; Herrera-Tapia, J.; Kuladinithi, K.; Kuppusamy, V.; Manzoni, P.; bin Muslim, A.; Udugama, A.; Vatandas, Z. Simulating Opportunistic Networks: Survey and Future Directions. IEEE Commun. Surv. Tutor. 2018, 20, 1547–1573. [Google Scholar] [CrossRef]
- Trifunovic, S.; Kouyoumdjieva, S.T.; Distl, B.; Pajevic, L.; Karlsson, G.; Plattner, B. A Decade of Research in Opportunistic Networks: Challenges, Relevance, and Future Directions. IEEE Commun. Mag. 2017, 55, 168–173. [Google Scholar] [CrossRef]
- Yao, X.; Chen, Y.; Zhang, R.; Zhang, Y.; Lin, Y. Beware of What You Share: Inferring User Locations in Venmo. IEEE Internet Things J. 2018. [Google Scholar] [CrossRef]
- Yao, X.; Zhang, R.; Zhang, Y.; Lin, Y. Verifiable Social Data Outsourcing. In Proceedings of the IEEE INFOCOM 2017 Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017. [Google Scholar]
- Chen, Z.; Guo, L.; Zhang, D.; Chen, X. Energy and channel transmission management algorithm for resource harvesting body area networks. Int. J. Distrib. Sens. Netw. 2018, 14, 155014771875923. [Google Scholar] [CrossRef]
- Wu, J.; Chen, Z. Sensor communication area and node extend routing algorithm in opportunistic network. Peer-to-Peer Netw. Appl. 2018, 11, 90–100. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Z.; Wu, J. An Opportunistic Routing for Data Forwarding Based on Vehicle Mobility Association in Vehicular Ad Hoc Networks. Information 2017, 8, 140. [Google Scholar] [CrossRef]
- Cacciapuoti, A.S.; Calabrese, F.; Caleffi, M.; Di Lorenzo, G.; Paura, L. Human-mobility enabled wireless networks for emergency communications during special events. Pervasive Mob. Comput. 2013, 9, 472–483. [Google Scholar] [CrossRef]
- Cacciapuoti, A.S.; Calabrese, F.; Caleffi, M.; Di Lorenzo, G.; Paura, L. Human-mobility enabled networks in urban environments: Is there any (mobile wireless) small world out there? Ad Hoc Netw. 2012, 10, 1520–1531. [Google Scholar] [CrossRef]
- Yao, L.; Man, Y.; Huang, Z.; Deng, J.; Wang, X. Secure Routing Based on Social Similarity in Opportunistic Networks. IEEE Trans. Wirel. Commun. 2016, 15, 594–605. [Google Scholar] [CrossRef]
- Baudic, G.; Auger, A.; Ramiro, V.; Lochin, E. Using emulation to validate applications on opportunistic networks. arXiv, 2016; arXiv:1606.06925. [Google Scholar]
- Jia, W.U.; Chen, Z.; Zhao, M. Effective information transmission based on socialization nodes in opportunistic networks. Comput. Netw. 2017, 129, 297–305. [Google Scholar] [CrossRef]
- Lenando, H.; Alrfaay, M. EpSoc: Social-Based Epidemic-Based Routing Protocol in Opportunistic Mobile Social Network. Mob. Infor. Syst. 2018, 2018, 6462826. [Google Scholar] [CrossRef]
- Zhou, H.; Leung, V.C.; Zhu, C.; Xu, S.; Fan, J. Predicting Temporal Social Contact Patterns for Data Forwarding in Opportunistic Mobile Networks. IEEE Trans. Veh. Technol. 2017, 66, 10372–10383. [Google Scholar] [CrossRef]
- Egami, M.; Kevkhishvili, R. On the Optimal Stopping Problem of Linear Diffusions in Regime-Switching Models. In Proceedings of the 30th Asian Finance Association Annual Meeting. Hitotsubashi Hall, Tokyo, Japan, 25–27 June 2018; pp. 1–29. [Google Scholar]
- Wang, Y.; Liu, Y.; Zhang, J.; Ye, H.; Tan, Z. Cooperative Store-Carry-Forward Scheme for Intermittently Connected Vehicular Networks. IEEE Trans. Veh. Technol. 2017, 66, 777–784. [Google Scholar] [CrossRef]
- Bocquillon, R.; Jouglet, A. Robust routing in deterministic delay-tolerant networks. Comput. Oper. Res. 2018, 92, 77–86. [Google Scholar] [CrossRef]
- Borrego, C.; Sánchez-Carmona, A.; Li, Z.; Robles, S. Explore and wait: A composite routing-delivery scheme for relative profile-casting in opportunistic networks. Comput. Netw. 2017, 123, 51–63. [Google Scholar] [CrossRef]
- Borah, S.J.; Dhurandher, S.K.; Tibarewala, S.; Woungang, I.; Obaidat, M.S. Energy-Efficient Prophet-PRoWait-EDR Protocols for Opportunistic Networks. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017. [Google Scholar]
- Spyropoulos, T.; Psounis, K.; Raghavendra, C.S. Spray and wait: An efficient routing scheme for intermittently connected mobile networks. In Proceedings of the ACM Workshop on Delaytolerant Networking, Philadelphia, PA, USA, 26 August 2005; pp. 252–259. [Google Scholar]
- Yuan, Q.; Cardei, I.; Wu, J. Predict and relay: An efficient routing in disruption-tolerant networks. In Proceedings of the ACM Interational Symposium on Mobile Ad Hoc NETWORKING and Computing, MOBIHOC 2009, New Orleans, LA, USA, 18–21 May 2009; pp. 95–104. [Google Scholar]
- Burgess, J.; Gallagher, B.; Jensen, D.; Levine, B.N. MaxProp: Routing for vehicle-based disruption-tolerant networks. In Proceedings of the 25th IEEE International Conference on Computer Communications (INFOCOM ’06), Barcelona, Spain, 23–29 April 2006. [Google Scholar]
- Wu, J.; Chen, Z.; Zhao, M. Information cache management and data transmission algorithm in opportunistic social networks. Wirel. Netw. 2018, 1–12. [Google Scholar] [CrossRef]
- Leguay, J.; Lopez-Ramos, M.; Jean-Marie, K.; Conan, V. An efficient service oriented architecture for heterogeneous and dynamic wireless sensor networks. In Proceedings of the 33rd IEEE Conference on Local Computer Networks (LCN), Montreal, QC, Canada, 14–17 October 2008; pp. 740–747. [Google Scholar]
- Leguay, J.; Friedman, T.; Conan, V. DTN routing in a mobility pattern space. In Proceedings of the ACM SIGCOMM Workshop on Delay-Tolerant Networking (WDTN’05), Philadelphia, PA, USA, 26 August 2005; pp. 276–283. [Google Scholar]
- Peng, B.T. Opportunistic Networks Routing Algorithm with Contact Probability and Data Packet Freshness Perception. J. Chin. Comput. Syst. 2017, 38, 1459–1463. [Google Scholar]
- Zhang, G.H.; Pang, S.B.; Yang, Y.H.; Chen, Z.G. Improved epidemic algorithm based on trust mechanism in opportunistic networks. In Chinese. J. Netw. Inf. Secur. 2017, 3, 1–7. [Google Scholar]
- Nguyen, H.A.; Giordano, S. Context information prediction for social-based routing in opportunistic networks. Ad Hoc Netw. 2012, 10, 1557–1569. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Zhang, L.; Lin, Y.; Zhao, R. A Routing Algorithm Based on the Prediction of Node Meeting Location in Opportunistic Networks; Springer: Singapore, 2017. [Google Scholar]
- Jinie, P.; Song, Y.T. Health Capability Maturity Model: Person-centered approach in Personal Health Record System. In Proceedings of the Americas Conference on Information Systems, San Diego, CA, USA, 11–14 August 2016. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).