Personalised and Coordinated Demand-Responsive Feeder Transit Service Design: A Genetic Algorithms Approach
Abstract
:1. Introduction
2. Literature
3. Methodology
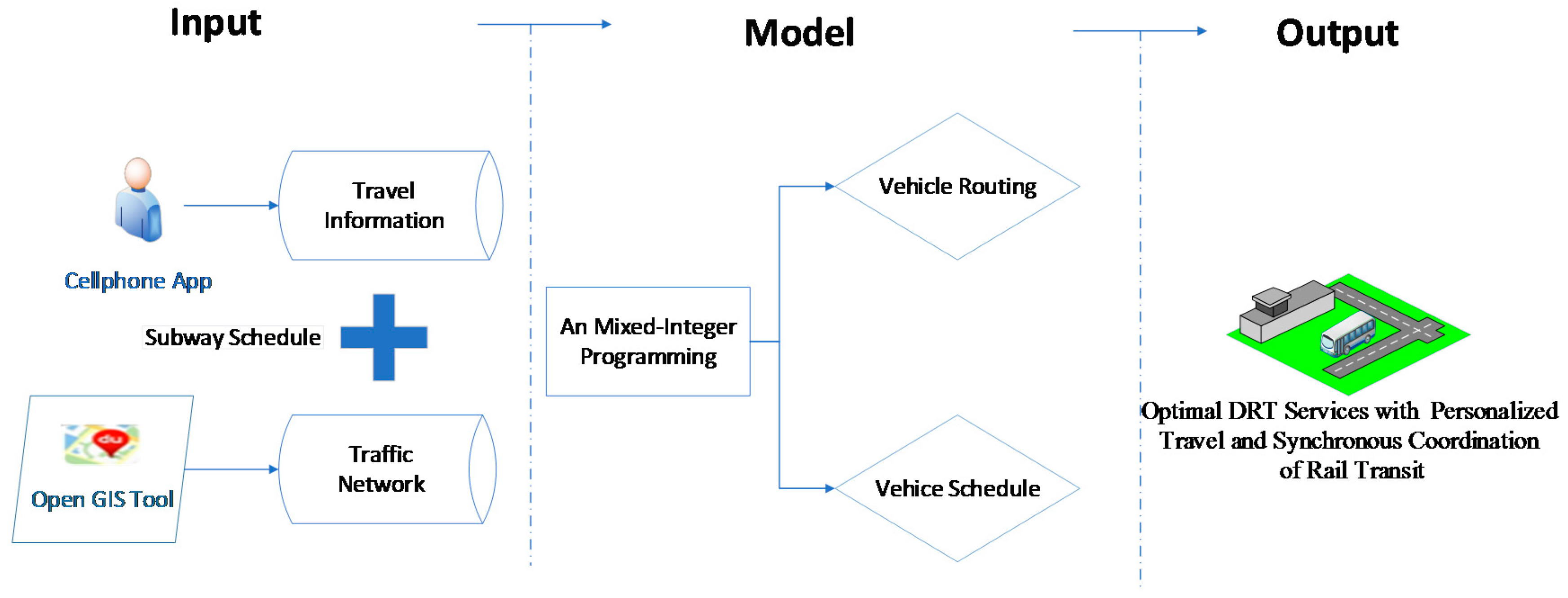
3.1. Research Framework
- (1)
- The pickup locations, the number of passengers, the boarding time window, and the predetermined subway schedule are collected by using a cell phone app.
- (2)
- The travel distance or time between demand points, bus depots, and rail stations in the real traffic network are easily obtained by using the Open GIS tool.
- (3)
- The demand point can only be visited by one feeder bus.
3.2. Model Formulation
3.2.1. Notation
3.2.2. Formulation
4. A GA-Based Heuristic Algorithm
4.1. Coding of GA Chromosomes
- (1)
- The first part of the GA chromosome, (the vector of integer variables) is used to represent the decision of the feeder bus route. The element () is the number of the demand point, and the element () is the number of the vehicle, i.e., .
- (2)
- The second part of the GA chromosome, (the vector of real variables) is used to represent the decision of schedule of the feeder bus. The element denotes the departure time of feeder bus k leaving the bus depot.
4.2. Fitness Evaluation
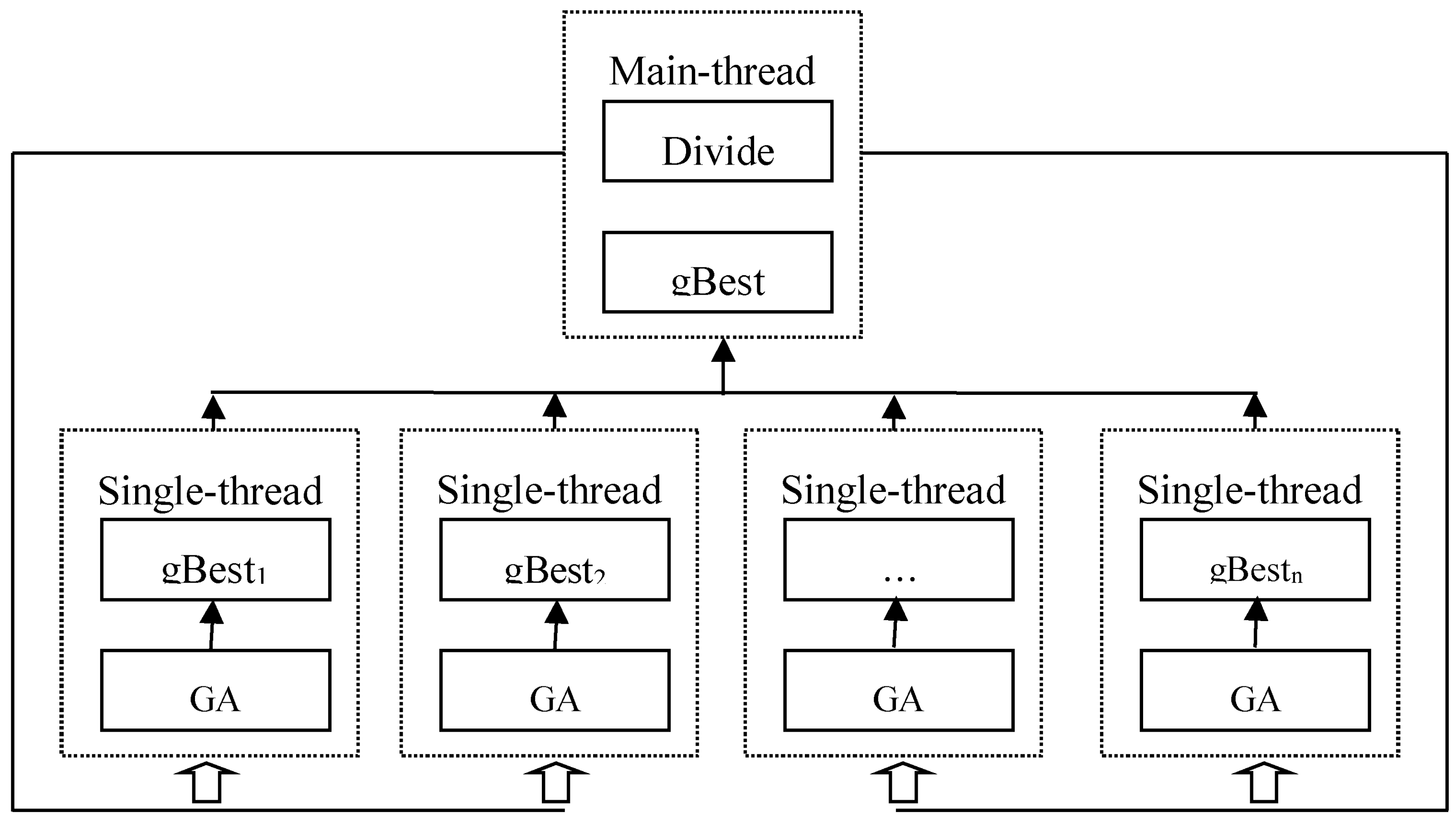
4.3. A Heuristic Algorithm of Generating the Initial Population
- Step 1.
- For , if , find all pairs of feasible adjacent nodes, i.e., .
- Step 2.
- Let denote the set of feeder buses, and each vehicle is randomly and initially placed at the nodes .
- Step 3.
- For each vehicle , find the next feasible nodes in , according to the constraints described by Equations (11)–(13),and randomly select a pair . Let and , and continue to step 4.
- Step 4.
- If , turn to the step 2; otherwise, the algorithm is terminated to output the result.
4.4. Genetic Operators
4.5. Stopping Criteria
5. Numerical Example
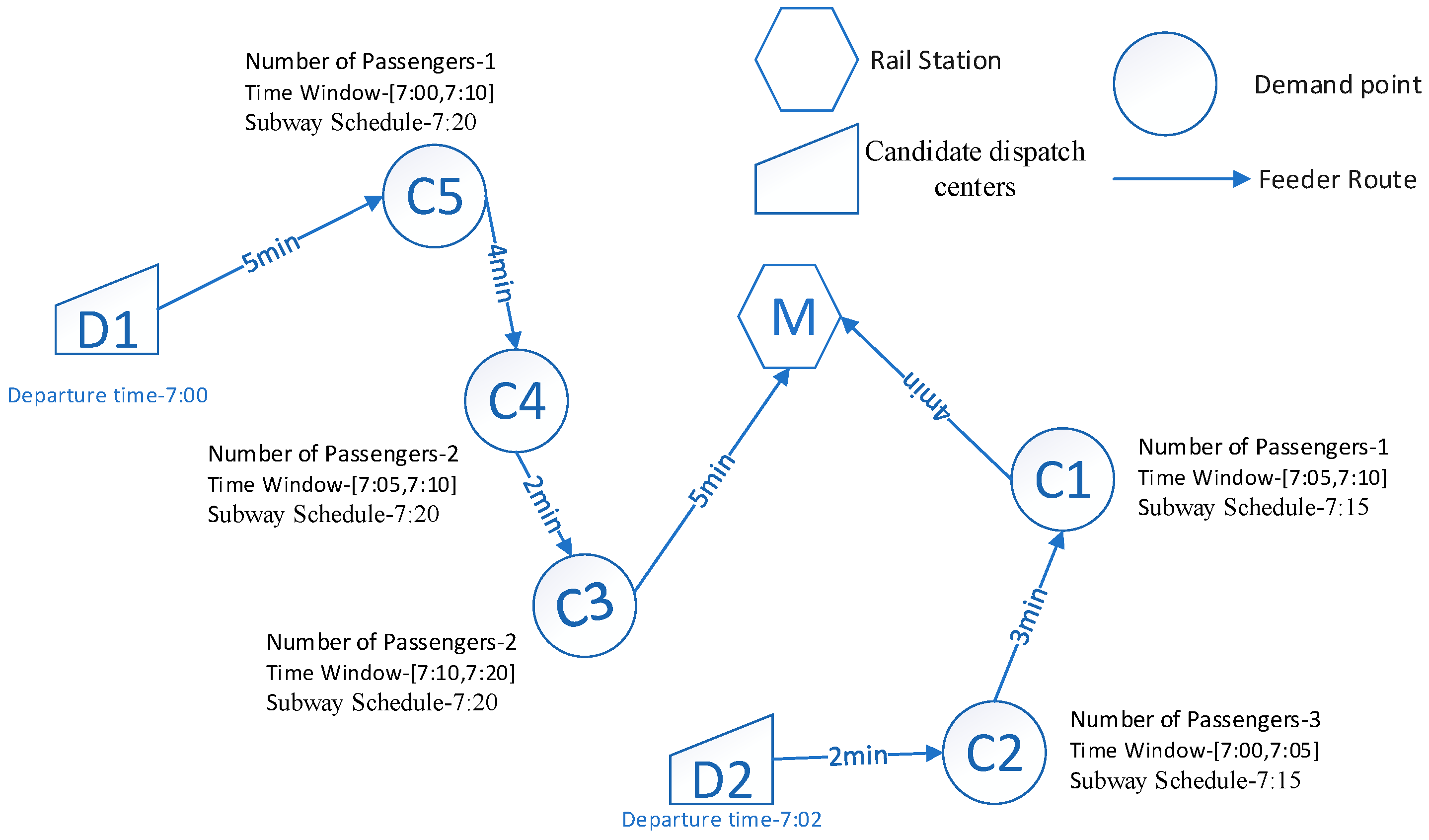
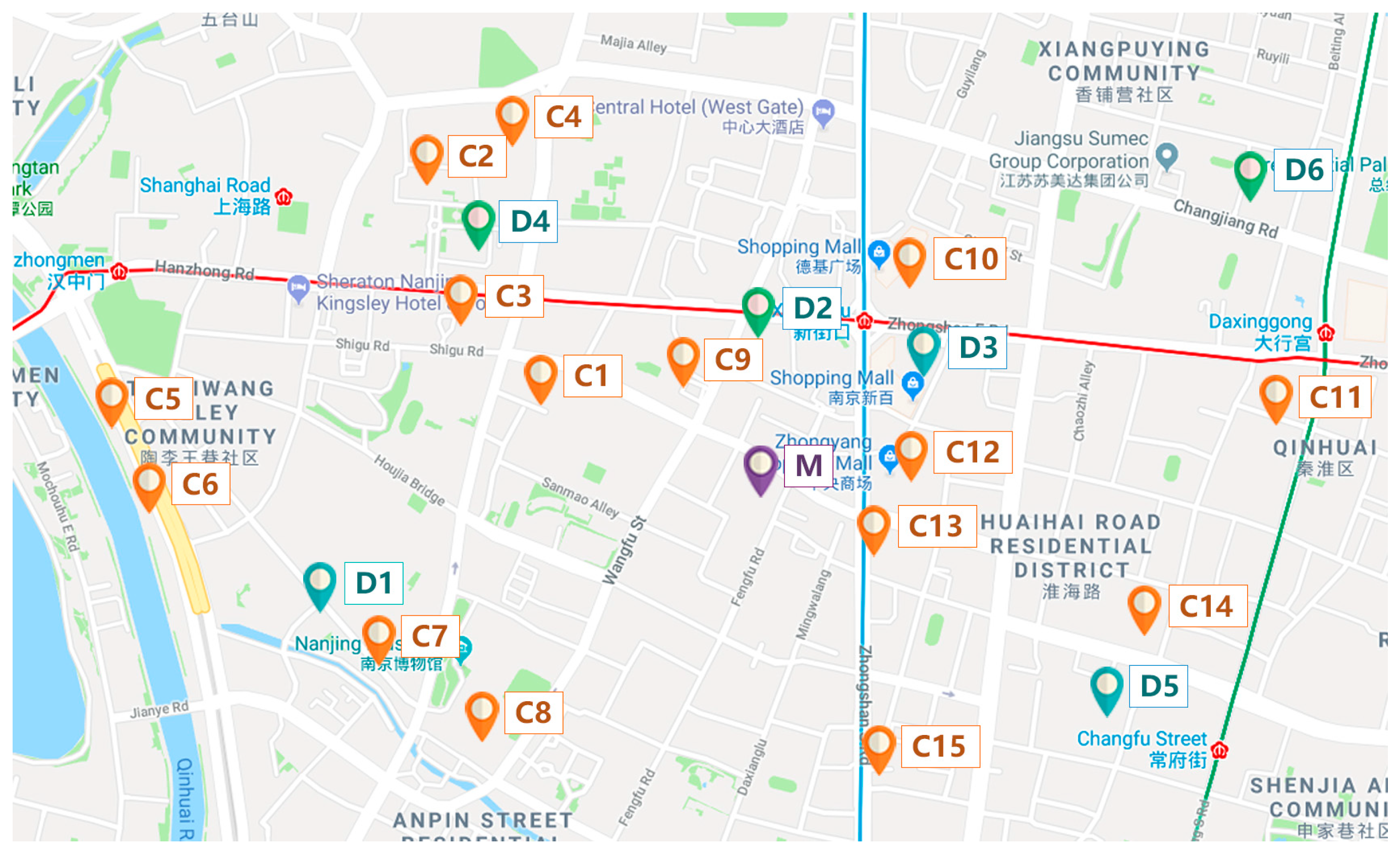
5.1. Example Description
- Number of bus routes: 3;
- Route capacity: Q = 10 people;
- Maximum and minimum length of the vehicle route: = 3 km and = 25 km;
- Maximum travel time of the feeder bus route: = 25 min;
- Walking time for passengers from the drop-off point of the rail station to the subway platform: Tw = 3 km; and
- The parameters of the hybrid algorithm: the number of maximum iterations = 500, the number of chromosomes = 40, the crossover rate = 0.7, and the mutation rate = 0.1.
5.2. Results
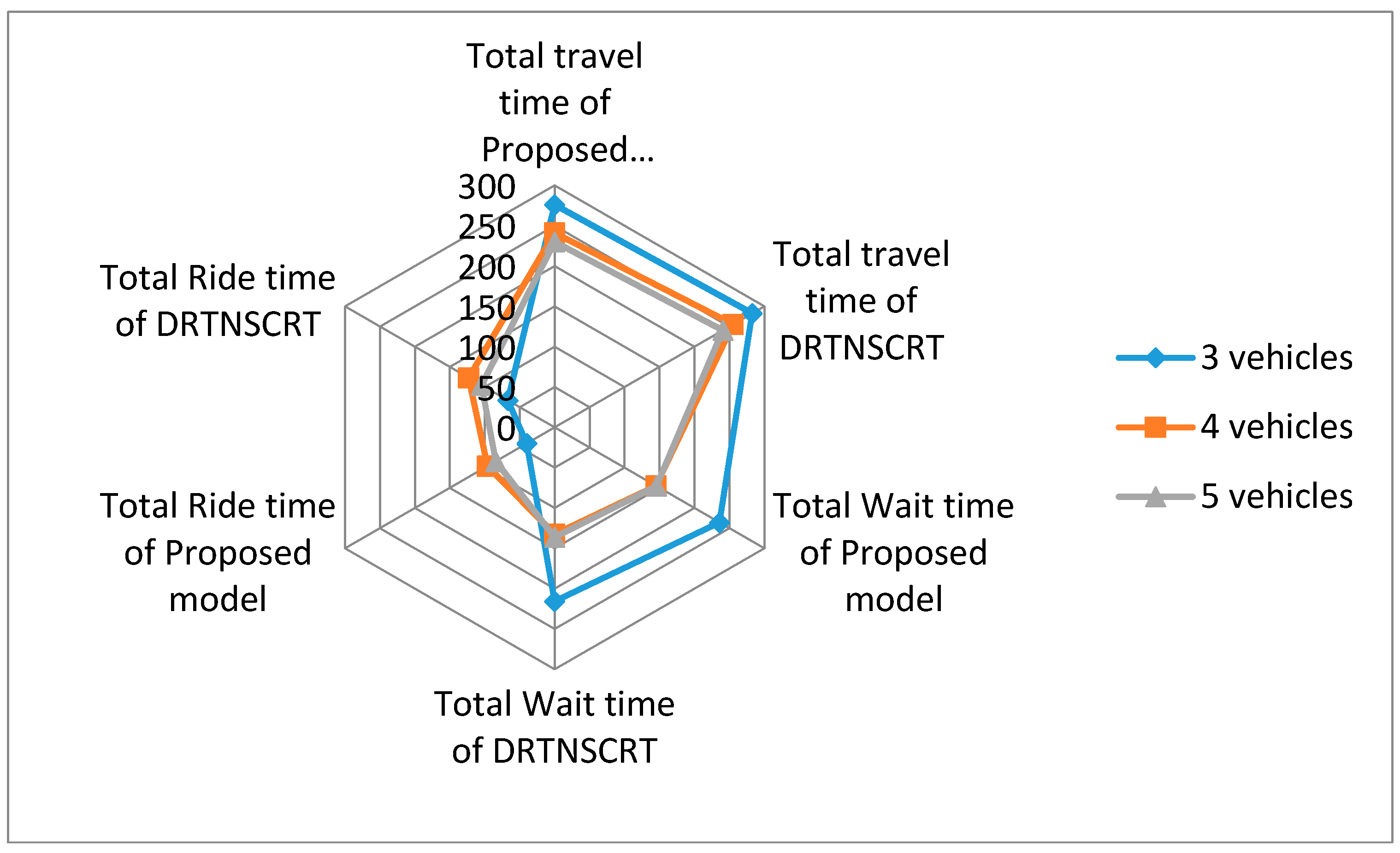
5.3. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ceder, A. Stepwise multi-criteria and multi-strategy design of public transit shuttles. J. Multi-Criteria Decis. Anal. 2009, 16, 21–38. [Google Scholar] [CrossRef]
- Fu, L.P.; Liu, Q.; Calamai, P.; Zhu, S.L. Real-time optimization model for dynamic scheduling of transit operations. Transp. Res. Rec. 2003, 1857, 48–54. [Google Scholar] [CrossRef]
- Savelsbergh, A.L.M. An extended demand responsive connector. EUROJ. Transp. Logist. 2017, 6, 25–50. [Google Scholar]
- Shen, J.X.; Yang, S.Q.; Gao, X.M.; Qiu, F. Vehicle routing and scheduling of demand-responsive connector with on-demand stations. Adv. Mech. Eng. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Maral, S.; Saeed, K.; Iraj, M.; Nezam, M.A. A partial delivery bi-objective vehicle routing model with time windows and customer satisfaction function. Mediterr. J. Soc. Sci. 2016, 7, 101–111. [Google Scholar]
- Azi, N.; Gendreau, M.; Potvin, J.Y. An exact algorithm for a single-vehicle routing problem with time windows and multiple routes. Eur. J. Oper. Res. 2007, 178, 755–766. [Google Scholar] [CrossRef]
- Laporte, G. Fifty years of vehicle routing. Transp. Sci. 2009, 43, 408–416. [Google Scholar] [CrossRef]
- Parragh, S.N.; Doerner, K.F.; Hartl, R.F. A survey on pickup and delivery problems. J. Betriebswirtsch. 2008, 58, 21–51. [Google Scholar] [CrossRef]
- Savelsbergh, M.W.P.; Sol, M. The general pickup and delivery problem. Transp. Sci. 1995, 29, 17–29. [Google Scholar] [CrossRef]
- Desaulniers, G.; Desrosiers, J.; Erdmann, A.; Solomon, M.M.; Soumis, F. VRP with pickup and delivery. In The Vehicle Routing Problem; Toth, P., Vigo, D., Eds.; SIAM Monographs on Discrete Mathematics and Applications: Philadelphia, PA, USA, 2002. [Google Scholar]
- Cordeau, J.F.; Laporte, G. The dial-a-ride problem: Models and algorithms. Ann. Oper. Res. 2007, 153, 29–46. [Google Scholar] [CrossRef]
- Cordeau, J.; Laporte, G.; Potvin, J.Y.; Savelsbergh, M. Chapter 7 transportation on demand. Handb. Oper. Res. Manag. Sci. 2007, 14, 429–466. [Google Scholar]
- Hurdle, V.F. Minimum cost locations for parallel public transit lines. Transp. Sci. 1973, 7, 340–350. [Google Scholar] [CrossRef]
- Kuan, S.N.; Ong, H.L.; Ng, K.M. Solving the Feeder Bus Network Design Problem by Genetic Algorithms and Ant Colony Optimization. Adv. Eng. Softw. 2006, 37, 351–359. [Google Scholar] [CrossRef]
- Wirasinghe, S.C. Nearly Optimal Parameters for a Rail/Feeder-bus System on a Rectangular Grid. Transp. Res. A 1980, 14, 33–40. [Google Scholar] [CrossRef]
- Kuah, G.K.; Perl, J. Optimization of Feeder Bus Routes and Bus-stop Spacing. J. Transp. Eng. 1988, 114, 341–354. [Google Scholar] [CrossRef]
- Kuah, G.K.; Perl, J. The Feeder-bus Network-design Problem. J. Oper. Res. Soc. 1989, 40, 751–767. [Google Scholar] [CrossRef]
- Chowdhury, S.M.; Chien, S.I.J. Intermodal transit system coordination. Transp. Plan. Technol. 2002, 25, 257–287. [Google Scholar] [CrossRef]
- Chang, Y.H.; Chang, B.W. Developing an Integrated Operational Plan between Metro Systems and Feeder-bus Services. J. Chin. Inst. Transp. 1997, 10, 41–72. [Google Scholar]
- Martins, L.C.; Pato, M.V. Search Strategies for the Feeder Bus Network Design Problem. Eur. J. Oper. Res. 1998, 106, 425–440. [Google Scholar] [CrossRef]
- Mohaymany, A.S.; Gholami, A. Multimodal Feeder Network Design Problem: Ant Colony Optimization Approach. J. Transp. Eng. 2010, 136, 323–331. [Google Scholar] [CrossRef]
- Shrivastava, P.; Dhingra, S.L. Development of Feeder Routes for Suburban Railway Stations Using Heuristic Approach. J. Transp. Eng. 2001, 127, 334–341. [Google Scholar] [CrossRef]
- Shrivastava, P.; O’Mahony, M. A Model for Development of Optimized Feeder Routes and Coordinated Schedules: A Genetic Algorithms Approach. Transp. Policy 2006, 13, 413–425. [Google Scholar] [CrossRef]
- Shrivastava, P.; O’Mahony, M. Design of Feeder Route Network Using Combined Genetic Algorithm and Specialized Repair Heuristic. J. Public Transp. 2007, 10, 109–133. [Google Scholar] [CrossRef] [Green Version]
- Shrivastava, P.; O’Mahony, M. Use of Hybrid Algorithm for Modeling Coordinated Feeder Bus Route Network at Suburban Railway Station. J. Transp. Eng. 2009, 135, 1–8. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, D.; Zhou, Z.H.; Li, N.; Atmaca, T.; Li, S. B-Planner: Night bus route planning using large-scale taxi GPS traces. In Proceedings of the 2013 IEEE International Conference on Pervasive Computing and Communications (PerCom), San Diego, CA, USA, 18–22 March 2013; pp. 225–233. [Google Scholar]
- Deng, L.B.; Gao, W.; Zhou, W.L.; Lai, T.Z. Optimal design of feeder-bus network related to urban rail line based on transfer system. Procedia-Soc. Behav. Sci. 2013, 96, 2383–2394. [Google Scholar] [CrossRef]
- Pan, S.; Yu, J.; Yang, X.; Liu, Y.; Zou, N. Designing a Flexible Feeder Transit System Serving Irregularly Shaped and Gated Communities: Determining Service Area and Feeder Route Planning. J. Urban Plan. Dev. 2014, 141, 0401–4028. [Google Scholar] [CrossRef]
- Yu, Y.; Machemehl, R.; Hakimi, S. Real-Time Optimization of Passenger Collection for Commuter Rail Systems; Technical report 600451-00082-1; Center of Transportation Research, University of Texas at Austin, National Technical Information Service: Springfield, VA, USA, 2014. [Google Scholar]
- Sun, Y.; Sun, X.; Li, B.; Gao, D. Joint optimization of a rail transit route and bus routes in a transit corridor. Procedia-Soc. Behav. Sci. 2013, 96, 1218–1226. [Google Scholar] [CrossRef]
- Yan, Y.; Liu, Z.; Meng, Q.; Jiang, Y. Robust optimization model of bus transit network design with stochastic travel time. J. Transp. Eng. 2013, 139, 625–634. [Google Scholar] [CrossRef]
- Sun, B.; Wei, M.; Zhu, S.L. Optimal Design of Demand-Responsive Feeder Transit Services with Passengers’ Multiple Time Windows and Satisfaction. Future Internet 2018, 10, 30–45. [Google Scholar] [CrossRef]
- Wei, M.; Sun, B.; Sun, R. Expected value model of bus gas station site layout problem with fuzzy demand in supplementary fuel using genetic algorithm. Clust. Comput. 2017, 1, 1–10. [Google Scholar] [CrossRef]
- Wei, M.; Sun, B. Bi-level programming model for multi-modal regional bus timetable and vehicle dispatch with stochastic travel time. Clust. Comput. 2017, 20, 1–11. [Google Scholar] [CrossRef]
- Nandy, A.; Chakraborty, D.; Shah, M.S. Optimal Sensors/Actuators Placement in Smart Structure Using Island Model Parallel Genetic Algorithm. Int. J. Comput. Methods 2017, 1, 184–187. [Google Scholar] [CrossRef]
- Yang, D.; Liu, Z.; Shu, T.; Yang, L.; Ouyang, J.; Shen, Z. An Improved Genetic Algorithm for Multiobjective Optimization of Helical Coil Electromagnetic Launchers. IEEE Trans. Plasma Sci. 2017, 99, 1–7. [Google Scholar] [CrossRef]
| Indices | |
| Node(demand point, bus depot and rail station) index | |
| Feeder bus index | |
| Subway schedule trip index | |
| Sets | |
| I | Set of demand points |
| K | Set of feeder buses |
| Set of bus depots | |
| Set of rail transit stations | |
| Set of subway schedule trips at rail station ; | |
| Parameters | |
| Number of passengers at the demand point ; | |
| The boarding time window of the demand point ; | |
| The subway schedule trip p of rail station m chosen by passengers at demand points ; , , | |
| Distance from the node i to node ; | |
| Travel time from the node i to node ; | |
| Depature time of subway schedule trip p at rail station m; , | |
| Walking time for passengers from the drop-off point of the rail station to the subway platform | |
| Maximum travel time of feeder bus route | |
| and | Maximum and minimum travel mileage of feeder bus |
| Q | Maximum capacity of feeder bus |
| A very large fixed value | |
| Decision Variables | |
| Whether the node i precedes the node on the vehicle k, or not; , | |
| Whether the node i is covered by the vehicle k, or not; , | |
| The time of vehicle k arriving the node ; | |
| Number of passengers at node assigned to vehicle k; | |
| An auxiliary (real) variable for sub-tour elimination constraint in vehicle k; | |
| Demand Point | qi (Person) | Time Window | Preferred Subway Schedule |
|---|---|---|---|
| C1 | 1 | 6:10–6:20 | 6:28 |
| C2 | 2 | 6:20–6:30 | 6:32 |
| C3 | 1 | 6:10–6:20 | 6:36 |
| C4 | 3 | 6:10–6:20 | 6:32 |
| C5 | 2 | 6:15–6:25 | 6:28 |
| C6 | 3 | 6:15–6:25 | 6:28 |
| C7 | 1 | 6:20–6:30 | 6:32 |
| C8 | 2 | 6:20–6:30 | 6:32 |
| C9 | 1 | 6:10–6:20 | 6:36 |
| C10 | 3 | 6:20–6:30 | 6:28 |
| C11 | 2 | 6:20–6:30 | 6:36 |
| C12 | 3 | 6:10–6:20 | 6:36 |
| C13 | 1 | 6:00–6:10 | 6:28 |
| C14 | 3 | 6:10–6:20 | 6:36 |
| C15 | 2 | 6:20–6:30 | 6:32 |
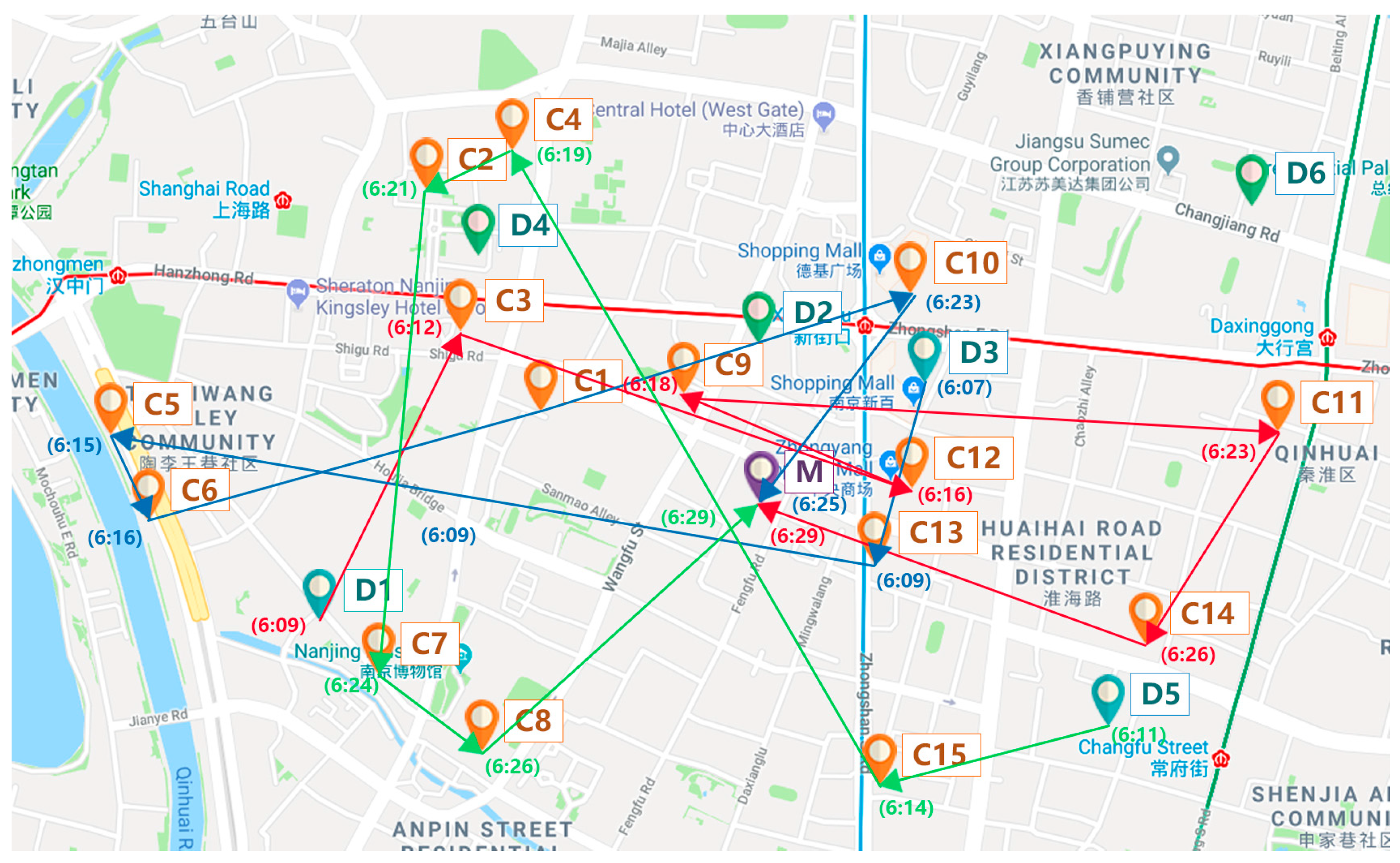
| Vehicle | Sequence of Demand Points Visited by the Vehicle | Travel Distance (km) | Travel Time (min) | Number of Passengers | Wait-Time (min) |
|---|---|---|---|---|---|
| V1 | D1(6:09)-C3(6:12)-C12(6:16)-C9(6:18)-C11(6:23)-C14(6:26)-M(6:29) | 5.0 | 19.9 | 10 | 4 |
| V2 | D3(6:07)-C13(6:09)-C5(6:15)-C6(6:16)-C1(6:19)-C10(6:23)-M(6:25) | 4.4 | 17.8 | 10 | 0 |
| V3 | D5(6:11)-C15(6:14)-C4(6:19)-C2(6:21)-C7(6:24)-C8(6:26)-M(6:29) | 4.5 | 17.5 | 10 | 0 |
| Demand Point | Boarding Time | Ride-Time | Wait-Time | Vehicle |
|---|---|---|---|---|
| C3 | 6:12 | 17 | 4 | V1 |
| C9 | 6:18 | 11 | 4 | |
| C11 | 6:23 | 6 | 4 | |
| C12 | 6:16 | 13 | 4 | |
| C14 | 6:26 | 3 | 4 | |
| C1 | 6:19 | 6 | 0 | V2 |
| C5 | 6:15 | 10 | 0 | |
| C6 | 6:16 | 9 | 0 | |
| C10 | 6:23 | 2 | 0 | |
| C13 | 6:09 | 16 | 0 | |
| C2 | 6:21 | 8 | 0 | V3 |
| C4 | 6:19 | 10 | 0 | |
| C7 | 6:24 | 5 | 0 | |
| C8 | 6:26 | 3 | 0 | |
| C15 | 6:14 | 15 | 1 |
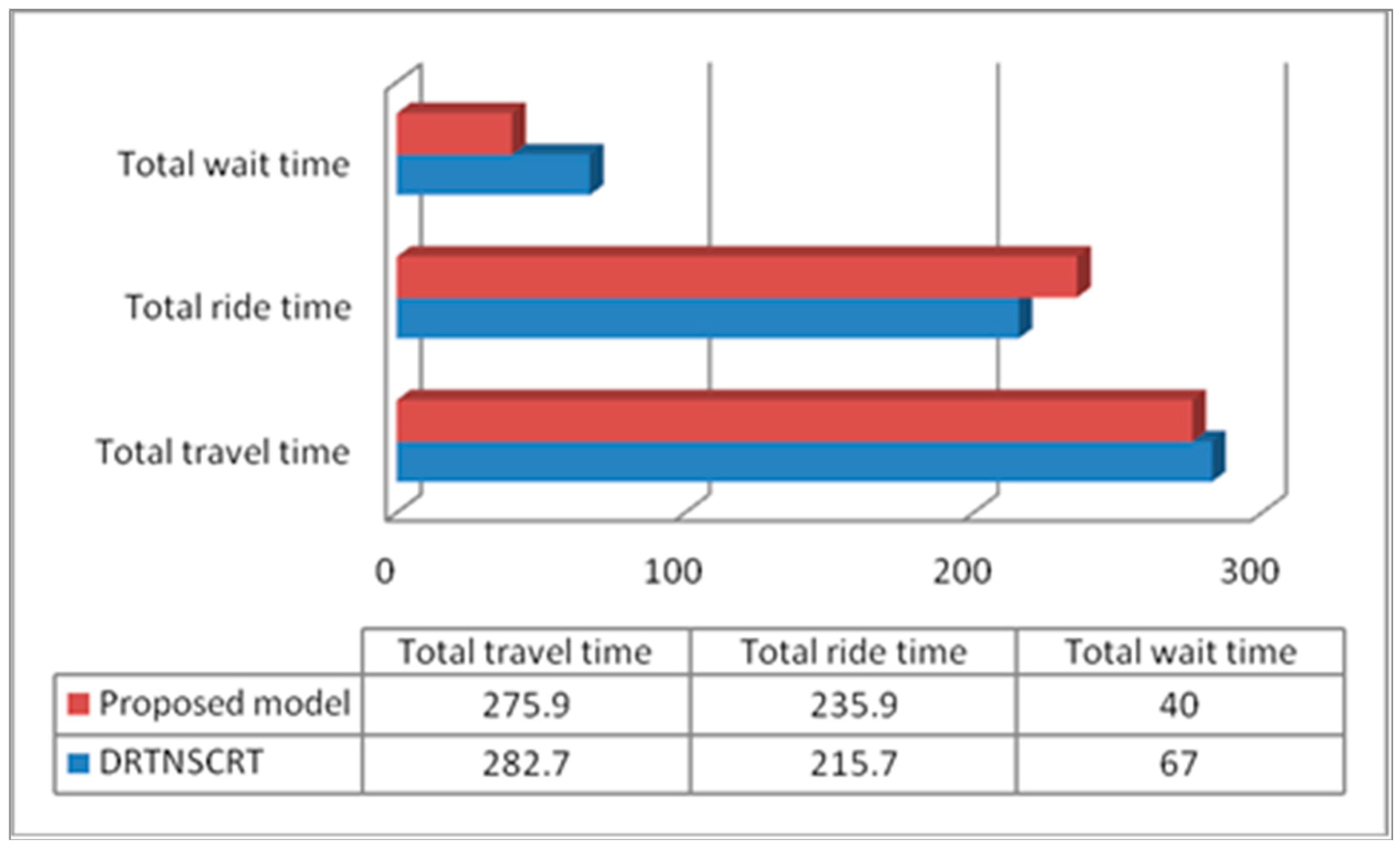
| Scenario | Objective(min) | Average Caculate Time (min) | Total Ride Time (min) | Total Wait Time (min) | Total Route Mileages (km) | Total Route Times(min) | ||
|---|---|---|---|---|---|---|---|---|
| Cplex | Improved GA | Cplex | Improved GA | |||||
| 3 Vehicles | 275.9 | 295.2 | 20.1 | 3.6 | 235.9 | 40 | 13.9 | 55.2 |
| 4 Vehicles | 241.2 | 253.3 | 120.2 | 4.2 | 145.2 | 96 | 14.3 | 57.0 |
| 5 Vehicles | 230.0 | 246.1 | 1500.3 | 4.6 | 145.7 | 84.3 | 18.1 | 72.1 |
| Number of Demand Points | Improved GA | Standard GA | Difference | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Iteration Times of Convergence | Best Solution | Worst Solution | Average Solution | Iteration Times of Convergence | Best Solution | Worst Solution | Average Solution | ||
| 50 | 67 | 416.1 | 438.7 | 423.3 | 112 | 416.1 | 449.2 | 438.9 | 3.7% |
| 100 | 87 | 785.2 | 868.2 | 827.6 | 197 | 792.7 | 902.6 | 880.6 | 6.4% |
| 200 | 104 | 1442.7 | 1566.4 | 1506.5 | 345 | 1472.3 | 1728.6 | 1676.7 | 11.3% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, B.; Wei, M.; Yang, C.; Xu, Z.; Wang, H. Personalised and Coordinated Demand-Responsive Feeder Transit Service Design: A Genetic Algorithms Approach. Future Internet 2018, 10, 61. https://doi.org/10.3390/fi10070061
Sun B, Wei M, Yang C, Xu Z, Wang H. Personalised and Coordinated Demand-Responsive Feeder Transit Service Design: A Genetic Algorithms Approach. Future Internet. 2018; 10(7):61. https://doi.org/10.3390/fi10070061
Chicago/Turabian StyleSun, Bo, Ming Wei, Chunfeng Yang, Zhihuo Xu, and Han Wang. 2018. "Personalised and Coordinated Demand-Responsive Feeder Transit Service Design: A Genetic Algorithms Approach" Future Internet 10, no. 7: 61. https://doi.org/10.3390/fi10070061
APA StyleSun, B., Wei, M., Yang, C., Xu, Z., & Wang, H. (2018). Personalised and Coordinated Demand-Responsive Feeder Transit Service Design: A Genetic Algorithms Approach. Future Internet, 10(7), 61. https://doi.org/10.3390/fi10070061




