Influence of Crowd Participation Features on Mobile Edge Computing
Abstract
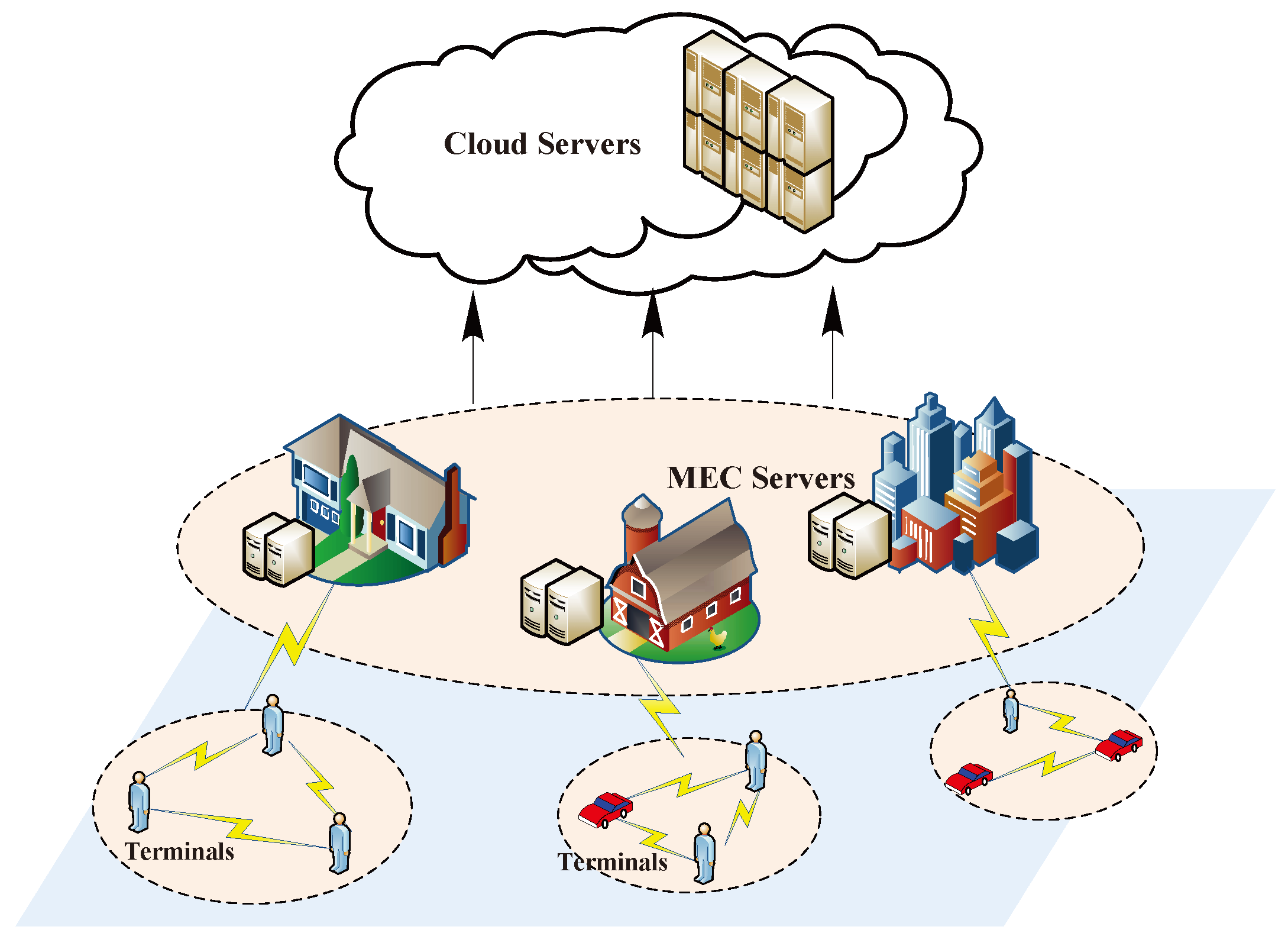
:1. Introduction
- Opportunistic caching: The application can independently decide which content should be stored and shared, without active participation from end users.
- Opportunistic transmission: The routing path cannot be decided in advance, and the content is delivered in a store-carry-forward style.
2. Opportunistic Caching
- (1)
- How big a buffer space should each node reserve?
- (2)
- How many copies should be stored for each content?
- (3)
- Where should these copies be stored?
2.1. Cache Size: How Big Is the Buffer Space?
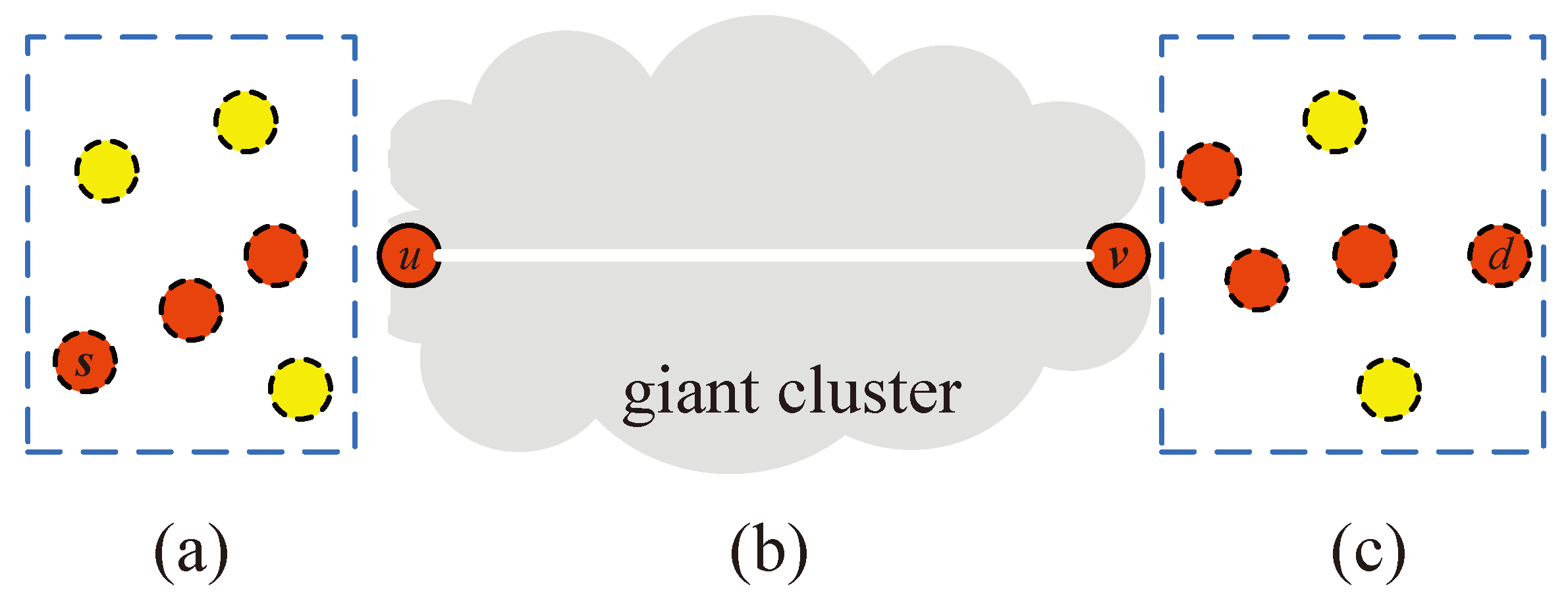
Upper Bound Analysis
2.2. Content Copies: How Many Copies Should Be Stored?
2.3. Content Allocation: Where to Store the Copies?
2.3.1. Cache Contents in the UTs and FAE
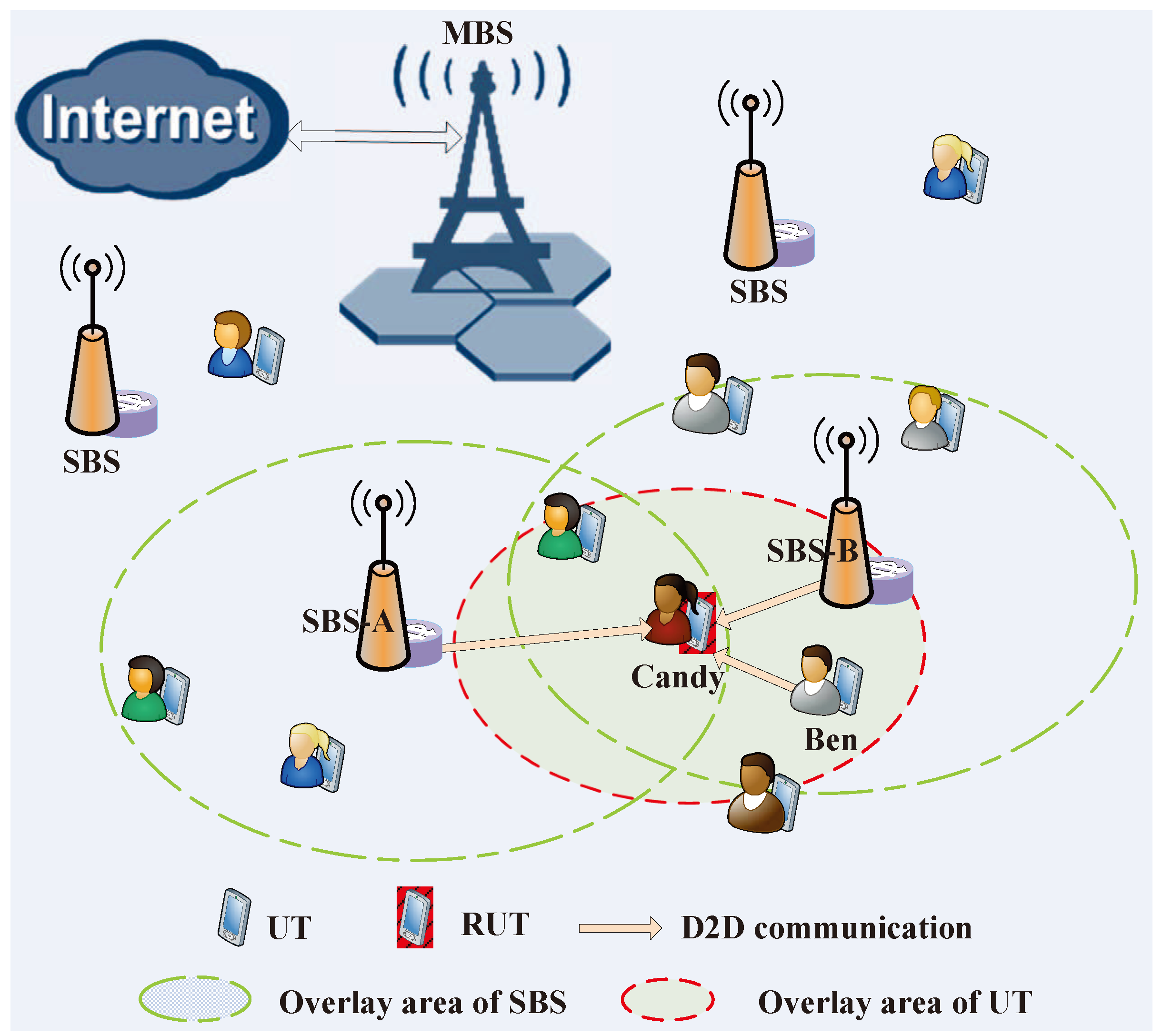
2.3.2. Cache Contents in the D2D Group
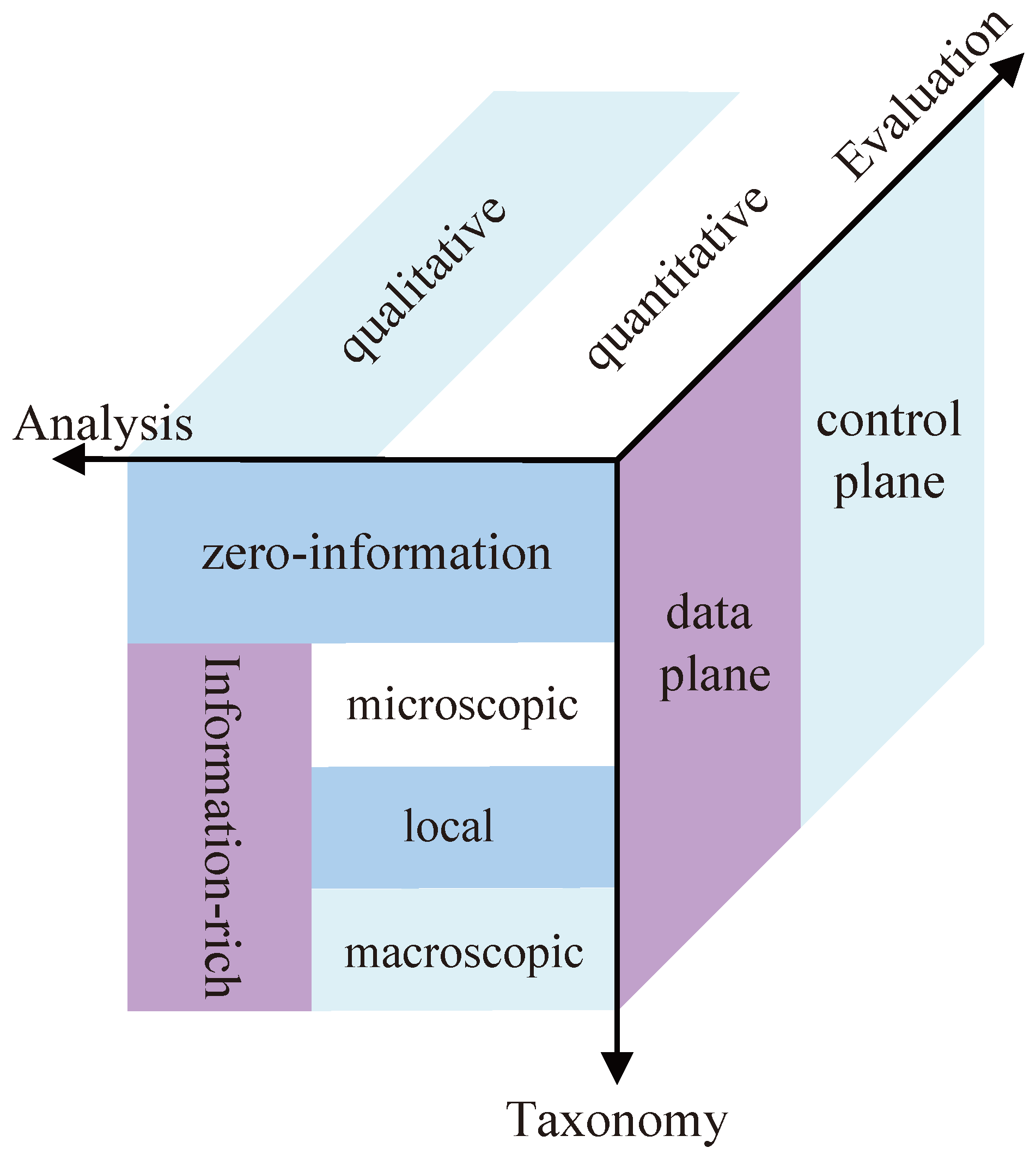
3. Opportunistic Transmission
3.1. Control Plane: How to Collect the Heuristic Information?
3.2. Data Plane: How to Select the Desired Relay?
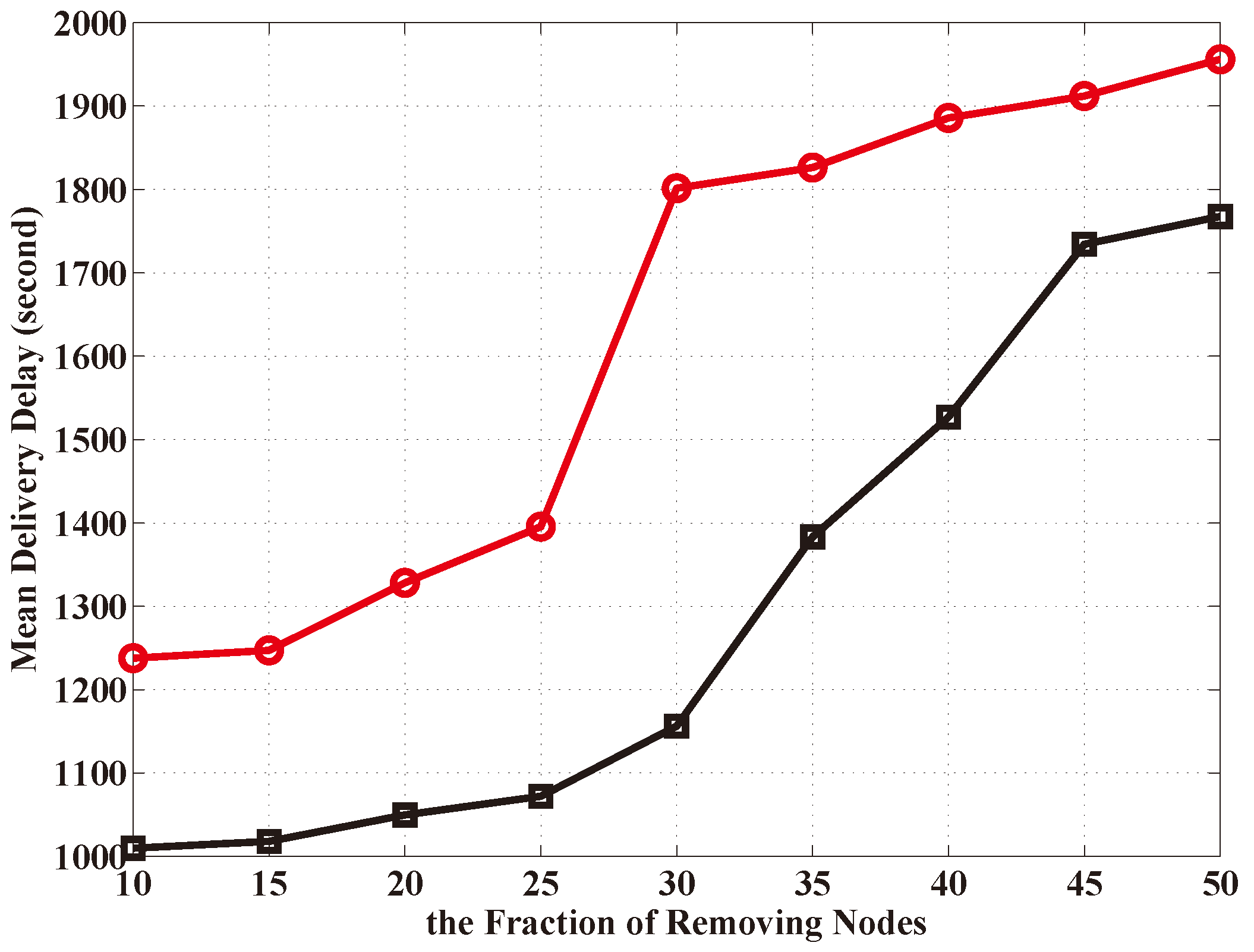
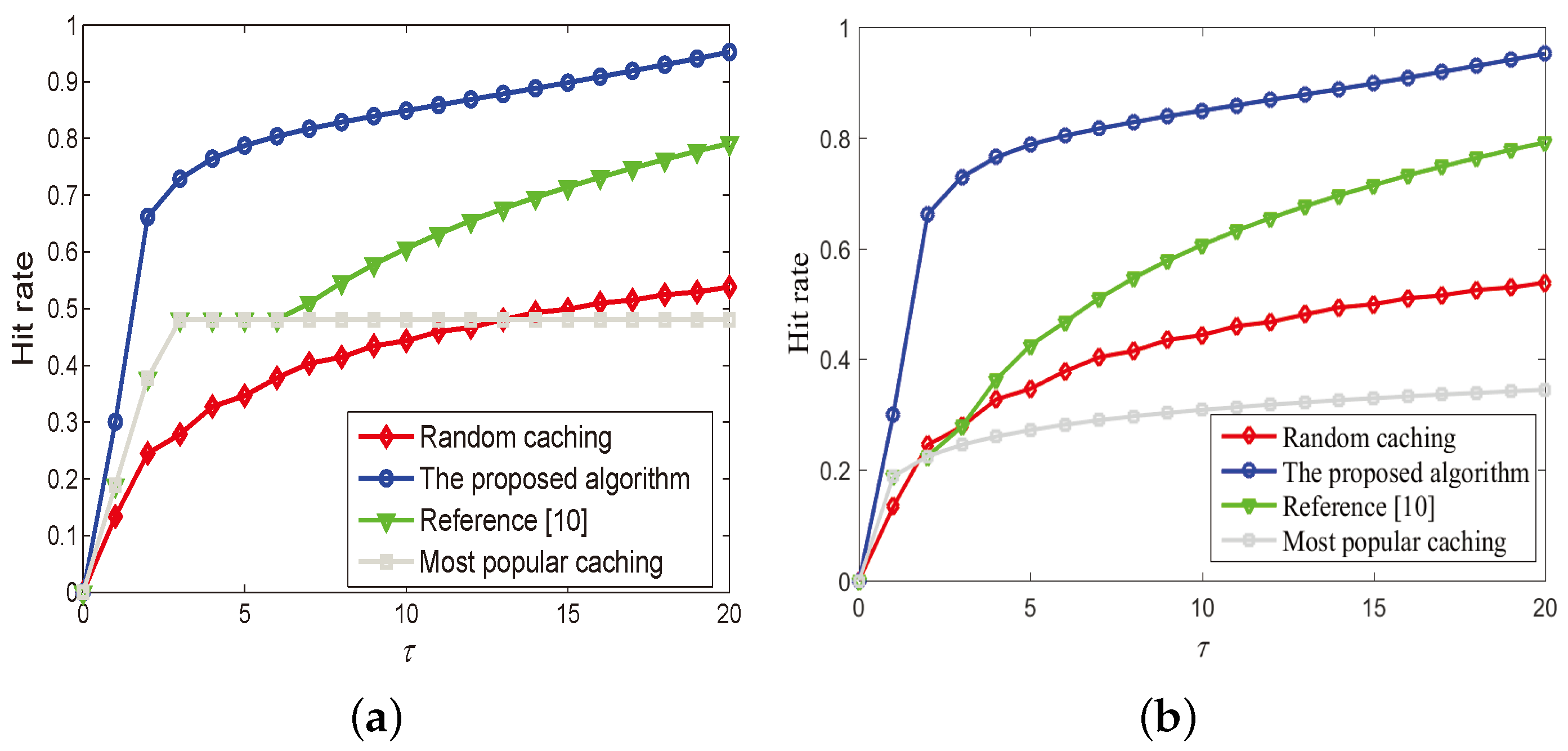
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ma, H.; Liu, L.; Zhou, A.; Zhao, D. On networking of internet of things: Explorations and challenges. IEEE Internet Things J. 2016, 3, 441–452. [Google Scholar] [CrossRef]
- Huang, J.; Xing, C.C.; Wang, C. Simultaneous Wireless Information and Power Transfer: Technologies, Applications, and Research Challenges. IEEE Commun. Mag. 2017, 55, 26–32. [Google Scholar] [CrossRef]
- Wang, X.; Chen, M.; Taleb, T.; Ksentini, A.; Leung, V. Cache in the air: exploiting content caching and delivery techniques for 5G systems. IEEE Commun. Mag. 2014, 52, 131–139. [Google Scholar] [CrossRef]
- Bilal, K.; Khalid, O.; Erbad, A.; Khan, S.U. Potentials, trends, and prospects in edge technologies: Fog, cloudlet, mobile edge, and micro data centers. Comput. Netw. 2018, 130, 94–120. [Google Scholar] [CrossRef]
- Yang, C.; Yao, Y.; Chen, Z.; Xia, B. Analysis on Cache-Enabled Wireless Heterogeneous Networks. IEEE Trans. Wirel. Commun. 2016, 15, 131–145. [Google Scholar] [CrossRef]
- Ma, H.; Zhao, D.; Yuan, P. Opportunities in mobile crowd sensing. IEEE Commun. Mag. 2014, 52, 29–35. [Google Scholar] [CrossRef]
- Ma, H.; Liu, Y. On coverage problems of directional sensor networks. In Proceedings of the International Conference on Mobile Ad-Hoc and Sensor Networks, Wuhan, China, 13–15 December 2005; pp. 721–731. [Google Scholar]
- Yuan, P.; Ma, H.; Fu, H. Hotspot-entropy based data forwarding in opportunistic social networks. Pervasive Mob. Comput. 2015, 16, 136–154. [Google Scholar] [CrossRef]
- Luo, H.; Luo, J.; Liu, Y.; Das, S.K. Adaptive data fusion for energy efficient routing in wireless sensor networks. IEEE Trans. Comput. 2006, 55, 1286–1299. [Google Scholar]
- Zhao, X.; Yuan, P.; Chen, Y.; Chen, P. Femtocaching assisted multi-source D2D content delivery in cellular networks. EURASIP J. Wirel. Commun. Netw. 2017, 2017, 125. [Google Scholar] [CrossRef] [Green Version]
- Gerla, M.; Tsai, J.T.C. Multicluster, mobile, multimedia radio network. Wirel. Netw. 1995, 1, 255–265. [Google Scholar] [CrossRef]
- Lin, C.R.; Gerla, M. Adaptive clustering for mobile wireless networks. IEEE J. Sel. Areas Commun. 1997, 15, 1265–1275. [Google Scholar] [CrossRef] [Green Version]
- Tsiropoulou, E.E.; Paruchuri, S.T.; Baras, J.S. Interest, energy and physical-aware coalition formation and resource allocation in smart IoT applications. In Proceedings of the 2017 51st Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 22–24 March 2017; pp. 1–6. [Google Scholar]
- Tsiropoulou, E.E.; Mitsis, G.; Papavassiliou, S. Interest-aware energy collection & resource management in machine to machine communications. Ad Hoc Netw. 2018, 68, 48–57. [Google Scholar]
- Zhao, X.; Yuan, P.; Chen, Y.; Chen, P. Cooperative D2D for Content Delivery in Heterogeneous Networks. In Proceedings of the International Conference on Big Data Computing and Communications, Chengdu, China, 10–11 August 2017; pp. 265–271. [Google Scholar]
- Becchetti, L.; Clementi, A.; Pasquale, F.; Resta, G.; Santi, P.; Silvestri, R. Flooding time in opportunistic networks under power law and exponential intercontact times. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 2297–2306. [Google Scholar] [CrossRef]
- Yuan, P.; Wu, H.; Zhao, X.; Dong, Z. Percolation-theoretic bounds on the cache size of nodes in mobile opportunistic networks. Sci. Rep. 2017, 7, 5662. [Google Scholar] [CrossRef] [PubMed]
- Yuan, P.; Wu, H.; Zhao, X.; Dong, Z. Cache Potentiality of MONs: A Prime. In Proceedings of the IEEE International Conference on Distributed Computing Systems, Atlanta, GA, USA, 5–8 June 2017; pp. 2650–2653. [Google Scholar]
- Zhu, H.; Huang, C.; Li, H. Information diffusion model based on privacy setting in online social networking services. Comput. J. 2014, 58, 536–548. [Google Scholar] [CrossRef]
- Zhao, X.; Yuan, P.; Li, H.; Tang, S. Collaborative edge caching in context-aware D2D networks. IEEE Trans. Veh. Technol. 2018. [Google Scholar] [CrossRef]
- Fan, L.; Dong, Z.; Yuan, P. The capacity of Device-to-device communication underlaying cellular networks with relay links. IEEE Access 2017, 5, 16840–16846. [Google Scholar] [CrossRef]
- Yuan, P.; Fan, L.; Liu, P.; Tang, S. Recent progress in routing protocols of mobile opportunistic networks. J. Netw. Comput. Appl. 2016, 62, 163–170. [Google Scholar] [CrossRef]
- Lindgren, A.; Doria, A.; Schelen, O. Probabilistic routing in intermittently connected networks. In Service Assurance with Partial and Intermittent Resources; Springer: Berlin, Germany, 2004; pp. 239–254. [Google Scholar]
- Daly, E.M.; Haahr, M. Social network analysis for information flow in disconnected delay-tolerant MANETs. IEEE Trans. Mob. Comput. 2009, 8, 606–621. [Google Scholar] [CrossRef]
- Hui, P.; Crowcroft, J.; Yoneki, E. Bubble rap: Social-based forwarding in delay-tolerant networks. IEEE Trans. Mob. Comput. 2011, 10, 1576–1589. [Google Scholar] [CrossRef]
- Yuan, P.; Song, M.; Zhao, X. Effective and efficient collection of control messages for opportunistic routing algorithms. J. Netw. Comput. Appl. 2017, 125–130. [Google Scholar] [CrossRef]
- Mtibaa, A.; May, M.; Diot, C.; Ammar, M. Peoplerank: Social opportunistic forwarding. In Proceedings of the Infocom, San Diego, CA, USA, 14–19 March 2010; pp. 1–5. [Google Scholar]
- Yuan, P.; Liu, P.; Tang, S. RIM: Relative-importance based data forwarding in people-centric networks. J. Netw. Comput. Appl. 2016, 62, 100–111. [Google Scholar] [CrossRef]
- Pietilänen, A.K.; Diot, C. Dissemination in opportunistic social networks: the role of temporal communities. In Proceedings of the Thirteenth ACM international Symposium on Mobile Ad Hoc Networking and Computing, Hilton Head, SC, USA, 11–14 June 2012; pp. 165–174. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, P.; Pang, X.; Zhao, X. Influence of Crowd Participation Features on Mobile Edge Computing. Future Internet 2018, 10, 94. https://doi.org/10.3390/fi10100094
Yuan P, Pang X, Zhao X. Influence of Crowd Participation Features on Mobile Edge Computing. Future Internet. 2018; 10(10):94. https://doi.org/10.3390/fi10100094
Chicago/Turabian StyleYuan, Peiyan, Xiaoxiao Pang, and Xiaoyan Zhao. 2018. "Influence of Crowd Participation Features on Mobile Edge Computing" Future Internet 10, no. 10: 94. https://doi.org/10.3390/fi10100094
APA StyleYuan, P., Pang, X., & Zhao, X. (2018). Influence of Crowd Participation Features on Mobile Edge Computing. Future Internet, 10(10), 94. https://doi.org/10.3390/fi10100094




