Proactive Caching at the Edge Leveraging Influential User Detection in Cellular D2D Networks

Abstract

Caching close to users in a radio access network (RAN) has been identified as a promising method to reduce a backhaul traffic load and minimize latency in 5G and beyond. In this paper, we investigate a novel community detection inspired by a proactive caching scheme for device-to-device (D2D) enabled networks. The proposed scheme builds on the idea that content generated/accessed by influential users is more probable to become popular and thus can be exploited for pro-caching. We use a Clustering Coefficient based Genetic Algorithm (CC-GA) for community detection to discover a group of cellular users present in close vicinity. We then use an Eigenvector Centrality measure to identify the influential users with respect to the community structure, and the content associated to it is then used for pro-active caching using D2D communications. The numerical results show that, compared to reactive caching, where historically popular content is cached, depending on cache size, load and number of requests, up to 30% more users can be satisfied using a proposed scheme while achieving significant reduction in backhaul traffic load.

1. Introduction

Generational shifts in the world of mobile networks have been driven by the unprecedented growth in mobile data traffic. The exponentially growing number of connected devices and the unquenchable thirst for better mobile broadband experience is also a driving force behind this evolution. The story of 5G is no more different as it is envisioned to provide a gigabit experience and virtually zero latency while withstanding an expected 500-fold increase in mobile video traffic over the next ten years. It is predicted that 75% of global mobile data will be video content in which 6.7% will be machine-to-machine (M2M) communication. Such massive growth of multimedia traffic was further fueled by social media feeds, such as Facebook and Twitter (representing 15% of the traffic [1]). This trend is undoubtedly going to stress the capacity of core networks, wireless links and mobile backhauls to their limits eventually leading to poor quality-of-experience (QoE).

In order to cope with this issue, a 5G network is gearing up with various technologies including device-to-device (D2D) communication [2], Massive MIMO (Multiple-input multiple-output) [3,4], Device-centric architecture [5], Small Cells, Caching, mmWave communication [6] all orchestrated by self organizing networks (SON) [7]. Among them, caching through D2D mode of communication is being considered a promising technology aimed for reducing backhaul load and minimizing latency [5]. The key idea of D2D enabled caching is to store the popular content of the network at the user end. The key benefit here is that it brings likely to be accessed content as close as possible to the users. This approach can reduce latency substantially, a key challenging requirement in 5G [8]. It can also increase the effective throughput and reduce the backhaul load [9]. The three key research questions in designing an optimal caching enabled next generation Radio Access Network (RAN) are: Where to cache? How to cache? and What to cache? Where to cache focuses on the problem of caching the content over the network in such a way that it reduces the network traffic. How to cache focuses on multiple ways of content caching, and what to cache focuses on the problem of finding content having the highest probabilities to be used in the near future. In order to address these questions, various attempts have been made by the researchers such as [9,10,11,12,13]. For a detailed review of caching in RAN, the reader is referred to [14,15]. However, to the best of the authors’ knowledge, this is a first study that investigates the potential of the leveraging detection of influential users via centrality measure in cellular networks and then uses that detection for identifying what to cache and pro-actively caching those likely to be accessing content using D2D communications.

Online Social Networks, one of the key sources of mobile data explosion, are known to be scale-free networks, which follow power-law distribution. For example, the Twitter network has millions of users and an enormous flow of information is published daily. There are small number of Twitter users who have a large number of followers while there is a huge number of users who have a small number of followers. In this paper, our key idea to design and evaluate a novel proactive yet low complexity caching solution is as follows. It is highly probable that content accessed or generated by influential users will become popular due to their relatively higher following and connectivity. Furthermore, popular content is expected to be in demand in the same community i.e., the community of the influential user first and then spread slowly in the remaining network. The mapping structure, information diffusion and influence phenomena of the social networks can thus be exploited for proactively caching those content which are expected to be highly demanded in the near future, for reducing the backhaul traffic load [16]. Therefore, we represent a mobile cellular network in the form of a graph and use graph theory and Social Network Analysis (SNA) techniques to improve QoE and reduce the backhaul traffic load.

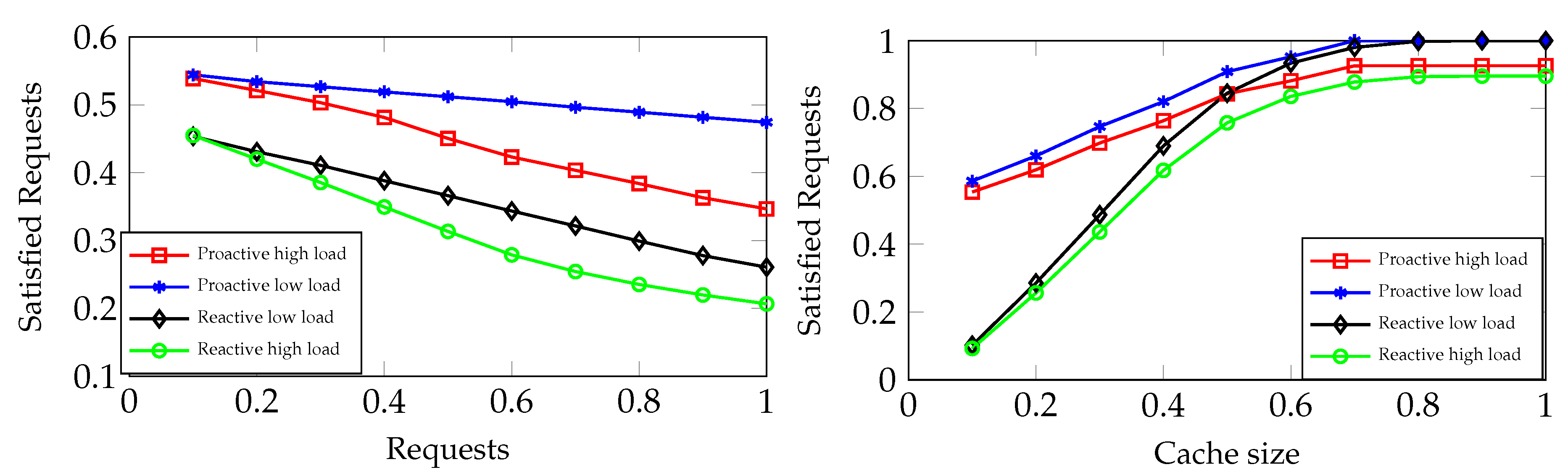
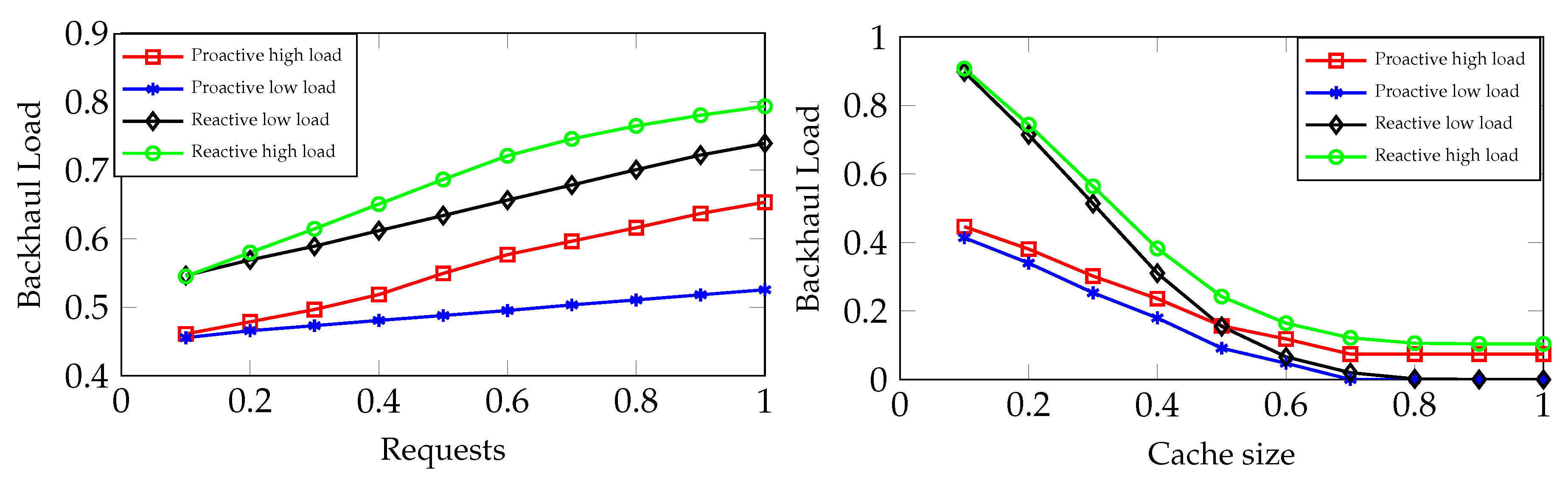
This study considers social networks aware D2D caching by focusing on influential users, their communities, and content. Initially, we use a preferential attachment model [17] for representing the mobile cellular network. We then perform clustering using a CC-GA algorithm [18], and find influential users using an eigenvector centrality measure [16]. Finally, based on the users’ previous history, we proactively cache the content of the influential users with respect to the available cache size. We perform extensive system level experiments to evaluate the gain of the proposed approach. The results reveal that 48% of backhaul traffic load can be reduced (48% satisfied requests) when users generating requests are 100% using the proposed approach.

The rest of the paper is organized as follows. Section 2 presents a brief background to caching methodologies in future cellular networks. Section 3 gives the most important related work. Section 4 discusses the methodology of the proposed approach. Section 5 presents the experimental setup and numerical results. Finally, Section 6 summarizes and concludes the paper.

2. Caching in Future Cellular Networks

We have seen a tremendous growth in cellular networks in the last decade. This growth is mainly driven by the exponentially growing demands of a high data rate by the end users. Various techniques have been employed to achieve a high data rate as well as spectral efficiency. Spectral efficiency can be achieved by efficiently managing cellular spectrum. These techniques range from control data split architecture (CDSA) [19], a cloud-radio access network (CRAN) to ultra-dense cellular networks (UDCN) [20] and D2D communication [21]. Almost all of these technologies are considered as enabling technologies for an upcoming fifth-generation (5G) cellular network. Among these, multi-tier architecture and D2D communication are well thought out as key enablers for providing access to a massive number of users as well as high data rate connectivity. In multi-tier architecture, there is an overlaid macro-cell (MC) comprising multiple micro-cells (mCs) operating in its coverage area. MC provides an overall coverage service and mobility management, whereas mCs can provide local area services and high data rate connectivity.

On the other hand, caching in cellular networks has been introduced to exploit storage capacity of diverse network devices. These devices range from user side (user equipment (UE), edge devices) to the network side (mCs, MC and extended packet core). In the following, we briefly describe how caching can be done on these diverse network devices.

Edge Caching: When an UE generates a request for specific content, first it will search for that content in its own memory and if that content is cached locally (edge), the UE will access that without any delay. This kind of caching can drastically reduce the backhaul traffic as well as access delay at the cost of large UE memory requirements.

Cluster-Head Caching: If the requested content is not available at UE itself, it will then ask its peers for that content through D2D communication. One way is to search for the content sequentially in every peer device. The other way could be to search for an influential user where it is highly probable that content accessed or generated by this influential user will become popular due to its relativity higher connectivity [22]. D2D communication will enable this kind of caching in the network. This mechanism also reduces backhaul traffic and access delay.

Micro-Cell Caching: If the requested content is not found using D2D communication, then mC will provide that content to the user if it is cached there. mC will utilize a radio access network (RAN) for delivering that content and not affect the backhaul channel.

Macro-Cell Caching: If the content can not be accessed using the above-mentioned ways, then MC will provide that content by downloading it from EPC (Evolved Packet Core) or from the cloud itself. It will ensure that content is delivered successfully. This mechanism can cause large access delays and an increase in backhaul traffic.

In the above, we answer the question where to cache?; however, in order to understand how to cache?, we might have two different approaches such as reactive and proactive. In the following, we describe these approaches in the context of cellular communication.

Reactive Caching: In the reactive caching approach, files are stored in cache if they were repeatedly requested in the past based on the history of the files accessed. In this caching, any content that remains in high demand for a specific period of time can be cached—for example, viral videos, popular tweets and other highly requested social media content.

Proactive Caching: It is a mechanism to predict future content that might be requested by the users. Based on previous content and user histories, certain content might become popular in the near future, which will be cached before they are actually requested, e.g., popular entities in various societies might trigger similar kinds of trends such as top trends on Twitter, etc. Due to the exponential increase of the demand of cellular data, it is very difficult to maintain the user satisfaction rate. Therefore, the importance of backhaul is increasing dramatically. Various studies [11,12] have shown that proactive caching in D2D communication can reduce a significant amount of backhaul traffic load, and is a smarter way to exploit D2D cellular networks. Using this approach in D2D communication in small cellular networks, the popular content is cached at the UE.

In the next section, we focus on the related work that deals with proactive caching using D2D communication.

3. Related Work

In recent years, a large number of studies have investigated caching on the edge in small cell networks. In [9], a proactive caching approach has been proposed. The authors studied two cases and utilized the spatial and social structure of the network. First, based on correlations among users and file popularity, files are cached during off-peak time. Secondly, influential users are detected and strategic content is cached using D2D communication and social networks. The authors used an eigenvector centrality measure for detecting influential users of the social network and model the content dissemination as a Dirichlet Process (CRP). In the experimental setup, a preferential attachment model is used to map the D2D small cellular network. The numerical results show a significant improvement in gain ratio; however, the proposed technique does not consider content of influential users in a specific community, which makes it less suitable for D2D communication in future cellular networks. The study in [11] introduced a new QoE metric for satisfying a given file request using proactive caching and then they proposed an optimization algorithm (propCaching) to maximize QoE. This algorithm is based on the popularity statistics of the requested files and cache files with highest popularity. However, unlike our proposed work, the algorithm has a limitation in that it chooses the popular files for caching based on their statistics or previous history. The work in [23] considers UE devices as cooperating nodes on which distributed cache is implemented for efficient downloading. However, this approach has certain drawbacks. Firstly, it does not consider the distance between D2D devices for cooperation and, secondly, it stores random content without prioritizing high in demand content. Golrezaei et al. [10] introduces a collaborative architecture which uses the distributed storage of popular content. In order to choose and cache random files at the user end, authors compute an average number of D2D links that can coexist without interference. However, this work also does not consider content of influential users to cache.

A probabilistic approach for optimizing scheduling policies and D2D caching is considered in [24]. The authors first derived approximated uploading probability for uploading gain and then they optimize the scheduling factor and caching distribution to optimize the successful offloading probability. In [25], authors investigate an optimal caching strategy by formulating an optimization problem and showing the relationship between D2D caching distribution and demand distribution for homogeneous Poisson Point Process models with different noise levels. With the exponential increase in multimedia traffic, content caching at every edge node might become a challenging task. To overcome this problem, authors in [26] proposed an idea of peer-to-peer content delivery networks. The authors have exploited the benefits of distrusted fog nodes for content delivery among the networks. In order to efficiently deploy enabling 5G technologies, authors in [27] proposed an algorithm to reduce total installation costs. The proposed algorithm considers both the hardware and cloud enabled softwarized components (reusable functional blocks) to ensure the users’ good performance as well as reduction in computation times. Kennington et al. [28] gives a comprehensive overview of modelling and solving optimization problems arising in wireless networks. Moreover, for a detailed review of applications of big data and caching techniques in mobile computing, the reader is referred to [9,29].

Table 1. Different caching techniques and their methodologies.

Objective	References	Cache Location	Methodology
Cache/Contents Placement	[9]	UE	Using SNA and CRP
	[10,11]	UE	Files popularity statistics
	[23]	UE	Random content
	[24]	UE	Probabilistic approach
	[25]	UE	Optimization
	[30]	Small Cell	Files instantaneous popularity learning and multi-armed bandit (MAB) technique
	[31,32]	Small Cell	Coded placement strategy
	[33]	Small Cell	Problem formulation using cost of files retrieval and bandwidth
	This paper	UE	SNA and influential users content as file popularity index

summarizes caching strategies in comparison with the one proposed in this paper.

Finding social hubs in social networks remains an active research area of Social Network Analysis (SNA). Various measures including Eigenvector Centrality measure, Betweenness measure, Closeness measure, Degree centrality measure and PageRank algorithm have been used extensively for finding the nodes importance in social graphs. Among these measures, Eigenvector centrality measure is the most widely used measure for detecting social hubs in social graphs. This measure has been used by three popular methods: PageRank [34], HITS (Hypertext Induced Topic Search) [35], and SALSA (Stochastic Approach for Link Structure Analysis) [36] for retrieving web information.

It is worth mentioning that several prior studies exist that propose various design approaches for proactive caching schemes [9,16,37]. However, the novelty of the proposed work stems from the simple yet under-explored idea of considering the content of influential users as popular content. Furthermore, our work uses a new community detection algorithm for detecting communities in the network and then k influential users are found, one for each community. In the next section, we will explain our proposed methodology for proactive caching in socially aware D2D networks.

4. Proposed Methodology

We exploit the social and spatial structure of social networks and use SNA approaches to find the content of the network that is expected to become viral in the future and proactively cache them in order to reduce the backhaul load. As the number of active users increases in the network, load on Small Base Station (SBS) increases. Therefore, D2D communication can play a vital role in reducing the load and increasing the user satisfaction rate. The D2D communication paradigm can be exploited to perform proactive caching and store highly probable content in the users’ caches. In this paper, we introduce a new proactive caching approach, which uses SNA techniques to address this problem. In the following subsection, after describing the system model and the essentials, we shall present our proposed algorithm.

4.1. System Model

Assume that there are n number of users who generate number of requests $R=\{r_1,r_2,\dots r_n\}$, number of files $F=\{f_1,f_2,\dots f_n\}$ with lengths $L=\{l_1,l_2,\dots l_n\}$, and bit rate $B_r=\{b_1,b_2,\dots b_n\}$. Note that bit rate of the file represents the transferring rate of the file per unit time. The requests are generated by the users in different time frames $T=\{t_1,t_2,\dots t_n\}$. A request $r_1\in R$ generated by user n is said to be satisfied iff D2D link capacity is higher than the bit rate of the file. The user satisfaction can be formulated as follows:

$$B_r\le \frac{l_i}{t_i^{\prime }-t_i},$$

(1)

where $l_i$ is the size(length) of the file, $t_i^{\prime }$ and $t_i$ is the end and starting time of delivery of file i. $B_r$ represents the bit rate of file f. Based on Equation (1), the user satisfaction rate $S_r$ can be defined as:

$$S_r=\frac{1}{R}\sum _{r\in R}{x}_r,$$

(2)

where

$$x_r=\{\begin{array}{cc}\hfill 1,& \mathrm{if}\frac{L}{t_z^{\prime }-t_z}\ge B_r,\\ \hfill 0,& \mathrm{otherwise}.\end{array}$$

In order to reduce backhaul traffic load, our main goal is to maximize $S_r$.

The users are considered to be connected with other users of their community in a D2D mode of communication. Thus, the request r of the user i for a file f is directed to its nearest user to search the requested file and will be served if the file exists in the nearby cache. Thus, a good proactive caching strategy can satisfy more requests at the user end, which results in reducing the backhaul traffic load.

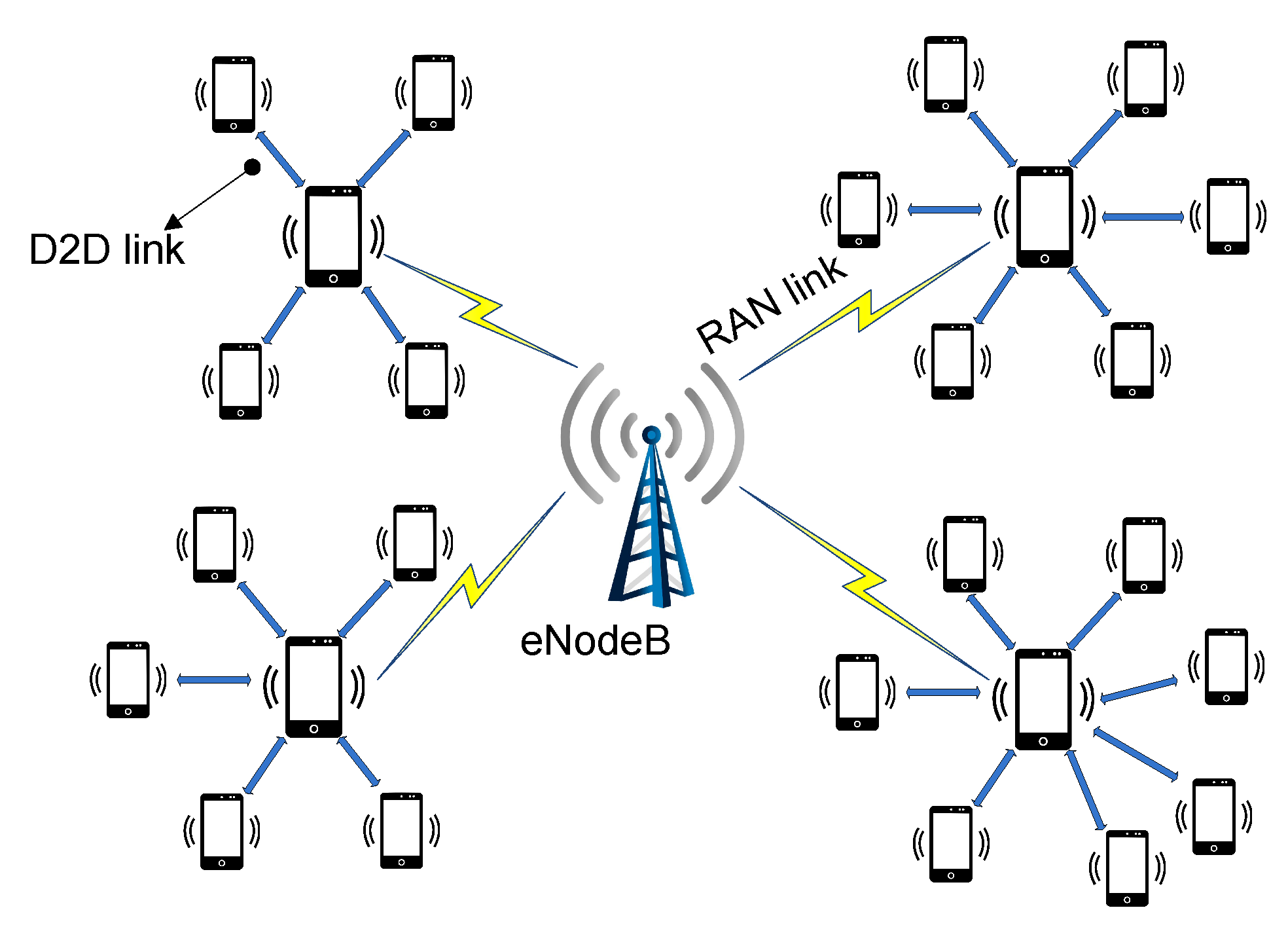
The architecture considered in this work assumes the D2D communication enabled small cellular network. Every community in the network finds a central node that can serve a maximum number of D2D users with a minimum distance as shown in Figure 1. There are a total of n number of users that are connected with each other via D2D communication with a link capacity $C_b$. The users are also connected with the small cell base station with a link capacity $C_w$. Assume that the $\sum C_w\le \sum C_b$, then the average backhaul traffic load due to each file of length $l_i$ can be formulated as follows [13]:

$$B_l\left(r\right)=\frac{1}{R}\sum _{r\in R}\frac{1}{l_i}\sum _{t=tr}^{t=t^{\prime }}{\lambda }_r\left(t\right),$$

(3)

where ${\lambda }_r\left(t\right)$ is the backhaul data rate during the content delivery for request r.

We consider the network as a graph $G=(V,E)$ where V represents set of users $V=\{v_1,v_2,v_3,\dots v_n\}$ and E is set of social links $(E\subseteq \left(\genfrac{}{}{0pt}{}{v}{2}\right))$ between the users. For generating the social network for our experimental setup, we used a well known model called preferential attachment proposed by Albert Barabasi [17] to form the small cellular network. This model basically represents degree distribution of the random generated network i.e., how users connect to each other. The core idea behind the preferential attachment model is that new users prefer to connect to well-connected users over less-connected users proportional to the probability of their degree. The generated network using this model follows power law distribution with exponent $\alpha =3$. This process is also known as rich-get-richer or cumulative advantage or Matthew effect. The process starts with some initial subgraph. Each new user comes with some initial m links. The probability $\mathsf{\Pi }\left(u\right)$ of connecting user u with other users j in the network is:

$$\mathsf{\Pi }\left(u\right)=m\frac{k_u}{{\sum }_j{k}_j},$$

(4)

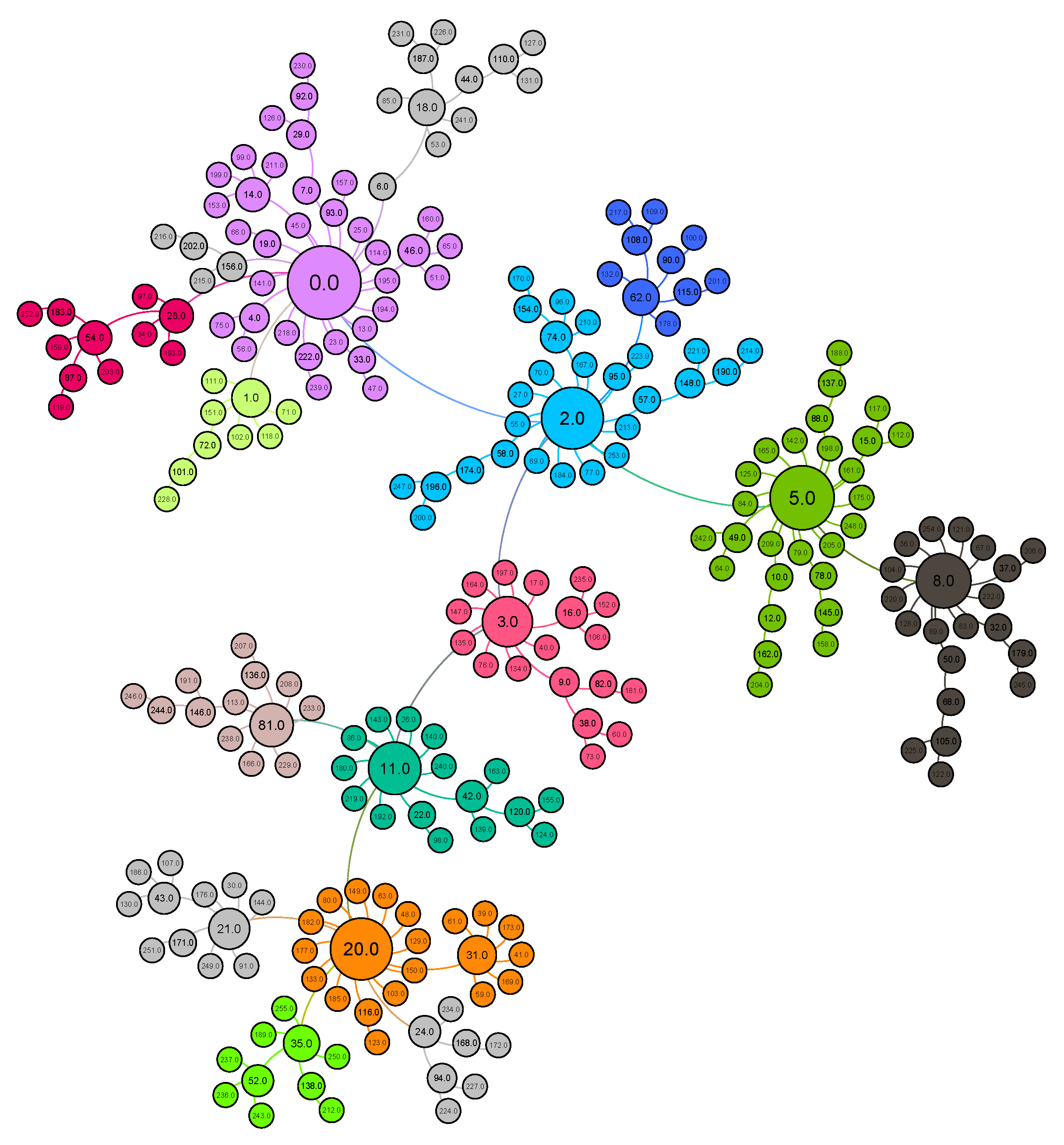
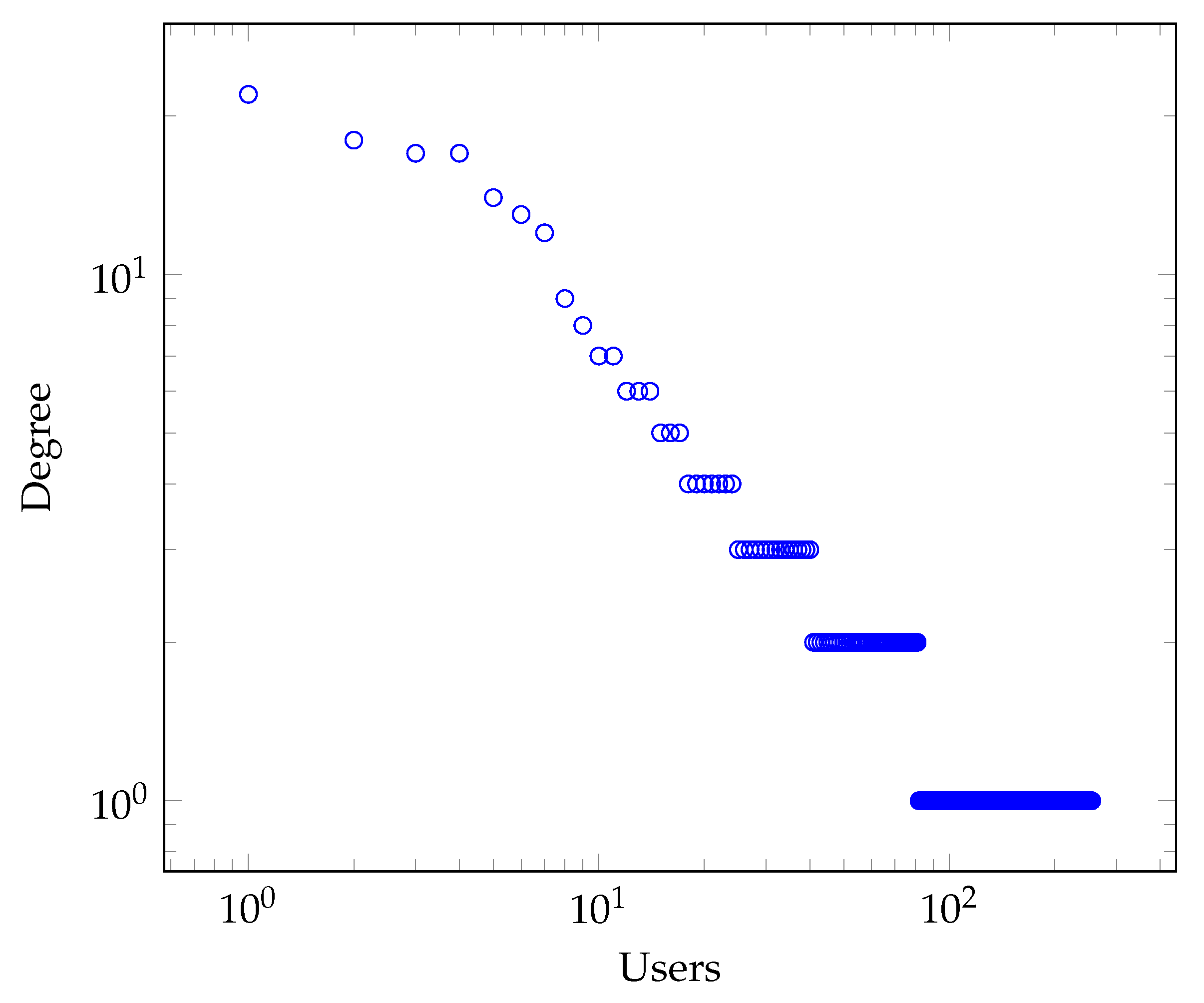
where $\mathsf{\Pi }\left(u\right)$ represents the probability of connecting user u with other users j in the network. m represents the number of links to which the new user joins the network and k represents the degree of each user in the network. This process results in a network with a power-law distribution with exponent = 3. Figure 2 shows a network of 256 users generated using a preferential attachment model where nodes represent users while links represent the D2D communication. We see that the network contains very few users having a large number of links while the rest of the users have very few links. The degree distribution of the generated network on a log–log scale is plotted in Figure 3. We can see that the network degree distribution follows power-law distribution.

4.2. Cluster Formation in a Social Network

The first step of our proposed approach is to detect the cluster of each user in the social network as discussed in the previous subsection. For a given graph $G=(V,E)$, there exist partitions $C=\{c_1,c_2,\dots .c_k\}$ of V, where $|c_i|>$ 0. Our goal is to identify a set of clusters that are densely intra-connected and sparsely interconnected. The process of identifying clusters in social networks is known as community detection.

Various kinds of community detection algorithms have been proposed. In this paper, we use the CC-GA algorithm [18]. The main reason for using CC-GA is its promising results when compared to other state-of-the-art algorithms such as the information theoretic algorithm (Infomap) [38] and the label prorogation algorithm (LPA) [39] on various kinds of networks including power-law and Forest fire models. This algorithm uses a well-known SNA measure called a Clustering Coefficient (CC) for generating an initial population. CC gives a better population for a genetic algorithm and results in better clustering of the network. Additionally, the algorithm using CC has shown that it converges very quickly [18]. In the following equation, $C_{v_i}$ represents the value of clustering coefficient of node $v_i$:

$$C_{v_i}=\frac{2L_{v_i}}{k_{v_i}(k_{v_i}-1)},$$

(5)

where $L_{v_i}$ represents the total number of links between the $k_{v_i}$ neighbors. The higher value of $C_{v_i}$ represents the dense neighborhood of a node. The main intuition behind using CC is that if the neighborhood of a node is densely populated, then it is more likely that all of the neighborhood nodes belong to the same cluster. Furthermore, CC-GA uses Modularity measure [40] as an objective function that is a quality index for clustering of social networks. It can be formally defined as follows:

$$Q=\sum _{C\in c}\left[\frac{\left|E\right(C\left)\right|}{m}-{\left(\frac{\left|E\left(C\right)\right|+{\sum }_{C^{\prime }\in c}\left|E(C,C^{\prime })\right|}{\left|2m\right|}\right)}^2\right],$$

(6)

where $\left|E\right(C\left)\right|$ represents the number internal links within the cluster while $E(C,C^{\prime })$ represents the links between clusters. m represents the total number of links in the whole network. Equation (6) can be rewritten into a precise mathematical formulation as given below:

$$\begin{array}{c}\hfill Q=\sum _{C\in c}\left[\frac{\left|E\right(C\left)\right|}{m}-{\left(\frac{{\sum }_{v\in c}deg\left(v\right)}{\left|2m\right|}\right)}^2\right].\end{array}$$

(7)

In Equation (7), the first fraction represents the true intra-connectivity of the users, while the second fraction represents the expected number of links within the cluster. The value of modularity ranges between $-1$ and 1. Greater value of modularity indicates better clustering of the network while a negative value represents an absence of true clustering in the network.

CC-GA tries to maximize the value of modularity in order to get nearly optimal clustering of the network. It is to be noted that modularity optimization is an NP-hard problem, which can not be solved with a guaranteed optimal solution. Algorithm 1 presents the pseudocode of CC-GA. Initially, the algorithm requires a graph consisting of vertices (V) and edges (E) as inputs. It also requires a set of input parameters including: the termination criteria (r), population size ($P_n$), crossover rate $\left(P_s\right)$, mutation rate $\left(P_m\right)$, mutation extension rate $\left(\alpha \right)$ and percentage of population $\left(T_c\right)$ to be selected for the next iteration. Initially, the algorithm computes CC of all nodes (steps 2–4) and generates the initial population (step 5). Afterwards, the genetic operators (crossover and mutation) are performed iteratively until the termination criterion is satisfied (steps 5-25). The algorithm also uses extension of mutation to merge small communities (step 19), and uses modularity measure as an objective function (steps 9, 15, 21). In the end, the algorithm returns the community structure of the input network. For more details about this algorithm, readers are referred to [18]. The interested readers are referred to [41,42] for more about genetic algorithms.

Algorithm 1 CC-GA (G)

Inputs: $P_s=$ Crossover rate; $P_m=$ Mutation rate; $P_n=$ Population size; $\alpha =$ Rate of mutation extension; $r=$ Termination criteria; $T_c=$ Selection criteria; Output: $C^{\ast }$ = $\{c_1,c_2,\dots ..c_k\}$; 1: procedure CC-GA($G,P_n,T_c,P_s,P_m,r,$ $\alpha$) 2:     for $\mathit{i}\leftarrow 1,\left|V\right|$ do 3:         ${\displaystyle C_{v_i}=\frac{2L_{v_i}}{K_{v_i}(K_{v_i}-1)}}$ 4:     end for 5:     $P=\left\{P_1,P_2,P_3\dots \dots P_n\right\}\leftarrow$ Initialize population $(g,P_n,C_v);$ 6:     repeat 7:         $O\leftarrow$ Apply Crossover ($P,T_c,P_s,$); 8:         Q = Compute fitness (P); 9:         $Q^{\prime }\leftarrow$ Compute modularity (O); 10:         if $Q^{\prime }>Q$ then 11:            P ← update population (O); 12:         end if 13:         O← Apply mutation (O, $P_m$); 14:         Q = Compute fitness (P); 15:         $Q^{″}\leftarrow$ Compute modularity (O); 16:         if $Q^{″}>Q$ then 17:            P ← update population (O); 18:         end if 19:         O ← Apply mutation extension (O, $\alpha$); 20:         Q = Compute fitness (P); 21:         $Q^{\prime \prime \prime }\leftarrow$ Compute modularity (O); 22:         if $Q^{\prime \prime \prime }>Q$ then 23:            P ← update population (O); 24:         end if 25:     until (termination-criterion(r)) 26:     $C^{\ast }\leftarrow$ Chromosome having highest fitness value 27:     Return $C^{\ast }$ 28: end procedure

4.3. Finding Influential Users and Popular Content

After clustering of the social network, our task is to find the Influential Users (IUs) of the network and then find their content. An influential user can be defined as the most connected and active user of the network [43]. In order to find the IUs, we use the notion of centrality [44], which is a well-known concept in SNA. The centrality measure provides a way to quantify the importance of nodes with respect to their positions and neighborhood connectivity within a social network. While various centrality measures exist, eigenvalue centrality is the most successful measure for detecting the social hubs or IUs within a social network. It is a widely used measure for finding the nodes centrality in the networks [16,45,46].

In order to find the IUs, we exploit the EigenVector Centrality measure. This measure uses the notion of eigenvector and eigenvalue of the adjacency matrix. It quantifies centrality of nodes based on centrality of its neighbors. Based on this measure, a node having more central neighbors will have greater centrality value. It can be formally defined as follows:

$$x_{v_i}=\frac{1}{\lambda }\sum _{N\in G}{a}_{i,j}{x}_{v_i},$$

(8)

where $\lambda$ is a normalization constant and N represents neighbors of node $v_i$. $a_{i,j}$ is 1 if nodes i and j are directly connected to each other, and 0, otherwise. The greatest value of $x_{v_i}$ represents the highest influence of the user in the network. Equation (8) can be rewritten in a vector form as follows:

$$\lambda x=Ax,$$

(9)

where A represents the adjacency matrix of the graph, and x is the vector of the eigenvalue scores. Based on eigenvector centrality measure, if our clustering algorithm returns K clusters of the network, then we find K influential users, one for each cluster in our social network. As we are considering D2D communication, it is necessary to identify at least one influential user in each cluster in order to communicate with other users directly. In our social network model shown in Figure 2, different clusters of the network have been shown in different colors after applying our clustering algorithm. There is one central influential user (nodes with greater sizes) found by using an eigenvector centrality measure. For example, user 11 is the influential user of its community represented with the green color, and there are 16 members of its community. Overall, the network is divided into 15 different communities and each community has one influential user. Furthermore, users who join the network earlier have more of a chance to become more connected and are hence more popular and influential (users 0–20).

Once we know the influential users and their communities, our next step is to determine the popular content of each community. For this purpose, inspired by the pervasive use of online social media, we assume that the content requested, generated, or accessed by the influential users is going to be the popular content for the same community, and we proactively cache this content based on the available cache size.

Algorithm 2 shows a pseudocode for computing the centrality values. We initialize an empty matrix $M^N$ for storing the centrality value of each node. Then, the algorithm recomputes the centrality score of each node as a weighted sum for centralities of all nodes in a node neighborhood. In order to normalize the centrality score, $\lambda$ is used. We set the value of $\lambda$ to the largest value of $x_u$. The procedure repeats until the values of each node converge.

After describing all the essentials in the following, we shall now present the proposed algorithm.

Algorithm 2 Compute Centrality

1: procedureCompute Centrality(A) 2:     Initialize matrix $M^N$ by 1 3:     repeat 4:         for $v\in V$ do 5:            $x_u=\frac{1}{\lambda }{\sum }_{u\in \left|A\right|}{A}_{u,v}{x}_u$ 6:            Update $M_u$ 7:         end for 8:     until values of $x_u$ converge 9: end procedure 10: Return M

4.4. Proposed Algorithm

Algorithm 3 presents our proposed approach for centrality based D2D proactive caching. Initially, we model the system based on the procedure presented in Section 4.1. After designing the model (step 2), we apply the CC-GA algorithm (step 3) for identifying clusters in the network that returns a set C depicting the communities of the network (communities and clustering have the same meaning and we use them interchangeably). Afterwards, we initialize a matrix M (step 4) having the dimensions $(C\times U)$, where C represents the total number of clusters ($C_i$ row contains the centrality values of cluster $C_i$) and U equals $max\left(\right|C_i\left|\right)$. This matrix stores the centrality value of each node with respect to its community. Note that $C_i$ has $|C_i|$ values and the remaining indexes which are $max\left(\right|C_i\left|\right)-\left(\right|C_i\left|\right)$ will have 0 entries. We also initialize an $IU$ matrix to find and store the influential users. The dimensions of this matrix are $(C\times 2)$. Then, we call the compute centrality algorithm (step 5), presented in Algorithm 2, which returns a vector of centrality values ($M^{\prime }$) indexes by node labels that are in the form of integers. As we need matrix M for computing the influential users, we therefore compute it from $M^{\prime }$ (step 6). We compute the primary influential users and secondary influential users from the matrix in each cluster and store them in the matrix (steps 7–10). The reason for finding secondary influential users is to ensure reliability of the system. In the end, we compute the popular content of influential users as described in Section 4.3 and load it into the cache (step 12).

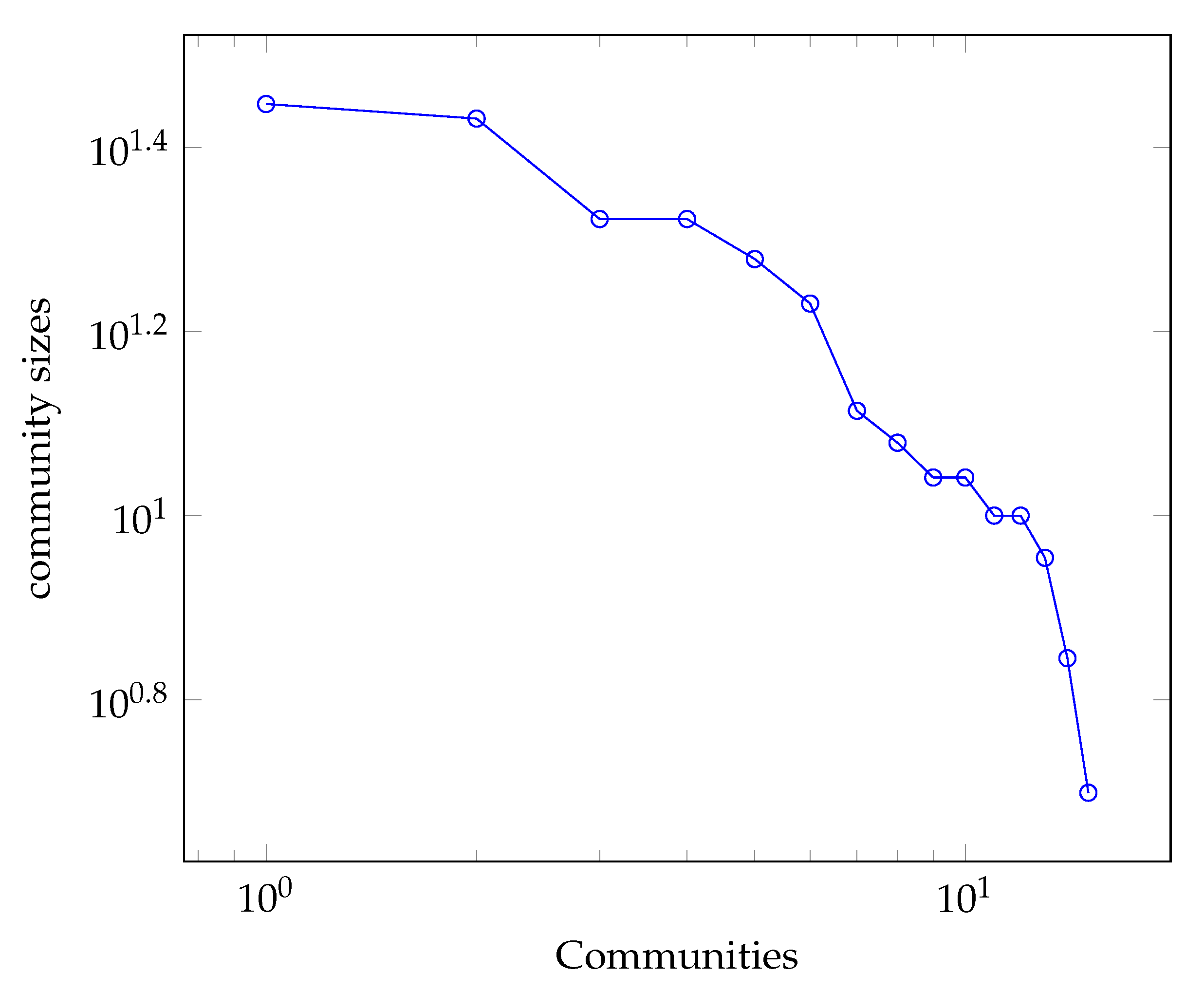
We see that the proposed Algorithm 3 relies on one primary influential user from one cluster, which raises important questions such as how many clusters the network has and how many users each cluster contains. To answer these questions, we present the distribution of community sizes in power-law networks in Figure 4. The figure shows the community sizes distribution of the network shown in Figure 2. We can see that the community size also follows a power law distribution that implies that there are no such communities who have either a large number of users that cover a great part of the network and neither there are such communities who have very few numbers of nodes. Taking this into consideration, we also follow network community size distribution to load the content in the cache of influential users. The user that has a greater community size has more content in the cache and vice versa.

The cellular networks suffer from a network outage problem, which can be in the form of power failure, signal loss or link break down. For maintaining the reliability of the network, we also maintain a list of secondary influential users as shown in Algorithm 3. In case of network outage problems, the secondary influential users will be used for D2D communication.

Algorithm 3 Proactive Caching

1: procedure D2D Proactive Caching 2:     $G=$ Model the system 3:     $C=$ CC-GA (G) 4:     initialize $M^{C\times U}$ and $I{U}^{C\times 2}$ matrix by 0 5:     $M^{\prime }=$ Compute Centrality(G) 6:     compute matrix M from $M^{\prime }$ 7:     for $\mathit{i}\leftarrow 1,\left|C\right|$ do 8:         $I{U}_0=max\left(M_i\right)$ 9:         remove($max\left(M_i\right)$) 10:         $I{U}_1$ = $max\left(M_i\right)$ 11:     end for 12:     Compute the popular content of influential users and load into cache 13: end procedure

5. Experimental Setup and Results

In this section, we present simulation setup and experimental results for evaluating the effectiveness of the proposed approach.

5.1. Simulation Setup

Currently, simulations are performed in Python 3. For community detection, CC-GA is implemented using Python’s library NetworkX to interact with the system model. Initial parameters for the genetic algorithm are initialized with the values shown in

Table 2. Simulation parameters.

(a) Genetic Algorithm Parameters
Parameter	Description	Value
$P_n$	Population size	500
$P_m$	Mutation rate	0.2
$P_s$	Crossover rate	0.2
$T_c$	Selection criteria	0.1
$\alpha$	Mutation extension rate	0.02
r	Termination criteria	50
(b) Proposed Approach Parameters
Parameter	Description	Value
K	Total of communities	15
N	Users	256
$\left|F\right|$	Total number of files	1024
$l_i$	Length of each file	1 Mbits
$b_i$	Bitrate of each file	1 Mbits/s
$C_w$	Total small base link capacity	64 Mbits/s
$C_b$	Total D2D link capacity	128 Mbits/s
R	Maximum number of requests	10,000
D	Total D2D cache size	256 Mbits

a. Typically, for network clustering problems, GA parameters like population size, termination criteria and mutation probability are set as 200, 50, and 0.15, respectively [18,47,48]. However, we performed experiments with different parameter settings to select values that perform best in our case. We set population size, termination criteria and mutation probability values as 500, 50 and 0.2, respectively. Note that the higher values of population size and mutation probability may increase the running time of the algorithm but give better results.

Table 2b shows a parameter setup for performing simulations. Two parameters, R and D2D cache size (D), are considered for performance evaluation as we are interested in evaluating backhaul traffic load with respect to cache size and the number of requests. For simulation purposes, we selected values of bitrate and size of each file, link capacity, and total number of requests from well-studied and well-cited papers on proactive caching [9,13]. Moreover, for a total number of files, number of users, and cache size, we selected higher values, in order to evaluate our proposed algorithm in more scalable scenarios. Table 2b presents simulation parameter values.

5.2. Simulation Results

In order to evaluate the performance of proposed approach, results are compared with a reactive caching approach, in which files are stored in the cache if they were repeatedly requested in the past based on the history of files accessed. Initially, a system model is generated using a preferential attachment model [17], and uniform distribution is considered for user requests’ generation. Based on the parameters setup shown in Table 2, the proposed algorithm is evaluated for a different number of requests and cache size.

In Figure 5, we plot satisfaction rate with respect to the number of requests generated by the users and the user’s cache size. Our experimental tests are based on number of active users in the network. We considered two main scenarios, first high load scenario when 100% users are active i.e., 256 users and second, and a low load scenario when 50% of the users are active i.e., 128 users. In Figure 5 (left), we measured satisfied requests of the proposed approach based on proactive caching with low and high load against reactive caching with respect to the number of requests. We see that the performance of reactive caching decreases more as compared with proactive caching when the number of requests increases. We see that with 100% requests, the number of satisfied requests is about 48%. We also note that, with 50% of requests, the proposed approach satisfies 52% requests on average with low load and satisfies 45% requests with high load, whereas these are 36% and 31%, respectively, in the case of the reactive approach. In Figure 5 (right), the effect of cache size on satisfaction rate is shown. We can see that with caching 20% of files, 65% of requests are satisfied by the proposed approach while caching 80% files increases the satisfied requests to 100% with low load, whereas these are 30% and 100%, respectively, in the case of reactive caching.

In Figure 6, we plot backhaul traffic load, with respect to the number of requests generated by the users and also with respect to the user’s cache size. It can be seen from Figure 6 (left) that, as we increase the number of requests, the backhaul traffic also increases. High load scenarios cause more backhaul traffic to increase as compared to low load scenarios. With the proposed approach, we see that on 100% requests, the backhaul load is 52% on low load and 65% on high load, whereas these are 75% and 79%, respectively, in the reactive approach. The proposed approach thus obtains significant reduction in backhaul traffic load as compared with the reactive caching approach. The effect of cache size on backhaul traffic is shown in Figure 6 (right). We see that with low values of cache size, the backhaul traffic load is significantly lower in the case of the proposed approach as compared to the reactive approach. For instance, with cache size of 10%, the backhaul traffic load is more than 90% in the case of reactive caching, whereas it is half of this in the proposed approach. As we increase cache size of the influential user, backhaul traffic decreases. For a low load scenario, using the proposed approach with 60% of the files cached, backhaul traffic load drops down to less than 10% and, when 80% of the files are cached, there is no backhaul traffic.

Figure 5 and Figure 6 also reveal the effect of increasing the number of users. Specifically from plots in Figure 5 (left) and Figure 6 (left), we see that as the number of active users increases, the number of satisfied requests decreases, leading to an increase in backhaul traffic. On the other hand, reducing the number of active users increases the number of satisfied requests and decreases the backhaul traffic load.

6. Conclusions and Future Directions

In this paper, we present a proactive caching approach for D2D in small cellular communication networks. We exploit the social and spatial structure of social networks and represent the D2D cellular network as a social graph. In order to find the influential users and clusters formation, we use an eigenvector centrality measure and CC-GA clustering algorithms, and cache the content of influential users of each community. Based on the experimental results, we conclude that caching content of influential users at the user cache can reduce a significant amount of backhaul load and increase the user satisfaction rate, compared to reactive caching or no caching. The key advantage of the proposed scheme is the simplicity of its popular content identification process, which is a key high complexity challenge in both reactive and proactive caching.

This work can be extended in the following directions:

• Event-driven influential users detection: When there is a change in the network being detected, it is possible that current influential users may not be available or as influential as they were before the change. In such scenarios, the system should be able to dynamically detect the influential users through re-computing the centrality scores.
• Joint optimization techniques for D2D enabled caching: Another interesting future work would be to investigate joint optimization of proactive content caching, scheduling techniques, and interference management.
• Machine learning for network optimization: For optimizing D2D caching, effective machine learning approaches can be exploited for clustering the network users and detection of influential users.
• Mobility aware proactive caching: Most of the work discussed in the literature focuses on cache placement and delivery strategy while the user is stationary. Caching becomes challenging when a user is moving. For example, when a user with a live streaming session moves from the connectivity of one influential user to another, the user will not be able to stream if the content is not available at the new influential user cache. In such scenarios, deep learning and big data analytics are essential tools that can be leveraged.