Occlusion-Aware Unsupervised Learning of Monocular Depth, Optical Flow and Camera Pose with Geometric Constraints
Abstract
:1. Introduction
- Jointly learn an unsupervised deep neural network from monocular videos that predicts depth, optical flow, and camera motion simultaneously at training time coupled by combined loss term.
- Modeling occlusion all through entire process explicitly through bidirectional flow from consecutive frames to make the model occlusion-aware and non-occluded region better constrained.
- Mutually supervise each component of the network in use of both 2D and 3D geometric constraints combined with occlusion module. The 2D image reconstruction loss takes optical flow into consideration. The 3D constraint contains two part: 3D point alignment loss and a novel 3D flow loss.
2. Related Work
2.1. Deep Learning vs. Geometry for Scene Understanding
2.2. Deep Learning with Geometry for Scene Understanding
2.2.1. Supervised Videos Learning
2.2.2. Unsupervised Videos Learning
3. Method
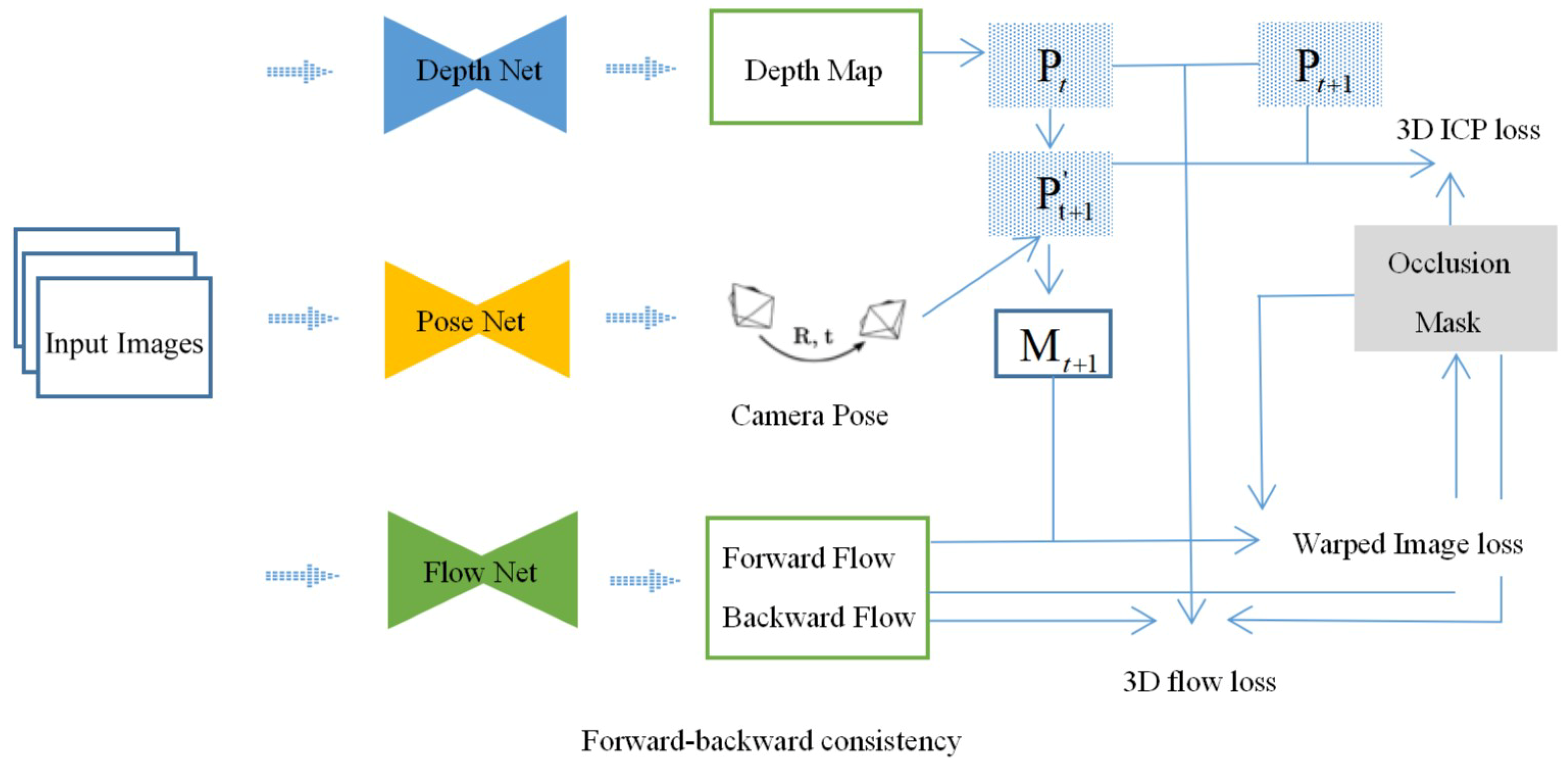
3.1. System Overview
3.2. Bidirectional Flow Loss as Occlusion Mask
3.3. 2D Image Reconstruction Loss as Supervision
3.4. Mutually Supervised 3D Geometric Consistency Loss
3.4.1. 3D Point Alignment Loss
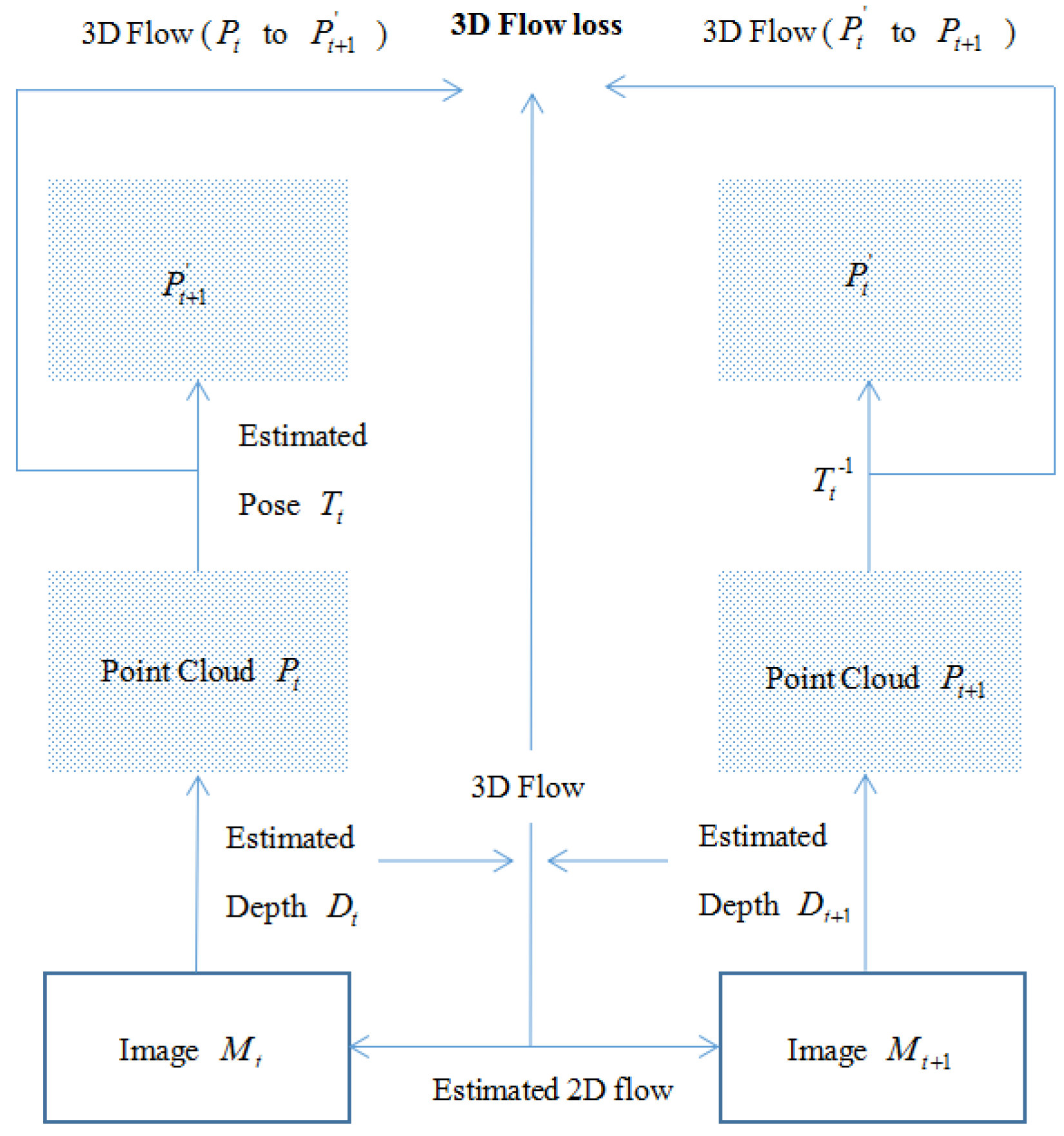
3.4.2. 3D Flow Loss
3.5. Smoothness Constraint
4. Experiments
4.1. Implementation Specification
4.1.1. Network Architecture
4.1.2. Training Details
4.2. Experimental Evaluation
4.2.1. Depth Evaluation
4.2.2. Optical Flow Evaluation
4.2.3. Pose Evaluation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, L.; Cheng, H.; Hao, J.; Ji, Y.; Kuang, Y. A Survey on Media Interaction in Social Robotics; Springer: Cham, Switzerland, 2015; pp. 181–190. [Google Scholar]
- Chen, C.; Seff, A.; Kornhauser, A.; Xiao, J. DeepDriving: Learning Affordance for Direct Perception in Autonomous Driving. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; Volume 00, pp. 2722–2730. [Google Scholar]
- Carmigniani, J.; Furht, B.; Anisetti, M.; Ceravolo, P.; Damiani, E.; Ivkovic, M. Augmented reality technologies, systems and applications. Multimed. Tools Appl. 2011, 51, 341–377. [Google Scholar] [CrossRef]
- Torresani, L.; Hertzmann, A.; Bregler, C. Nonrigid Structure-from-Motion: Estimating Shape and Motion with Hierarchical Priors. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 878–892. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, C. Towards Linear-Time Incremental Structure from Motion. In Proceedings of the International Conference on 3dtv-Conference, Seattle, WA, USA, 29 June–1 July 2013; pp. 127–134. [Google Scholar]
- Agudo, A.; Morenonoguer, F.; Calvo, B.; Montiel, J.M. Sequential Non-Rigid Structure from Motion Using Physical Priors. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 979–994. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-Time Single Camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1052–1067. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mur-Artal, R.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef] [Green Version]
- Mur-Artal, R.; Tardós, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef] [Green Version]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth Map Prediction from a Single Image using a Multi-Scale Deep Network. In Proceedings of the Annual Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2366–2374. [Google Scholar]
- Godard, C.; Aodha, O.M.; Brostow, G.J. Unsupervised Monocular Depth Estimation with Left-Right Consistency. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 6602–6611. [Google Scholar]
- Kendall, A.; Martirosyan, H.; Dasgupta, S.; Henry, P. End-to-End Learning of Geometry and Context for Deep Stereo Regression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 66–75. [Google Scholar]
- Brahmbhatt, S.; Gu, J.; Kim, K.; Hays, J.; Kautz, J. MapNet: Geometry-Aware Learning of Maps for Camera Localization. arXiv 2017, arXiv:1712.03342. [Google Scholar]
- Dosovitskiy, A.; Fischery, P.; Ilg, E.; Hausser, P.; Hazirbas, C.; Golkov, V.; Smagt, P.V.D.; Cremers, D.; Brox, T. FlowNet: Learning Optical Flow with Convolutional Networks. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2758–2766. [Google Scholar]
- Zhou, T.; Brown, M.; Snavely, N.; Lowe, D.G. Unsupervised Learning of Depth and Ego-Motion from Video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6612–6619. [Google Scholar]
- Ummenhofer, B.; Zhou, H.; Uhrig, J.; Mayer, N.; Ilg, E.; Dosovitskiy, A.; Brox, T. DeMoN: Depth and Motion Network for Learning Monocular Stereo. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5622–5631. [Google Scholar]
- Vijayanarasimhan, S.; Ricco, S.; Schmid, C.; Sukthankar, R.; Fragkiadaki, K. SfM-Net: Learning of Structure and Motion from Video. arXiv 2017, arXiv:1704.07804. [Google Scholar]
- Mahjourian, R.; Wicke, M.; Angelova, A. Unsupervised Learning of Depth and Ego-Motion from Monocular Video Using 3D Geometric Constraints. arXiv 2018, arXiv:1802.05522. [Google Scholar]
- Yin, Z.; Shi, J. GeoNet: Unsupervised Learning of Dense Depth, Optical Flow and Camera Pose. arXiv 2018, arXiv:1803.02276. [Google Scholar]
- Ilg, E.; Mayer, N.; Saikia, T.; Keuper, M.; Dosovitskiy, A.; Brox, T. FlowNet 2.0: Evolution of Optical Flow Estimation with Deep Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1647–1655. [Google Scholar]
- Garg, R.; Vijay, K.B.G.; Carneiro, G.; Reid, I. Unsupervised CNN for Single View Depth Estimation: Geometry to the Rescue. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 740–756. [Google Scholar]
- Li, R.; Wang, S.; Long, Z.; Gu, D. UnDeepVO: Monocular Visual Odometry through Unsupervised Deep Learning. arXiv 2017, arXiv:1709.06841. [Google Scholar]
- Meister, S.; Hur, J.; Roth, S. UnFlow: Unsupervised Learning of Optical Flow with a Bidirectional Census Loss. arXiv 2017, arXiv:1711.07837. [Google Scholar]
- Jaderberg, M.; Simonyan, K.; Zisserman, A.; Kavukcuoglu, K. Spatial Transformer Networks. In Proceedings of the Annual Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 2017–2025. [Google Scholar]
- Menze, M.; Geiger, A. Object scene flow for autonomous vehicles. In Proceedings of the Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3061–3070. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2015, arXiv:1603.04467. [Google Scholar]
- Liu, F.; Shen, C.; Lin, G.; Reid, I. Learning Depth from Single Monocular Images Using Deep Convolutional Neural Fields. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2024–2039. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Saxena, A.; Sun, M.; Ng, A.Y. Make3D: Learning 3D Scene Structure from a Single Still Image. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 31, 824–840. [Google Scholar] [CrossRef] [PubMed]
- Karsch, K.; Liu, C.; Kang, S.B. Depth Transfer: Depth Extraction from Video Using Non-Parametric Sampling. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 36, 2144. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Salzmann, M.; He, X. Discrete-Continuous Depth Estimation from a Single Image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 716–723. [Google Scholar]
- Laina, I.; Rupprecht, C.; Belagiannis, V.; Tombari, F.; Navab, N. Deeper Depth Prediction with Fully Convolutional Residual Networks. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 239–248. [Google Scholar]
- Revaud, J.; Weinzaepfel, P.; Harchaoui, Z.; Schmid, C. EpicFlow: Edge-preserving interpolation of correspondences for optical flow. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 7–12 June 2015; pp. 1164–1172. [Google Scholar]
- Ren, Z.; Yan, J.; Ni, B.; Liu, B.; Yang, X.; Zha, H. Unsupervised Deep Learning for Optical Flow Estimation. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]



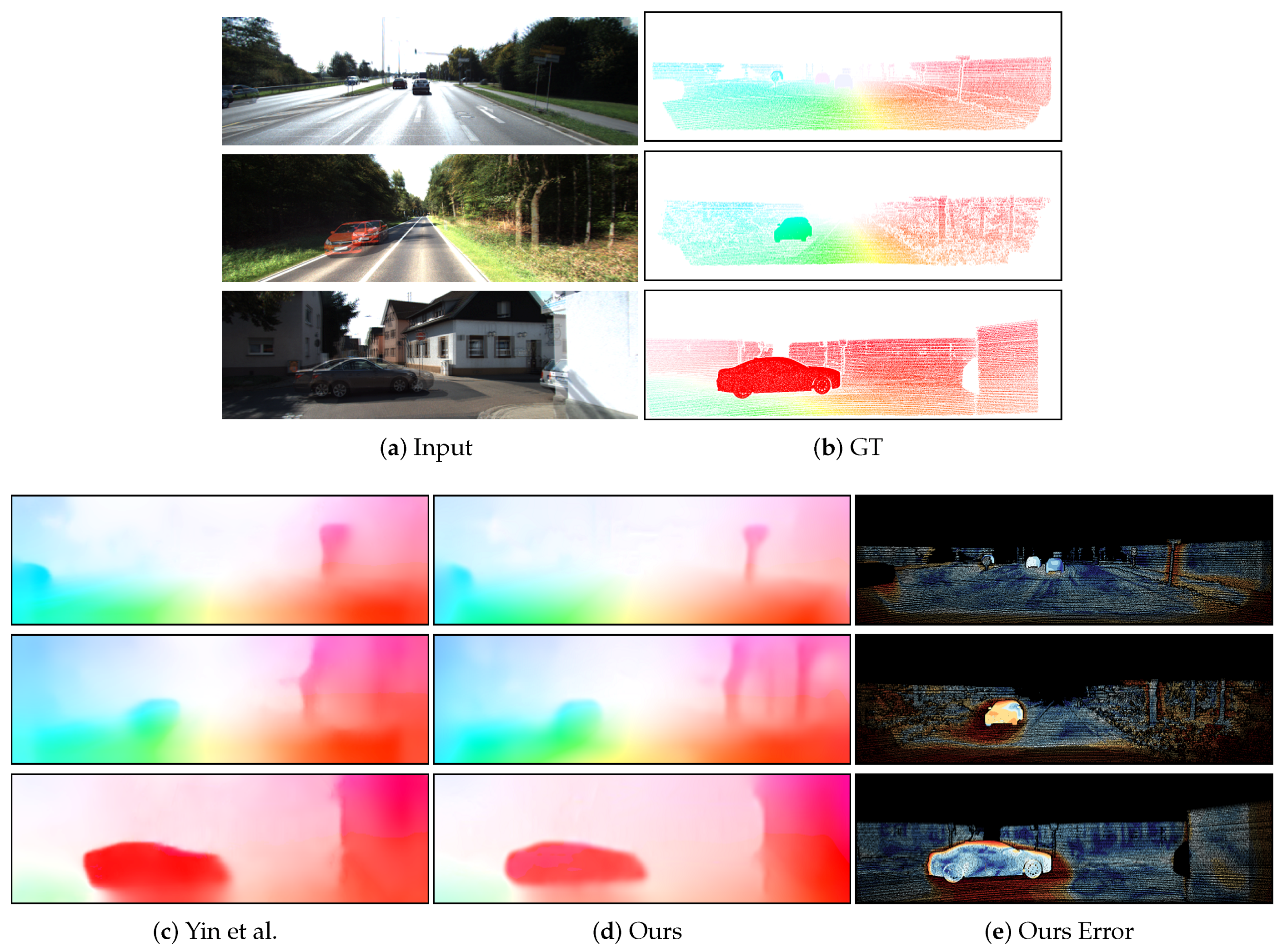
| Method | Supervise | Abs Rel | Sq Rel | RMSE | RMSE Log | |||
|---|---|---|---|---|---|---|---|---|
| Eigen [10] Coarse | Depth | 0.214 | 1.605 | 6.563 | 0.292 | 0.673 | 0.884 | 0.957 |
| Eigen [10] Fine | Depth | 0.203 | 1.548 | 6.307 | 0.282 | 0.702 | 0.890 | 0.958 |
| Liu [27] | Depth | 0.202 | 1.614 | 6.523 | 0.275 | 0.678 | 0.895 | 0.965 |
| Godard [11] | Stereo | 0.148 | 1.344 | 5.927 | 0.247 | 0.803 | 0.922 | 0.964 |
| Zhou [15] | No | 0.208 | 1.768 | 6.856 | 0.283 | 0.678 | 0.885 | 0.957 |
| Mahjourian [18] | No | 0.163 | 1.240 | 6.220 | 0.250 | 0.762 | 0.916 | 0.968 |
| Yin [19] | No | 0.155 | 1.296 | 5.857 | 0.233 | 0.793 | 0.931 | 0.973 |
| Ours (VGG) | No | 0.157 | 1.229 | 5.960 | 0.238 | 0.799 | 0.932 | 0.973 |
| Ours (ResNet) | No | 0.149 | 1.223 | 5.732 | 0.225 | 0.829 | 0.944 | 0.978 |
| Method | Supervise | Abs Rel | Sq Rel | RMSE | RMSE Log | |||
|---|---|---|---|---|---|---|---|---|
| Garg [21] | Stereo | 0.169 | 1.080 | 5.104 | 0.273 | 0.740 | 0.904 | 0.962 |
| Mahjourian [18] | No | 0.155 | 0.927 | 4.549 | 0.231 | 0.781 | 0.931 | 0.975 |
| Yin [19] | No | 0.147 | 0.936 | 4.348 | 0.218 | 0.810 | 0.941 | 0.977 |
| Ours (Resnet) | No | 0.142 | 0.909 | 4.306 | 0.203 | 0.832 | 0.949 | 0.978 |
| Method | Supervise | Abs Rel | Sq Rel | RMSE | RMSE Log | |||
|---|---|---|---|---|---|---|---|---|
| Godard [11] | Stereo | 0.124 | 1.076 | 5.311 | 0.219 | 0.847 | 0.942 | 0.973 |
| Zhou [15] | No | 0.198 | 1.836 | 6.565 | 0.275 | 0.718 | 0.901 | 0.960 |
| Mahjourian [18] | No | 0.159 | 1.231 | 5.912 | 0.243 | 0.784 | 0.923 | 0.970 |
| Yin [19] | No | 0.153 | 1.328 | 5.737 | 0.232 | 0.802 | 0.934 | 0.972 |
| Ours (Resnet) | No | 0.146 | 1.253 | 5.614 | 0.224 | 0.838 | 0.941 | 0.973 |
| Method | Abs Rel | Sq Rel | RMSE | RMSE Log | |||
|---|---|---|---|---|---|---|---|
| No Occ-Mask | 0.161 | 1.367 | 6.017 | 0.236 | 0.805 | 0.934 | 0.972 |
| No 3D ICP Loss | 0.160 | 1.594 | 5.775 | 0.226 | 0.826 | 0.945 | 0.976 |
| No 3D Flow Loss | 0.157 | 1.353 | 5.971 | 0.232 | 0.811 | 0.938 | 0.975 |
| All losses | 0.149 | 1.223 | 5.732 | 0.225 | 0.829 | 0.944 | 0.978 |
| Method | Supervision | Abs Rel | Sq Rel | RMSE | RMSE Log |
|---|---|---|---|---|---|
| Train set mean | Depth | 0.876 | 13.98 | 12.27 | 0.307 |
| Karsch [30] | Depth | 0.428 | 5.079 | 8.389 | 0.149 |
| Liu [31] | Depth | 0.475 | 6.562 | 10.05 | 0.165 |
| Laina [32] | Depth | 0.204 | 1.840 | 5.683 | 0.084 |
| Godard [11] | Pose | 0.544 | 10.94 | 11.76 | 0.193 |
| Zhou [15] | No | 0.383 | 5.321 | 10.47 | 0.478 |
| Ours | No | 0.406 | 4.071 | 9.624 | 0.385 |
| Method | Dataset | Noc | All |
|---|---|---|---|
| EpicFlow [33] | - | 4.45 | 9.57 |
| FlowNetS [14] | C+S | 8.12 | 14.19 |
| FlowNet2 [20] | C+T | 4.93 | 10.06 |
| DSTFlow [34] | K | 6.96 | 16.79 |
| UnFlow-C [23] | K | 4.29 | 8.80 |
| GeoNet (FlowNetS) [19] | K | 6.77 | 12.21 |
| GeoNet [19] | K | 8.05 | 10.81 |
| Ours | K | 4.41 | 9.24 |
| Method | Seq.09 | Seq.10 |
|---|---|---|
| ORB-SLAM (full) | 0.014 ± 0.008 | 0.012 ± 0.011 |
| ORB-SLAM (short) | 0.064 ± 0.141 | 0.064 ± 0.130 |
| Zhou [15] | 0.021 ± 0.017 | 0.020 ± 0.015 |
| Mahjourian [18] | 0.013 ± 0.010 | 0.012 ± 0.011 |
| Yin [19] | 0.012 ± 0.007 | 0.012 ± 0.009 |
| Ours (naive) | 0.011 ± 0.007 | 0.011 ± 0.009 |
| Ours | 0.011 ± 0.006 | 0.010 ± 0.008 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, Q.; Chen, Y.; Huang, C. Occlusion-Aware Unsupervised Learning of Monocular Depth, Optical Flow and Camera Pose with Geometric Constraints. Future Internet 2018, 10, 92. https://doi.org/10.3390/fi10100092
Teng Q, Chen Y, Huang C. Occlusion-Aware Unsupervised Learning of Monocular Depth, Optical Flow and Camera Pose with Geometric Constraints. Future Internet. 2018; 10(10):92. https://doi.org/10.3390/fi10100092
Chicago/Turabian StyleTeng, Qianru, Yimin Chen, and Chen Huang. 2018. "Occlusion-Aware Unsupervised Learning of Monocular Depth, Optical Flow and Camera Pose with Geometric Constraints" Future Internet 10, no. 10: 92. https://doi.org/10.3390/fi10100092
APA StyleTeng, Q., Chen, Y., & Huang, C. (2018). Occlusion-Aware Unsupervised Learning of Monocular Depth, Optical Flow and Camera Pose with Geometric Constraints. Future Internet, 10(10), 92. https://doi.org/10.3390/fi10100092




