Elastic Scheduling of Scientific Workflows under Deadline Constraints in Cloud Computing Environments

Abstract

Scientific workflow applications are collections of several structured activities and fine-grained computational tasks. Scientific workflow scheduling in cloud computing is a challenging research topic due to its distinctive features. In cloud environments, it has become critical to perform efficient task scheduling resulting in reduced scheduling overhead, minimized cost and maximized resource utilization while still meeting the user-specified overall deadline. This paper proposes a strategy, Dynamic Scheduling of Bag of Tasks based workflows (DSB), for scheduling scientific workflows with the aim to minimize financial cost of leasing Virtual Machines (VMs) under a user-defined deadline constraint. The proposed model groups the workflow into Bag of Tasks (BoTs) based on data dependency and priority constraints and thereafter optimizes the allocation and scheduling of BoTs on elastic, heterogeneous and dynamically provisioned cloud resources called VMs in order to attain the proposed method’s objectives. The proposed approach considers pay-as-you-go Infrastructure as a Service (IaaS) clouds having inherent features such as elasticity, abundance, heterogeneity and VM provisioning delays. A trace-based simulation using benchmark scientific workflows representing real world applications, demonstrates a significant reduction in workflow computation cost while the workflow deadline is met. The results validate that the proposed model produces better success rates to meet deadlines and cost efficiencies in comparison to adapted state-of-the-art algorithms for similar problems.

1. Introduction

Various scientific domains such as biology, medicine, planetary science, astronomy, physics, bioinformatics and environmental science, often involves the use of simulations of large-scale complex applications for validating behavior of different real-world activities. Most of such scientific applications are constructed as workflows containing a set of computational tasks linked via control and data dependencies. The workflow is partitioned into multiple tasks which may have different sizes and require different running times ranging from tens of seconds to multiple minutes [1]. Workflow scheduling is a process of mapping workflow tasks to processing resources called Virtual Machines (VMs) and managing their execution while satisfying all dependencies, constraints and objective functions. It is well-known that workflow scheduling problems are Nondeterministic Polynomial time (NP)-complete [2], so finding the perfect solution in polynomial time is not viable in all cases. Efficiently executing such workflows within a reasonable amount of time usually require massive storage and large-scale distributed computing infrastructures such as cluster, grid, or cloud. Among such infrastructures, cloud computing has emerged as an economical and scalable distributed computing environment for the design and execution of large and complex scientific workflow applications [3]. However, cloud environments may incur significant computing overheads that can adversely affect the overall performance and costs of the workflow execution [4]. In real cloud environment, some factors can cause delays. The overall workflow execution time and scheduling time overheads may include the additional times for queuing delay, workflow engine delay, tasks grouping delay, data transfer overhead, resource allocation, resource preparation, VM provisioning and deprovisioning delays, task runtime variance, VM boot time, VM idle times and other unexpected delays in real environments. IaaS providers make no guarantees on the value of these delays and it can have higher or lower variability and impact on the execution of a workflow. Data communication overheads may be critical in case of data-intensive workflows. For instance, the execution of two dependent tasks on one less powerful resource but with zero or negligible transfer overhead would be more efficient than the execution on two more powerful but separate resources with significant transfer overhead. Therefore, in order to minimize the overheads incurred, the most challenging problems in workflow schedulers are the minimization of execution time and monetary budget of workflow execution and capability of dynamic adaptation to any unexpected delays.

The majority of existing strategies which focus on both of these objectives simultaneously, lack in consideration of one or more crucial aspects of workflow scheduling. For example, dynamic provisioning of resources is not considered in [5,6,7,8], scalability in terms of large number of tasks is not considered in [9], heterogeneity of resources is not considered in [8,10], resource auto-scaling is not considered in [11], data dependencies are not considered in [12] and task clustering technique in [5] is not fully autonomous. Moreover, unlike multiple independent BoTs or single task-based workflows, the concept of using multiple connected and constrained BoTs for reducing the data transfer time is not considered in most existing scheduling algorithms [13,14].

To address the limitations of previous research, we propose a dynamic and scalable cost-efficient deadline constrained algorithm for scheduling workflows using dynamic provisioning of resources in a single cloud environment, using CPLEX solver (https://www.ibm.com/analytics/data-science/prescriptive-analytics/cplex-optimizer) and Mixed Integer Programming (MIP). We call our algorithm as Dynamic Scheduling of Bag of Tasks based workflows (DSB). The main contributions of this study are summarized as follows.

(1)

Grouping homogeneous tasks with the same depth into BoTs according to their priorities and dependency constraints in order to minimize queuing overheads and then distributing the overall workflow deadline over different BoTs.

(2)

Implementation of a technique for scheduling of tasks on dynamic and scalable set of VMs in order to optimize cost while satisfying their deadlines.

(3)

The proposed algorithm involves dynamic provisioning of resources as MIP problem by the use of IBM ILOG CPLEX.

(4)

Extensive simulations with results for real world scientific applications.

The rest of the paper is organized as follows. Section 2 provides an overview of the related work. Section 3 presents the scientific workflow application model, the cloud resource model and the workflow execution model assumed in this work. Section 4 provides the proposed scheduling algorithm. Section 5 presents results and finally Section 6 concludes the paper.

2. Related Work

In the last two decades, several research studies have been conducted that address the problem of workflow scheduling due to its NP-completeness. The Quality of Service (QoS)-constrained workflow scheduling algorithms tries to maximize the performance while meeting other user-defined QoS constraints, for example, cost minimization of a workflow execution under deadline constraints, as in IC-PCP and IC-PCP2 [15], URH [16], DPDS [17] and EPSM [18].

Rodriguez and Buyya [19] considered an application model similar to the one addressed in this paper and proposed a scheduling algorithm for optimizing a workflow’s execution time (that is, makespan) under a budget constraint. They proposed resource provisioning plan for a subset of the workflow tasks as a mixed integer linear programming (MILP) model. However, their solution is tailored for fine-grained billing periods such as per-minute billing. Moreover, the algorithm’s objective is to minimize the makespan instead of meeting a deadline constraint. Despite these differences, we consider their work relevant as the authors not only consider dynamic resource provisioning and delays but also consider several VM instance types with different characteristics and prices.

Dziok et al. [20] presented an adaptive algorithm and used the MIP approach to schedule workflows in IaaS clouds for optimizing cost under a deadline constraint. However, they do not consider reusing of already assigned VMs and also do not consider data transfer time.

Malawski et al. [8] presented a dynamic resource provisioning and scheduling algorithm called DPDS. It schedules workflows under given deadline and budget constraints along with the information about resource utilization for VM provisioning and scheduling. However, it attempts to maximize the number of completed workflows rather than minimizing the rental cost of a single BoT workflow. Moreover, it supports single instance type and do not consider resource heterogeneity which is in contrast to the current IaaS cloud model that offer a wide variety of instance types and dynamic provisioning and scheduling of resources.

Task granularity has been addressed in several research studies for reducing the impact of overheads that may arise when executing scientific workflows in distributed environments, such as the cloud [4,12,21]. Task grouping methods reduce computational granularity by reducing the number of computational activities by grouping fine-grained tasks into course-grained tasks. These techniques attempt to minimize queuing times and scheduling overheads when resources are limited. However, task granularity may limit the degree of inherent parallelism, therefore it must be done optimally.

Mao and Humphrey [9] proposed an auto-scaling mechanism that schedules workflow jobs in order to minimize the monetary cost while meeting the application deadlines on clouds. A static resource provisioning plan is made based on a global optimization heuristic and then adapted to dynamic changes by running the global optimization algorithm every time a task is scheduled. However, they do not consider the different priorities of each job and considered dynamic and unpredictable workloads of workflow. Furthermore, the high computational overhead in Scaling-Consolidation-Scheduling (SCS) hinders its scalability in terms of the number of tasks in the workflow and they do not provide a near-optimal solution.

Malawski et al. [22] explicate a deadline and budget constraint scheduling algorithm which tries to maximize the amount of work completed. The scheduling algorithm proposed by Byun et al. [10] estimated the minimum number of resources needed to execute the workflow in a cost- effective way. But, they considered a single type of VM and fails to consider the heterogeneous nature of clouds.

The proposed Dynamic Scheduling of Bag of Tasks based workflows (DSB) algorithm covers all of these deficits and presents a dynamic and scalable cost-efficient deadline constrained algorithm for scheduling workflows using dynamic provisioning of resources in a single cloud environment.

3. System Model

This section presents the application model, cloud resource model and the overall workflow model for the execution of our proposed method for scheduling of scientific workflows in the cloud. The parameters and their semantics used throughout this paper are summarized in

Table 1. Notations.

Notation	Description
$W$	Workflow represented by Directed Acyclic Graph (DAG)
$V$	Set of tasks of the workflow, represented by vertices of the DAG
$E$	Set of directed edges between the vertices
$BoT$	Set of BoTs
$VM$	Set of Virtual Machines (VMs)
$n$	Number of tasks
$k$	Number of VM types
$u$	Number of BoTs
$v_i$	A task such that $v_i\in V$
$v_j$	A task such that $v_j\in V$
$v_{entry}$	Virtual entry node
$v_{exit}$	Virtual exit node
$v_{run}$	Running task
$e_{ij}$	An edge such that $e_{ij}\in E$ between the tasks $v_i$ and $v_j$
$e_{p,i}$	Inward edges of task $v_i$
$e_{i,c}$	Outward edges of task $v_i$
$bo{t}_q$	A BoT such that $bo{t}_q\in BoT$
$m_r$	A virtual machine of type $r$ such that $m_r\in VM$
$pred\left(v_i\right)$	Immediate predecessor of task $v_i$
$succ\left(v_i\right)$	Immediate successor of task $v_i$
$R{T}_i^r$	Estimated Runtime of task $v_i$ on VM $m_r$
$C{T}_{ij}^r$	Communication time of edge $e_{ij}$ from tasks $v_i$ and $v_j$ on a VM $m_r$
$E{T}_i^r$	Execution time of task $v_i$ on VM $m_r$
$S{T}_i^r$	Start time of task $v_i$ on VM $m_r$
$F{T}_i^r$	Finish time of task $v_i$ on VM $m_r$
$E{C}_i^r$	Execution cost of task $v_i$ on VM $m_r$
$l_i$	Service length of task $v_i$
$p_r$	Processing power of VM $m_r$
$h_r$	Billing interval length of VM type $m_r$
$c_r$	Cost per interval unit of VM type $m_r$
$b_r$	Bandwidth capacity of VM $m_r$
$d_r$	Provisioning delay in VM allocation
$p{v}_r$	VM performance variability
$sl{t}_r$	Start leasing time of VM $m_r$
$t{c}_{ij}$	Data transfer cost of communicating data from task $v_i$ to $v_j$
$s_{ij}$	Size of data needed to be communicated from task $v_i$ and $v_j$
$uran{k}_i$	Upward rank of a task
$d{d}_i$	Degree of dependency of task $v_i$
$lv\left(v_j\right)$	Maximum number of edges from task $v_{entry}$ to $v_j$
$coun{t}_{lv}$	Number of tasks in the level $lv$
$D{L}_W$	Deadline associated with the workflow $W$ to complete its execution
$M{P}_W$	Overall schedule length of workflow $W$
$A{S}_W$	Elapsed time between $D{L}_W$ and the estimated $M{P}_W$
$A{S}_{lv}$	Available spare time of a level $lv$
$A{S}_i$	Available spare time of a task level $v_i$
$S{D}_i$	Estimated sub-deadline for task $v_i$ of the workflow
$EF{T}_i^r$	Earliest finish time of task $v_i$ on VM $m_r$
$CP{T}^{sel}$	Cumulative processing time of submitted tasks on VM $m_{sel}$
$y_{r,u}$	Variable representing number of tasks assigned to $u^{th}$ VM of type $r$
$n_{bot}^r$	Number of tasks in $bot\in BoT$ assigned to VM of type $r$

.

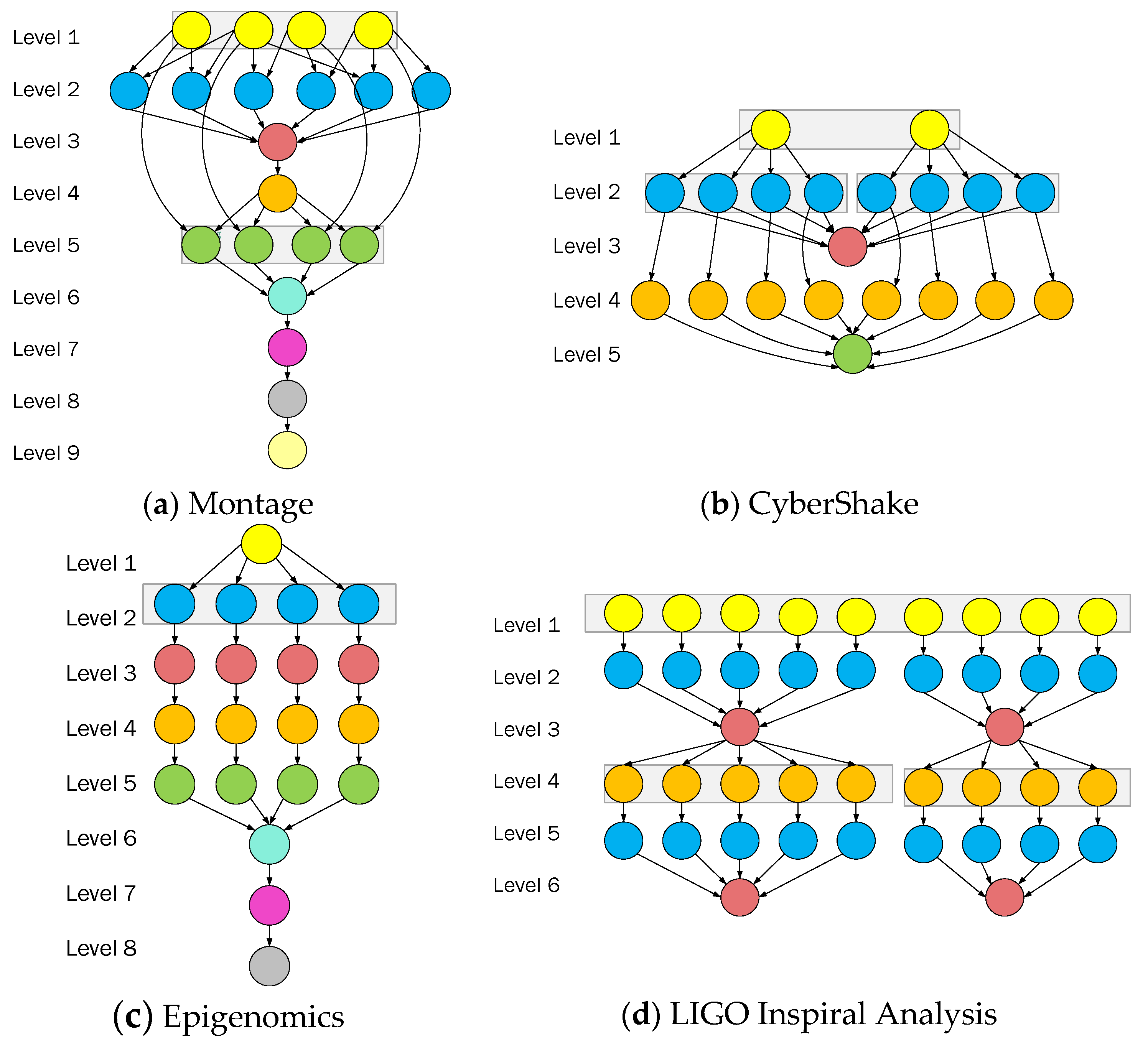
3.1. Scientific Workflow Application Model

The standard way to represent a BoT-based workflow is a Directed Acyclic Graph (DAG) $W=\left(V,E,B\right)$ in which $V=\left\{v_1,v_2,\dots ,v_n\right\}$ is the set of vertices representing n different tasks of the workflow, $E=\left\{e_{ij}\left|\right(1\le i\le n,1\le j\le n,i\ne j\right\}$ is the set of directed edges between the vertices, representing data or control dependencies between the tasks $v_i$ and $v_j$, indicating a task $v_j$ cannot start its execution before $v_i$ finishes and sends all the needed output data to task $v_j$ and $BoT=\{bo{t}_1,bo{t}_2,\dots ,bo{t}_u\}$ is the set of BoTs, in which $bo{t}_q$ is the set of $q^{th}$ BoT. Each task has an estimated runtime $R{T}_i$ which denotes the precedence constraint assigned to task $v_i$. Also, each edge $e_{ij}$ has a communication time $C{T}_{ij}$ which denotes the amount of data needed to be communicated and the precedence constraint from tasks $v_i$ and $v_j$, if they are executed on different resources. It is predetermined and known a priori. In this case, task $v_i$ is considered one of the immediate predecessor of task $v_j$ and task $v_j$ is considered one of the immediate successor of task $v_i$. The predecessor task of $v_i$ is denoted as $pred\left(v_i\right)$ and the successor task as $succ\left(v_i\right)$. Task $v_i$ can have multiple predecessors and multiple successor tasks. A task is considered as a ready task when all its predecessors have finished execution. Any task without a predecessor task is called as the entry task $v_{entry}$ and a task with no successor task is called the exit task $v_{exit}$. Since the proposed method needs a graph with individual entry and exit nodes, virtual entry and exit nodes denoted by $v_{entry}$ and $v_{exit}$ respectively, with zero execution time and zero transmission time have been inserted into the DAG.

The crux of the proposed research is scheduling a BoT-based workflow based on the deadline constraint while minimizing the budget of the application. The proposed approach, called DSB, considers pay-as-you-go IaaS cloud model having inherent features such as elasticity, abundance, heterogeneity, dynamic provision of resources, interval-based pricing model and VM provisioning delays. A user-defined deadline is submitted initially with the workflow DAG.

3.2. Cloud Resource Model

The IaaS cloud model, adopted in this work, offers virtualized resources containing various instance types at different costs. In this study, the cloud resource model is based on Amazon Elastic Compute Cloud (Amazon EC2), where VM instances are dynamically provisioned on-demand for executing scientific workflow applications. Under this pay-per-use interval-based model, the IaaS providers charge customers for used hours of VM instances and each partial hour consumed is billed as a full hour. We assume that the users have access to unlimited number of instances represented by a set of heterogeneous virtual machines, $VM=\left\{m_1,m_2,m_3,\dots ,m_k\right\}$ where $m_r\in VM|1\le r\le k$ and $r$ is an index of the instance type having varied prices and configurations.

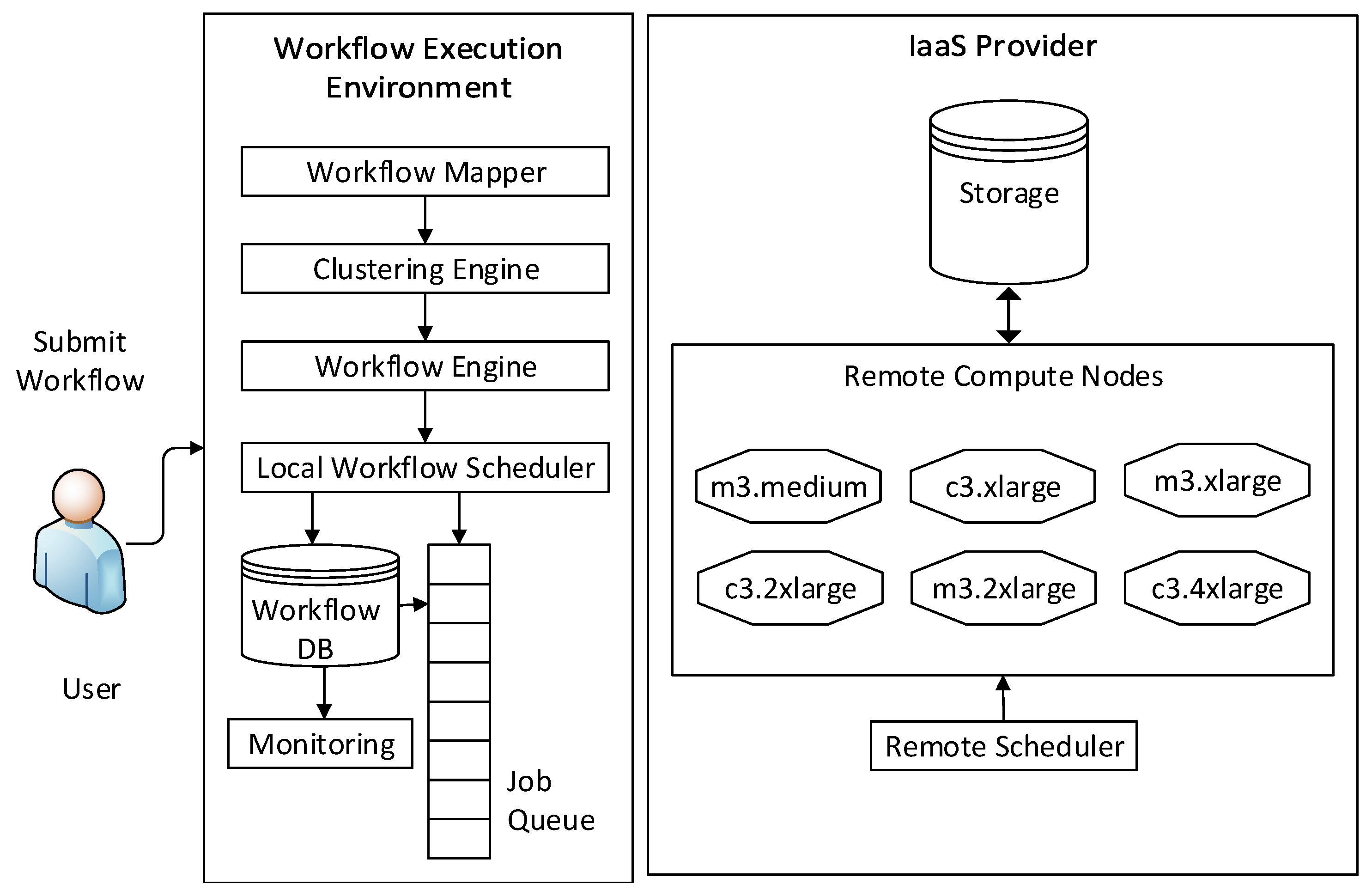
3.3. Workflow Execution Model

The workflow execution model used in the proposed method is shown in Figure 1. The scientific workflow is described as DAG where the nodes denote individual executional tasks and the edges denote control and data constraints (i.e. the set of parameters) between the tasks. The output data in the form of files by one task is used as input data for another task. In the model used in this study, the scientific workflow is abstract, i.e. the workflow is unaware of the details of physical locations of the executables and the data. This model fits a number of workflow management systems (WMSs). IaaS providers allow WMSs to access to infinite pool of VMs for lease. For instance, Pegasus (https://pegasus.isi.edu/) and Galaxy [23,24]. An introduction of the main components of the workflow execution environment are given below, details of which may be found in [25].

• Workflow submission: The user submits the workflow application to the WMS for scheduling of the workflow tasks. The WMS resides on the host machine which may be a user’s laptop or a community resource.
• Target execution environment: It can be a local machine, like the user’s laptop, or a virtual environment such as the cloud or a remote physical cluster or a grid [26]. On the basis of the available resources, the WMS maps given abstract workflow into an executable workflow and execute them. Moreover, it monitors the execution and manages the input data, intermediate files and output files of the workflow tasks. An overview of the main components of the target execution environment are discussed below:
  • Workflow mapper: The workflow mapper produces an executable workflow on the basis of the abstract workflow submitted by the user. It identifies the appropriate data and the software and hardware resources required for the execution. Moreover, the mapper can restructure the workflow for performance optimization.
  • Clustering engine: To reduce system overheads, one or more small tasks are clustered into single execution unit called job in WMS.
  • Workflow engine: The workflow engine submits the jobs defined by the workflow in order of their dependency constraints. Thereafter, the jobs are submitted to the local workflow scheduling queue.
  • Local workflow scheduler and local queue: The local workflow scheduler manages and supervises individual workflow jobs on local and remote resources. The elapsed time between the submission of a job to the job scheduler and its execution in a remote compute node (potentially on cloud) is denoted as the queue delay.
  • Remote execution engine: It manages the execution of clustered jobs on one or more remote compute nodes.

4. The Proposed DSB Workflow Scheduling Algorithm

4.1. Assumptions

The current study assumes that the workflow application executes in a single cloud data center so that one possible source of execution delay and data transfer cost between data centers is eliminated. The average bandwidth between the VM instances is assumed to be fixed during the execution of $W$. The estimated runtime of task on a VM instance, denoted as $R{T}_i^r$ is known to the scheduler in advance. It is obtained by Equation (1). The runtime of virtual entry and exit nodes is zero. Moreover, the tasks do not have the ability to checkpoint their work or get preemption. In other words, a task has to be restarted in case of its failure. Furthermore, we assume that for every VM type, the processing capacity is furnished either from the IaaS provider or can be estimated based on the work of [27]. We assume a VM boot time of 97 s based on the measurements presented by Mao and Humphrey [9] for EC2 cloud. We adopted a performance degradation model based on results achieved in Amazon EC2 clouds by Jackson et al. [28]. Therefore, we consider the loss in VM performance based on a normal distribution with mean of 15% and standard deviation of 10% in our proposed approach as well.

Similarly, the amount of data needed to be communicated between the tasks of a workflow are considered to be known in advance. The communication time for the tasks allocated to the same VM is considered to be zero. Moreover, data communication cost between resources are assumed to be zero, since in IaaS clouds, data communication inside a data center is free. Furthermore, the cloud datacenter is considered to have unlimited resources, so resource contention is almost negligible. Additionally, we assume that all VMs have enough memory to run any task of the workflow.

4.2. Problem Statement

The scheduling problem addressed in the present study can be defined as dynamically scaling a set of VMs and assigning each task to a given VM in order to minimize the cost of the application while fulfilling the deadline constraint.

4.3. Basic Definitions

Definition 1.

Estimated runtime of task $v_i$ on a VM $m_r$, denoted by $R{T}_i^r$, is computed using Equation (1).

$$R{T}_i^r=\frac{l_i}{p_r\times \left(1-p{v}_r\right)}$$

(1)

where $l_i$ is the service length of task $v_i$ measured in Floating Point Operations (FLOP), $p_r$ is the Central Processing Unit (CPU) processing capacity of VM $m_r$ in Million Floating Point Operations Per Second (MFLOPS) based on the number of EC2 compute units and $p{v}_r$ is the VM performance variability which represent the uncertainties such as potential variability or degradation in CPU performance in real cloud environments.

Definition 2.

Communication time of edge $e_{ij}$ between tasks $v_i$ and $v_j$ on VM $m_r$, denoted by $C{T}_{ij}^r$, is computed using Equation (2).

$$C{T}_{ij}^r=s_{ij}/b_r$$

(2)

where $s_{ij}$ is the size of data needed to be communicated from tasks $v_i$ and $v_j$ in Megabytes (MB) and $b_r$ is the bandwidth capacity of VM $m_r$ in Megabytes Per Second (MBps).

Definition 3.

Execution time of task $v_i$ on a VM, denoted by $E{T}_i^r$, is computed using Equation (3).

$$E{T}_i^r=R{T}_i^r+\underset{v_i\in pred\left(j\right)}{\max }C{T}_{ij}^r+d_r$$

(3)

In IaaS cloud, provisioning delay in VM allocation, that is $d_r$ can be caused by multiple factors such as, data center location, VM setup time, software setup time, VM migration time, quantity of simultaneous VM provisioning requests and variations in VM types, Operating Systems (OS) and time zones.

Definition 4.

Start time of running task $v_i$ on VM $m_r$, denoted by $S{T}_i^r$, is computed as in Equation (4).

$$S{T}_i^r=sl{t}_r+{\displaystyle \sum }_{v_p\in pred\left(v_i\right)}E{T}_p^r$$

(4)

where $sl{t}_r$ is start leasing time of VM $m_r$ and ${{\displaystyle \sum }}_{v_p\in pred\left(v_i\right)}E{T}_p^r$ is the total execution time of assigned tasks to VM $m_r$.

Definition 5.

Execution cost of task $v_i$ on VM $m_r$, denoted by $E{C}_i^r$, is computed as in Equation (5).

$$E{C}_i^r=\left(\frac{E{T}_i^r\times c_r}{h_r}\right)+\left(s_{ij}\times t{c}_{ij}\right)$$

(5)

where $h_r$ represents used billing interval of VM $m_r$, $c_r$ represents the cost per interval unit of VM $m_r$, $s_{ij}$ is the size of the data to be transferred from $v_i$ to $v_j$ and $t{c}_{ij}$ represents the data transfer cost (per MB) of communicating data from task $v_i$ to $v_j$. It becomes zero, if the tasks are scheduled on VMs within the same data center. So, we also do not consider this price when calculating the workflow’s execution cost.

Definition 6.

The upward rank for a task $v_i$ is the length of critical/longest path from task $v_i$ to the exit task $\left(v_{exit}\right)$, including the execution time of $v_i$. Thus, the priority of each task is defined as given by Topcuoglu et al. [29].

$$uran{k}_i=R{T}_i+\underset{v_j\in succ\left(v_i\right)}{\max }\left(C{T}_{ij}+uran{k}_j\right)$$

(6)

Definition 7.

The Degree of Dependency of each task $v_i$, denoted as $D{D}_i$, is provided by Equation (7).

$$d{d}_i=\left({\displaystyle \sum }_{v_p\in pred\left(v_i\right)}{e}_{p,i}+{\displaystyle \sum }_{v_c\in succ\left(v_i\right)}{e}_{i,c}\right)$$

(7)

where ${{\displaystyle \sum }}_{v_p\in pred\left(v_i\right)}{e}_{p,i}$ is the sum of all inward edges of task $v_i$ and ${{\displaystyle \sum }}_{v_p\in pred\left(v_i\right)}{e}_{p,i}$ is the sum of all outward edges of task $v_i$.

Definition 8.

Level of a task $v_j$ in the workflow, denoted as $lv\left(v_j\right)$, is defined as the maximum number of edges from the task $v_{entry}$ to $v_j$ . All the tasks in a BoT have same level. It is computed by Equation (8). Level of $v_{entry}$ is assumed to be zero.

$$lv\left(v_j\right)=1+\underset{v_i\in pred\left(v_j\right)}{\max }\left(lv\left(v_i\right)\right)$$

(8)

Definition 9.

Finish Time of task $v_i$ on VM $m_r$ is computed as in Equation (9).

$$F{T}_i^r=S{T}_i^r+E{T}_i^r$$

(9)

Definition 10.

Makespan (that is, schedule length) of workflow W is calculated by Equation (9).

$$M{P}_W=F{T}_{sink}^r$$

(10)

In other words, the overall makespan of the workflow is computed as the elapsed time between $v_{entry}$ and $v_{exit}$.

Definition 11.

Available spare time of a workflow is the amount of elapsed time between the user-defined deadline and the makespan, as computed by Equation (11).

$$A{S}_W=D{L}_W-M{P}_W$$

(11)

Definition 12.

Available spare time of a level is provided by Equation (12).

$$A{S}_{lv}=\left(\frac{R{T}_{lv}}{R{T}_W}\right)\times A{S}_W$$

(12)

where $R{T}_{lv}$ is the runtime of all tasks in the corresponding level $lv$ and $R{T}_W$ is the runtime of all tasks of the workflow $W$.

Definition 13.

Available spare time of a level is distributed among the tasks in the corresponding level, as provided by Equation (13).

$$A{S}_i=\left(\frac{coun{t}_{lv}}{n}\right)\times A{S}_{lv}$$

(13)

where $coun{t}_{lv}$ is the number of all tasks in the corresponding level $lv$ and $n$ is the number of all tasks in the workflow $W$.

Definition 14.

Sub-deadline of a task is the maximum limit of finish time of the corresponding task. The sub-deadline of each task $v_i$ is calculated by recursive traversal of the workflow DAG downwards, starting from $v_{entry}$, as provided by Equation (14).

$$S{D}_{run}=\underset{v_i\in pred\left(v_{run}\right)}{\min }\{S{D}_i+C{T}_{run,i}^r+R{T}_{run}^r+A{S}_i\}$$

(14)

Definition 15.

Sub-deadline of a BoT is initialized as

$$S{D}_{bot}=d_r+\underset{v_i\in bot}{\max }S{D}_i^r.$$

(15)

Definition 16.

Earliest Finish Time of a task $v_i$ on VM, denoted as $EF{T}_i^r$, is given by Equation (16).

$$EF{T}_i^r=\min \left(R{T}_i^r\right)+\underset{v_p\in pred\left(v_i\right)}{\max }\left(C{T}_{pi}^r+S{D}_p\right)$$

(16)

where $\min \left(R{T}_i^r\right)$ is the minimum finish time of task $v_i$ over all instances and $S{D}_p$ is the estimated sub-deadline for predecessor of $v_i$.

4.4. Proposed Algorithm

The main objective of the proposed DSB technique for scheduling scientific workflows in cloud computing is achieving high success rates with lower pay-per-use cost while satisfying the deadline constraint. The proposed DSB includes five distinct steps, namely task prioritization, task grouping, deadline distribution, task selection and elastic resource provisioning phase as presented next.

4.4.1. Task Prioritization

In the first step which is called task prioritization, we propose a task ordering strategy for optimizing task assignment. First, the tasks of the workflow are assigned priorities in order to guarantee task dependencies. For assigning priorities to the workflow tasks, their upward ranks [29] are calculated by Equation (6). The priority of tasks calculated using this technique has several benefits, which make it a worthy candidate for the prioritizing phase. Its implementation is simple. It considers the execution time of the workflow tasks, the transfer time between each pair of the tasks and the critical path of the workflow. Besides, this technique ensures that every task of the workflow has a higher priority over its successor tasks. It is calculated recursively for each task, beginning from the ending task to the first task of the workflow. The degree of dependency of each task is calculated by Equation (7). The tasks in the workflow having higher number of inward and outward edges have higher priority than others for scheduling them on the available VMs. Finally, the task scheduling sequence after the first phase, contain tasks sorted in descending order of their priorities. By assigning a priority to each task of the workflow, this method creates tasks with higher priorities earlier than the other tasks.

4.4.2. Task Grouping

Subsequently, in the second step, the tasks are combined into BoTs by applying horizontal grouping so that the tasks in each BoT have the same functionality and the same level (that is, depth) in the workflow DAG and are guaranteed to be ready for processing in parallel [19]. Figure 2 shows our example benchmark scientific workflows after applying horizontal grouping. The homogeneous tasks are represented by same color in Figure 2. Each BoT can comprise a single task or multiple tasks. Tasks within each BoT are homogeneous and share the same single immediate predecessor, have identical data distribution structure and have same type in terms of data size, input/output size and computational cost.

Table 2. Characteristics of the benchmark workflows. CU: Compute Unit.

Workflow	Number of Nodes	Number of Edges	Mean Data Size (MB)	Mean Runtime (CU = 1)
Montage_1000	1000	4485	3.21	11.36 s
CyberShake_1000	1000	3988	102.29	22.71 s
Epigenomics_997	997	3228	388.59	3858.67 s
LIGO_1000	1000	3246	8.90	2227.25 s
SIPHT_1000	1000	3528	5.91	179.05 s

shows the published details of these real-world workflows including the DAG, the average data size and the reference runtime of tasks based on [email protected] GHz CPUs (Compute Units $\cong$ 8) [25,30,31].

4.4.3. Deadline Distribution

The third step of the proposed algorithm is called deadline distribution. First, the cheapest VM type ($m_{sel}$) is determined among all the available VM instances such that, if assigned to all the workflow tasks, their estimated makespan (calculated by using Equation (10)) would be lower than the user-defined deadline ($D{L}_W$). If the estimated makespan exceeds deadline, then the next cheapest VM type ($m_{sel}$) is selected until the estimated execution time of the workflow on $m_{sel}$ is lower than $D{L}_W$. The elapsed time between the deadline and the estimated makespan, denoted as the available spare time $A{S}_W$ is calculated according to Equation (11). $A{S}_W$ is distributed proportionally over all levels of the workflow on the basis of runtime of tasks according to Equation (12). Then, $A{S}_{lv}$ is distributed among all tasks of each level proportional to the number of tasks in the corresponding level according to Equation (13). Afterwards, an estimated sub-deadline $S{D}_i$ is computed for each task of the workflow under the determined VM type $m_{sel}$, by using Equation (14). This sub-deadline will be a guiding factor for taking decisions at runtime about whether to reuse existing VM or rent a new one. It is larger for the BoTs with longer running tasks. The sub-deadline of each BoT is assumed to be the maximum finish time of its tasks corresponding to $m_{sel}$ (Equation (15)). In other words, the tasks within a BoT are assigned the same sub-deadline which would be equal to the estimated start time of the successor task. The algorithm for distributing deadlines to the BoTs is given in Algorithm 1.

Algorithm 1 Deadline Distribution

procedure DD(Workflow $W$, Deadline $D{L}_W$, Runtime of tasks on VMs $R{T}_i^r$) 1: $m_{sel}\leftarrow$ Find cheapest VM type such that $M{P}_W<D{L}_W$ 2: if $m_{sel}=null$ then 3: while $m_{sel}\ne null$ do 4:  $m_{sel}\leftarrow$ Next cheapest VM type such that $M{P}_W<D{L}_W$ 5: end while 6:end if 7: Calculate available spare time of workflow $A{S}_W$      //according to Equation (11) 8: Distribute $A{S}_W$ proportionally over all levels        //according to Equation (12) 9: Distribute $A{S}_W$ proportionally over all tasks in each level $lv$ //according to Equation (13) 10: Calculate estimated sub-deadline $S{D}_i$ for each task     //according to Equation (14) 11: Update sub-deadline of each BoT as the maximum finish time of its tasks

4.4.4. Task Selection

The set of tasks ready for execution are put in the execution queue. A task is considered as ready after all of its predecessors are already scheduled. The tasks in each BoT can be executed in parallel because they have no dependency constraints as well as sequentially to improve the utilization of leased billing intervals. However, there may exist dependency constraints between BoTs at the upper or lower levels. In order to exploit parallelism of such BoTs, the currently running tasks can send the data to their dependent tasks as soon as it is prepared, so that the dependent tasks at the consequent level can start their execution. Consequently, more tasks will execute in less time resulting in faster schedules. All the tasks in a BoT are homogeneous and share the same predecessor, therefore they become ready at the same time and have identical VM performance requirements.

4.4.5. Elastic Resource Provisioning

The resource provisioning phase is based on the optimization of a QoS metric cost and used to dynamically adjust the number of required VM instances to ensure the completion of workflow within the deadline. Its primary purpose is to prioritize the reuse of already leased VMs by utilizing idle times on previous rented intervals when possible instead of renting a new VM instance. When all the tasks in a BoT are ready for execution, they are put in the execution queue from the priority queue. Tasks in a BoT can be scheduled one by one to an elastic number of VMs for parallel, or serial executions. Scheduling plan is created based on tasks in the same BoT to decide the number and type of VM instances that can be launched to schedule the BoT. The plan needs to be made once for all the tasks in each BoT using MIP. The MIP problem was formulated to provide an estimate of the number and types of VMs that can optimize total cost of the workflow execution with the given deadline. It can be formally modeled as follows:

$$\mathrm{minimize}{\displaystyle \sum }_{v_i\in V}{\displaystyle \sum }_{m_r\in VM}E{C}_i^r$$

(17)

subject to:

$$x_i^r=1,x_i^r\in \left\{0,1\right\},\forall v_i\in V,\forall m_r\in VM$$

(18)

$$F{T}_i^r\le F{T}_j^r-E{T}_j^r,\forall \left(v_i,v_j\right)\in V,i<j$$

(19)

$${{\displaystyle \sum }}_{m_r\in VM,u\in m_r}{y}_{r,u}=n_{bot}^{r,u},\forall bot\in BoT$$

(20)

$$D{L}_{bot\in BoT}\le D{L}_W$$

(21)

$$F{T}_{sink}^r\le D{L}_W$$

(22)

Constraint (18) is a binary variable and ensures that each task is assigned to one and only one VM type. Constraint (19) ensures the precedence constraint. Constraint (20) ensures that the number of tasks of a BoT assigned to the u^th VM of type $r$ process all the tasks. Constraint (21) guarantees that the sum of sub-deadlines of all BoTs is not greater than the workflow deadline. Constraint (22) ensures that the deadline is met.

The problem is solved in CPLEX solver and a scheduling plan ${\mathcal{S}\mathcal{P}}_q^r=(m_r,n_q^r,k_{bo{t}_q}^{m_r})$ is obtained for each BoT to obtain VMs that can process the BoTs while meeting the deadline and with minimum cost. $n_q^r$ corresponds to the maximum number of tasks in the BoT $bo{t}_q$ that can be executed by the VM type $m_r$ without exceeding the deadline and $k_{bo{t}_q}^{m_r}$ is the number of VMs of type $m_r$ to use.

The VM selection for the task $v_i\in BoT$ requires the estimation of its actual execution time which is computed by taking the sum of execution time and provisioning delay. Then each ready task is checked to available times of rented intervals on existing VMs. The execution cost is calculated by Equation (5). Since, each partial hour consumed is billed as a full hour, therefore the execution cost of other tasks submitted to the same VM during the available partial hour is zero. If such VMs exist that incur no execution cost for the remaining intervals as well as satisfy the sub-deadline, then the scheduler selects the VM $m_{sel}$, that can execute the running task with the estimated earliest finish time (according to Equation (16)). The number of tasks allotted to current billing interval of $m_{sel}$ depends on the number of tasks that can meet their sub-deadline. It can improve resource utilization by minimizing wastage of already leased intervals without affecting the execution time of the workflow. The total execution time of assigned tasks to VM $m_r$ is updated dynamically after every task assignment. If no such VMs exist with remaining available billing intervals, all the tasks in the BoT from the execution queue are scheduled to subsequent billing interval of existing VMs only if the BoT still meets the sub-deadline. If none of the existing active VMs can satisfy the BoT sub-deadline, the resource scaling-up strategy will be triggered to create a new VM type with the minimum execution cost among others and that can meet the BoT’s sub-deadline. In extreme cases in which no such VM type exist that can complete the tasks within deadline, a fastest VM type can be rented. Whenever a BoT completes its execution, the sub-deadline of all the remaining BoTs is updated dynamically. Since all the tasks within a BoT are homogeneous, so they have the same VM type preference. Therefore, the current VM type $m_{sel}$ can be assigned to all tasks in BoT. The algorithms for this phase are given in Algorithms 2–4.

Algorithm 2 Elastic Resource Provisioning
procedure ERP(Execution queue containing set of ready BoTs $ExeQ$, Set of VM types VM)
1	$Exe{Q}^{new}\leftarrow null$
2	for all $bo{t}_q\in ExeQ$
3	if $bo{t}_q.count\left(tasks\right)>1$ then
4	Solve the MIP problem by CPLEX and get ${\mathcal{S}\mathcal{P}}_{bot}^r$
5	for all ${\mathcal{S}\mathcal{P}}_q^r=(m_r,n_q^r,k_{bo{t}_q}^{m_r})$ do
6	for all $m_r\in {\mathcal{S}\mathcal{P}}_q^r$ do
7	$ExeQ\leftarrow n_q^r$
8	$VM\leftarrow k_{bo{t}_q}^{m_r}$
9	$\mathit{E}\mathit{x}\mathit{e}{\mathit{Q}}^{\mathit{n}\mathit{e}\mathit{w}}\leftarrow$ Call LFI($\mathit{E}\mathit{x}\mathit{e}\mathit{Q},\mathit{V}\mathit{M}$)
10	if $\mathit{E}\mathit{x}\mathit{e}{\mathit{Q}}^{\mathit{n}\mathit{e}\mathit{w}}\ne \mathit{n}\mathit{u}\mathit{l}\mathit{l}$ then
11	Call RSU($Exe{Q}^{new},VM$)
12	end if
13	end for
14	end for
15	else if $\mathit{b}\mathit{o}{\mathit{t}}_{\mathit{q}}.\mathit{c}\mathit{o}\mathit{u}\mathit{n}\mathit{t}\left(\mathit{t}\mathit{a}\mathit{s}\mathit{k}\mathit{s}\right)=\mathbf{1}$ then
16	$v_{run}\leftarrow bo{t}_q$
17	$m_{sel}\leftarrow$ select cheapest VM that can run task within deadline
18	Schedule $v_{run}$ to $m_{sel}$
19	$ExeQ\leftarrow ExeQ-\left\{v_{run}\right\}$
20	${CPT}^{sel}\leftarrow {CPT}^{sel}+{ET}_{sel}^{run}$
21	Update next available time of $m_{sel}$
22	end if
23	end for

Algorithm 3 Lease Free Interval
procedure LFI(Set of ready tasks of BoT $ExeQ$, $\mathrm{Set}\mathrm{of}\mathrm{VMs}VM$)
1	$v_{run}\leftarrow$ Get the next ready task with highest priority from $ExeQ$
2	$m_{sel}\leftarrow null$
3	$M_{sel}\leftarrow null$
4	$m\leftarrow null$
5	$freeInterval\leftarrow false$
6	for all $m_r\in VM$ do
7	Calculate $E{C}_{run}^r$        //according to Equation (5)
8	Calculate $F{T}_{run}^r$        //according to Equation (9)
9	if $E{C}_{run}^r<S{D}_{run}$ and $F{T}_{run}^r<S{D}_{run}$ then
10	$freeInterval\leftarrow true$
11	$M_{sel}\leftarrow M_{sel}\cup \{m_r\}$
12	end if
13	end for
14	$m_{sel}\leftarrow m_r\in M_{sel}$ such that $EF{T}_{run}^{sel}$ is minimum
15	if $m_{sel}\ne null$ then
16	$m\leftarrow m_{sel}$
17	end if
18	if $freeInterval=true$ then
19	Schedule $v_{run}$ to $m_{sel}$
20	$ExeQ\leftarrow ExeQ-\left\{v_{run}\right\}$
21	$CP{T}^{sel}\leftarrow CP{T}^{sel}+E{T}_{run}^{sel}$
22	Update next available time of $m_{sel}$
23	else
24	$Exe{Q}^{new}\leftarrow Exe{Q}^{new}\cup \left\{v_{run}\right\}$
25	end if

Algorithm 4 Resource Scaling Up
procedure RSU(Set of ready BoTs $Exe{Q}^{new}$, Set of VMs $VM$)
1	$v_{run}\leftarrow$ next ready task with highest priority
2	$m_{sel}\leftarrow null$
3	$M_{sel}\leftarrow null$
4	$newVM\leftarrow false$
5	for all $m_r\in VM$ do
6	Calculate $E{C}_{run}^r$        //according to Equation (5)
7	Calculate $F{T}_{run}^r$        //according to Equation (9)
8	if $F{T}_{run}^r<S{D}_{run}$ then
9	$newVM\leftarrow true$
10	$M_{sel}\leftarrow M_{sel}\cup \left\{m_r\right\}$
11	end if
12	end for
13	$m_{sel}\leftarrow m_r\in M_{sel}$ such that $EF{T}_{run}^{sel}$ is minimum
14	if $m_{sel}=null$ then
15	$m_{sel}\leftarrow m_r\in M_{sel}$ such that $E{T}_{run}^{sel}$ is maximum
16	end if
17	if $newVM=\mathit{true}$ then
18	Lease new interval $m_{sel}$ and schedule task $v_{run}$ on it
19	$Exe{Q}^{new}\leftarrow Exe{Q}^{new}-\left\{v_{run}\right\}$
20	$S{T}^{sel}\leftarrow CurrentTime()$
21	end if

In order to adapt to unexpected delays such as variations in task runtime estimations, network congestion and resource provisioning delays, the sub-deadline of remaining workflow tasks is adjusted whenever a task finishes either earlier or later than expected. In this way, if a task finishes earlier, the remaining tasks will have more time to run and hence they can either be assigned to a cheaper VM or delayed, to be scheduled in subsequent cycles. If a task finishes later than expected, adjusting the deadline of the remaining tasks may prevent the deadline from being missed. The VM scaling-down strategy is used by the scheduler during execution to shut down any leased VMs that are idle for a long time and approaching their subsequent billing interval. An overview of resource scaling down technique is shown in Algorithm 6.

The algorithm of the proposed method is shown in Algorithm 5.

Algorithm 5 The Proposed DSB
Input: Workflow $W$, Deadline $D{L}_W$, Runtime of tasks on VMs $R{T}_i^r$
1	Add $v_{entry}$ and $v_{exit}$ and their corresponding edges to the workflow W
2	for all $v_i\in V$ do
3	Calculate upward rank $uran{k}_i$         //according to Equation (6)
4	Calculate degree of dependency $d{d}_i$       //according to Equation (7)
5	end for
6	Sort the tasks in descending order of priorities
7	Calculate level of each task $lv\left(v_i\right)$         //according to Equation (8)
8	Identify all the BoTs in the workflow
9	Call DD($W,D{L}_W,R{T}_i^r$)
10	for all $bo{t}_q\in BoT$ do
11	Put BoTs in priority queue and sort them based on the rules mentioned in Section 4.4.4
12	end for
13	Put ready BoTs in execution queue $ExeQ$
14	Call ERP($ExeQ,VM$)

Algorithm 6 Resource Scaling Down
procedure RSD(Set of leased VMs $M_{lease}$)
1	$M_{lease} \leftarrow$ Set of all leased VMs
2	for each $m_r\in M_{lease}$ do
3	if $m_r$ is currently idle then
4	if $m_r$ has no waiting tasks then
5	if $m_r$ is currently approaching the next pricing interval then
6	$M_{lease}\leftarrow M_{lease}-\left\{m_r\right\}$
7	Shut down $m_r$
8	end if
9	end if
10	end if
11	end for

4.5. Computational Complexity

Consider n as the total number of workflow tasks, m as the number of BoTs, k as the total number of available VMs, d as the number of dependency constraints and e as the number of directed edges. The time complexity of this scheduling algorithm requires the computation of some basic operations. Calculating priority, dependency constraints and sub-deadline of all tasks have complexity $O\left(n.k\right)$. Sorting groups based on their priority $O\left(m\right)$. Computing start time, completion time and solving the MIP for all VMs $O\left(k\right)$. Mapping tasks on VMs $O\left(n.k\right)$. The total time is $O\left(n.k+n(m+k+nk)\right)$, therefore complexity of the proposed algorithm is $O\left(n^2.k\right).$

5. Performance Analysis and Discussion

5.1. Experiment Environment

WorkflowSim is a Java-based open source discrete event workflow engine that has been used to model a cloud execution environment for executing scientific workflow applications [32]. This trace-based framework is an extension of CloudSim [33]. WorkflowSim offers support for workflow DAGs and provides execution environment for workflow level resource provisioning, resource management, task clustering and task scheduling. For our experiments, WorkflowSim was adopted to evaluate the performance of the proposed method on real traces under dynamically provisioned on-demand cloud VMs and a pay-per-use model derived from Amazon EC2 pricing model (http://aws.amazon.com/ec2). The correctness of WorkflowSim has been proved in [32]. Moreover, it supports the analysis of various scheduling overheads and failures.

An IaaS provider offering a single data center and six types of VMs was modelled.

Table 3. VM types specifications. ECU: EC2 Compute Unit.

VM Type	ECU	Memory	Price ($/h)
m3.medium	1	3.75	0.067
c3.xlarge	4	3.75	0.21
m3.xlarge	4	15	0.266
c3.2xlarge	8	15	0.42
m3.2xlarge	16	30	0.532
c3.4xlarge	16	30	0.84

lists the configurations of the VM types based on EC2.

The workflow generator toolkit, Pegasus, was used to generate synthetic workflows of various sizes for each workflow application in terms of total number of nodes. Five real-world scientific applications were chosen, namely: Cybershake (data-intensive, memory-intensive, resource-intensive), Epigenomics (CPU-bound), LIGO Inspiral Analysis (memory-intensive, resource-intensive), Montage (I/O bound) and SIPHT [30].

5.2. Performance Metric

The goal of scheduling algorithm considered here is to find a schedule map in such a way that the cost is optimized under user-defined deadline constraint. The performance metrics used to evaluate the proposed DSB algorithm are given below.

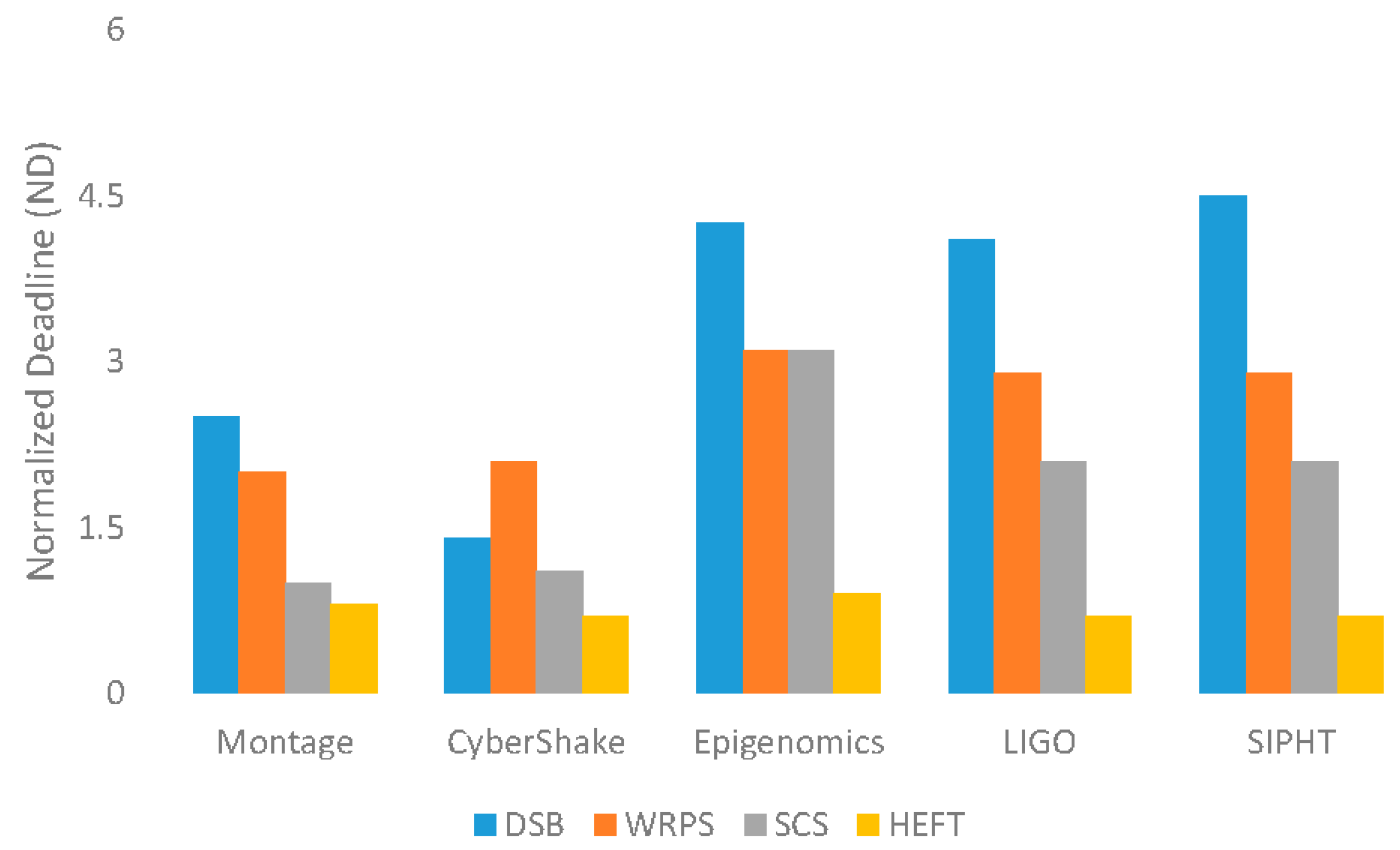
5.2.1. Normalized Deadline (ND)

To investigate the quality of results and for the purpose of comparison, deadline is normalized, called ND (Normalized Deadline). $M{P}_W$ is the minimum makespan or schedule length of the workflow DAG. It can be obtained by computing the makespan of the workflow on fastest VM types with a maximum level of parallelism and ignoring delays. With these values, the normalized user-defined deadline constraint is computed by Equation (23):

$$ND=\frac{D{L}_W}{\min \left(M{P}_W\right)}$$

(23)

For successful schedule map that meet the deadline constraint, the value of ND could not be less than 1.

5.2.2. Improvement Rate (IR)

It is defined as the percentage improvement obtained in the performance of the proposed algorithm in the overall execution of workflow DAG with respect to other algorithms. Reduction in the cost of the proposed algorithm over other considered algorithms can be calculated by IR(%).

$$IR(\%)=\frac{cost\left(other\right)-cost\left(proposed\right)}{cost\left(proposed\right)}\times 100.$$

(24)

5.2.3. Success Rate (SR)

It is defined as the success rate of finding a cost optimized schedule while satisfying the user-defined deadline, as given by Equation (25):

$$SR=\frac{Numberofsimulationrunsthatsuccessfullymeetdeadline}{Totalnumberofsimulationruns}\times 100$$

(25)

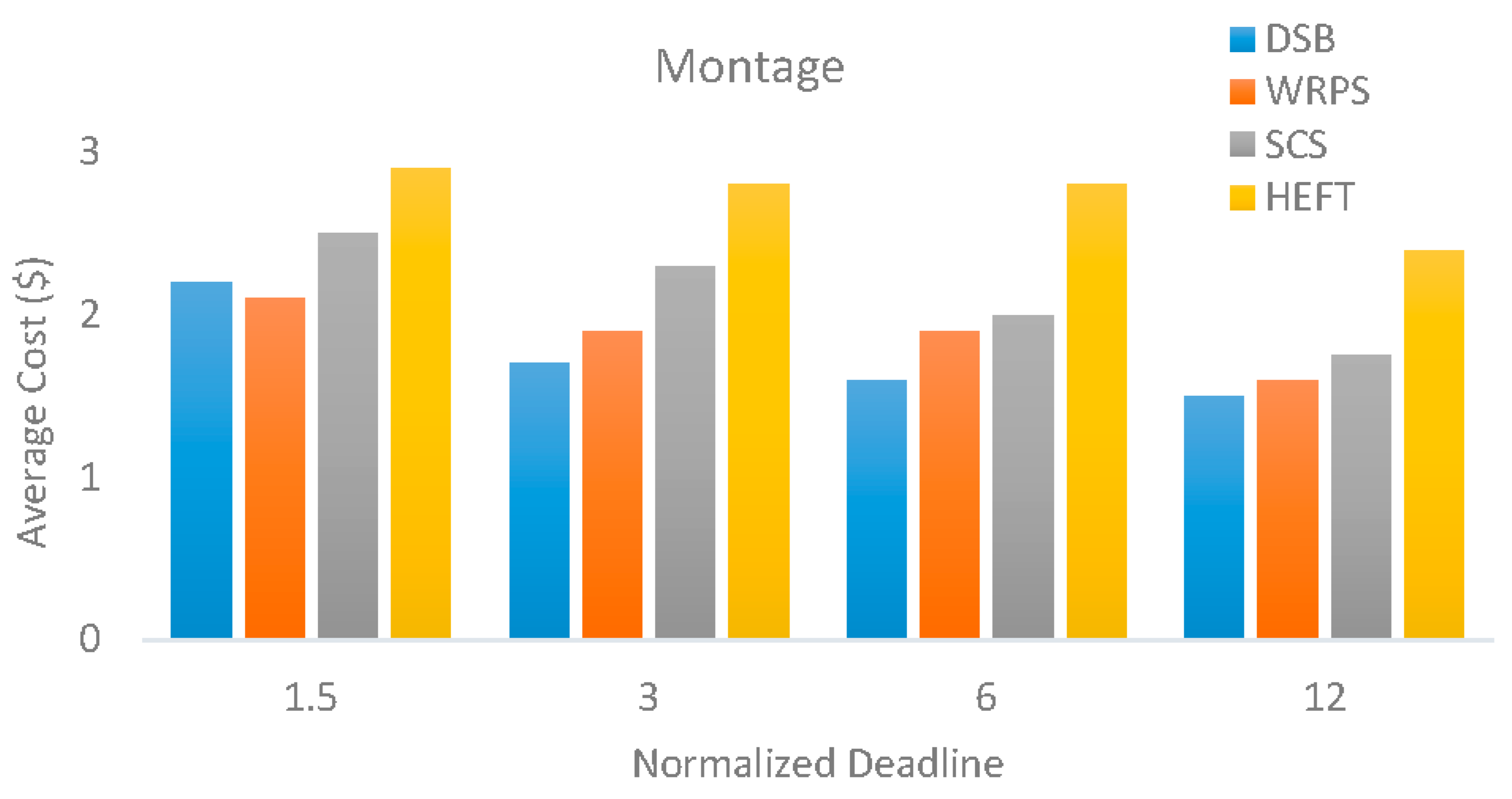
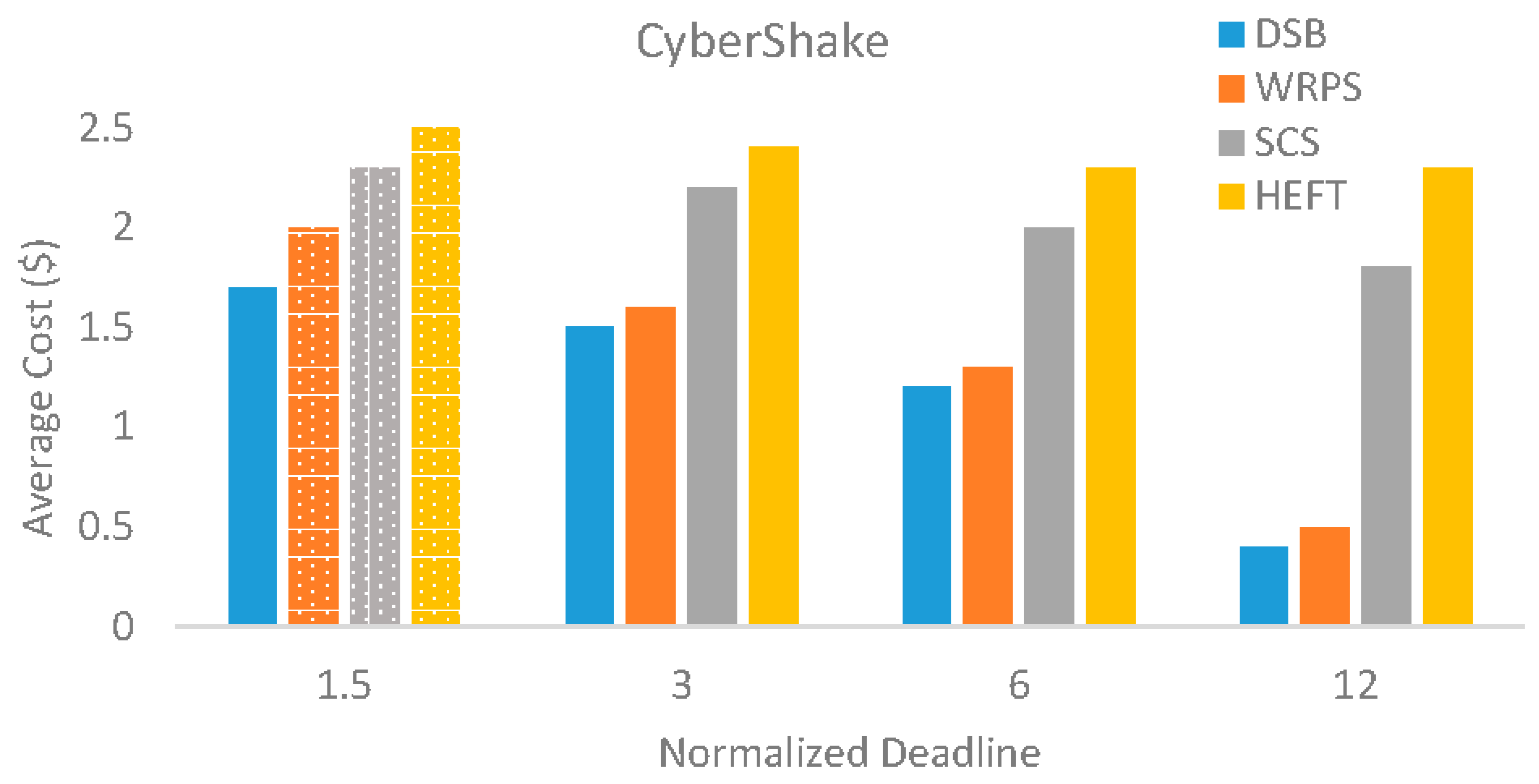
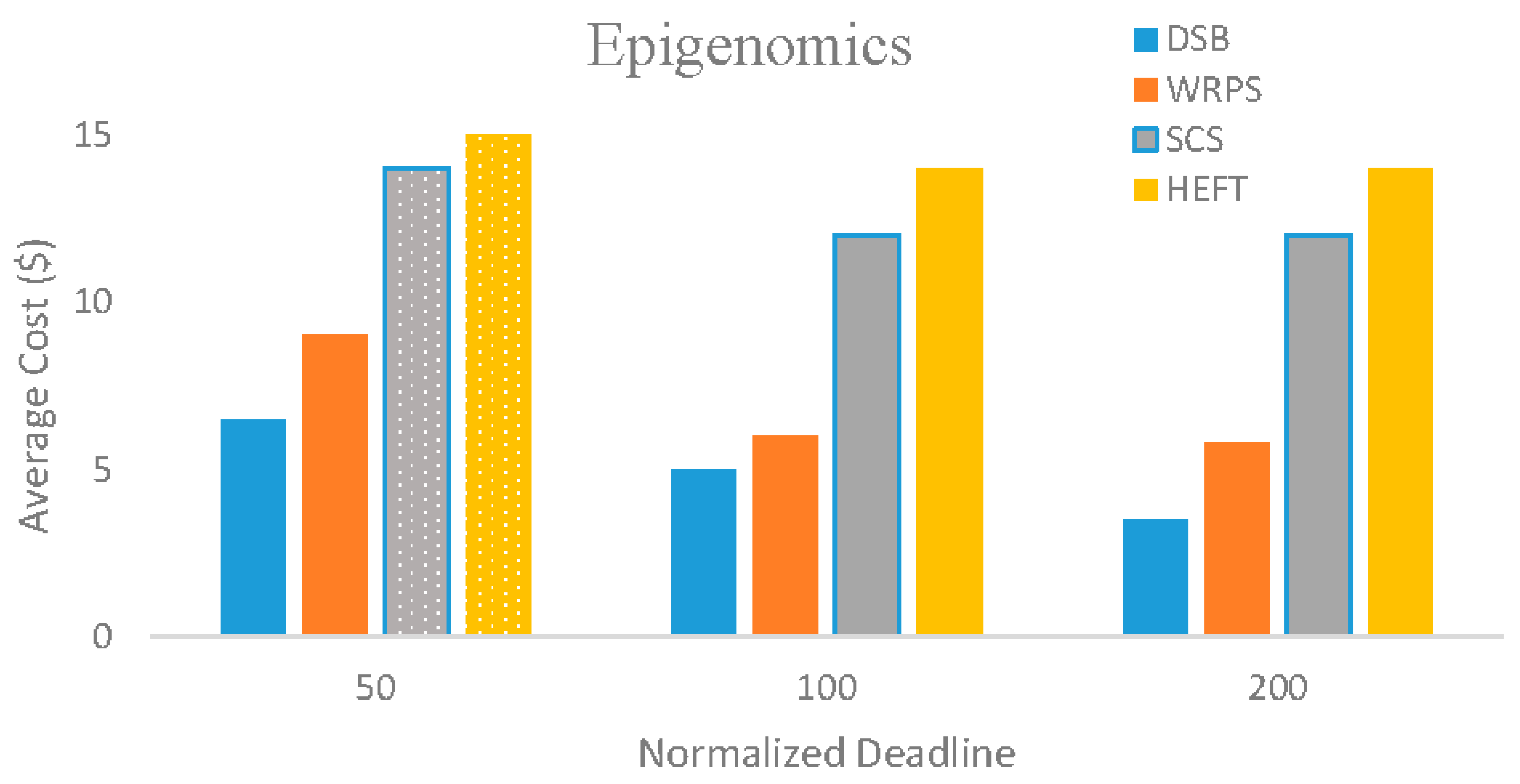
5.3. Evaluation Results

We implemented WRPS [34], SCS [9] and HEFT [29] algorithms. Then, we evaluated these scheduling methods and our proposed DSB scheduling algorithm on a standard and real set of scientific workflow applications. Finally, we compared their results with our scheduling model.

The workflows were executed by changing the deadline. The experiments were repeated 30 times for each workload instance and the average value of output metrics are reported in this section. The effect of varying deadline over the cost was evaluated, as shown in Figure 3 and Figure 4. The proposed DSB scheduling algorithm successfully scheduled maximum number of tasks while meeting the deadline constraint with the average success rate of 97.93% compared to the success rates of WRPS, SCS and HEFT which are 92.68%, 82.86% and 66.93% respectively. Figure 3 and Figure 4 shows the average cost of Montage and CyberShake workflow respectively for 1000 tasks. The structure of Montage and CyberShake consists of many small-sized tasks in each level with almost same priorities, dependency constraints and deadline. It can be seen that the average cost of the proposed DSB is lower because the workflow tasks are ordered on the basis of their priorities, dependency constraints and sub-deadlines and afterwards partitioned into horizontal BoTs. The cost of SCS and HEFT are comparatively high because these methods take longer to process tasks of large size. Similarly, it can be seen that the cost of the proposed DSB was comparatively lower than the other algorithms which shows that the proposed DSB exhibits better performance than its counterparts. Figure 5 shows that SCS and HEFT missed the deadline when it is minimum for executing Epigenomics workflow, while in all other cases, the deadline was successfully met. The proposed method not only execute maximum number of tasks successfully without violating the deadline but also achieves lowest cost for Epigenomics workflows. Figure 6 illustrates that the proposed DSB shows best performance under hard deadline. This is due to the fact that LIGO Inspiral Analysis workflow consists of blocks of tasks and each block create specific results on a portion of data. These results must be created with minimum makespan. Our proposed method can execute the blocks in each level in parallel by partitioning them in horizontal groups while taking care of the deadline and dependency constraints. The SIPHT workflow has different parts and their intermediate output is required as input to the last node to achieve the final output. Our proposed algorithm prioritizes reuse of rented intervals and schedule the different parts of the SIPHT by considering priority and sub-deadline of each task and map it with the VM that leads to minimum cost of the task on the assigned VM, as shown in Figure 7.

It can be seen from the results that the proposed method DSB shows significant improvement in cost when the deadline was minimum. Moreover, it showed better resource management by exploiting efficient level of parallelism.

Figure 8 shows the normalized deadline obtained for each workflow with different scheduling algorithms. In the proposed DSB, the greater value of ND represents that it could achieve an efficient schedule map with lowest cost under the user-defined deadline constraint. Its value less than 1 denotes that the algorithm was unable to generate a schedule map while satisfying the deadline constraint. Moreover, the proposed DSB achieves lower cost with workflows having longer deadlines because they are scheduled on least expensive VMs.

The average success rate achieved for the workflows are shown in Figure 9. It can be seen that the performance of the proposed DSB is better in terms of cost achieved under user-defined deadline as compared to the other baseline algorithms.

5.4. Sensitivity of Overheads, VM Performance Variations and Task Failures

In real cloud environment, unexpected delays, VM provisioning delays, inaccuracies in task runtime estimations and VM performance variations can cause failures. The sensitivity of our mechanism to overheads, delays and performance variations was evaluated. It was modeled using a normal distribution around the real value with 30% provisioning delay and task failure probability. The loss in VM performance was considered based on a normal distribution with mean of 15% and standard deviation of 10%. The relative performance of our method is given in Figure 10. It shows four curves, each representing (i) accurate estimations and no delays and failures; (ii) inaccurate estimations of VM performance variation; (iii) inaccurate estimations of provisioning delays and (iv) task failures respectively. These results demonstrate the algorithm’s good sensitivity to inaccurate estimations. It is also found that the proposed mechanism is successful in meeting its deadline constraint in most of the cases. However, task failure has a larger impact on performance due to its direct effect on overall makespan.

5.5. Analysis of Variance (ANOVA) Test

In this section, the statistical significance of the obtained experimental results is checked by the one-way ANOVA test [35].

Table 4. One-way ANOVA test result.

Workflow	Source of Variation	SS	df	MS	F	p-Value
Montage_1000	Between groups	561,231.4	2	280615.7	35.683	3.04 × 10−8
	Within groups	212,330	27	7864.074
	Total	773,561.4	29
	Between groups	1,519,506.153	2	759,753.076	21.027	3.12× 10−6
CyberShake_1000	Within groups	975,550.9	27	36,131.515
	Total	2,495,057.053	29
	Between groups	1,630,867.799	2	815,433.8995	60.632	0.0
Epigenomics_997	Within groups	363,117.4	27	13,448.792
	Total	1,993,985.199	29
LIGO_1000	Between groups	1,000,549.365	2	500,274.682	63.815	0.0
	Within groups	211,665.6	27	7839.467
	Total	1,212,214.965	29
SIPHT_1000	Between groups	4,717,007.744	2	2,358,503.872	24.935	7.3 × 10−7
	Within groups	2,553,788	27	94,584.741
	Total	7,270,795.744	29

Note: SS = Sum of Squares, MS = Mean Sum of Squares, df = Degree of Freedom.

shows that most of the variation in the obtained results is the variation between and not the variation within. It is evident that the ANOVA test is statistically significant due to the greater F-statistic and lower p-value. In other words, there is statistically significant difference between the two algorithms. Therefore, the null hypothesis (H₀) which states that the mean of all the algorithms are equal, can be rejected.

6. Conclusions

In this paper, a BoT based workflow scheduling algorithm has been proposed for the dynamic and elastic provisioning of VM instances, that considers resource renting cost minimization constrained to user-defined deadline. The proposed model groups the workflow into BoTs based on data dependency and priority constraints and thereafter optimizes the allocation and scheduling of BoTs on elastic, heterogeneous and dynamically provisioned cloud resources called VMs in order to attain the proposed method’s objectives. The proposed approach considers pay-as-you-go IaaS clouds having inherent features such as elasticity, abundance, heterogeneity, VM performance variation and VM provisioning delays. Mathematical model was successfully used for the dynamic provisioning of resources. The traces for the experiments were taken from real-world scientific workflow applications. Experimental results demonstrate that our proposed DSB increases the chance of deadline being satisfied and minimizes the execution cost compared to other approaches for the real-world scientific workflow applications considered.

The future work is intended to investigate more accurate models to predict potential failures, uncertainties and performance variations of time critical applications in the real IaaS environment. Another future direction is to extend the proposed model to implement fault tolerant energy efficient elastic resource provisioning and scheduling. Moreover, future research will also evaluate the proposed model on VMs with different lengths of pricing intervals. Finally, the algorithms will be implemented in a workflow execution engine for their effective utilization in real life.