Abstract
As more and more items are tagged with RFID (Radio Frequency Identification) tags, grouping-proof technology is widely utilized to provide a coexistence evidence for a group of related items. Due to the wireless channel used in RFID systems, a security risk exists in the communication between the reader and tags. How to ensure the tag’s information security and to generate reliable grouping-proof becomes a hot research topic. To protect the privacy of tags, the verification of grouping-proof is traditionally executed by the verifier, and the reader is only used to collect the proof data. This approach can cause the reader to submit invalid proof data to the verifier in the event of DoP (Deny of Proof) attack. In this paper, an ECC-based, off-line anonymous grouping-proof protocol (EAGP) is proposed. The protocol authorizes the reader to examine the validity of grouping-proof without knowing the identities of tags. From the security and performance analysis, the EAGP can protect the security and privacy of RFID tags, and defence impersonation and replay attacks. Furthermore, it has the ability to reduce the system overhead caused by the invalid submission of grouping-proofs. As a result, the proposed EAGP equips practical application values.
1. Introduction
RFID grouping-proof technology is a mechanism that can prove a group of tagged items appeared at the same time and the same place [1]. The grouping-proof protocol can be widely adopted to many applications that need coexistence proof to guarantee the items with RFID tags have been scanned simultaneously, such as supply-chain, health care, and evidence in law [2,3,4]. For example, in logistics management, we can generate a proof to guarantee the integrity of the container and the goods in it by scanning their tags simultaneously. In the intelligent health care environment, we can validate the correctness of the medicine taking through scanning the patients and their unit-dose medications at the same time and place [5]. In the manufacturing field, a manufacturer of aircraft equipment can certify that a certain part always leaves its factories with a safety cap attached by scanning their RFID tags simultaneously.
According to the connection method between the reader and the verifier, there are two different modes: online and offline [4]. The online mode requires a stable connection between the reader and the verifier, such as [6,7]. In this model, the verifier can send and receive messages from a specific tag (via the reader) during the whole protocol execution. This mode has good real-time performance and high security, but the network condition requirement is relatively high. In some application fields, it is difficult to maintain the network connection between the reader and the background. In addition, the consistent network connection should take the energy efficiency into account [8,9,10]. On the other hand, in the offline mode, the stable connection between the reader and the background is unnecessary; the reader can collect tag information and generate multiple grouping-proofs without the participation of the verifier. After these processes, the reader can finally send these proof data to the verifier. In this vein, the verifier in offline mode does not need to communicate with any specific tag (via the reader), it only needs the connection before and after the generation of grouping-proof. The connection requirement is more flexible during the protocol, however, there are many security problems need to be solved in this mode, which has become the research focus in many works proposed in the state of the art [3,4,11,12,13,14,15,16,17,18].
Figure 1 shows a common offline mode of RFID grouping-proof system. The tags are divided into M groups: . Each group represents items with RFID tags. The reader receives group information from the verifier and communicates with tags. If it can simultaneously scan all tags in the ith group, the reader generates a grouping-proof . After all groups are scanned, the reader sends to the verifier. The verifier checks these proofs and stores them as a record. In the grouping-proof protocol, the simultaneous scan means all tags are scanned by a same reader in a short time interval.
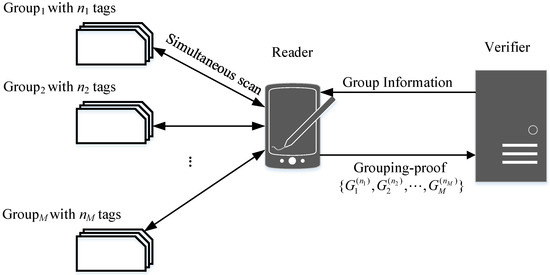
Figure 1.
The offline mode of grouping-proof protocol.
1.1. Motivation
In this study, we focus on the offline mode of grouping-proof protocols. There are many works that engage in this mode. At first, the grouping-proof can show the presence of group items as a whole. Note that each single item intends to be sold or transported to other owners. To protect the privacy of these items, the anonymity should be considered as an important security property. In order to do this, the authentication should be anonymous so that any unauthorized third party cannot obtain a tag’s identity during the protocol execution. The second point is the secret key distribution. Considering there are a large number of tags in RFID system, the management of secret keys becomes a complicated problem, the use of symmetric encryption schemes is not practical. So the PKI systems are considered. The encryption and decryption in the RSA algorithm need to perform modular exponentiation of great numbers to guarantee security, since the length of the modulus is always larger than 1024 bits, which makes multiplication and division a time-consuming calculation, it is impossible to apply the RSA algorithm in RFID tags in reality. The Ellipse Curve Cryptography (ECC) method is used instead. The point or scalar multiplication is the basic operation for ECC protocols; it is easily performed via repeated group operations which is applicable to low-cost RFID tags. The third problem of offline grouping-proof protocol is that the validity check can only be performed by the verifier. That means the invalid grouping-proof will not be found before submission to the background. This problem greatly reduces the response speed to illegal data. Our solution allows the reader to check the tag’s identity before submitting the proof data. However, this solution needs the reader to store the tag’s identity, which may bring a potential safety hazard about the tag’s privacy information. Therefore, it is essentially necessary to find a way to guarantee the legality of grouping-proof without revealing the secret information of tags.
1.2. Our Contributions
The main contributions of this paper are shown as follows.
- (1)
- We investigate Kang’s protocol [19] and provide improvements in key distribution [20], communication overhead, and resistance to impersonation attack and DoP (Denial of Proof) attack.
- (2)
- We establish a scheme to seal the identity of the tag into the grouping-proof message by the group key and session key. So the proof data include two types of tag information: the group member identity and the individual identity.
- (3)
- We propose an ECC based offline anonymous grouping-proof protocol with two tags, denoted as EAGP. Based on EAGP, we extend the protocol into n tags condition , expressed as EAGP. The EAGP has two verification stages. The first stage is used to verify the legality of the tag’s group member identity and check the grouping-proof briefly. The second stage is used to verify the identity of the tag and further confirm the grouping-proof.
- (4)
- We carry out the security analysis, performance analysis and correctness proof about the EAGP, and obtain a conclusion that this protocol can resist DoP attack [21] and impersonation attack. It can also protect the tag’s information when the reader was compromised. Moreover, EAGP has good scalability in multiple tags condition.
The rest of the paper is organized as follows. An overview of related RFID grouping-proof protocols is presented in Section 2. Section 3 describes the preliminaries of EAGP. Section 4 introduces the Kang’s protocol [19]. The system model and definition are described in Section 5. Section 6 shows the EAGP protocol. The security analysis about EAGP are described in Section 7. In Section 8, we provides a performance analysis of our protocols. Section 9 draws a conclusion about this work. The correctness proof about EAGP is described in Appendix.
2. Related Work
The idea of grouping-proof was first introduced in [1], the protocol was called yoking-proof, which only involves two tags coexistence proof in the protocol. Since its introduction, the yoking-proof has evolved to include multiple tags and is now known as the “grouping-proof”. In succeeding studies, the grouping-proof protocol is applied in many application fields. In [2,3,4,5], the authors used the protocol to generate the medical process evidence for inpatient medication safety. Chien et al. [13] constructed a tree-based tag organization to provide grouping-proof for a complicated system. In addition, there are many other promotions to enhance the security and privacy of this protocol. Burmester et al. in [22] pointed out that there are some problems in grouping-proof protocols: (1) vulnerability to replay attack; (2) unrelated tags can participate in a protocol session, and that the failure can only be found by the verifier; and (3) the protocol does not take the presence of a rogue reader into account. To mitigate these drawbacks, the authors improve the protocol by using group key, proposing the grouping-proof protocol with forward security. Li et al. [16] proposed a yoking-proof protocol with tag anonymous and prove the security within the Universally Composable (U.C.) framework [23]. Cho et al. [18] described a grouping-proof protocol resisted replay attack. In [24], the authors used the code scheme to check the tag information and improve the protocol security. In [4], the authors analyze the existing grouping-proof protocol, and declared the guidelines for future sound protocols. In order to further improve safety of RFID systems, the application of encryption algorithm is necessary. The work in [25] discussed the feasibility of the ECC in RFID systems. In [26], the authors proposed a RFID chip scheme to support ECC. After that, a RFID mutual authentication protocol based on ECC (ID-Transfer) was proposed [27]. Based on the ID-Transfer, Batina proposed the first grouping-proof protocol based on the ECC in [28] and proved it can provide proof validation and privacy protection in the presence of untrusted tags or reader. The literature [29] showed that Batina’s protocol is vulnerable to malicious tracking and proposed the improvement scheme. Kang in [19] further showed that the Batina’s protocol is not secure with respect to impersonation attack and they proposed to use the authentication of the reader during the grouping-proof procedure to solve this problem.
3. Preliminaries
In this section, we introduce the ECC and the related hardness problem. The details are described as follows.
3.1. The Ellipse Curve Cryptography
Elliptic curves are algebraic structures that constitute a basic class of cryptographic primitives which rely on a mathematical hard problem. An elliptic curve E over a finite field with characteristic can be defined by the Equation (1):
where and . The point is a point on the elliptic curve. Let P be a fixed point on the curve with prime order n and k is a large integer scalar in . Due to the hardness of Elliptic Curve Discrete Logarithm Problem [30], it is easy to compute the scalar multiplication but hard to find k by knowing only Q and P.
3.2. Elliptic Curve Discrete Logarithm Problem (ECDLP)
ECDLP Definition: Given an elliptic curve E defined over a finite field , a point of order n, and a point where , determine k.
The well-known hardness of the ECDLP is crucial for the security of our elliptic curve scheme.
4. Investigation of Kang’s Protocol
Literature [19] proposed a grouping-proof protocol based on ECC. The framework of this protocol is shown in Figure 2. Table 1 describes the notations in this protocol.
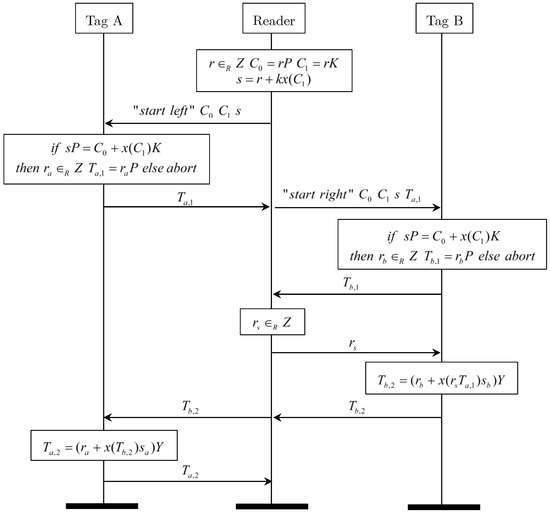
Figure 2.
The Kang’s protocol.

Table 1.
Summary of notations in Kang’s protocol.
The protocol has four stages: (1) initialization stage, (2) authentication stage, (3) grouping-proof generation stage, and (4) verification stage. In initialization stage, the server writes the into tag A, the into tag B. The authentication stage is used to authenticate the identity of a reader. It can prevent the reader impersonation attack. In this stage, the reader generates its authentication code and uses it to identify itself to two tags. Then the reader starts the grouping-proof stage:
- (1)
- According to the random number broadcasted by the reader, tag A generates random number , calculates and sends it to tag B via the reader.
- (2)
- Tag B calculates and sends to tag A via the reader.
- (3)
- Tag A calculates and send it to the reader.
- (4)
- Finally, the reader passes these data as grouping-proof to the verifier for validation.
Kang’s protocol uses authentication to solve the impersonation attack, and there are some flaws which need to be pointed out.
- (1)
- The key distribution: in Kang’s protocol, tag A and tag B need to store the reader’s public key. If the reader is changed, the new public key needs to be written into all the tags. If the amount of tags is very big, the overhead is too serious.
- (2)
- The DoP attack: the reader in Kang’s protocol can not validate the proof and is unable to check the legality of tags. If the reader suffered from DoP attack or some unrelated tags taken part into the proof process, before the proof be sent to the verifier, the failure can not be identified immediately which will reduce the system real-time performance.
- (3)
- Communication overhead: the using of authentication stage increases the number of communication times between the tag and the reader, which leads to the additional overhead of communication.
5. The System Model and Security Requirement
5.1. The System Model
In our work, the RFID grouping-proof system is consist of three parts: reader, RFID tags and verifier.
- Tag: the tags in our protocol are passive low-cost devices which have a relative small storage and limited computational capacity. The tags are divided into several groups.
- Reader: the RFID reader is a powerful device which is controlled by an untrusted third party. For security reasons, the privacy information of tag and verifier is unknown to the reader.
- Verifier: an offline trusted third party (TTP) which maintains all the keys and identities of groups.
There are two types of channels in our protocol. The channel between the tag and the reader and the channel between the reader and the verifier. We assume the former is not secure and can be attacked by the adversary. The second channel is secure and the message transferred in this channel cannot be eavesdropped.
5.2. The Adversary Model
In grouping-proof protocols, the adversary has two purposes: (1) forge the grouping-proof which can pass the validation of verifier; and (2) get the privacy information of the reader and tags. According to the attacker described in [23], the adversary in our protocol can completely control the communication channel between the reader and tags, in terms of modifying, delaying and replaying any message in the protocol. In addition, the adversary can also hack the tag and fully control it.
5.3. The Security Requirement of Grouping-Proof System
The security requirements include these parts:
- AnonymityThe anonymity of tags and readers, which means the adversary cannot get the identity of a tag or a reader by eavesdropping the protocol message.
- Location PrivacyThe adversary cannot track the location of a reader and tags through the protocol messages.
- Resist to replay attackThe adversary cannot use the message in previous sessions to cheat the reader or tags to generate grouping-proof.
- Defense the DoP AttackThe adversary cannot use illegal tag involved in the protocol to disturb the proof validation execute by the verifier [21].
- Tag secret information protectionIf the reader is hacked in, the adversary can’t use the information stored in it to extract any secret information of tags.
6. Description of EAGP
To overcome the weakness of the grouping-proof protocol which is put forward in [19], we come up with the improvement protocol EAGP.
6.1. EAGP
The simultaneous scan is the basic requirement in grouping-proof protocols. To ensure this, the EAGP uses the timeout mechanism to guarantee the tags are scanned by a reader in a very short interval. When the protocol starts, both the reader and tag activate a timer. If a session of grouping-proof do not complete before the timeout, then the protocol is terminated. For simplicity, we assume each group has two tags. Without loss of generality, we assume the verifier can be trusted. The reader and tag are untrusted and can be impersonated or even controlled by an adversary. The notations used in EAGP are summarized in Table 2.

Table 2.
Summary of notations in EAGP.
In EAGP, without losing any security characteristics, we cut down the times of communication between the reader and tags to reduce the communication overhead. The proposed protocol consists of three phases: initial phase, grouping-proof generation phase and verification phase.
The descriptions of the protocol are as follows:
6.1.1. Initial Phase
The verifier divides the tag A and tag B into one group, allocates group parameters as: the verifier chooses a random number and computes as its public key. The group’s public key Y is stored in the tag, while keeping the private key y. Both tags share their secret keys or with verifier; in addition, the verifier stores the public key and . The reader gets the group key y from the verifier.
6.1.2. Grouping-Proof Generation Phase
The framework is demonstrated in Figure 3.
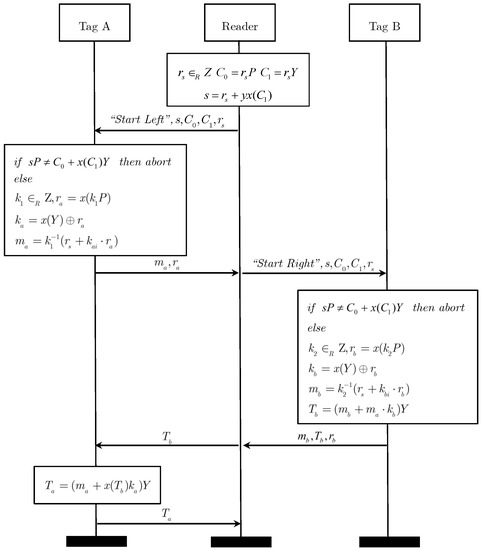
Figure 3.
The EAGP.
- (1)
- Reader generates a random number , calculates , , and . Then, the is sent to the tag A along with the message of “start left”.
- (2)
- Tag A verifies the equation . If it does not hold, the protocol is terminated. Otherwise, it generates a random number , calculates , generates the session secret key . Then, it seals its secret key into message as follows:Finally, tag A sends to the reader.
- (3)
- Reader sends along with the message of “start right” to tag B.
- (4)
- Tag B verifies the equation . If it does not hold, the protocol is terminated. Otherwise, it generates a random number , calculates and sends to the reader.
- (5)
- Reader sends the message to tag A.
- (6)
- Tag A calculates , and sends it to the reader.
- (7)
6.1.3. Verification Phase
There are two steps in the verification phase: (1) Reader verification step, (2) Verifier verification step.
- (1)
- Reader verification step:The utilization of group key y can prove that tag A and B belong to the same group and be scanned by the reader simultaneously.
- (2)
- Verifier verification step:The second verification stage is executed by the verifier to authenticate the tag’s identity in grouping-proof. The procedure of tag A is described as follows, the verification of tag B is the same as it:
- Calculate the following equations
- If is valid, the validation is successful, and the verifier stores the proof in the server as a record. Otherwise, the validation fails and the proof is abandoned.
6.2. Extension to Tags
In previous description, we assume the group only has two tags, in this section, the EAGP can be extended to multiple tags.
6.2.1. Initial Phase
We describe the group with multiple tags as . The notation of EAGP with n tags can be described by Table 3.

Table 3.
Summary of notations in EAGP.
6.2.2. Grouping-Proof Generation Phase
The framework is shown in Figure 4. The solid arrow represents the direct communication, the dotted arrow represents the tag-to-tag communication via the reader.
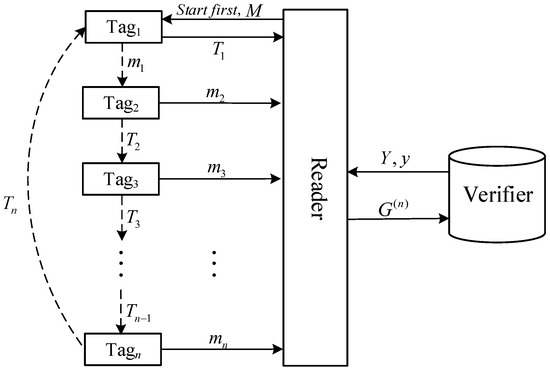
Figure 4.
The EAGP with n tags.
- (1)
- Reader selects as the first tag to calculate the grouping-proof. It generates message as Figure 3, and sends it to with the “Start first” query.
- (2)
- authorizes the reader, generates message by Equation (2) and sends it to by the reader.
- (3)
- selects a random number , calculates ,then sends to the reader, to via the reader, where
- (4)
- generates and the same way as , calculates as below.sends to the reader, to via the reader.
- (5)
- generates and , calculates as below.Then sends to the reader, to via the reader.
- (6)
- The last tag calculates , and sends to via the reader.
- (7)
- calculates by Equation (16), and sends it to the reader.
- (8)
- The reader generates the grouping-proof shown in Equation (17).
6.2.3. Verification Phase
Reader verification step:
The reader verification includes n equations below:
Verifier verification step:
7. Security Analysis and Comparison
7.1. Security Analysis
7.1.1. The Anonymous of Tag and Reader
During the execution of the protocol, the communication message set can be expressed as . Among them, are the random numbers generated by tags and reader, while the other messages are calculated from these random numbers. The adversary cannot get any information concerning protocol participants from the communication messages.
7.1.2. The Location Privacy of Tag and Reader
All the messages sent from the EAGP are random numbers or generated from random numbers. In each protocol session, the temporary session key and random numbers are different. Adversary cannot figure out the protocol participants by the messages they send. Therefore, it is difficult for the adversary to track any tag or reader, since the locations of readers and tags are protected.
7.1.3. Defense Against DoP Attack
The EAGP adds the reader verification in protocol. When the reader sends the proof to a verifier, the reader can verify the tag’s group member identity and proof data before hand. If the adversary does not know the group key, it cannot generate the legal grouping-proof to satisfy the Equation (21), then it is impossible to cheat the reader to sending invalid grouping-proof to the verifier.
7.1.4. Tag Secret Information Protect
In EAGP, the reader only stores the group’s private key y. No tag information is stored in the reader’s memory. Even if the adversary gets the group’s private key by hacking the reader, it still cannot get any secret information about tag, which makes sure the information security of tags.
7.1.5. Resist to Impersonation Attack
The impersonation attack includes two methods: impersonate tag, and impersonate reader. In the first type, the adversary impersonates the tag, tries to cheat the reader to pass the grouping-proof verification, and further cheats the verifier. In the second type, the adversary impersonates the reader to collect the tag’s information, or generates the valid grouping-proof without scanning to the real tag. The attack process is described as follows.
- Impersonate tagThere are two situations where the adversary impersonate a tag: (1) the adversary does not know any secret key, that means it cannot deduce legal . In this situation, the grouping-proof generated in presence of attack cannot pass the reader validation Equation (21). This attack can be detected before the proof is sent to the verifier, protecting the system from DoP attack. (2) The adversary gets the group’s public key Y. From Y, the adversary can deduce the session key . Then the adversary can generate the grouping-proof that can satisfy Equations (21). However, due to the lack of tag ’s authentication secret key , to forge the legal need solve the ECDLP described in Section II, thus the probability is negligible. So it is nearly impossible to pass the verifier validation. In conclusion, EAGP can resist the tag impersonation attack in both situations.
- Impersonate readerIf the adversary impersonate the reader, it needs the group key y to generate s, which is used by tag to authenticate the reader. Without the correct s, the tag will abort the protocol, and the adversary cannot get any information about .From the above, it is difficult for the adversary to impersonate tag or reader. The EAGP can resist impersonation attack.
7.1.6. Resist to Eavesdrop Attack
If the adversary eavesdrop the protocol, the message set it can collect is , all the information is transferred in the ciphertext. Without knowing the secret key of tag, the adversary cannot deduce the tag’s identity and forge valid grouping-proof without scanning legal tags.
7.1.7. Resist to Replay Attack
The replay attack denotes when the adversary uses a tag’s response to a rogue reader’s challenge to impersonate the tag. Suppose the adversary collected the message of : in EAGP session , trying to replay these messages in session in order to forge a valid grouping-proof including while it is absent. The adversary begins the attack as follows:
- (1)
- The adversary sends to the reader.
- (2)
- The adversary sends as to via the reader.
- (3)
- calculates
Due to the different session , we know , so , we get:
The grouping proof cannot pass the validation of the reader. EAGP can resist the replay attack.
7.2. Security Comparison
Table 4 lists the comparison of the existing grouping-proof schemes and EAGP. It can be seen from the comparison that the EAGP basically satisfies the security requirements of the grouping-proof protocol.

Table 4.
The comparison of grouping-proof protocols.
8. Performance Analysis
In this section, we analyze the communication overhead of the proposed protocol. The communication overhead denotes the length of the messages transmitted between the reader and tags when they execute the protocol. According to [32], we assume that an elliptic curve with length of 160 bits is used in our schemes. The length of an elliptic curve point is 320 bits. The communicational overhead comparisons about the Kang’s protocol [19], EAGP and EAGP are shown in Table 5.

Table 5.
The comparison of communication overhead.
According to the Table 5, we know that the amount of data transferred in EAGP/EAGP and Kang’s protocol is very close. However, our protocols reduce the transmission number to six, this will cut down the communication overhead. When the tag number increases to n (EAGP), the transmission data amount of each tag is the same as (EAGP), EAGP has good scalability in multiple tags condition.
9. Conclusions
In this paper, we use the ECC as encryption means, cut down the transmission times and propose an offline grouping-proof protocol. In this protocol, the reader can verify the validity of grouping-proof before submitting it to the verifier. The protocol is described in condition of two tags at first (EAGP), then we extend it to n tags condition (EAGP). Through the security and performance analysis, EAGP can resist impersonation, DoP and replay attack, protect the security and privacy of tag’s secret information.
Acknowledgments
This work is supported in part by the National Natural Science Foundation of China under Grant Numbers 61632009, 61472451 and 61402161, the High Level Talents Program of Higher Education in Guangdong Province under Grant Number 2016ZJ01, the Hunan Provincial Education Department of China under Grant Number 2015C0589, the Hunan Provincial Natural Science Foundation of China under Grant Number 2015JJ3046, the Fundamental Research Funds for the Central Universities of Central South University under Grant Number 2016zzts058.
Author Contributions
Zhibin Zhou contributed to the conception of the study and wrote the paper. Pin Liu contributed significantly to analysis and manuscript preparation; Qin Liu performed the data analyses and wrote the manuscript; Guojun Wang helped perform the analysis with constructive discussions.
Conflicts of Interest
The authors declare no conflict of interest. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A. Correctness Proof of EAGP
Proof of the Correctness about Reader Verify.
For :
If is known, according to Equation (16) we have:
Then, the right side of Equation (18) can be simplified to . Therefore, the Equation (18) is proved.
For :
According to Equation (11), we have
In a similar way, for we have
The Equantion (21) is proved.
In conclusion, the correctness proof of reader verification is completed. ☐
References
- Juels, A. “Yoking-proofs” for RFID tags. In Proceedings of the IEEE Annual Conference on Pervasive Computing and Communications Workshops, Orlando, FL, USA, 14–17 March 2004; pp. 138–143. [Google Scholar]
- Chen, Y.-Y.; Tsai, M.-L. An RFID solution for enhancing inpatient medication safety with real-time verifiable grouping-proof. Int. J. Med. Inform. 2014, 83, 70–81. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.-L.; Wu, C.-Y. Using RFID yoking proof protocol to enhance inpatient medication safety. J. Med. Syst. 2012, 36, 2849–2864. [Google Scholar] [CrossRef] [PubMed]
- Peris-Lopez, P.; Orfila, A.; Hernandez-Castro, J.C.; van der Lubbe, J.C.A. Flaws on RFID grouping-proofs. Guidelines for future sound protocols. J. Netw. Comput. Appl. 2011, 34, 833–845. [Google Scholar] [CrossRef]
- Zhibin, Z.; Qin, L.; Guojun, W.; Weijia, J. Secure Medication Scheme Using the Grouping-proof Technology. J. Chin. Comput. Syst. 2015, 36, 2349–2353. [Google Scholar]
- Huang, H.; Ku, C. A RFID grouping proof protocol for medicationsafety of inpatient. J. Med. Syst. 2009, 33, 467–474. [Google Scholar] [CrossRef] [PubMed]
- Chien, H.-Y.; Yang, C.-C.; Wu, T.-C.; Lee, C.-F. Two RFID-based solutions to enhance inpatient medication safety. J. Med. Syst. 2011, 35, 369–375. [Google Scholar] [CrossRef] [PubMed]
- Xie, K.; Cao, J.; Wang, X.; Wen, J. Optimal resource allocation for reliable and energy efficient cooperative communications. IEEE Trans. Wirel. Commun. 2013, 12, 4994–5007. [Google Scholar] [CrossRef]
- Pizzolante, R.; Carpentieri, B.; Castiglione, A.; Castiglione, A.; Palmieri, F. Text Compression and Encryption through Smart Devices for Mobile Communication. In Proceedings of the 2013 Seventh International Conference on Innovative Mobile and Internet Services in Ubiquitous Computing, Taichung, Taiwan, 3–5 July 2013; pp. 672–677. [Google Scholar]
- Castiglione, A.; Palmieri, F.; Fiore, U.; Castiglione, A.; De Santis, A. Modeling energy-efficient secure communications in multi-mode wireless mobile devices. J. Comput. Syst. Sci. 2015, 81, 1464–1478. [Google Scholar] [CrossRef]
- Sundaresan, S.; Doss, R.; Zhou, W. Offline grouping proof protocol for RFID systems. In Proceedings of the 2013 IEEE 9th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Lyon, France, 7–9 October 2013; pp. 247–252. [Google Scholar]
- Liu, H.; Ning, H.; Zhang, Y.; He, D.; Xiong, Q.; Yang, L. Grouping-Proofs-Based Authentication Protocol for Distributed RFID Systems. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 1321–1330. [Google Scholar] [CrossRef]
- Chien, H.-Y.; Liu, S.-B. Tree-based RFID yoking proof. In Proceedings of the International Conference on Networks Security, Wireless Communications and Trusted Computing, Wuhan, China, 25–26 April 2009; pp. 550–553. [Google Scholar]
- Lien, Y.; Leng, X.; Mayes, K.; Chiu, J.-H. Reading order independent grouping proof for RFID tags. In Proceedings of the Intelligence and Security Informatics, Taipei, China, 17–20 June 2008; pp. 128–136. [Google Scholar]
- Piramuthu, S. On existence proofs for multiple RFID tags. In Proceedings of the 2006 ACS/IEEE Pervasive Services, Lyon, France, 26–29 June 2006; pp. 317–320. [Google Scholar]
- Li, N.; Mu, Y.; Susilo, W.; Varadharajan, V. Anonymous yoking-group proofs. In Proceedings of the Proceedings of the 10th ACM Symposium on Information, Computer and Communications Security, Singapore, 14–17 April 2015; pp. 615–620. [Google Scholar]
- Ma, C.; Lin, J.; Wang, Y.; Shang, M. Offline RFID grouping proofs with trusted timestamps. In Proceedings of the 2012 IEEE 11th International Conference on Trust, Security and Privacy in Computing and Communications, Liverpool, UK, 25–27 June 2012; pp. 674–681. [Google Scholar]
- Cho, J.S.; Yeo, S.S.; Hwang, S.; Rhee, S.Y.; Kim, S.K. Enhanced Yoking Proof Protocols for RFID Tags and Tag Groups. In Proceedings of the Advanced Information Networking and Applications—Workshops, Okinawa, Japan, 25–28 March 2008; pp. 1591–1596. [Google Scholar]
- Kang, H.-Y. Analysis and Improvement of ECC-based Grouping-proof Protocol for RFID. Int. J. Control Autom. 2016, 9, 343–352. [Google Scholar]
- Castiglione, A.; de Santis, A.; Masucci, B.; Palmieri, F.; Castiglione, A.; Li, J.; Huang, X. Hierarchical and Shared Access Control. IEEE Trans. Inf. Forensics Secur. 2016, 11, 850–865. [Google Scholar] [CrossRef]
- Lo, N.-W.; Yeh, K.-H. Anonymous coexistence proofs for RFID tags. J. Inf. Sci. Eng. 2010, 26, 1213–1230. [Google Scholar] [CrossRef]
- Burmester, M.; De Medeiros, B.; Motta, R. Provably secure grouping-proofs for RFID tags. In International Conference on Smart Card Research and Advanced Applications; Springer: Berlin/Heidelberg, Germay, 2008; pp. 176–190. ISBN 978-3-540-85892-8. [Google Scholar]
- Canetti, R. Universally composable security: A new paradigm for cryptographic protocols. In Proceedings of the 42nd IEEE Symposium on Foundations of Computer Science, Las Vegas, NV, USA, 14–17 October 2001; pp. 136–145. [Google Scholar]
- Burmester, M.; Munilla, J. An Anonymous RFID Grouping-Proof with Missing Tag Identification. In Proceedings of the 10th IEEE International Conference on Radio-Frequency Identification, Orlando, FL, USA, 3–5 May 2016; pp. 3–5. [Google Scholar]
- Wolkerstorfer, J. Is elliptic-curve cryptography suitable to secure RFID tags. In Proceedings of the Handout of the Ecrypt Workshop on RFID and Lightweight Crypto, Graz, Austria, 14–15 July 2005. [Google Scholar]
- Batina, L.; Guajardo, J.; Kerins, T.; Mentens, N.; Tuyls, P.; Verbauwhede, I. An Elliptic Curve Processor Suitable For RFID-Tags. IACR Cryptol. ePrint Arch. 2006, 2006, 227. [Google Scholar]
- Lee, Y.K.; Batina, L.; Verbauwhede, I. Untraceable RFID authentication protocols: Revision of EC-RAC. In Proceedings of the RFID, 2009 IEEE International Conference, Orlando, FL, USA, 27–28 April 2009; pp. 178–185. [Google Scholar]
- Batina, L.; Lee, Y.K.; Seys, S. Extending ECC-based RFID authentication protocols to privacy-preserving multi-party grouping proofs. Pers. Ubiquitous Comput. 2012, 16, 323–335. [Google Scholar] [CrossRef]
- Lv, C.; Li, H.; Ma, J.; Niu, B.; Jiang, H. Security Analysis of a Privacy-preserving ECC-based Grouping-proof Protocol. J. Converg. Inf. Technol. 2011, 6, 113–119. [Google Scholar] [CrossRef]
- Menezes, A. Evaluation of Security Level of Cryptography: The Elliptic Curve Discrete Logarithm Problem (ECDLP); University of Waterloo: Waterloo, ON, Canada, 2001. [Google Scholar]
- Lin, Q.; Zhang, F. ECC-based grouping-proof RFID for inpatient medication safety. J. Med. Syst. 2012, 36, 3527–3531. [Google Scholar] [CrossRef] [PubMed]
- He, D.; Kumar, N.; Chilamkurti, N.; Lee, J.H. Lightweight ECC Based RFID Authentication Integrated with an ID Verifier Transfer Protocol. J. Med. Syst. 2014, 38, 116. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).