Characterization of VitE-TPGS Micelles Linked to Poorly Soluble Pharmaceutical Compounds Exploiting Pair Distribution Function’s Moments
Abstract
:1. Introduction
2. Analytical Method
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| VitE-TPGS | D-α-tocopherol polyethylene glycol 1000 succinate |
| PSC | Poorly soluble pharmaceutical compound |
| Pair Distribution Function | |
| SAXS | Small-Angle X-ray Scattering |
| WAXS | Wide-Angle X-ray Scattering |
| RES | Reticuloendothelial system |
| EPR | Enhanced permeability and retention |
| DLS | Dynamic light scattering |
| TEM | Transmission electron microscopy |
| Cryo-EM | Cryogenic electron microscopy |
| AFM | Atomic force microscopy |
| LSM | Least square minimum |
| PEG | Polyethylene glycol |
Appendix A
Determination of the Micelles’ Structure by Evaluating the PDF’s Moments Through a Least-Square Approach
References
- Kabanov, A.V.; Alakhov, V.Y. Micelles of amphiphilic block copolymers as vehicles for drug delivery. J. Control. Release 2007, 2000, 347–376. [Google Scholar] [CrossRef]
- Torchili, V.P. Micellar Nanocarriers: Pharmaceutical Perspectives. Pharm. Res. 2007, 24, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Lammers, T. Nanomedicine and tumor targeting. Adv. Mater. 2024, 36, 2312169. [Google Scholar] [CrossRef] [PubMed]
- Blanco, E.; Shen, H.; Ferrari, M. Principles of nanoparticle design for overcoming biological barriers to drug delivery. Nat. Biotechnol. 2015, 33, 941–951. [Google Scholar] [CrossRef] [PubMed]
- Discher, D.E.; Eisenberg, A. Polymer vesicles. Science 2002, 297, 967–973. [Google Scholar] [CrossRef] [PubMed]
- Kinnear, C.; Moore, T.L.; Rodriguez-Lorenzo, L.; Rothen-Rutishauser, B.; Petri-Fink, A. Form Follows Function: Nanoparticle Shape and Its Implications for Nanomedicine. Chem. Rev. 2017, 117, 11476–11521. [Google Scholar] [CrossRef] [PubMed]
- Fang, J.; Nakamura, H.; Maeda, H. The EPR effect: Unique features of tumor blood vessels for drug delivery, factors involved, and limitations and augmentation of the effect. Adv. Drug Deliv. Rev. 2011, 63, 136–151. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Tan, J.; Thomas, A.; Ou-Yang, D.; Muzykantov, V.R. The Shape of Things to Come: Importance of Design in Nanotechnology for Drug Delivery. Ther. Deliv. 2012, 3, 181–194. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Zhong, Z.; Feijen, J. Stimuli-responsive polymersomes for programmed drug delivery. Biomacromolecules 2009, 10, 197–209. [Google Scholar] [CrossRef] [PubMed]
- Petros, R.A.; De Simone, J.M. Strategies in the design of nanoparticles for therapeutic applications. Nat. Rev. Drug Discov. 2010, 9, 615–627. [Google Scholar] [CrossRef] [PubMed]
- Verma, A.; Stellacci, F. Effect of surface properties on nanoparticle-cell interactions. Small 2010, 6, 12–21. [Google Scholar] [CrossRef] [PubMed]
- Ghezzi, M.; Pescina, S.; Padula, C.; Santi, P.; Del Favero, E.; Cantù, L.; Nicoli, S. Polymeric micelles in drug delivery: An insight of the techniques for their characterization and assessment in biorelevant conditions. J. Control. Release 2021, 332, 312–336. [Google Scholar] [CrossRef] [PubMed]
- De Caro, L.; Del Giudice, A.; Morin, M.; Reinle-Schmitt, M.; Grandeury, A.; Gozzo, F.; Giannini, C. Small Angle X-Ray Scattering Data Analysis and Theoretical Modelling for the Size and Shape Characterization of Drug Delivery Systems Based on Vitamin E TPGS Micelles. J. Pharm. Sci. 2023, 112, 243–249. [Google Scholar] [CrossRef] [PubMed]
- De Caro, L.; Stoll, T.; Grandeury, A.; Gozzo, F.; Giannini, C. Characterization of Surfactant Spheroidal Micelle Structure for Pharmaceutical Applications: A Novel Analytical Framework. Pharmaceutics 2024, 16, 604. [Google Scholar] [CrossRef] [PubMed]
- U.S. Food and Drug Administration. Drug Approval Package: Promacta (Eltrombopag) NDA#022291; U.S. Food and Drug Administration: Silver Spring, MD, USA, 2008. Available online: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2008/022291s000_TOC.cfm (accessed on 18 February 2025).
- Beth Wire, M.; Bruce, J.; Gauvin, J.; Pendry, C.J.; McGuire, A.; Qian, Y.; Brainsky, A. A Randomized, Open-Label, 5-Period, Balanced Crossover Study to Evaluate the Relative Bioavailability of Eltrombopag Powder for Oral Suspension (PfOS) and Tablet Formulations and the Effect of a High-Calcium Meal on Eltrombopag Pharmacokinetics When Administered with or 2 Hours Before or After PfOS. Clin. Ther. 2012, 34, 699–709. [Google Scholar] [CrossRef]
- Svergun, D.I. Determination of the regularization parameter in indirect-transform methods using perceptual criteria. J. Appl. Crystallogr. 1992, 25, 495–503. [Google Scholar] [CrossRef]
- Williams, D.D.; Peng, B.; Bailey, C.K.; Wire, M.B.; Deng, Y.; Park, J.W.; Collins, D.A.; Kapsi, S.G.; Jenkins, J.M. Effects of food and antacids on the pharmacokinetics of eltrombopag in healthy adult subjects: Two single-dose, open-label, randomized-sequence, crossover studies. Clin. Ther. 2009, 31, 764–776. [Google Scholar] [CrossRef] [PubMed]
- Rathod, S.; Bahadur, P.; Tiwari, S. Nanocarriers based on vitamin E-TPGS: Design principle and molecular insights into improving the efficacy of anticancer drugs. Int. J. Pharm. 2021, 592, 120045. [Google Scholar] [CrossRef] [PubMed]
- Puig-Rigall, J.; Grillo, I.; Dreiss, C.A.; González-Gaitano, G. Structural and Spectroscopic Characterization of TPGS Micelles: Disruptive Role of Cyclodextrins and Kinetic Pathways. Langmuir 2017, 33, 4737–4747. [Google Scholar] [CrossRef] [PubMed]
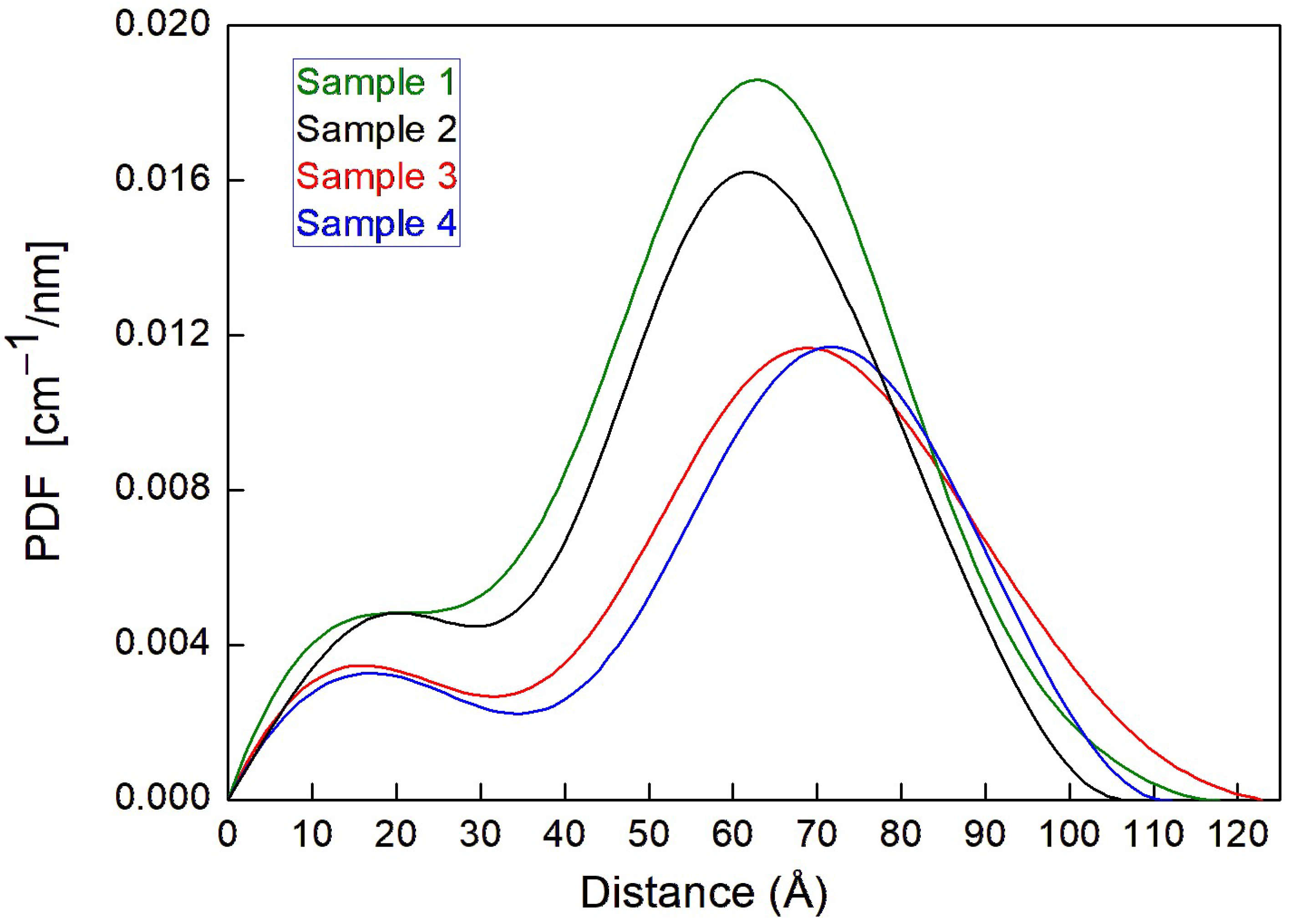

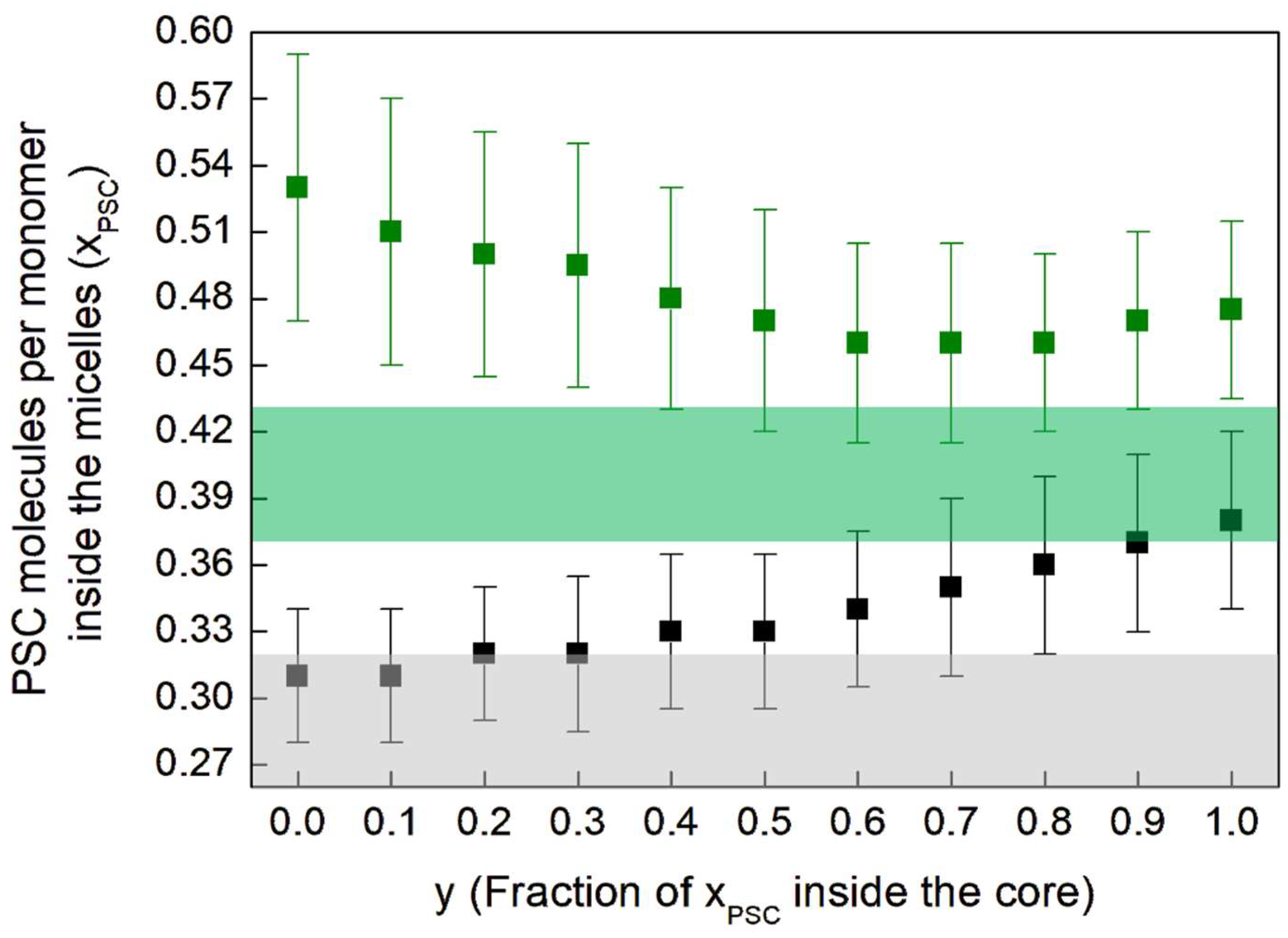
| Sample | VitE-TPGS | PSC | CaCl2 | pH Measured | |
|---|---|---|---|---|---|
| 1 | 19.9 g of buffer 50 mM | 82.6 mg (0.415 wt%) | No | No | 6.87 |
| 2 | 2.4 g of sample 1 | Yes (0.415 wt%) | No | 0.55 mg (0.024 wt%) | 6.82 |
| 3 | 10 g of sample 1 | Yes (0.415 wt%) | 8 mg (0.08 wt%) | No | 6.91 |
| 4 | 2.8 g of sample 3 | Yes (0.415 wt%) | Yes (0.08 wt%) | 0.8 mg (0.029 wt%) | 6.84 |
| Sample | (Å) | (Å) | Equatorial Core Radius − (Å) | (ne/Å3) | (ne/Å3) | (Å) | I(0) (cm−1) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 (without PSC and CaCl2) | 16.7 ± 0.1 | 122.0 ± 0.1 | 29.3 ± 0.2 | −0.026 ± 0.001 | 0.032 ± 0.001 | 1.51 ± 0.01 | 127 ± 2 | 53 ± 4 | 47.3 ± 0.5 | 0.056 ± 0.001 |
| 2 (without PSC, with CaCl2) | 14.2 ± 0.1 | 113.8 ± 0.1 | 30.5 ± 0.2 | −0.031 ± 0.001 | 0.039 ± 0.001 | 1.40 ± 0.01 | 122 ± 3 | 36 ± 4 | 47.3 ± 0.4 | 0.055 ± 0.001 |
| 3 (with PSC, without CaCl2) | 16.4 ± 0.1 | 116.7 ± 0.1 | 27.1 ± 0.2 | −0.026 ± 0.001 | 0.036 ± 0.001 | 1.55 ± 0.01 | 118 ± 4 | 44 ± 4 | 43.5 ± 0.5 | 0.085 ± 0.001 |
| 4 (with PSC and CaCl2) | 12.3 ± 0.1 | 107.7 ± 0.1 | 27.7 ± 0.2 | −0.030 ± 0.001 | 0.055 ± 0.001 | 1.51 ± 0.01 | 125 ± 4 | 12 ± 5 | 42.8 ± 0.3 | 0.079 ± 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Caro, L.; Stoll, T.; Grandeury, A.; Gozzo, F.; Giannini, C. Characterization of VitE-TPGS Micelles Linked to Poorly Soluble Pharmaceutical Compounds Exploiting Pair Distribution Function’s Moments. Pharmaceutics 2025, 17, 431. https://doi.org/10.3390/pharmaceutics17040431
De Caro L, Stoll T, Grandeury A, Gozzo F, Giannini C. Characterization of VitE-TPGS Micelles Linked to Poorly Soluble Pharmaceutical Compounds Exploiting Pair Distribution Function’s Moments. Pharmaceutics. 2025; 17(4):431. https://doi.org/10.3390/pharmaceutics17040431
Chicago/Turabian StyleDe Caro, Liberato, Thibaud Stoll, Arnaud Grandeury, Fabia Gozzo, and Cinzia Giannini. 2025. "Characterization of VitE-TPGS Micelles Linked to Poorly Soluble Pharmaceutical Compounds Exploiting Pair Distribution Function’s Moments" Pharmaceutics 17, no. 4: 431. https://doi.org/10.3390/pharmaceutics17040431
APA StyleDe Caro, L., Stoll, T., Grandeury, A., Gozzo, F., & Giannini, C. (2025). Characterization of VitE-TPGS Micelles Linked to Poorly Soluble Pharmaceutical Compounds Exploiting Pair Distribution Function’s Moments. Pharmaceutics, 17(4), 431. https://doi.org/10.3390/pharmaceutics17040431







