Optimization of Spray Drying Process Parameters for the Preparation of Inhalable Mannitol-Based Microparticles Using a Box-Behnken Experimental Design
Abstract
1. Introduction
2. Materials and Methods
2.1. Spray Drying Process
2.2. Particle Size and Aerodynamic Diameter
2.3. Bulk and Tapped Density, Hausner Ratio
2.4. Particle Morphology
2.5. Experimental Design
2.6. Data Analysis
- Data checking; descriptive statistics; basic data visualization (histograms, box plots).
- Choosing a suitable mathematical model for the obtained data.
- Testing the assumptions required for ANOVA and regression analysis (MLR), primarily using visual assessment of graphical outputs (histograms, residual graphs); eventually, exclusion of the outliers from the analysis and subsequent building of a new model.
- Simplification of the model by gradual backward elimination of insignificant terms (assessment of their p-values in ANOVA table) while monitoring and comparing values of coefficient of determination R2, adjusted R2, Akaike information criterion, and p-value of the original and simplified model to achieve the best quality of the model fit. Percentage prediction error (PPE) was assessed to ensure the validity of the generated regression equation. PPE for each experimental run was calculated as: (observed value—predicted value)/predicted value × 100 (%).
- Visualization of MLR results: RSM via 3D perspective plots.
- Interpretation of obtained regression equation and graphical outputs: investigation of the effects of independent factors (process conditions) and their possible interactions on the response (quality attributes of microparticles) and the determination of optimal process conditions for the desired response.
3. Results and Discussion
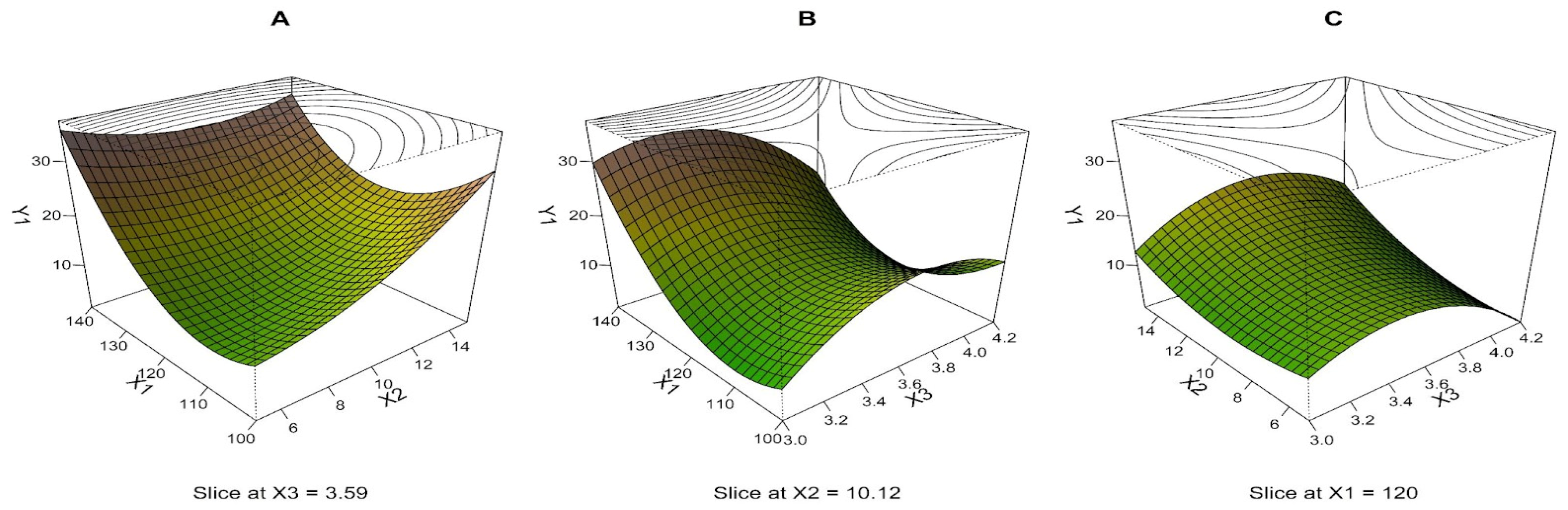
3.1. Laser Diffraction Median Size—S (Y1)
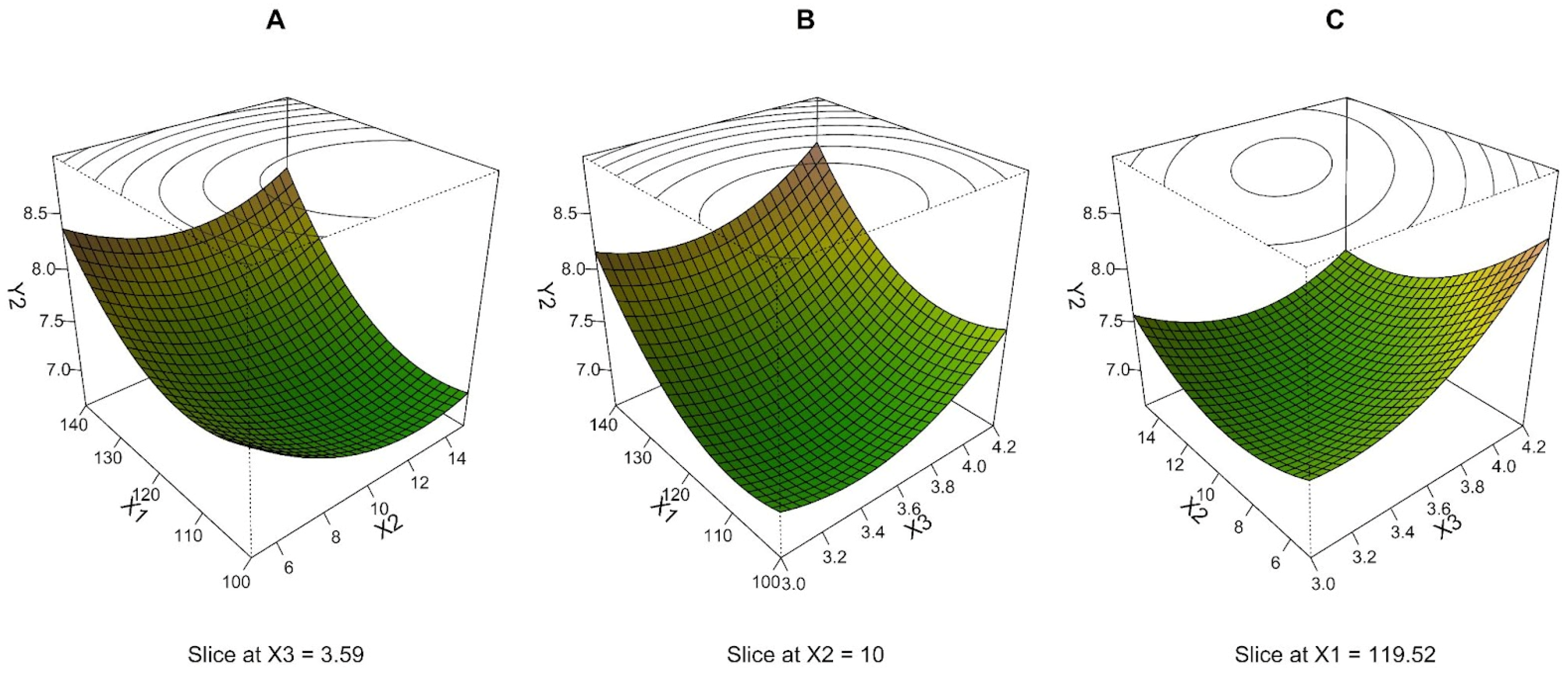
3.2. Mass Median Aerodynamic Diameter—MMAD (Y2)
3.3. Numeric Median Aerodynamic Diameter—NMAD (Y3)
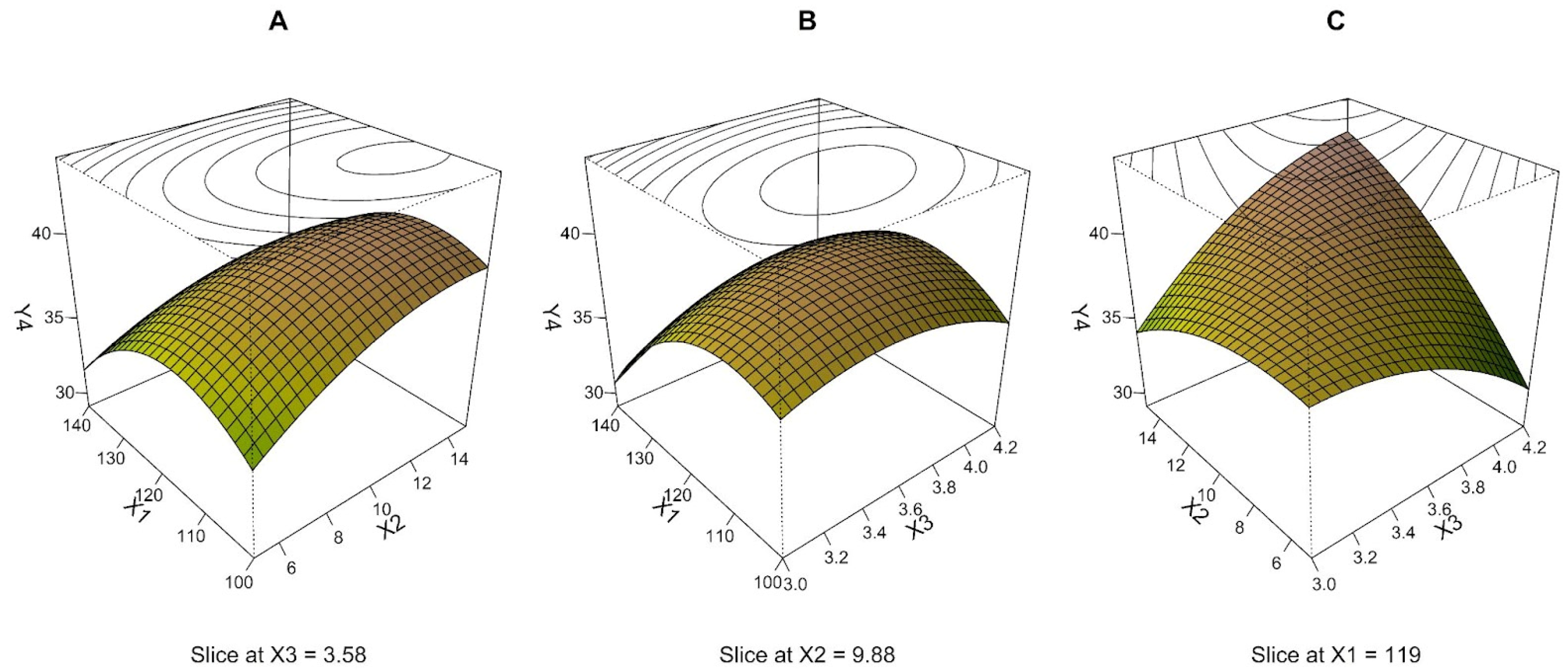
3.4. Relative Standard Deviation of Mass Median Aerodynamic Diameter—MMAD RSD (Y4)
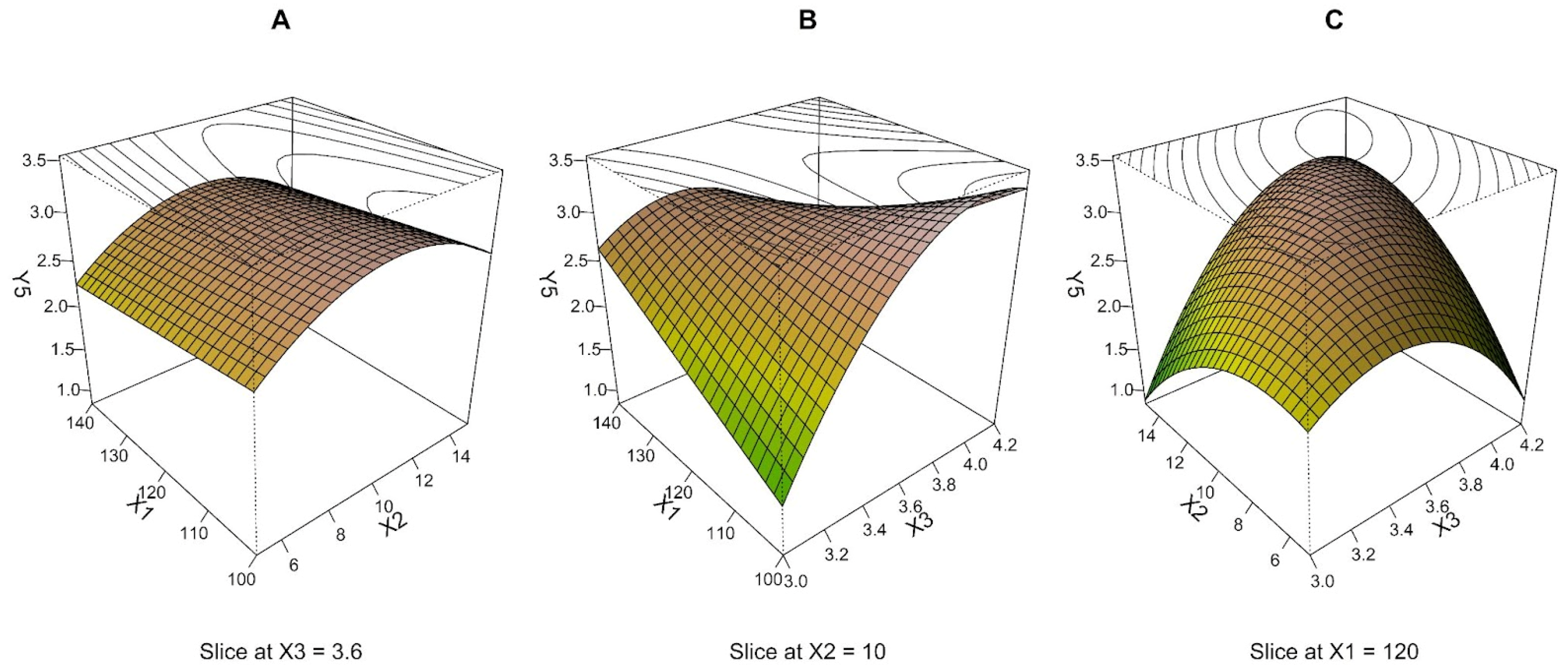
3.5. Particle Morphology Characterized by SEM (Y5)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Labiris, N.R.; Dolovich, M.B. Pulmonary drug delivery. Part I: Physiological factors affecting therapeutic effectiveness of aerosolized medications. Brit. J. Clin. Pharmaco. 2003, 56, 588–599. [Google Scholar] [CrossRef] [PubMed]
- Bahrainian, S.; Mirmoeini, M.S.; Gilani, Z.; Gilani, K. Engineering of levodopa inhalable microparticles in combination with leucine and dipalmitoylphosphatidylcholine by spray drying technique. Eur. J. Pharm. Sci. 2021, 167, 106008. [Google Scholar] [CrossRef] [PubMed]
- Karas, J.; Vetchý, D.; Gajdziok, J. Práškové částice pro plicní podání. Chem. Listy 2022, 116, 28–34. [Google Scholar] [CrossRef]
- Hoppentocht, M.; Hagendoorn, P.; Frijlink, H.W.; De Boer, A.H. Technological and practical challenges of dry powder inhalers and formulations. Adv. Drug Deliver. Rev. 2014, 75, 18–31. [Google Scholar] [CrossRef] [PubMed]
- Silva, D.; Jacinto, T. Inhaled β2-agonists in asthma management: An evolving story. Breathe 2016, 12, 375–377. [Google Scholar] [CrossRef] [PubMed]
- Gentile, D.A.; Skoner, D.P. New asthma drugs: Small molecule inhaled corticosteroids. Curr. Opin. Pharmacol. 2010, 10, 260–265. [Google Scholar] [CrossRef] [PubMed]
- Barnett, A.H. Exubera inhaled insulin: A review. Int. J. Clin. Prac. 2004, 58, 394–401. [Google Scholar] [CrossRef]
- Mishra, M.; Mishra, B. Formulation optimization and characterization of spray dried microparticles for inhalation delivery of doxycycline hyclate. Yakugaku Zasshi 2011, 131, 1813–1825. [Google Scholar] [CrossRef]
- Elversson, J.; Millqvist-Fureby, A.; Alderborn, G.; Elofsson, U. Droplet and particle size relationship and shell thickness of inhalable lactose particles during spray drying. J. Pharm. Sci. 2003, 92, 900–910. [Google Scholar] [CrossRef]
- Rahimpour, Y.; Kouhsoltani, M.; Hamishehkar, H. Alternative carriers in dry powder inhaler formulations. Drug Discov. Today 2014, 19, 618–626. [Google Scholar] [CrossRef]
- Nelson, H.S. Inhalation devices, delivery systems, and patient technique. Ann. Allerg. Asthma Immunol. 2016, 117, 606–612. [Google Scholar] [CrossRef]
- Edwards, D.A.; Hanes, J.; Caponetti, G.; Hrkach, J.; Ben-Jebria, A.; Eskew, M.L.; Mintzes, J.; Deaver, D.; Lotan, N.; Langer, R. Large porous particles for pulmonary drug delivery. Science 1997, 276, 1868–1871. [Google Scholar] [CrossRef]
- Heyder, J.; Gebhart, J.; Rudolf, G.; Schiller, C.F.; Stahlhofen, W. Deposition of particles in the human respiratory tract in the size range 0.005–15 μm. J. Aerosol Sci. 1986, 17, 811–825. [Google Scholar] [CrossRef]
- Cryan, S.A.; Ssivadas, N.; Garcia-Contreras, L. In vivo animal models for drug delivery across the lung mucosal barrier. Adv. Drug Deliver. Rev. 2007, 59, 1133–1151. [Google Scholar] [CrossRef]
- Musante, C.J.; Schroeter, J.D.; Rosati, J.A.; Crowder, T.M.; Hickey, A.J.; Martonen, T.B. Factors affecting the deposition of inhaled porous drug particles. J. Pharm. Sci. 2002, 91, 1590–1600. [Google Scholar] [CrossRef]
- Geller, D.E.; Weers, J.; Heuerding, S. Development of an inhaled dry-powder formulation of tobramycin using PulmoSphereTM technology. J. Aerosol Med. Pulm. Drug Deliv. 2011, 24, 175. [Google Scholar] [CrossRef]
- Hersey, J.A. Ordered mixing: A new concept in powder mixing practice. Powder Technol. 1975, 11, 41–44. [Google Scholar] [CrossRef]
- Thalberg, K.; Papathanasiou, F.; Fransson, M.; Nicholas, M. Controlling the performance of adhesive mixtures for inhalation using mixing energy. Int. J. Pharm. 2021, 592, 120055. [Google Scholar] [CrossRef] [PubMed]
- Islam, N.; Stewart, P.; Larson, I.; Hartley, P. Effect of carrier size on the dispersion of salmeterol xinafoate from interactive mixtures. J. Pharm. Sci. 2004, 93, 1030–1038. [Google Scholar] [CrossRef]
- Rasenack, N.; Steckel, H.; Müller, B.W. Micronization of anti-inflammatory drugs for pulmonary delivery by a controlled crystallization process. J. Pharm. Sci. 2003, 92, 35–44. [Google Scholar] [CrossRef]
- Karner, S.; Urbanetz, N.A. The impact of electrostatic charge in pharmaceutical powders with specific focus on inhalation-powders. J. Aerosol Sci. 2011, 42, 428–445. [Google Scholar] [CrossRef]
- Chougule, M.B.; Padhi, B.K.; Jinturkar, K.A.; Misra, A. Development of dry powder inhalers. Recent Pat. Drug Deliv. Formul. 2008, 1, 11–21. [Google Scholar] [CrossRef] [PubMed]
- Gradon, L.; Sosnowski, T.R. Formation of particles for dry powder inhalers. Adv. Powder Technol. 2014, 25, 43–55. [Google Scholar] [CrossRef]
- Kailay, W.; Nokhodchi, A. Freeze-dried mannitol for superior pulmonary drug delivery via dry powder inhaler. Pharm. Res. 2013, 30, 458–477. [Google Scholar] [CrossRef]
- Van Drooge, D.J.; Hinrichs, W.L.J.; Dickhoff, B.H.J.; Elli, M.N.A.; Visser, M.R.; Zijlstra, G.S.; Ffrijlink, H.W. Spray freeze drying to produce a stable Delta(9)-tetrahydrocannabinol containing inulin-based solid dispersion powder suitable for inhalation. Eur. J. Pharm. Sci. 2005, 26, 231–240. [Google Scholar] [CrossRef]
- Moura, C.; Casimiro, T.; Costa, E.; Aguiar-Ricardo, A. Optimization of supercritical CO2-assisted spray drying technology for the production of inhalable composite particles using quality-by-design principles. Powder Technol. 2019, 357, 387–397. [Google Scholar] [CrossRef]
- Du, Z.; Guan, Y.X.; Yao, S.J.; Zhu, Z.Q. Supercritical fluid assisted atomization introduced by an enhanced mixer for micronization of lysozyme: Particle morphology, size and protein stability. Int. J. Pharm. 2011, 421, 258–268. [Google Scholar] [CrossRef]
- Cal, K.; Sollohub, K. Spray drying technique. I: Hardware and process parameters. J. Pharm. Sci. 2010, 99, 575–586. [Google Scholar] [CrossRef]
- Santos, D.; Maurício, A.C.; Sencadas, V.; Santos, J.D.; Fernandes, M.H.; Gomes, P.S. Spray drying: An overview. In Biomaterials-Physics and Chemistry-New Edition; Pignatello, R., Ed.; IntechOpen: London, UK, 2018; pp. 9–35. [Google Scholar]
- Broadhead, J.; Edmond Rouan, S.K.; Rhodes, C.T. The spray drying of pharmaceuticals. Drug Dev. Ind. Pharm. 1992, 18, 1169–1206. [Google Scholar] [CrossRef]
- Ameri, M.; Maa, Y.F. Spray drying of biopharmaceuticals: Stability and process considerations. Dry. Technol. 2006, 24, 763–768. [Google Scholar] [CrossRef]
- Hertel, N.; Birk, G.; Scherliess, R. Particle engineered mannitol for carrier-based inhalation–A serious alternative? Int. J. Pharm. 2020, 577, 118901. [Google Scholar] [CrossRef]
- Grangeia, H.B.; Silva, C.; Simões, S.P.; Reis, M.S. Quality by design in pharmaceutical manufacturing: A systematic review of current status, challenges and future perspectives. Eur. J. Pharm. Biopharm. 2020, 147, 19–37. [Google Scholar] [CrossRef]
- Box, G.E.P.; Behnken, D.W. Some new three level designs for the study of quantitative variables. Technometrics 1960, 2, 455–475. [Google Scholar] [CrossRef]
- Littringer, E.M.; Mescher, A.; Eckhard, S.; Schröttner, H.; Langes, C.; Fries, M.; Griesser, U.; Walzel, P.; Urbanetz, N.A. Spray drying of mannitol as a drug carrier—The impact of process parameters on product properties. Dry. Technol. 2011, 30, 114–124. [Google Scholar] [CrossRef]
- Kramek-Romanowska, K.; Odziomek, M.; Sosnowski, T.R.; Gradoń, L. Effects of process variables on the properties of spray-dried mannitol and mannitol/disodium cromoglycate powders suitable for drug delivery by inhalation. Ind. Eng. Chem. Res. 2011, 50, 13922–13931. [Google Scholar] [CrossRef]
- Li, X.; Vogt, F.G.; Hayes, D.; Mansour, H.M. Design, characterization, and aerosol dispersion performance modeling of advanced spray-dried microparticulate/nanoparticulate mannitol powders for targeted pulmonary delivery as dry powder inhalers. J. Aerosol Med. Pulm. Drug Deliv. 2014, 27, 81–93. [Google Scholar] [CrossRef]
- Guimarães, T.F.; Lanchote, A.D.; Da Costa, J.S.; Viçosa, A.L.; De Freitas, L.A.P. A multivariate approach applied to quality on particle engineering of spray-dried mannitol. Adv. Powder Technol. 2015, 26, 1094–1101. [Google Scholar] [CrossRef]
- Laser Diffraction Particle Size Analyzer LA-960-HORIBA. Available online: https://static.horiba.com/fileadmin/Horiba/Products/Scientific/Particle_Characterization/LA/LA-960.pdf (accessed on 10 November 2022).
- Model 3321 Aerodynamic Particle Sizer® Spectrometer Instruction Manual. Available online: http://www.lisa.u-pec.fr/~formenti/Tools/Manuals/APS-3321-manual.pdf (accessed on 10 November 2022).
- European Pharmacopoeia Commision. European Pharmacopoeia, 9th ed.; Deutscher Apotheker Verlag: Stuttgart, Germany, 2017. [Google Scholar]
- Farkas, Á.; Lízal, F.; Jedelský, J.; Elcner, J.; Karas, J.; Bělka, M.; Mišík, O.; Jícha, M. The role of the combined use of experimental and computational methods in revealing the differences between the micron-size particle deposition patterns in healthy and asthmatic subjects. J. Aerosol Sci. 2020, 147, 105582. [Google Scholar] [CrossRef]
- The R Project for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 10 November 2022).
- Broadhead, J.; Rouan, S.K.E.; Hau, I.; Rhodes, C.T. The effect of process and formulation variables on the properties of dpray-dried β-galactosidase. J. Pharm. Pharmacol. 1994, 46, 458–467. [Google Scholar] [CrossRef]
- Ståhl, K.; Claesson, M.; Lilliehorn, P.; Lindén, H.; Bäckström, K. The effect of process variables on the degradation and physical properties of spray dried insulin intended for inhalation. Int. J. Pharm. 2002, 233, 227–237. [Google Scholar] [CrossRef]
- Maltesen, M.J.; Bjessegaard, S.; Hovgaard, L.; Havelund, S.; Van Da Weert, M. Quality by design–Spray drying of insulin intended for inhalation. Eur. J. Pharm. Biopharm. 2008, 70, 828–838. [Google Scholar] [CrossRef] [PubMed]
- Chew, N.Y.K.; Chan, H.-K. Effect of powder polydispersity on aerosol generation. J. Pharm. Pharm. Sci. 2002, 5, 162–168. [Google Scholar]
- Schiavone, H.; Palakodaty, S.; Clark, A.; York, P.; Tzannis, S.T. Evaluation of SCF-engineered particle-based lactose blends in passive dry powder inhalers. Int. J. Pharm. 2004, 281, 55–66. [Google Scholar] [CrossRef]
- Vanbever, R.; Mintzes, J.D.; Wang, J.; Nice, J.; Chen, D.; Batycky, R.; Langer, R.; Edwards, D.A. Formulation and physical characterization of large porous particles for inhalation. Pharm. Res. 1999, 16, 1735–1742. [Google Scholar] [CrossRef]


| Input Variable (Process Parameter) | Unit | Code Level | ||
|---|---|---|---|---|
| Low (−1) | Medium (0) | Hight (+1) | ||
| Drying temperature (X1) | °C | 100 | 120 | 140 |
| Pump speed (X2) | mL/min | 5 | 10 | 15 |
| Air speed (X3) | m/s | 3.0 | 3.6 | 4.2 |
| Run | Drying Temperature (X1) | Pump Speed (X2) | Air Speed (X3) | S (Y1) | MMAD (Y2) | NMAD (Y3) | MMAD RSD (Y4) | SEM (Y5) | Bulk Density | Tapped Density | Hausner Ratio |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [°C] | [mL/min] | [m/s] | [μm] | [μm] | [μm] | [%] | [Grade] | [g/cm3] | [g/cm3] | ||
| 1 | 100 | 5 | 3.6 | 9.13 ± 3.40 | 7.67 ± 2.69 | 3.60 ± 3.24 | 35.2 | G | 0.31 | 0.39 | 1.28 |
| 2 | 140 | 5 | 3.6 | 26.33 ± 3.98 | 8.28 ± 2.67 | 3.65 ± 3.60 | 32.3 | A | 0.29 | 0.38 | 1.32 |
| 3 | 100 | 15 | 3.6 | 39.39 ± 4.81 | 7.07 ± 2.71 | 3.48 ± 3.19 | 38.4 | G | 0.25 | 0.34 | 1.39 |
| 4 | 140 | 15 | 3.6 | 35.80 ± 5.32 | 8.27 ± 2.68 | 3.22 ± 4.51 | 32.4 | A | 0.29 | 0.37 | 1.28 |
| 5 | 100 | 10 | 3.0 | 5.60 ± 3.45 | 7.20 ± 2.62 | 3.70 ± 3.59 | 36.4 | B | 0.30 | 0.41 | 1.37 |
| 6 | 140 | 10 | 3.0 | 32.07 ± 5.10 | 8.42 ± 2.89 | 2.68 ± 4.93 | 30.0 | G | 0.28 | 0.35 | 1.25 |
| 7 | 100 | 10 | 4.2 | 11.08 ± 3.65 | 7.34 ± 2.66 | 3.20 ± 1.14 | 36.3 | G | 0.27 | 0.39 | 1.43 |
| 8 | 140 | 10 | 4.2 | 18.34 ± 3.88 | 8.33 ± 2.87 | 3.02 ± 3.70 | 34.8 | A | 0.27 | 0.40 | 1.47 |
| 9 | 120 | 5 | 3.0 | 12.75 ± 4.03 | 7.19 ± 2.68 | 3.47 ± 3.43 | 37.2 | A | 0.25 | 0.35 | 1.39 |
| 10 | 120 | 15 | 3.0 | 8.22 ± 3.23 | 7.33 ± 2.58 | 4.14 ± 2.78 | 35.2 | B | 0.26 | 0.38 | 1.46 |
| 11 | 120 | 5 | 4.2 | 7.80 ± 3.97 | 8.68 ± 2.63 | 3.34 ± 4.99 | 30.3 | B | 0.26 | 0.35 | 1.32 |
| 12 | 120 | 15 | 4.2 | 11.08 ± 4.10 | 7.59 ± 4.25 | 2.98 ± 4.35 | 42.5 | G | 0.27 | 0.37 | 1.39 |
| 13a | 120 | 10 | 3.6 | 15.54 ± 4.74 | 7.14 ± 2.73 | 3.03 ± 4.24 | 38.5 | G | 0.26 | 0.36 | 1.39 |
| 13b | 120 | 10 | 3.6 | 12.40 ± 3.97 | 6.99 ± 2.74 | 2.97 ± 4.26 | 38.8 | G | 0.28 | 0.39 | 1.42 |
| 13c | 120 | 10 | 3.6 | 12.09 ± 4.08 | 6.93 ± 2.79 | 3.18 ± 3.29 | 40.2 | G | 0.27 | 0.37 | 1.40 |
| Regression Coefficient (Constant)/Model Parameter | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Coefficient | p-Value | Coefficient | p-Value | Coefficient | p-Value | Coefficient | p-Value | Coefficient | p-Value | |
| −93.3966 0.0178 | 0.361 (ns) | 30.9155 −0.0015 | <0.001 *** | 11.3003 0.0000 | <0.001 *** | −64.8662 0.0246 | 0.144 (ns) | −45.0000 0.0000 | 0.005 ** | |
| −4.2188 −8.6415 | <0.001 *** | −0.2635 −6.2616 | <0.001 *** | −0.0725 −0.3614 | 0.001 ** | 1.6284 7.6038 | <0.001 *** | 0.2188 −0.1157 | 0.011 * | |
| 1.3080 −0.6524 | 0.653 (ns) | −0.1182 −1.8881 | 0.491 (ns) | 0.0149 −2.7110 | 0.885 (ns) | −1.8425 1.5110 | 0.118 (ns) | −0.4750 1.9670 | 0.169 (ns) | |
| 185.4160 6.2569 | <0.001 *** | −5.3053 −4.8503 | 0.023 * | −1.5371 −0.3748 | 0.043 * | 10.3711 3.8965 | 0.485 (ns) | 20.4167 8.5640 | 0.004 ** | |
| 0.0271 9.1212 | <0.001 *** | 0.0012 6.8800 | <0.001 *** | – | (ns) | −0.0083 −8.0185 | <0.001 *** | – | (ns) | |
| 0.1386 0.9664 | 0.038 * | 0.0134 1.6753 | 0.002 ** | 0.0145 2.7490 | <0.001 *** | −0.0566 −1.1837 | 0.037 * | −0.0200 −1.8780 | 0.057 (ns) | |
| −20.6202 −6.3651 | <0.001 *** | 0.9863 5.1313 | <0.001 *** | – | (ns) | −4.4550 −3.8149 | 0.019 * | −2.0833 −8.3460 | 0.011 * | |
| −0.0520 −0.2600 | 0.004 ** | 0.0015 0.1380 | 0.101 (ns) | – | (ns) | −0.0077 −0.1199 | 0.192 (ns) | – | (ns) | |
| 0.8419 0.1291 | 0.115 (ns) | −0.1025 −0.2833 | 0.002 ** | −0.0856 −0.3589 | <0.001 *** | 1.1762 0.5370 | <0.001 *** | 0.2500 0.5249 | 0.009 ** | |
| −0.4000 −0.2513 | 0.003 ** | −0.0032 −0.0346 | 0.684 (ns) | 0.0174 0.2926 | 0.005 ** | 0.0905 0.1613 | 0.099 (ns) | −0.0625 −0.5249 | 0.009 ** | |
| 0.813 | 0.810 | 0.679 | 0.775 | 0.866 | ||||||
| 0.761 | 0.756 | 0.625 | 0.708 | 0.732 | ||||||
| p-value | <0.001 *** | <0.001 *** | <0.001 *** | <0.001 *** | 0.012 * | |||||
| Run | Pattern of Coded Factors (X1, X2, X3) | Y1 | Y2 | Y3 | Y4 | Y5 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| O (μm) | P (μm) | PPE (%) | O (μm) | P (μm) | PPE (%) | O (μm) | P (μm) | PPE (%) | O (%) | P (%) | PPE (%) | O (Grade) | P (Grade) | PPE (%) | ||
| 1 | −1, −1, 0 | 9.1 | 11.4 | −20.3 | 7.67 | 7.65 | 0.2 | 3.60 | 3.69 | −2.3 | 35.2 | 34.2 | 2.7 | 3.0 | 2.5 | 20.0 |
| 2 | +1, −1, 0 | 26.3 | 35.2 | −25.1 | 8.28 | 8.38 | −1.2 | 3.65 | 3.30 | 10.8 | 32.3 | 31.5 | 2.3 | 2.0 | 2.3 | −11.1 |
| 3 | −1, +1, 0 | 39.4 | 30.6 | 28.9 | 7.07 | 6.96 | 1.5 | 3.48 | 3.65 | −4.6 | 38.4 | 39.1 | −1.9 | 3.0 | 2.8 | 9.1 |
| 4 | +1, +1, 0 | 35.8 | 33.5 | 6.9 | 8.27 | 8.29 | −0.2 | 3.22 | 3.26 | −1.2 | 32.4 | 33.4 | −2.8 | 2.0 | 2.5 | −20.0 |
| 5 | −1, 0, −1 | 5.6 | 6.9 | −18.8 | 7.20 | 7.06 | 2.0 | 3.70 | 3.70 | 0.1 | 36.4 | 37.0 | −1.6 | 1.0 | 2.6 | −61.9 |
| 6 | +1, 0, −1 | 32.1 | 29.8 | 7.6 | 8.42 | 8.16 | 3.2 | 2.68 | 2.89 | −7.2 | 30.0 | 30.6 | −1.9 | 3.0 | 2.6 | 14.3 |
| 7 | −1, 0, +1 | 11.1 | 13.3 | −17.0 | 7.34 | 7.60 | −3.5 | 3.20 | 2.92 | 9.8 | 36.3 | 35.9 | 1.1 | 3.0 | 3.4 | −11.1 |
| 8 | +1, 0, +1 | 18.3 | 17.0 | 7.6 | 8.33 | 8.55 | −2.5 | 3.02 | 2.94 | 2.5 | 34.8 | 33.9 | 2.6 | 2.0 | 1.6 | 23.1 |
| 9 | 0, −1, −1 | 12.7 | 9.1 | 39.6 | 7.19 | 7.35 | −2.2 | 3.47 | 3.42 | 1.5 | 37.2 | 37.6 | −0.9 | 2.0 | 2.1 | −5.9 |
| 10 | 0, +1, −1 | 8.2 | 12.8 | −35.8 | 7.33 | 7.58 | −3.2 | 4.14 | 3.90 | 6.3 | 35.2 | 33.9 | 3.9 | 1.0 | 0.9 | 14.3 |
| 11 | 0, −1, +1 | 7.8 | 0.9 | 748.9 | 8.68 | 8.43 | 2.9 | 3.34 | 3.57 | −6.5 | 30.3 | 31.6 | −4.2 | 1.0 | 1.1 | −11.1 |
| 12 | 0, +1, +1 | 11.1 | 14.7 | −24.6 | 7.59 | 7.43 | 2.2 | 2.98 | 3.02 | −1.2 | 42.5 | 42.0 | 1.2 | 3.0 | 2.9 | 4.3 |
| 13a | 0, 0, 0 | 15.5 | 13.3 | 16.5 | 7.14 | 7.01 | 1.9 | 3.03 | 3.11 | −2.5 | 38.5 | 39.3 | −2.1 | 3.0 | 3.0 | 0.0 |
| 13b | 0, 0, 0 | 12.4 | 13.3 | −7.1 | 6.99 | 7.01 | −0.3 | 2.97 | 3.11 | −4.6 | 38.7 | 39.3 | −1.4 | 3.0 | 3.0 | 0.0 |
| 13c | 0, 0, 0 | 12.1 | 13.3 | −9.4 | 6.93 | 7.01 | −1.1 | 3.18 | 3.11 | 2.2 | 40.2 | 39.3 | 2.3 | 3.0 | 3.0 | 0.0 |
| Goal | >10 μm; Minimize | Minimize | Minimize | Minimize | Maximize | |||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karas, J.; Pavloková, S.; Hořavová, H.; Gajdziok, J. Optimization of Spray Drying Process Parameters for the Preparation of Inhalable Mannitol-Based Microparticles Using a Box-Behnken Experimental Design. Pharmaceutics 2023, 15, 496. https://doi.org/10.3390/pharmaceutics15020496
Karas J, Pavloková S, Hořavová H, Gajdziok J. Optimization of Spray Drying Process Parameters for the Preparation of Inhalable Mannitol-Based Microparticles Using a Box-Behnken Experimental Design. Pharmaceutics. 2023; 15(2):496. https://doi.org/10.3390/pharmaceutics15020496
Chicago/Turabian StyleKaras, Jakub, Sylvie Pavloková, Hana Hořavová, and Jan Gajdziok. 2023. "Optimization of Spray Drying Process Parameters for the Preparation of Inhalable Mannitol-Based Microparticles Using a Box-Behnken Experimental Design" Pharmaceutics 15, no. 2: 496. https://doi.org/10.3390/pharmaceutics15020496
APA StyleKaras, J., Pavloková, S., Hořavová, H., & Gajdziok, J. (2023). Optimization of Spray Drying Process Parameters for the Preparation of Inhalable Mannitol-Based Microparticles Using a Box-Behnken Experimental Design. Pharmaceutics, 15(2), 496. https://doi.org/10.3390/pharmaceutics15020496






