5.1. Calibration of the Simulation Model
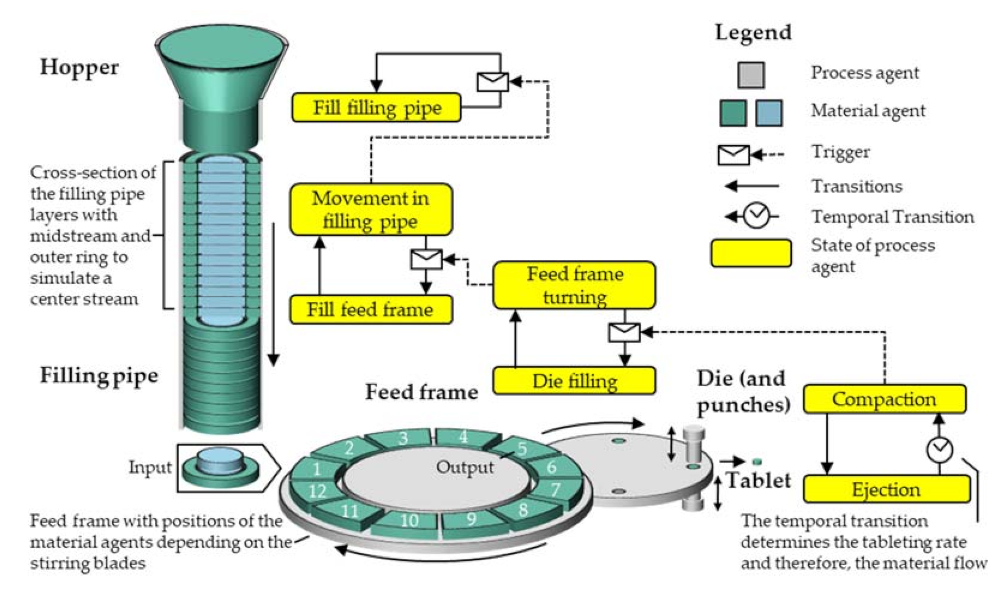
The sensitivity of the system towards two parameters is characterized and their calibration is necessarily conducted based on comparison with experimental data, as these parameters are not directly assessable by experiments, so far. Firstly, the effect of the theoretical diameter of the midstream, assuming a constant velocity ratio of 2:1 to the outer ring of the filling pipe, is investigated within the simulation. Secondly, the filling pattern from the feed frame fragments to the die, defining what fraction of the whole die volume is filled by successive feed frame compartments passing over the die during one filling event is also evaluated within the simulation.
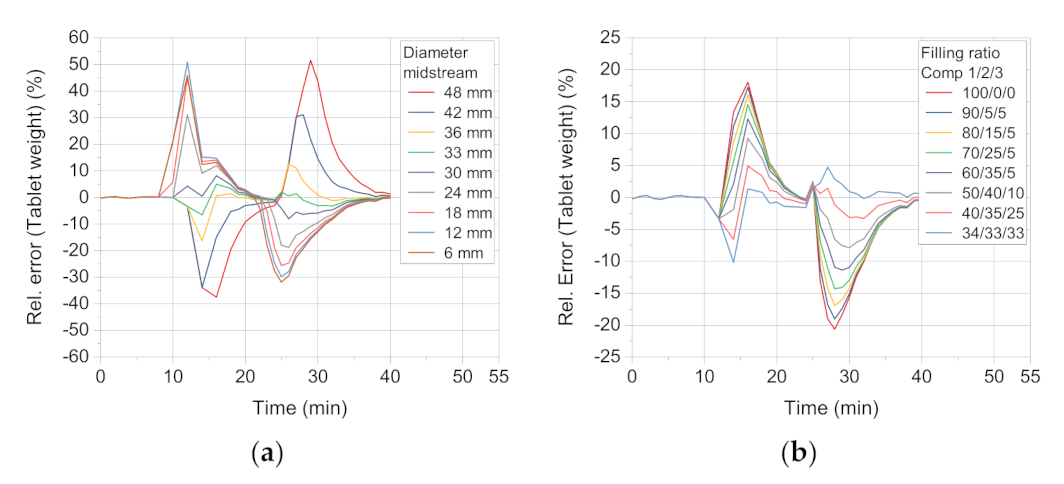
The sensitivity of the simulation towards deviation of the repeated midstream diameter increasing by always 6 mm shows that the relative error between the midstream diameter of 36 mm and 30 mm has the lowest relative errors (
Figure 9a). Therefore, the mean of those two values (33 mm) is chosen as the midstream diameter. This proved well suited, as its
f value of 1.32% is the lowest in this data set (see
Table 6).
The sensitivity of the distribution of filling over three compartments was studied by reducing the fraction filled by the first compartment in steps of 10%-points, distributing the rest of the filling reasonably over the second and the third compartment with the assumption that the ratio declines over the compartment number.
The lowest values are found for the ratio 40/35/25 and 34/33/33 (
Table 7). This finding shows that a distribution of the die filling is better described by filling from more than one compartment of the feed frame. However, it must be born in mind that this value most likely depends on the flowability of the formulation as well as on the process parameters of turret and paddle speed. A descending pattern of 40/35/25 was used for the case study.
5.2. Validation of the Sub-Process Models
The behavior of the agents in the sub-processes plays an important role in the simulation, as they determine the interim results and thus the input of the subsequent sub-process models. Therefore, a careful prior validation of the underlying mathematical models is necessary and useful to investigate their accuracy and to identify possible sources of error for the simulation results. In the following, the three empirical models regarding the compressibility curve, the elastic recovery and the tensile strength are compared to experimental data examined by the compaction simulator. Subsequently, the results of the simulation are compared with the experimental data and discussed.
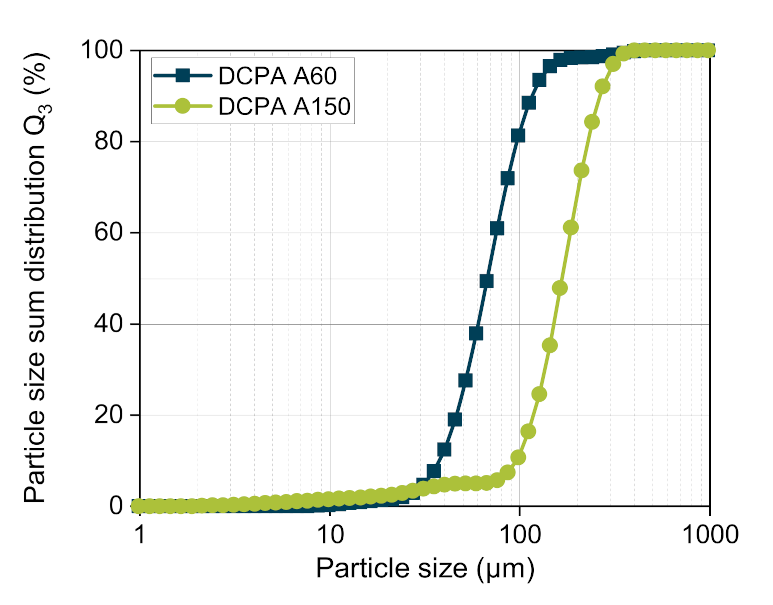
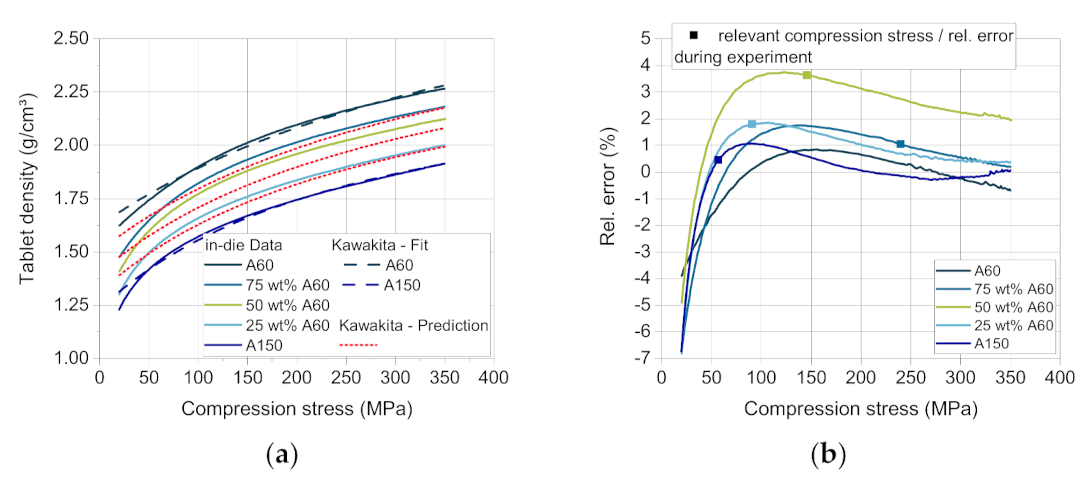
According to Busignies et al., the compressibility curves of DCPA A60 and DCPA A150 are fitted by the model of Kawakita (
Figure 10a, dashed lines) to gain the material-specific coefficients
a,
b and
ρ0. Using Equation (4) and the coefficients, the compressibility curves of the mixtures with a mass fraction of 25, 50 and 75 wt.% DCPA A60 were calculated. The comparison of the predicted and the measured curves present errors between highly negative deviation (lower values of experimental data) for all materials at a very low compression stress < 50 MPa, displaying that the lower stress range is less well described by the Kawakita model.
In the validation experiment as well as in the simulation, only specific compression stresses were reached for each blend composition, as the compression height stays approximately constant. These compression stresses and the corresponding relative errors are marked with a square (
Figure 10b). The maximum positive deviation (4%) occurs for the blend with 50 wt.% DCPA A60 at about 100–150 MPa (
Figure 10b), which was most likely to occur as it is the furthest from the support points of the two pure materials. The higher relative error for the blend with 50 wt.% DCPA A60 over the whole compression stress range may result from the volume-additive approach. The higher measured tablet density probably results from a volume contraction of the mixed powders in contrast to the additive volume of the single components. The small particles of DCPA A60 and their fragments may fill the pores between particles and fragments of DCPA A150, resulting in a higher tablet density than calculated. This trend can also be observed for the blends with 25 and 75 wt.% DCPA A60, although the relative error is smaller.
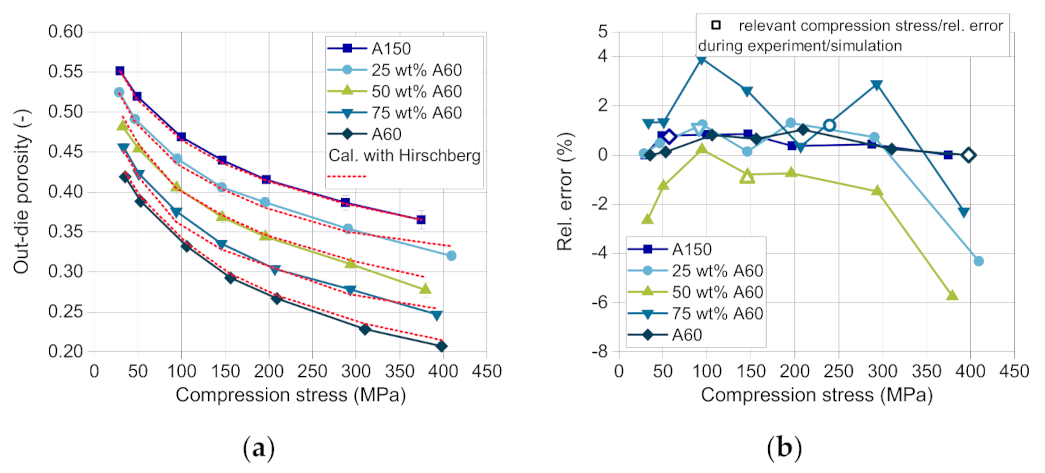
After the stress maximum during compaction and after ejection of the tablets, the elastic recovery takes place. As proposed by Hirschberg et al., the out-die porosity is calculated based on Equations (5)–(7) with consideration of the solid density. The relative error between the measured and the predicted out-die porosities of all substances and blends is considerably low with maximal 4% for 75 wt.% DCPA A60 and minimal −6% for 50 wt.% DCPA A60 (
Figure 11b). The relevant compression stresses and the related relative errors, which occur in the validation experiment as well as in the simulation, are marked with a hollow symbol (
Figure 11b).
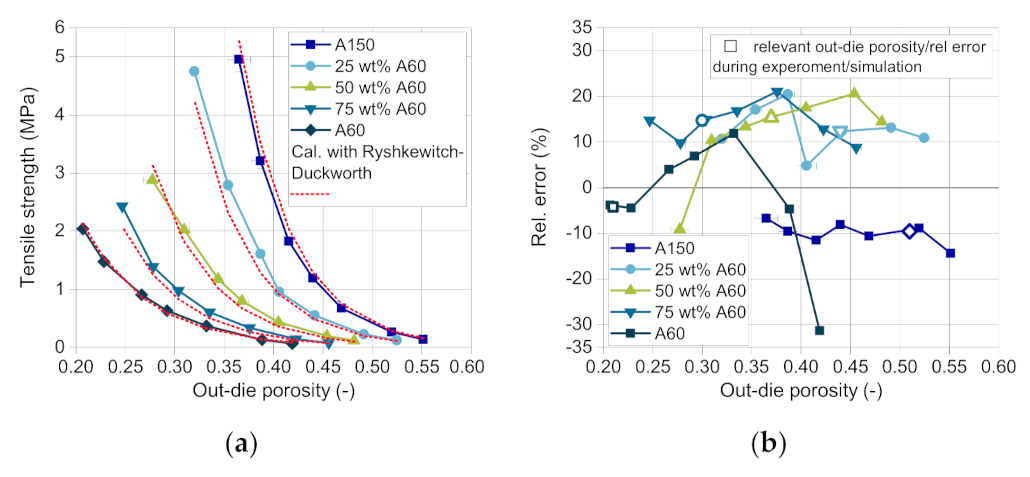
Finally, the tablet tensile strength was estimated in dependence on the out-die porosity using the model of Ryshkewitch and Duckworth. As described in
Section 4.3, a new mixing rule was developed to predict the tensile strength of tablets consisting of two different components. The coefficients of the model are calculated based on the mass fraction of DCPA A150 (Equations (9) and (10)). The compactability curves of A150 and the mixture 25 wt.% A60 (
Figure 12a) show a strong increase in tensile strength with decreasing out-die porosity. With increasing mass fraction of A60, the curve flattens. The correct mathematical description of the curves is challenging due to high changes in tensile strength for low differences in the out-die porosity. This causes the high relative error between the measured and the predicted tensile strength with about −30 up to 20% (
Figure 12b). Although, the calculated tensile strength curves fit the experimental values very well, as it can be seen in a first approximation in
Figure 12a. Nevertheless, it has to be taken into account that the data for each composition is only relevant in a specific compression stress range and thus a porosity range, as the stress changes with the composition and so does the out-die porosity. The relevant relative errors of the tensile strength are marked for each blend composition with hollow symbols (
Figure 12b).
5.3. Comparison of the Simulative and Experimental Results
In order to determine the quality of the AB model, the resulting CQAs obtained by the simulation are compared with the experimental results achieved from the rotary press XL 100.
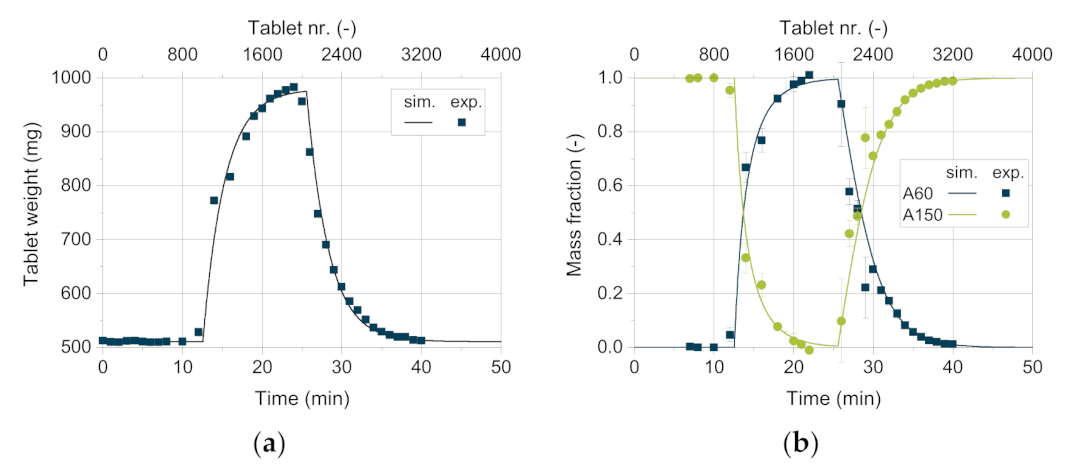
Figure 13 shows the tablet weight as well as the mass fraction of the respective excipient as a function of time. The tablets weigh about 500 mg at the beginning of the experiment, containing 100 wt.% DCPA A150. After about twelve minutes, the tablet weight increases significantly as the DCPA A60 content starts to rise. This can be traced back to the increasing apparent bulk density with higher DCPA A60 content as its small particles fill pores and lead to a denser arrangement of the powder bed. Therefore, the weight filled into the die increases, resulting in a higher tablet weight. With increasing mass content of DCPA A60, the change in mass fraction as well as tablet weight flattens. Due to the residence time distribution of DCPA A150, it takes a certain time to fill remaining DCPA A150 particles into the dies, leading to change in content inside the feed frame.
The good agreement between the simulative data and the measured values for the tablet weight and mass fraction (
Figure 13) are particularly worth to mention. Only for high DCPA A60 mass fractions, simulative data exhibit slightly lower tablet weights compared to the measured values. This underestimation might be linked to die filling, where apparent densities above the bulk density are possible due to particle rearrangements during forced feeding and especially during dosing [
47]. To meet the tablet weight, obtained by the experiment, an apparent consolidated bulk density after filling of 0.73 g/cm
3 had to be used, which is considerably higher than the bulk density of 0.68 g/cm
3. As described in the literature, good flowing powder as dicalcium phosphate consolidates at high paddle speeds and low turret speeds inside the die. The process parameters selected here as well as the material properties support this hypothesis. The same observations were made for DCPA A60, so the apparent consolidated bulk density after filling was taken to be 1.41 g/cm
3 compared to the bulk density of 1.33 g/cm
3.
Although no specific mixing model is introduced in the AB simulation, mixing and the distribution of the newly entering DCPA A60 can be represented by the set-up of the simulation itself. As described in
Section 3, the midstream with a diameter of 33 mm simulates a flow profile inside the filling pipe according to its geometry, by having double the velocity as the surrounding powder flow (compare
Section 3). Thus, a powder flow similar to the actually expected is aspired. As soon as the powder, represented by the
blend in filling pipe, enters the feed frame, the mass fraction of the respective compartment is recalculated. Therefore, the twelve compartments work as independent continuous stirred tank reactors (CSTRs), as the mixing ratio is constant within the entire compartment in each time step. Comparing this setting to the visual observations on the tablet press using a transparent feed frame, a completely homogenous concentration of the excipients is not realistic, especially not directly after new powder with a different composition entered the feed frame. Mixing in the feed frame over time can be observed, while the powder is not only mixed inside an interspace but is also able to change the compartment if the particles are close to the bottom or flow over the paddles in real experiments. Due to the high paddle speed of 60 rpm and the simultaneously low turret speed of 20 rpm, leading to a high residence time, the powder can mix quickly inside the feed frame. Puckhaber et al. investigated the residence time distribution on the XL 100 for a pure dicalcium phosphate with similar powder properties as DCPA A150, showing strong intermixing for the process parameters used in this study [
50]. This improves the model quality in so far that the simulated mass fraction, resulting from the compartments, modeled as CSTRs, is in good agreement with the experimental data. In future work different combinations of paddle and turret speed shall be looked at to investigate whether the concept of the CSTRs is still valid or must be refined for combinations of free flowing with poorly flowing materials, for example.
For the experimental data of the mass fraction, a very good correlation between experimental and simulative values was found (
Figure 13b). However, higher standard deviations are observed for the experimentally determined mass fraction than for the tablet weight, which shows standard deviations below 1.5%. The mass fraction is determined by using dyed DCPA A60, which intrinsically shows higher standard deviations of the loading as ten samples à 100 mg presented a relative standard deviation of 11.7%. Therefore, the tablet weight (
n = 6) is a more reliable and more facile to determine parameter to compare the simulative and experimental data.
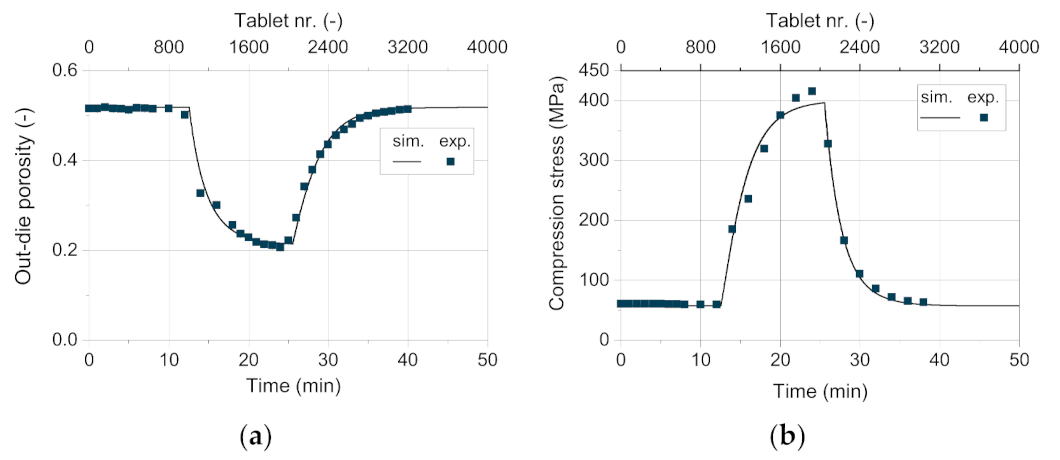
Besides the tablet weight, the out-die porosity and the tensile strength are of particular interest regarding their possible correlation to disintegration time and the handling stability of the tablets, respectively. The out-die porosity exhibited by the simulation fits very well with the experimental data (
Figure 14a). To achieve this degree of convergence, the models used to describe the maximum compression stress and the total elastic recovery as function of filling weight and blend density do present a very good applicability.
As shown for the validation of the process models, the in-die tablet density and thus the in-die tablet porosity have a deviation between −2 and 4% above 50 MPa (
Figure 10b). As the tablets contain only DCPA A150 at a compression stress of about 60 Mpa in this case, the apparent error due to the Kawakita model is close to 0%. As
Figure 15a shows, the resulting simulated compression stress in this study for 75 wt.% DCPA A60 is around 200 Mpa. In this stress range, the deviation for the respective content is small (
Figure 11b, hollow symbol). Although tablets with 50 wt.% and 25 wt.% DCPA A60 present high relative errors around 400 Mpa (
Figure 11b), they do not affect the simulation results as the apparent compression stress is lower than 150 Mpa for these mass fractions. Therefore, the total mean error for the out-die porosity is low with 2.13% as listed in
Table 8.
For the comparison of the experimentally recorded compression stress on the rotary press and the simulated values, a very good match can be observed (
Figure 14b). In the high stress range, the simulative data underestimates the experimental values. This might be due to the slightly lower simulated tablet weight at high DCPA A60 content. At such a high compression state, a low change in weight has a relatively strong effect on the corresponding compression stress (compare
Figure 10a). For further research, the consolidation of the powder during and after filling has to be addressed in more detail to better calculate the tablet weight and thus predict the compression stress even more accurately.
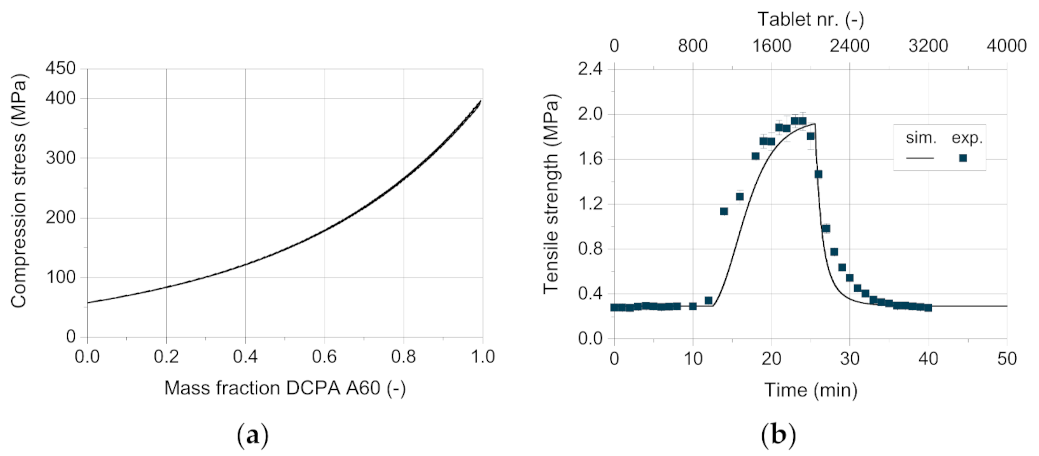
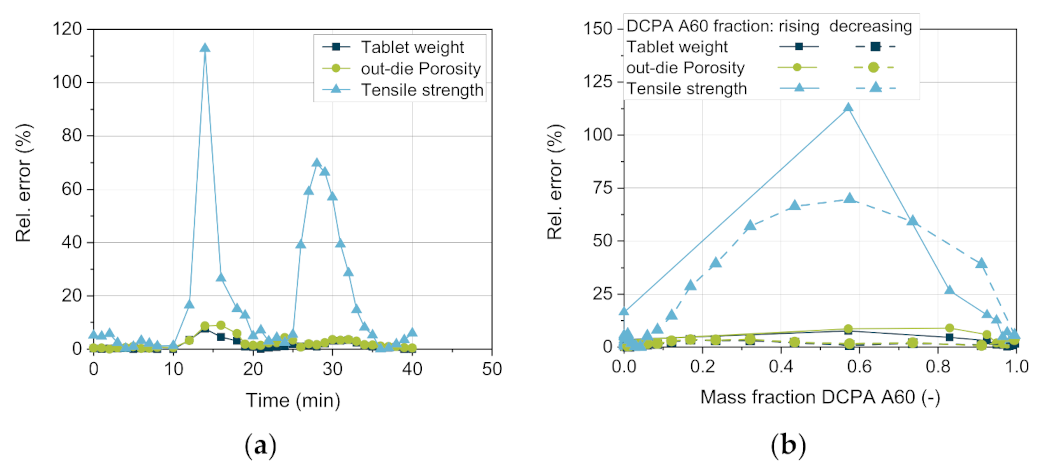
Regarding the tensile strength, considerably higher deviations between the simulative and the experimental data are observed (
Figure 15b). While the measured values match well for pure DCPA A150 and pure A60, the correct prediction of the tensile strength during the change in content is challenging (
Figure 16). The tensile strength obtains the highest relative errors for the simulative data with over 100% with rising mass fraction of DCPA A60 and about 70% with decreasing content (
Figure 16a). The lower quality of the predicted data of the tensile strength can be traced back to the model and especially the mixing rule used. For the model validation, already relative errors of -35 up to 20% are obtained, while no specific trend for the mass fraction is observable (
Figure 12b). Nevertheless, the model of Ryshkewitch uses the out-die porosity as input parameter to calculate the corresponding tensile strength, which includes previous errors. Due to the strong increase in strength for low changes in porosity, small differences in the porosity have a high impact. A parabolic shape of the relative error over the mass content can be observed, which indicates a systematic error for the determination of the tensile strength (
Figure 16b).
Interestingly, comparing the increasing and decreasing DCPA A60 fractions, the relative errors of all three parameters present higher values with increasing DCPA A60 fraction than vice versa (
Figure 16b). This might be due to the change in the apparent bulk density as the actual volume of the powder is lower than the calculated one by adding the respective volumes of each powder. Additionally, the higher deviation with rising DCPA A60 content in comparison to the decreasing content can indicate different residence time distributions and thus, different distribution profiles of the two excipients. Both will be investigated in future research.
Considering the overall accuracy of the simulation results, the mean absolute relative error
f (compare Equation (11)) of the CQAs can be seen in
Table 8.
Besides the tensile strength of the tablets, all other CQAs have a mean relative error of less than or equal to 6.99%. However, the quality of the AB model can only be as good as the quality of the physical models used to calculate product properties. For the calculation of the tensile strength a better model and, moreover, a better bulk density determination of the component mixture is necessary.
From a simulation point of view, the AB modeling approach allows the observation of each agent over the complete simulation time. Furthermore, the input materials have been digitally marked and allow a tracking and tracing over the whole process. This fact allows to investigate the output in relation to the input on a specific matter. With this, several processing questions can be answered, e.g., the characterization of tablets that have fractions of a specific input material. This shows the potential of AB models to be capable of model particle-based processes chains at low computational cost, prospectively making their application in real time control of pharmaceutical production processes feasible.