Numerical Simulation of Particle Dynamics in a Spiral Jet Mill via Coupled CFD-DEM
Abstract
:1. Introduction
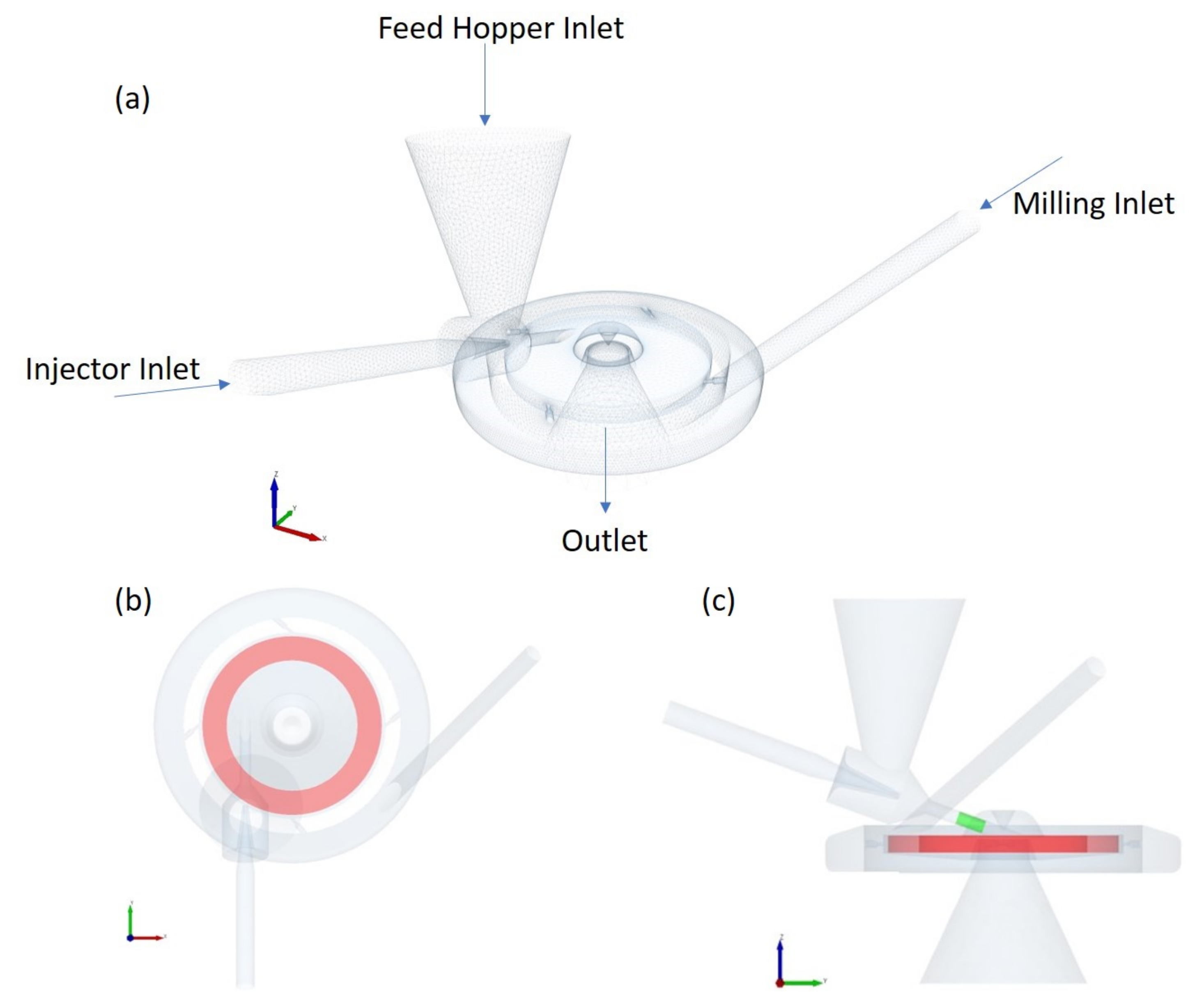
2. Numerical Methods
3. Results
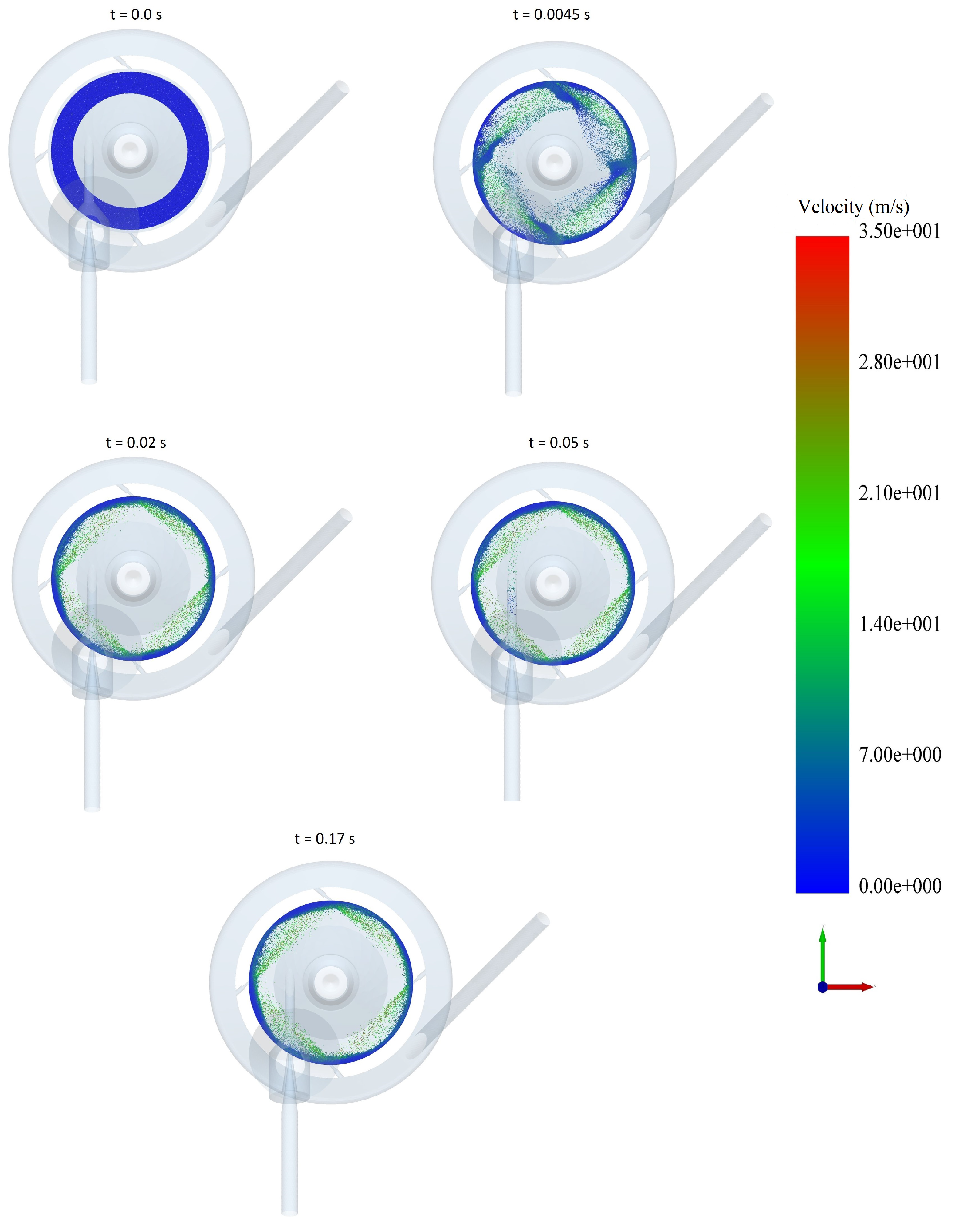
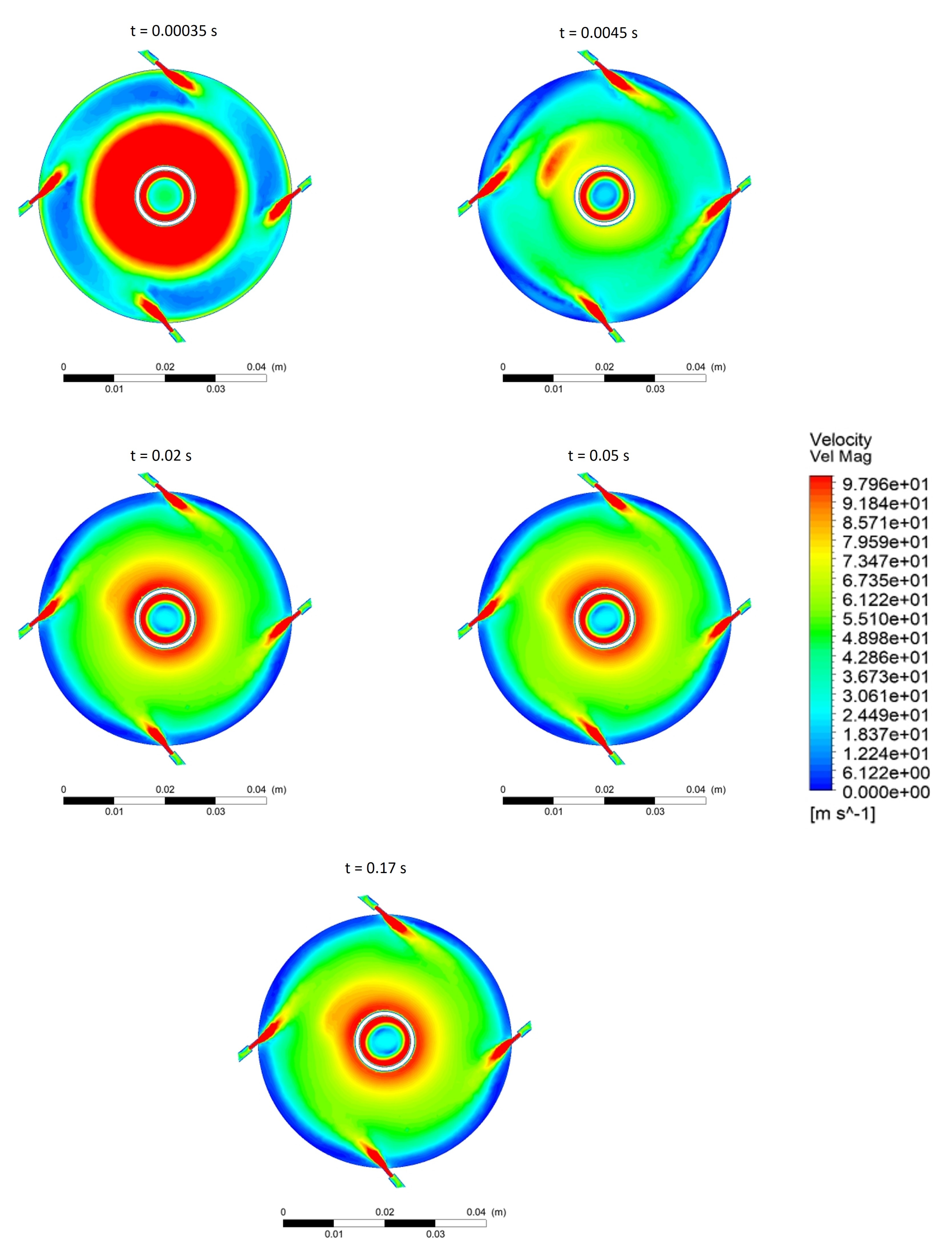
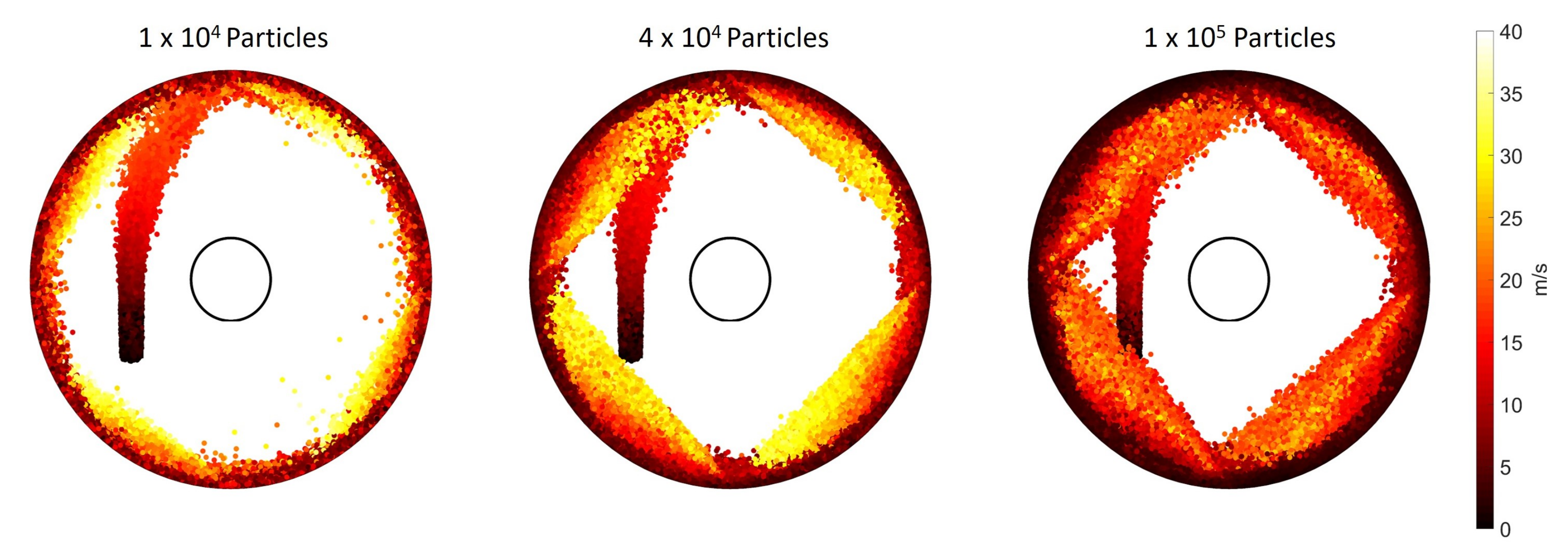
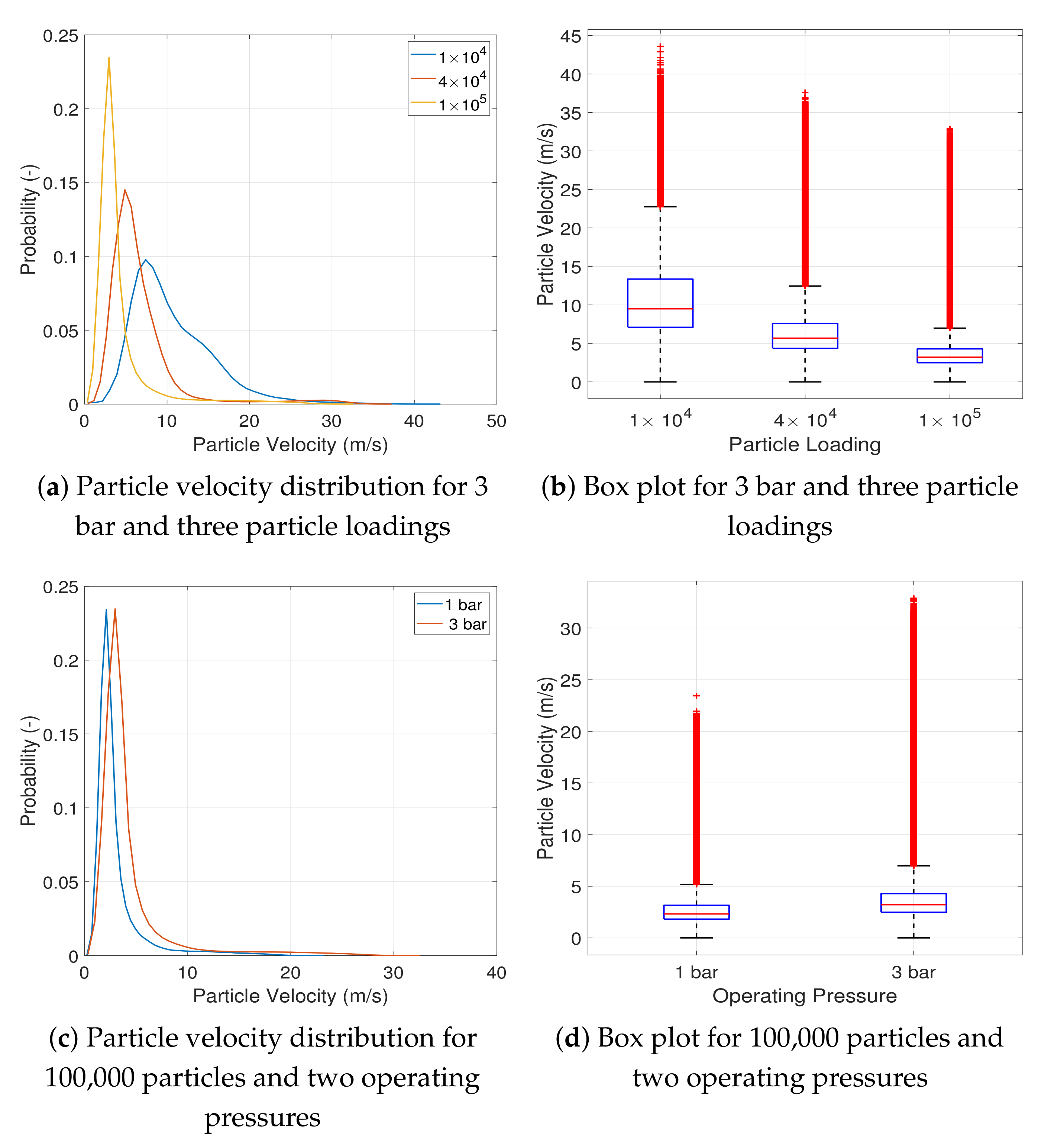
3.1. Fluid and Particle Dynamics
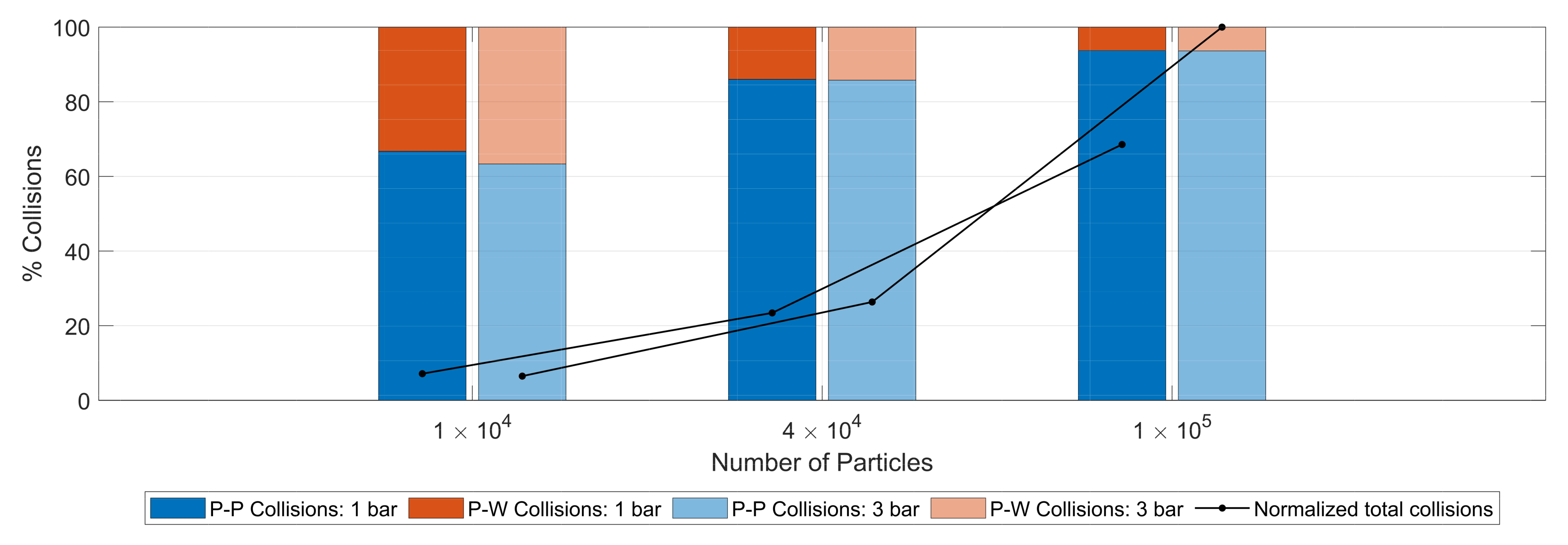
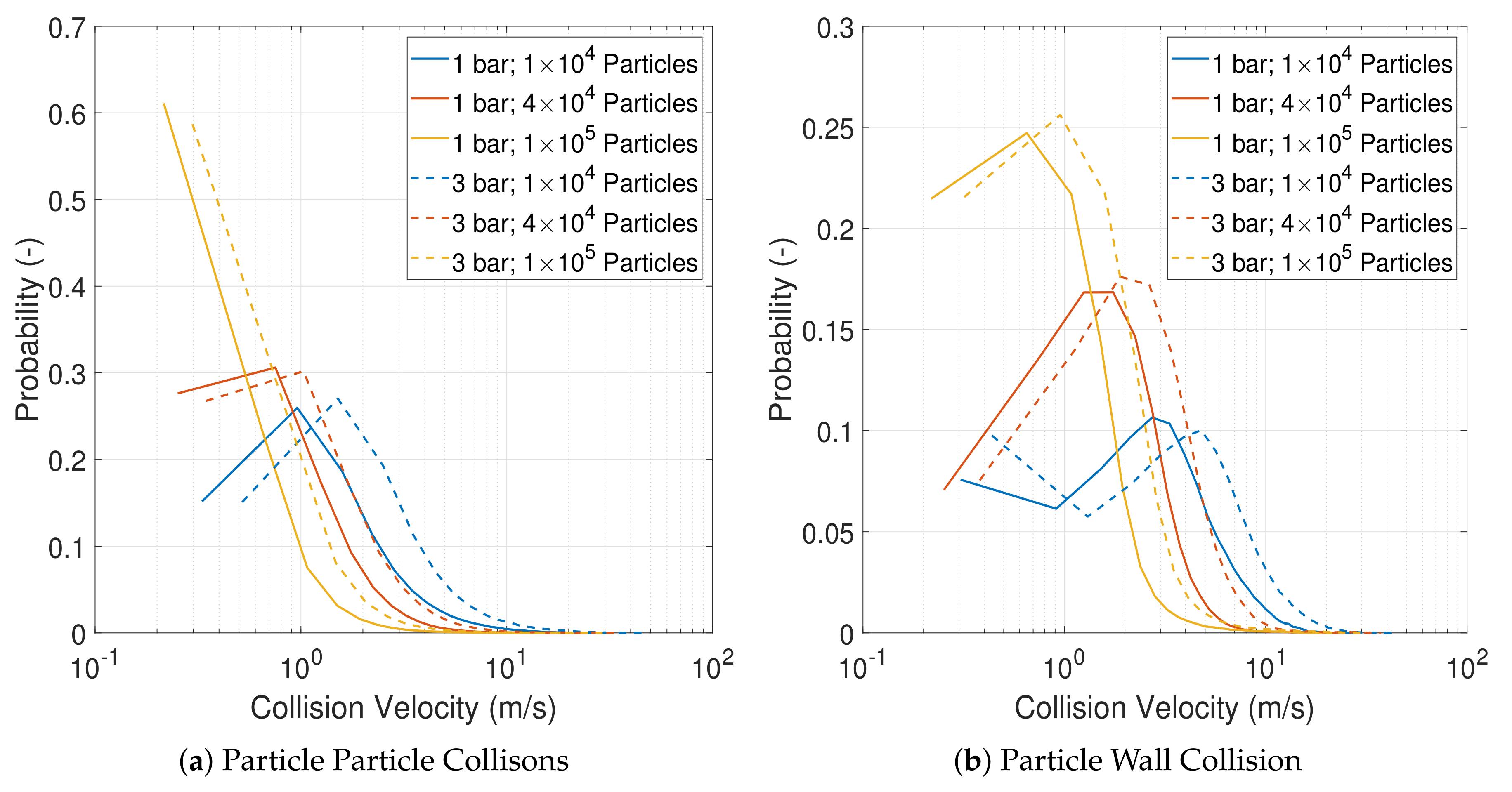
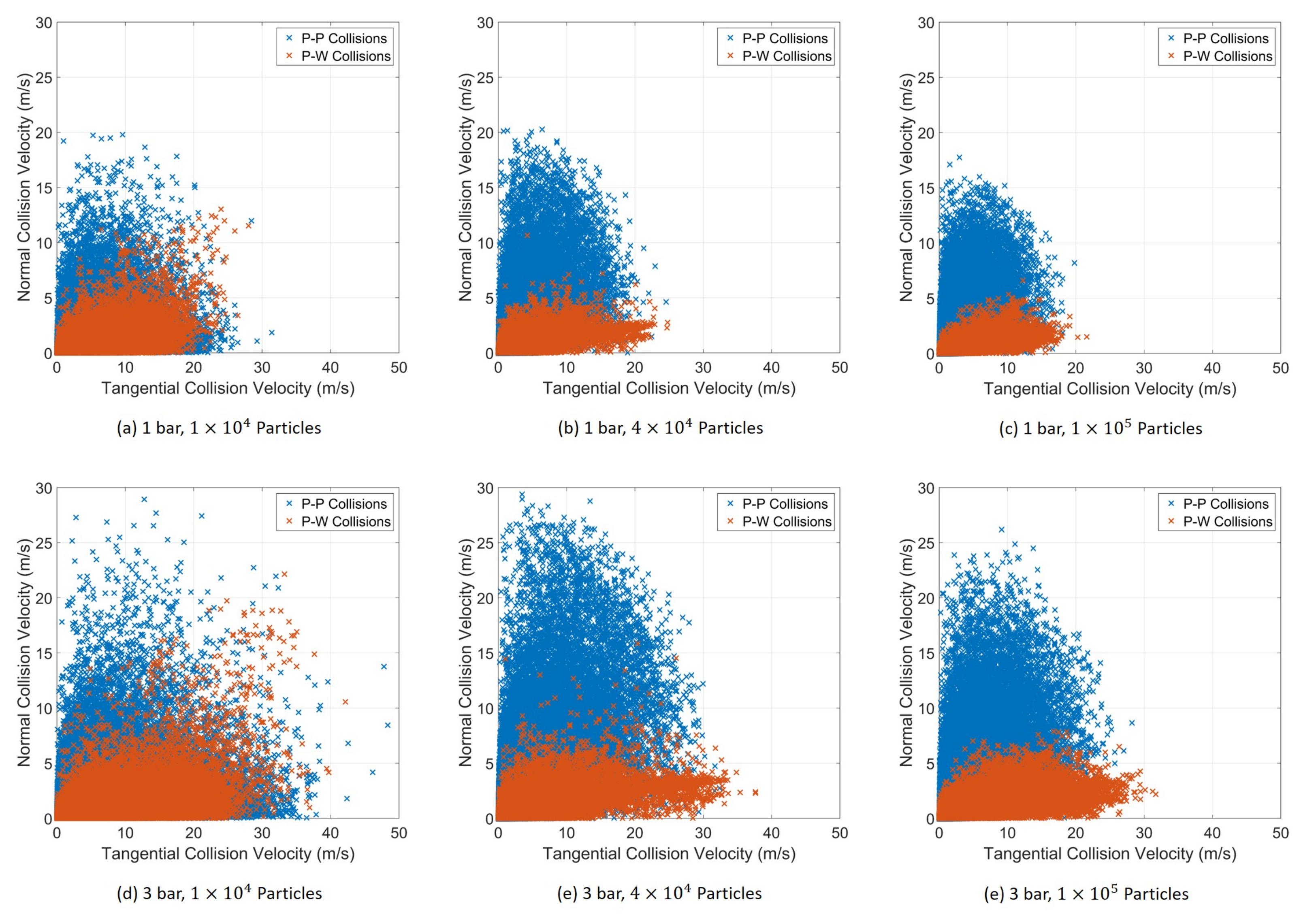
3.2. Particle Collision Statistics
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nakach, M.; Authelin, J.R.; Chamayou, A.; Dodds, J. Comparison of various milling technologies for grinding pharmaceutical powders. Int. J. Miner. Process. 2004, 74, S173–S181. [Google Scholar] [CrossRef]
- Parrott, E.L. Milling of Pharmaceutical Solids. J. Pharm. Sci. 1974, 63, 813–829. [Google Scholar] [CrossRef] [PubMed]
- Andrews, N. Method and Apparatus for Providing Material in Finely Divided Form. U.S. Patent US002032827, 3 March 1936. [Google Scholar]
- Dobson, B.; Rothwell, E. Particle size reduction in a fluid energy mill. Powder Technol. 1969, 3, 213–217. [Google Scholar] [CrossRef]
- Liu, G. Hammer Milling and Jet Milling Fundamentals. Chem. Eng. Prog. 2017, 113, 48–54. [Google Scholar]
- Teng, S.; Wang, P.; Zhu, L.; Young, M.W.; Gogos, C.G. Experimental and numerical analysis of a lab-scale fluid energy mill. Powder Technol. 2009, 195, 31–39. [Google Scholar] [CrossRef]
- Katz, A.; Kalman, H. Preliminary Experimental Analysis of a Spiral Jet Mill Performance. Part. Part. Syst. Charact. 2007, 24, 332–338. [Google Scholar] [CrossRef]
- Midoux, N.; Hošek, P.; Pailleres, L.; Authelin, J. Micronization of pharmaceutical substances in a spiral jet mill. Powder Technol. 1999, 104, 113–120. [Google Scholar] [CrossRef]
- Müller, F.; Polke, R.; Schädel, G. Spiral jet mills: Hold up and scale up. Int. J. Miner. Process. 1996, 44–45, 315–326. [Google Scholar] [CrossRef]
- Ramanujam, M.; Venkateswarlu, D. Studies in fluid energy grinding. Powder Technol. 1969, 3, 92–101. [Google Scholar] [CrossRef]
- Tuunila, R.; Nyström, L. Effects of grinding parameters on product fineness in jet mill grinding. Miner. Eng. 1998, 11, 1089–1094. [Google Scholar] [CrossRef]
- Teng, S.; Wang, P.; Zhang, Q.; Gogos, C. Analysis of Fluid Energy Mill by gas-solid two-phase flow simulation. Powder Technol. 2011, 208, 684–693. [Google Scholar] [CrossRef]
- Luczak, B.; Müller, R.; Kessel, C.; Ulbricht, M.; Schultz, H.J. Visualization of flow conditions inside spiral jet mills with different nozzle numbers—Analysis of unloaded and loaded mills and correlation with grinding performance. Powder Technol. 2019, 342, 108–117. [Google Scholar] [CrossRef]
- MacDonald, R.; Rowe, D.; Martin, E.; Gorringe, L. The spiral jet mill cut size equation. Powder Technol. 2016, 299, 26–40. [Google Scholar] [CrossRef]
- Rodnianski, V.; Krakauer, N.; Darwesh, K.; Levy, A.; Kalman, H.; Peyron, I.; Ricard, F. Aerodynamic classification in a spiral jet mill. Powder Technol. 2013, 243, 110–119. [Google Scholar] [CrossRef]
- Tanaka, T. Scale-Up Theory of Jet Mills on Basis of Comminution Kinetics. Ind. Eng. Chem. Process Des. Dev. 1972, 11, 238–241. [Google Scholar] [CrossRef]
- Gommeren, H.; Heitzmann, D.; Kramer, H.; Heiskanen, K.; Scarlett, B. Dynamic modeling of a closed loop jet mill. Int. J. Miner. Process. 1996, 44-45, 497–506. [Google Scholar] [CrossRef]
- Starkey, D.; Taylor, C.; Morgan, N.; Winston, K.; Svoronos, S.; Mecholsky, J.; Powers, K.; Iacocca, R. Modeling of continuous self-classifying spiral jet mills part 1: Model structure and validation using mill experiments. AIChE J. 2014, 60, 4086–4095. [Google Scholar] [CrossRef]
- Starkey, D.; Taylor, C.; Siddabathuni, S.; Parikh, J.; Svoronos, S.; Mecholsky, J.; Powers, K.; Iacocca, R. Modeling of continuous self-classifying spiral jet mills part 2: Powder-dependent parameters from characterization experiments. AIChE J. 2014, 60, 4096–4103. [Google Scholar] [CrossRef]
- Kozawa, K.; Seto, T.; Otani, Y. Development of a spiral-flow jet mill with improved classification performance. Adv. Powder Technol. 2012, 23, 601–606. [Google Scholar] [CrossRef]
- Levy, A.; Kalman, H. Numerical Study of Particle Motion in Jet Milling. Part. Sci. Technol. 2007, 25, 197–204. [Google Scholar] [CrossRef]
- Bhonsale, S.S.; Telen, D.; Stokbroekx, B.; Impe, J.V. Comparison of numerical solution strategies for population balance model of continuous cone mill. Powder Technol. 2019, 345, 739–749. [Google Scholar] [CrossRef]
- Bhonsale, S.S.; Stokbroekx, B.; Van Impe, J. Assessment of the parameter identifiability of population balance models for air jet mills. Comput. Chem. Eng. 2020, 143, 107056. [Google Scholar] [CrossRef]
- Han, T.; Kalman, H.; Levy, A. DEM Simulation of Particle Comminutionin Jet Milling. Part. Sci. Technol. 2002, 20, 325–340. [Google Scholar] [CrossRef]
- Brosh, T.; Kalman, H.; Levy, A.; Peyron, I.; Ricard, F. DEM–CFD simulation of particle comminution in jet-mill. Powder Technol. 2014, 257, 104–112. [Google Scholar] [CrossRef]
- Kalman, H.; Rodnianski, V.; Haim, M. A new method to implement comminution functions into DEM simulation of a size reduction system due to particle–wall collisions. Granul. Matter 2009, 11, 253–266. [Google Scholar] [CrossRef]
- Bnà, S.; Ponzini, R.; Cestari, M.; Cavazzoni, C.; Cottini, C.; Benassi, A. Investigation of particle dynamics and classification mechanism in a spiral jet mill through computational fluid dynamics and discrete element methods. Powder Technol. 2020, 364, 746–773. [Google Scholar] [CrossRef]
- Scott, L.; Borissova, A.; Burns, A.; Ghadiri, M. Influence of holdup on gas and particle flow patterns in a spiral jet mill. Powder Technol. 2021, 377, 233–243. [Google Scholar] [CrossRef]
- Dogbe, S. Predictive Milling of Active Pharmaceutical Ingredients and Excipients. Ph.D. Thesis, School of Chemical and Process Engineering, The University of Leeds, Leeds, UK, 2016. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Agrawal, V.; Shinde, Y.; Shah, M.T.; Utikar, R.P.; Pareek, V.K.; Joshi, J.B. Effect of drag models on CFD–DEM predictions of bubbling fluidized beds with Geldart D particles. Adv. Powder Technol. 2018, 29, 2658–2669. [Google Scholar] [CrossRef]
- Marchelli, F.; Hou, Q.; Bosio, B.; Arato, E.; Yu, A. Comparison of different drag models in CFD-DEM simulations of spouted beds. Powder Technol. 2020, 360, 1253–1270. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, L.; Bai, L.; Shi, W.; Li, W.; Wang, C.; Agarwal, R. Experimental study and transient CFD/DEM simulation in a fluidized bed based on different drag models. RSC Adv. 2017, 7, 12764–12774. [Google Scholar] [CrossRef] [Green Version]
- Norouzi, H.R.; Zarghami, R.; Sotudeh-Gharebagh, R.; Mostoufi, N. Coupled CFD-DEM Modeling: Formulation, Implementation and Application to Multiphase Flows; Wiley: Newark, NJ, USA, 2016. [Google Scholar]
- Tsuji, Y.; Tanaka, T.; Ishida, T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe. Powder Technol. 1992, 71, 239–250. [Google Scholar] [CrossRef]
- Dogbe, S.; Ghadiri, M.; Hassanpour, A.; Hare, C.; Wilson, D.; Storey, R.; Crosley, I. Fluid-particle energy transfer in spiral jet milling. EPJ Web Conf. 2017, 140, 09040. [Google Scholar] [CrossRef]
- Rodnianski, V.; Levy, A.; Kalman, H. A new method for simulation of comminution process in jet mills. Powder Technol. 2019, 343, 867–879. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhonsale, S.; Scott, L.; Ghadiri, M.; Van Impe, J. Numerical Simulation of Particle Dynamics in a Spiral Jet Mill via Coupled CFD-DEM. Pharmaceutics 2021, 13, 937. https://doi.org/10.3390/pharmaceutics13070937
Bhonsale S, Scott L, Ghadiri M, Van Impe J. Numerical Simulation of Particle Dynamics in a Spiral Jet Mill via Coupled CFD-DEM. Pharmaceutics. 2021; 13(7):937. https://doi.org/10.3390/pharmaceutics13070937
Chicago/Turabian StyleBhonsale, Satyajeet, Lewis Scott, Mojtaba Ghadiri, and Jan Van Impe. 2021. "Numerical Simulation of Particle Dynamics in a Spiral Jet Mill via Coupled CFD-DEM" Pharmaceutics 13, no. 7: 937. https://doi.org/10.3390/pharmaceutics13070937
APA StyleBhonsale, S., Scott, L., Ghadiri, M., & Van Impe, J. (2021). Numerical Simulation of Particle Dynamics in a Spiral Jet Mill via Coupled CFD-DEM. Pharmaceutics, 13(7), 937. https://doi.org/10.3390/pharmaceutics13070937







