Bottom-Up Physiologically Based Oral Absorption Modeling of Free Weak Base Drugs
Abstract
:1. Introduction
2. Theory
2.1. Solubility in the Stomach
2.2. Dissolution Rate in the Stomach
2.3. Fraction Dissolved in the Stomach
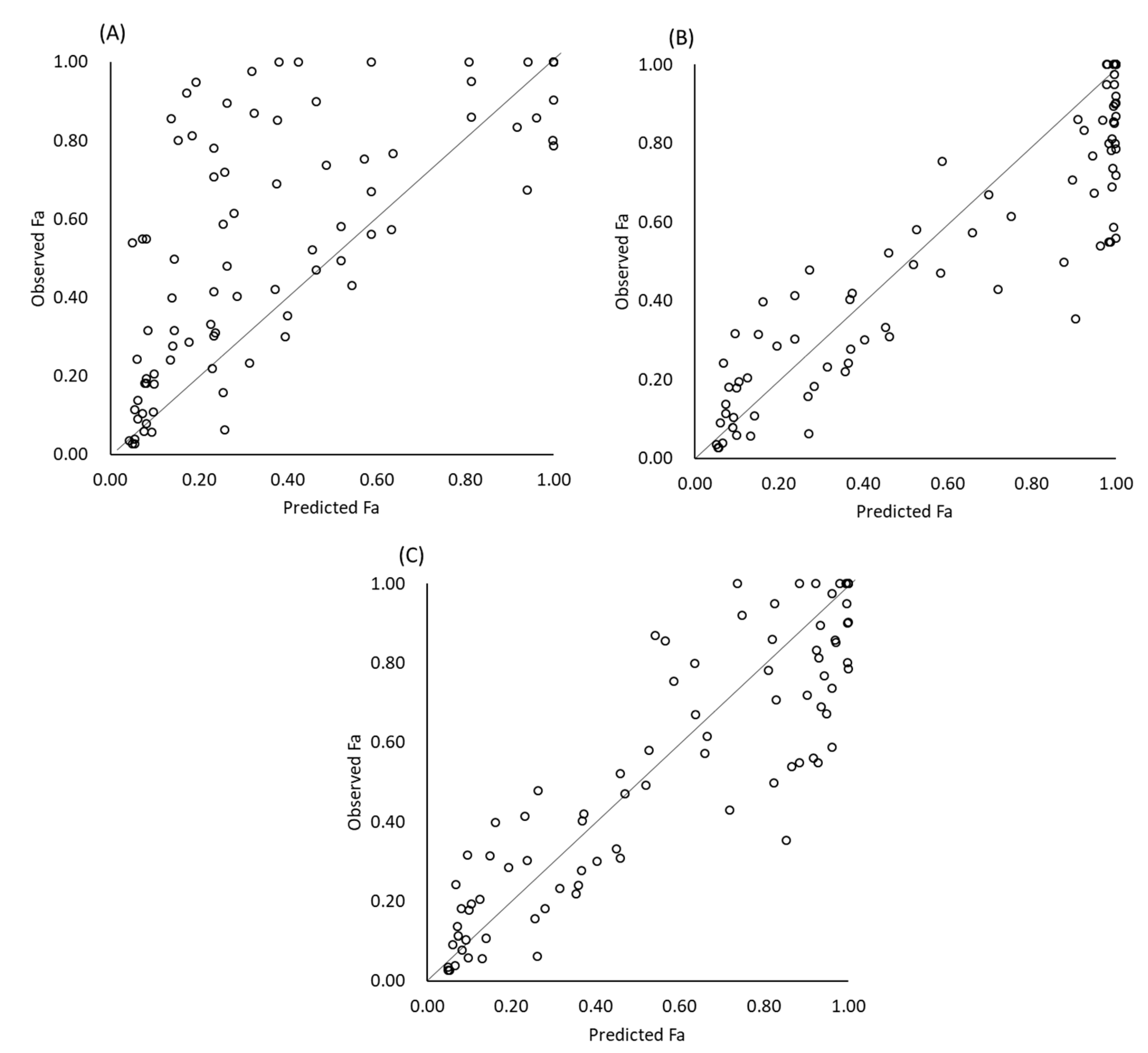
2.4. Calculation of the Fraction of a Dose Absorbed Considering Gastric Dissolution
- (A)
- No gastric dissolution
- (B)
- Using bulk pH
- (C)
- Using pHsurface and pHeq.
2.5. Fa Rate-Limiting Steps (FaRLS)
2.6. Physiological Parameters
2.7. In Vivo Fa Data
- (I)
- Fa described in the literature was used as it was.
- (II)
- Relative bioavailability of solution vs. solid form formulation.
- (III)
- Relative bioavailability in the fasted state vs. in the fed state (especially when DoSI < 1 in the fed state).
- (IV)
- Relative bioavailability with the low vs. high pH stomach when DoSI < 1 in the stomach (for basic drugs) (not used in this study)
- (V)
- Dose-normalized relative bioavailability at DoSI < 1 vs. DoSI > 1 when the terminal elimination half-life is consistent.
- (VI)
- From absolute bioavailability (F) and hepatic clearance using Fa = F/(1 − CLh/Qh).
2.8. Statistics
3. Results
3.1. Model Drugs
3.2. Prediction Model
3.3. Results of Fa Prediction
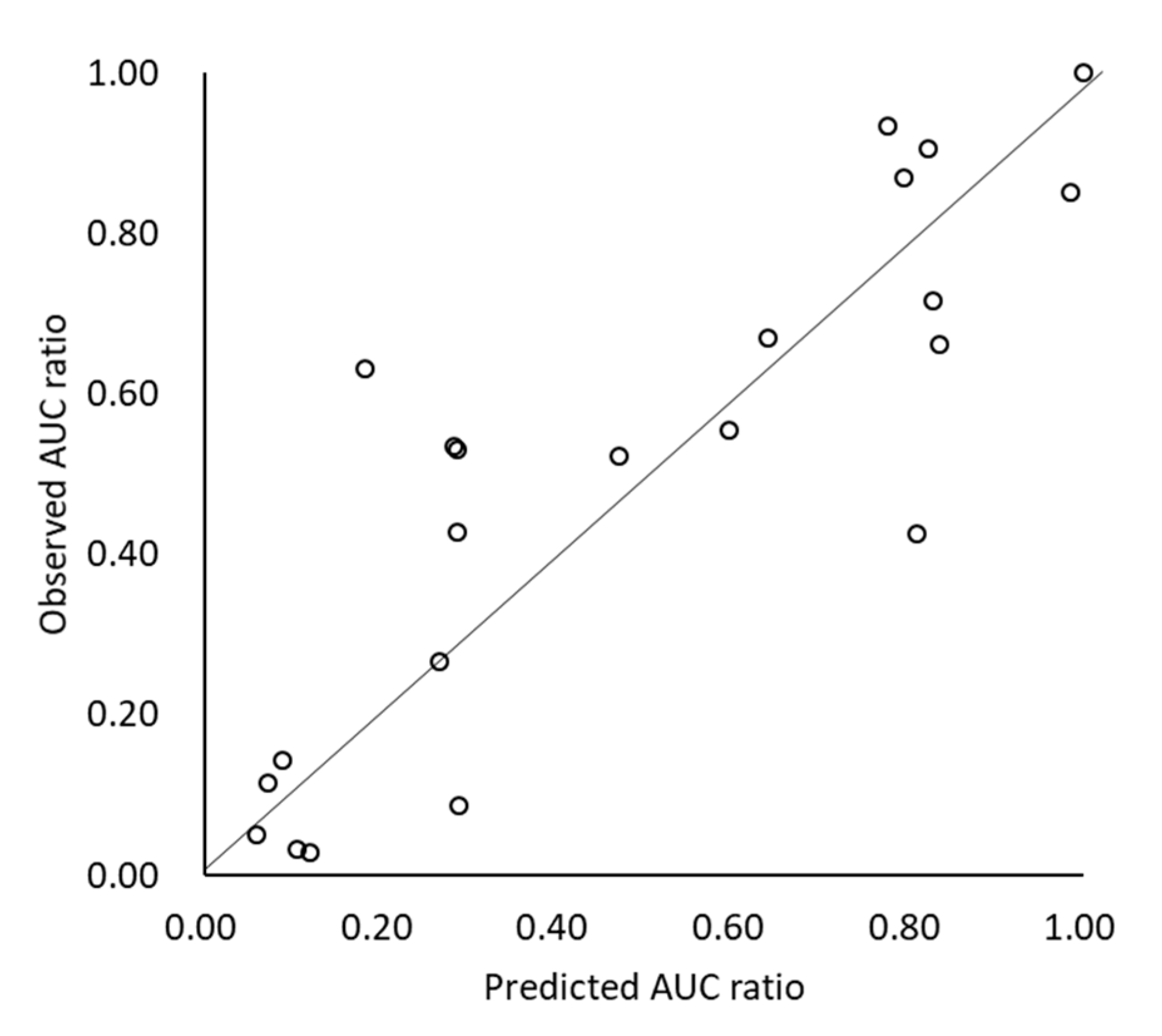
3.4. Prediction of Drug-Drug Interaction (DDI) with Acid-Reducing Agents (ARA)
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Thayer, A.M. Custom manufacturers take on DRUG SOLUBILITY ISSUES to help pharmaceutical firms move products through development. Chem. Eng. News 2010, 88, 13–18. [Google Scholar]
- Sugano, K.; Okazaki, A.; Sugimoto, S.; Tavornvipas, S.; Omura, A.; Mano, T. Solubility and dissolution profile assessment in drug discovery. Drug Metab. Pharmacokinet. 2007, 22, 225–254. [Google Scholar]
- Abrahamsson, B.; McAllister, M.; Augustijns, P.; Zane, P.; Butler, J.; Holm, R.; Langguth, P.; Lindahl, A.; Müllertz, A.; Pepin, X.; et al. Six years of progress in the oral biopharmaceutics area—A summary from the IMI OrBiTo project. Eur. J. Pharm. Biopharm. 2020, 152, 236–247. [Google Scholar]
- Sugano, K. Introduction to computational oral absorption simulation. Expert Opin. Drug Metab. Toxicol. 2009, 5, 259–293. [Google Scholar]
- Sugano, K. Biopharmaceutics Modeling and Simulations: Theory, Practice, Methods, and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Budha, N.R.; Frymoyer, A.; Smelick, G.S.; Jin, J.Y.; Yago, M.R.; Dresser, M.J.; Holden, S.N.; Benet, L.Z.; Ware, J.A. Drug absorption interactions between oral targeted anticancer agents and PPIs: Is pH-dependent solubility the Achilles heel of targeted therapy? Clin. Pharmacol. Ther. 2012, 92, 203–213. [Google Scholar]
- Indini, A.; Petrelli, F.; Tomasello, G.; Rijavec, E.; Facciorusso, A.; Grossi, F.; Ghidini, M. Impact of Use of Gastric-Acid Suppressants and Oral Anti-Cancer Agents on Survival Outcomes: A Systematic Review and Meta-Analysis. Cancers 2020, 12, 998. [Google Scholar]
- Patel, D.; Bertz, R.; Ren, S.; Boulton, D.W.; Någård, M. A Systematic Review of Gastric Acid-Reducing Agent-Mediated Drug-Drug Interactions with Orally Administered Medications. Clin. Pharmacokinet. 2020, 59, 447–462. [Google Scholar]
- Morihara, M.; Aoyagi, N.; Kaniwa, N.; Kojima, S.; Ogata, H. Assessment of gastric acidity of Japanese subjects over the last 15 years. Biol. Pharm. Bull. 2001, 24, 313–315. [Google Scholar]
- Russell, T.L.; Berardi, R.R.; Barnett, J.L.; Dermentzoglou, L.C.; Jarvenpaa, K.M.; Schmaltz, S.P.; Dressman, J.B. Upper gastrointestinal pH in seventy-nine healthy, elderly, North American men and women. Pharm. Res. 1993, 10, 187–196. [Google Scholar]
- van de Waterbeemd, H.; Gifford, E. ADMET in silico modelling: Towards prediction paradise? Nat. Rev. Drug Discov. 2003, 2, 192–204. [Google Scholar]
- Arora, S.; Pansari, A.; Kilford, P.; Jamei, M.; Gardner, I.; Turner, D.B. Biopharmaceutic In Vitro In Vivo Extrapolation (IVIV_E) Informed Physiologically-Based Pharmacokinetic Model of Ritonavir Norvir Tablet Absorption in Humans Under Fasted and Fed State Conditions. Mol. Pharm. 2020, 17, 2329–2344. [Google Scholar]
- Kato, T.; Nakagawa, H.; Mikkaichi, T.; Miyano, T.; Matsumoto, Y.; Ando, S. Establishment of a clinically relevant specification for dissolution testing using physiologically based pharmacokinetic (PBPK) modeling approaches. Eur. J. Pharm. Biopharm. 2020, 151, 45–52. [Google Scholar]
- Mitra, A.; Parrott, N.; Miller, N.; Lloyd, R.; Tistaert, C.; Heimbach, T.; Ji, Y.; Kesisoglou, F. Prediction of pH-Dependent Drug-Drug Interactions for Basic Drugs Using Physiologically Based Biopharmaceutics Modeling: Industry Case Studies. J. Pharm. Sci. 2020, 109, 1380–1394. [Google Scholar]
- Tistaert, C.; Heimbach, T.; Xia, B.; Parrott, N.; Samant, T.S.; Kesisoglou, F. Food Effect Projections via Physiologically Based Pharmacokinetic Modeling: Predictive Case Studies. J. Pharm. Sci. 2019, 108, 592–602. [Google Scholar]
- Yu, Y.; DuBois, S.G.; Wetmore, C.; Khosravan, R. Physiologically Based Pharmacokinetic Modeling and Simulation of Sunitinib in Pediatrics. AAPS J. 2020, 22, 31. [Google Scholar]
- Margolskee, A.; Darwich, A.S.; Pepin, X.; Pathak, S.M.; Bolger, M.B.; Aarons, L.; Rostami-Hodjegan, A.; Angstenberger, J.; Graf, F.; Laplanche, L.; et al. IMI—Oral biopharmaceutics tools project—Evaluation of bottom-up PBPK prediction success part 1: Characterisation of the OrBiTo database of compounds. Eur. J. Pharm. Sci. 2017, 96, 598–609. [Google Scholar]
- Sjögren, E.; Thörn, H.; Tannergren, C. Reply to “Comment on ‘In Silico Modeling of Gastrointestinal Drug Absorption: Predictive Performance of Three Physiologically Based Absorption Models’”. Mol. Pharm. 2017, 14, 340–343. [Google Scholar]
- Li, M.; Zhao, P.; Pan, Y.; Wagner, C. Predictive Performance of Physiologically Based Pharmacokinetic Models for the Effect of Food on Oral Drug Absorption: Current Status. CPT Pharmacomet. Syst. Pharmacol. 2018, 7, 82–89. [Google Scholar]
- Dodd, S.; Kollipara, S.; Sanchez-Felix, M.; Kim, H.; Meng, Q.; Beato, S.; Heimbach, T. Prediction of ARA/PPI Drug-Drug Interactions at the Drug Discovery and Development Interface. J. Pharm. Sci. 2019, 108, 87–101. [Google Scholar]
- Mooney, K.G.; Mintun, M.A.; Himmelstein, K.J.; Stella, V.J. Dissolution kinetics of carboxylic acids I: Effect of pH under unbuffered conditions. J. Pharm. Sci. 1981, 70, 13–22. [Google Scholar]
- Ozturk, S.S.; Palsson, B.O.; Dressman, J.B. Dissolution of ionizable drugs in buffered and unbuffered solutions. Pharm. Res. 1988, 5, 272–282. [Google Scholar]
- Pudipeddi, M.; Zannou, E.A.; Vasanthavada, M.; Dontabhaktuni, A.; Royce, A.E.; Joshi, Y.M.; Serajuddin, A.T. Measurement of surface pH of pharmaceutical solids: A critical evaluation of indicator dye-sorption method and its comparison with slurry pH method. J. Pharm. Sci. 2008, 97, 1831–1842. [Google Scholar]
- Serajuddin, A.T.; Jarowski, C.I. Effect of diffusion layer pH and solubility on the dissolution rate of pharmaceutical bases and their hydrochloride salts. I: Phenazopyridine. J. Pharm. Sci. 1985, 74, 142–147. [Google Scholar]
- Johnson, K.C. Dissolution and absorption modeling: Model expansion to simulate the effects of precipitation, water absorption, longitudinally changing intestinal permeability, and controlled release on drug absorption. Drug Dev. Ind. Pharm. 2003, 29, 833–842. [Google Scholar]
- Sugano, K. Computational oral absorption simulation of free base drugs. Int. J. Pharm. 2010, 398, 73–82. [Google Scholar]
- Serajuddin, A.T. Salt formation to improve drug solubility. Adv. Drug Deliv. Rev. 2007, 59, 603–616. [Google Scholar]
- Sugano, K. A simulation of oral absorption using classical nucleation theory. Int. J. Pharm. 2009, 378, 142–145. [Google Scholar]
- Koyama, H.; Ito, M.; Terada, K.; Sugano, K. Effect of Seed Particles on Precipitation of Weak Base Drugs in Physiological Intestinal Conditions. Mol. Pharm. 2016, 13, 2711–2717. [Google Scholar]
- Oki, J.; Watanabe, D.; Uekusa, T.; Sugano, K. Mechanism of Supersaturation Suppression in Dissolution Process of Acidic Drug Salt. Mol. Pharm. 2019, 16, 1669–1677. [Google Scholar]
- Omori, M.; Uekusa, T.; Oki, J.; Inoue, D.; Sugano, K. Solution-mediated phase transformation at particle surface during cocrystal dissolution. J. Drug Deliv. Sci. Technol. 2020, 56, 101566. [Google Scholar]
- Uekusa, T.; Oki, J.; Omori, M.; Watanabe, D.; Inoue, D.; Sugano, K. Effect of buffer capacity on dissolution and supersaturation profiles of pioglitazone hydrochloride. J. Drug Deliv. Sci. Technol. 2019, 55, 101492. [Google Scholar]
- Uekusa, T.; Sugano, K. Effect of buffer capacity on dissolution and supersaturation profiles of poorly soluble drug salt. In Proceedings of the APSTJ Annual Meeting, Toyama, Japan, 16–18 May 2019; p. 236. [Google Scholar]
- Akiyama, Y.; Kimoto, T.; Mukumoto, H.; Miyake, S.; Ito, S.; Taniguchi, T.; Nomura, Y.; Matsumura, N.; Fujita, T.; Sugano, K. Prediction Accuracy of Mechanism-Based Oral Absorption Model for Dogs. J. Pharm. Sci. 2019, 108, 2728–2736. [Google Scholar]
- Matsumura, N.; Hayashi, S.; Akiyama, Y.; Ono, A.; Funaki, S.; Tamura, N.; Kimoto, T.; Jiko, M.; Haruna, Y.; Sarashina, A.; et al. Prediction Characteristics of Oral Absorption Simulation Software Evaluated Using Structurally Diverse Low-Solubility Drugs. J. Pharm. Sci. 2020, 109, 1403–1416. [Google Scholar]
- Sugano, K. Fraction of a dose absorbed estimation for structurally diverse low solubility compounds. Int. J. Pharm. 2011, 405, 79–89. [Google Scholar]
- Vertzoni, M.; Pastelli, E.; Psachoulias, D.; Kalantzi, L.; Reppas, C. Estimation of intragastric solubility of drugs: In what medium? Pharm. Res. 2007, 24, 909–917. [Google Scholar]
- Sugano, K. Calculation of fraction of dose absorbed: Comparison between analytical solution based on one compartment steady state concentration approximation and dynamic seven compartment model. CBI J. 2009, 9, 75–93. [Google Scholar]
- Grimm, M.; Koziolek, M.; Kühn, J.P.; Weitschies, W. Interindividual and intraindividual variability of fasted state gastric fluid volume and gastric emptying of water. Eur. J. Pharm. Biopharm. 2018, 127, 309–317. [Google Scholar]
- Grimm, M.; Scholz, E.; Koziolek, M.; Kühn, J.P.; Weitschies, W. Gastric Water Emptying under Fed State Clinical Trial Conditions Is as Fast as under Fasted Conditions. Mol. Pharm. 2017, 14, 4262–4271. [Google Scholar]
- Koziolek, M.; Grimm, M.; Garbacz, G.; Kühn, J.P.; Weitschies, W. Intragastric volume changes after intake of a high-caloric, high-fat standard breakfast in healthy human subjects investigated by MRI. Mol. Pharm. 2014, 11, 1632–1639. [Google Scholar]
- McConnell, E.L.; Fadda, H.M.; Basit, A.W. Gut instincts: Explorations in intestinal physiology and drug delivery. Int. J. Pharm. 2008, 364, 213–226. [Google Scholar]
- Mudie, D.M.; Amidon, G.L.; Amidon, G.E. Physiological parameters for oral delivery and in vitro testing. Mol. Pharm. 2010, 7, 1388–1405. [Google Scholar]
- Shingaki, T.; Takashima, T.; Wada, Y.; Tanaka, M.; Kataoka, M.; Ishii, A.; Shigihara, Y.; Sugiyama, Y.; Yamashita, S.; Watanabe, Y. Imaging of gastrointestinal absorption and biodistribution of an orally administered probe using positron emission tomography in humans. Clin. Pharmacol. Ther. 2012, 91, 653–659. [Google Scholar]
- Ehrlein, H.J.; Pröve, J. Effect of viscosity of test meals on gastric emptying in dogs. Q. J. Exp. Physiol. 1982, 67, 419–425. [Google Scholar]
- Gupta, P.K.; Robinson, J.R. Gastric emptying of liquids in the fasted dog. Int. J. Pharm. 1988, 43, 45–52. [Google Scholar]
- Mizuta, H.; Kawazoe, Y.; Haga, K.; Ogawa, K. Effects of meals on gastric emptying and small intestinal transit times of a suspension in the beagle dog assessed using acetaminophen and salicylazosulfapyridine as markers. Chem. Pharm. Bull. 1990, 38, 2224–2227. [Google Scholar]
- Wyse, C.A.; McLellan, J.; Dickie, A.M.; Sutton, D.G.; Preston, T.; Yam, P.S. A review of methods for assessment of the rate of gastric emptying in the dog and cat: 1898–2002. J. Vet. Intern. Med. 2003, 17, 609–621. [Google Scholar]
- Wang, C.; Zhai, B.; Guo, H.; Wang, P.; Liu, Z.; Gu, H.; Ho, H.; Langguth, P.; Li, K.; Wang, C.; et al. In vivo measurement of gastric fluid volume in anesthetized dogs. J. Drug Deliv. Sci. Technol. 2020, 55, 101488. [Google Scholar]
- Martinez, M.N.; Papich, M.G. Factors influencing the gastric residence of dosage forms in dogs. J. Pharm. Sci. 2009, 98, 844–860. [Google Scholar]
- Wu, Y.; Loper, A.; Landis, E.; Hettrick, L.; Novak, L.; Lynn, K.; Chen, C.; Thompson, K.; Higgins, R.; Batra, U.; et al. The role of biopharmaceutics in the development of a clinical nanoparticle formulation of MK-0869: A Beagle dog model predicts improved bioavailability and diminished food effect on absorption in human. Int. J. Pharm. 2004, 285, 135–146. [Google Scholar]
- Zollers, B.; Rhodes, L.; Heinen, E. Capromorelin oral solution (ENTYCE®) increases food consumption and body weight when administered for 4 consecutive days to healthy adult Beagle dogs in a randomized, masked, placebo controlled study. BMC Vet. Res. 2017, 13, 10. [Google Scholar]
- Dressman, J.B.; Berardi, R.R.; Dermentzoglou, L.C.; Russell, T.L.; Schmaltz, S.P.; Barnett, J.L.; Jarvenpaa, K.M. Upper gastrointestinal (GI) pH in young, healthy men and women. Pharm. Res. 1990, 7, 756–761. [Google Scholar]
- Fletcher, J.; Wirz, A.; Young, J.; Vallance, R.; McColl, K.E. Unbuffered highly acidic gastric juice exists at the gastroesophageal junction after a meal. Gastroenterology 2001, 121, 775–783. [Google Scholar]
- Dressman, J.B. Comparison of canine and human gastrointestinal physiology. Pharm. Res. 1986, 3, 123–131. [Google Scholar]
- Sagawa, K.; Li, F.; Liese, R.; Sutton, S.C. Fed and fasted gastric pH and gastric residence time in conscious beagle dogs. J. Pharm. Sci. 2009, 98, 2494–2500. [Google Scholar]
- Akimoto, M.; Nagahata, N.; Furuya, A.; Fukushima, K.; Higuchi, S.; Suwa, T. Gastric pH profiles of beagle dogs and their use as an alternative to human testing. Eur. J. Pharm. Biopharm. 2000, 49, 99–102. [Google Scholar]
- Koziolek, M.; Grimm, M.; Bollmann, T.; Schäfer, K.J.; Blattner, S.M.; Lotz, R.; Boeck, G.; Weitschies, W. Characterization of the GI transit conditions in Beagle dogs with a telemetric motility capsule. Eur. J. Pharm. Biopharm. 2019, 136, 221–230. [Google Scholar]
- Polentarutti, B.; Albery, T.; Dressman, J.; Abrahamsson, B. Modification of gastric pH in the fasted dog. J. Pharm. Pharmacol. 2010, 62, 462–469. [Google Scholar]
- Castell, D.; Bagin, R.; Goldlust, B.; Major, J.; Hepburn, B. Comparison of the effects of immediate-release omeprazole powder for oral suspension and pantoprazole delayed-release tablets on nocturnal acid breakthrough in patients with symptomatic gastro-oesophageal reflux disease. Aliment. Pharmacol. Ther. 2005, 21, 1467–1474. [Google Scholar]
- Miner, P.B., Jr.; Allgood, L.D.; Grender, J.M. Comparison of gastric pH with omeprazole magnesium 20.6 mg (Prilosec OTC) o.m. famotidine 10 mg (Pepcid AC) b.d. and famotidine 20 mg b.d. over 14 days of treatment. Aliment. Pharmacol. Ther. 2007, 25, 103–109. [Google Scholar]
- Kalantzi, L.; Persson, E.; Polentarutti, B.; Abrahamsson, B.; Goumas, K.; Dressman, J.B.; Reppas, C. Canine intestinal contents vs. simulated media for the assessment of solubility of two weak bases in the human small intestinal contents. Pharm. Res. 2006, 23, 1373–1381. [Google Scholar]
- Takano, R.; Sugano, K.; Higashida, A.; Hayashi, Y.; Machida, M.; Aso, Y.; Yamashita, S. Oral absorption of poorly water-soluble drugs: Computer simulation of fraction absorbed in humans from a miniscale dissolution test. Pharm. Res. 2006, 23, 1144–1156. [Google Scholar]
- Chiou, W.L.; Jeong, H.Y.; Chung, S.M.; Wu, T.C. Evaluation of using dog as an animal model to study the fraction of oral dose absorbed of 43 drugs in humans. Pharm. Res. 2000, 17, 135–140. [Google Scholar]
- Mitra, A.; Kesisoglou, F.; Beauchamp, M.; Zhu, W.; Chiti, F.; Wu, Y. Using absorption simulation and gastric pH modulated dog model for formulation development to overcome achlorhydria effect. Mol. Pharm. 2011, 8, 2216–2223. [Google Scholar]
- Pepin, X.J.H.; Moir, A.J.; Mann, J.C.; Sanderson, N.J.; Barker, R.; Meehan, E.; Plumb, A.P.; Bailey, G.R.; Murphy, D.S.; Krejsa, C.M.; et al. Bridging in vitro dissolution and in vivo exposure for acalabrutinib. Part II. A mechanistic PBPK model for IR formulation comparison, proton pump inhibitor drug interactions, and administration with acidic juices. Eur. J. Pharm. Biopharm. 2019, 142, 435–448. [Google Scholar]
- Ono, A.; Matsumura, N.; Kimoto, T.; Akiyama, Y.; Funaki, S.; Tamura, N.; Hayashi, S.; Kojima, Y.; Fushimi, M.; Sudaki, H.; et al. Harmonizing solubility measurement to lower inter-laboratory variance—Progress of consortium of biopharmaceutical tools (CoBiTo) in Japan. ADMET DMPK 2019, 7, 183. [Google Scholar]
- Vogt, M.; Kunath, K.; Dressman, J.B. Dissolution improvement of four poorly water soluble drugs by cogrinding with commonly used excipients. Eur. J. Pharm. Biopharm. 2008, 68, 330–337. [Google Scholar]
- Andersson, S.B.E.; Alvebratt, C.; Bevernage, J.; Bonneau, D.; da Costa Mathews, C.; Dattani, R.; Edueng, K.; He, Y.; Holm, R.; Madsen, C.; et al. Interlaboratory Validation of Small-Scale Solubility and Dissolution Measurements of Poorly Water-Soluble Drugs. J. Pharm. Sci. 2016, 105, 2864–2872. [Google Scholar]
- Parrott, N.; Lukacova, V.; Fraczkiewicz, G.; Bolger, M.B. Predicting pharmacokinetics of drugs using physiologically based modeling—Application to food effects. AAPS J. 2009, 11, 45–53. [Google Scholar]
- Takano, R.; Furumoto, K.; Shiraki, K.; Takata, N.; Hayashi, Y.; Aso, Y.; Yamashita, S. Rate-limiting steps of oral absorption for poorly water-soluble drugs in dogs; prediction from a miniscale dissolution test and a physiologically-based computer simulation. Pharm. Res. 2008, 25, 2334–2344. [Google Scholar]
- Gesenberg, C.; Mathias, N.R.; Xu, Y.; Crison, J.; Savant, I.; Saari, A.; Good, D.J.; Hemenway, J.N.; Narang, A.S.; Schartman, R.R.; et al. Utilization of In Vitro, In Vivo and In Silico Tools to Evaluate the pH-Dependent Absorption of a BCS Class II Compound and Identify a pH-Effect Mitigating Strategy. Pharm. Res. 2019, 36, 164. [Google Scholar]
- Fagerberg, J.H.; Tsinman, O.; Sun, N.; Tsinman, K.; Avdeef, A.; Bergstrom, C.A. Dissolution rate and apparent solubility of poorly soluble drugs in biorelevant dissolution media. Mol. Pharm. 2010, 7, 1419–1430. [Google Scholar]
- Bloomer, J.C.; Ambery, C.; Miller, B.E.; Connolly, P.; Garden, H.; Henley, N.; Hodnett, N.; Keel, S.; Kreindler, J.L.; Lloyd, R.S.; et al. Identification and characterisation of a salt form of Danirixin with reduced pharmacokinetic variability in patient populations. Eur. J. Pharm. Biopharm. 2017, 117, 224–231. [Google Scholar]
- Dasatinib Drug Information. Available online: https://www.info.pmda.go.jp/go/pack/4291020F1027_1_15/ (accessed on 9 August 2020).
- Vaidhyanathan, S.; Wang, X.; Crison, J.; Varia, S.; Gao, J.Z.H.; Saxena, A.; Good, D. Bioequivalence Comparison of Pediatric Dasatinib Formulations and Elucidation of Absorption Mechanisms Through Integrated PBPK Modeling. J. Pharm. Sci. 2019, 108, 741–749. [Google Scholar]
- Avdeef, A. Absorption and Drug Development: Solubility, Permeability, and Charge State, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Ross, D.L.; Riley, C.M. Aqueous solubilities of some variously substituted quinolone antimicrobials. Int. J. Pharm. 1990, 63, 237–250. [Google Scholar]
- Völgyi, G.; Vizserálek, G.; Takács-Novák, K.; Avdeef, A.; Tam, K.Y. Predicting the exposure and antibacterial activity of fluoroquinolones based on physicochemical properties. Eur. J. Pharm. Sci. 2012, 47, 21–27. [Google Scholar]
- Okumu, A.; DiMaso, M.; Löbenberg, R. Computer simulations using GastroPlus to justify a biowaiver for etoricoxib solid oral drug products. Eur. J. Pharm. Biopharm. 2009, 72, 91–98. [Google Scholar]
- Wilson, C.G.; O’Mahony, B.; Connolly, S.M.; Cantarini, M.V.; Farmer, M.R.; Dickinson, P.A.; Smith, R.P.; Swaisland, H.C. Do gastrointestinal transit parameters influence the pharmacokinetics of gefitinib? Int. J. Pharm. 2009, 376, 7–12. [Google Scholar]
- de Zwart, L.; Snoeys, J.; De Jong, J.; Sukbuntherng, J.; Mannaert, E.; Monshouwer, M. Ibrutinib Dosing Strategies Based on Interaction Potential of CYP3A4 Perpetrators Using Physiologically Based Pharmacokinetic Modeling. Clin. Pharmacol. Ther. 2016, 100, 548–557. [Google Scholar]
- Shi, X.; Song, S.; Ding, Z.; Fan, B.; Xu, T.; Huang, W. Improving the Solubility and Dissolution of Ibrutinib by Preparing Solvates. J. Pharm. Innov. 2019. [Google Scholar]
- Palbociclib PMDA Approval Document. Available online: https://www.pmda.go.jp/drugs/2017/P20170830001/ (accessed on 9 August 2020).
- Ibrahim, F.M.L.; Mullarney, M.P.; Shanker, R.M.; Spong, B.R.; Wang, J. Solid Dosage Forms of. Palbociclib. Patent WO2016193860A1, 8 December 2016. [Google Scholar]
- Sun, W.; Klamerus, K.J.; Yuhas, L.M.; Pawlak, S.; Plotka, A.; O’Gorman, M.; Kirkovsky, L.; Kosa, M.; Wang, D. Impact of Acid-Reducing Agents on the Pharmacokinetics of Palbociclib, a Weak Base With pH-Dependent Solubility, With Different Food Intake Conditions. Clin. Pharmacol. Drug Dev. 2017, 6, 614–626. [Google Scholar]
- Brouwers, J.; Pauwels, H.; Augustijns, P. In vitro evaluation of intestinal precipitation as a rate-limiting factor in fasted state absorption of posaconazole. In Proceedings of the AAPS Annual Meeting and Exposition, Washington, DC, USA, 23–27 October 2011. [Google Scholar]
- Hens, B.; Pathak, S.M.; Mitra, A.; Patel, N.; Liu, B.; Patel, S.; Jamei, M.; Brouwers, J.; Augustijns, P.; Turner, D.B. In Silico Modeling Approach for the Evaluation of Gastrointestinal Dissolution, Supersaturation, and Precipitation of Posaconazole. Mol. Pharm. 2017, 14, 4321–4333. [Google Scholar]
- Fossati, L.; Dechaume, R.; Hardillier, E.; Chevillon, D.; Prevost, C.; Bolze, S.; Maubon, N. Use of simulated intestinal fluid for Caco-2 permeability assay of lipophilic drugs. Int. J. Pharm. 2008, 360, 148–155. [Google Scholar]
- Jantratid, E.; Janssen, N.; Reppas, C.; Dressman, J.B. Dissolution media simulating conditions in the proximal human gastrointestinal tract: An update. Pharm. Res. 2008, 25, 1663–1676. [Google Scholar]
- Higashino, H.; Hasegawa, T.; Yamamoto, M.; Matsui, R.; Masaoka, Y.; Kataoka, M.; Sakuma, S.; Yamashita, S. In vitro-in vivo correlation of the effect of supersaturation on the intestinal absorption of BCS Class 2 drugs. Mol. Pharm. 2014, 11, 746–754. [Google Scholar]
- Psachoulias, D.; Vertzoni, M.; Butler, J.; Busby, D.; Symillides, M.; Dressman, J.; Reppas, C. An in vitro methodology for forecasting luminal concentrations and precipitation of highly permeable lipophilic weak bases in the fasted upper small intestine. Pharm. Res. 2012, 29, 3486–3498. [Google Scholar]
- Psachoulias, D.; Vertzoni, M.; Goumas, K.; Kalioras, V.; Beato, S.; Butler, J.; Reppas, C. Precipitation in and supersaturation of contents of the upper small intestine after administration of two weak bases to fasted adults. Pharm. Res. 2011, 28, 3145–3158. [Google Scholar]
- Frank, K.J.; Locher, K.; Zecevic, D.E.; Fleth, J.; Wagner, K.G. In vivo predictive mini-scale dissolution for weak bases: Advantages of pH-shift in combination with an absorptive compartment. Eur. J. Pharm. Sci. 2014, 61, 32–39. [Google Scholar]
- Hate, S.S.; Reutzel-Edens, S.M.; Taylor, L.S. Absorptive Dissolution Testing of Supersaturating Systems: Impact of Absorptive Sink Conditions on Solution Phase Behavior and Mass Transport. Mol. Pharm. 2017, 14, 4052–4063. [Google Scholar]
- Shi, Y.; Erickson, B.; Jayasankar, A.; Lu, L.; Marsh, K.; Menon, R.; Gao, P. Assessing Supersaturation and Its Impact on In Vivo Bioavailability of a Low-Solubility Compound ABT-072 With a Dual pH, Two-Phase Dissolution Method. J. Pharm. Sci. 2016, 105, 2886–2895. [Google Scholar]
- Yeap, Y.Y.; Lock, J.; Lerkvikarn, S.; Semin, T.; Nguyen, N.; Carrier, R.L. Intestinal mucus is capable of stabilizing supersaturation of poorly water-soluble drugs. J. Controll. Release 2019, 296, 107–113. [Google Scholar]
- Kambayashi, A.; Yasuji, T.; Dressman, J.B. Prediction of the precipitation profiles of weak base drugs in the small intestine using a simplified transfer (“dumping”) model coupled with in silico modeling and simulation approach. Eur. J. Pharm. Biopharm. 2016, 103, 95–103. [Google Scholar]
- Tokumura, T.; Tsushima, Y.; Tatsuishi, K.; Kayano, M.; Machida, Y.; Nagai, T. Evaluation of bioavailability upon oral administration of cinnarizine-beta-cyclodextrin inclusion complex to beagle dogs. Chem. Pharm. Bull. 1985, 33, 2962–2967. [Google Scholar]
- Hens, B.; Brouwers, J.; Corsetti, M.; Augustijns, P. Supersaturation and Precipitation of Posaconazole upon Entry in the Upper Small Intestine in Humans. J. Pharm. Sci. 2016, 105, 2677–2684. [Google Scholar]
| Parameters | Human | Dog | ||
|---|---|---|---|---|
| Fasted | Fed | Fasted | Fed | |
| Stomach 1 | ||||
| Initial gastric pH, pHSTini (normal/ with ARA) | 2.0/6.0 | 2.7/6.0 | 2.0/6.0 | 2.0/6.0 |
| Gastric emptying half-life, TST1/2 (min) 2 | 10 | 60 | 10 | 180 |
| Gastric fluid volume, VST (mL) | 125 | 250 | 50 | 250 |
| Small intestine 3 | ||||
| Small intestinal pH | 6.5 | 6.0 | 7.0 | 6.0 |
| Small intestinal bile micelle concentration, Cbm (mM) | 3.0 | 15 | 5.0 | 18 |
| Small intestinal transit time, TSI (min) | 210 | 210 | 120 | 120 |
| Small intestinal fluid volume, VSI (mL) | 130 | 156 | 19 | 22 |
| Plicate expansion, PE | 3 | 3 | 1 | 1 |
| Villi expansion, VE | 10 | 10 | 10 | 10 |
| Radius of small intestine, RGI (cm) | 1.5 | 1.5 | 0.5 | 0.5 |
| Degree of flatness, DF | 1.7 | 1.7 | 1.7 | 1.7 |
| Paracellular radius, RParaMW | 8.46 | 8.46 | 12.9 | 12.9 |
| Unstirred water layer thickness, hUWL (cm) | 0.03 | 0.03 | 0.03 | 0.03 |
| Particle-drifting coefficient, Cpd | 2.2 | 2.2 | 2.2 | 2.2 |
| Nominal pore radius, Rmucus (μm) | 2.9 | 2.9 | 2.9 | 2.9 |
| Drugs | MW | pKa | logPoct | Solubility (mg/mL) | Ref. | ||
|---|---|---|---|---|---|---|---|
| Buffer 3 | FaSSIF 4 | FeSSIF 4 | |||||
| Acalabrutinib | 466 | 5.8 | 2.0 | 0.048 (pH 8.0) | 0.12 5 | [66] | |
| Albendazole | 265 | 4.2 | 3.1 | 0.0009 | 0.0021 | [67,68] | |
| Aprepitant | 534 | 4.2 | 4.8 | 0.0008 | 0.019, 0.021 7 | 0.119 | [69,70,71] |
| BMS | 550 | 6.3 | 2.3 | 0.019 (pH 6.6) | 0.043 | [72] | |
| Cinnarizine | 369 | 7.5 | 5.7 | 0.0014 | 0.013 | 0.112 | [73] |
| Danixirin | 442 | 4.8 | 1.2 1 | 0.004 (pH 6.0) | 0.009 | [74] | |
| Dasatinib | 488 | 6.8 | 3.2 | 0.01 (pH 6.0) | 0.032 | [75,76] | |
| Dipyridamole | 505 | 4.9 | 3.9 | 0.006 | 0.017 | [63,77] | |
| Enoxacin | 320 | 6.2 | −0.2 2 | 0.38 | 0.54 5 | 0.83 (pH 5.8) 5 | [20,78,79] |
| Etoricoxib | 359 | 4.6 | 3.1 | 0.16 | 0.16 | [80] | |
| Gefitinib | 447 | 7.2 | 4.1 | 0.002 (pH 6.9) | 0.085 (pH 6.4) | 2.0 (pH 5.4) | [81] |
| Iburtinib | 441 | 3.8 | 4.0 | 0.0021 (pH 6.8) | 0.016 (pH 7.0) | [82,83] | |
| Ketoconazole | 531 | 6.5 | 4.3 | 0.012 | 0.021 | [63] | |
| Palbociclib | 448 | 7.4 | 1.3 2 | 0.009 (pH 7.9) 6 | [84,85,86] | ||
| Posaconazole | 701 | 4.6 | 5.4 | 0.0001 | 0.005 | [87,88] | |
| Drugs | Physiological Condition | Dose (mg) | d (μm) | Predicted | Observed | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Fa | AUCr | FaFdST% | Fa | AUCr | ||||||
| (A) 1 | (B) 1 | (C) 1 | (C) 1 | (C) 1,2 | ||||||
| Acalabrutinib | Human, Fasted | 100 | 98 | 0.54 | 1.00 | 0.94 | 88% (DRL) | |||
| Human, Fasted, ARA | 100 | 98 | 0.54 | 0.57 | 0.56 | 0.60 | 6% (SL) | 0.56 | ||
| Albendazole | Human, Fasted | 350 | 3.4 | 0.10 | 0.14 | 0.14 | 32% (SL) | 0.11 | ||
| Human, Fasted | 400 | 3.4 | 0.09 | 0.13 | 0.13 | 30% (SL) | 0.06 | |||
| Human, Fed | 400 | 3.4 | 0.18 | 0.19 | 0.19 | 8% (SL) | 0.29 | |||
| Human, Fasted | 700 | 3.4 | 0.08 | 0.10 | 0.10 | 23% (SL) | 0.06 | |||
| Human, Fasted | 800 | 3.4 | 0.07 | 0.09 | 0.09 | 22% (SL) | 0.10 | |||
| Human, Fasted | 1400 | 3.4 | 0.05 | 0.07 | 0.07 | 17% (SL) | 0.04 | |||
| Human, Fasted, ARA | 1400 | 3.4 | 0.05 | 0.05 | 0.05 | 0.83 | 0% (SL) | 0.03 | 0.72 | |
| Human, Fasted | 2100 | 3.4 | 0.04 | 0.05 | 0.05 | 15% (SL) | 0.03 | |||
| Aprepitant | Human, Fasted | 40 | 0.12 | 1.00 | 1.00 | 1.00 | 28% (SL) | 0.90 | ||
| Human, Fasted | 100 | 5.0 | 0.23 | 0.36 | 0.35 | 38% (SL) | 0.22 | |||
| Human, Fasted | 125 | 0.12 | 1.00 | 1.00 | 1.00 | 11% (SL) | 0.79 | |||
| Human, Fasted | 250 | 0.12 | 0.96 | 0.97 | 0.97 | 6% (SL) | 0.86 | |||
| Human, Fasted | 375 | 0.12 | 0.94 | 0.95 | 0.95 | 4% (SL) | 0.67 | |||
| Human, Fasted | 500 | 0.12 | 0.92 | 0.92 | 0.92 | 3% (SL) | 0.83 | |||
| Human, Fed | 125 | 0.12 | 1.00 | 1.00 | 1.00 | 5% (SL) | 1.00 | |||
| Dog, Fasted | 20 | 0.12 | 0.94 | 0.98 | 0.98 | 24% (SL) | 1.00 | |||
| Dog, Fed | 20 | 0.12 | 1.00 | 1.00 | 1.00 | 61% (DRL) | 1.00 | |||
| Dog, Fasted | 20 | 0.48 | 0.54 | 0.72 | 0.72 | 33% (SL) | 0.43 | |||
| Dog, Fasted | 20 | 1.9 | 0.24 | 0.46 | 0.46 | 52% (SL) | 0.31 | |||
| Dog, Fasted | 20 | 2.0 | 0.23 | 0.45 | 0.45 | 53% (SL) | 0.33 | |||
| Dog, Fasted | 20 | 5.0 | 0.14 | 0.37 | 0.37 | 63% (SL) | 0.28 | |||
| Dog, Fasted | 20 | 5.5 | 0.14 | 0.36 | 0.36 | 64% (SL) | 0.24 | |||
| Dog, Fed | 20 | 5.5 | 0.64 | 0.95 | 0.94 | 64% (DRL) | 0.77 | |||
| Dog, Fasted | 20 | 25 | 0.08 | 0.28 | 0.28 | 74% (SL) | 0.18 | |||
| BMS | Human, Fasted | 150 | 3.0 | 0.80 | 1.00 | 1.00 | 82% (DRL) | |||
| Human, Fasted, ARA | 150 | 3.0 | 0.80 | 0.82 | 0.81 | 0.81 | 1% (SL) | 0.43 | ||
| Dog, Fasted | 150 | 40 | 0.08 | 1.00 | 0.70 | 91% (DRL) | ||||
| Dog, Fasted, ARA | 150 | 40 | 0.08 | 0.09 | 0.08 | 0.12 | 5% (SL) | 0.03 | ||
| Cinnarizine | Human, Fasted | 25 | 25 | 0.25 | 0.99 | 0.96 | 98% (DRL) | 0.59 | ||
| Human, Fasted, ARA | 25 | 25 | 0.25 | 0.27 | 0.26 | 0.27 | 1% (SL) | 0.16 | 0.27 | |
| Human, Fasted | 25 | 60 | 0.08 | 0.99 | 0.93 | 99% (DRL) | 0.55 | |||
| Human, Fasted, ARA | 25 | 60 | 0.08 | 0.09 | 0.08 | 0.09 | 2% (SL) | 0.08 | 0.14 | |
| Human, Fasted | 50 | 25 | 0.18 | 0.99 | 0.93 | 96% (DRL) | 0.81 | |||
| Human, Fed | 50 | 25 | 0.38 | 1.00 | 0.92 | 83% (DRL) | 1.00 | |||
| Human, Fasted | 50 | 60 | 0.07 | 0.98 | 0.89 | 99% (DRL) | 0.55 | |||
| Human, Fed | 50 | 60 | 0.19 | 0.98 | 0.82 | 92% (DRL) | 0.95 | |||
| Dog, Fasted | 25 | 25 | 0.05 | 0.96 | 0.87 | 97% (DRL) | 0.54 | |||
| Dog, Fasted, ARA | 25 | 25 | 0.05 | 0.06 | 0.05 | 0.06 | 2% (SL) | 0.03 | 0.05 | |
| Danixirin | Human, Fed | 50 | 2.0 | 0.40 | 0.91 | 0.85 | 70% (DRL) | 0.35 | ||
| Human, Fasted | 100 | 1.8 | 0.23 | 0.90 | 0.83 | 80% (DRL) | 0.71 | |||
| Human, Fasted, ARA | 100 | 1.8 | 0.23 | 0.24 | 0.24 | 0.29 | 2% (SL) | 0.30 | 0.43 | |
| Human, Fed | 100 | 1.8 | 0.28 | 0.75 | 0.66 | 65% (SL) | 0.61 | |||
| Dasatinib | Human, Fasted | 50 | 27 | 0.38 | 1.00 | 0.97 | 94% (DRL) | 0.85 | ||
| Human, Fasted | 70 | 27 | 0.32 | 1.00 | 0.96 | 92% (DRL) | 0.98 | |||
| Human, Fasted | 100 | 27 | 0.26 | 0.99 | 0.93 | 91% (DRL) | 0.90 | |||
| Human, Fasted, ARA | 100 | 27 | 0.26 | 0.27 | 0.26 | 0.28 | 1% (SL) | 0.48 | 0.54 | |
| Dipyridamole | Human, Fasted | 50 | 75 | 0.14 | 0.88 | 0.82 | 95% (DRL) | 0.50 | ||
| Human, Fasted, ARA | 50 | 75 | 0.14 | 0.15 | 0.15 | 0.18 | 5% (DRL) | 0.31 | 0.63 | |
| Dog, Fasted | 50 | 75 | 0.04 | 0.78 | 0.68 | 96% (DRL) | ||||
| Dog, Fasted, ARA | 50 | 75 | 0.04 | 0.05 | 0.05 | 0.07 | 9% (SL) | 0.11 | ||
| Enoxacin | Human, Fasted | 400 | 25 | 0.59 | 0.98 | 0.89 | 57% (DRL) | 1.00 | ||
| Human, Fed | 400 | 25 | 0.81 | 1.00 | 0.99 | 36% (SL) | 1.00 | |||
| Human, Fasted, ARA | 400 | 25 | 0.59 | 0.70 | 0.64 | 0.64 | 11% (SL) | 0.67 | 0.67 | |
| Etoricoxib | Human, Fasted | 120 | 40 | 1.00 | 1.00 | 1.00 | 78% (DRL) | 1.00 | ||
| Human, Fasted, ARA | 120 | 40 | 1.00 | 1.00 | 1.00 | 1.00 | 13% (SL) | 1.00 | 1 | |
| Gefitinib | Human, Fasted | 50 | 30 | 0.49 | 0.99 | 0.96 | 94% (DRL) | 0.74 | ||
| Human, Fasted | 100 | 30 | 0.38 | 0.99 | 0.94 | 89% (DRL) | 0.69 | |||
| Human, Fasted | 250 | 30 | 0.23 | 0.99 | 0.81 | 83% (DRL) | 0.78 | |||
| Human, Fasted, ARA | 250 | 30 | 0.23 | 0.24 | 0.23 | 0.29 | 0% (SL) | 0.41 | 0.53 | |
| Human, Fed | 250 | 30 | 1.00 | 1.00 | 1.00 | 46% (SL) | 0.80 | |||
| Human, Fasted | 500 | 30 | 0.15 | 0.98 | 0.64 | 81% (DRL) | 0.80 | |||
| Ibrutinib | Human, Fasted | 560 | 10 | 0.10 | 0.13 | 0.13 | 21% (SL) | 0.21 | ||
| Human, Fasted, ARA | 560 | 10 | 0.10 | 0.10 | 0.10 | 0.80 | 0% (SL) | 0.18 | 0.87 | |
| Human, Fed | 560 | 10 | 0.39 | 0.40 | 0.40 | 3% (SL) | 0.30 | |||
| Ketoconazole | Human, Fasted | 200 | 25 | 0.26 | 1.00 | 0.90 | 84% (DRL) | 0.72 | ||
| Human, Fasted, ARA | 200 | 25 | 0.26 | 0.27 | 0.26 | 0.29 | 2% (SL) | 0.06 3 | 0.09 3 | |
| Human, Fed | 200 | 25 | 0.59 | 1.00 | 0.92 | 61% (DRL) | 0.56 | |||
| Human, Fasted | 400 | 25 | 0.17 | 1.00 | 0.75 | 83% (DRL) | 0.92 | |||
| Human, Fed | 400 | 25 | 0.42 | 1.00 | 0.74 | 53% (SL) | 1.00 | |||
| Human, Fasted | 800 | 25 | 0.14 | 0.99 | 0.57 | 79% (SL) | 0.86 | |||
| Human, Fed | 800 | 25 | 0.32 | 1.00 | 0.54 | 45% (SL) | 0.87 | |||
| Dog, Fasted | 200 | 25 | 0.06 | 0.99 | 0.62 | 91% (DRL) | ||||
| Dog, Fasted, ARA | 200 | 25 | 0.06 | 0.07 | 0.06 | 0.10 | 3% (SL) | 0.03 | ||
| Palbociclib | Human, Fasted | 125 | 16 | 0.46 | 1.00 | 1.00 | 82% (DRL) | 0.90 | ||
| Human, Fasted, ARA | 125 | 16 | 0.46 | 0.58 | 0.47 | 0.47 | 2% (SL) | 0.47 | 0.52 | |
| Human, Fed | 125 | 16 | 0.81 | 1.00 | 1.00 | 64% (DRL) | 0.95 | |||
| Human, Fed, ARA | 125 | 16 | 0.81 | 0.91 | 0.82 | 0.82 | 2% (SL) | 0.86 | 0.91 | |
| Posaconazole | Human, Fed | 50 | 1.7 | 0.63 | 0.66 | 0.66 | 6% (SL) | 0.57 | ||
| Human, Fed | 100 | 1.7 | 0.57 | 0.59 | 0.59 | 3% (SL) | 0.75 | |||
| Human, Fasted | 200 | 1.7 | 0.08 | 0.11 | 0.11 | 23% (SL) | 0.19 | |||
| Human, Fasted, ARA | 200 | 1.7 | 0.08 | 0.08 | 0.08 | 0.78 | 0% (SL) | 0.18 | 0.93 | |
| Human, Fed | 200 | 1.7 | 0.52 | 0.53 | 0.53 | 2% (SL) | 0.58 | |||
| Human, Fed, ARA | 200 | 1.7 | 0.52 | 0.52 | 0.52 | 0.99 | 0% (SL) | 0.49 | 0.85 | |
| Human, Fasted | 400 | 1.7 | 0.06 | 0.07 | 0.07 | 17% (SL) | 0.14 | |||
| Human, Fasted, ARA | 400 | 1.7 | 0.06 | 0.06 | 0.06 | 0.84 | 0% (SL) | 0.09 | 0.66 | |
| Human, Fed | 400 | 1.7 | 0.46 | 0.46 | 0.46 | 1% (SL) | 0.52 | |||
| Human, Fed | 800 | 1.7 | 0.37 | 0.37 | 0.37 | 1% (SL) | 0.42 | |||
| Human, Fed | 1200 | 1.7 | 0.31 | 0.32 | 0.32 | 1% (SL) | 0.23 | |||
| Dog, Fasted | 100 | 1.7 | 0.05 | 0.07 | 0.07 | 26% (SL) | 0.11 | |||
| Dog, Fed | 100 | 1.7 | 0.29 | 0.37 | 0.37 | 24% (SL) | 0.40 | |||
| Dog, Fed | 400 | 1.7 | 0.14 | 0.16 | 0.16 | 15% (SL) | 0.40 | |||
| Dog, Fed | 800 | 1.7 | 0.08 | 0.10 | 0.10 | 13% (SL) | 0.32 | |||
| Dog, Fed | 1200 | 1.7 | 0.06 | 0.07 | 0.07 | 12% (SL) | 0.24 | |||
| Statistics | Prediction Scenario 1 | ||
|---|---|---|---|
| (A) No Gastric Dissolution | (B) Bulk pH | (C) pHeq/pHsurface | |
| All drug | |||
| N | 85 | 85 | 85 |
| AAFE | 1.85 | 1.41 | 1.40 |
| AFE | 0.64 | 1.10 | 1.04 |
| r2 | 0.47 | 0.83 | 0.79 |
| % within 2-fold error | 64 | 89 | 91 |
| Without posaconazole | |||
| N | 69 | 69 | 69 |
| AAFE | 1.87 | 1.37 | 1.36 |
| AFE | 0.64 | 1.23 | 1.15 |
| r2 | 0.43 | 0.83 | 0.78 |
| % within 2-fold error | 65 | 93 | 94 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsumura, N.; Ono, A.; Akiyama, Y.; Fujita, T.; Sugano, K. Bottom-Up Physiologically Based Oral Absorption Modeling of Free Weak Base Drugs. Pharmaceutics 2020, 12, 844. https://doi.org/10.3390/pharmaceutics12090844
Matsumura N, Ono A, Akiyama Y, Fujita T, Sugano K. Bottom-Up Physiologically Based Oral Absorption Modeling of Free Weak Base Drugs. Pharmaceutics. 2020; 12(9):844. https://doi.org/10.3390/pharmaceutics12090844
Chicago/Turabian StyleMatsumura, Naoya, Asami Ono, Yoshiyuki Akiyama, Takuya Fujita, and Kiyohiko Sugano. 2020. "Bottom-Up Physiologically Based Oral Absorption Modeling of Free Weak Base Drugs" Pharmaceutics 12, no. 9: 844. https://doi.org/10.3390/pharmaceutics12090844
APA StyleMatsumura, N., Ono, A., Akiyama, Y., Fujita, T., & Sugano, K. (2020). Bottom-Up Physiologically Based Oral Absorption Modeling of Free Weak Base Drugs. Pharmaceutics, 12(9), 844. https://doi.org/10.3390/pharmaceutics12090844





