Gellan Gum/Laponite Beads for the Modified Release of Drugs: Experimental and Modeling Study of Gastrointestinal Release
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Rheological Measurements
2.3. Beads Preparation
2.4. Determination of Swelling Degree
2.5. Preparation of Drug Loaded Beads
2.6. Drug Entrapment Efficiency
2.7. In Vitro Release Studies
2.8. Statistics
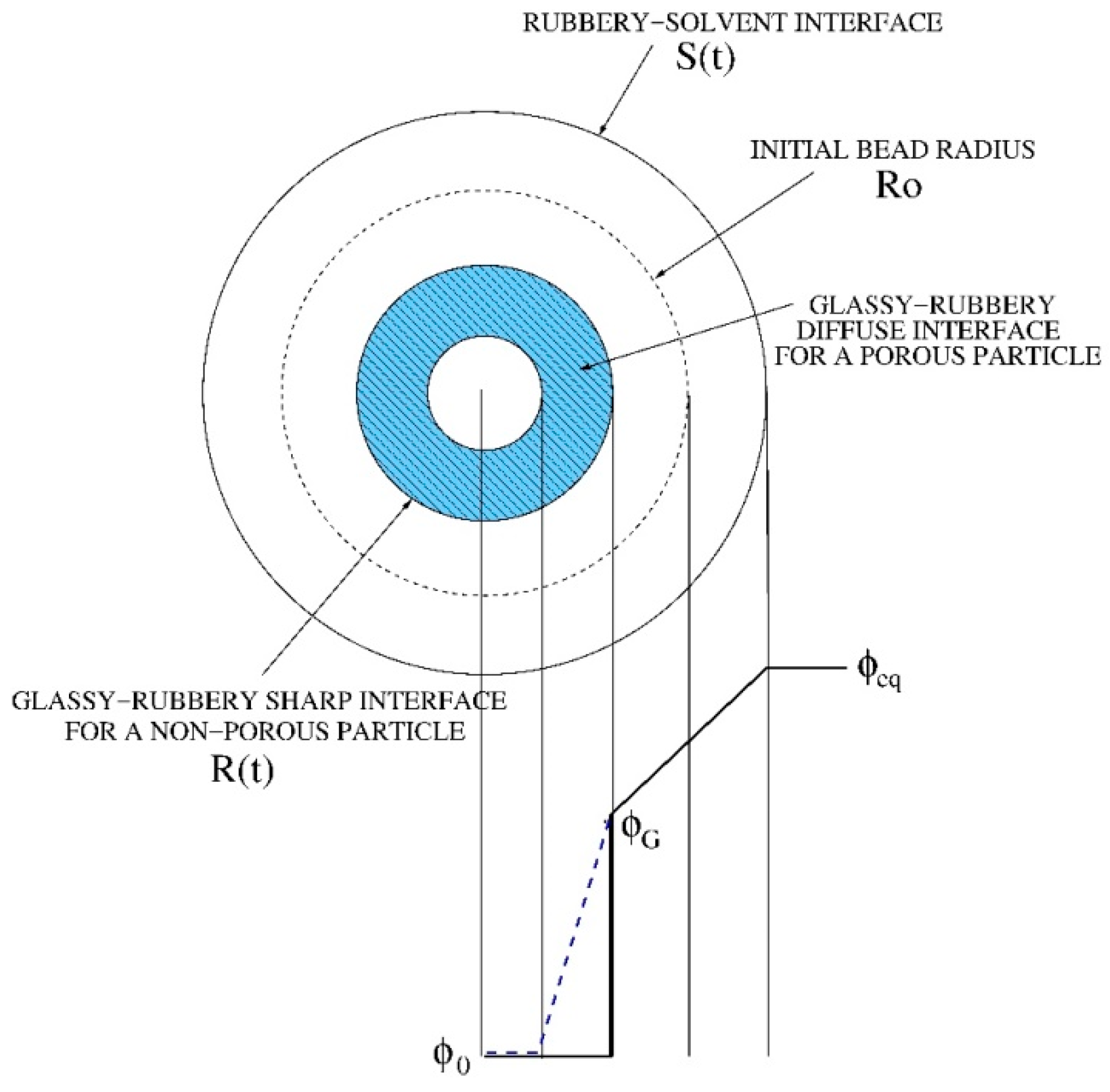
3. Mathematical Modeling of Swelling and Drug release of Highly Porous Beads
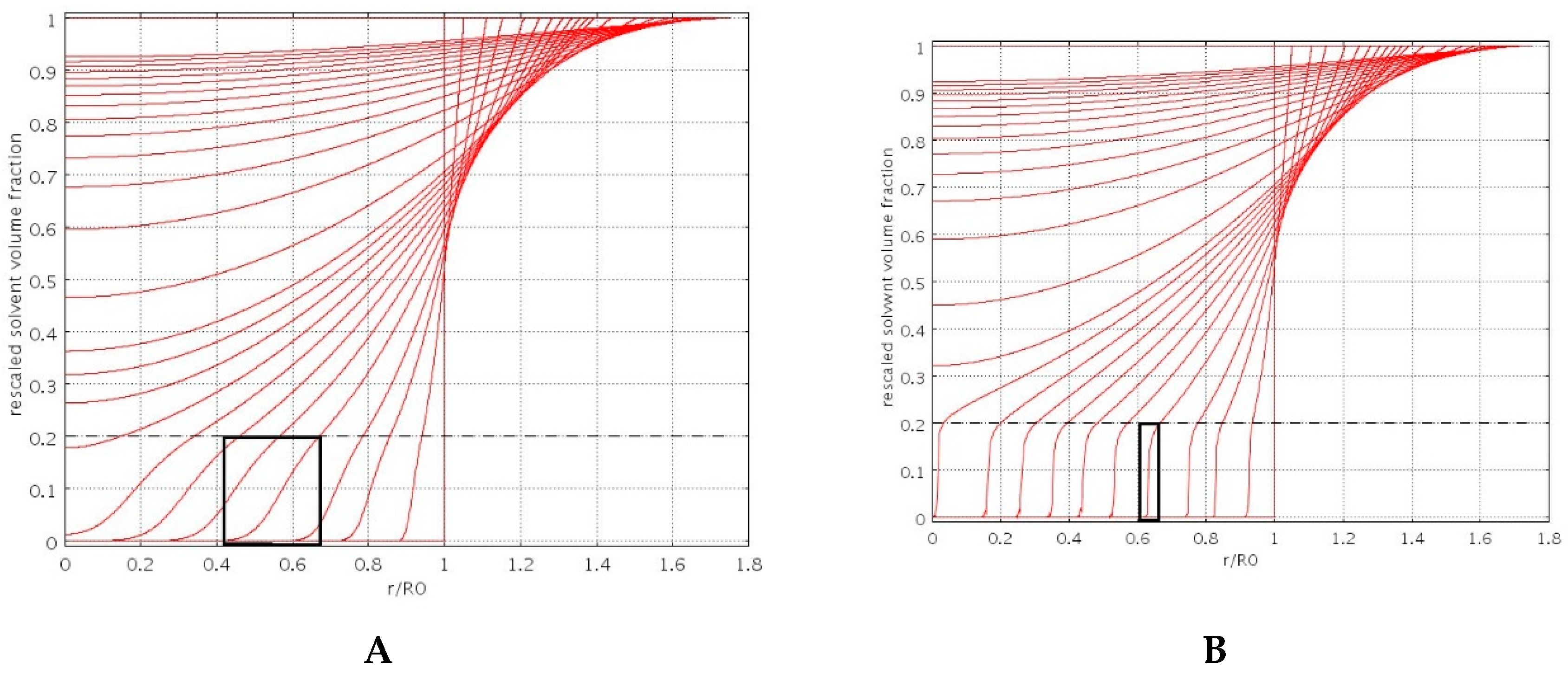
3.1. Swelling Modeling
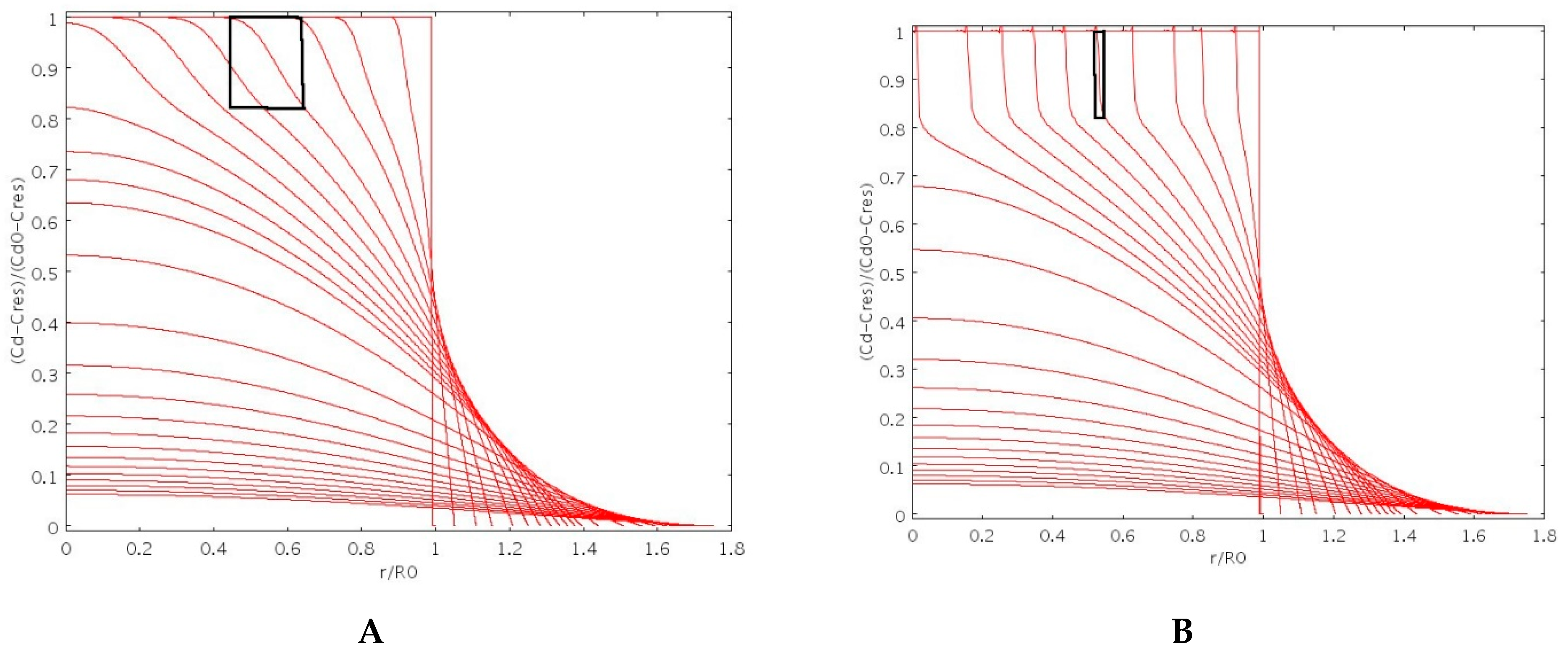
3.2. Drug Release Modeling of No-Interacting Drugs
3.3. Drug Release Modeling of Interacting Drugs
3.4. Numerical Issues
4. Results and Discussion
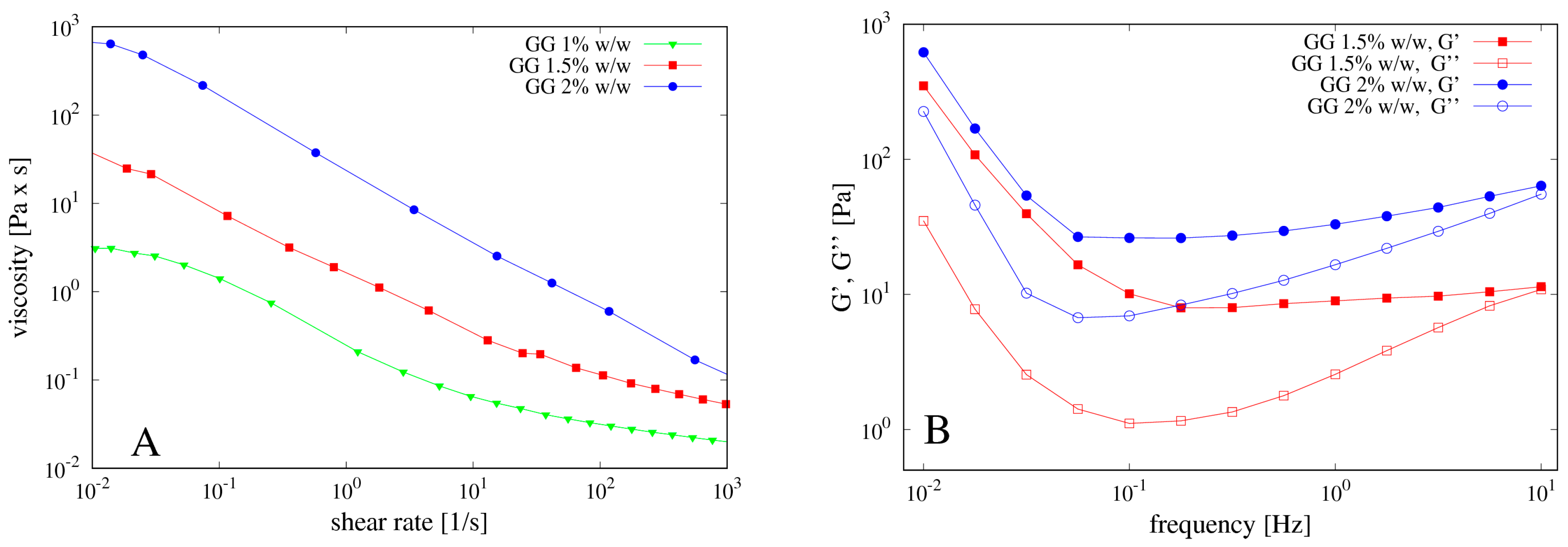
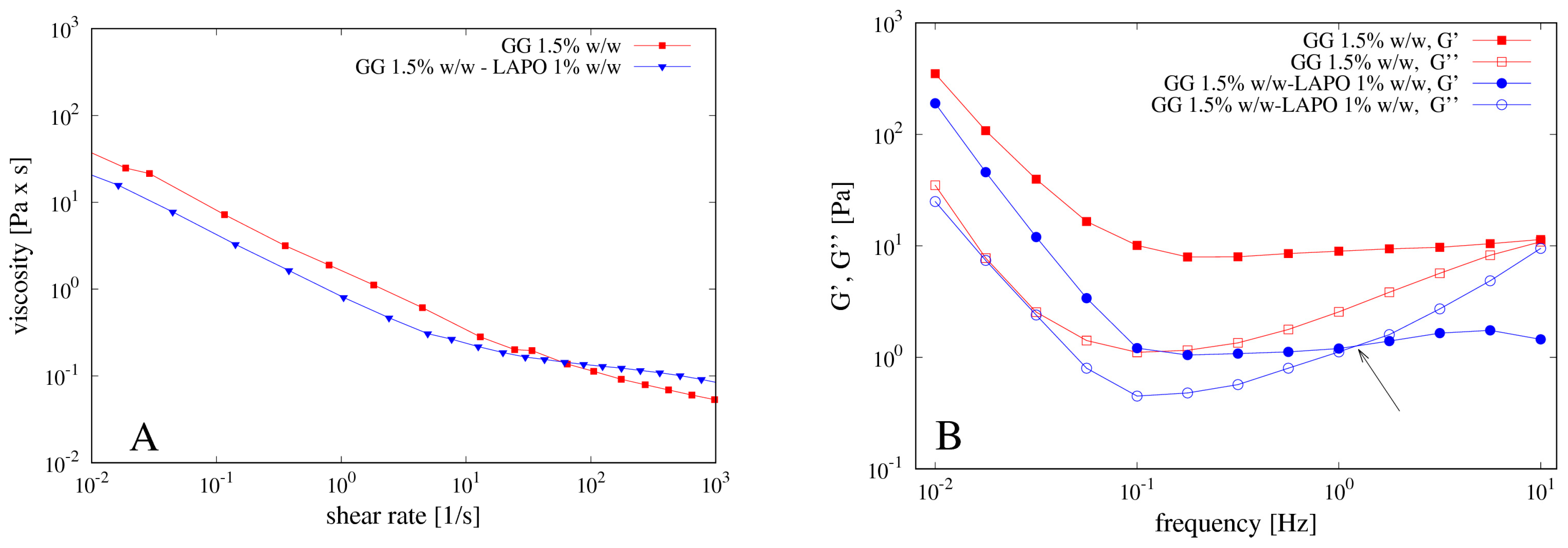
4.1. Rheological Measurements
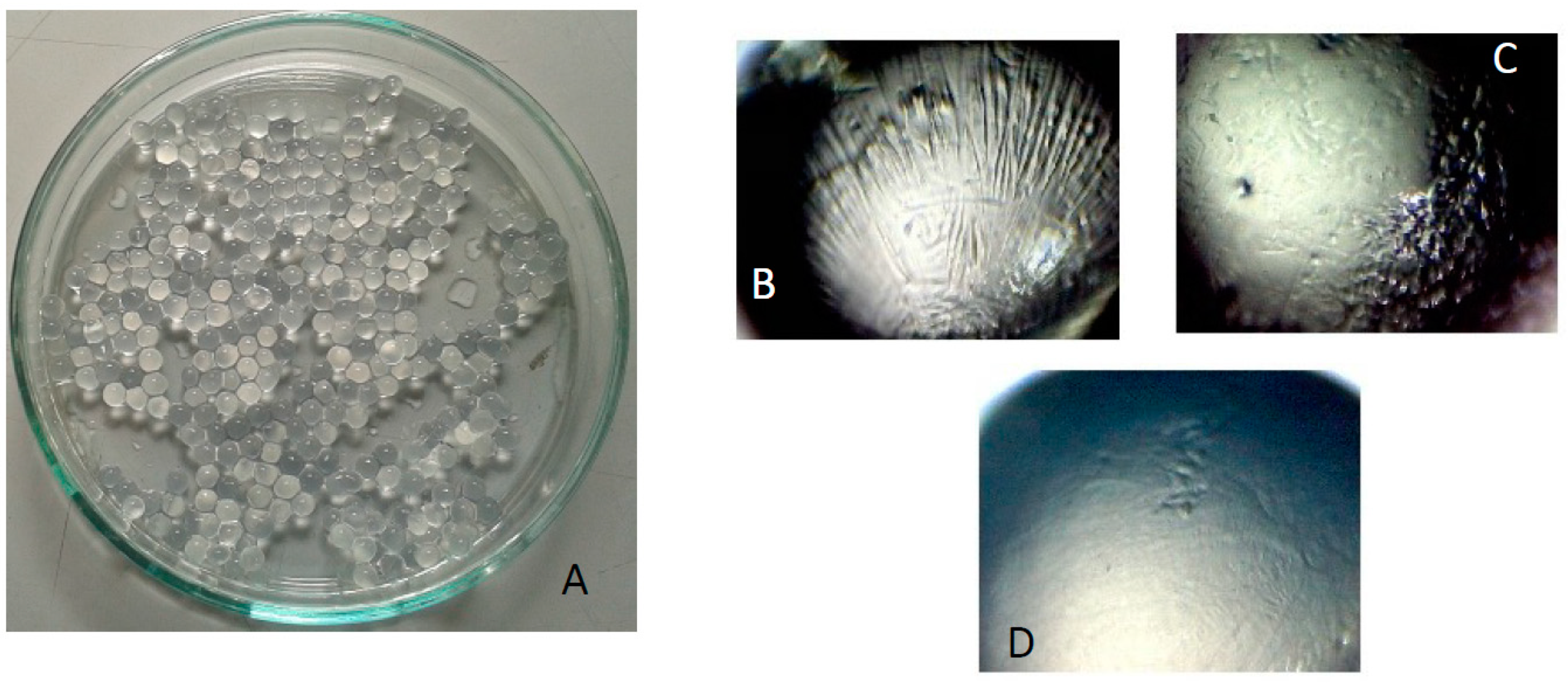
4.2. Beads Preparation
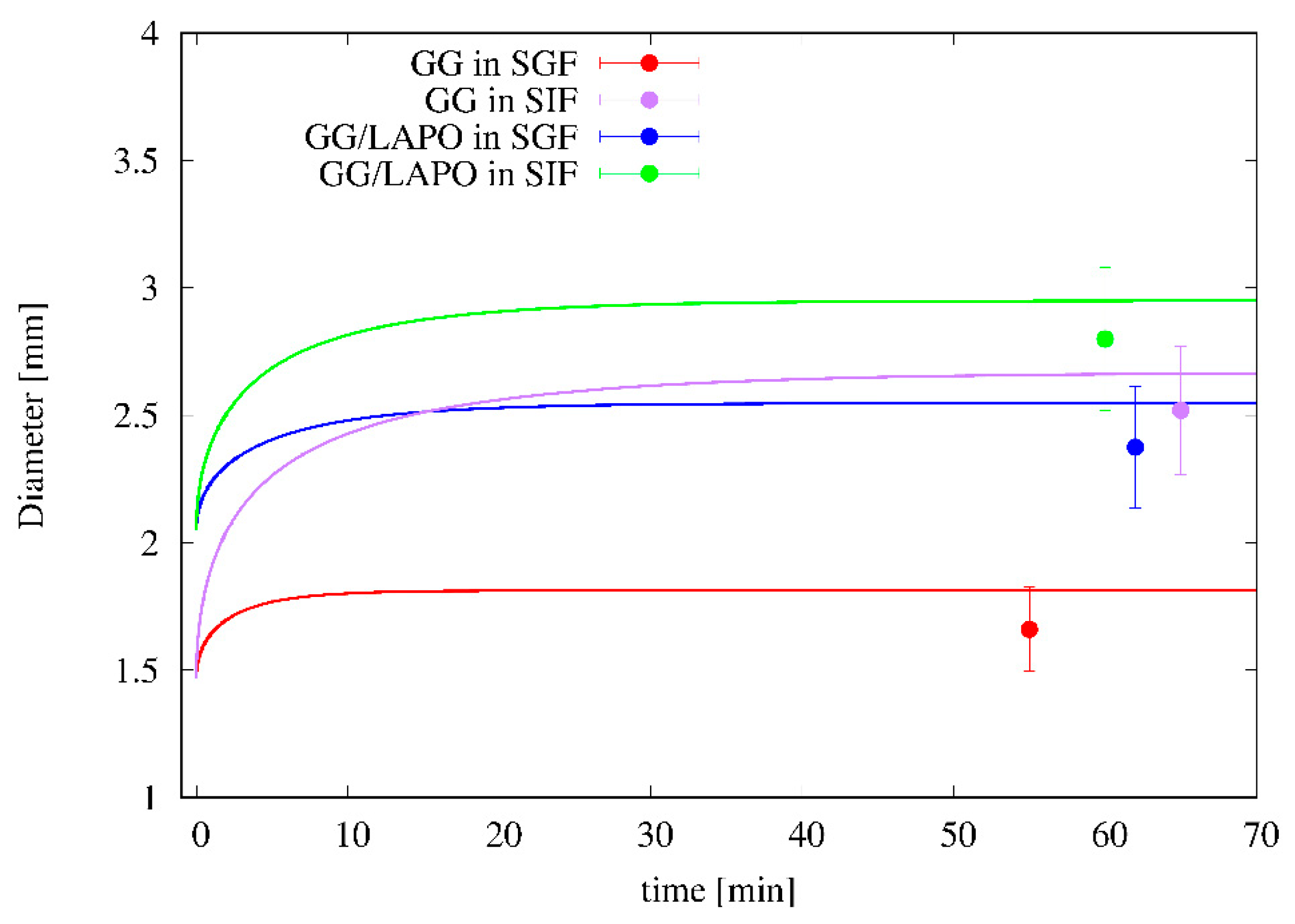
4.3. Swelling Experiments
- (1)
- the parameter β has been set to the value β = 2 in order to account for the large porosity/small density of beads;
- (2)
- the solvent volume fraction (SGF or SIF) at equilibrium φeq is directly estimated from the equilibrium swelling degree Seq aswhere xeq is the solvent weight fraction at equilibrium and ρb is the dry particle density;
- (3)
- φG has been set to φG = 0.1φeq, given the ease of beads re-hydration after freeze-drying.
4.4. Entrapment Efficiency
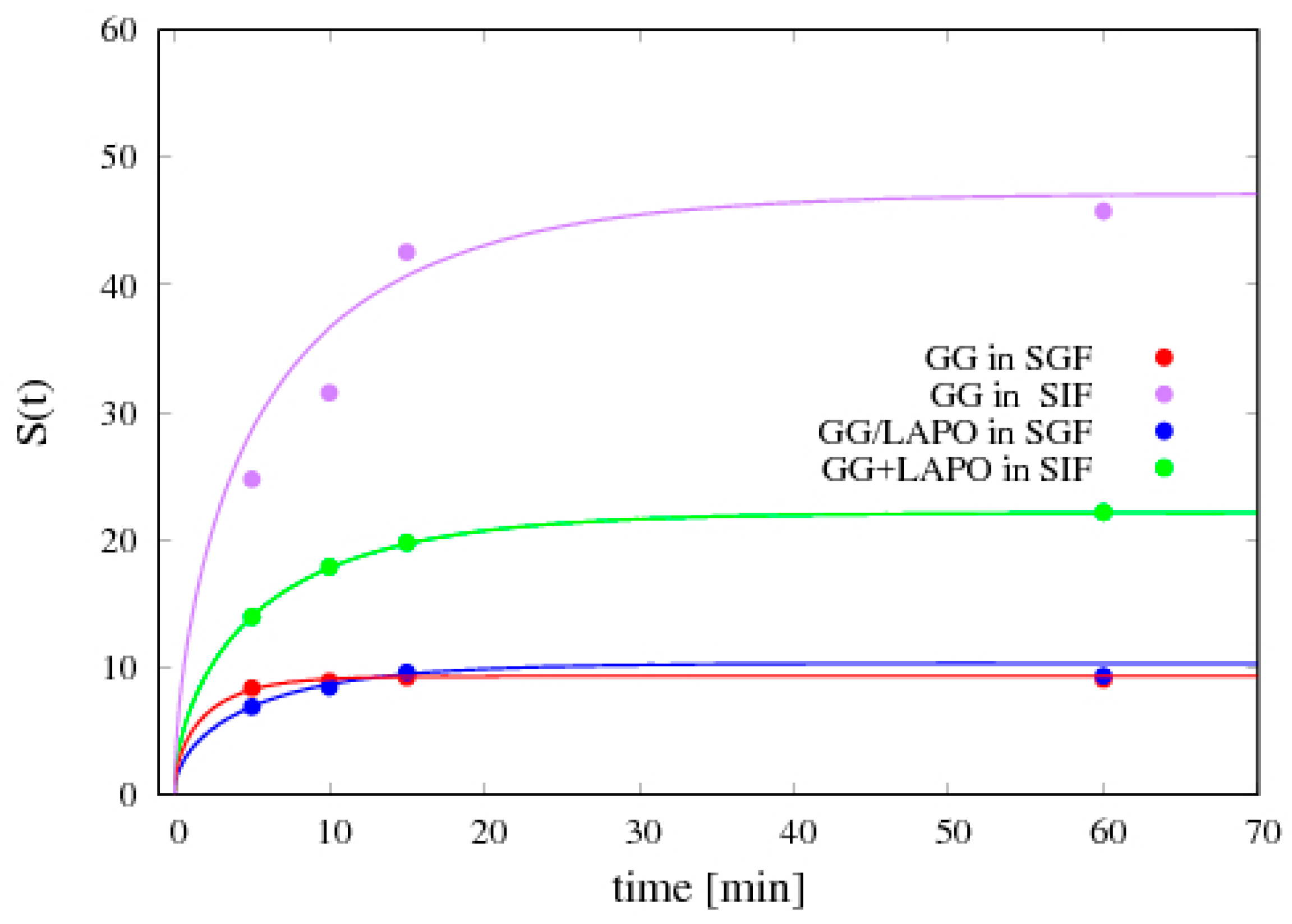
4.5. Release Data Analysis
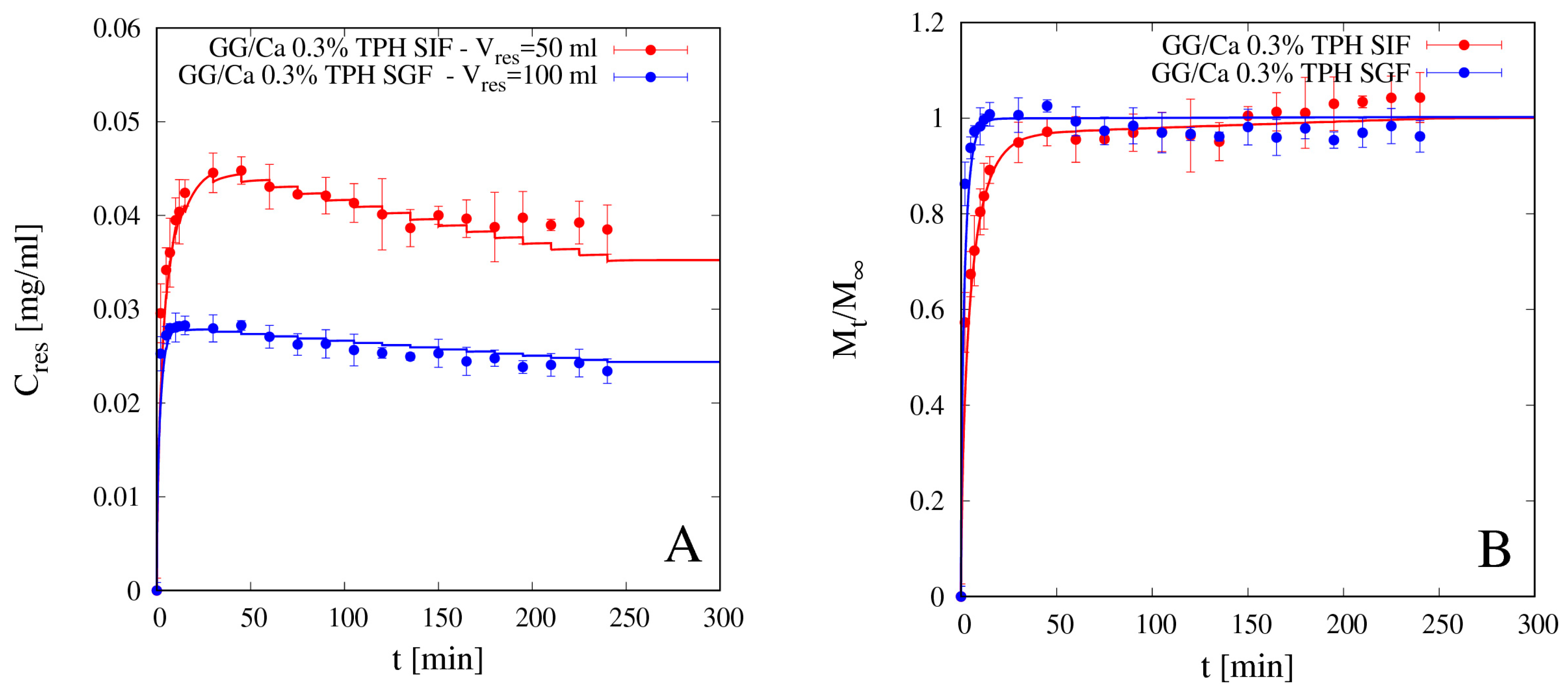
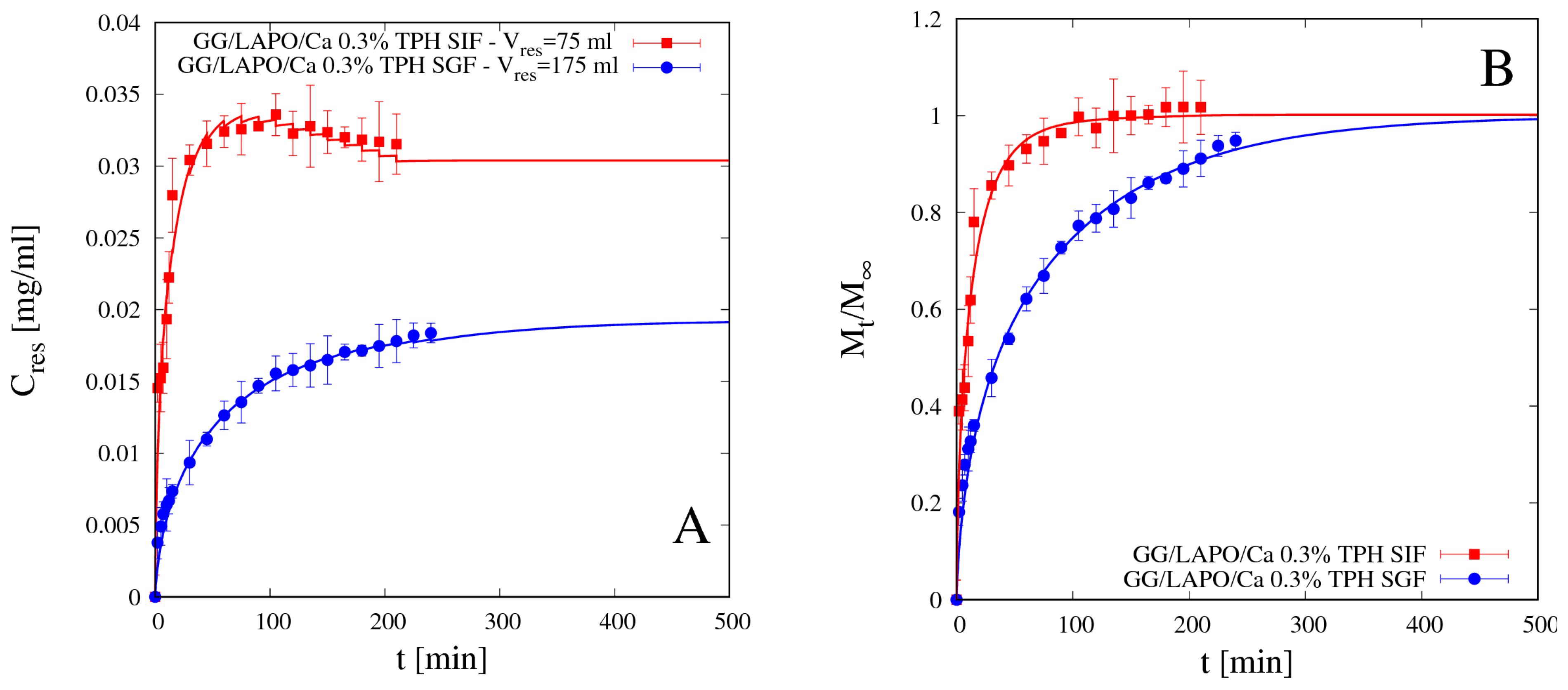
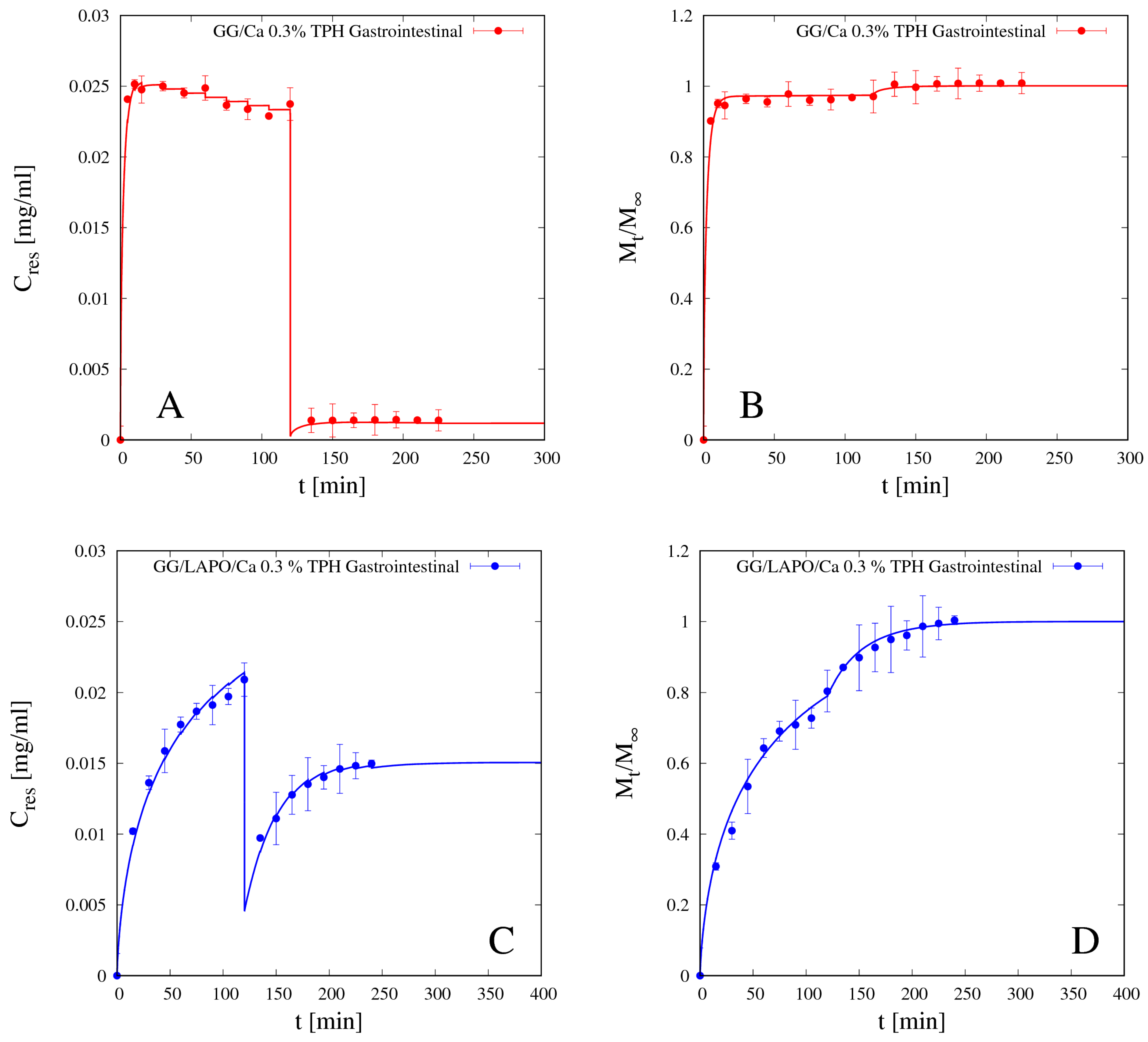
4.5.1. Theophylline Release
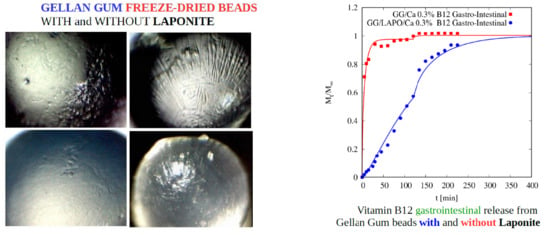
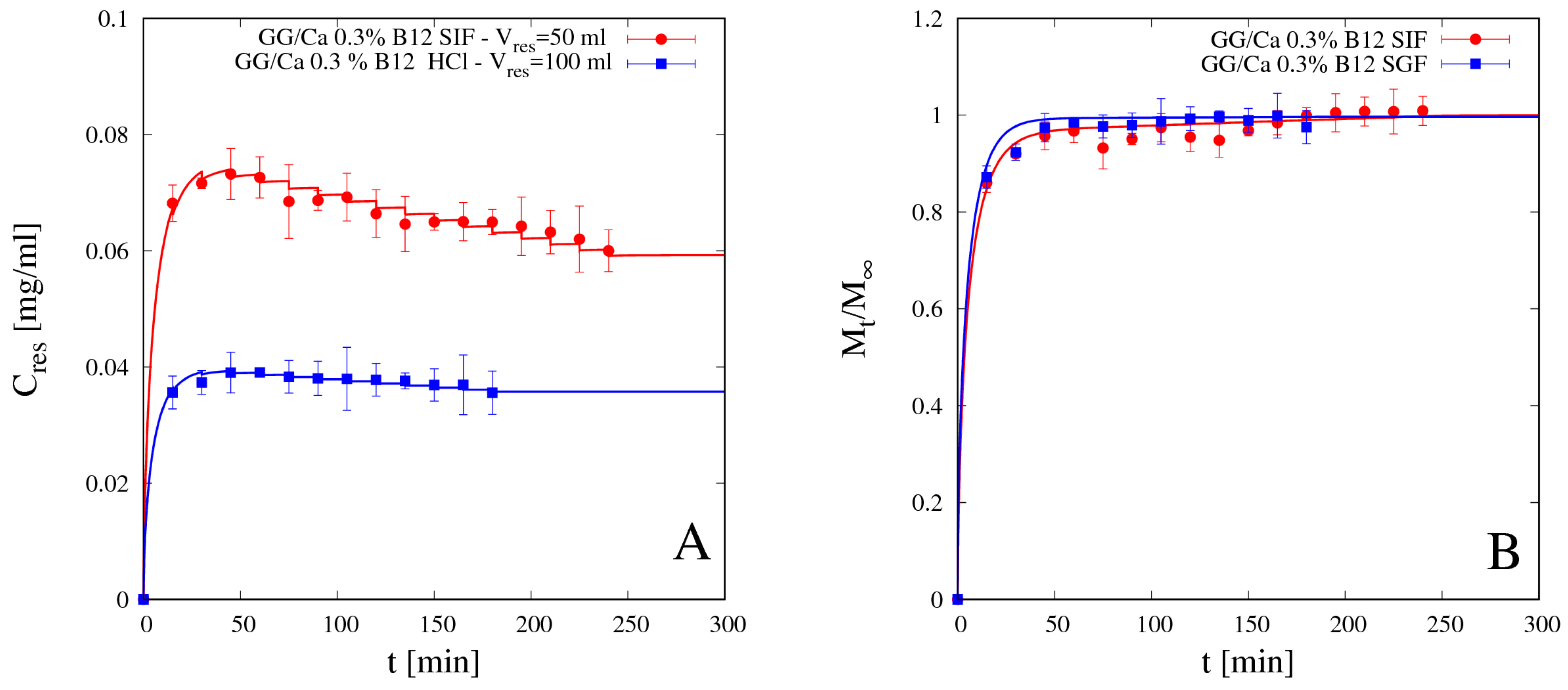
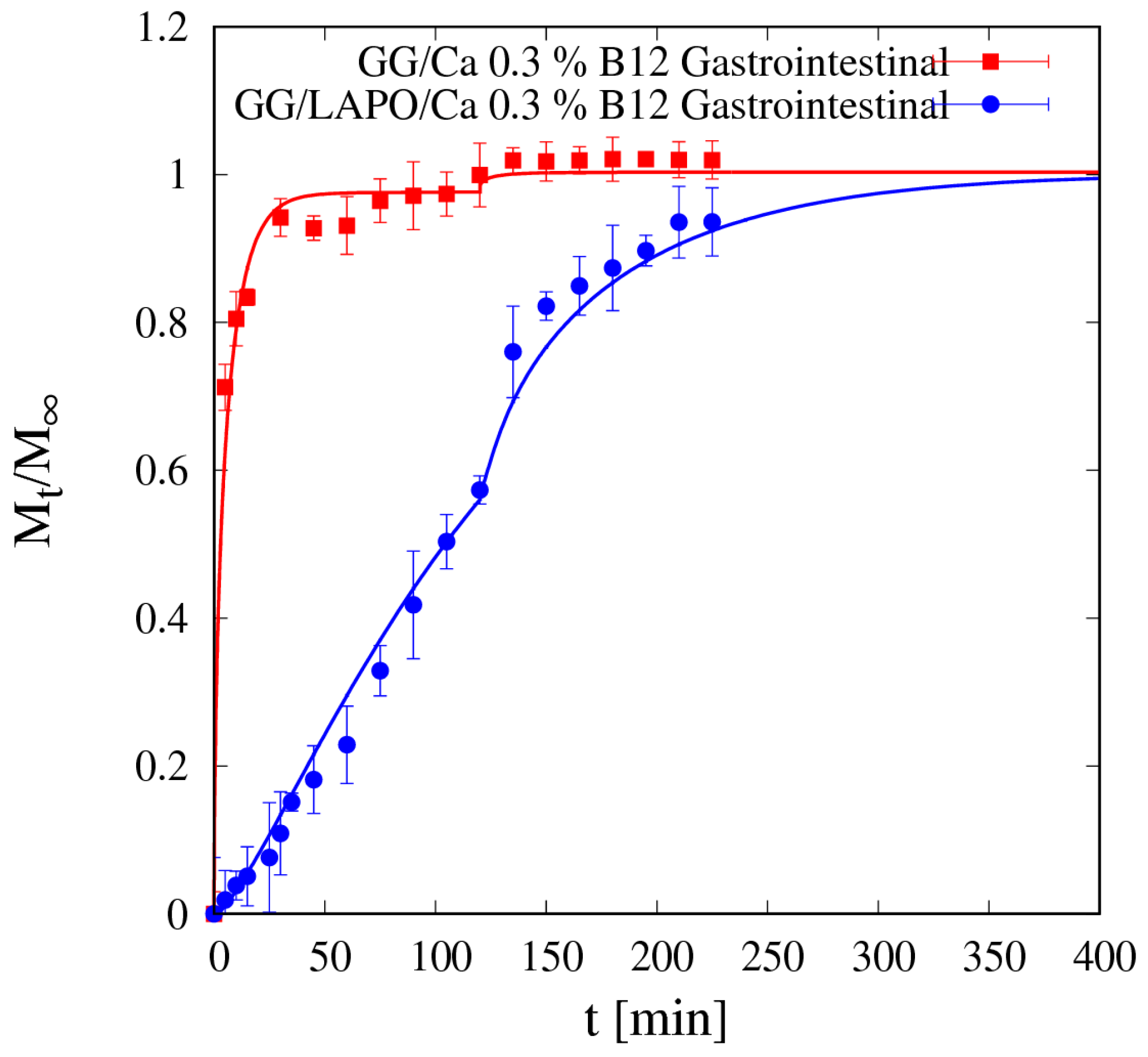
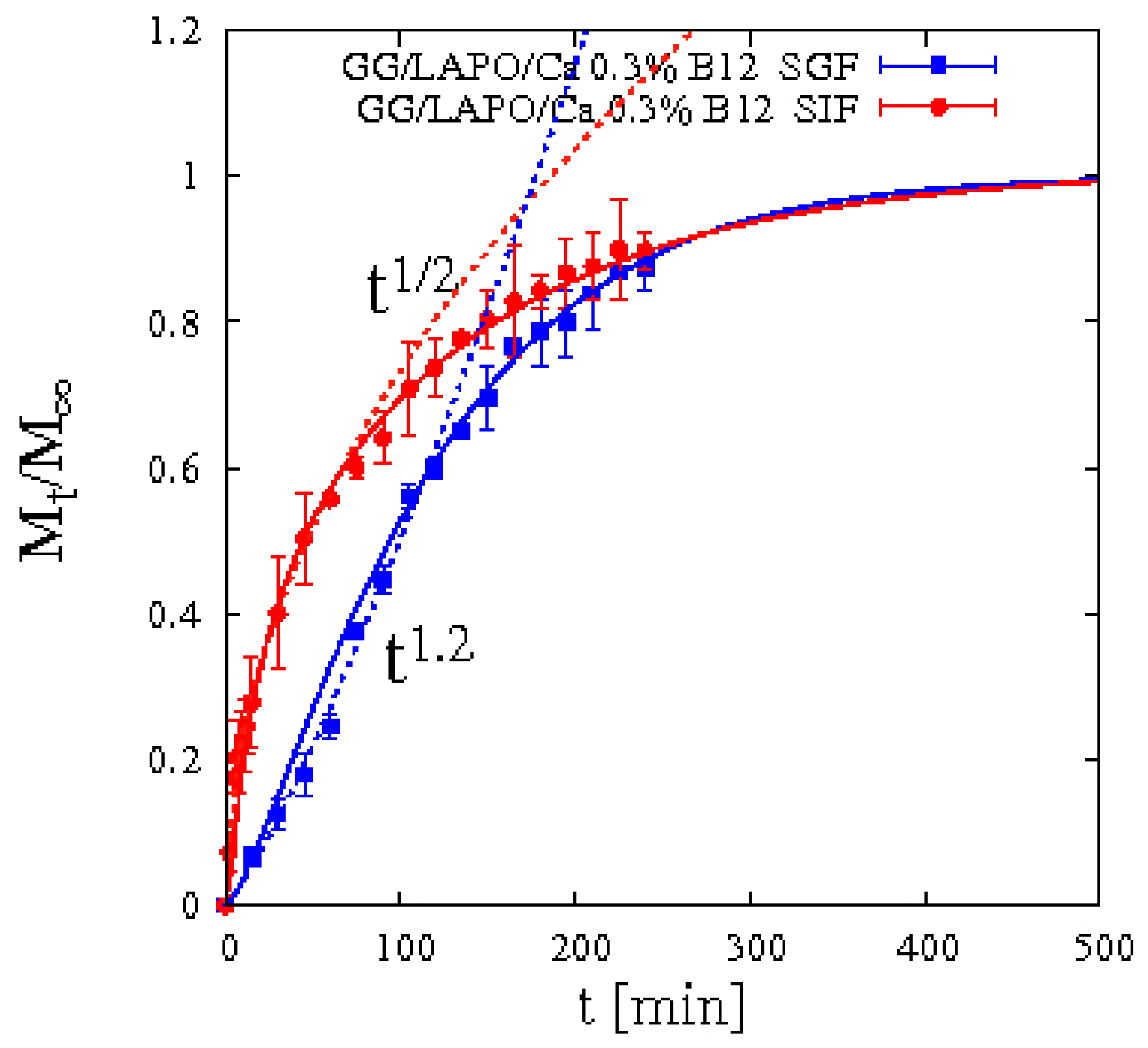
4.5.2. Vitamin B12 Release
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Debotton, N.; Dahan, A. Applications of Polymers as Pharmaceutical Excipients in Solid Oral Dosage Forms. Med. Res. Rev. 2017, 37, 52–97. [Google Scholar] [CrossRef] [PubMed]
- Borges, A.F.; Silva, C.; Coelho, J.F.J.; Simoes, S. Oral films: Current status and future perspectives: I-Galenical development and quality attributes. J. Control. Release 2015, 206, 1–19. [Google Scholar] [CrossRef]
- Qui, Y.; Park, K. Environment sensitive hydrogels for drug delivery. Adv. Drug Deliv. Rev. 2012, 64, 49–60. [Google Scholar]
- Giannuzzo, M.; Feeney, M.; Paolicelli, P.; Casadei, M.A. pH-sensitive hydrogels of dextran. J. Drug Deliv. Sci. Technol. 2006, 16, 49–54. [Google Scholar] [CrossRef]
- Singh, B.N.; Kim, K.H. Floating drug delivery systems: An approach to oral controlled drug delivery via gastric retention. J. Control. Release 2000, 63, 235–259. [Google Scholar] [CrossRef]
- Bardonnet, P.L.; Faivre, V.; Pugh, W.J.; Piffaretti, J.C.; Falson, F. Gastro-retentive dosage forms: Overview and special case of Helicobacter pylori. J. Control. Release 2006, 111, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Bera, H.; Boddupalli, S.; Nandikonda, S.; Kumar, S.; Nayak, A.K. Alginate gel-coated oil-entrapped alginate-tamarind gum-magnesium stearate buoyant beads of risperidone. Int. J. Biol. Macromol. 2015, 78, 102–111. [Google Scholar] [CrossRef] [PubMed]
- Baumgartner, S.; Kristil, J.; Vrecer, F.; Vodopivec, P.; Zorko, B. Optimization of floating matrix tablets and evalutation of their gastric residence time. Int. J. Pharm. 2000, 195, 125–135. [Google Scholar] [CrossRef]
- Osmałek, T.; Froelich, A.; Tasarek, S. Application of gellan gum in pharmacy and medicine. Int. J. Pharm. 2014, 466, 328–340. [Google Scholar]
- Patil, P.; Chavanke, D.; Wagh, M. A review on ionotropic gelation method: Novel approach for controlled gastroretentive gelispheres. Int. J. Pharm. Pharm. Sci. 2012, 4, 27–32. [Google Scholar]
- Lopez-Cebral, R.; Paolicelli, P.; Romero-Caamaño, V.; Sejio, B.; Casadei, M.A.; Sanchez, A. Spermidine cross-linked hydrogels as novel potential platforms for pharmaceutical applications. J. Pharm. Sci. 2013, 102, 2632–2643. [Google Scholar] [CrossRef] [PubMed]
- Patela, A.M.; Mohamed, H.H.; Schryer-Pragaa, J.V.; Chadwicka, K. The effect of ionotropic gelation residence time on alginate cross-linking and properties. Carbohydr. Polym. 2017, 155, 362–371. [Google Scholar] [CrossRef]
- Cerciello, A.; Del Gaudio, P.; Granatac, V.; Sala, M.; Aquino, R.P.; Russo, P. Synergistic effect of divalent cations in improving technological properties of cross-linked alginate beads. Int. J. Biol. Macromol. 2017, 101, 100–106. [Google Scholar] [CrossRef] [PubMed]
- Benfattoum, K.; Haddadine, N.; Bouslah, N.; Benaboura, A.; Maincent, P.; Barillé, R.; Sapin-Minet, A.; El-Shall, M.S. Formulation characterization and in vitro evaluation of acacia gum–calcium alginate beads for oral drug delivery systems. Polym. Adv. Technol. 2018, 29, 884–895. [Google Scholar] [CrossRef]
- Gupta, K.C.; Ravi, K.M.N.V. Drug release behavior of beads and microgranules of chitosan. Biomaterials 2000, 21, 1115–1119. [Google Scholar] [CrossRef]
- Meirelles, L.M.A.; Raffin, F.N. Clay and Polymer-Based Composites Applied to Drug Release: A Scientific and Technological Prospection. J. Pharm. Pharm. Sci. 2017, 20, 115–134. [Google Scholar] [CrossRef]
- Li, Y.; Maciel, D.; Tom, H.; Rodrigues, J.; Ma, H.; Shi, X. pH sensitive Laponite/alginate hybrid hydrogels: Swelling behaviour and release mechanism. Soft Matter 2011, 7, 6231–6238. [Google Scholar] [CrossRef]
- Wu, C.J.; Gaharwar, A.K.; Schexnailder, P.J.; Schmidt, G. Development of Biomedical Polymer-Silicate Nanocomposites: A Materials Science Perspective. Materials 2010, 3, 2986–3005. [Google Scholar] [CrossRef]
- Haraguchi, K.; Takehisa, T. Nanocomposite Hydrogels: A Unique Organic–Inorganic Network Structure with Extraordinary Mechanical, Optical, and Swelling/De-swelling Properties. Adv. Mater. 2002, 14, 1120–1124. [Google Scholar] [CrossRef]
- Raut, S.Y.; Gahane, A.; Joshi, M.B.; Kalthur, G.; Mutalik, S. Nanocomposite clay-polymer microbeads for oral controlled drug delivery: Development and, in vitro and in vivo evaluations. J. Drug Deliv. Sci. Technol. 2019, 51, 234–243. [Google Scholar] [CrossRef]
- Yang, H.; Hua, S.; Wang, W.; Wang, A. Composite hydrogel beads based on chitosan and laponite: Preparation, swelling, and drug release behavior. Iran. Polym. J. 2011, 20, 479–490. [Google Scholar]
- Li, P.; Siddaramaiah; Kim, N.H.; Yoo, G.H.; Lee, J.H. Poly(acrylamide/laponite) nanocomposite hydrogels: Swelling and cationic dye adsorption properties. J. Appl. Polym. Sci. 2009, 111, 1786–1798. [Google Scholar] [CrossRef]
- Pacelli, S.; Paolicelli, P.; Moretti, G.; Petralito, S.; Di Giacomo, S.; Vitalone, A.; Casadei, M.A. Gellan gum methacrylate and laponite as an innovative nanocomposite hydrogel for biomedical applications. Eur. Polym. J. 2016, 77, 114–126. [Google Scholar] [CrossRef]
- Haraguchi, K. Synthesis and properties of soft nanocomposite materials with novel organic/inorganic network structures. Polym. J. 2011, 43, 223–241. [Google Scholar] [CrossRef]
- Da Silva Fernandes, R.; de Moura, M.R.; Glenn, G.M.; Aouada, F.A. Thermal, microstructural, and spectroscopic analysis of Ca2+ alginate/clay nanocomposite hydrogel beads. J. Mol. Liq. 2018, 265, 327–336. [Google Scholar] [CrossRef]
- Papanu, J.S.; Soane, D.S.; Bell, A.T.; Hess, D.M. Transport Models for swelling and dissolution of thin polymer films. J. Appl. Polym. Sci. 1989, 38, 859–885. [Google Scholar] [CrossRef]
- Adrover, A.; Nobili, M. Release kinetics from oral thin films: Theory and experiments. Chem. Eng. Res. Des. 2015, 98, 188–211. [Google Scholar] [CrossRef]
- Adrover, A.; Varani, G.; Paolicelli, P.; Petralito, S.; Di Muzio, L.; Casadei, M.A.; Tho, I. Experimental and Modeling Study of Drug Release from HPMC-Based Erodible Oral Thin Films. Pharmaceutics 2018, 10, 222. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.; Lumpkin, J.A.; Rosenblatt, J. Mathematical modeling of drug release from hydrogel matrices via a diffusion coupled with desorption mechanism. J. Control. Release 1994, 32, 17–25. [Google Scholar] [CrossRef]
- Paolicelli, P.; Varani, G.; Pacelli, S.; Ogliani, E.; Nardoni, M.; Petralito, S.; Adrover, A.; Casadei, M.A. Design and characterization of a biocompatible physical hydrogel based on scleroglucan for topical drug delivery. Carbohydr. Polym. 2017, 174, 960–969. [Google Scholar] [CrossRef] [PubMed]
- Morris, E.R.; Nishinari, K.; Rinaudo, M. Gelation of gellan—A review. Food Hydrocoll. 2012, 28, 373–411. [Google Scholar] [CrossRef]
- Osmałek, T.; Milanowski, B.; Froelich, A.; Szybowicz, M.; Białowąs, W.; Kapela, M.; Gadziński, P.; Ancukiewicz, K. Design and characteristics of gellan gum beads for modified release of meloxicam. Drug. Dev. Ind. Pharm. 2017, 43, 1314–1329. [Google Scholar] [CrossRef] [PubMed]
- Narkar, M.; Sher, P.; Pawar, A. Stomach-specific controlled release gellan beads of acid-soluble drug prepared by ionotropic gelation method. AAPS PharmSciTech 2010, 11, 267–277. [Google Scholar] [CrossRef] [PubMed]
- Babu, R.J.; Sathigari, S.; Kumar, M.T.; Pandit, J.K. Formulation of controlled release gellan gum macro beads of amoxicillin. Curr. Drug Deliv. 2010, 7, 36–43. [Google Scholar] [CrossRef]
- Cohen, J.L. Theophylline. Anal. Profiles Drug Subst. 1975, 4, 466–493. [Google Scholar]
- Kirschbaum, J. Cyanocobalamin. Anal. Profiles Drug Subst. 1981, 10, 183–288. [Google Scholar]
- Coviello, T.; Grassi, M.; Rambone, G.; Santucci, E.; Carafa, M.; Murtas, E.; Riccieri, F.M.; Alhaique, F. Novel hydrogel system from scleroglucan: Synthesis and characterization. J. Control. Release 1999, 60, 367–378. [Google Scholar] [CrossRef]
- Coviello, T.; Grassi, M.; Palleschi, A.; Bocchinfuso, G.; Coluzzi, G.; Banishoeib, F.; Alhaique, F. A new scleroglucan/borax hydrogel: Swelling and drug release studies. Int. J. Pharm. 2005, 289, 97–107. [Google Scholar] [CrossRef] [PubMed]
| Beads Formulation | Beads Diameter (mm ± SD) | Freeze-Dried Beads Diameter (mm ± SD) |
|---|---|---|
| GG/Ca 0.3% | 2.41 ± 0.06 | 1.63 ± 0.03 |
| GG/Ca 0.6% | 2.44 ± 0.07 | 1.56 ± 0.09 |
| GG/LAPO/Ca 0.3% | 2.79 ± 0.11 | 2.06 ± 0.08 |
| Beads Formulation | Seq in SGF | Seq in SIF | Dssg in SGF [m2/s] | Dssg in SIF [m2/s] |
|---|---|---|---|---|
| GG/Ca 0.3% | 9.08 ± 0.3 | 45.80 ± 0.9 | (8.8 ± 0.3) × 10−10 | (1.5 ± 0.1) × 10−9 |
| GG/Ca 0.6% | 8.97 ± 0.2 | 25.44 ± 0.6 | - | - |
| GG/LAPO/Ca 0.3% | 9.14 ± 0.3 | 20.60 ± 0.3 | (6.5 ± 0.3) × 10−10 | (1.1 ± 0.1) × 10−9 |
| Beads | Drug Molecule | Entrapment Efficiency (%) |
|---|---|---|
| GG/Ca 0.3% | Vitamin B12 | 53.62 |
| GG/LAPO/Ca 0.3% | Vitamin B12 | 61.26 |
| GG/Ca 0.3% | Theophylline | 20.26 |
| GG/LAPO/Ca 0.3% | Theophylline | 36.49 |
| Beads | Ddsg in SGF [m2/s] | Ddsg in SIF [m2/s] |
|---|---|---|
| GG/Ca 0.3% | (4.26 ± 0.15) × 10−10 | (2.62 ± 0.2) × 10−10 |
| GG/LAPO/Ca 0.3% | (2.73 ± 0.3) × 10−11 | (1.43 ± 0.1) × 10−10 |
| Beads | Ddsg in SGF [m2/s] | Ddsg in SIF [m2/s] | kbgsg in SGF [1/s] | kbgsg in SIF [1/s] |
|---|---|---|---|---|
| GG/Ca 0.3% | (1.53 ± 0.15) × 10−10 | (1.85 ± 0.15) × 10−10 | - | - |
| GG/LAPO/Ca 0.3% | (2.87 ± 0.1) × 10−11 | (5.33 ± 0.1) × 10−11 | 2.35 × 10−4 | 4.12 × 10−3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adrover, A.; Paolicelli, P.; Petralito, S.; Di Muzio, L.; Trilli, J.; Cesa, S.; Tho, I.; Casadei, M.A. Gellan Gum/Laponite Beads for the Modified Release of Drugs: Experimental and Modeling Study of Gastrointestinal Release. Pharmaceutics 2019, 11, 187. https://doi.org/10.3390/pharmaceutics11040187
Adrover A, Paolicelli P, Petralito S, Di Muzio L, Trilli J, Cesa S, Tho I, Casadei MA. Gellan Gum/Laponite Beads for the Modified Release of Drugs: Experimental and Modeling Study of Gastrointestinal Release. Pharmaceutics. 2019; 11(4):187. https://doi.org/10.3390/pharmaceutics11040187
Chicago/Turabian StyleAdrover, Alessandra, Patrizia Paolicelli, Stefania Petralito, Laura Di Muzio, Jordan Trilli, Stefania Cesa, Ingunn Tho, and Maria Antonietta Casadei. 2019. "Gellan Gum/Laponite Beads for the Modified Release of Drugs: Experimental and Modeling Study of Gastrointestinal Release" Pharmaceutics 11, no. 4: 187. https://doi.org/10.3390/pharmaceutics11040187
APA StyleAdrover, A., Paolicelli, P., Petralito, S., Di Muzio, L., Trilli, J., Cesa, S., Tho, I., & Casadei, M. A. (2019). Gellan Gum/Laponite Beads for the Modified Release of Drugs: Experimental and Modeling Study of Gastrointestinal Release. Pharmaceutics, 11(4), 187. https://doi.org/10.3390/pharmaceutics11040187