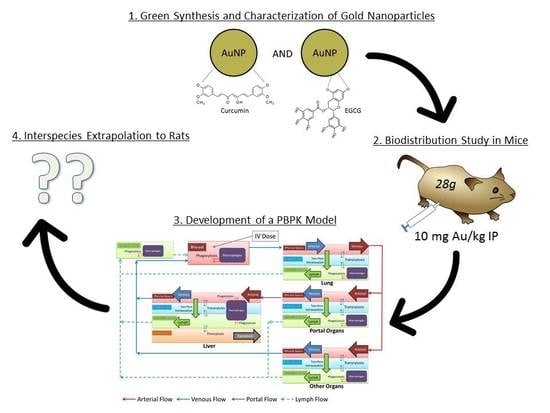
Biodistribution and Physiologically-Based Pharmacokinetic Modeling of Gold Nanoparticles in Mice with Interspecies Extrapolation
Abstract
1. Introduction
- Anatomy and physiology of the individual
- Physicochemical properties of the drug
- System of equations governing the movement and interaction of the drug within the body (model processes).
2. Materials and Methods
2.1. Materials
2.2. Synthesis and Isolation
2.3. Characterization
2.3.1. Ultraviolet Visible (UV-Vis) Absorption Spectroscopy
2.3.2. Dynamic Light Scattering (DLS)
2.3.3. Transmission Electron Microscopy (TEM)
2.4. Animal Study
2.5. Gold Quantification
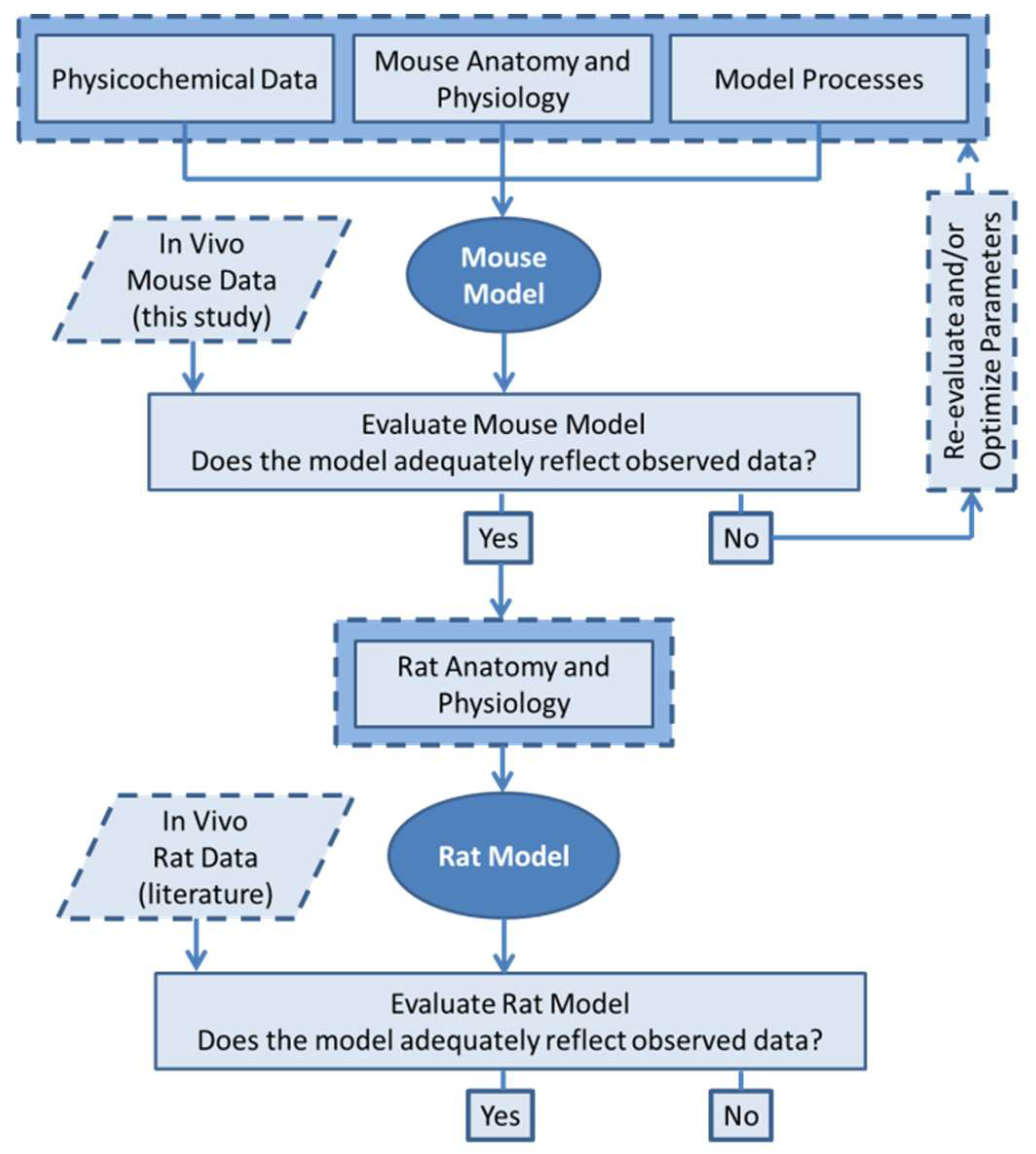
2.6. PBPK Modelling Workflow
2.7. Software
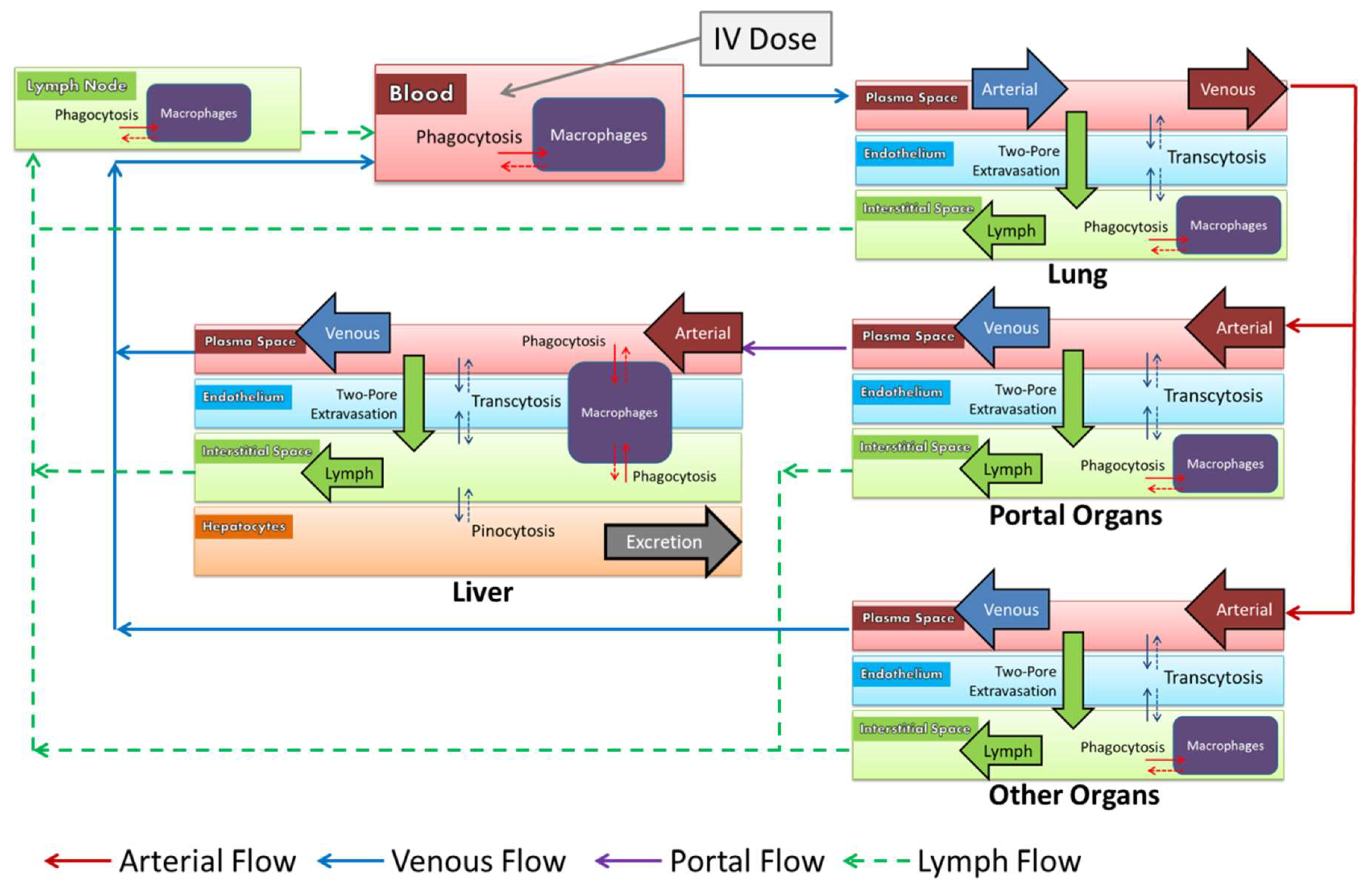
2.8. Model Structure
2.9. Model Parameterization
2.9.1. Anatomy
2.9.2. Extravasation
2.9.3. Vascular Endothelium
2.9.4. Macrophages
- Complete blood counts indicate that 1% of the blood volume is comprised of phagocytic cells, based on an average white blood cell volume of 1.25 pL [36]
2.9.5. Hepatocytes
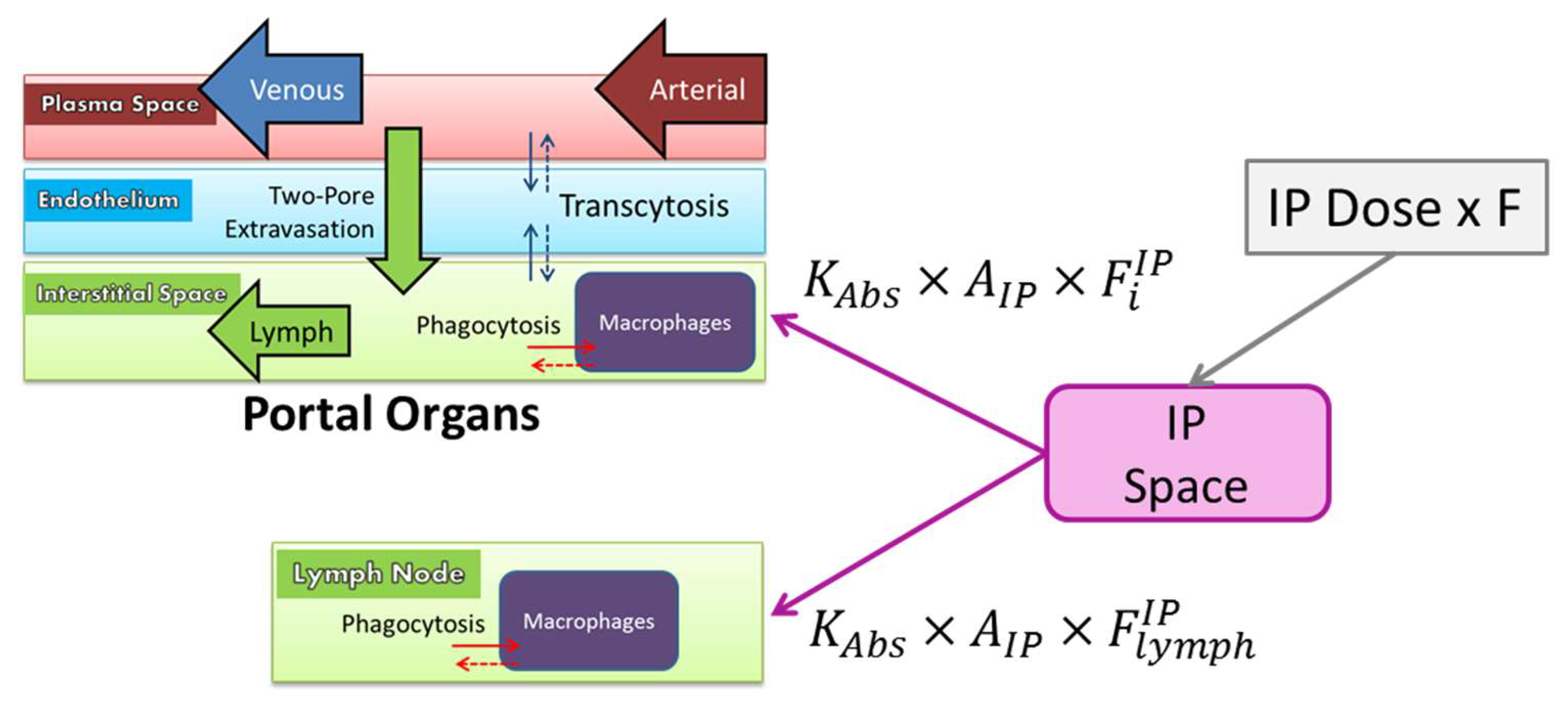
2.9.6. Intraperitoneal Administration
2.9.7. Optimization
2.10. Model Evaluation
2.11. Sensitivity Analysis
3. Results
3.1. Characterization
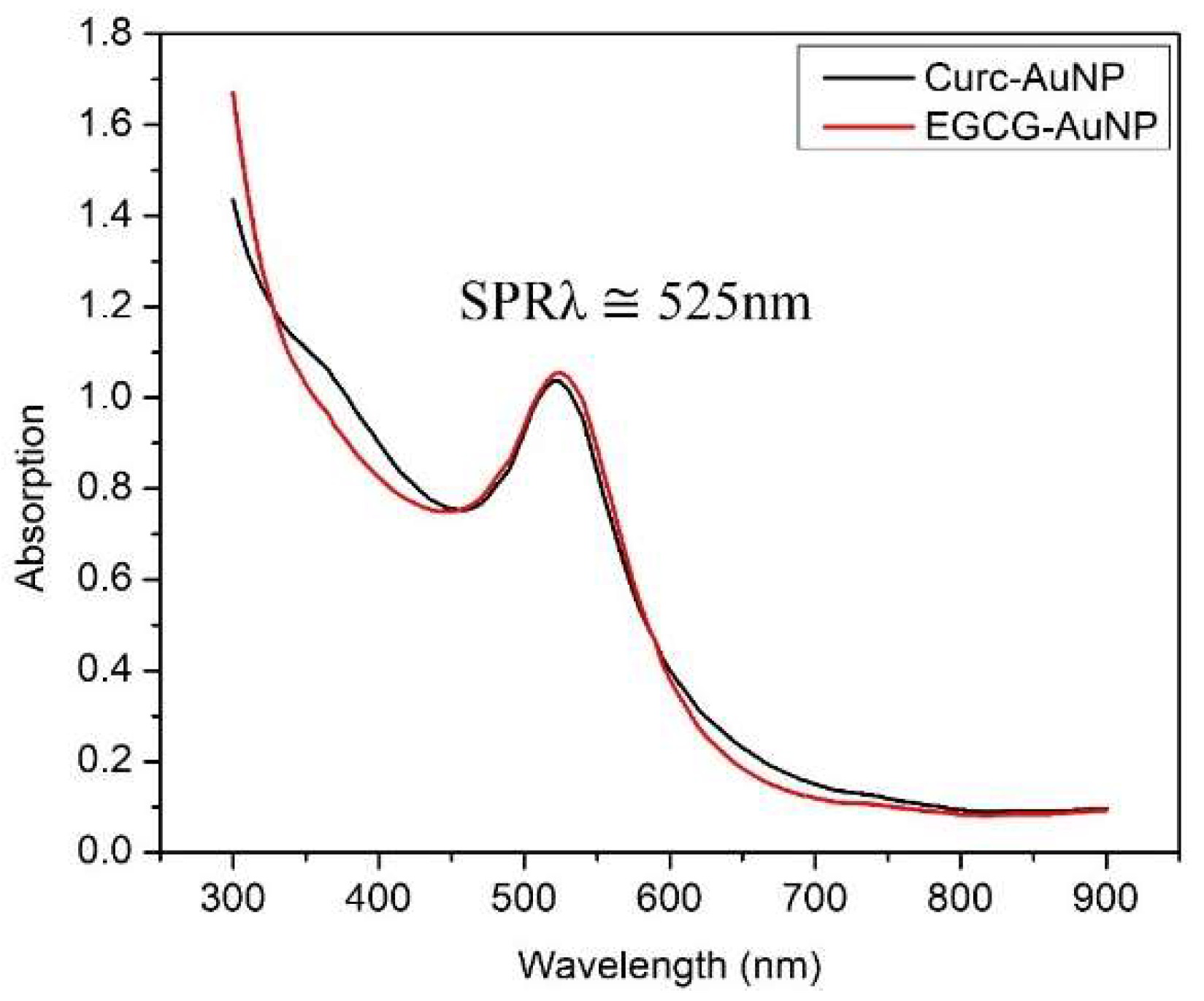
3.1.1. Ultraviolet Visible (UV-Vis) Absorption Spectroscopy
3.1.2. Dynamic Light Scattering (DLS)
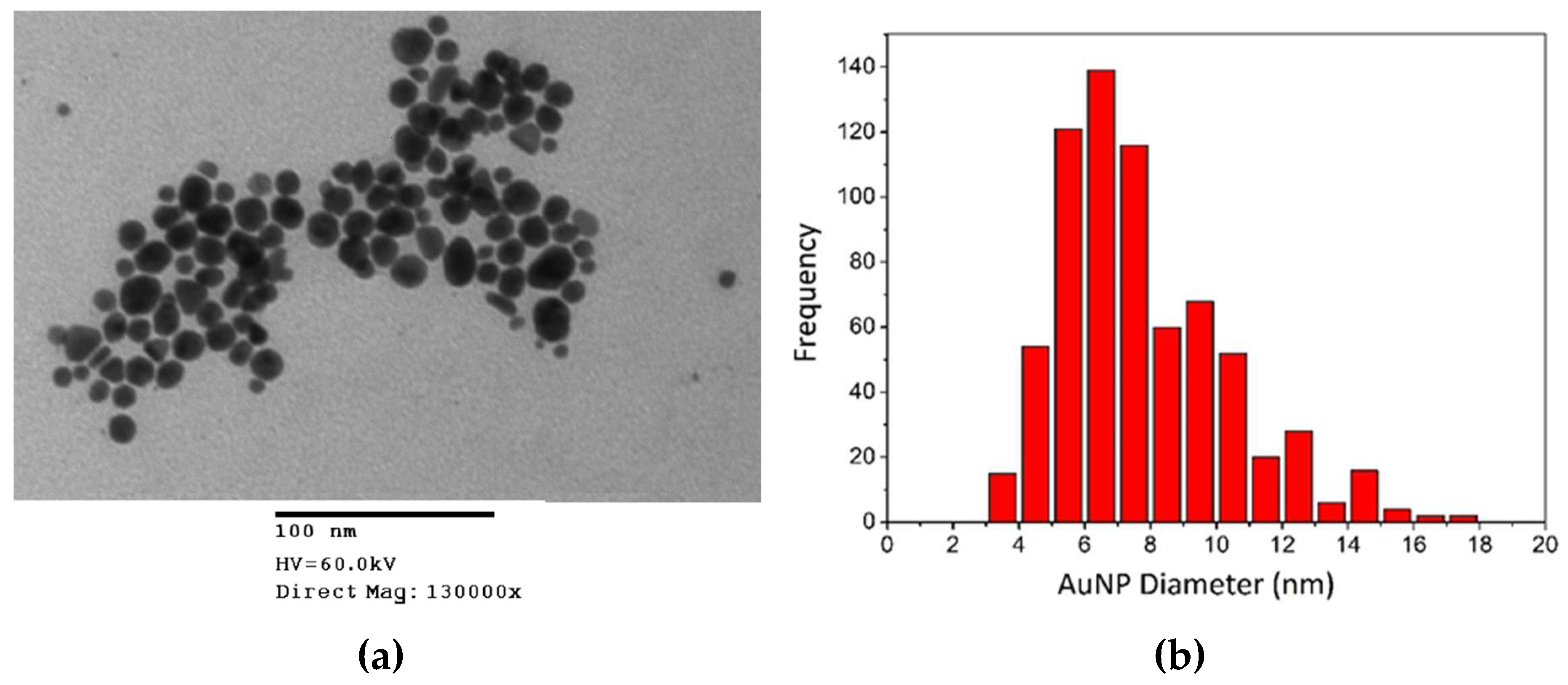
3.1.3. Transmission Electron Microscopy (TEM)
3.2. Animal Study
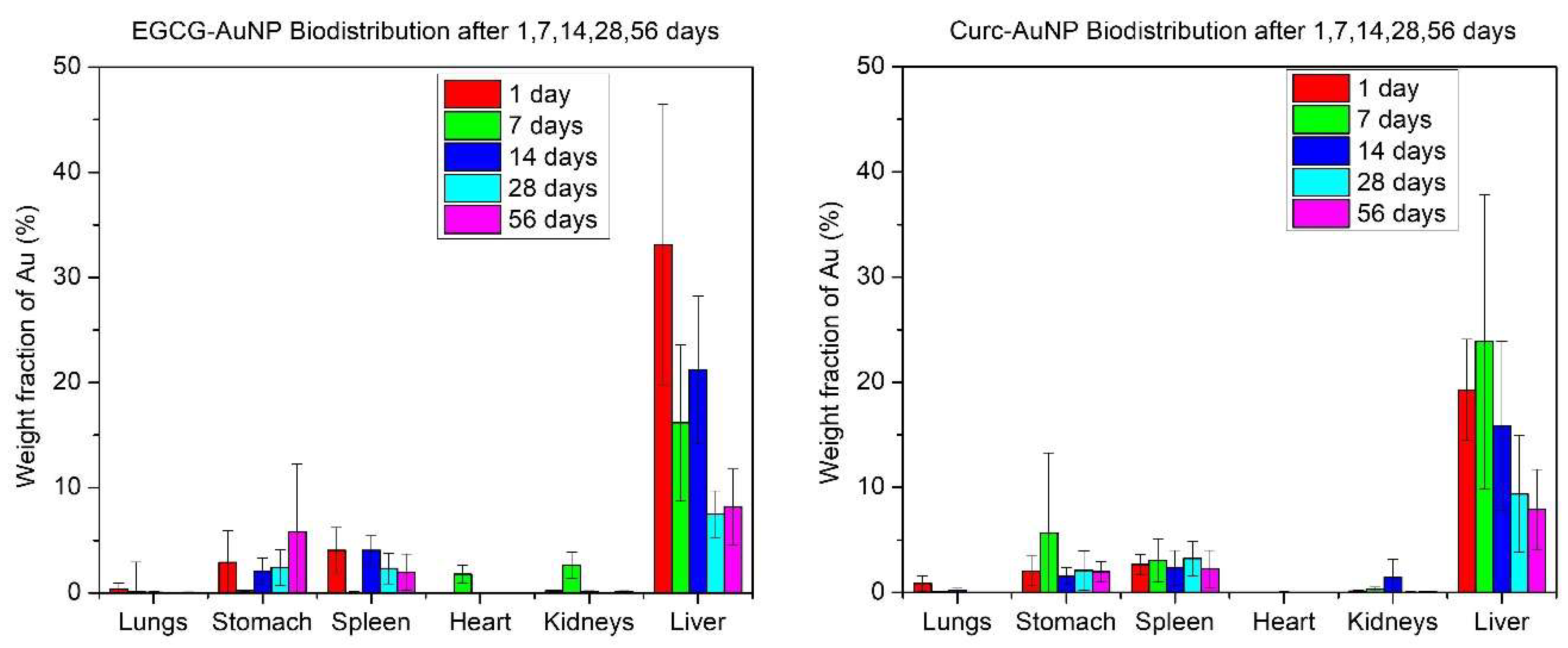
3.3. Gold Quantification
3.4. Model ParameterizationOptimization
Optimization
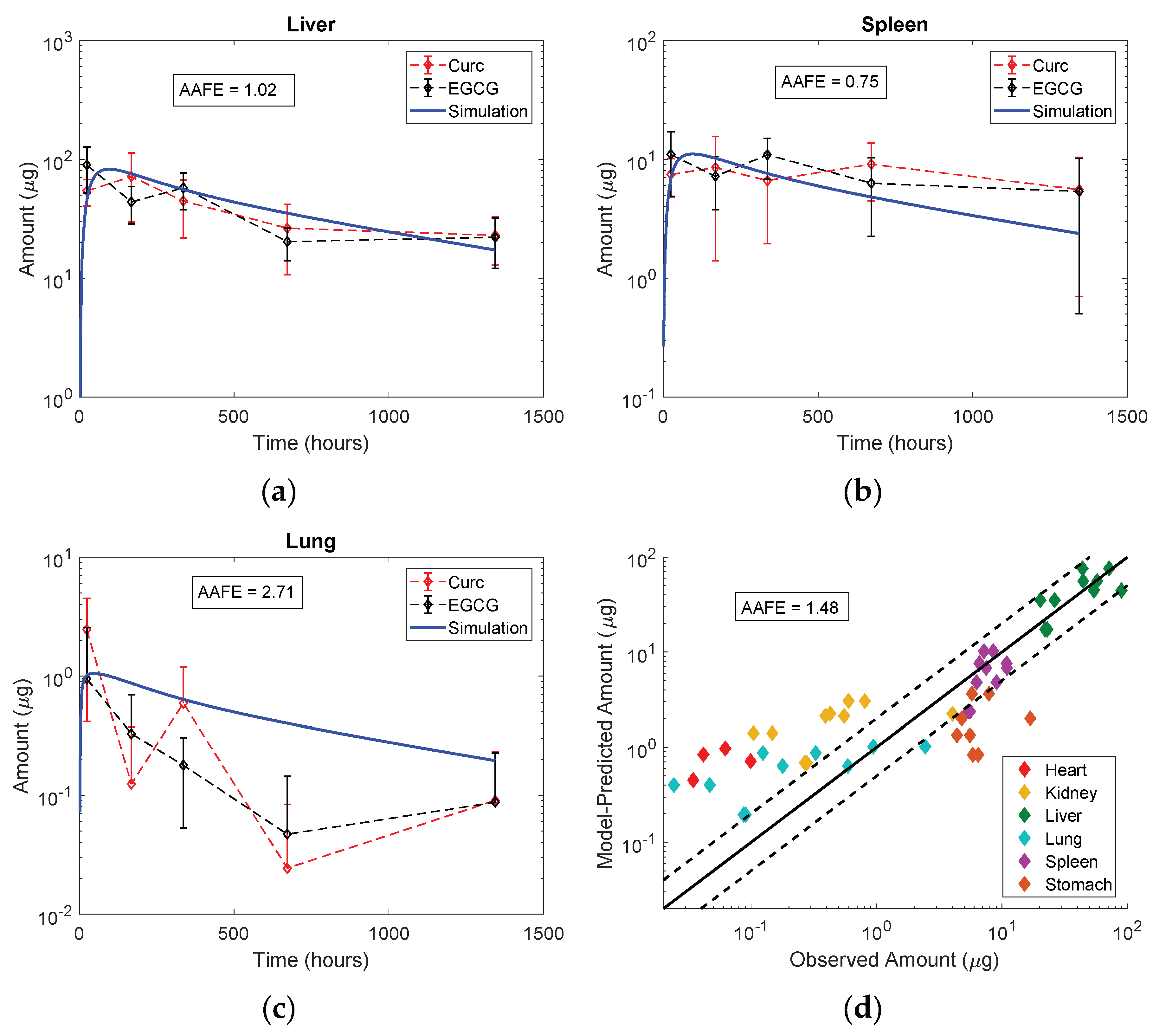
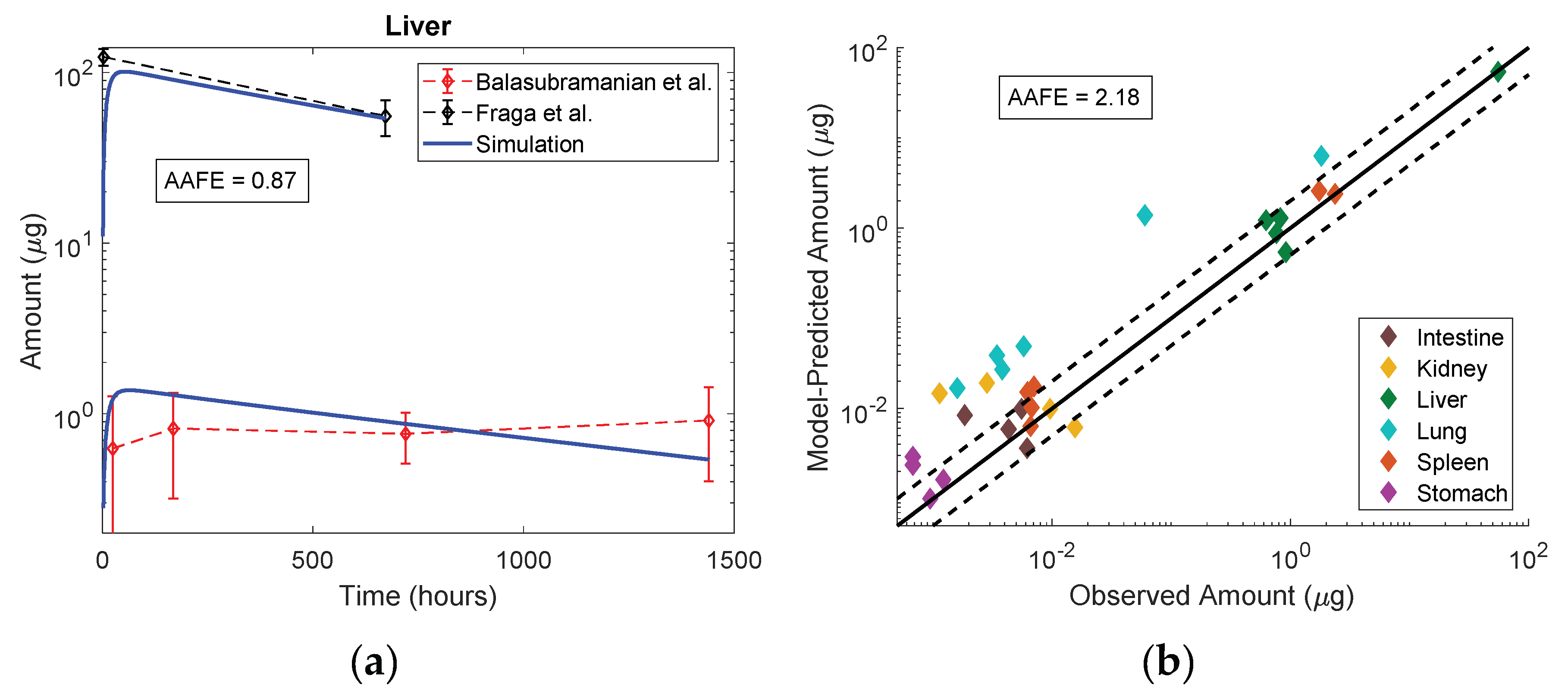
3.5. Model Evaluation
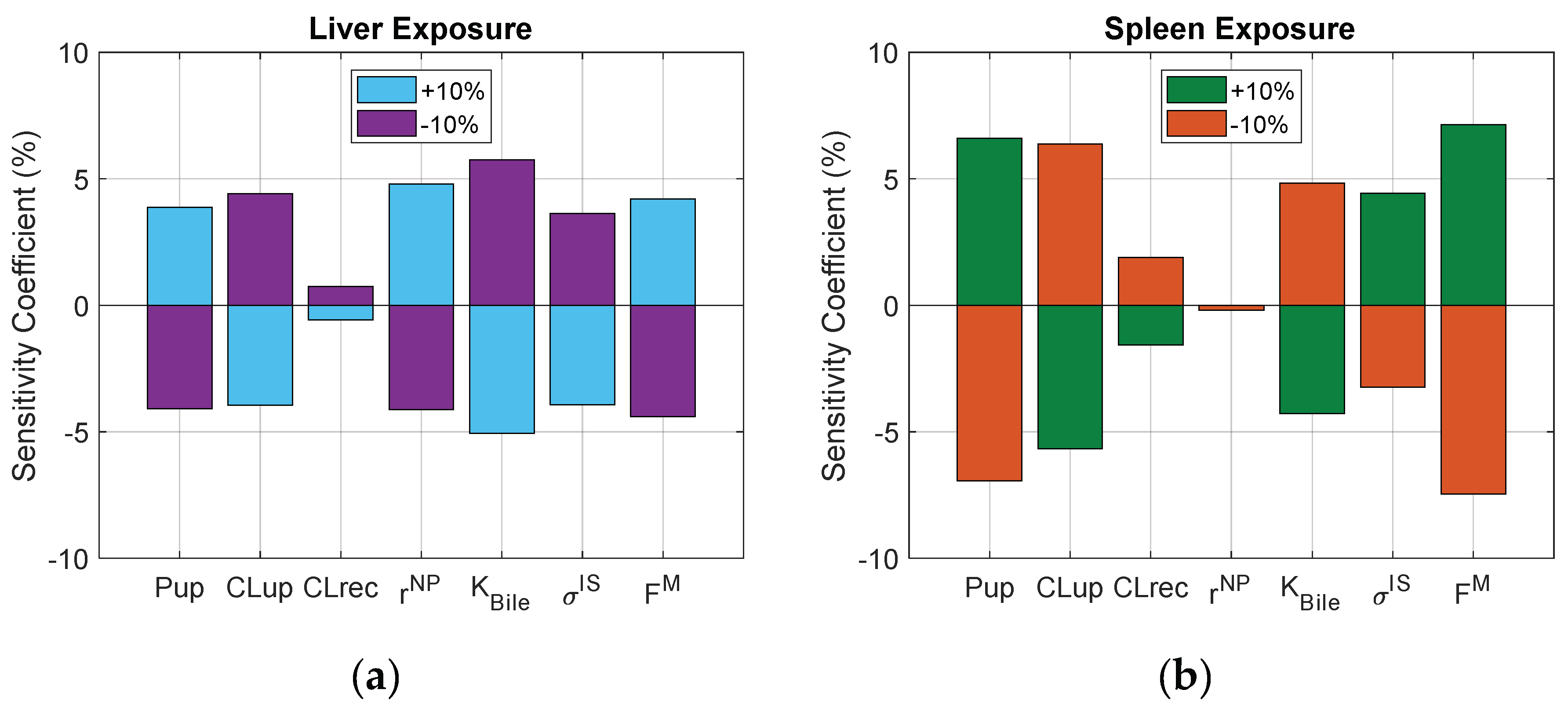
3.6. Sensitivity Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eustis, S.; El-Sayed, M.A. Why gold nanoparticles are more precious than pretty gold: Noble metal surface plasmon resonance and its enhancement of the radiative and nonradiative properties of nanocrystals of different shapes. Chem. Soc. Rev. 2006, 35, 209–217. [Google Scholar] [CrossRef]
- Daniela, C.; Andreea, C.; Rebecca, P.; Alexandru Mihai, G. Biomedical Applications of Gold Nanoparticles. Curr. Top. Med. Chem. 2015, 15, 1605–1613. [Google Scholar] [CrossRef]
- Xu, Z.P.; Zeng, Q.H.; Lu, G.Q.; Yu, A.B. Inorganic nanoparticles as carriers for efficient cellular delivery. Chem. Eng. Sci. 2006, 61, 1027–1040. [Google Scholar] [CrossRef]
- Qiu, Y.; Liu, Y.; Wang, L.; Xu, L.; Bai, R.; Ji, Y.; Wu, X.; Zhao, Y.; Li, Y.; Chen, C. Surface chemistry and aspect ratio mediated cellular uptake of Au nanorods. Biomaterials 2010, 31, 7606–7619. [Google Scholar] [CrossRef]
- Giljohann, D.A.; Seferos, D.S.; Patel, P.C.; Millstone, J.E.; Rosi, N.L.; Mirkin, C.A. Oligonucleotide Loading Determines Cellular Uptake of DNA-Modified Gold Nanoparticles. Nano Lett. 2007, 7, 3818–3821. [Google Scholar] [CrossRef]
- Boisselier, E.; Astruc, D. Gold nanoparticles in nanomedicine: Preparations, imaging, diagnostics, therapies and toxicity. Chem. Soc. Rev. 2009, 38, 1759–1782. [Google Scholar] [CrossRef]
- Stoner, G.D.; Mukhtar, H. Polyphenols as cancer chemopreventive agents. J. Cell. Biochem. 1995, 59, 169–180. [Google Scholar] [CrossRef]
- Mittal, A.K.; Chisti, Y.; Banerjee, U.C. Synthesis of metallic nanoparticles using plant extracts. Biotechnol. Adv. 2013, 31, 346–356. [Google Scholar] [CrossRef]
- American Association for Laboratory Animal Science. Laboratory Animal Data: Quick Reference Guide for Researchers; The National Academies Press: Washington, DC, USA, 2002. [Google Scholar]
- Page Faulk, W.; Malcolm Taylor, G. Communication to the editors: An immunocolloid method for the electron microscope. Immunochemistry 1971, 8, 1081–1083. [Google Scholar] [CrossRef]
- Anselmo, A.C.; Mitragotri, S.J.T.A.J. A Review of Clinical Translation of Inorganic Nanoparticles. AAPS J. 2015, 17, 1041–1054. [Google Scholar] [CrossRef]
- Khlebtsov, N.; Dykman, L. Biodistribution and toxicity of engineered gold nanoparticles: A review of in vitro and in vivo studies. Chem. Soc. Rev. 2011, 40, 1647–1671. [Google Scholar] [CrossRef]
- Chithrani, B.D.; Ghazani, A.A.; Chan, W.C.W. Determining the Size and Shape Dependence of Gold Nanoparticle Uptake into Mammalian Cells. Nano Lett. 2006, 6, 662–668. [Google Scholar] [CrossRef]
- Mager, D.E.; Mody, V.; Xu, C.; Forrest, A.; Lesniak, W.G.; Nigavekar, S.S.; Kariapper, M.T.; Minc, L.; Khan, M.K.; Balogh, L.P. Physiologically based pharmacokinetic model for composite nanodevices: Effect of charge and size on in vivo disposition. Pharm. Res. 2012, 29, 2534–2542. [Google Scholar] [CrossRef]
- Sadauskas, E.; Wallin, H.; Stoltenberg, M.; Vogel, U.; Doering, P.; Larsen, A.; Danscher, G. Kupffer cells are central in the removal of nanoparticles from the organism. Part. Fibre Toxicol. 2007, 4, 10. [Google Scholar] [CrossRef]
- Gustafson, H.H.; Holt-Casper, D.; Grainger, D.W.; Ghandehari, H. Nanoparticle Uptake: The Phagocyte Problem. Nano Today 2015, 10, 487–510. [Google Scholar] [CrossRef]
- Li, M.; Zou, P.; Tyner, K.; Lee, S. Physiologically Based Pharmacokinetic (PBPK) Modeling of Pharmaceutical Nanoparticles. AAPS J. 2017, 19, 26–42. [Google Scholar] [CrossRef]
- Niederalt, C.; Kuepfer, L.; Solodenko, J.; Eissing, T.; Siegmund, H.U.; Block, M.; Willmann, S.; Lippert, J. A generic whole body physiologically based pharmacokinetic model for therapeutic proteins in PK-Sim. J. Pharmacokinet. Pharmacodyn. 2018, 45, 235–257. [Google Scholar] [CrossRef]
- Carlander, U.; Li, D.; Jolliet, O.; Emond, C.; Johanson, G. Toward a general physiologically-based pharmacokinetic model for intravenously injected nanoparticles. Int. J. Nanomed. 2016, 11, 625–640. [Google Scholar] [CrossRef]
- Ferl, G.Z.; Theil, F.-P.; Wong, H. Physiologically based pharmacokinetic models of small molecules and therapeutic antibodies: A mini-review on fundamental concepts and applications. Biopharm. Drug Dispos. 2016, 37, 75–92. [Google Scholar] [CrossRef]
- Malik, P.R.V.; Hamadeh, A.; Phipps, C.; Edginton, A.N. Population PBPK modelling of trastuzumab: A framework for quantifying and predicting inter-individual variability. J. Pharmacokinet. Pharmacodyn. 2017, 44, 277–290. [Google Scholar] [CrossRef]
- Nambiar, S.; Osei, E.; Fleck, A.; Darko, J.; Mutsaers, A.J.; Wettig, S. Synthesis of curcumin-functionalized gold nanoparticles and cytotoxicity studies in human prostate cancer cell line. Appl. Nanosci. 2018, 8, 347–357. [Google Scholar] [CrossRef]
- Blanco, E.; Shen, H.; Ferrari, M. Principles of nanoparticle design for overcoming biological barriers to drug delivery. Nat. Biotechnol. 2015, 33, 941. [Google Scholar] [CrossRef]
- Guerrero, S.; Araya, E.; Fiedler, J.L.; Arias, J.I.; Adura, C.; Albericio, F.; Giralt, E.; Arias, J.L.; Fernández, M.S.; Kogan, M.J. Improving the brain delivery of gold nanoparticles by conjugation with an amphipathic peptide. Nanomedcine 2010, 5, 897–913. [Google Scholar] [CrossRef]
- Balasubramanian, S.K.; Jittiwat, J.; Manikandan, J.; Ong, C.-N.; Yu, L.E.; Ong, W.-Y. Biodistribution of gold nanoparticles and gene expression changes in the liver and spleen after intravenous administration in rats. Biomaterials 2010, 31, 2034–2042. [Google Scholar] [CrossRef]
- Fraga, S.; Brandão, A.; Soares, M.E.; Morais, T.; Duarte, J.A.; Pereira, L.; Soares, L.; Neves, C.; Pereira, E.; Bastos, M.d.L.; et al. Short- and long-term distribution and toxicity of gold nanoparticles in the rat after a single-dose intravenous administration. Nanomed. Nanotechnol. Biol. Med. 2014, 10, 1757–1766. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Monteiro-Riviere, N.A.; Riviere, J.E. A physiologically based pharmacokinetic model for polyethylene glycol-coated gold nanoparticles of different sizes in adult mice. Nanotoxicology 2016, 10, 162–172. [Google Scholar] [CrossRef]
- Bachler, G.; von Goetz, N.; Hungerbühler, K. A physiologically based pharmacokinetic model for ionic silver and silver nanoparticles. Int. J. Nanomed. 2013, 8, 3365–3382. [Google Scholar] [CrossRef]
- Rippe, B.; Haraldsson, B. Transport of macromolecules across microvascular walls: The two-pore theory. Physiol. Rev. 1994, 74, 163–219. [Google Scholar] [CrossRef]
- Longmire, M.; Choyke, P.L.; Kobayashi, H. Clearance properties of nano-sized particles and molecules as imaging agents: Considerations and caveats. Nanomedicine 2008, 3, 703–717. [Google Scholar] [CrossRef]
- Shah, D.K.; Betts, A.M. Towards a platform PBPK model to characterize the plasma and tissue disposition of monoclonal antibodies in preclinical species and human. J. Pharmacokinet. Pharmacodyn. 2012, 39, 67–86. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Balthasar, J.P. Evaluation of a catenary PBPK model for predicting the in vivo disposition of mAbs engineered for high-affinity binding to FcRn. AAPS J. 2012, 14, 850–859. [Google Scholar] [CrossRef]
- Li, T.; Balthasar, J.P. Application of Physiologically Based Pharmacokinetic Modeling to Predict the Effects of FcRn Inhibitors in Mice, Rats, and Monkeys. J. Pharm. Sci. 2019, 108, 701–713. [Google Scholar] [CrossRef]
- Morales-Navarrete, H.; Segovia-Miranda, F.; Klukowski, P.; Meyer, K.; Nonaka, H.; Marsico, G.; Chernykh, M.; Kalaidzidis, A.; Zerial, M.; Kalaidzidis, Y. A versatile pipeline for the multi-scale digital reconstruction and quantitative analysis of 3D tissue architecture. eLife 2015, 4, e11214. [Google Scholar] [CrossRef] [PubMed]
- Baratta, J.L.; Ngo, A.; Lopez, B.; Kasabwalla, N.; Longmuir, K.J.; Robertson, R.T. Cellular organization of normal mouse liver: A histological, quantitative immunocytochemical, and fine structural analysis. Histochem. Cell Biol. 2009, 131, 713–726. [Google Scholar] [CrossRef]
- Blood Basics. Available online: https://www.hematology.org/Patients/Basics/ (accessed on 1 February 2019).
- Veerman, A.J.P.; van Ewijk, W. White pulp compartments in the spleen of rats and mice. Cell Tissue Res. 1975, 156, 417–441. [Google Scholar] [CrossRef] [PubMed]
- Markoe, A.M.; Okunewick, J.P. Changes in Spleen Cellularity and Erythrocyte Accumulation Following Rauscher Virus Infection in the Mouse. Scand. J. Haematol. 1973, 10, 273–281. [Google Scholar] [CrossRef] [PubMed]
- Beran, M.; Tribukait, B. The Quantitative Bone Marrow and Spleen Composition in Male NMRI and CBA Mice. Acta Haematol. 1971, 45, 55–64. [Google Scholar] [CrossRef]
- Alkilany, A.M.; Murphy, C.J. Toxicity and cellular uptake of gold nanoparticles: What we have learned so far? J. Nanopart. Res. 2010, 12, 2313–2333. [Google Scholar] [CrossRef] [PubMed]
- Park, J.W.; Shumaker-Parry, J.S. Structural study of citrate layers on gold nanoparticles: Role of intermolecular interactions in stabilizing nanoparticles. J. Am. Chem. Soc. 2014, 136, 1907–1921. [Google Scholar] [CrossRef]
- Sindhu, K.; Rajaram, A.; Sreeram, K.J.; Rajaram, R. Curcumin conjugated gold nanoparticle synthesis and its biocompatibility. RSC Adv. 2014, 4, 1808–1818. [Google Scholar] [CrossRef]
- Hirn, S.; Semmler-Behnke, M.; Schleh, C.; Wenk, A.; Lipka, J.; Schäffler, M.; Takenaka, S.; Möller, W.; Schmid, G.; Simon, U.; et al. Particle size-dependent and surface charge-dependent biodistribution of gold nanoparticles after intravenous administration. Eur. J. Pharm. Biopharm. 2011, 77, 407–416. [Google Scholar] [CrossRef] [PubMed]
- Hoshyar, N.; Gray, S.; Han, H.; Bao, G. The effect of nanoparticle size on in vivo pharmacokinetics and cellular interaction. Nanomedcine 2016, 11, 673–692. [Google Scholar] [CrossRef] [PubMed]
- Takeuchi, I.; Nobata, S.; Oiri, N.; Tomoda, K.; Makino, K. Biodistribution and excretion of colloidal gold nanoparticles after intravenous injection: Effects of particle size. Bio-Med. Mater. Eng. 2017, 28, 315–323. [Google Scholar] [CrossRef] [PubMed]
- Sahneh, F.D.; Scoglio, C.M.; Monteiro-Riviere, N.A.; Riviere, J.E. Predicting the impact of biocorona formation kinetics on interspecies extrapolations of nanoparticle biodistribution modeling. Nanomedcine 2015, 10, 25–33. [Google Scholar] [CrossRef]
- Sasidharan, A.; Riviere, J.E.; Monteiro-Riviere, N.A. Gold and silver nanoparticle interactions with human proteins: Impact and implications in biocorona formation. J. Mater. Chem. 2015, 3, 2075–2082. [Google Scholar] [CrossRef]
- Riviere, J.E. Of mice, men and nanoparticle biocoronas: Are in vitro to in vivo correlations and interspecies extrapolations realistic? Nanomedicine 2013, 8, 1357–1359. [Google Scholar] [CrossRef]
| Time Point (Days) | Number of Mice in EGCG-AuNP Arm | Number of Mice in Curc-AuNP Arm |
|---|---|---|
| 1 | 5C, 5T (10 total) | 5C, 6T (11 total) |
| 7 | 5C, 5T (10 total) | 5C, 6T (11 total) |
| 14 | 5C, 5T (10 total) | 5C, 6T (11 total) |
| 28 | 7C, 8T (15 total) | 7C, 8T (15 total) |
| 56 | 7C, 7T (14 total) | 7C, 8T (15 total) |
| Dataset | Species | Particle a | Dose | Organ PK b | Meas. Time |
|---|---|---|---|---|---|
| Balasubramanian et al. [25] | Rat | 20 nm Au with citrate | 0.01 mg Au/kg IV | Liver, Spleen, Lung, Kidney, Stomach, Intestine | 1, 7, 30 and 60 days |
| Fraga et al. [26] | Rat | 16 nm Au with citrate | 0.7 mg Au/kg IV | Liver, Spleen, Lung | 30 min and 28 days |
| AuNP | Hydrodynamic Diameter (nm) | Polydispersity Index (PDI) | Zeta Potential (mV) | Au Conc. (µg/mL) | Au Core Diameter (nm) | Nanoparticle Concentration (AuNP/mL) |
|---|---|---|---|---|---|---|
| EGCG-AuNP | 25.00 ± 0.172 | 0.173 ± 0.007 a | −22 | 422.790 | 7.78 ± 2.59 | |
| Curc-AuNP | 19.62 ± 0.09 | 0.167 ± 0.002 | −20 | 391.430 | 6.21 ± 3.36 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aborig, M.; Malik, P.R.V.; Nambiar, S.; Chelle, P.; Darko, J.; Mutsaers, A.; Edginton, A.N.; Fleck, A.; Osei, E.; Wettig, S. Biodistribution and Physiologically-Based Pharmacokinetic Modeling of Gold Nanoparticles in Mice with Interspecies Extrapolation. Pharmaceutics 2019, 11, 179. https://doi.org/10.3390/pharmaceutics11040179
Aborig M, Malik PRV, Nambiar S, Chelle P, Darko J, Mutsaers A, Edginton AN, Fleck A, Osei E, Wettig S. Biodistribution and Physiologically-Based Pharmacokinetic Modeling of Gold Nanoparticles in Mice with Interspecies Extrapolation. Pharmaceutics. 2019; 11(4):179. https://doi.org/10.3390/pharmaceutics11040179
Chicago/Turabian StyleAborig, Mohamed, Paul R. V. Malik, Shruti Nambiar, Pierre Chelle, Johnson Darko, Anthony Mutsaers, Andrea N. Edginton, Andre Fleck, Ernest Osei, and Shawn Wettig. 2019. "Biodistribution and Physiologically-Based Pharmacokinetic Modeling of Gold Nanoparticles in Mice with Interspecies Extrapolation" Pharmaceutics 11, no. 4: 179. https://doi.org/10.3390/pharmaceutics11040179
APA StyleAborig, M., Malik, P. R. V., Nambiar, S., Chelle, P., Darko, J., Mutsaers, A., Edginton, A. N., Fleck, A., Osei, E., & Wettig, S. (2019). Biodistribution and Physiologically-Based Pharmacokinetic Modeling of Gold Nanoparticles in Mice with Interspecies Extrapolation. Pharmaceutics, 11(4), 179. https://doi.org/10.3390/pharmaceutics11040179