A Bioinformatic Pipeline for Monitoring of the Mutational Stability of Viral Drug Targets with Deep-Sequencing Technology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of Libraries for the Deep Sequencing of RNA Interference Targets
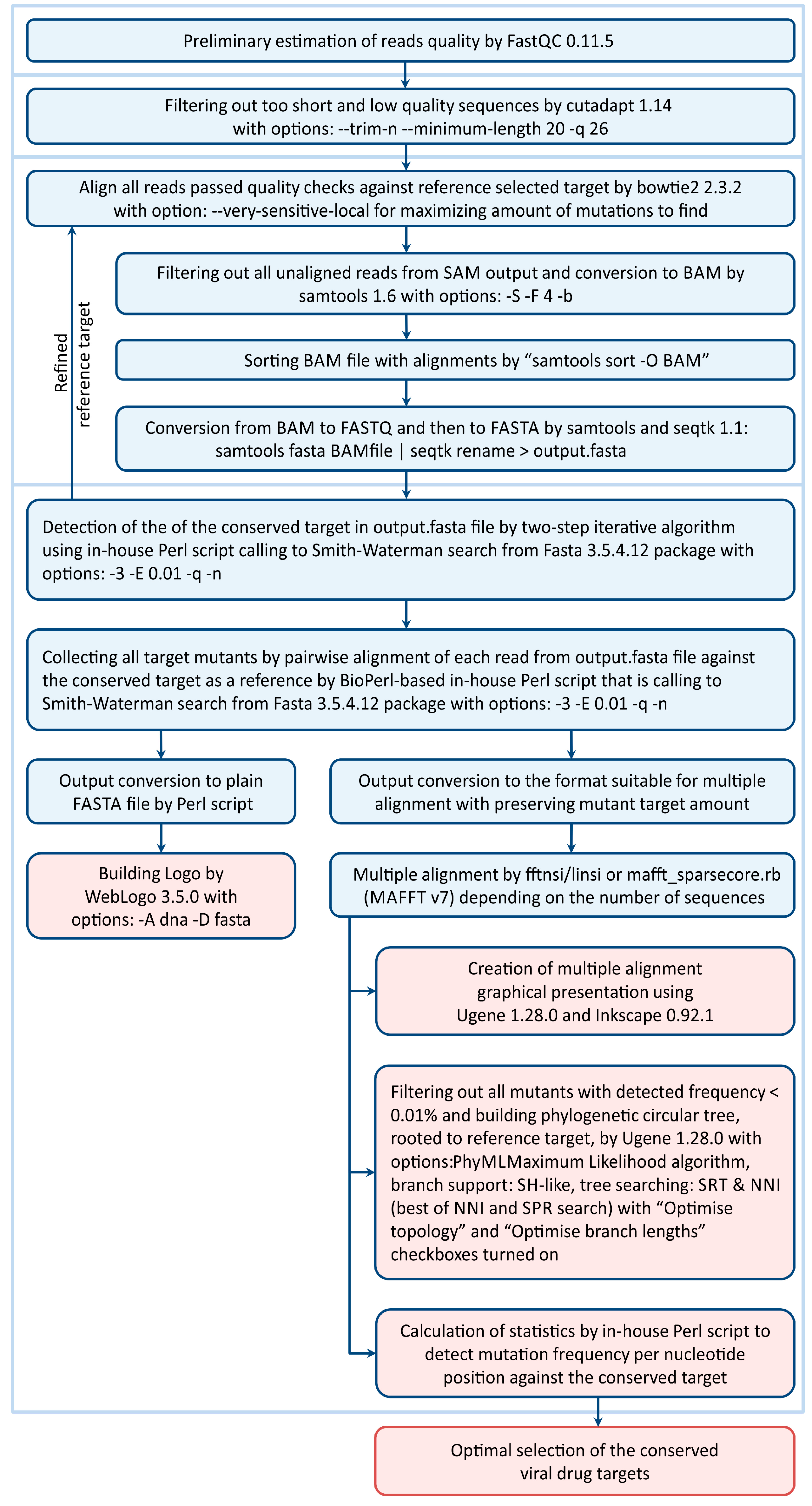
2.2. Bioinformatic Pipeline and Data Processing
3. Results
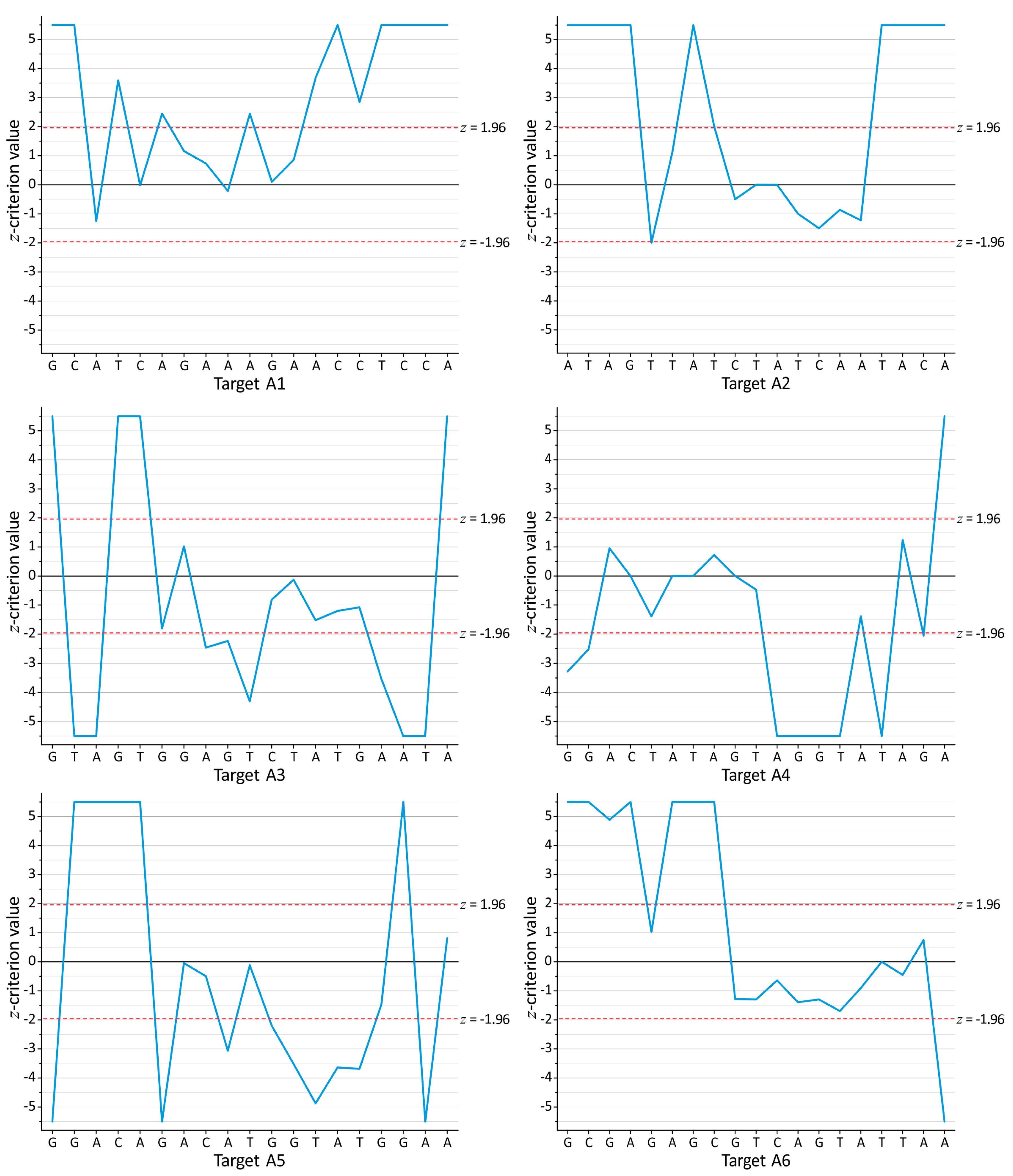
3.1. Search for the Conserved Targets and Statistical Criteria for Deep Sequencing Data Arrays
3.2. The Scheme of the Bioinformatic Pipeline
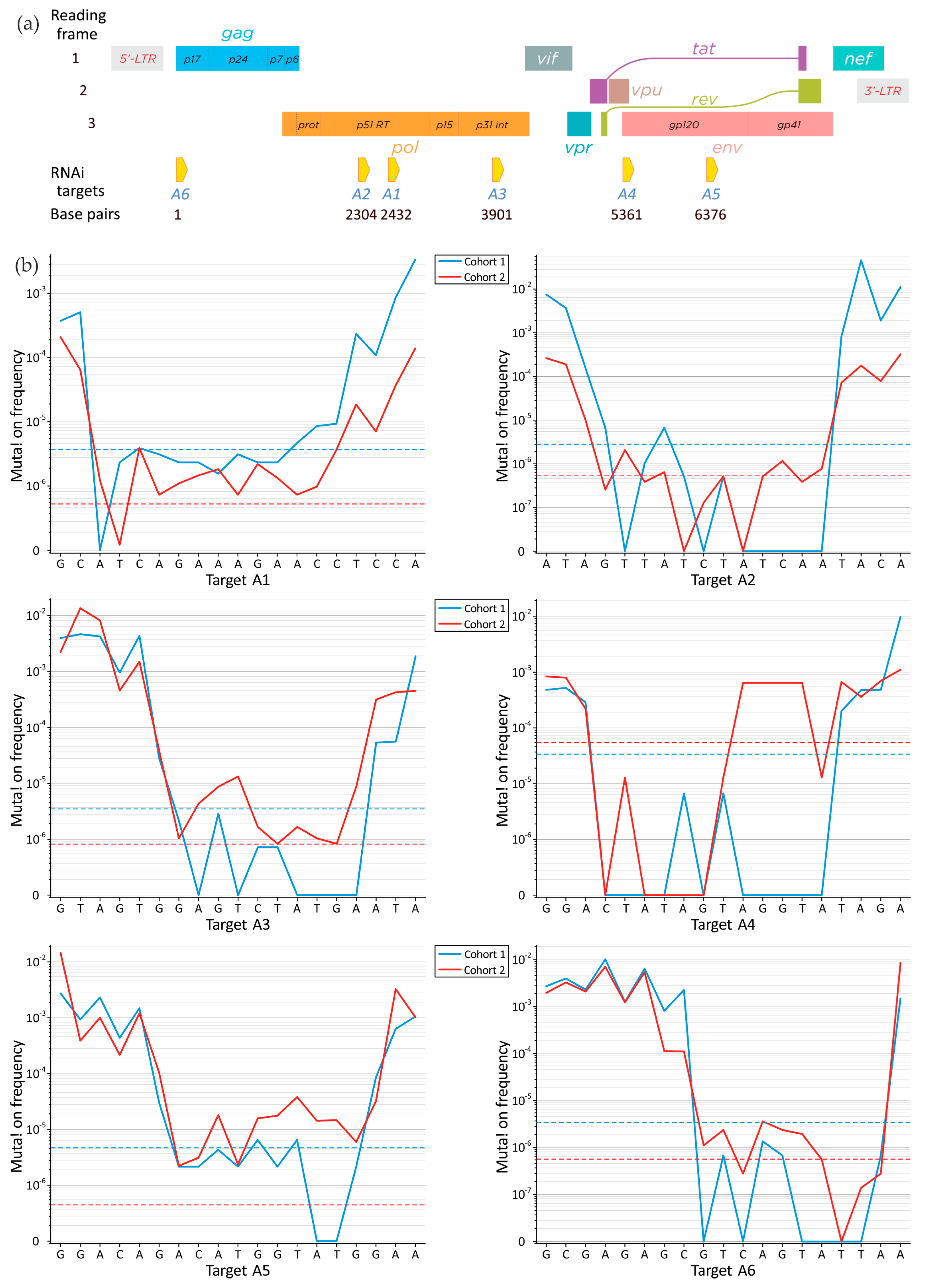
3.3. Mutations in RNA Interference Targets for HIV-1 Subtype A
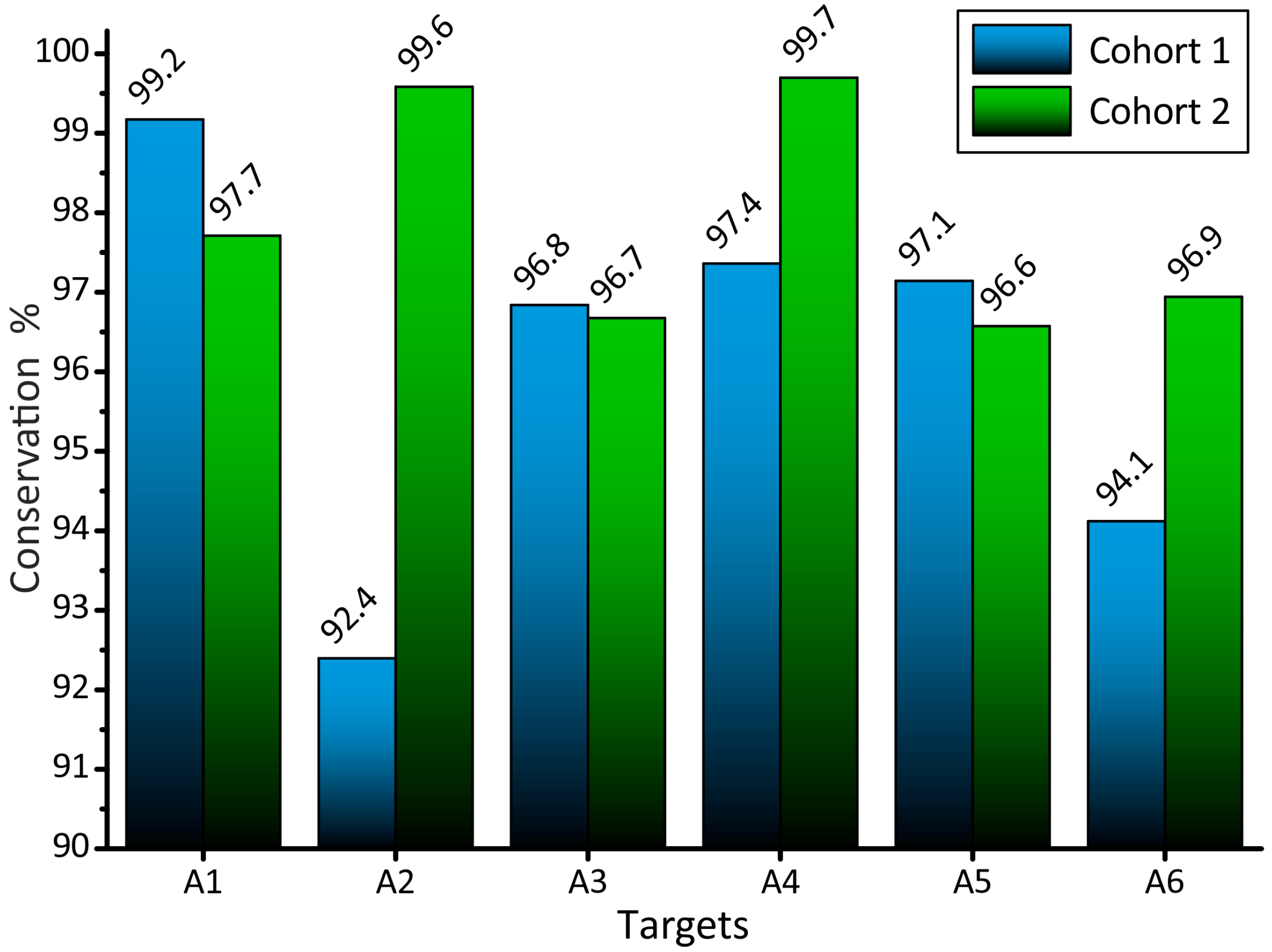
3.4. Conservation of RNA Interference Targets for HIV-1 Subtype A
4. Discussion
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yacoby, I.; Benhar, I. Targeted anti bacterial therapy. Infect. Disord. Drug Targets 2007, 7, 221–229. [Google Scholar] [CrossRef] [PubMed]
- Muller, B.; Krausslich, H.G. Antiviral strategies. Handb. Exp. Pharmacol. 2009, 1–24. [Google Scholar] [CrossRef]
- Lou, Z.; Sun, Y.; Rao, Z. Current progress in antiviral strategies. Trends Pharmacol. Sci. 2014, 35, 86–102. [Google Scholar] [CrossRef] [PubMed]
- Wainberg, M.A.; Zaharatos, G.J.; Brenner, B.G. Development of antiretroviral drug resistance. N. Engl. J. Med. 2011, 365, 637–646. [Google Scholar] [CrossRef] [PubMed]
- Houldcroft, C.J.; Beale, M.A.; Breuer, J. Clinical and biological insights from viral genome sequencing. Nat. Rev. Microbiol. 2017, 15, 183–192. [Google Scholar] [CrossRef] [PubMed]
- Dye, C.; Mertens, T.; Hirnschall, G.; Mpanju-Shumbusho, W.; Newman, R.D.; Raviglione, M.C.; Savioli, L.; Nakatani, H. WHO and the future of disease control programmes. Lancet 2013, 381, 413–418. [Google Scholar] [CrossRef]
- Quiñones-Mateu, M.E.; Ávila, S.; Reyes-Terán, G.; Martínez, M.A. Deep sequencing: Becoming a critical tool in clinical virology. J. Clin. Virol. 2014, 61, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Chabria, S.B.; Gupta, S.; Kozal, M.J. Deep sequencing of HIV: Clinical and research applications. Annu. Rev. Genom. Hum. Genet. 2014, 15, 295–325. [Google Scholar] [CrossRef] [PubMed]
- Lefterova, M.I.; Suárez, C.J.; Banaei, N.; Pinsky, B.A. Next-Generation Sequencing for Infectious Disease Diagnosis and Management: A Report of the Association for Molecular Pathology. J. Mol. Diagn. 2015, 17, 623–634. [Google Scholar] [CrossRef] [PubMed]
- Van Laethem, K.; Theys, K.; Vandamme, A.M. HIV-1 genotypic drug resistance testing: Digging deep, reaching wide? Curr. Opin. Virol. 2015, 14, 16–23. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zou, X.; He, J.; Zheng, J.; Chiarella, J.; Kozal, M.J. HIV Drug Resistance Mutations (DRMs) Detected by Deep Sequencing in Virologic Failure Subjects on Therapy from Hunan Province, China. PLoS ONE 2016, 11, 0149215. [Google Scholar] [CrossRef] [PubMed]
- Yin, Q.Q.; Li, Z.P.; Zhao, H.; Pan, D.; Wang, Y.; Xu, W.S.; Xing, H.; Feng, Y.; Jiang, S.B.; Shao, Y.M.; et al. Distinctive Drug-resistant Mutation Profiles and Interpretations of HIV-1 Proviral DNA Revealed by Deep Sequencing in Reverse Transcriptase. Biomed. Environ. Sci. 2016, 29, 239–247. [Google Scholar] [CrossRef] [PubMed]
- Leipzig, J. A review of bioinformatic pipeline frameworks. Brief. Bioinform. 2017, 18, 530–536. [Google Scholar] [CrossRef] [PubMed]
- Posada-Céspedes, S.; Seifert, D.; Beerenwinkel, N. Recent advances in inferring viral diversity from high-throughput sequencing data. Virus Res. 2017, 239, 17–32. [Google Scholar] [CrossRef] [PubMed]
- Sharma, R.K. A review on new horizons of bioinformatics in next generation sequencing, viral and cancer genomics. Int. J. Biomed. Data Min. 2016, 5, 122. [Google Scholar] [CrossRef]
- Tchurikov, N.A.; Fedoseeva, D.M.; Gashnikova, N.M.; Sosin, D.V.; Gorbacheva, M.A.; Alembekov, I.R.; Chechetkin, V.R.; Kravatsky, Y.V.; Kretova, O.V. Conserved sequences in the current strains of HIV-1 subtype A in Russia are effectively targeted by artificial RNAi in vitro. Gene 2016, 583, 78–83. [Google Scholar] [CrossRef] [PubMed]
- Kretova, O.V.; Chechetkin, V.R.; Fedoseeva, D.M.; Kravatsky, Y.V.; Sosin, D.V.; Alembekov, I.R.; Gorbacheva, M.A.; Gashnikova, N.M.; Tchurikov, N.A. Analysis of variability in HIV-1 subtype a strains in Russia suggests a combination of deep sequencing and multitarget RNA interference for silencing of the virus. AIDS Res. Hum. Retrovir. 2017, 33, 194–201. [Google Scholar] [CrossRef] [PubMed]
- Kravatsky, Y.V.; Chechetkin, V.R.; Fedoseeva, D.M.; Gorbacheva, M.A.; Kretova, O.V.; Tchurikov, N.A. Mutation frequencies in HIV-1 subtype-A genome in regions containing efficient RNAi targets. Mol. Biol. 2016, 50, 480–485. [Google Scholar] [CrossRef]
- Casadella, M.; Paredes, R. Deep sequencing for HIV-1 clinical management. Virus Res. 2017, 239, 69–81. [Google Scholar] [CrossRef] [PubMed]
- Noguera-Julián, M.; Edgil, D.; Harrigan, P.R.; Sandstrom, P.; Godfrey, C.; Paredes, R. Next-generation human immunodeficiency virus sequencing for patient management and drug resistance surveillance. J. Infect. Dis. 2017. [Google Scholar] [CrossRef] [PubMed]
- Andrews, S. FastQC: A Quality Control Tool for High Throughput Sequence Data. 2010. Available online: http://www.bioinformatics.babraham.ac.uk/projects/fastqc (accessed on 22 November 2017).
- Martin, M. Cutadapt removes adapter sequences from high-throughput sequencing reads. EMBnet J. 2011, 3. [Google Scholar] [CrossRef]
- Del Fabbro, C.; Scalabrin, S.; Morgante, M.; Giorgi, F.M. An extensive evaluation of read trimming effects on Illumina NGS data analysis. PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed]
- Langmead, B.; Salzberg, S.L. Fast gapped-read alignment with Bowtie 2. Nat. Methods 2012, 9, 357–359. [Google Scholar] [CrossRef] [PubMed]
- Liao, Y.; Smyth, G.K.; Shi, W. The Subread aligner: Fast, accurate and scalable read mapping by seed-and-vote. Nucleic Acids Res. 2013, 41. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Handsaker, B.; Wysoker, A.; Fennell, T.; Ruan, J.; Homer, N.; Marth, G.; Abecasis, G.; Durbin, R.; Genome Project Data Processing Subgroup. The Sequence Alignment/Map format and SAMtools. Bioinformatics 2009, 25, 2078–2079. [Google Scholar] [CrossRef] [PubMed]
- Katoh, K.; Standley, D.M. MAFFT multiple sequence alignment software version 7: Improvements in performance and usability. Mol. Biol. Evol. 2013, 30, 772–780. [Google Scholar] [CrossRef] [PubMed]
- Okonechnikov, K.; Golosova, O.; Fursov, M.; the UGENE team. Unipro UGENE: A unified bioinformatics toolkit. Bioinformatics 2012, 28, 1166–1167. [Google Scholar] [CrossRef] [PubMed]
- Crooks, G.E.; Hon, G.; Chandonia, J.M.; Brenner, S.E. WebLogo: A sequence logo generator. Genom. Res. 2004, 14, 1188–1190. [Google Scholar] [CrossRef] [PubMed]
- Johnson, N.L.; Leone, F.C. Statistics and Experimental Design in Engineering and the Physical Sciences, 2nd ed.; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Weir, B.S. Genetic Data Analysis II: Methods for Discrete Population Genetic Data; Sinauer Associates: Sunderland, MA, USA, 1996; pp. 32–51. [Google Scholar]
- Archer, J.; Rambaut, A.; Taillon, B.E.; Harrigan, P.R.; Lewis, M.; Robertson, D.L. The evolutionary analysis of emerging low frequency HIV-1 CXCR4 using variants through time—An ultra-deep approach. PLoS Comput. Biol. 2010, 6. [Google Scholar] [CrossRef] [PubMed]
- Lebbink, R.J.; de Jong, D.C.; Wolters, F.; Kruse, E.M.; van Ham, P.M.; Wiertz, E.J.; Nijhuis, M. A combinational CRISPR/Cas9 gene-editing approach can halt HIV replication and prevent viral escape. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Nair, M. A CRISPR/Cas9 guidance RNA screen platform for HIV provirus disruption and HIV/AIDS gene therapy in astrocytes. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kravatsky, Y.; Chechetkin, V.; Fedoseeva, D.; Gorbacheva, M.; Kravatskaya, G.; Kretova, O.; Tchurikov, N. A Bioinformatic Pipeline for Monitoring of the Mutational Stability of Viral Drug Targets with Deep-Sequencing Technology. Viruses 2017, 9, 357. https://doi.org/10.3390/v9120357
Kravatsky Y, Chechetkin V, Fedoseeva D, Gorbacheva M, Kravatskaya G, Kretova O, Tchurikov N. A Bioinformatic Pipeline for Monitoring of the Mutational Stability of Viral Drug Targets with Deep-Sequencing Technology. Viruses. 2017; 9(12):357. https://doi.org/10.3390/v9120357
Chicago/Turabian StyleKravatsky, Yuri, Vladimir Chechetkin, Daria Fedoseeva, Maria Gorbacheva, Galina Kravatskaya, Olga Kretova, and Nickolai Tchurikov. 2017. "A Bioinformatic Pipeline for Monitoring of the Mutational Stability of Viral Drug Targets with Deep-Sequencing Technology" Viruses 9, no. 12: 357. https://doi.org/10.3390/v9120357
APA StyleKravatsky, Y., Chechetkin, V., Fedoseeva, D., Gorbacheva, M., Kravatskaya, G., Kretova, O., & Tchurikov, N. (2017). A Bioinformatic Pipeline for Monitoring of the Mutational Stability of Viral Drug Targets with Deep-Sequencing Technology. Viruses, 9(12), 357. https://doi.org/10.3390/v9120357




