Bayesian Binary Mixture Models as a Flexible Alternative to Cut-Off Analysis of ELISA Results, a Case Study of Seoul Orthohantavirus
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
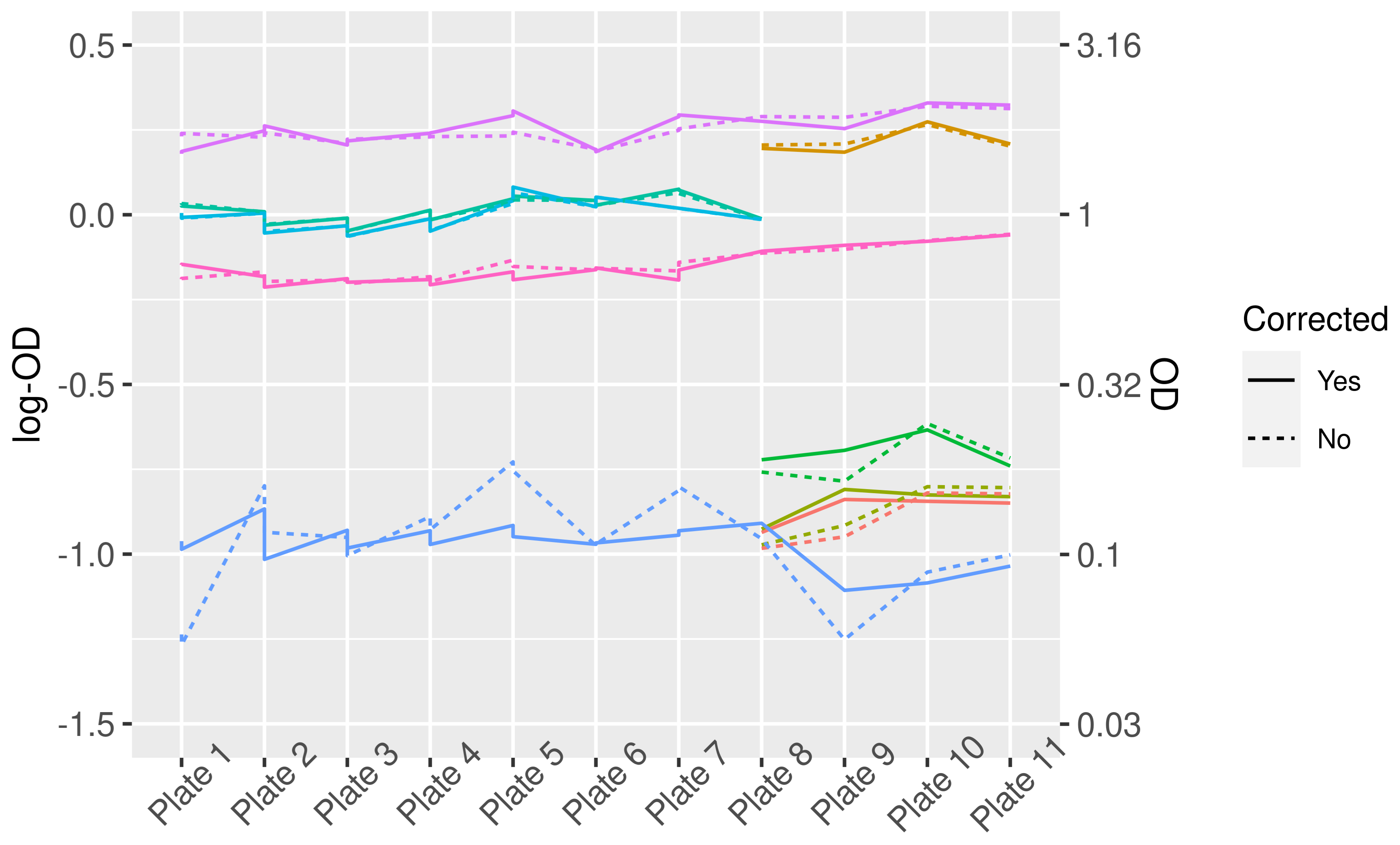
2.2. Plate-to-Plate Variation
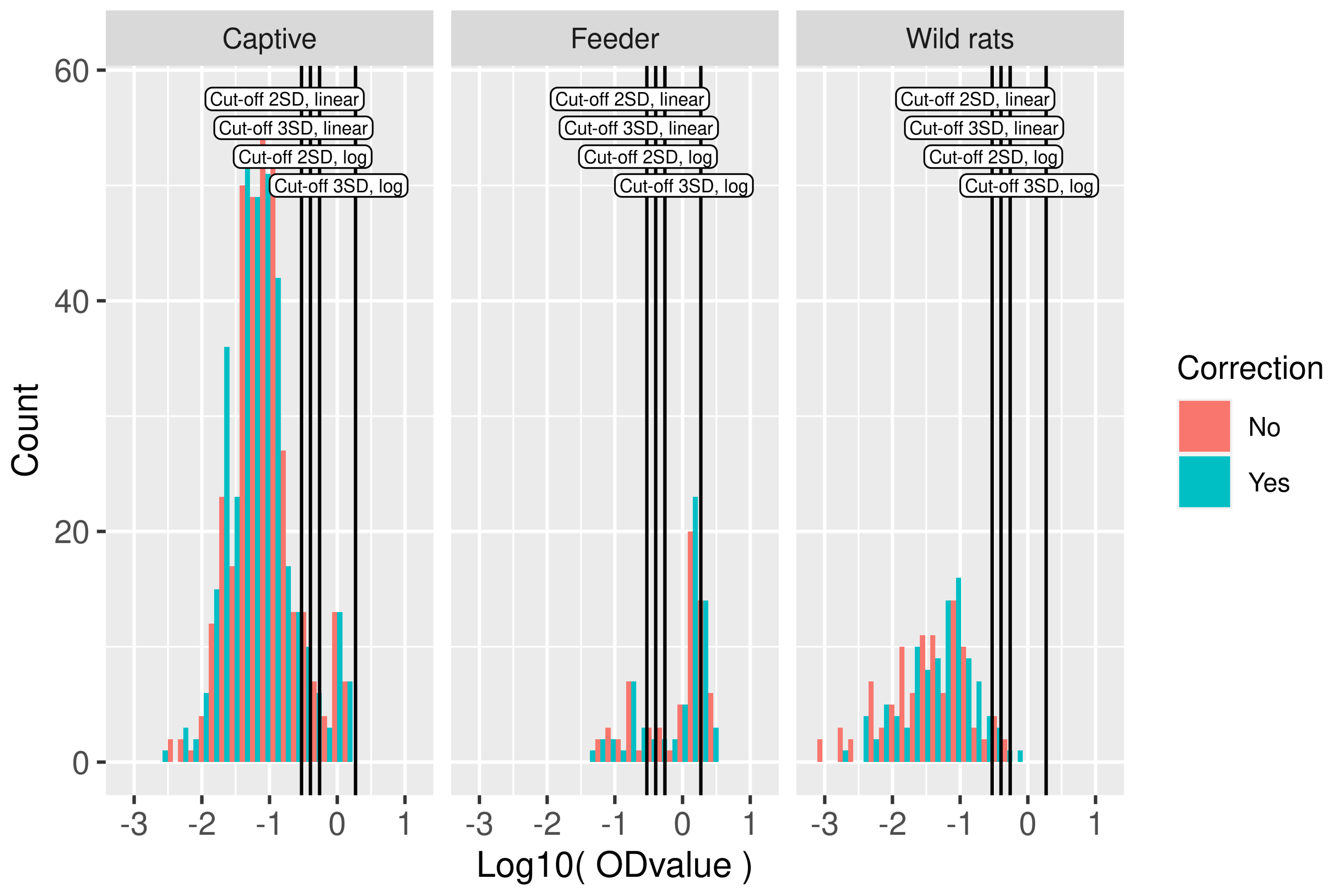
2.3. Cut-Off Analysis
2.4. Mixture Modeling
- The distribution of logOD values in both the positive and negative populations is Gaussian;
- The two components of the mixture each represent natural variation between animals.
2.5. Sample Matrices
2.6. Censoring
2.7. Prediction of Serological Status
2.8. Model Accuracy
2.9. Model Implementation and Checking
3. Results
3.1. Plate-to-Plate Variation
3.2. Serological Results and Cut-Off Value
3.3. Parameter Estimates from Mixture Modeling
3.4. Model Performance
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PPV | Positive predictive value |
| NPV | Negative predictive value |
| RT-qPCR | Real-time quantitative polymerase chain reaction |
| ELISA | Enzyme-linked immunosorbent assay (ELISA) |
| SEOV | Seoul orthohantavirus |
| HFRS | Hemorrhagic fever with renal syndrome |
| OD | Optical density |
| SPF | Specific-pathogen-free |
Appendix A
Appendix A.1. Equations
Appendix A.2. Accuracy Measures
Appendix A.3. Model Checks
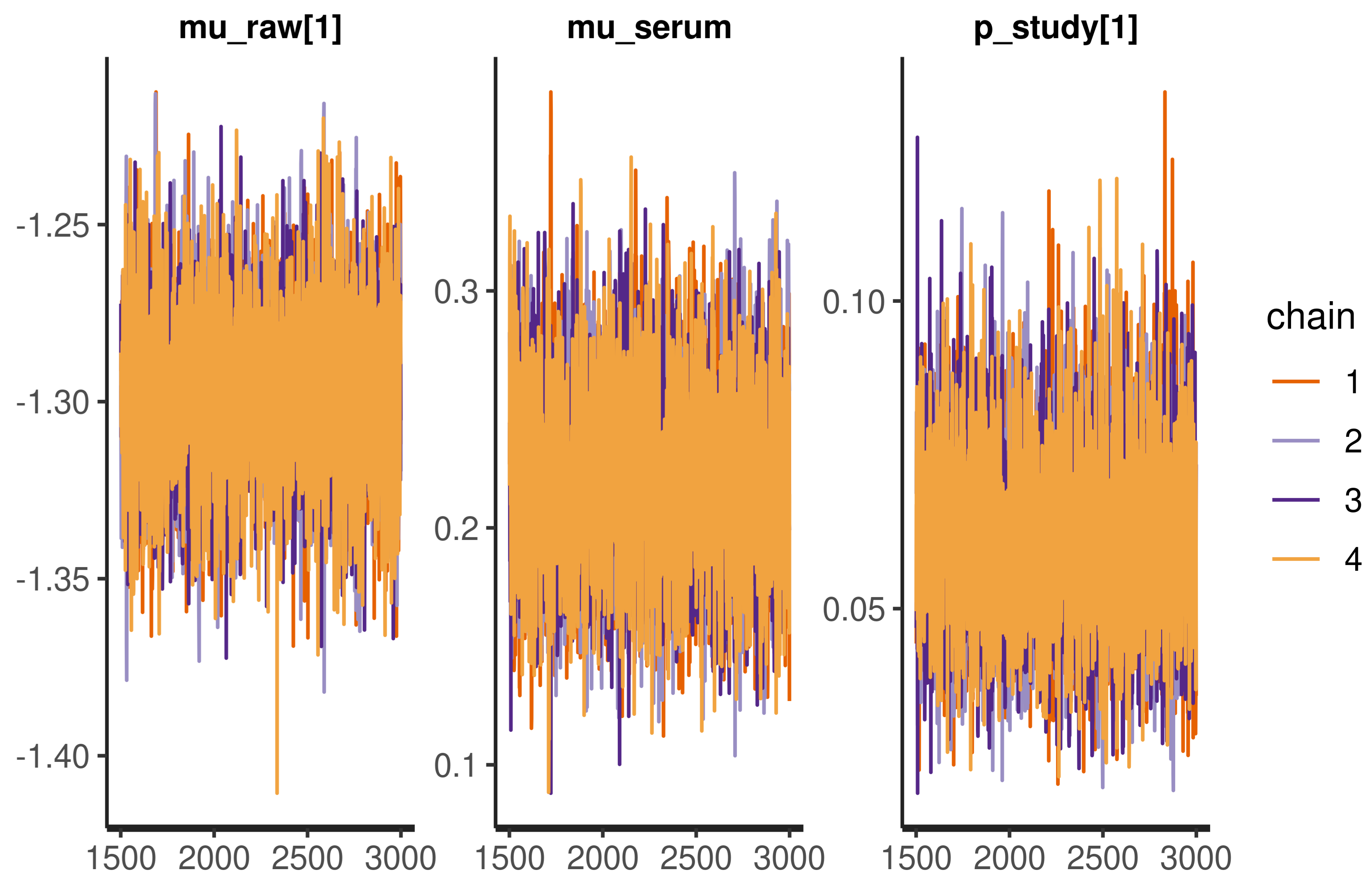

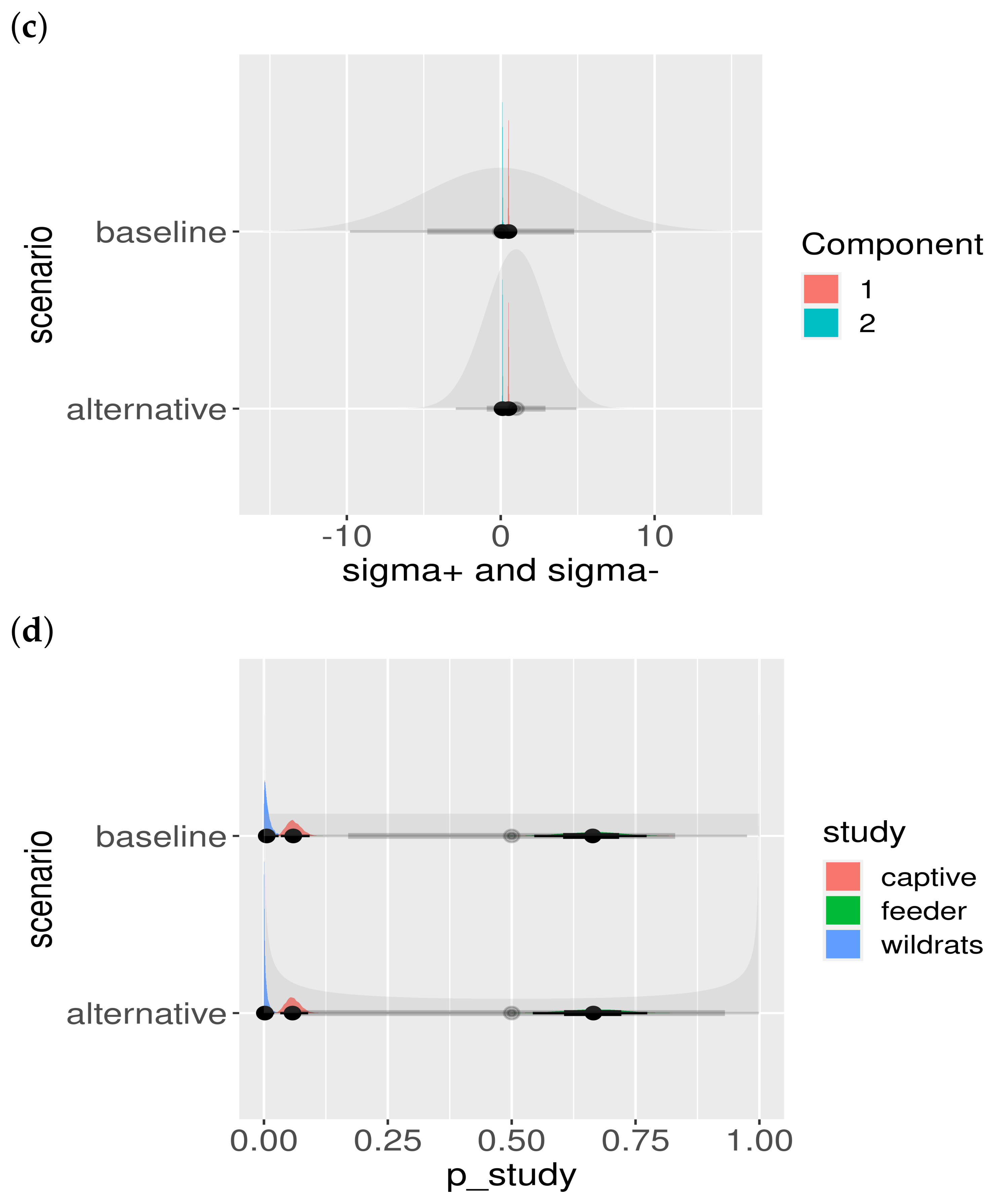
Appendix A.4. Appendix Classification Results
| Mixture | Cutoff 2SD Linear | Cutoff 3SD Linear | Cutoff 2SD | Cutoff 3SD | n |
|---|---|---|---|---|---|
| 11 | 20 | 15 | 13 | 0 | 175 |
| 67 | 67 | 67 | 67 | 67 | 67 |
| 20 | 23 | 21 | 21 | 20 | 69 |
Appendix A.5. Appendix Implementation

References
- Jacobson, R. Validation of serological assays for diagnosis of infectious diseases. Rev. Sci. Tech. Off. Int. Epizoot. 1998, 17, 469–486. [Google Scholar] [CrossRef]
- Greiner, M.; Gardner, I. Application of diagnostic tests in veterinary epidemiologic studies. Prev. Vet. Med. 2000, 45, 43–59. [Google Scholar] [CrossRef]
- Entine, O.A.; Small, D.S.; Jensen, S.T.; Sanchez, G.; Bastos, M.; Verastegui, M.R.; Levy, M.Z. Disease diagnosis from immunoassays with plate to plate variability: A hierarchical Bayesian approach. Stat. Biosci. 2015, 7, 206–224. [Google Scholar] [CrossRef]
- Zweig, M.H.; Campbell, G. Receiver-operating characteristic (ROC) plots: A fundamental evaluation tool in clinical medicine. Clin. Chem. 1993, 39, 561–577. [Google Scholar] [CrossRef]
- Rogan, W.J.; Gladen, B. Estimating prevalence from the results of a screening test. Am. J. Epidemiol. 1978, 107, 71–76. [Google Scholar] [CrossRef] [PubMed]
- Gardner, I.A. An epidemiologic critique of current microbial risk assessment practices: The importance of prevalence and test accuracy data. J. Food Prot. 2004, 67, 2000–2007. [Google Scholar] [CrossRef] [PubMed]
- McLachlan, G.J.; Lee, S.X.; Rathnayake, S.I. Finite mixture models. Annu. Rev. Stat. Appl. 2019, 6, 355–378. [Google Scholar] [CrossRef]
- Clement, J.; LeDuc, J.W.; Lloyd, G.; Reynes, J.M.; McElhinney, L.; Van Ranst, M.; Lee, H.W. Wild rats, laboratory rats, pet rats: Global Seoul hantavirus disease revisited. Viruses 2019, 11, 652. [Google Scholar] [CrossRef] [PubMed]
- Cuperus, T.; de Vries, A.; Hoornweg, T.; Fonville, M.; Jaarsma, R.I.; Opsteegh, M.; Maas, M. Seoul virus in pet and feeder rats in The Netherlands. Viruses 2021, 13, 443. [Google Scholar] [CrossRef] [PubMed]
- Swanink, C.; Reimerink, J.; Gisolf, J.; de Vries, A.; Claassen, M.; Martens, L.; Waegemaekers, T.; Rozendaal, H.; Valkenburgh, S.; Hoornweg, T.; et al. Autochthonous Human Case of Seoul Virus Infection, The Netherlands. Emerg. Infect. Dis. 2018, 24, 2158. [Google Scholar] [CrossRef] [PubMed]
- Maas, M.; van Heteren, M.; de Vries, A.; Kuiken, T.; Hoornweg, T.; Veldhuis Kroeze, E.; Rockx, B. Seoul virus tropism and pathology in naturally infected feeder rats. Viruses 2019, 11, 531. [Google Scholar] [CrossRef] [PubMed]
- Opsteegh, M.; Teunis, P.; Mensink, M.; Züchner, L.; Titilincu, A.; Langelaar, M.; van der Giessen, J. Evaluation of ELISA test characteristics and estimation of Toxoplasma gondii seroprevalence in Dutch sheep using mixture models. Prev. Vet. Med. 2010, 96, 232–240. [Google Scholar] [CrossRef] [PubMed]
- Stan Development Team. Stan Modeling Language Users Guide and Reference Manual, 2.25 2020.
- Stan Development Team. RStan: The R interface to Stan. R Package Version 2.21.2. 2020.
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Compton, S.; Jacoby, R.; Paturzo, F.; Smith, A. Persistent Seoul virus infection in Lewis rats. Arch. Virol. 2004, 149, 1325–1339. [Google Scholar] [CrossRef] [PubMed]
- Meyer, B.J.; Schmaljohn, C.S. Persistent hantavirus infections: Characteristics and mechanisms. Trends Microbiol. 2000, 8, 61–67. [Google Scholar] [CrossRef]
- Opsteegh, M.; Haveman, R.; Swart, A.; Mensink-Beerepoot, M.; Hofhuis, A.; Langelaar, M.; Van der Giessen, J. Seroprevalence and risk factors for Toxoplasma gondii infection in domestic cats in The Netherlands. Prev. Vet. Med. 2012, 104, 317–326. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Dam-Deisz, C.; Luttikholt, S.; Maas, M.; Nielen, M.; Swart, A.; Vellema, P.; van der Giessen, J.; Opsteegh, M. Risk factors related to Toxoplasma gondii seroprevalence in indoor-housed Dutch dairy goats. Prev. Vet. Med. 2016, 124, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Greiner, M.; Franke, C.; Böhning, D.; Schlattmann, P. Construction of an intrinsic cut-off value for the sero-epidemiological study of Trypanosoma evansi infections in a canine population in Brazil: A new approach towards an unbiased estimation of prevalence. Acta Trop. 1994, 56, 97–109. [Google Scholar] [CrossRef]
- Branscum, A.; Gardner, I.; Johnson, W. Estimation of diagnostic-test sensitivity and specificity through Bayesian modeling. Prev. Vet. Med. 2005, 68, 145–163. [Google Scholar] [CrossRef] [PubMed]
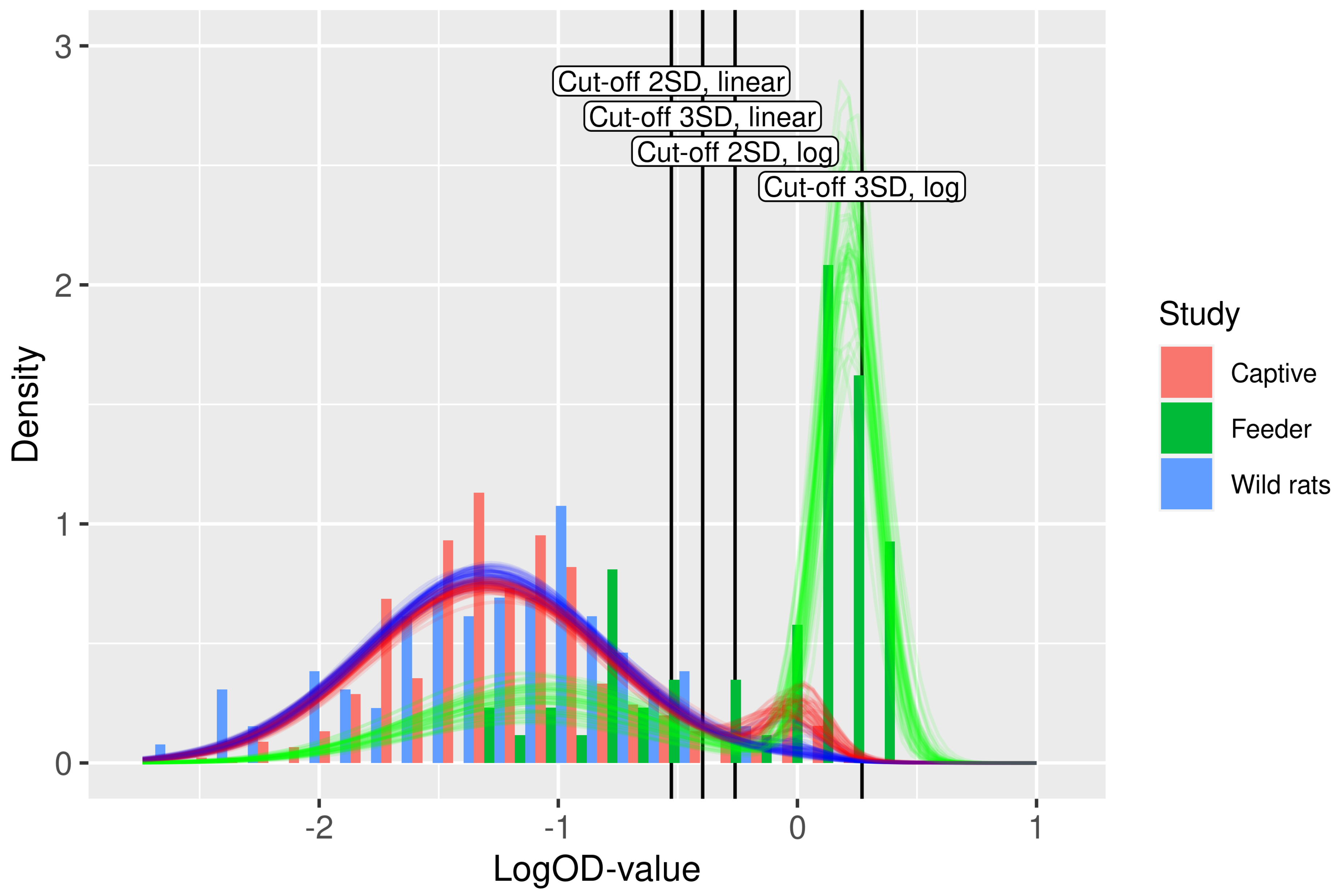
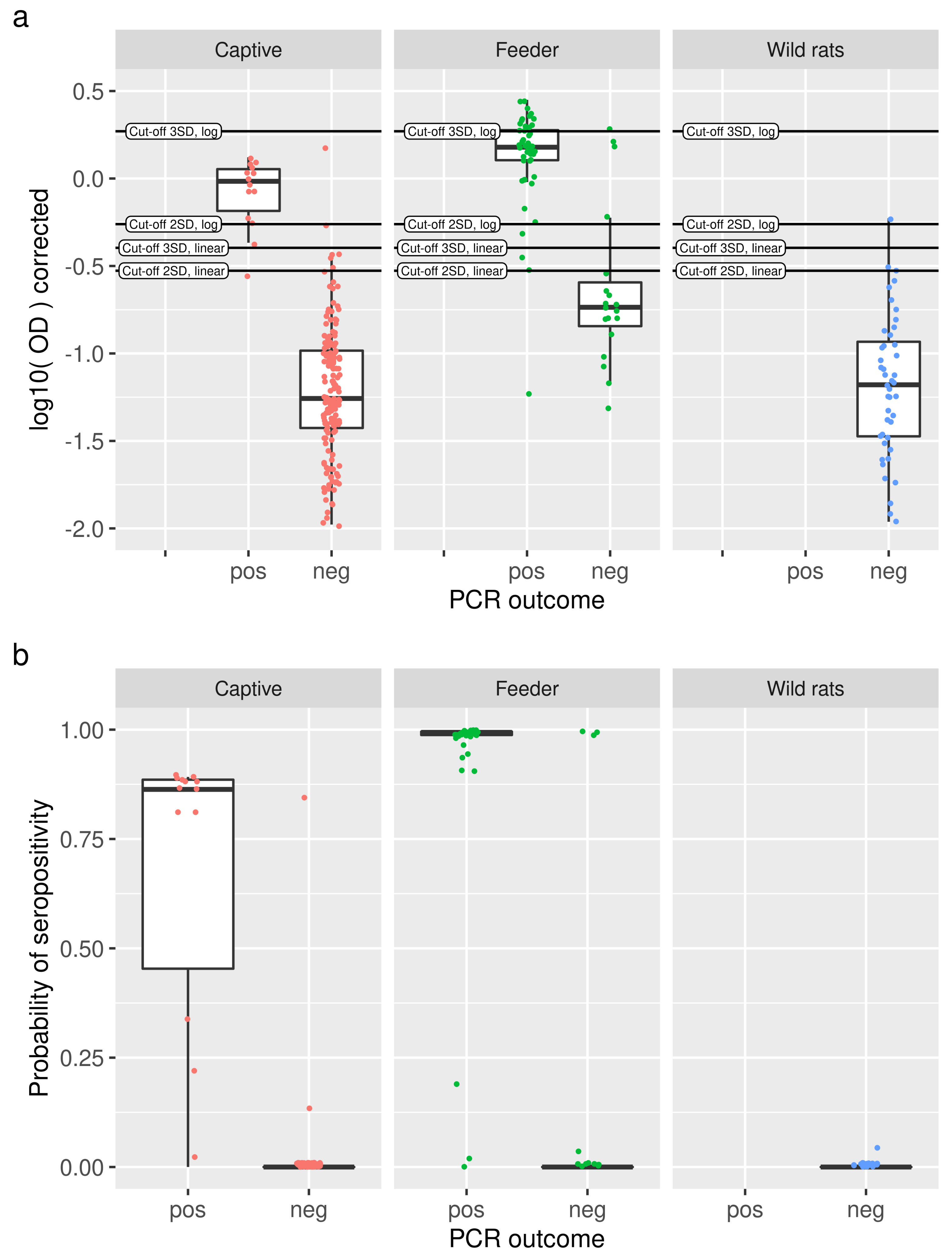
| Sample Matrix | 2018 | 2016 | |
|---|---|---|---|
| Captive Rat Study | Wild Rat Study | Feeder Rat Study | |
| heart fluid | 175 | 69 | 2 |
| serum | 0 | 0 | 67 |
| Parameter | Negative | Positive | Both |
|---|---|---|---|
| −1.30 (−1.35, −1.25) | −0.00 (−0.08, 0.06) | - | |
| - | - | 0.22 (0.15, 0.30) | |
| 0.51 (0.47, 0.55) | 0.12 (0.09, 0.15) | - | |
| - | - | 0.06 (0.03, 0.09) | |
| - | - | 0.66 (0.54, 0.77) | |
| - | - | 0.01 (0.00, 0.03) |
| Accuracy | Sensitivity | Specificity | PPV | NPV | |
|---|---|---|---|---|---|
| Captive study | |||||
| Binary mixture P(pos) > 0.5 | |||||
| Binary mixture theoretical | |||||
| Cutoff2 | |||||
| Cutoff2 linear | |||||
| Cutoff3 | - | - | |||
| Cutoff3 linear | |||||
| Feeder study | |||||
| Binary mixture P(pos) > 0.5 | - | ||||
| Binary mixture theoretical | |||||
| Cutoff2 | - | ||||
| Cutoff2 linear | - | ||||
| Cutoff3 | - | - | |||
| Cutoff3 linear | - | ||||
| Wild rats | |||||
| Binary mixture P(pos) > 0.5 | - | - | - | ||
| Cutoff2 | - | - | - | ||
| Cutoff2 linear | - | - | - | ||
| Cutoff3 | - | - | - | - | |
| Cutoff3 linear | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Swart, A.; Maas, M.; de Vries, A.; Cuperus, T.; Opsteegh, M. Bayesian Binary Mixture Models as a Flexible Alternative to Cut-Off Analysis of ELISA Results, a Case Study of Seoul Orthohantavirus. Viruses 2021, 13, 1155. https://doi.org/10.3390/v13061155
Swart A, Maas M, de Vries A, Cuperus T, Opsteegh M. Bayesian Binary Mixture Models as a Flexible Alternative to Cut-Off Analysis of ELISA Results, a Case Study of Seoul Orthohantavirus. Viruses. 2021; 13(6):1155. https://doi.org/10.3390/v13061155
Chicago/Turabian StyleSwart, Arno, Miriam Maas, Ankje de Vries, Tryntsje Cuperus, and Marieke Opsteegh. 2021. "Bayesian Binary Mixture Models as a Flexible Alternative to Cut-Off Analysis of ELISA Results, a Case Study of Seoul Orthohantavirus" Viruses 13, no. 6: 1155. https://doi.org/10.3390/v13061155
APA StyleSwart, A., Maas, M., de Vries, A., Cuperus, T., & Opsteegh, M. (2021). Bayesian Binary Mixture Models as a Flexible Alternative to Cut-Off Analysis of ELISA Results, a Case Study of Seoul Orthohantavirus. Viruses, 13(6), 1155. https://doi.org/10.3390/v13061155






