Estimating Vaccine-Driven Selection in Seasonal Influenza
Abstract
1. Introduction
2. Materials and Methods
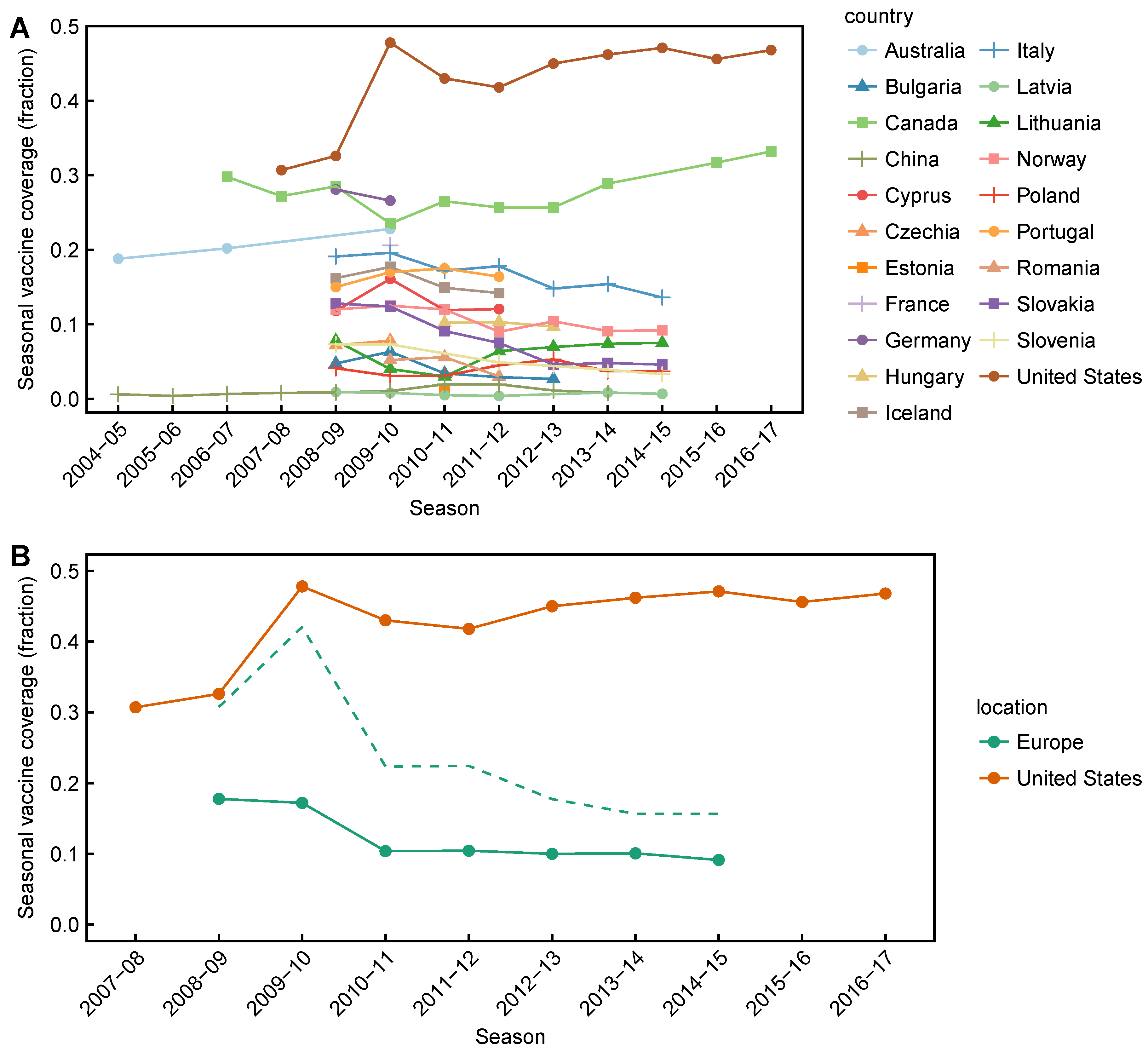
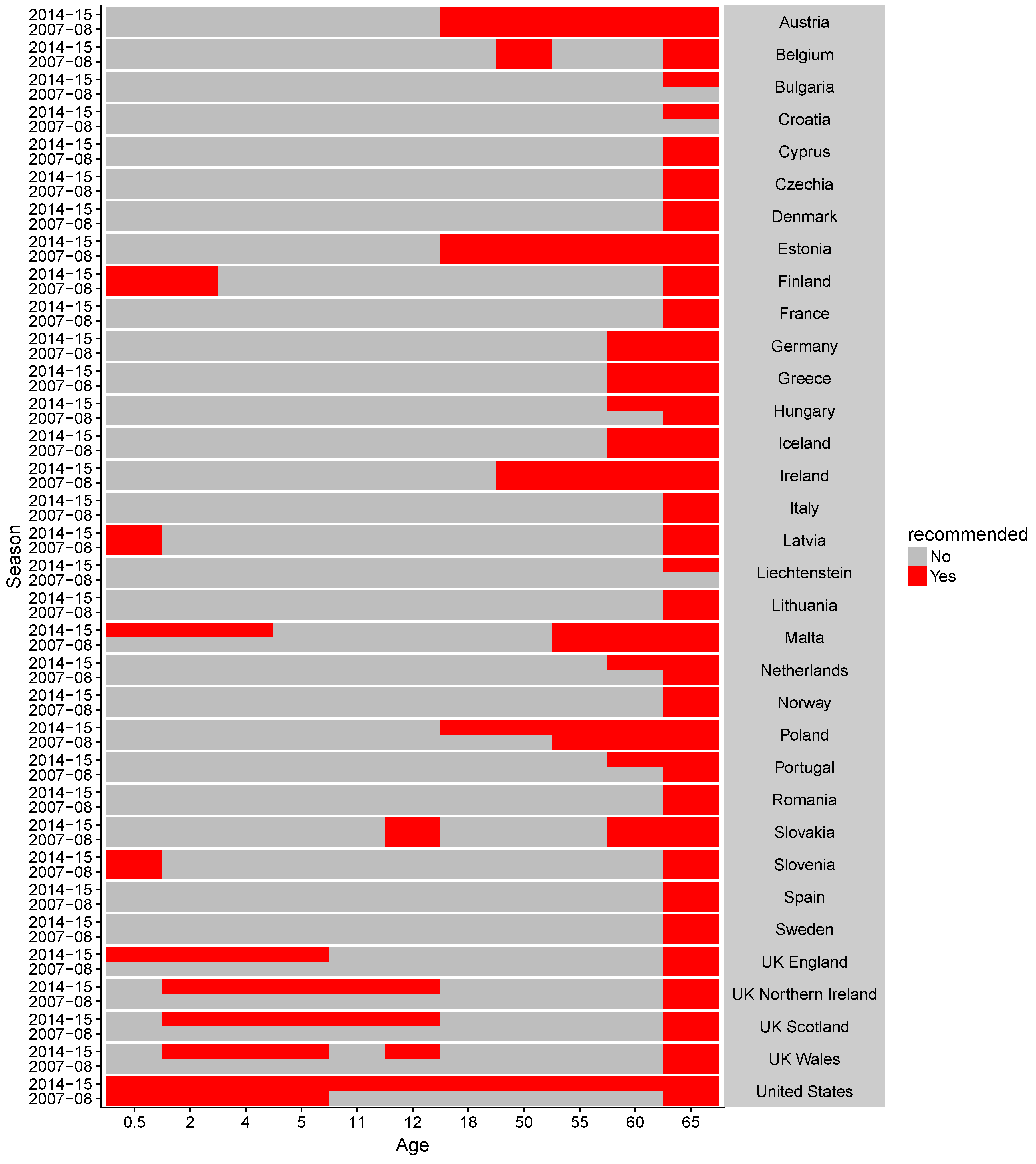
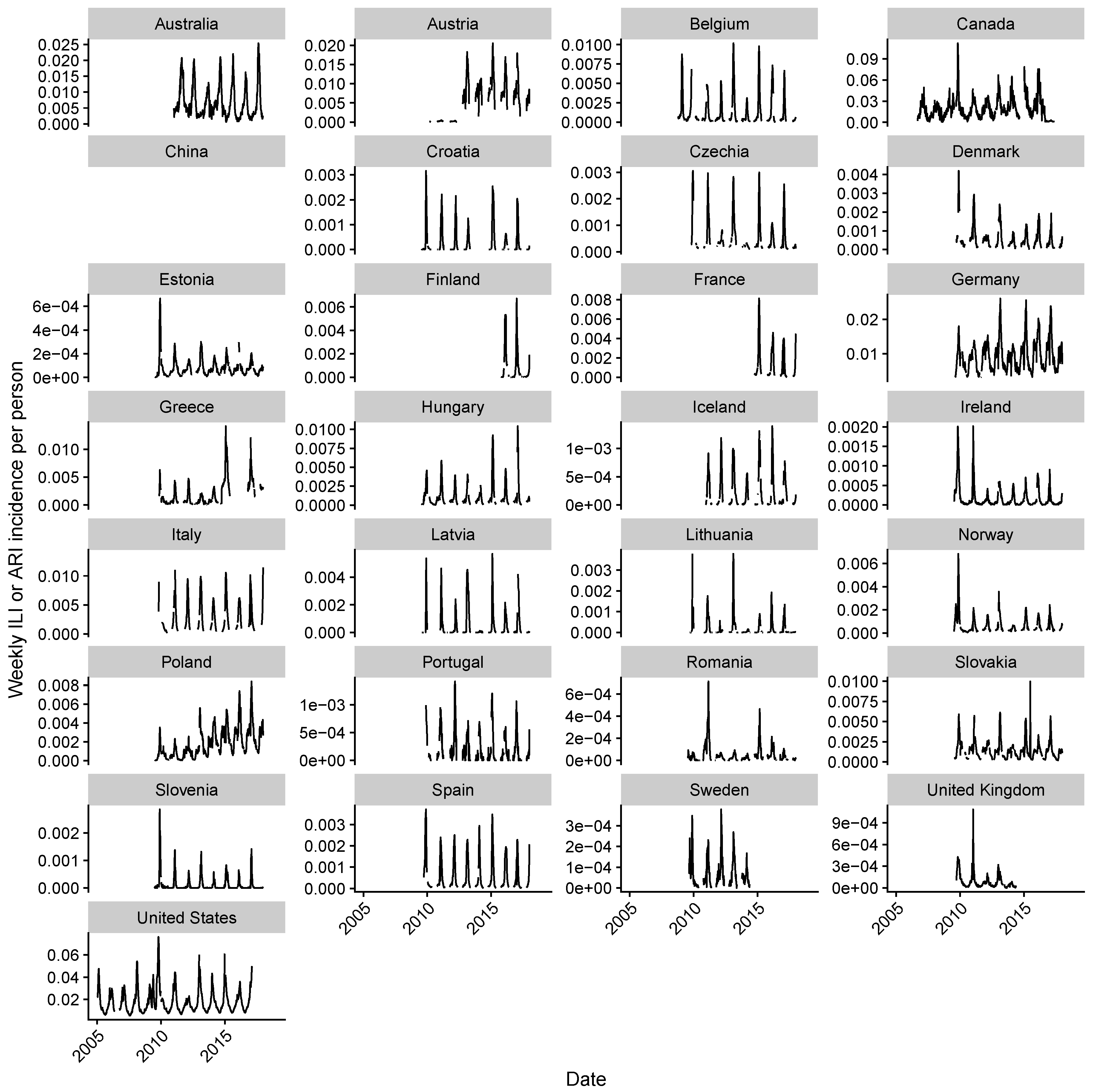
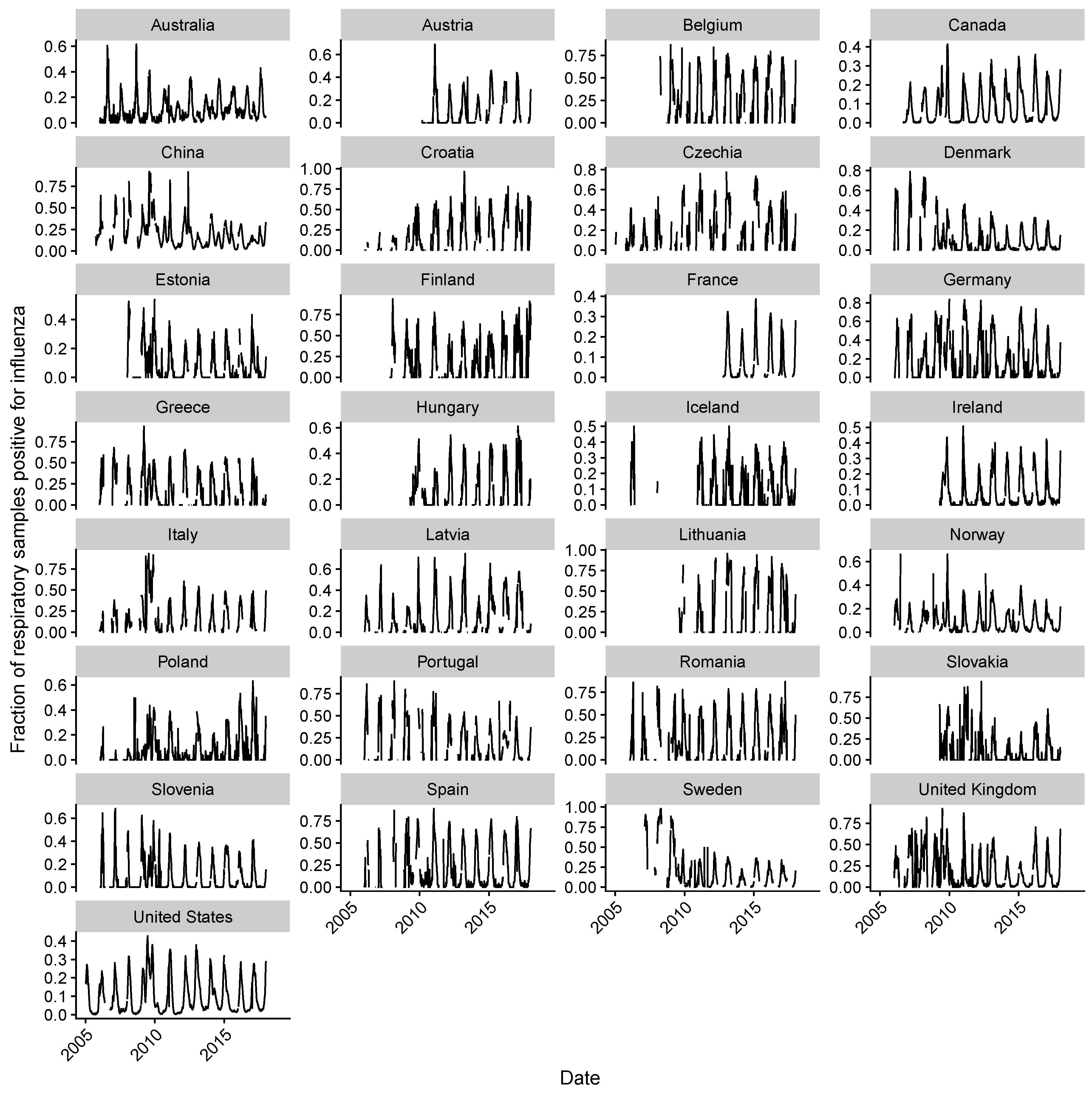
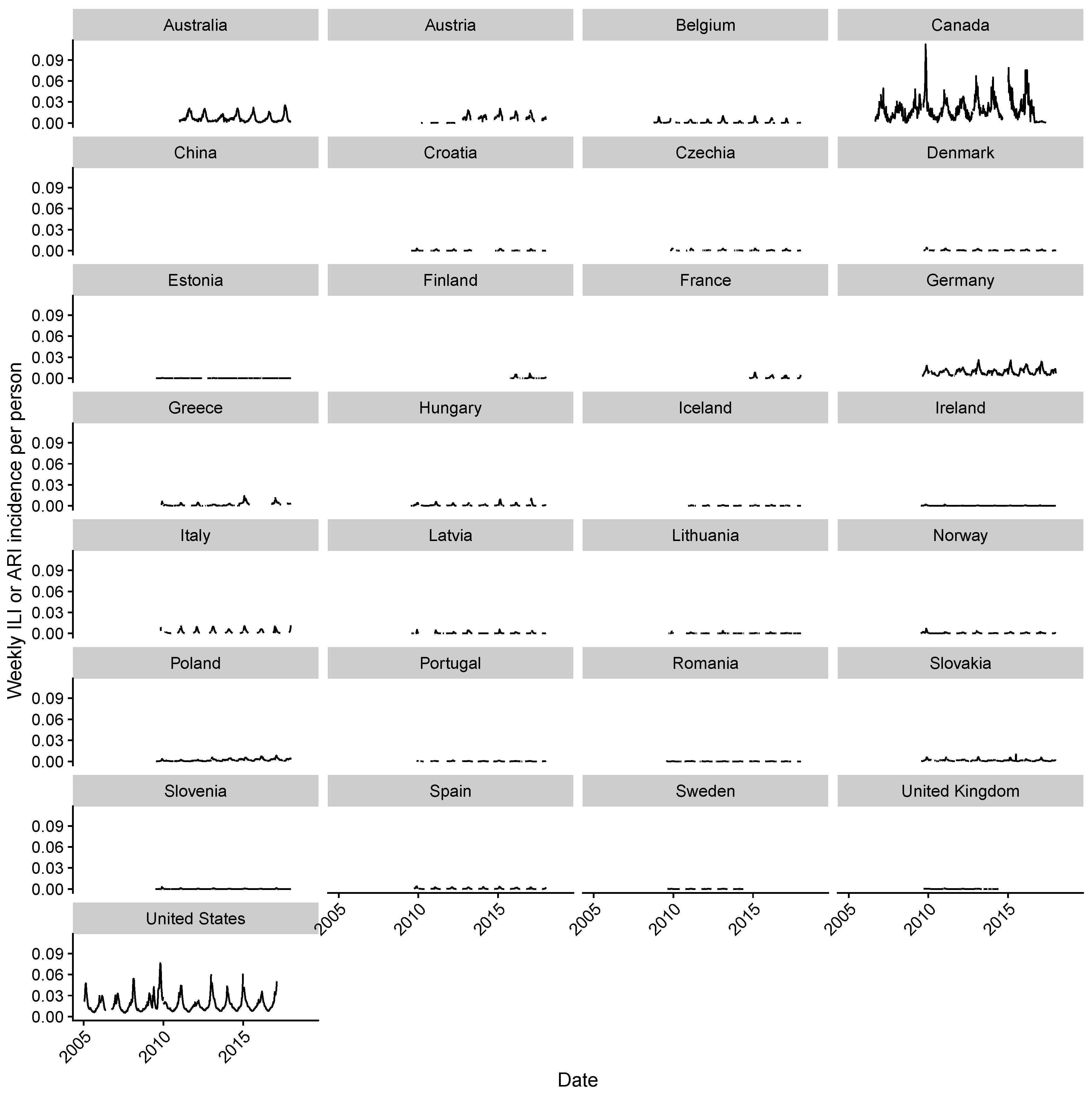
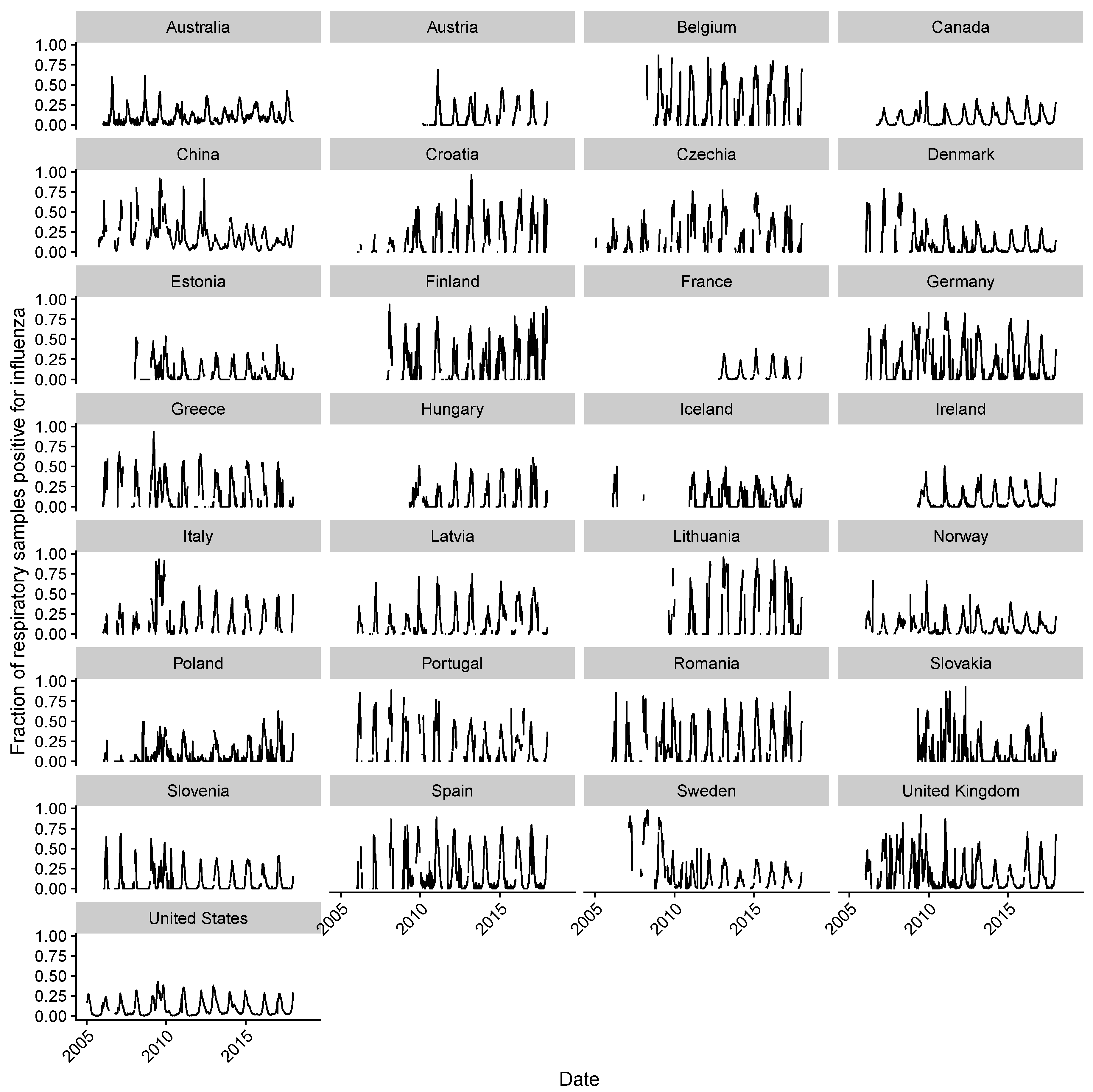
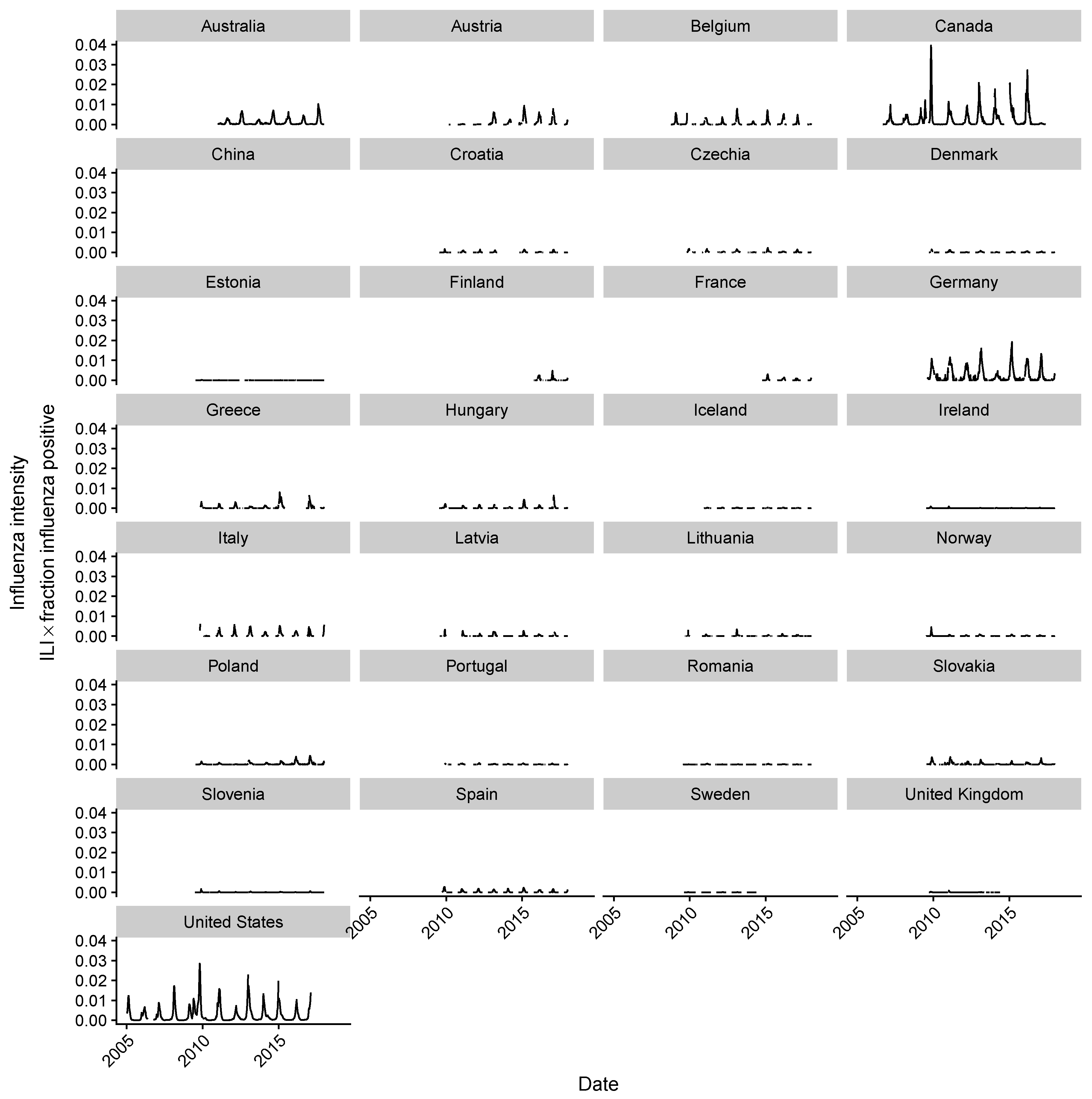
2.1. Data Collection
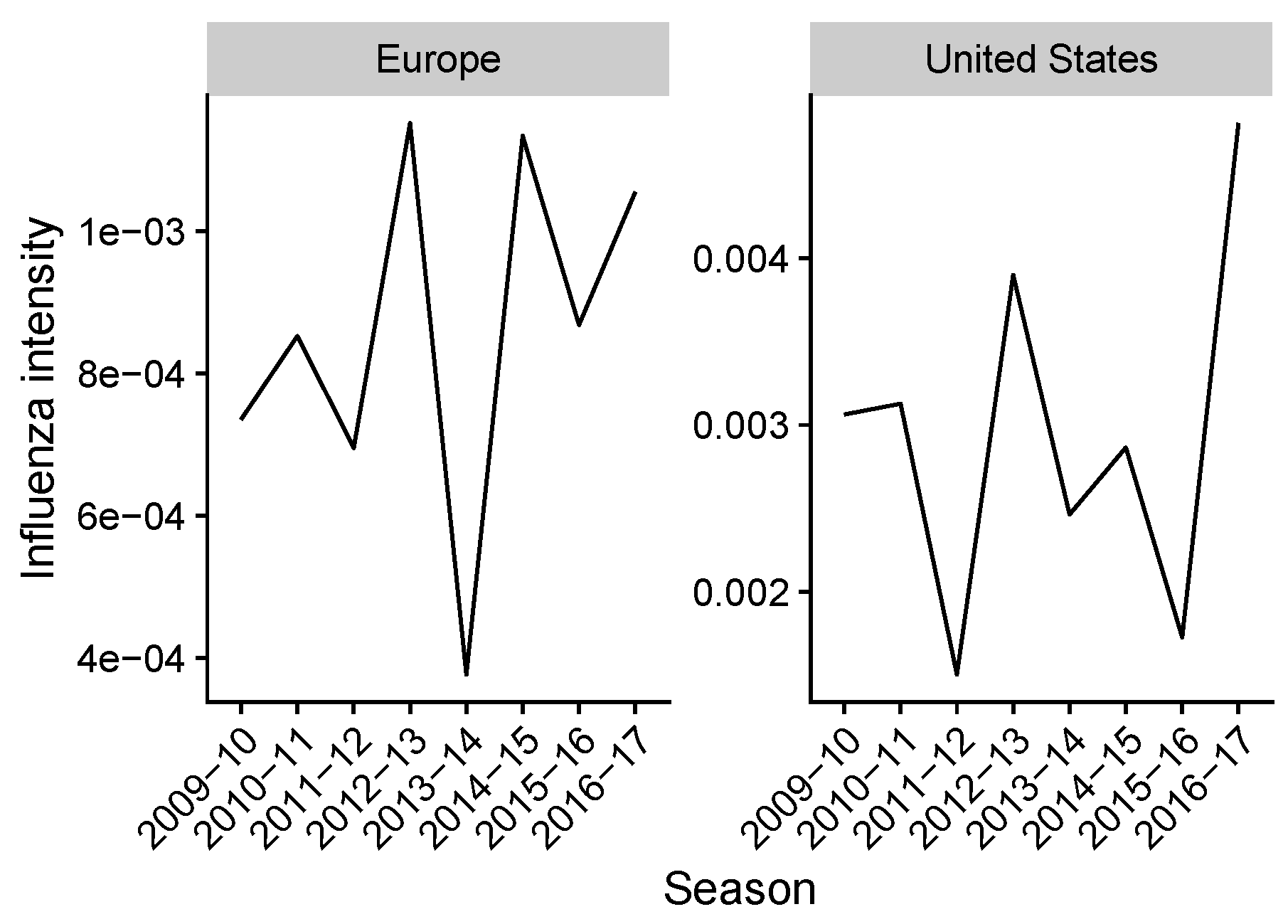
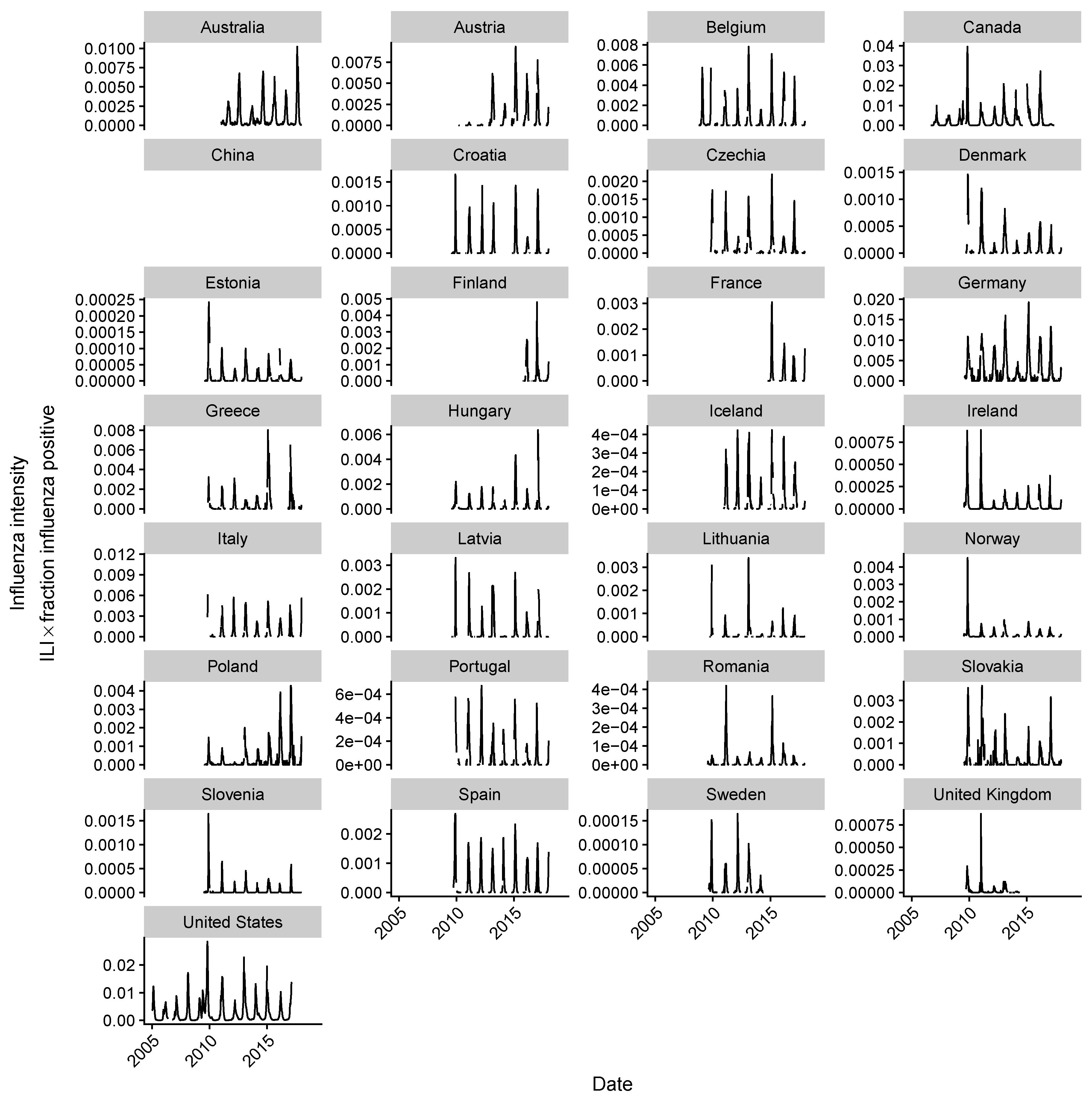
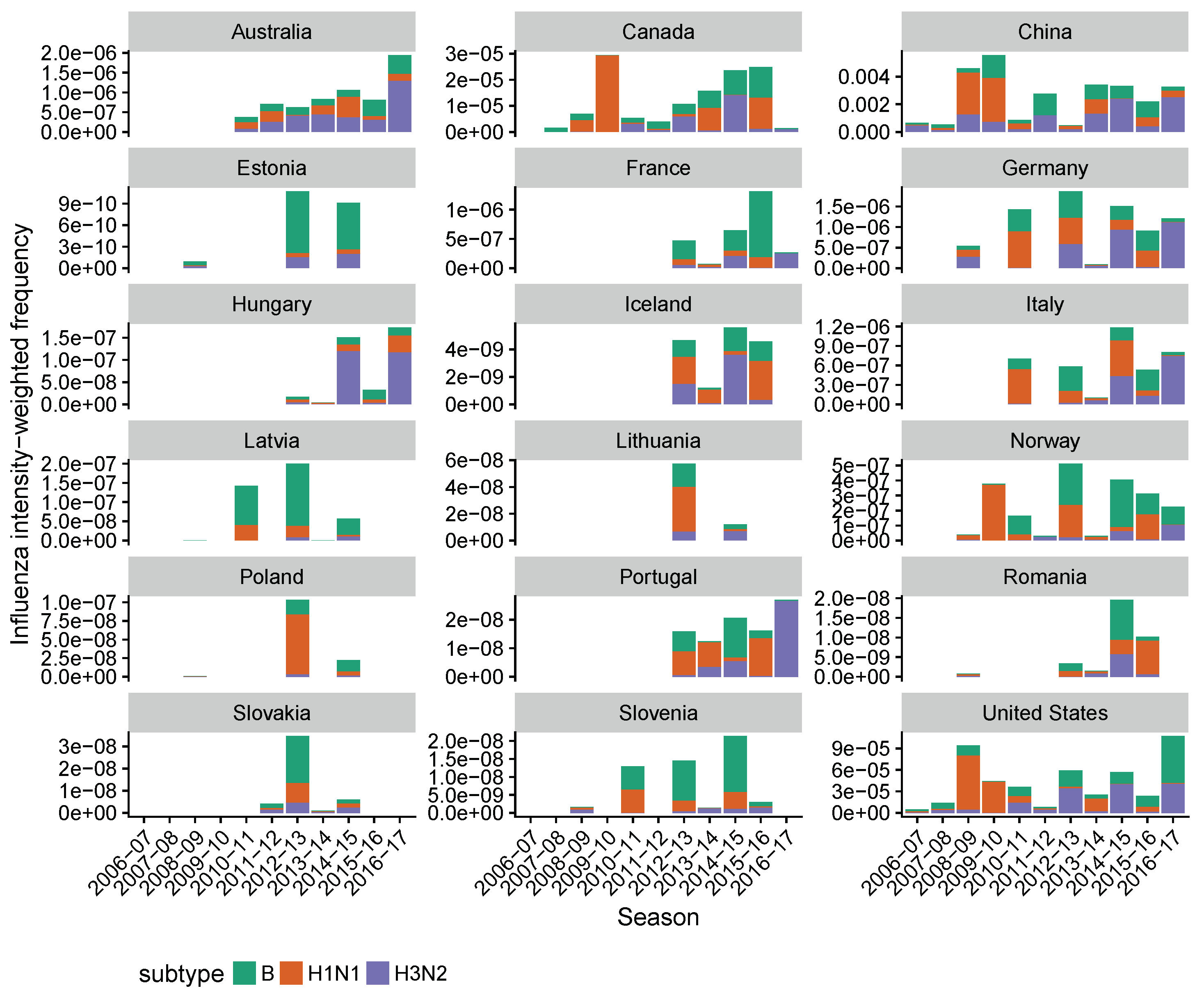
2.2. Estimating Influenza Intensity
2.3. Power Analysis
2.4. Estimating Antigenic Distances between H3N2 Strains and the Vaccine Strain
2.5. Data Availability
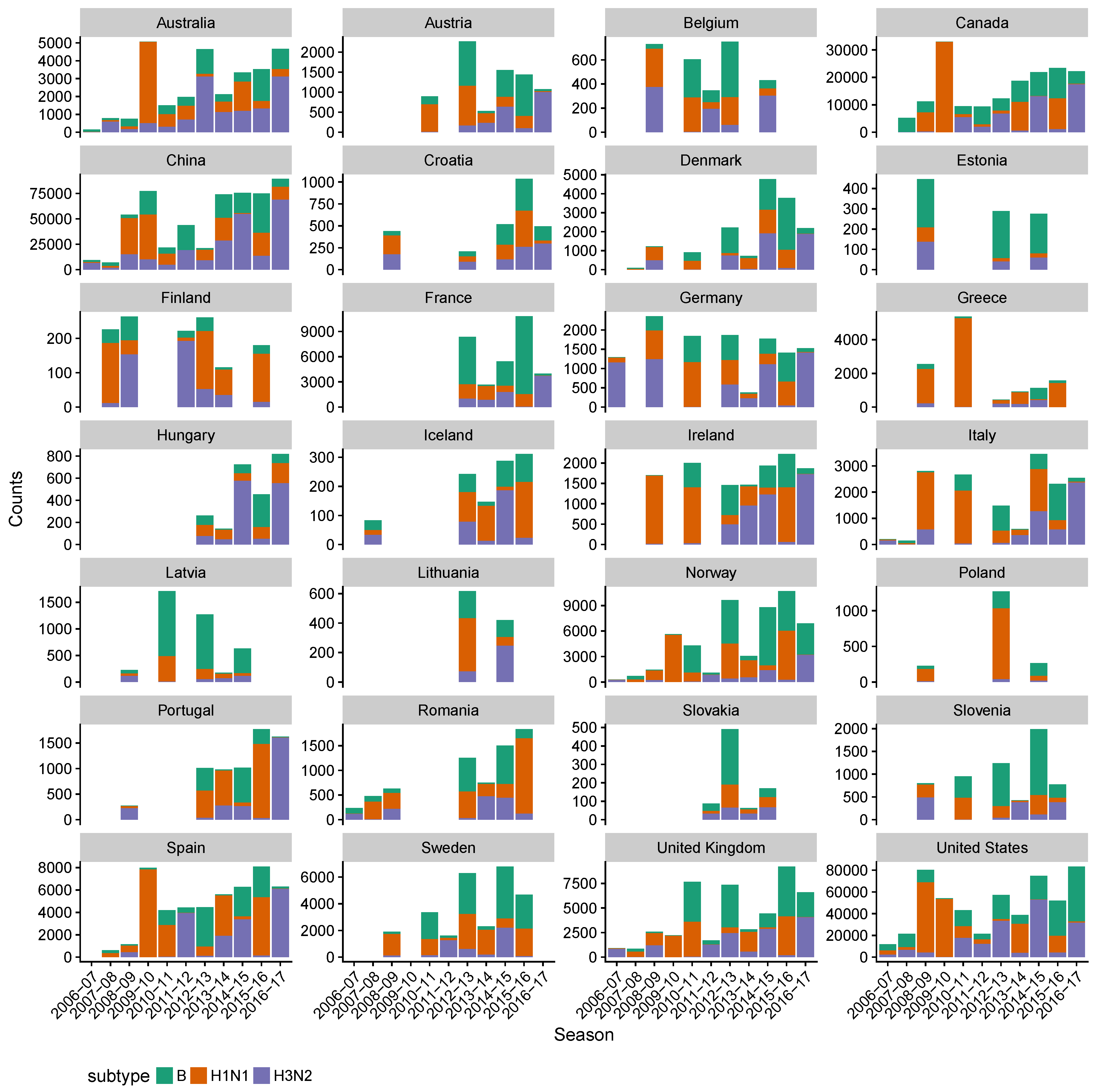
3. Results
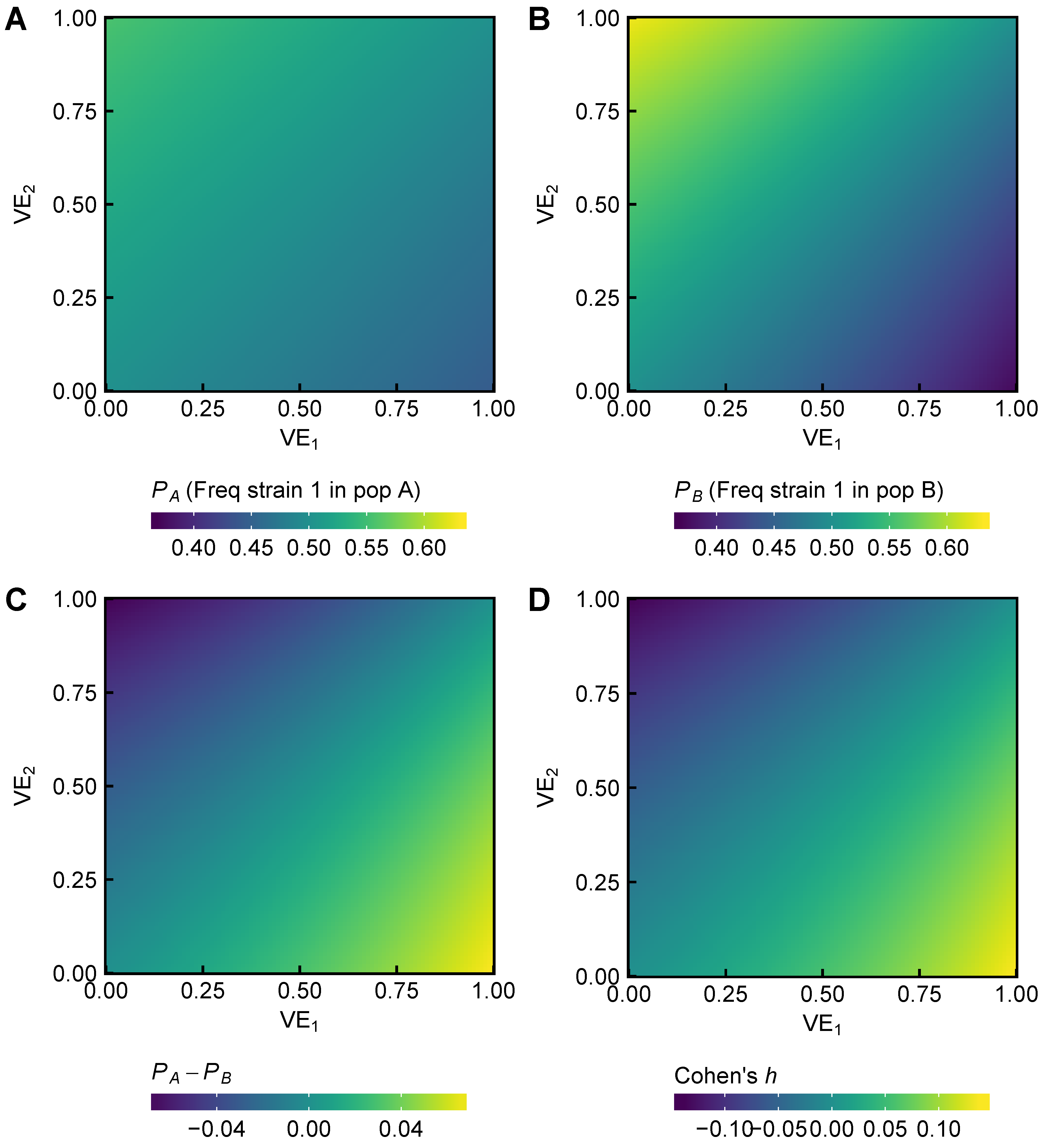
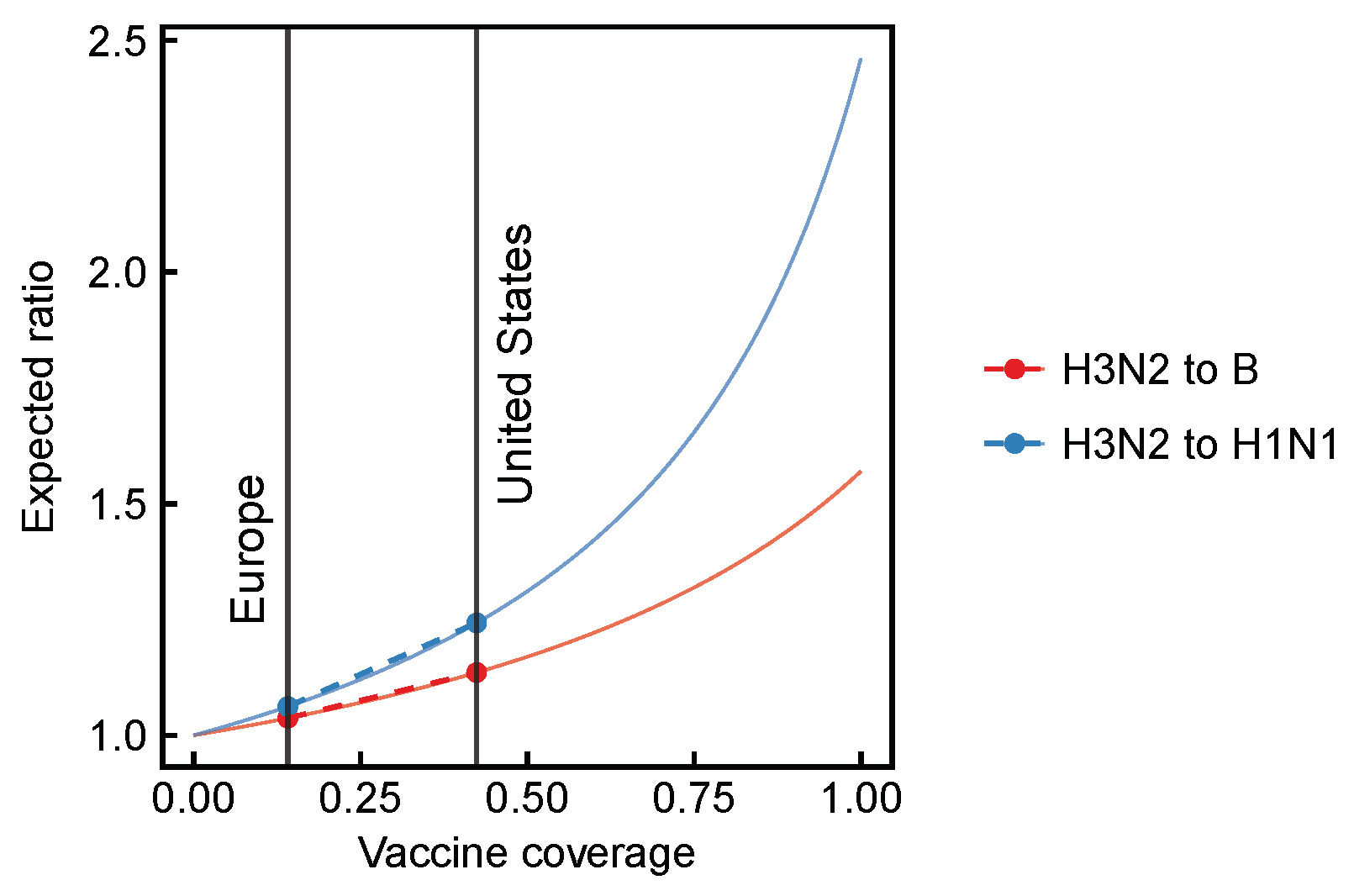
3.1. Expected Effect Sizes of Vaccination on Selection among Influenza Viruses Vary According to Vaccine Effectiveness
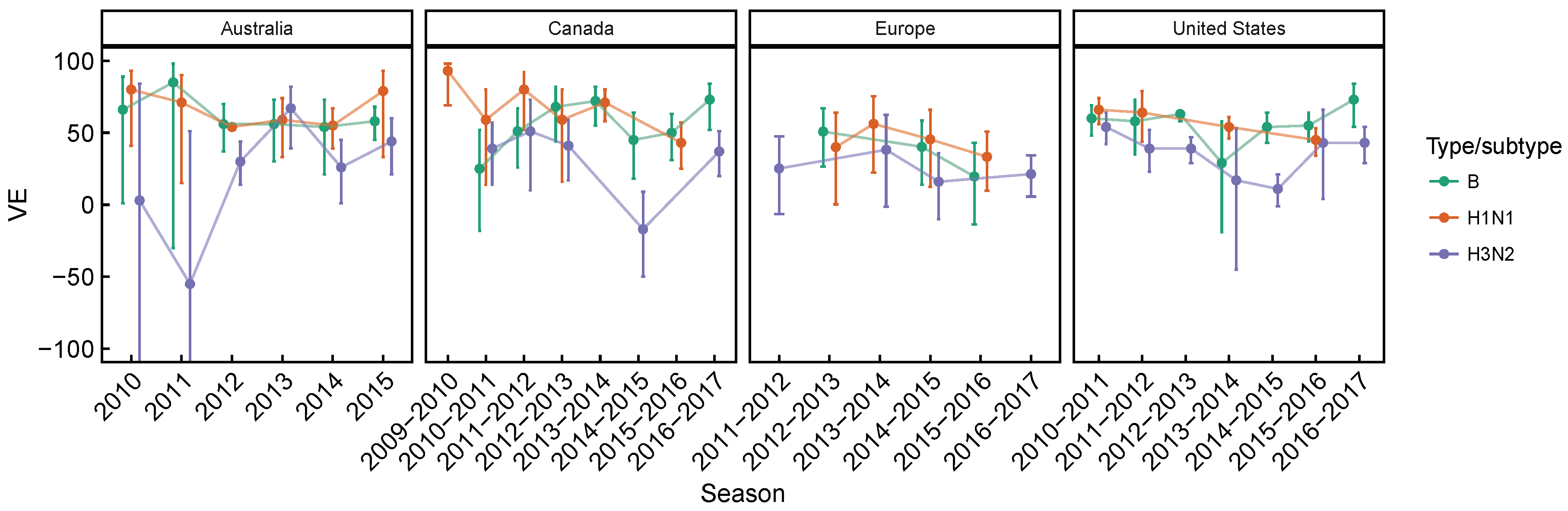
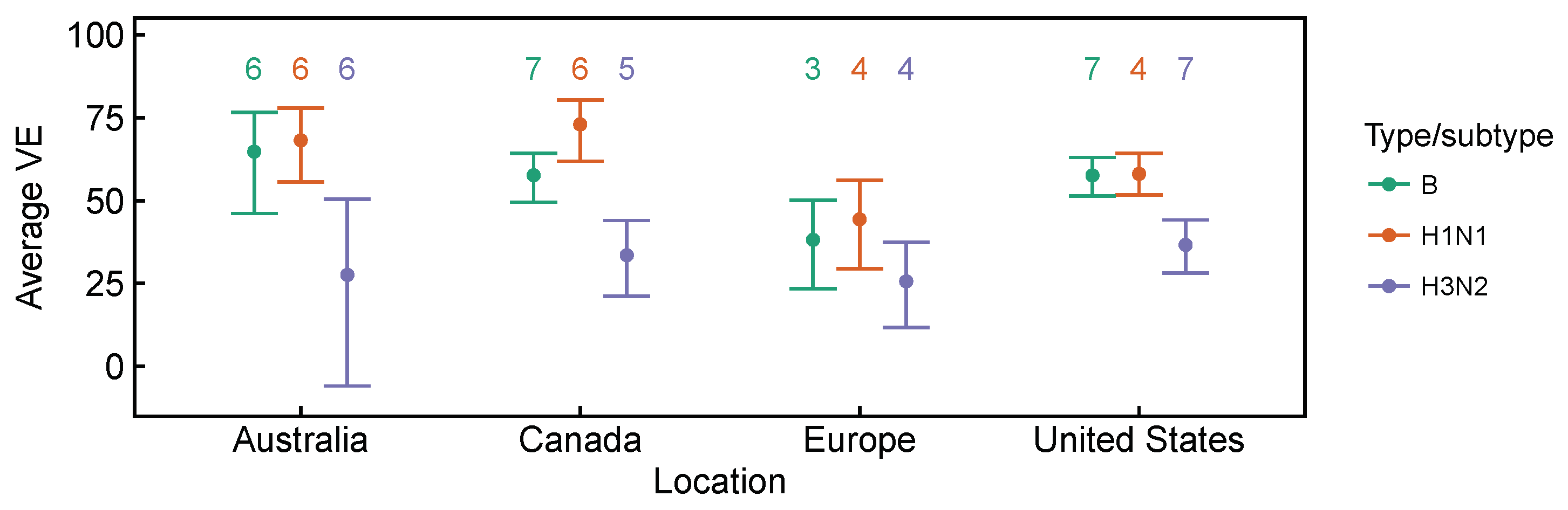
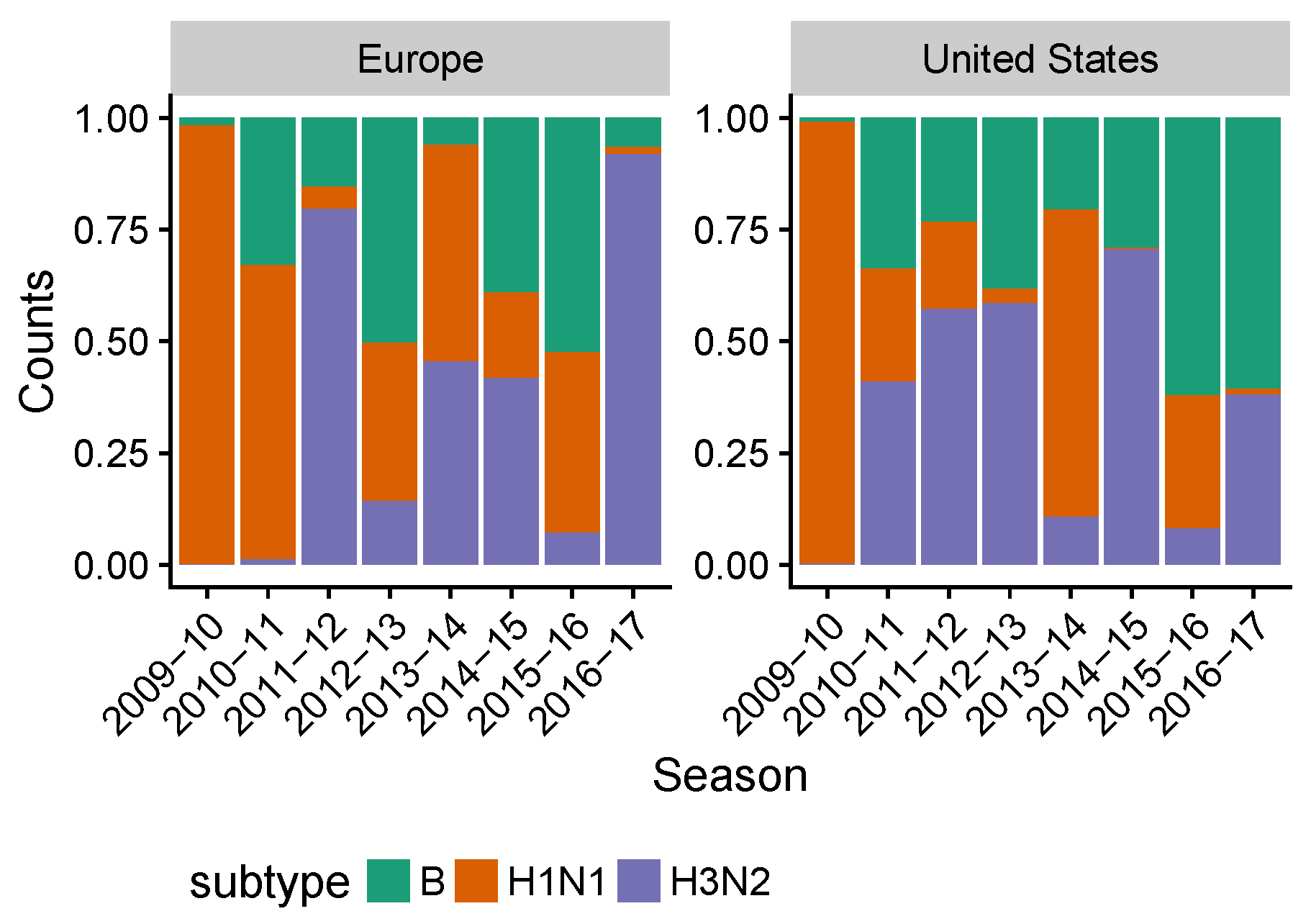
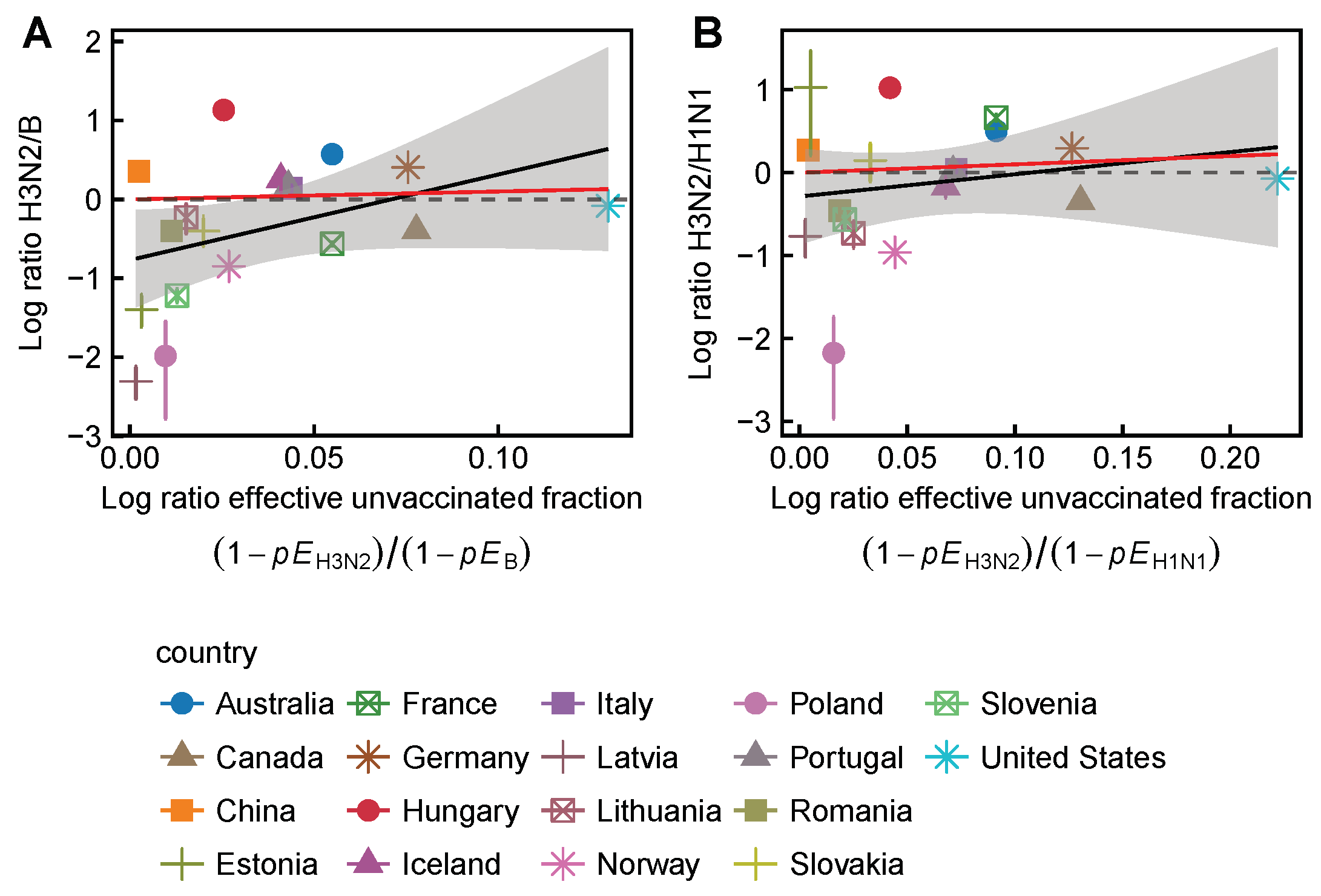
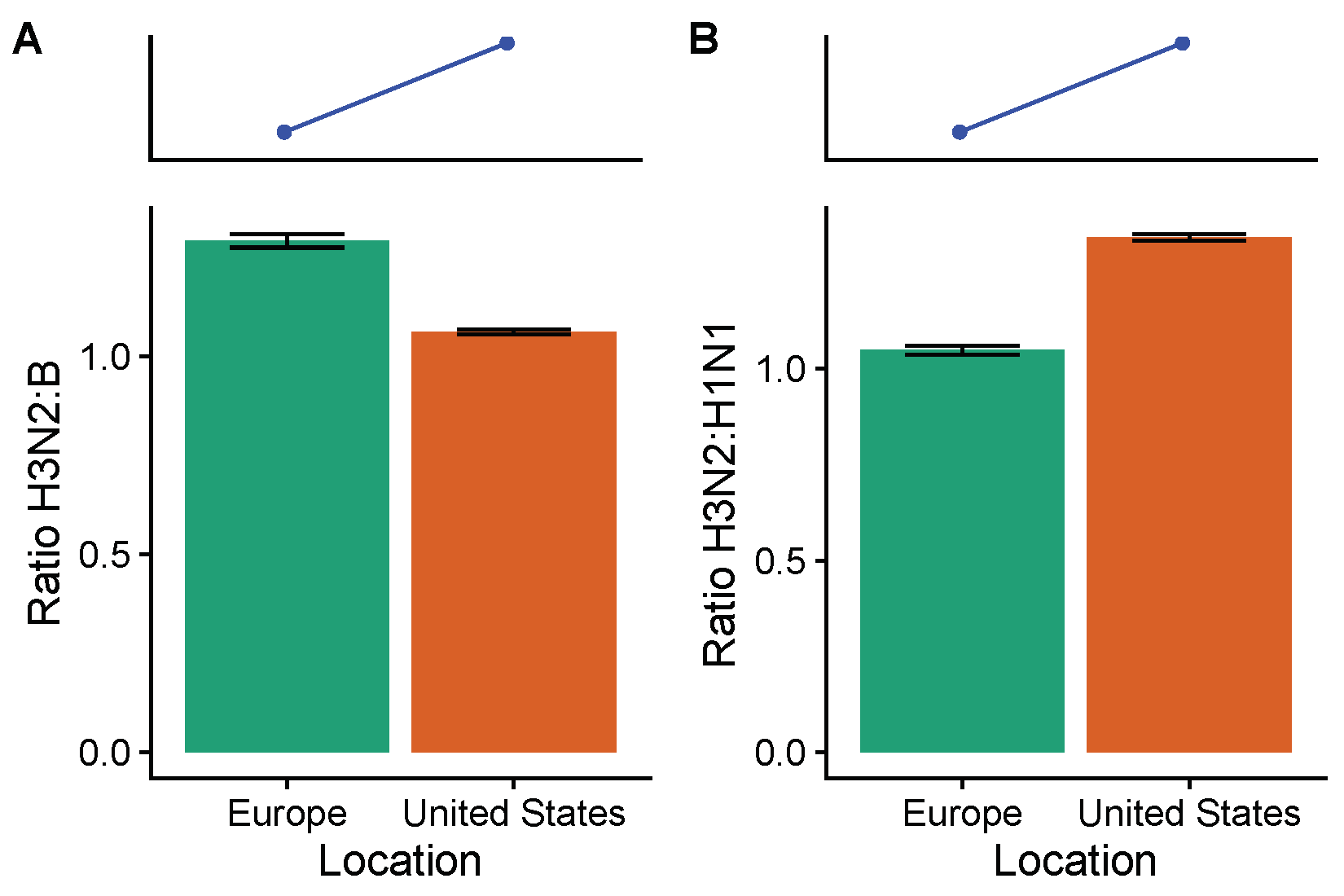
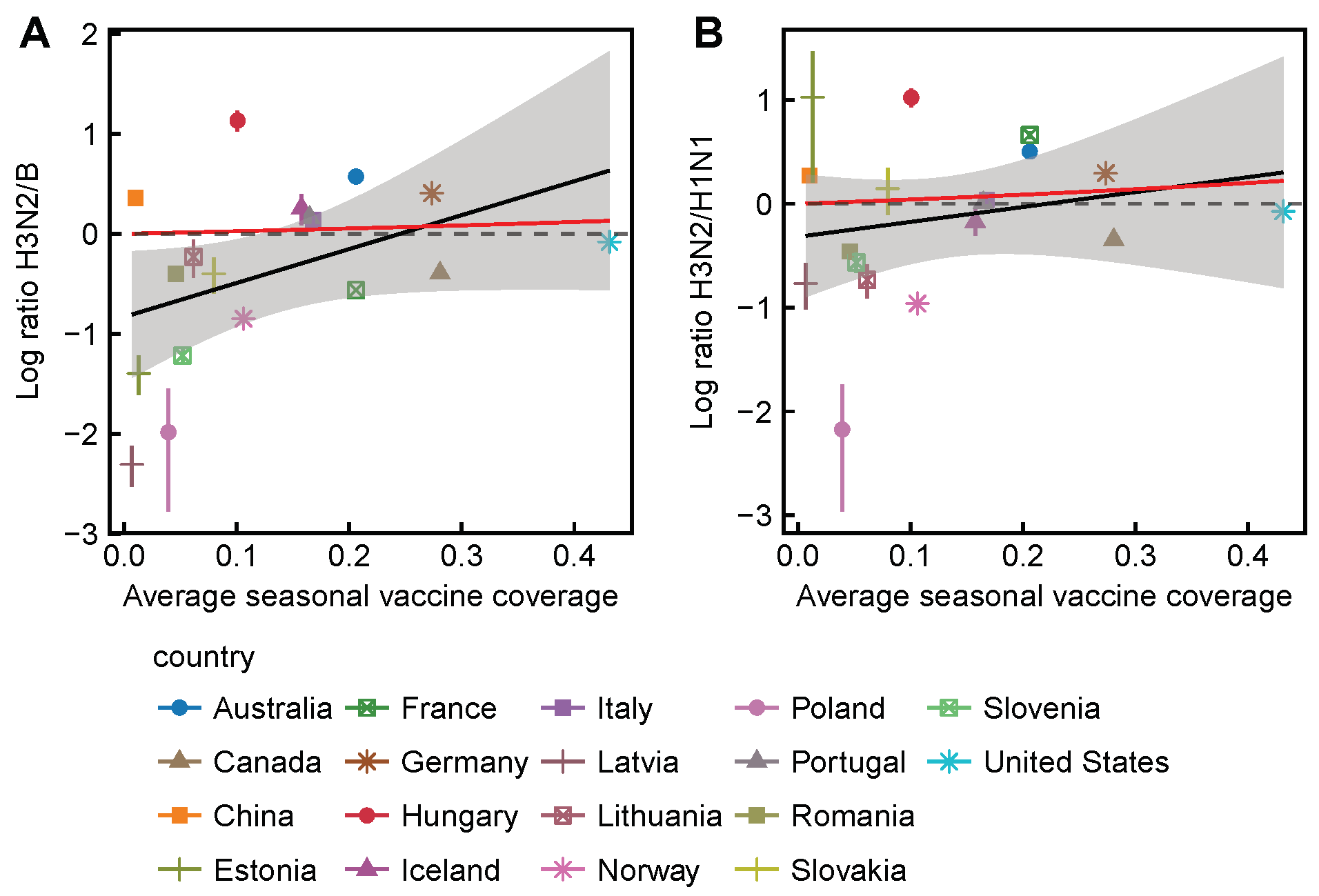
3.2. Spatial Differences in Influenza Subtype and Type Frequencies Are Not Always Consistent with Vaccine-Driven Selection Caused by Differential Vaccine Effectiveness
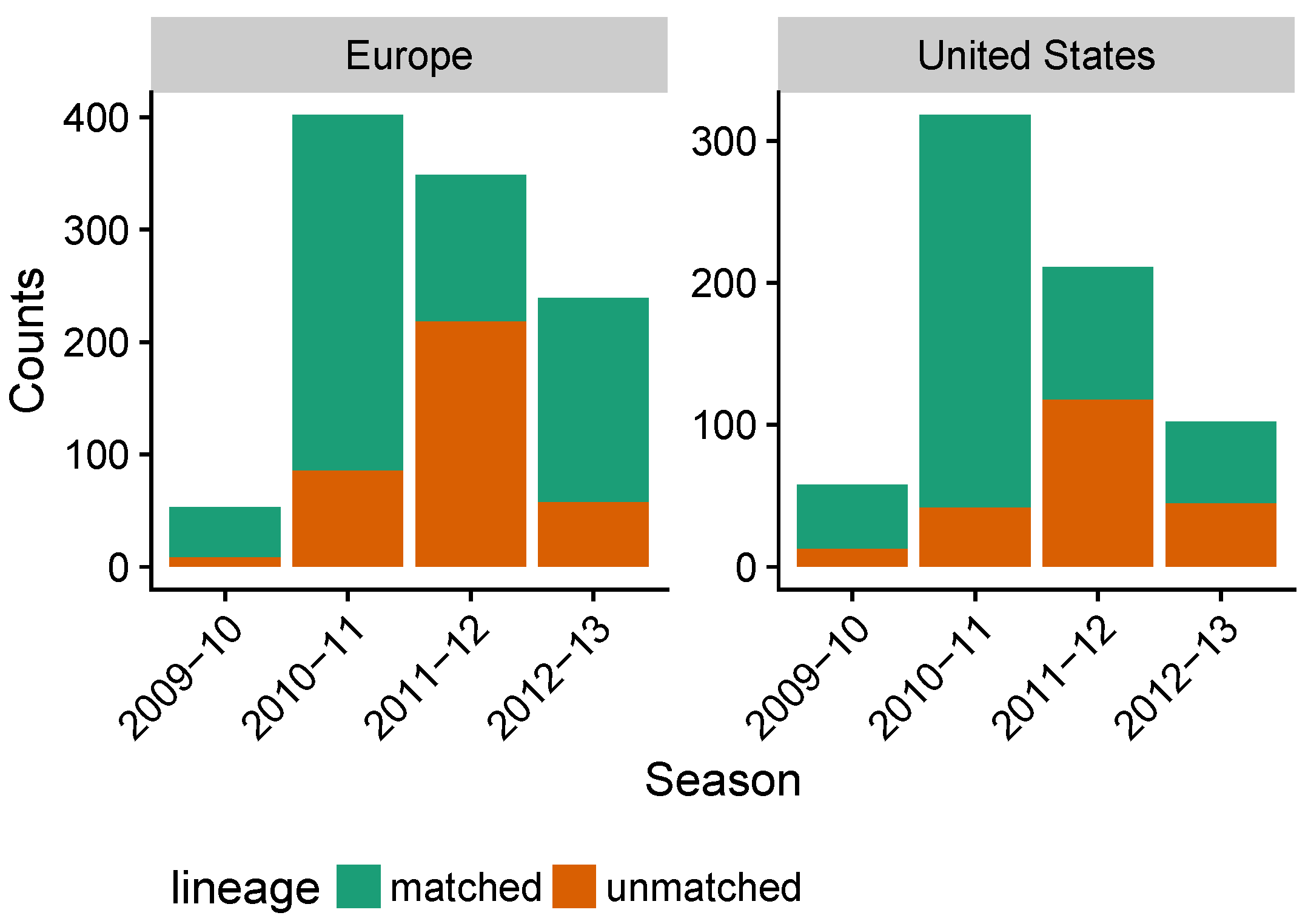
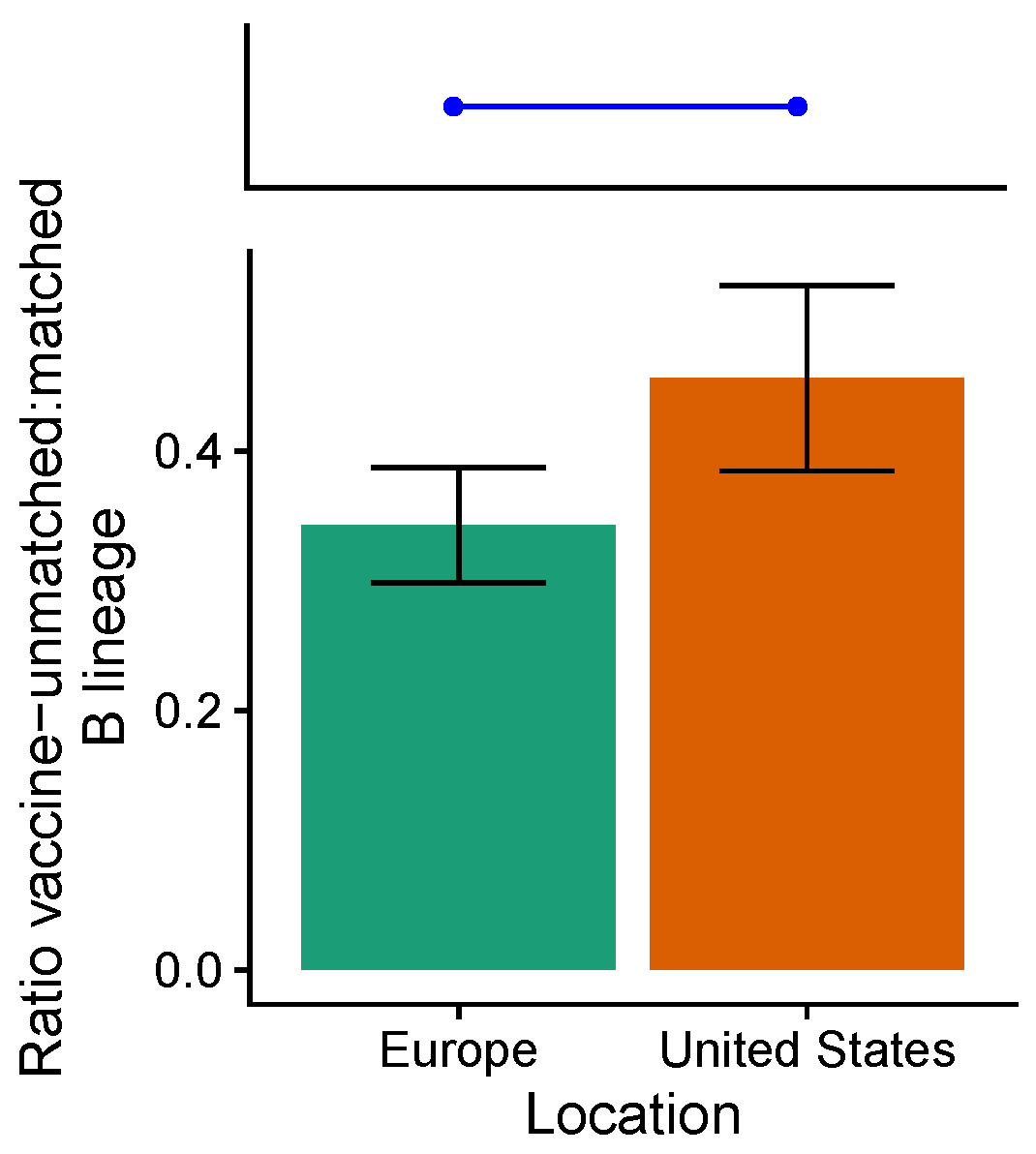
3.3. Influenza B Lineage Frequencies Differ Marginally Significantly between More and Less Vaccinated Populations during Seasons Where Only One Lineage Was Included in the Vaccine
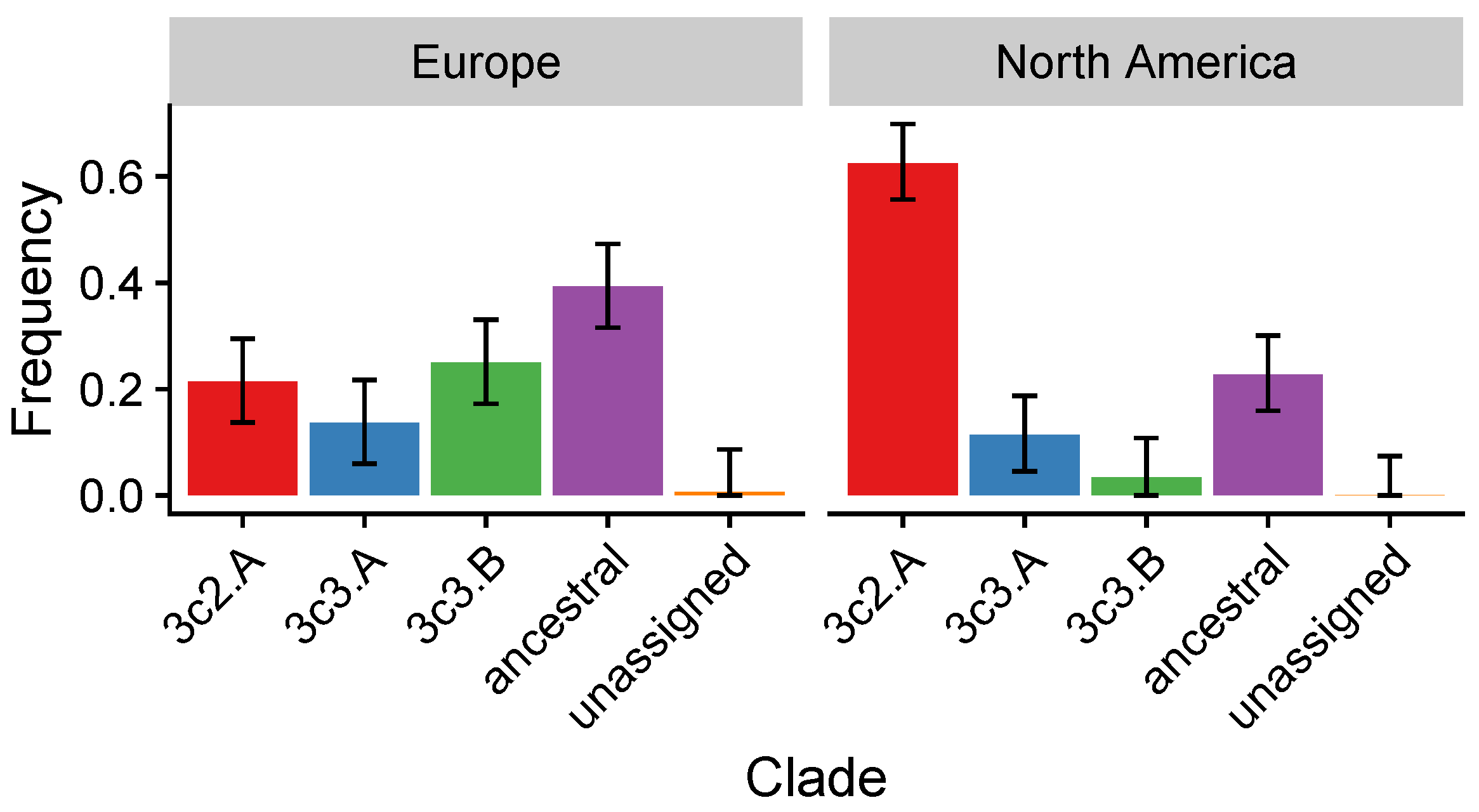
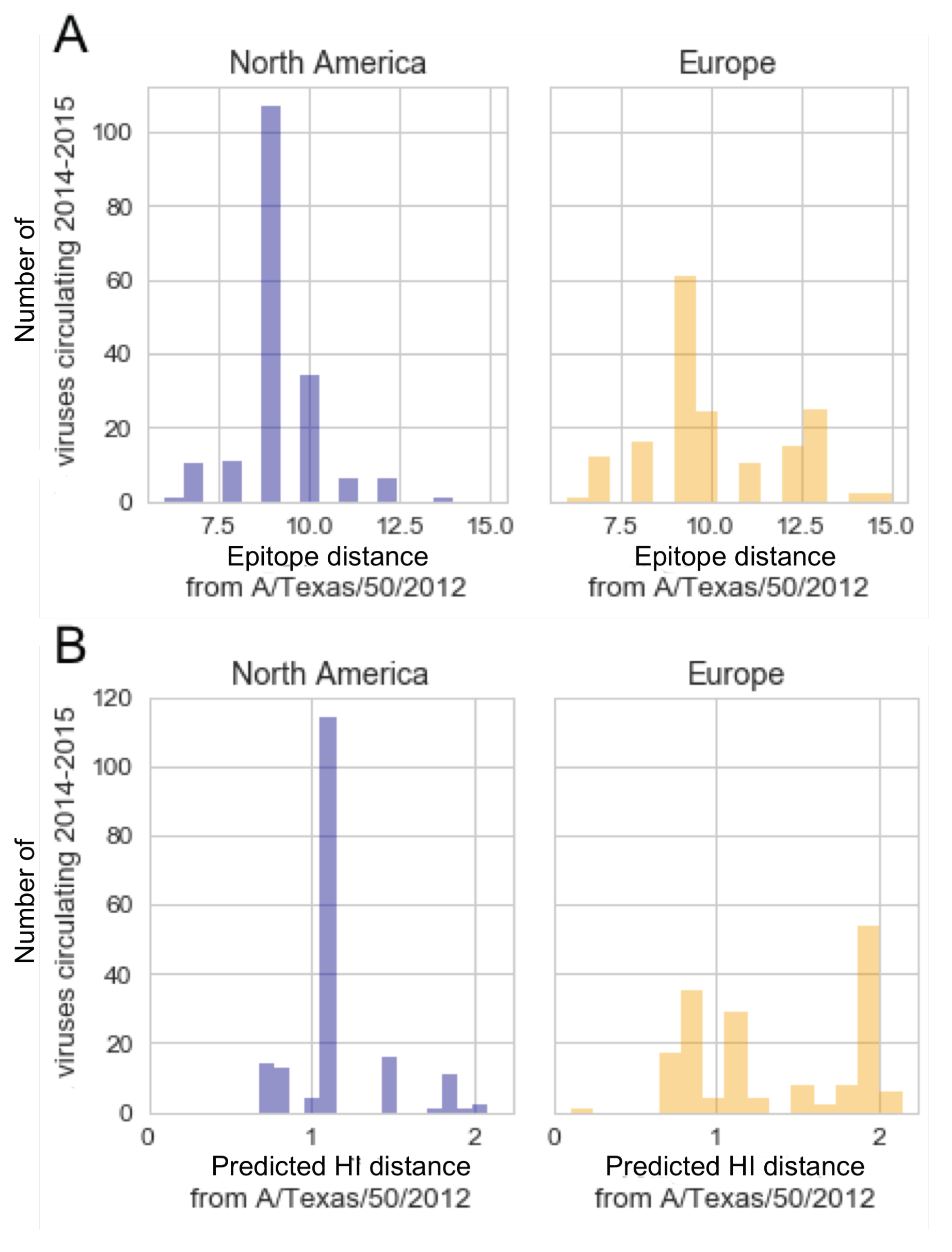
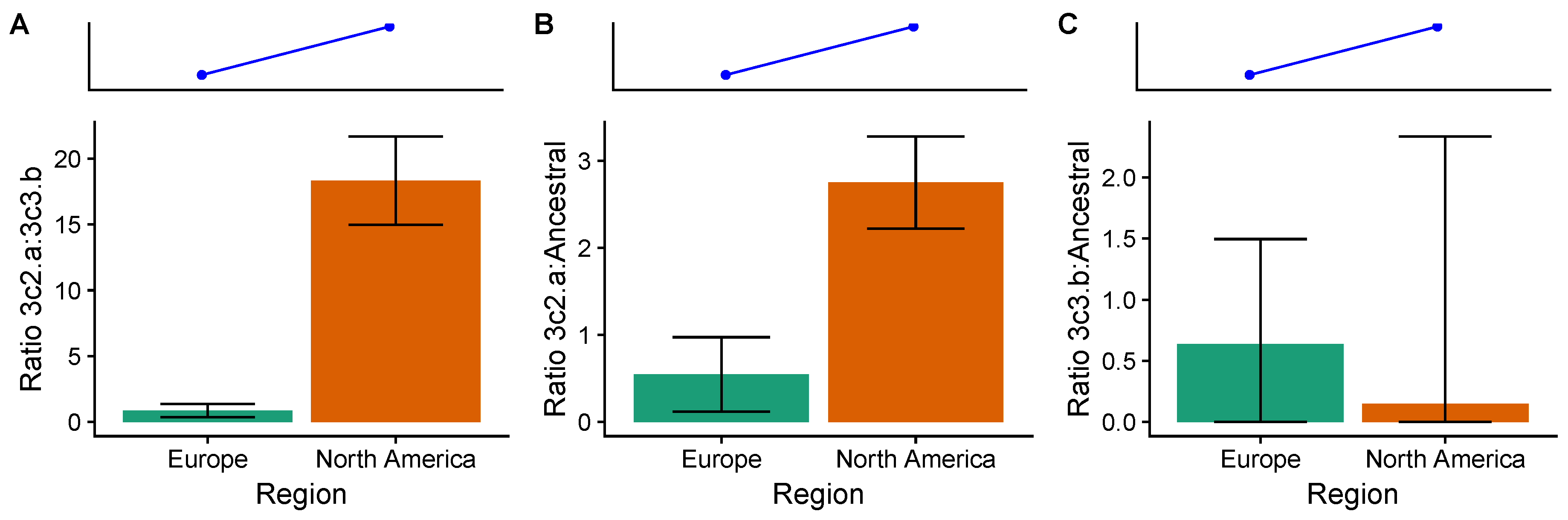
3.4. In the 2014–2015 Season, 3c2.A H3N2 Clades Were More Frequent in the United States Than Europe
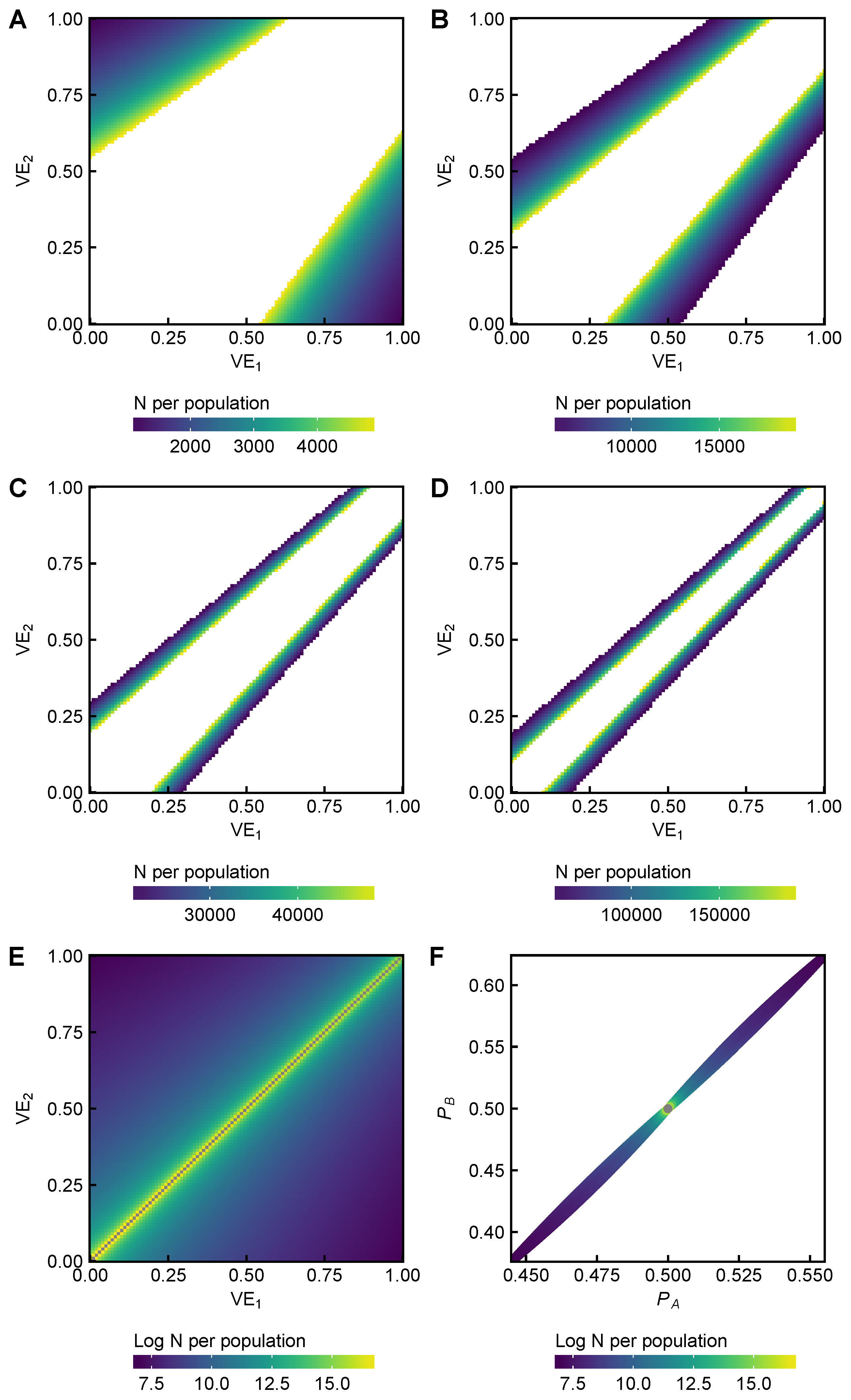
3.5. Power Analysis
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Approximate Effects of Vaccination on Prevalence
Appendix B. Estimating Average Vaccine Effectiveness by Subtype
Appendix C. Derivation of Theoretical Subtype Ratios
Appendix D. Supplementary Tables and Figures
| Efficacy (CI) | Inclusion in Averages | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ref. | Season | Overall | A | H3N2 | H1N1 | B | Type/Subtype Dominance | Location | H3N2 | H1N1 | B |
| [21] | 2008 | 41.0 (21.1, 55.9) | – | – | – | – | ∼50% B | Australia | (D) | (D) | (D) |
| [21] | 2009 | 42.7 (26.3, 55.4) | – | – | – | – | H1N1 dominated | Australia | (N) | I | (N) |
| [82] | 2004–2005 | 74 (37, 89) | – | – | – | – | 50% H3N2 50% B | USA | (D) | (D) | (D) |
| [83] | 2005–2006 | 22.3 (, 58.5) | 25.1 (, 82.2) | – | – | 21.5 (, 61.6) | Very few cases | Czechia | (F) | (F) | (F) |
| [84] | 2005–2006 | 49.4 (12.7, 70.7) | – | – | – | – | Majority H3N2 | USA | I | (D) | (D) |
| [82] | 2005–2006 | 23 (, 73) | – | – | – | – | Majority H3N2 | USA | (F) | (N) | (N) |
| [84] | 2006–2007 | 49.2 (, 75.3) | – | – | – | – | Majority H3N2 | USA | I | (D) | (D) |
| [20] | 2006–2007 | 61.6 (46, 72.8) | – | – | – | – | >99% H3N2 | Czechia, Finland | I | (N) | (N) |
| [85] | 2007–2008 | 63.0 (46.7) | – | 49.3 () | 81.5 (60.9) | 53.2 (22.2) | – | USA, Finland, Poland | I | I | I |
| [22] | 2007–2008 | – | 72 (49, 84) | – | – | 40 (, 86) | 90% H3N2 | USA | I | (F) | (F) |
| [23] | 2007–2008 | – | 49.0 (24.7, 65.9) | – | – | 37.2 (, 64.5) | 70% H3N2 among A | USA | I | (N) | I |
| [19] | 2008–2009 | 71.5 (54.7, 82.1) | – | 50.0 (, 90.8) | 75.2 (55.4, 86.2) | 60.1 (9.5, 82.4) | – | USA | (F) | I | I |
| Average Efficacy (Studies Used to Compute Average) | |||
|---|---|---|---|
| Season | H3N2 | H1N1 | B |
| 2005–2006 | 49.4 (12.7,70.7) [84] | – | – |
| 2006–2007 | 55.9 (35.5,70.4) [20,84] | – | – |
| 2007–2008 | 58.3 (40.9,66.9) [22,23,85] | 81.5 (60.9) [85] | 45.8 (21.2, 59.2) [23,85] |
| 2008–2009 | – | 62.3 (48.1, 72.6) [19,21] | 60.1 (9.5, 82.4) [19] |
| Average | 54.7 (41.8, 64.3) | 73.6 (60.3, 77.5) | 53.5 (27.0, 69.9) |
| Seasons | Observation | References | Interpretation |
|---|---|---|---|
| 2005–2006 to 2008–2009 | Lower vaccine efficacy against H3N2 (54.7%, 95% CI: 41.8-64.3%) compared to H1N1 (73.6%, 95% CI: 60.3, 77.5%), though not a statistically significant difference. Similar efficacy against H3N2 relative to B (53.5%, 95% CI: 27.0, 69.9%) reported in randomized control trials (RCTs) in adults (Table A2). | [19,20,21,22,23] | Possible selection for H3N2 relative to H1N1 but not necessarily relative to B. More recent RCTs have not yet been reported. |
| 2009–2010 to 2016–2017 | Lower vaccine effectiveness against H3N2, compared to H1N1 and B based on test-negative design studies averaged over time. Differences are significant in Canada [27,28,29,30,31,32,33,34] and the United States [36,37,38,39,40,41,42,43], but not in Australia [24,25,26] for H3N2 vs. B, and not in Europe [35] for both H3N2 vs. B and H3N2 vs. H1N1 (Figure A1 and Figure A2). | [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43] | Expect selection for H3N2 relative to relative to H1N1 and B. |
| Observation | References | Interpretation |
|---|---|---|
| Vaccination with a Victoria strain (B/Brisbane/60/2008-like) induced antibodies responses against Victoria and Yamagata strains by HI, but vaccination with a Yamagata strain (B/Florida/4/2006-like) only elicits antibody responses against Yamagata (in mice and in children using the LAIV). | [66,67] | Possible selection for Victoria during Yamagata vaccine seasons. No vaccine-driven selection for either lineage during Victoria vaccine seasons. |
| The quadrivalent vaccine elicited significantly greater HI titers against both lineages than did the trivalent vaccine against the heterologous lineage. | [64,65] | Possible selection for the unmatched lineage. |
| TIV effectiveness against clinical influenza infection was comparable against both lineages in the 2011-2012, 2012-2013, and 2015-2016 seasons. Trivalent vaccines were effective against influenza B even in seasons dominated by a lineage that mismatches the vaccine. | [29,34,36,38,39] | Vaccine-driven selection for either lineage is not expected. |
| Season | Observation | References | Interpretation |
|---|---|---|---|
| 2016–2017 | The egg-adapted vaccine strain lacks glycosylation site found in circulating 3c2.A viruses. | [86] | The vaccine is poorly immunogenic against circulating strains in general. Little vaccine-driven selection is expected. |
| 2014–2015 | Circulating 3c2.A viruses have a new glycosylation site and several other site B residues different from the vaccine strain. Clade-specific VEs differ: 3c2.A 3% (95% CI, % to 15%); 3c3.B 52% (95% CI, to 80%) | [28,44,45] | 3c2.A strains differ immunologically from the vaccine strain. Vaccine-driven selection for 3c2.A strains is expected. |
| 2012–2013 | In adults, the vaccine fails to induce responses to novel mutations on the vaccine strain’s HA. | [71] | The vaccine is poorly immunogenic against circulating strains in general. Little vaccine-driven selection is expected. |
References
- Jefferson, T.; Rivetti, A.; Di Pietrantonj, C.; Demicheli, V. Vaccines for preventing influenza in healthy children. Cochrane Database Syst. Rev. 2018, 2, CD004879. [Google Scholar] [PubMed]
- Demicheli, V.; Jefferson, T.; Ferroni, E.; Rivetti, A.; Di Pietrantonj, C. Vaccines for preventing influenza in healthy adults. Cochrane Database Syst. Rev. 2018, 2, CD001269. [Google Scholar] [PubMed]
- Hurwitz, E.S.; Haber, M.; Chang, A.; Shope, T.; Teo, S.; Ginsberg, M.; Waecker, N.; Cox, N.J. Effectiveness of influenza vaccination of day care children in reducing influenza-related morbidity among household contacts. JAMA 2000, 284, 1677–1682. [Google Scholar] [CrossRef] [PubMed]
- Principi, N.; Esposito, S.; Marchisio, P.; Gasparini, R.; Crovari, P. Socioeconomic impact of influenza on healthy children and their families. Pediatr. Infec. Dis. J. 2003, 22, S207–S210. [Google Scholar] [CrossRef] [PubMed]
- Loeb, M.; Russell, M.L.; Moss, L.; Fonseca, K.; Fox, J.; Earn, D.J.D.; Aoki, F.; Horsman, G.; Van Caeseele, P.; Chokani, K.; et al. Effect of influenza vaccination of children on infection rates in Hutterite communities: A randomized trial. JAMA 2010, 303, 943–950. [Google Scholar] [CrossRef] [PubMed]
- Pebody, R.G.; Green, H.K.; Andrews, N. Uptake and impact of vaccinating school age children against influenza during a season with circulation of drifted influenza A and B strains, England, 2014/15. Euro Surveill. 2015, 20, 1560–7917. [Google Scholar] [CrossRef] [PubMed]
- Centers for Disease Control and Prevention. Seasonal Influenza Vaccine and Total Doses Distributed; Technical Report; Centers for Disease Control and Prevention: Atlanta, GA, USA, 2016. [Google Scholar]
- Martcheva, M.; Bolker, B.M.; Holt, R.D. Vaccine-induced pathogen strain replacement: What are the mechanisms? J. R. Soc. Interface 2008, 5, 3–13. [Google Scholar] [CrossRef] [PubMed]
- McLean, A.R. Vaccination, evolution and changes in the efficacy of vaccines: A theoretical framework. R. Soc. 1995, 261, 389–393. [Google Scholar] [CrossRef] [PubMed]
- Lipsitch, M. Bacterial vaccines and serotype replacement: Lessons from Haemophilus influenzae and prospects for Streptococcus pneumoniae. Emerg. Infect. Dis. 1999, 5, 336. [Google Scholar] [CrossRef] [PubMed]
- Lipsitch, M. Vaccination against colonizing bacteria with multiple serotypes. Proc. Natl. Acad. Sci. USA 1997, 94, 6571–6576. [Google Scholar] [CrossRef] [PubMed]
- Pilishvili, T.; Lexau, C.; Farley, M.M.; Hadler, J.; Harrison, L.H.; Bennett, N.M.; Reingold, A.; Thomas, A.; Schaffner, W.; Craig, A.S.; et al. Sustained Reductions in Invasive Pneumococcal Disease in the Era of Conjugate Vaccine. J. Infect. Dis. 2010, 201, 32–41. [Google Scholar] [CrossRef] [PubMed]
- Feikin, D.R.; Kagucia, E.W.; Loo, J.D.; Link-Gelles, R.; Puhan, M.A.; Cherian, T.; Levine, O.S.; Whitney, C.G.; O’Brien, K.L.; Moore, M.R.; et al. Serotype-Specific Changes in Invasive Pneumococcal Disease after Pneumococcal Conjugate Vaccine Introduction: A Pooled Analysis of Multiple Surveillance Sites. PLoS Med. 2013, 10, e1001517. [Google Scholar] [CrossRef] [PubMed]
- Weinberger, D.M.; Malley, R.; Lipsitch, M. Serotype replacement in disease after pneumococcal vaccination Serotype replacement in disease following pneumococcal vaccination: A discussion of the evidence. Lancet 2011, 378, 1962–1973. [Google Scholar] [CrossRef]
- Carman, W.F.; Zanetti, A.R.; Karayiannis, P.; Waters, J.; Manzillo, G.; Tanzi, E.; Zuckerman, A.J.; Thomas, H.C. Vaccine-induced escape mutant of hepatitis B virus. Lancet 1990, 336, 325–329. [Google Scholar] [CrossRef]
- Adam, H.J.; Richardson, S.E.; Jamieson, F.B.; Rawte, P.; Low, D.E.; Fisman, D.N. Changing epidemiology of invasive Haemophilus influenzae in Ontario, Canada: Evidence for herd effects and strain replacement due to Hib vaccination. Vaccine 2010, 28, 4073–4078. [Google Scholar] [CrossRef] [PubMed]
- Genton, B.; Betuela, I.; Felger, I.; Al-Yaman, F.; Anders, R.F.; Saul, A.; Rare, L.; Baisor, M.; Lorry, K.; Brown, G.V.; et al. A Recombinant Blood-Stage Malaria Vaccine Reduces Plasmodium falciparum Density and Exerts Selective Pressure on Parasite Populations in a Phase 1–2b Trial in Papua New Guinea. J. Infect. Dis. 2002, 185, 820–827. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.W.; Senne, D.A.; Suarez, D.L. Effect of Vaccine Use in the Evolution of Mexican Lineage H5N2 Avian Influenza Virus. J. Virol. 2004, 78, 8372–8381. [Google Scholar] [CrossRef] [PubMed]
- Barrett, P.N.; Berezuk, G.; Fritsch, S.; Aichinger, G.; Hart, M.K.; El-Amin, W.; Kistner, O.; Ehrlich, H.J. Efficacy, safety, and immunogenicity of a Vero-cell-culture-derived trivalent influenza vaccine: A multicentre, double-blind, randomised, placebo-controlled trial. Lancet 2011, 377, 751–759. [Google Scholar] [CrossRef]
- Beran, J.; Vesikari, T.; Wertzova, V.; Karvonen, A.; Honegr, K.; Lindblad, N.; Van Belle, P.; Peeters, M.; Innis, B.L.; Devaster, J.M. Efficacy of inactivated split-virus influenza vaccine against culture-confirmed influenza in healthy adults: A prospective, randomized, placebo-controlled trial. J. Infect. Dis. 2009, 200, 1861–1869. [Google Scholar] [CrossRef] [PubMed]
- Mcbride, W.J.H.; Abhayaratna, W.P.; Barr, I.; Booy, R.; Carapetis, J.; Carson, S.; De Looze, F.; Ellis-Pegler, R.; Heron, L.; Karrasch, J.; et al. Efficacy of a trivalent influenza vaccine against seasonal strains and against 2009 pandemic H1N1: A randomized, placebo-controlled trial. Vaccine 2016, 34, 4991–4997. [Google Scholar] [CrossRef] [PubMed]
- Monto, A.S.; Ohmit, S.E.; Petrie, J.G.; Johnson, E.; Truscon, R.; Teich, E.; Rotthoff, J.; Boulton, M.; Victor, J.C. Comparative efficacy of inactivated and live attenuated influenza vaccines. N. Engl. J. Med. 2009, 361, 1260–1267. [Google Scholar] [CrossRef] [PubMed]
- Treanor, J.J.; El Sahly, H.; King, J.; Graham, I.; Izikson, R.; Kohberger, R.; Patriarca, P.; Cox, M. Protective efficacy of a trivalent recombinant hemagglutinin protein vaccine (FluBlok®) against influenza in healthy adults: A randomized, placebo-controlled trial. Vaccine 2011, 29, 7733–7739. [Google Scholar] [CrossRef] [PubMed]
- Fielding, J.E.; Grant, K.A.; Papadakis, G.; Kelly, H.A. Estimation of type- and subtype-specific influenza vaccine effectiveness in Victoria, Australia using a test negative case control method, 2007–2008. BMC Infect. Dis. 2011, 11, 170. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, S.G.; Carville, K.S.; Chilver, M.; Fielding, J.E.; Grant, K.A.; Kelly, H.; Levy, A.; Stocks, N.P.; Tempone, S.S.; Regan, A.K. Pooled influenza vaccine effectiveness estimates for Australia, 2012–2014. Epidemiol. Infect. 2016, 144, 2317–2328. [Google Scholar] [CrossRef] [PubMed]
- Levy, A.; Sullivan, S.G.; Tempone, S.S.; Wong, K.L.; Regan, A.K.; Dowse, G.K.; Effler, P.V.; Smith, D.W. Influenza vaccine effectiveness estimates for Western Australia during a period of vaccine and virus strain stability, 2010 to 2012. Vaccine 2014, 32, 6312–6318. [Google Scholar] [CrossRef] [PubMed]
- Skowronski, D.M.; Chambers, C.; Sabaiduc, S.; De Serres, G.; Winter, A.L.; Dickinson, J.A.; Gubbay, J.B.; Drews, S.J.; Martineau, C.; Charest, H.; et al. Beyond Antigenic Match: Possible Agent-Host and Immuno-epidemiological Influences on Influenza Vaccine Effectiveness During the 2015–2016 Season in Canada. J. Infect. Dis. 2017, 216, 1487–1500. [Google Scholar] [CrossRef] [PubMed]
- Skowronski, D.M.; Chambers, C.; Sabaiduc, S.; De Serres, G.; Winter, A.L.; Dickinson, J.A.; Krajden, M.; Gubbay, J.B.; Drews, S.J.; Martineau, C.; et al. A Perfect Storm: Impact of Genomic Variation and Serial Vaccination on Low Influenza Vaccine Effectiveness During the 2014–2015 Season. Clin. Infect. Dis. 2016, 63, 21–32. [Google Scholar] [CrossRef] [PubMed]
- Skowronski, D.M.; Janjua, N.Z.; Sabaiduc, S.; De Serres, G.; Winter, A.L.; Gubbay, J.B.; Dickinson, J.A.; Fonseca, K.; Charest, H.; Bastien, N.; et al. Influenza A/Subtype and B/Lineage Effectiveness Estimates for the 2011–2012 Trivalent Vaccine: Cross-Season and Cross-Lineage Protection With Unchanged Vaccine. J. Infect. Dis. 2014, 210, 126–137. [Google Scholar] [CrossRef] [PubMed]
- Skowronski, D.M.; Janjua, N.Z.; De Serres, G.; Sabaiduc, S.; Eshaghi, A.; Dickinson, J.A.; Fonseca, K.; Winter, A.L.; Gubbay, J.B.; Krajden, M.; et al. Low 2012–13 Influenza Vaccine Effectiveness Associated with Mutation in the Egg-Adapted H3N2 Vaccine Strain Not Antigenic Drift in Circulating Viruses. PLoS ONE 2014, 9, e92153. [Google Scholar] [CrossRef] [PubMed]
- Skowronski, D.M.; Janjua, N.Z.; De Serres, G.; Winter, A.L.; Dickinson, J.A.; Gardy, J.L.; Gubbay, J.; Fonseca, K.; Charest, H.; Crowcroft, N.S.; et al. A Sentinel Platform to Evaluate Influenza Vaccine Effectiveness and New Variant Circulation, Canada 2010–2011 Season. Clin. Infect. Dis. 2012, 55, 332–342. [Google Scholar] [CrossRef] [PubMed]
- Skowronski, D.M.; De Serres, G.; Crowcroft, N.S.; Janjua, N.Z.; Boulianne, N.; Hottes, T.S.; Rosella, L.C.; Dickinson, J.A.; Gilca, R.; Sethi, P.; et al. Association between the 2008–09 Seasonal Influenza Vaccine and Pandemic H1N1 Illness during Spring–Summer 2009: Four Observational Studies from Canada. PLoS Med. 2010, 7, e1000258. [Google Scholar] [CrossRef] [PubMed]
- Skowronski, D.M.; De Serres, G.; Dickinson, J.; Petric, M.; Mak, A.; Fonseca, K.; Kwindt, T.L.; Chan, T.; Bastien, N.; Charest, H.; et al. Component-Specific Effectiveness of Trivalent Influenza Vaccine as Monitored through a Sentinel Surveillance Network in Canada, 2006–2007. J. Infect. Dis. 2009, 199, 168–179. [Google Scholar] [CrossRef] [PubMed]
- Janjua, N.Z.; Skowronski, D.M.; De Serres, G.; Dickinson, J.; Crowcroft, N.S.; Taylor, M.; Winter, A.L.; Hottes, T.S.; Fonseca, K.; Charest, H.; et al. Estimates of Influenza Vaccine Effectiveness for 2007–2008 From Canada’s Sentinel Surveillance System: Cross-Protection Against Major and Minor Variants. J. Infect. Dis. 2012, 205, 1858–1868. [Google Scholar] [CrossRef] [PubMed]
- Valenciano, M.; Kissling, E.; Larrauri, A.; Nunes, B.; Pitigoi, D.; O’Donnell, J.; Reuss, A.; Horváth, J.K.; Paradowska-Stankiewicz, I.; Rizzo, C.; et al. Exploring the effect of previous inactivated influenza vaccination on seasonal influenza vaccine effectiveness against medically attended influenza: Results of the European I-MOVE multicentre test-negative case-control study, 2011/2012–2016/2017. Influ. Respir. Viruses 2018. [Google Scholar] [CrossRef] [PubMed]
- Jackson, M.L.; Chung, J.R.; Jackson, L.A.; Phillips, C.H.; Benoit, J.; Monto, A.S.; Martin, E.T.; Belongia, E.A.; McLean, H.Q.; Gaglani, M.; et al. Influenza Vaccine Effectiveness in the United States during the 2015–2016 Season. N. Engl. J. Med. 2017, 377, 534–543. [Google Scholar] [CrossRef] [PubMed]
- Zimmerman, R.K.; Nowalk, M.P.; Chung, J.; Jackson, M.L.; Jackson, L.A.; Petrie, J.G.; Monto, A.S.; McLean, H.Q.; Belongia, E.A.; Gaglani, M.; et al. 2014–2015 Influenza Vaccine Effectiveness in the United States by Vaccine Type. Clin. Infect. Dis. 2016, 63, 1564–1573. [Google Scholar] [CrossRef] [PubMed]
- McLean, H.Q.; Thompson, M.G.; Sundaram, M.E.; Kieke, B.A.; Gaglani, M.; Murthy, K.; Piedra, P.A.; Zimmerman, R.K.; Nowalk, M.P.; Raviotta, J.M.; et al. Influenza vaccine effectiveness in the United States during 2012–2013: Variable protection by age and virus type. J. Infect. Dis. 2015, 211, 1529–1540. [Google Scholar] [CrossRef] [PubMed]
- Ohmit, S.E.; Thompson, M.G.; Petrie, J.G.; Thaker, S.N.; Jackson, M.L.; Belongia, E.A.; Zimmerman, R.K.; Gaglani, M.; Lamerato, L.; Spencer, S.M.; et al. Influenza Vaccine Effectiveness in the 2011–2012 Season: Protection Against Each Circulating Virus and the Effect of Prior Vaccination on Estimates. Clin. Infect. Dis. 2014, 58, 319–327. [Google Scholar] [CrossRef] [PubMed]
- Belongia, E.A.; Kieke, B.A.; Donahue, J.G.; Coleman, L.A.; Irving, S.A.; Meece, J.K.; Vandermause, M.; Lindstrom, S.; Gargiullo, P.; Shay, D.K. Influenza vaccine effectiveness in Wisconsin during the 2007–2008 season: Comparison of interim and final results. Vaccine 2011, 29, 6558–6563. [Google Scholar] [CrossRef] [PubMed]
- Treanor, J.J.; Talbot, H.K.; Ohmit, S.E.; Coleman, L.A.; Thompson, M.G.; Cheng, P.Y.; Petrie, J.G.; Lofthus, G.; Meece, J.K.; Williams, J.V.; et al. Effectiveness of Seasonal Influenza Vaccines in the United States During a Season With Circulation of All Three Vaccine Strains. Clin. Infect. Dis. 2012, 55, 951–959. [Google Scholar] [CrossRef] [PubMed]
- Gaglani, M.; Pruszynski, J.; Murthy, K.; Clipper, L.; Robertson, A.; Reis, M.; Chung, J.R.; Piedra, P.A.; Avadhanula, V.; Nowalk, M.P.; et al. Influenza Vaccine Effectiveness Against 2009 Pandemic Influenza A(H1N1) Virus Differed by Vaccine Type During 2013–2014 in the United States. J. Infect. Dis. 2016, 213, 1546–1556. [Google Scholar] [CrossRef] [PubMed]
- Flannery, B. Preliminary end-of-season estimates of 2016–2017 seasonal influenza vaccine effectiveness against medically attended influenza from the US Flu VE Network. Natl. Adult Influ. Immun. Summit 2017, 337, 534–543. [Google Scholar]
- Chambers, B.S.; Parkhouse, K.; Ross, T.M.; Alby, K.; Hensley, S.E. Identification of Hemagglutinin Residues Responsible for H3N2 Antigenic Drift during the 2014–2015 Influenza Season. Cell Rep. 2015, 12, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Flannery, B.; Zimmerman, R.K.; Gubareva, L.V.; Garten, R.J.; Chung, J.R.; Nowalk, M.P.; Jackson, M.L.; Jackson, L.A.; Monto, A.S.; Ohmit, S.E.; et al. Enhanced Genetic Characterization of Influenza A(H3N2) Viruses and Vaccine Effectiveness by Genetic Group, 2014–2015. J. Infect. Dis. 2016, 214, 1010–1019. [Google Scholar] [CrossRef] [PubMed]
- ECDC. Seasonal influenza vaccination in Europe. In Vaccination Recommendations and Coverage Rates in the EU Member States for Eight Influenza Seasons: 2007–2008 to 2014–2015; Technical report; European Centre for Disease Prevention and Control: Solna Municipality, Sweden, 2017. [Google Scholar]
- Centers for Disease Control and Prevention. Seasonal Influenza Vaccination Resources for Health Professionals; Centers for Disease Control and Prevention: Atlanta, GA, USA, 2018. [Google Scholar]
- Bahl, J.; Nelson, M.I.; Chan, K.H.; Chen, R.; Vijaykrishna, D.; Halpin, R.A.; Stockwell, T.B.; Lin, X.; Wentworth, D.E.; Ghedin, E.; et al. Temporally structured metapopulation dynamics and persistence of influenza A H3N2 virus in humans. Proc. Natl. Acad. Sci. USA 2011, 108, 19359–19364. [Google Scholar] [CrossRef] [PubMed]
- Bedford, T.; Cobey, S.; Beerli, P.; Pascual, M. Global migration dynamics underlie evolution and persistence of human influenza A (H3N2). PLoS Pathog. 2010, 6, e1000918. [Google Scholar] [CrossRef] [PubMed]
- Russell, C.A.; Jones, T.C.; Barr, I.G.; Cox, N.J.; Garten, R.J.; Gregory, V.; Gust, I.D.; Hampson, A.W.; Hay, A.J.; Hurt, A.C.; et al. The Global Circulation of Seasonal Influenza A (H3N2) Viruses. Science 2008, 320, 340–346. [Google Scholar] [CrossRef] [PubMed]
- Finkelman, B.S.; Viboud, C.; Koelle, K.; Ferrari, M.J.; Bharti, N.; Grenfell, B.T. Global Patterns in Seasonal Activity of Influenza A/H3N2, A/H1N1, and B from 1997 to 2005: Viral Coexistence and Latitudinal Gradients. PLoS ONE 2007, 2, e1296. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. FluNet; World Health Organization: Geneva, Switzerland, 2018. [Google Scholar]
- World Health Organization. FluID—A gLobal Influenza Epidemiological Data Sharing Platform; World Health Organization: Geneva, Switzerland, 2018. [Google Scholar]
- World Health Organization, European Centre for Disease Prevention and Control. Influenza Surveillance Country, Territory, and Area Profiles 2017; Technical report; World Health Organization, European Centre for Disease Prevention and Control: Solna Municipality, Sweden, 2017. [Google Scholar]
- Shu, Y.; McCauley, J. GISAID: Global initiative on sharing all influenza data—From vision to reality. Eurosurveillance 2017, 22, 30494. [Google Scholar] [CrossRef] [PubMed]
- Hadfield, J.; Megill, C.; Bell, S.M.; Huddleston, J.; Potter, B.; Callender, C.; Sagulenko, P.; Bedford, T.; Neher, R.A. Nextstrain: real-time tracking of pathogen evolution. bioRxiv 2017, 224048. [Google Scholar] [CrossRef]
- Goldstein, E.; Cobey, S.; Takahashi, S.; Miller, J.C.; Lipsitch, M. Predicting the Epidemic Sizes of Influenza A/H1N1, A/H3N2, and B: A Statistical Method. PLoS Med. 2011, 8, e1001051. [Google Scholar] [CrossRef] [PubMed]
- Viboud, C.; Bjørnstad, O.N.; Smith, D.L.; Simonsen, L.; Miller, M.A.; Grenfell, B.T. Synchrony, waves, and spatial hierarchies in the spread of influenza. Science 2006, 312, 447–451. [Google Scholar] [CrossRef] [PubMed]
- Neher, R.A.; Bedford, T.; Daniels, R.S.; Russell, C.A.; Shraiman, B.I. Prediction, dynamics, and visualization of antigenic phenotypes of seasonal influenza viruses. Proc. Natl. Acad. Sci. USA 2016, 113, E1701–E1709. [Google Scholar] [CrossRef] [PubMed]
- Wolf, Y.I.; Viboud, C.; Holmes, E.C.; Koonin, E.V.; Lipman, D.J. Long intervals of stasis punctuated by bursts of positive selection in the seasonal evolution of influenza A virus. Biol. Direct 2006, 1, 34. [Google Scholar] [CrossRef] [PubMed]
- Wen, F.T.; Bell, S.M.B.; Bedford, T.; Cobey, S. Flu Vaccine Sieve. Available online: https://github.com/cobeylab/flu-vaccine-sieve (accessed on 22 August 2018).
- Bhatt, S.; Holmes, E.C.; Pybus, O.G. The Genomic Rate of Molecular Adaptation of the Human Influenza A Virus. Mol. Biol. Evol. 2011, 28, 2443–2451. [Google Scholar] [CrossRef] [PubMed]
- Centers for Disease Control and Prevention. Quadrivalent Influenza Vaccine; Centers for Disease Control and Prevention: Atlanta, GA, USA, 2018. [Google Scholar]
- Block, S.L.; Yi, T.; Sheldon, E.; Dubovsky, F.; Falloon, J. A randomized, double-blind noninferiority study of quadrivalent live attenuated influenza vaccine in adults. Vaccine 2011, 29, 9391–9397. [Google Scholar] [CrossRef] [PubMed]
- Block, S.L.; Falloon, J.; Hirschfield, J.A.; Krilov, L.R.; Dubovsky, F.; Yi, T.; Belshe, R.B. Immunogenicity and Safety of a Quadrivalent Live Attenuated Influenza Vaccine in Children. Pediatr. Infec. Dis. J. 2012, 31, 745–751. [Google Scholar] [CrossRef] [PubMed]
- Skowronski, D.M.; Hottes, T.S.; De Serres, G.; Ward, B.J.; Janjua, N.Z.; Sabaiduc, S.; Chan, T.; Petric, M. Influenza B/Victoria Antigen Induces Strong Recall of B/Yamagata But Lower B/Victoria Response in Children Primed With Two Doses of B/Yamagata. Pediatr. Infec. Dis. J. 2011, 30, 833–839. [Google Scholar] [CrossRef] [PubMed]
- Skowronski, D.M.; Hamelin, M.E.; Janjua, N.Z.; De Serres, G.; Gardy, J.L.; Rhéaume, C.; Bouhy, X.; Boivin, G. Cross-Lineage Influenza B and Heterologous Influenza A Antibody Responses in Vaccinated Mice: Immunologic Interactions and B/Yamagata Dominance. PLoS ONE 2012, 7, e38929. [Google Scholar] [CrossRef] [PubMed]
- Lewnard, J.A.; Tedijanto, C.; Cowling, B.J.; Lipsitch, M. Quantifying biases in test-negative studies of vaccine effectiveness. bioRxiv 2017. [Google Scholar] [CrossRef]
- Bonomo, M.E.; Deem, M.W. Predicting Influenza H3N2 Vaccine Efficacy from Evolution of the Dominant Epitope. Clin. Infect. Dis. 2018. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Deem, M.W. Influenza evolution and H3N2 vaccine effectiveness, with application to the 2014/2015 season. Protein Eng. Des. Sel. 2016, 29, 309–315. [Google Scholar] [CrossRef] [PubMed]
- Cobey, S.; Gouma, S.; Parkhouse, K.; Chambers, B.S.; Ertl, H.C.; Schmader, K.E.; Halpin, R.A.; Lin, X.; Stockwell, T.B.; Das, S.R.; et al. Poor immunogenicity, not vaccine strain egg adaptation, may explain the low H3N2 influenza vaccine effectiveness in 2012–2013. Clin. Infect. Dis. 2018, 67, 327–333. [Google Scholar] [CrossRef] [PubMed]
- Davenport, F.M.; Hennessy, A.V. A serologic recapitulation of past experiences with influenza A; antibody response to monovalent vaccine. J. Exp. Med. 1956, 104, 85–97. [Google Scholar] [CrossRef] [PubMed]
- Davenport, F.M.; Hennessy, A.V. Predetermination by infection and by vaccination of antibody response to influenza virus vaccines. J. Exp. Med. 1957, 106, 835–850. [Google Scholar] [CrossRef] [PubMed]
- Jester, B.; Schwerzmann, J.; Mustaquim, D.; Aden, T.; Brammer, L.; Humes, R.; Shult, P.; Shahangian, S.; Gubareva, L.; Xu, X.; et al. Mapping of the US Domestic Influenza Virologic Surveillance Landscape. Emerg. Infect. Dis. 2018, 24, 1300–1306. [Google Scholar] [CrossRef] [PubMed]
- Kwok, K.O.; Riley, S.; Perera, R.A.P.M.; Wei, V.W.I.; Wu, P.; Wei, L.; Chu, D.K.W.; Barr, I.G.; Malik Peiris, J.S.; Cowling, B.J. Relative incidence and individual-level severity of seasonal influenza A H3N2 compared with 2009 pandemic H1N1. BMC Infect. Dis. 2017, 17, 337. [Google Scholar] [CrossRef] [PubMed]
- White, L.J.; Cox, M.J.; Medley, G.F. Cross immunity and vaccination against multiple microparasite strains. IMA J. Math. Appl. Med. Biol. 1998, 15, 211–233. [Google Scholar] [CrossRef] [PubMed]
- Lewnard, J.; Cobey, S. Immune History and Influenza Vaccine Effectiveness. Vaccines 2018, 6, 28. [Google Scholar] [CrossRef] [PubMed]
- Clover, R.D.; Crawford, S.; Glezen, W.P.; Taber, L.H.; Matson, C.C.; Couch, R.B. Comparison of Heterotypic Protection against Influenza A/Taiwan/86 (H1N1) by Attenuated and Inactivated Vaccines to A/Chile/83-like Viruses. J. Infect. Dis. 1991, 163, 300–3004. [Google Scholar] [CrossRef] [PubMed]
- Gruber, W.C.; Taber, L.H.; Glezen, W.P.; Clover, R.D.; Abell, T.D.; Demmler, R.W.; Couch, R.B. Live Attenuated and Inactivated Influenza Vaccine in School-age Children. Arch. Pediatr. Adolesc. Med. 1990, 144, 595. [Google Scholar] [CrossRef]
- Hoberman, A.; Greenberg, D.P.; Paradise, J.L.; Rockette, H.E.; Lave, J.R.; Kearney, D.H.; Colborn, D.K.; Kurs-Lasky, M.; Haralam, M.A.; Byers, C.J.; et al. Effectiveness of Inactivated Influenza Vaccine in Preventing Acute Otitis Media in Young Children. JAMA 2003, 290, 1608–1616. [Google Scholar] [CrossRef] [PubMed]
- Osterholm, M.T.; Kelley, N.S.; Sommer, A.; Belongia, E.A. Efficacy and effectiveness of influenza vaccines: A systematic review and meta-analysis. Lancet. Infec. Dis. 2012, 12, 36–44. [Google Scholar] [CrossRef]
- Ohmit, S.E.; Victor, J.C.; Rotthoff, J.R.; Teich, E.R.; Truscon, R.K.; Baum, L.L.; Rangarajan, B.; Newton, D.W.; Boulton, M.L.; Monto, A.S. Prevention of antigenically drifted influenza by inactivated and live attenuated vaccines. N. Engl. J. Med. 2006, 355, 2513–2522. [Google Scholar] [CrossRef] [PubMed]
- Beran, J.; Wertzova, V.; Honegr, K.; Kaliskova, E.; Havlickova, M.; Havlik, J.; Jirincova, H.; Van Belle, P.; Jain, V.; Innis, B.; et al. Challenge of conducting a placebo-controlled randomized efficacy study for influenza vaccine in a season with low attack rate and a mismatched vaccine B strain: A concrete example. BMC Infect. Dis. 2009, 9, 2. [Google Scholar] [CrossRef] [PubMed]
- Jackson, L.A.; Gaglani, M.J.; Keyserling, H.L.; Balser, J.; Bouveret, N.; Fries, L.; Treanor, J.J. Safety, efficacy, and immunogenicity of an inactivated influenza vaccine in healthy adults: A randomized, placebo-controlled trial over two influenza seasons. BMC Infect. Dis. 2010, 10, 71. [Google Scholar] [CrossRef] [PubMed]
- Frey, S.; Vesikari, T.; Szymczakiewicz-Multanowska, A.; Lattanzi, M.; Izu, A.; Groth, N.; Holmes, S. Clinical Efficacy of Cell Culture–Derived and Egg–Derived Inactivated Subunit Influenza Vaccines in Healthy Adults. Clin. Infect. Dis. 2010, 51, 997–1004. [Google Scholar] [CrossRef] [PubMed]
- Zost, S.J.; Parkhouse, K.; Gumina, M.E.; Kim, K.; Diaz Perez, S.; Wilson, P.C.; Treanor, J.J.; Sant, A.J.; Cobey, S.; Hensley, S.E. Contemporary H3N2 influenza viruses have a glycosylation site that alters binding of antibodies elicited by egg-adapted vaccine strains. Proc. Natl. Acad. Sci. USA 2017. [Google Scholar] [CrossRef] [PubMed]
- Dyda, A.; Karki, S.; Hayen, A.; MacIntyre, C.R.; Menzies, R.; Banks, E.; Kaldor, J.M.; Liu, B. Influenza and pneumococcal vaccination in Australian adults: A systematic review of coverage and factors associated with uptake. BMC Infect. Dis. 2016, 16. [Google Scholar] [CrossRef] [PubMed]
- Buchan, S.A.; Kwong, J.C. Trends in influenza vaccine coverage and vaccine hesitancy in Canada, 2006/07 to 2013/14: Results from cross-sectional survey data. CMAJ Open 2016, 4, E455–E462. [Google Scholar] [CrossRef] [PubMed]
- Gionet, L. Health at a Glance: Flu vaccination rates in Canada. Natl. Advis. Comm. Immun. 2015, 7. [Google Scholar]
- Palache, A.; Oriol-Mathieu, V.; Abelin, A.; Music, T. Seasonal influenza vaccine dose distribution in 157 countries (2004–2011). Vaccine 2014, 32, 6369–6376. [Google Scholar] [CrossRef] [PubMed]
- Palache, A.; Oriol-Mathieu, V.; Fino, M.; Xydia-Charmanta, M.; Influenza Vaccine Supply task force (IFPMA IVS). Seasonal influenza vaccine dose distribution in 195 countries (2004–2013): Little progress in estimated global vaccination coverage. Vaccine 2015, 33, 5598–5605. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, F.T.; Bell, S.M.; Bedford, T.; Cobey, S. Estimating Vaccine-Driven Selection in Seasonal Influenza. Viruses 2018, 10, 509. https://doi.org/10.3390/v10090509
Wen FT, Bell SM, Bedford T, Cobey S. Estimating Vaccine-Driven Selection in Seasonal Influenza. Viruses. 2018; 10(9):509. https://doi.org/10.3390/v10090509
Chicago/Turabian StyleWen, Frank T., Sidney M. Bell, Trevor Bedford, and Sarah Cobey. 2018. "Estimating Vaccine-Driven Selection in Seasonal Influenza" Viruses 10, no. 9: 509. https://doi.org/10.3390/v10090509
APA StyleWen, F. T., Bell, S. M., Bedford, T., & Cobey, S. (2018). Estimating Vaccine-Driven Selection in Seasonal Influenza. Viruses, 10(9), 509. https://doi.org/10.3390/v10090509





