Neuraminidase Inhibitors in Influenza Treatment and Prevention–Is It Time to Call It a Day?
Abstract
1. Introduction
2. Materials and Methods
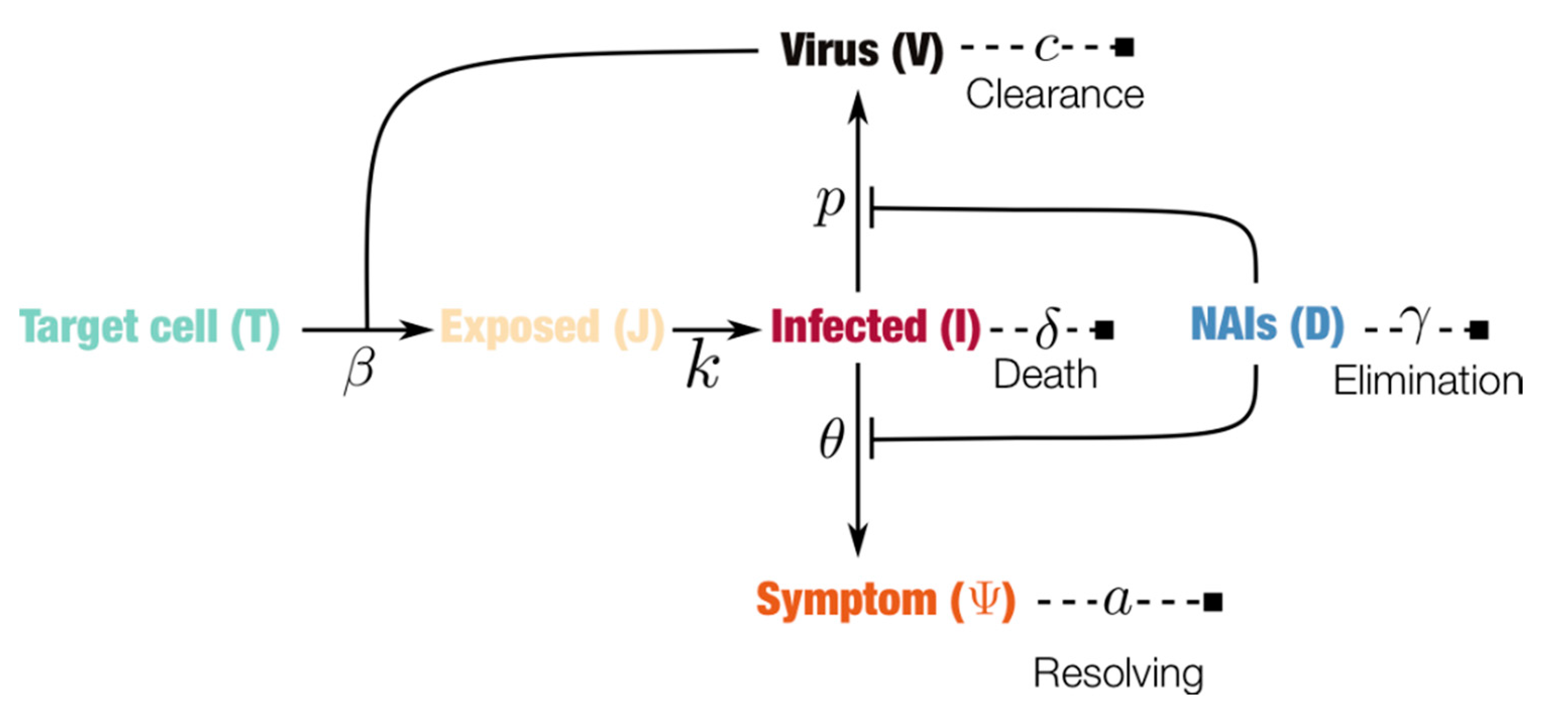
2.1. Within-Host Model
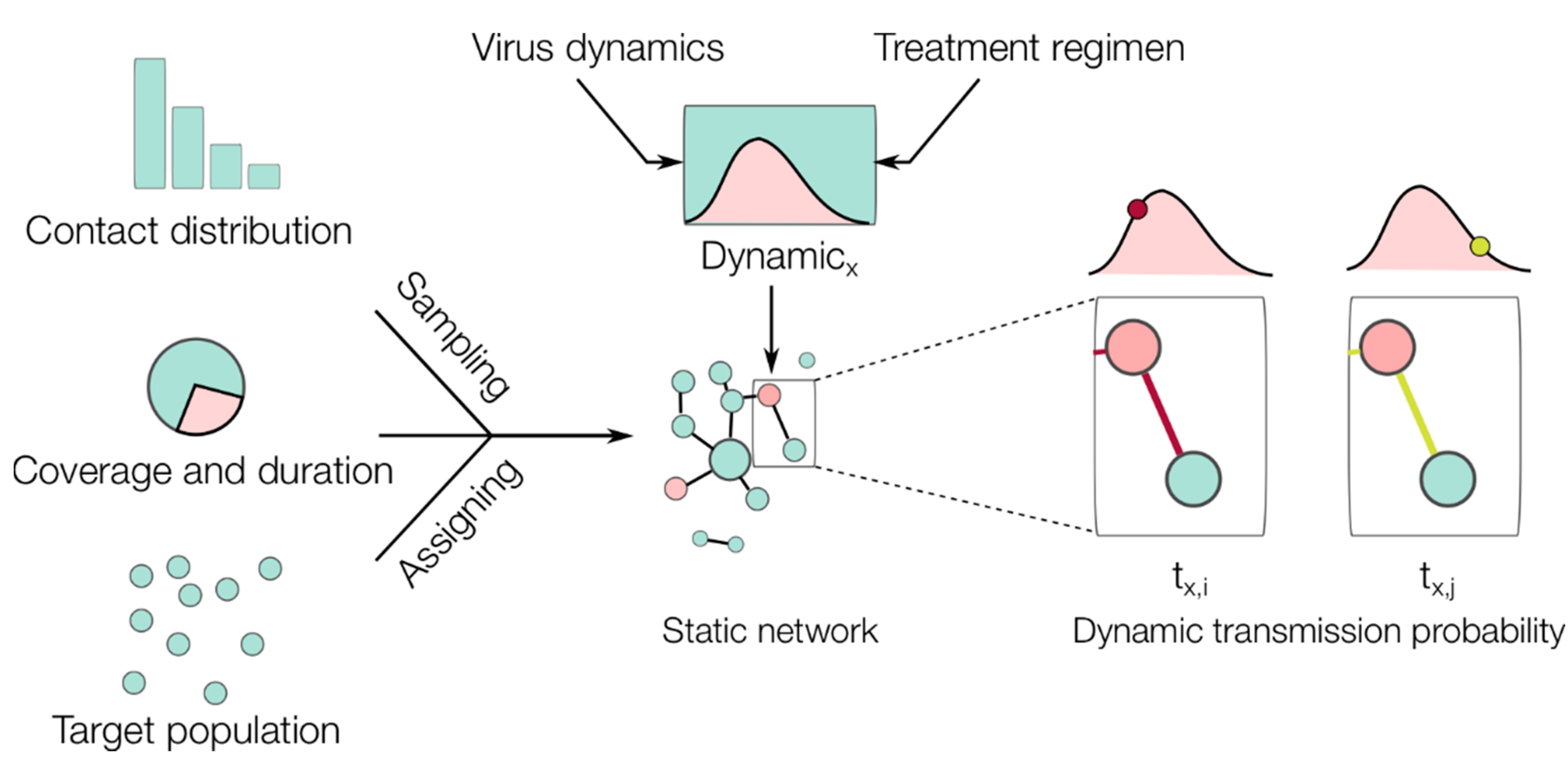
2.2. Population Model
2.3. Software and Algorithms
3. Results
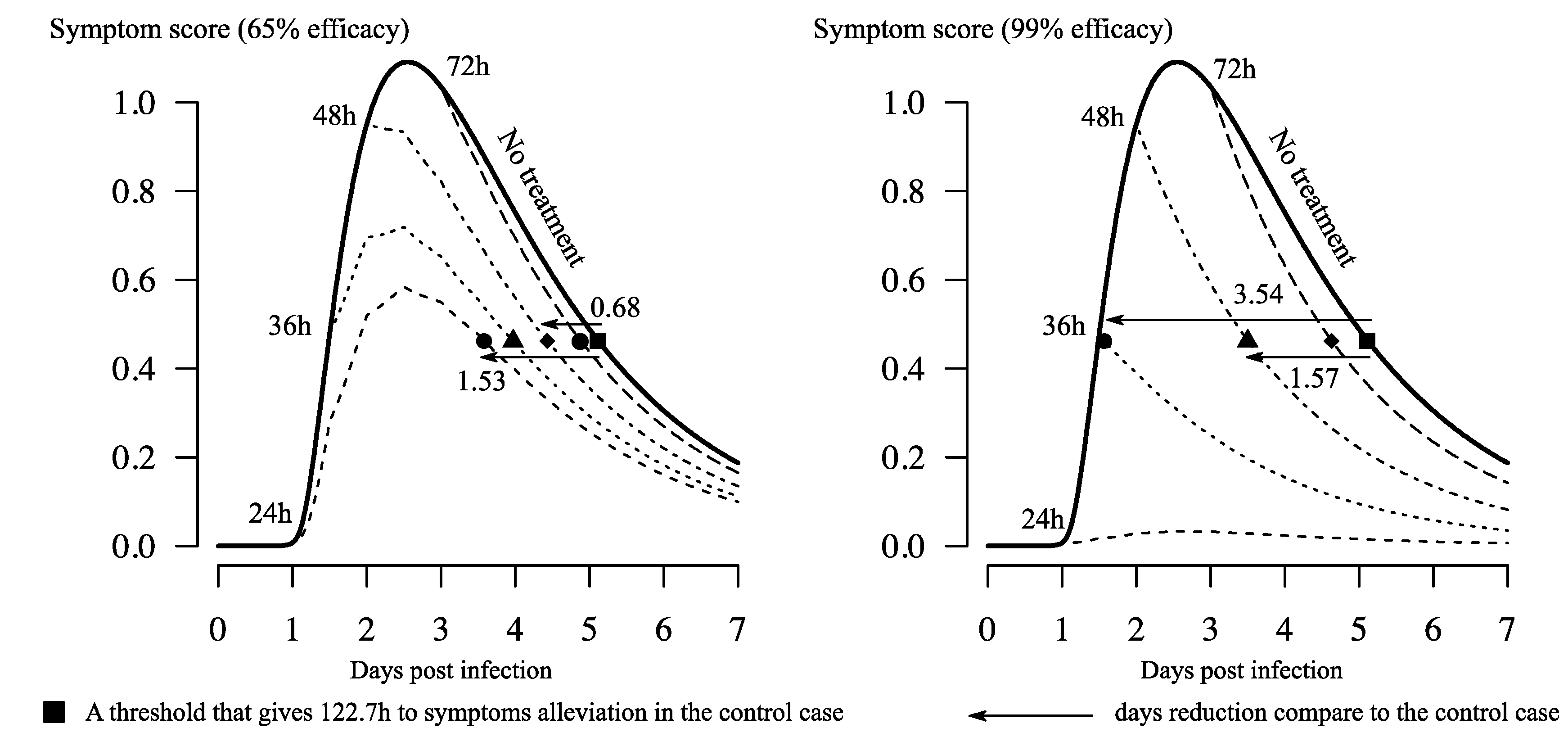
3.1. Reduction of Time to Symptom Alleviation
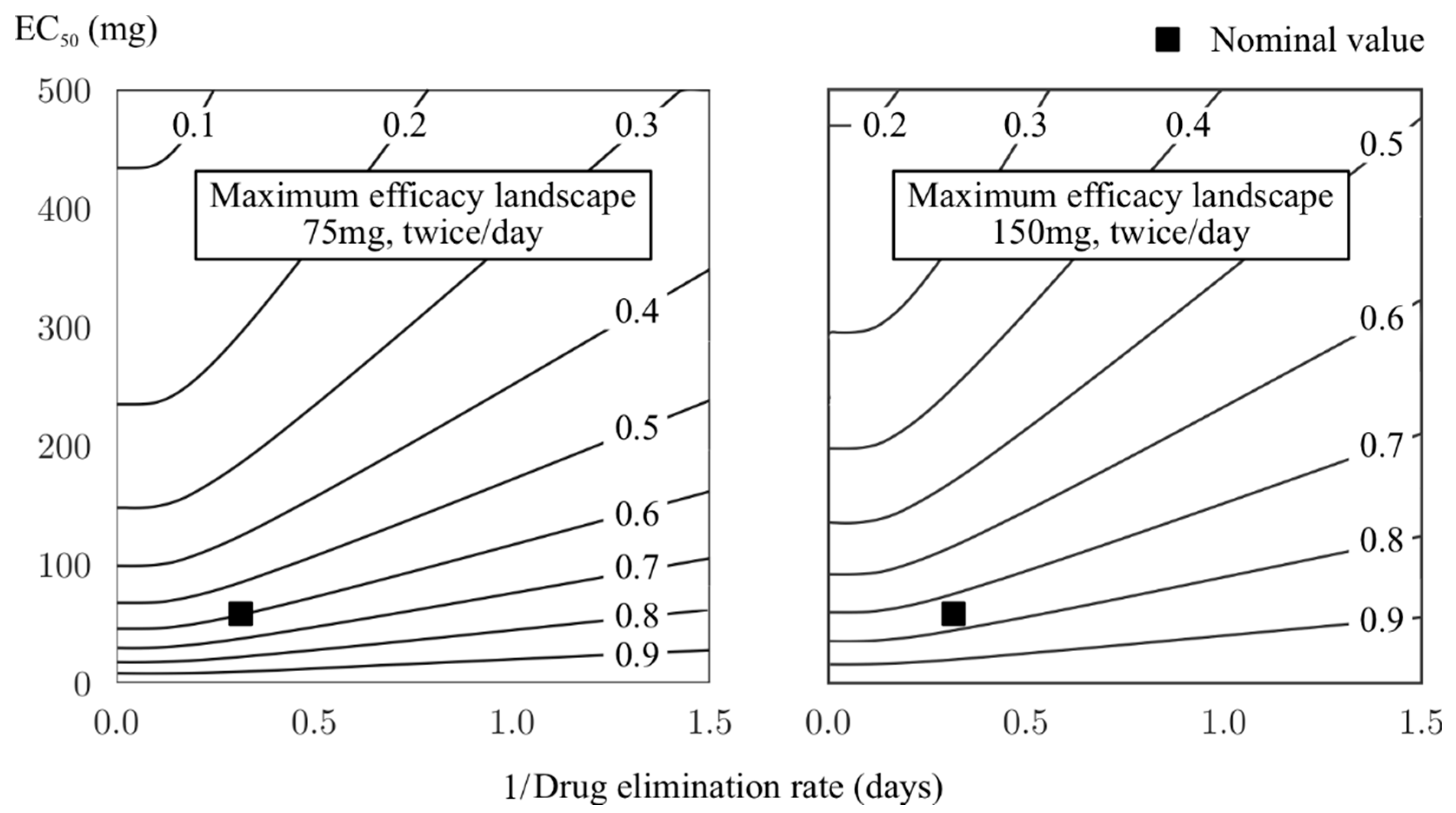
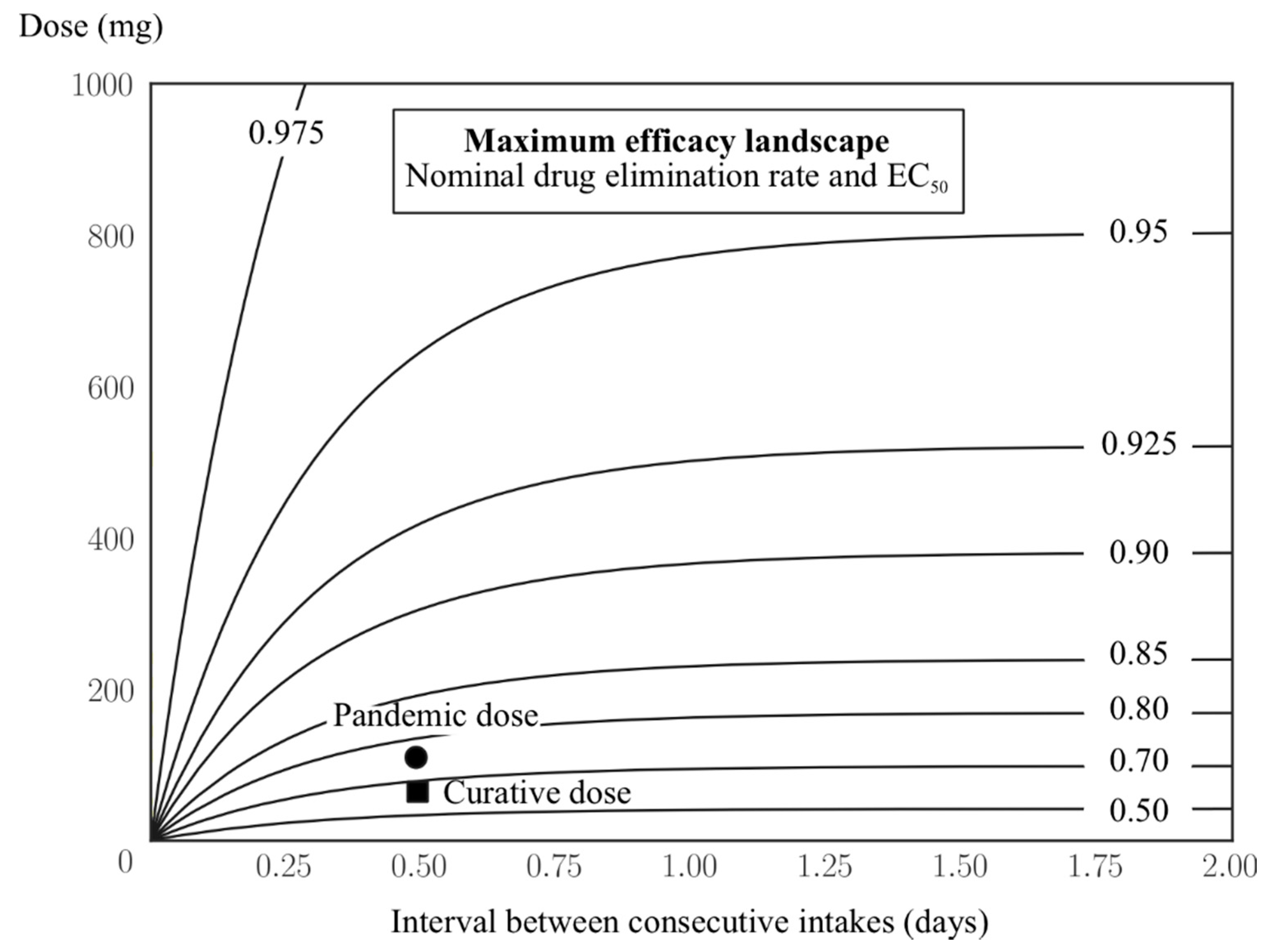
3.2. Inherently Limited Efficacy by Pharmacokinetic Parameters
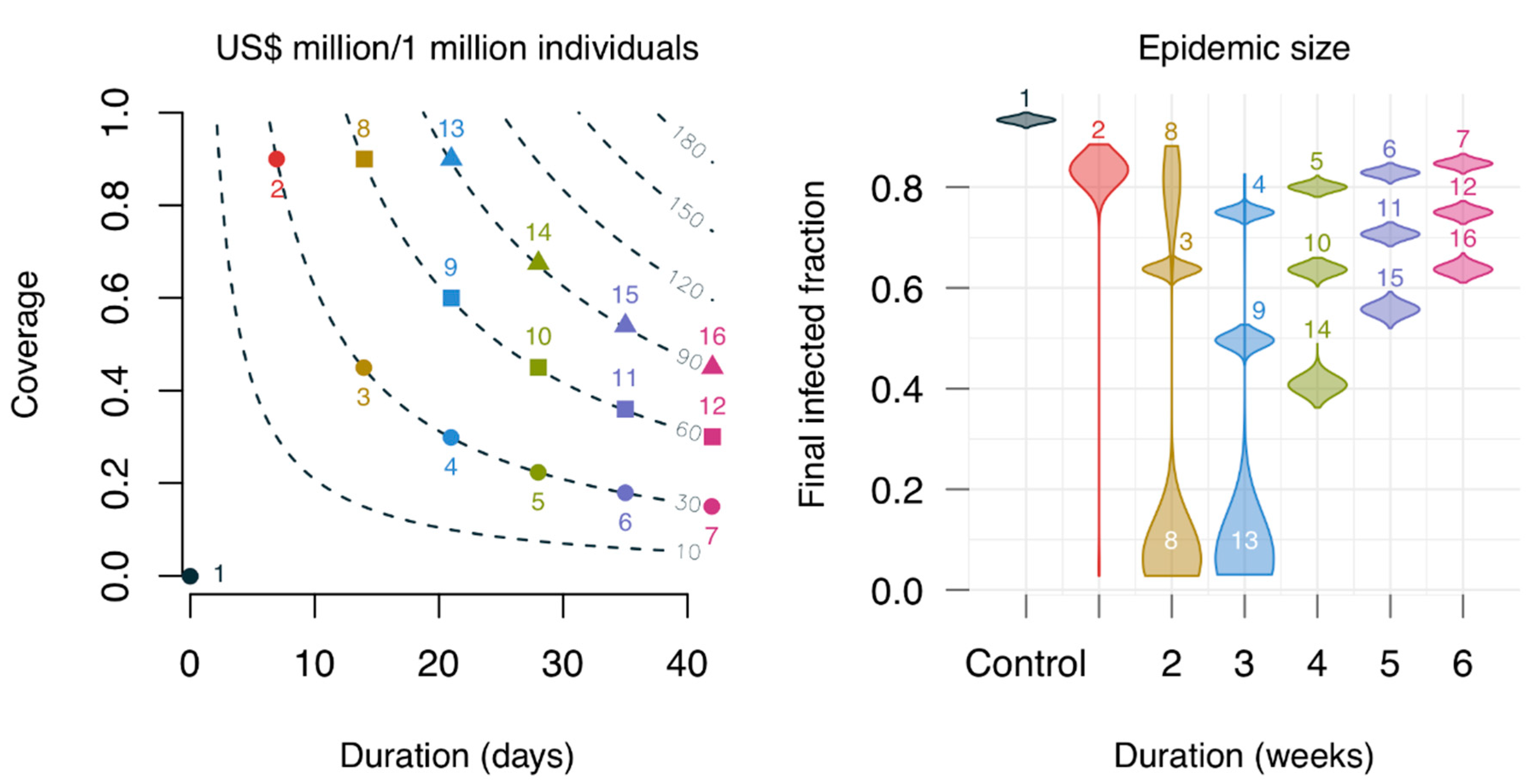
3.3. High Preventive Effect Observed only in a Fragile Setting
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
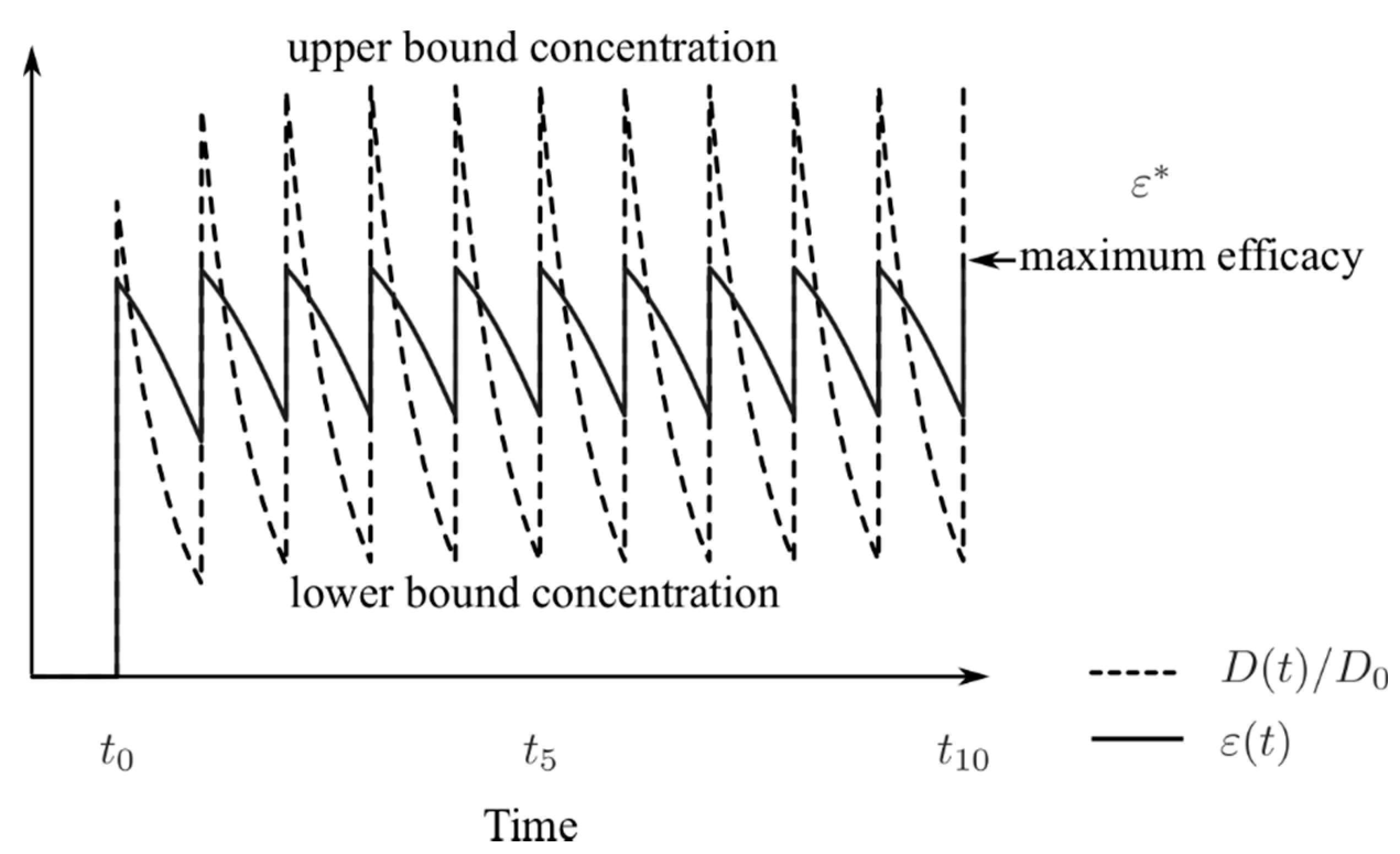
Appendix A.1. Model Analyses
Appendix A.2. Simulations of Viral Load Dynamics in Different Treatment Strategies
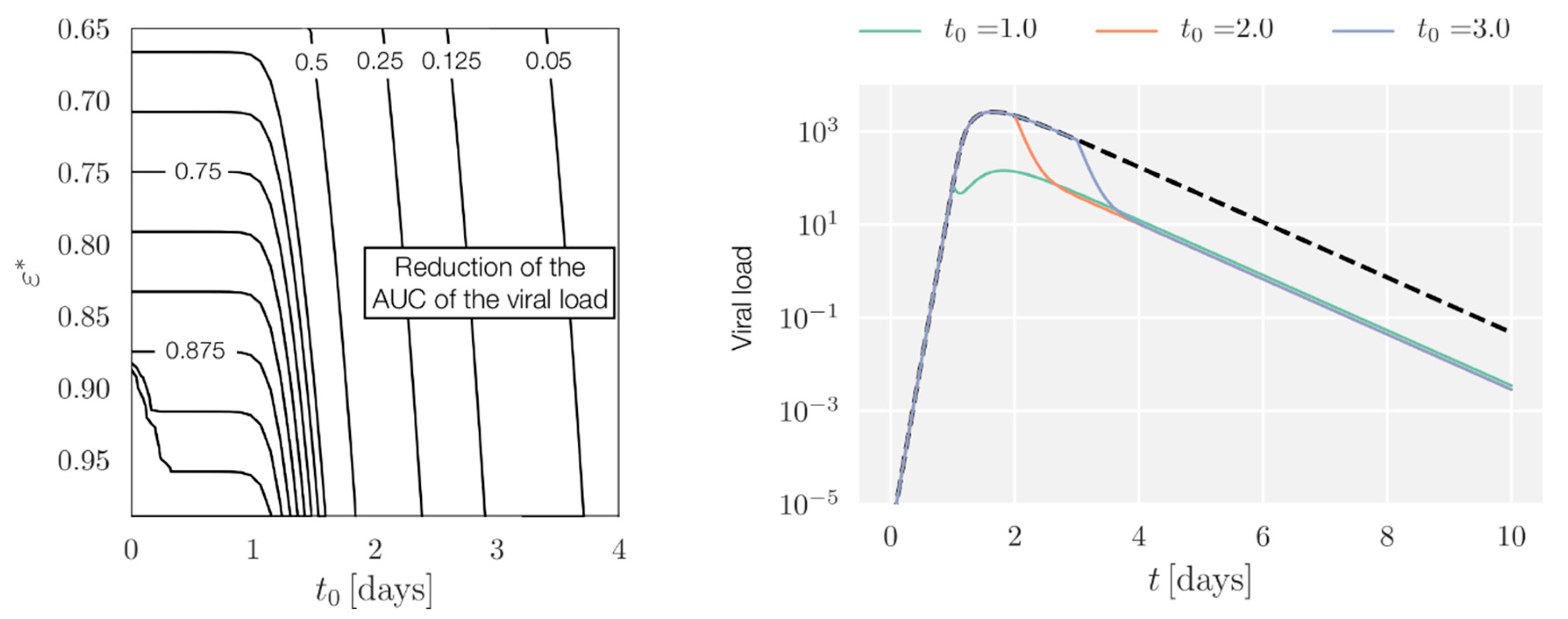
Appendix A.3. AUC Reduction with Full Pharmacokinetic-Pharmacodynamic (PK/PD)
References
- Moscona, A. Neuraminidase inhibitors for influenza. N. Engl. J. Med. 2005, 353, 1363–1373. [Google Scholar] [CrossRef] [PubMed]
- Stöhr, K. Avian influenza and pandemics—Research needs and opportunities. N. Engl. J. Med. 2005, 352, 405–407. [Google Scholar] [CrossRef] [PubMed]
- Centers for Disease Control and Prevention Seasonal Influenza Vaccine Effectiveness, 2005–2018. Available online: https://www.cdc.gov/flu/professionals/vaccination/effectiveness-studies.htm (accessed on 13 July 2018).
- Kelly, H.; Cowling, B.J. Influenza: The rational use of oseltamivir. Lancet 2017, 385, 1700–1702. [Google Scholar] [CrossRef]
- Dobson, J.; Whitley, R.J.; Pocock, S.; Monto, A.S. Oseltamivir treatment for influenza in adults: A meta-analysis of randomised controlled trials. Lancet 2015, 385, 1729–1737. [Google Scholar] [CrossRef]
- Hurt, A.C.; Kelly, H. Debate Regarding Oseltamivir Use for Seasonal and Pandemic Influenza. Emerg. Infect. Dis. 2016, 22, 949–955. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization Influenza (Seasonal). Fact Sheet N. 211. Available online: http://www.who.int/mediacentre/factsheets/2003/fs211/en/ (accessed on 13 July 2018).
- Jefferson, T.; Jones, M.A.; Doshi, P.; Del Mar, C.B.; Hama, R.; Thompson, M.J.; Spencer, E.A.; Onakpoya, I.; Mahtani, K.R.; Nunan, D.; et al. Neuraminidase inhibitors for preventing and treating influenza in healthy adults and children. Cochrane Database Syst. Rev. 2014, CD008965. [Google Scholar] [CrossRef]
- Gubareva, L.V.; Kaiser, L.; Hayden, F.G. Influenza virus neuraminidase inhibitors. Lancet 2000, 355, 827–835. [Google Scholar] [CrossRef]
- McClellan, K.; Perry, C.M. Oseltamivir. Drugs 2001, 61, 263–283. [Google Scholar] [CrossRef] [PubMed]
- Kamali, A.; Holodniy, M. Influenza treatment and prophylaxis with neuraminidase inhibitors: A review. Infect. Drug Resist. 2013, 6, 187–198. [Google Scholar] [PubMed]
- Ison, M.G. Clinical use of approved influenza antivirals: Therapy and prophylaxis. Influenza Other Respir. Viruses 2013, 7, 7–13. [Google Scholar] [CrossRef] [PubMed]
- South East Asia Infectious Disease Clinical Research Network. Effect of double dose oseltamivir on clinical and virological outcomes in children and adults admitted to hospital with severe influenza: Double blind randomised controlled trial. BMJ 2013, 346, f3039. [Google Scholar] [CrossRef] [PubMed]
- Jefferson, T.; Doshi, P. Multisystem failure: The story of anti-influenza drugs. BMJ 2014, 348, g2263. [Google Scholar] [CrossRef] [PubMed]
- Boianelli, A.; Nguyen, V.K.; Ebensen, T.; Schulze, K.; Wilk, E.; Sharma, N.; Stegemann-Koniszewski, S.; Bruder, D.; Toapanta, F.; Guzmán, C.A.; et al. Modeling Influenza Virus Infection: A Roadmap for Influenza Research. Viruses 2015, 7, 5274–5304. [Google Scholar] [CrossRef] [PubMed]
- Cohen, S.; Doyle, W.J.; Skoner, D.P. Psychological stress, cytokine production, and severity of upper respiratory illness. Psychosom. Med. 1999, 61, 175–180. [Google Scholar] [CrossRef] [PubMed]
- Jefferson, T.; Jones, M.A.; Doshi, P.; Del Mar, C.B.; Hama, R.; Thompson, M.J.; Spencer, E.A.; Onakpoya, I.J.; Mahtani, K.R.; Nunan, D.; et al. Neuraminidase Inhibitors for Preventing and Treating Influenza in Adults and Children; Cochrane Acute Respiratory Infections Group, Ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014; Volume 19. [Google Scholar]
- Lukens, S.; DePasse, J.; Rosenfeld, R.; Ghedin, E.; Mochan, E.; Brown, S.T.; Grefenstette, J.; Burke, D.S.; Swigon, D.; Clermont, G. A large-scale immuno-epidemiological simulation of influenza A epidemics. BMC Public Health 2014, 14. [Google Scholar] [CrossRef] [PubMed]
- Wattanagoon, Y.; Stepniewska, K.; Lindegårdh, N.; Pukrittayakamee, S.; Silachamroon, U.; Piyaphanee, W.; Singtoroj, T.; Hanpithakpong, W.; Davies, G.; Tarning, J. Pharmacokinetics of high-dose oseltamivir in healthy volunteers. Antimicrob. Agents Chemother. 2009, 53, 945–952. [Google Scholar] [CrossRef] [PubMed]
- Tamiflu™ (Oseltamivir Phosphate) Capsules and for Oral Suspension. 2009. Available online: https://www.accessdata.fda.gov/drugsatfda_docs/label/2000/21246LBL.pdf (accessed on 13 July 2018).
- World Health Organization. WHO Guidelines for Pharmacological Management of Pandemic (H1N1) 2009 Influenza and Other Influenza Viruses Part I: Recommendations. Available online: http://www.who.int/csr/resources/publications/swineflu/h1n1_guidelines_pharmaceutical_mngt.pdf (accessed on 13 July 2018).
- Enserink, M. Oseltamivir Becomes Plentiful--But Still Not Cheap. Science 2006, 312, 382–383. [Google Scholar] [CrossRef] [PubMed]
- Mossong, J.; Hens, N.; Jit, M.; Beutels, P.; Auranen, K.; Mikolajczyk, R.; Massari, M.; Salmaso, S.; Tomba, G.S.; Wallinga, J.; et al. Social Contacts and Mixing Patterns Relevant to the Spread of Infectious Diseases. PLoS Med. 2008, 5, e74. [Google Scholar] [CrossRef] [PubMed]
- Britton, T. Stochastic epidemic models: A survey. Math. Biosci. 2010, 225, 24–35. [Google Scholar] [CrossRef] [PubMed]
- Rayner, C.R.; Chanu, P.; Gieschke, R.; Boak, L.M.; Jonsson, E.N. Population pharmacokinetics of oseltamivir when coadministered with probenecid. J. Clin. Pharmacol. 2008, 48, 935–947. [Google Scholar] [CrossRef] [PubMed]
- Canini, L.; Conway, J.M.; Perelson, A.S.; Carrat, F. Impact of different oseltamivir regimens on treating influenza A virus infection and resistance emergence: Insights from a modelling study. PLoS Comput. Biol. 2014, 10, e1003568. [Google Scholar] [CrossRef] [PubMed]
- Doll, M.K.; Winters, N.; Boikos, C.; Kraicer-Melamed, H.; Gore, G.; Quach, C. Safety and effectiveness of neuraminidase inhibitors for influenza treatment, prophylaxis, and outbreak control: A systematic review of systematic reviews and/or meta-analyses. J. Antimicrob. Chemother. 2017, 72, 2990–3007. [Google Scholar] [CrossRef] [PubMed]
- Noel, Z.R.; Bastin, M.L.T.; Montgomery, A.A.; Flannery, A.H. Comparison of High-Dose Versus Standard Dose Oseltamivir in Critically III Patients With Influenza. J. Intensive Care Med. 2016, 32, 574–577. [Google Scholar] [CrossRef] [PubMed]
- Davies, B.E. Pharmacokinetics of oseltamivir: An oral antiviral for the treatment and prophylaxis of influenza in diverse populations. J. Antimicrob. Chemother. 2010, 65. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez-Mendoza, L.M.; Schwartz, B.; Méndez de Lira, J.; Wirtz, V.J. Oseltamivir storage, distribution and dispensing following the 2009 H1N1 influenza outbreak in Mexico. Bull. World Health Organ. 2012, 90, 782–787. [Google Scholar] [CrossRef] [PubMed]
- Lipsitch, M.; Cohen, T.; Murray, M.; Levin, B.R. Antiviral resistance and the control of pandemic influenza. PLoS Med. 2007, 4, e15. [Google Scholar] [CrossRef] [PubMed]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; United States Department of Commerce, National Institute of Standards and Technology (NBS): New York, NY, USA, 1965. [Google Scholar]
| Parameter | Value | Unit | Source or Notes |
|---|---|---|---|
| β | 0.0674 | TCID50 mL day−1 | [18] |
| k | 3.684 | day−1 | [18] |
| δ | 1.364 | day−1 | [18] |
| p | 40,356 | TCID50 mL−1 day−1 | [18] |
| c | 8.0 | day−1 | [18] |
| θ | 2.75 | day−1 S * | [18] |
| a | 0.498 | day−1 | [18] |
| γ | 3.26 | day−1 | [19] |
| EC50 | 0.01–500 † | mg | [20] |
| D0 | 75 (c) and 150 (p) ** | mg | [21] |
| τ | 0.5 | day | twice a day |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parra-Rojas, C.; Nguyen, V.K.; Hernandez-Mejia, G.; Hernandez-Vargas, E.A. Neuraminidase Inhibitors in Influenza Treatment and Prevention–Is It Time to Call It a Day? Viruses 2018, 10, 454. https://doi.org/10.3390/v10090454
Parra-Rojas C, Nguyen VK, Hernandez-Mejia G, Hernandez-Vargas EA. Neuraminidase Inhibitors in Influenza Treatment and Prevention–Is It Time to Call It a Day? Viruses. 2018; 10(9):454. https://doi.org/10.3390/v10090454
Chicago/Turabian StyleParra-Rojas, César, Van Kinh Nguyen, Gustavo Hernandez-Mejia, and Esteban A. Hernandez-Vargas. 2018. "Neuraminidase Inhibitors in Influenza Treatment and Prevention–Is It Time to Call It a Day?" Viruses 10, no. 9: 454. https://doi.org/10.3390/v10090454
APA StyleParra-Rojas, C., Nguyen, V. K., Hernandez-Mejia, G., & Hernandez-Vargas, E. A. (2018). Neuraminidase Inhibitors in Influenza Treatment and Prevention–Is It Time to Call It a Day? Viruses, 10(9), 454. https://doi.org/10.3390/v10090454





