Sensitivity of Codispersion to Noise and Error in Ecological and Environmental Data
Abstract
:1. Introduction
2. Methods
2.1. Preliminaries and Notation
2.2. Types of Error
- 1.
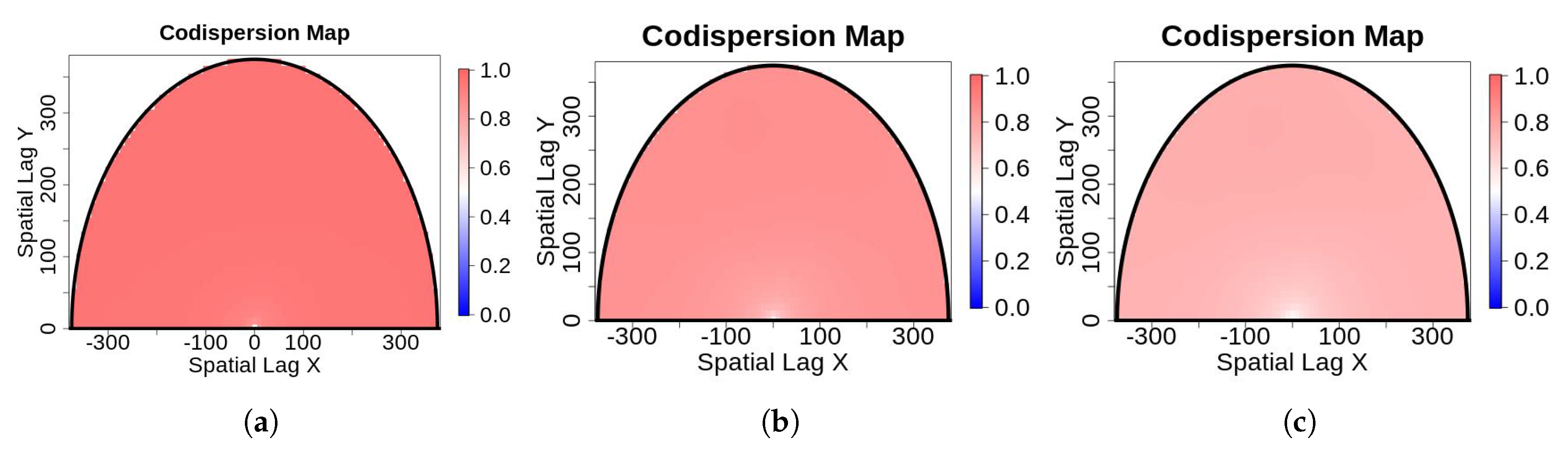
- “Salt-and-pepper” noise on an image: Salt-and-pepper noise—so-called because of its resemblance to dust on images that appears to have been distributed by a salt or pepper shaker—is used widely in image processing and computational statistics to represent real distortions [12] and to generate different scenarios via Monte Carlo simulation [13]. Salt-and-pepper noise can be added to an image using a simple algorithm:Assume that is the original image whose individual observations are points or pixels representing leaves or trees and is the contaminated image with salt-and-pepper noise such that the additive noise is drawn from a normal distribution with mean = 0 and variance , with , where is the variance of . The contamination is located randomly in space such that a small percentage of observations are corrupted with a probability [3]. Specifically,where the is an outlier generating process such that is a zero-one process with and , and .We used Monte Carlo simulations of (3) to generate salt-and-pepper noise on a 5616 × 3744-pixel aerial image of a forest stand at Harvard Forest in Petersham, MA, USA (Figure 1). We considered , and the percentage of contamination We conjectured that the codispersion coefficient would be robust for That is, for relatively small amounts of measurement error, we could still recover the relevant spatial information present in the remotely-sensed image.In Figure 1a, we illustrate the noise-free image. Figure 1c,e,g is contaminated versions of the original one when . The corresponding perspective plots shown in Figure 1b,d,f,h depict the effect of contamination on the gray intensities. The greater the contamination, the greater the dispersion, which is plotted on the z-axis of the three-dimensional scatter plots displayed in Figure 1.We then compared the codispersion calculated for the original image to that calculated for the contaminated images. In addition to the reference image shown in Figure 1a, we considered other aerial images. The codispersion maps of these images are presented in the supplementary material for this paper. We emphasize that the computation of the codispersion coefficient requires that both processes are measured over the same domain, thus the codispersion between a reference image and its contaminated versions make sense. To address the codispersion between two images taken from different scenarios (for instance, images displayed in the supplementary material), rasterized versions of the original images could be considered following the guidelines given in [4].
- 2.
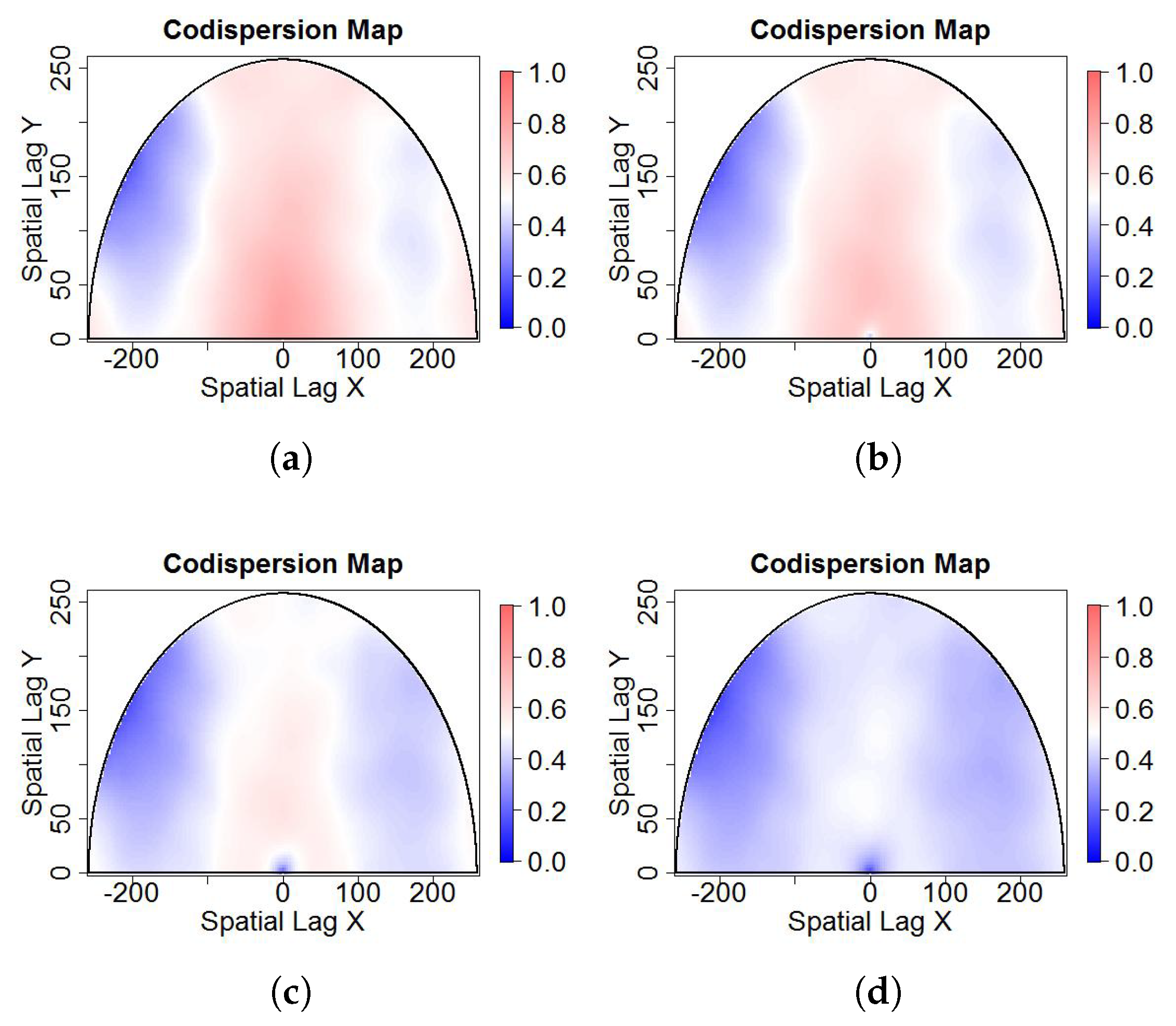
- Salt-and-pepper noise on dependent processes: More generally, Reference [14] extended the well known Matérn class of covariance functions to a multivariate random field. For multivariate Gaussian and second-order processes, the multivariate Matérn covariance function is defined aswhere is the distance lag, is a modified Bessel function of the second kind, is a spatial scale parameter, and is a smoothness parameters that defines the Hausdorff dimension and the differentiability of the sample paths. In particular, a Gaussian and second-order stationary process , has a bivariate Matérn covariance matrix ifwhere are the marginal covariance functions, with variance parameter , smoothness parameter , and scale parameter for . is the cross-covariance function, with correlation coefficient , smoothness parameter , and scale parameter . In all cases, is the function defined in Equation (4). The parsimonious bivariate Matérn model has the restrictionThe correlation between the spatial variables and is controlled by the parameter which allows one to generate bivariate Gaussian spatial processes with different levels of dependence. The spatial correlation defined by Equation (6) is not necessarily bounded by 1. Without loss of generality, it can be assumed that the mean of the bivariate process is zero, but the theory works well for any bivariate process with mean Any type of contamination can be applied over the generated dependence data. In this case, we applied salt-and-pepper noise.We generated dependent random fields from the bivariate Matérn class of covariance functions described in Equation (5) by Monte Carlo simulation using the R package RandomFields [15]. We then added the salt-and-pepper noise, varying the additional parameter , which represents the known correlation between processes and .Figure 2 shows one realization of size from a bivariate Gaussian process (images (a) and (b)) with correlation equal to 0.8, and , , and . Figure 2c,d,e show versions of (b) contaminated with salt-and-pepper noise with the percentage of contamination equal to 5%, 15%, and 25%, respectively. Because the Gaussian process is stationary, images (a) and (b) look very regular (approximately constant mean and variance), and any correlation between them (if it exists) is difficult to observe in the printed images. Other parameters used in the simulation study are , , , , and . The results are similar to the shown here, but with a codispersion map close to zero.
- 3.
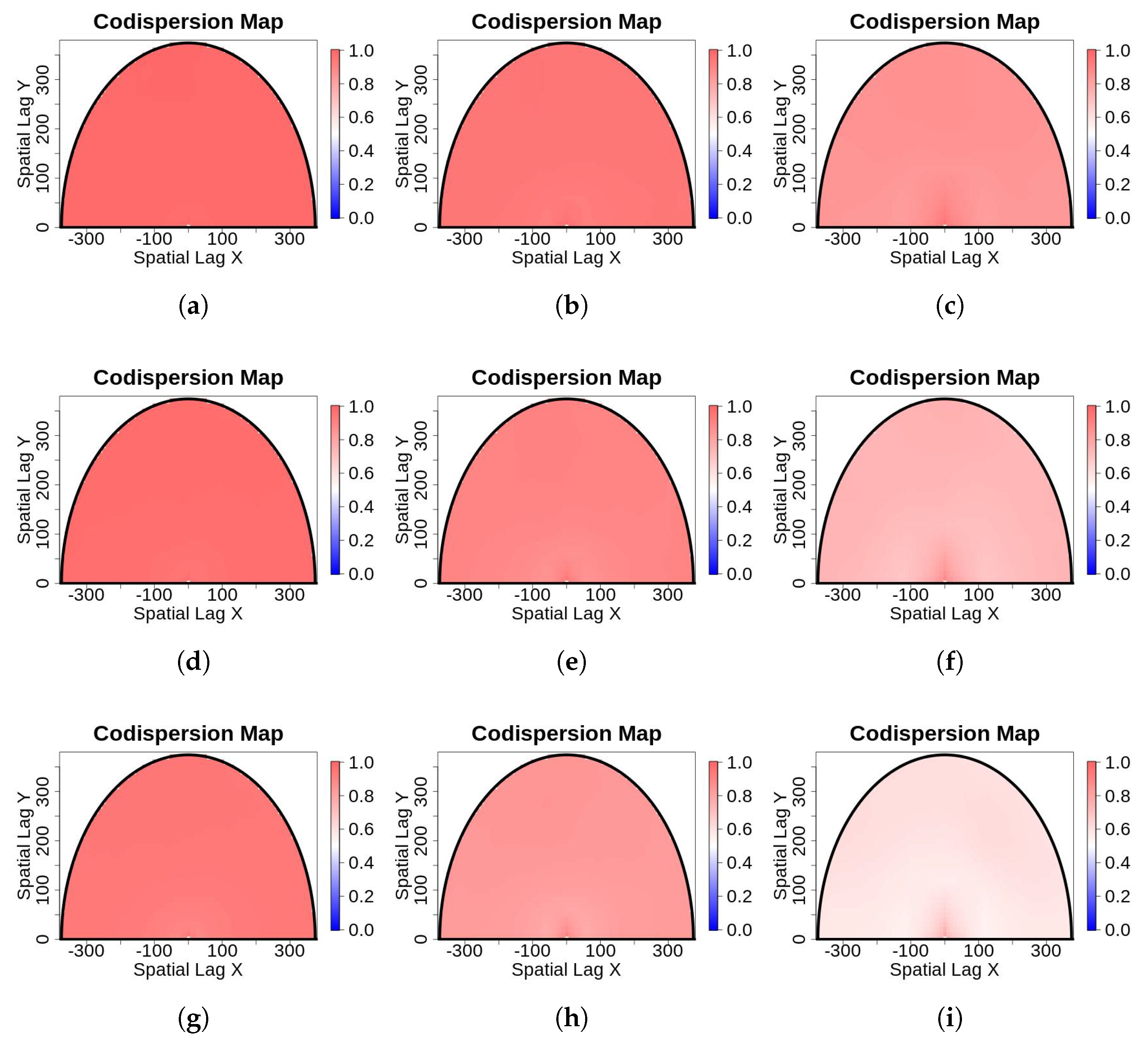
- Missing observations at random locations: We used the salt-and-pepper scheme to randomly delete n observations. We first defined the percentage of contamination (), and then deleted that many observations from the dataset. In practice, we replaced observations with non-observed (NA) at the randomly-selected locations. The main feature of these missing observations is that they are spatially independent of one another, but, for the posterior data analysis, they will remain fixed. The imputation algorithm described in the Appendix A was not applied here because codispersion calculations are not affected when the percentage of contamination is small.In Figure 3, we illustrate the missing-observations-at-random-locations with nine contaminated versions of the original image shown in Figure 1a. The columns show the effect of increasing the percentage of contamination (5%, 15%, and 25%, respectively), and the rows depict the effect of increasing the block size of contaminated pixels, which are , , and respectively. The contaminated pixels have been colored in white. NAs were ignored in the computation of the codispersion coefficients because for large gaps of missing observations the computation of the codispersion coefficient will be affected for those directions such that is less than the maximum diameter of the missing block.
- 4.
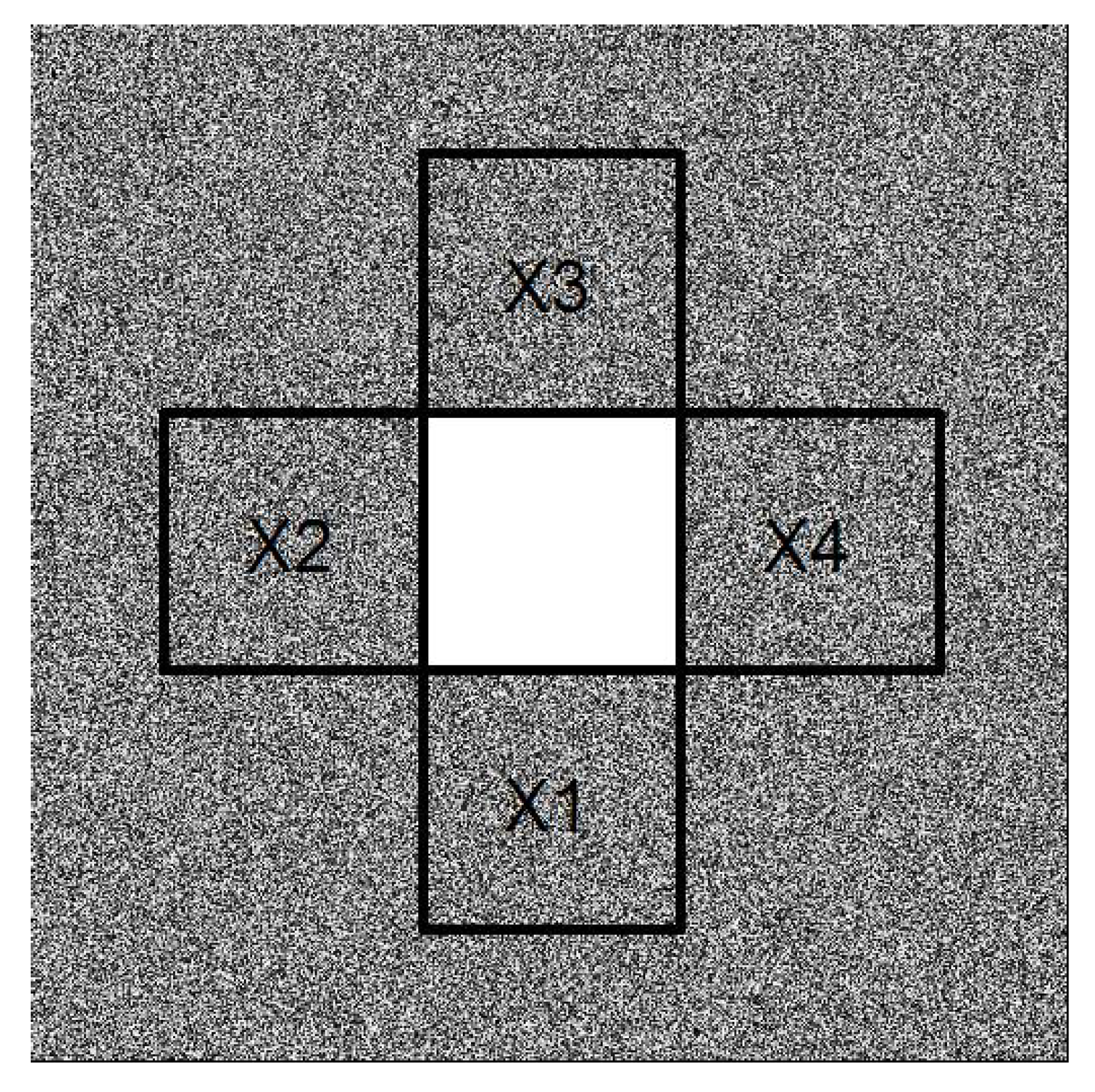
- Gaps resulting from clusters of missing observations: Missing values may be clustered, for example, either because of local difficulties in sampling or because large sections of a remotely-sensed image are obscured by, for example, clouds or shadows. We simulated clustered missing observations for the image shown in Figure 1a, given three different pixel sizes for the contaminated block: , , and (Figure 4). We used simple clustered geometries (squares) for ease of computation. The difference between the previous type of contamination and this one is that, in the former, the contamination consisted of several blocks of small size. Here, we introduced just one gap containing a large number of pixels, which, in Figure 4, is located for illustrative purposes in the center of the image. In our simulations and analysis, the size of the missing block and its location were fixed.To compute codispersion coefficients for datasets with such large blocks of missing data, we needed to fill the missing gaps (impute missing data) prior to computing the codispersion coefficient. We used and compared two different methods of imputation (gap-filling).First, the image with a missing gap was represented by a first-order spatial autoregressive process. The fitting of the parameters of the models was done via least-squares estimation following the guidelines given in [16]. This estimation method was studied in [17] and found to yield an approximated image of the original one X (see Algorithm 1 in the Appendix A).Second, to predict the values of the process in the locations belonging to the missing block, we applied Algorithm 1 to predict missing values in the four closest blocks to the missing gap as is illustrated in Figure A1. This prediction scheme is summarized in Algorithm 2 (Appendix A). Briefly, the first step represents the image intensity by an autoregressive process that assumes that the intensity of any pixel is a weighted average of the intensity of the surrounding pixels. This is a model-based alternative to the average or median commonly computed using the intensities of a moving window across the image. The second step predicts the missing values using similar autoregressive models to represent the surrounding blocks. The predicted value of a pixel belonging to the missing block is a weighted average where the weights are proportional to the distance from the missing pixel to the surrounding blocks.
- 5.
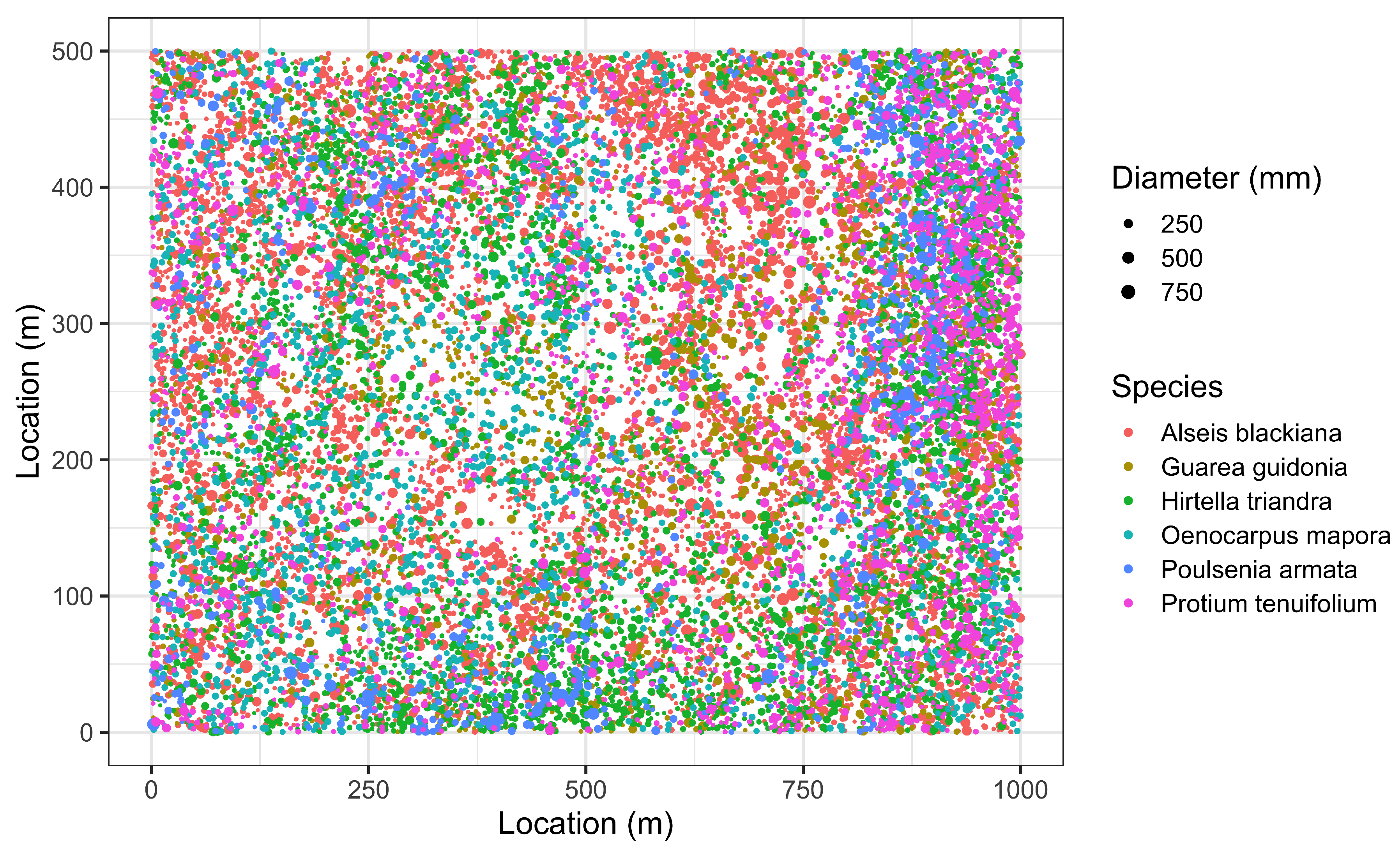
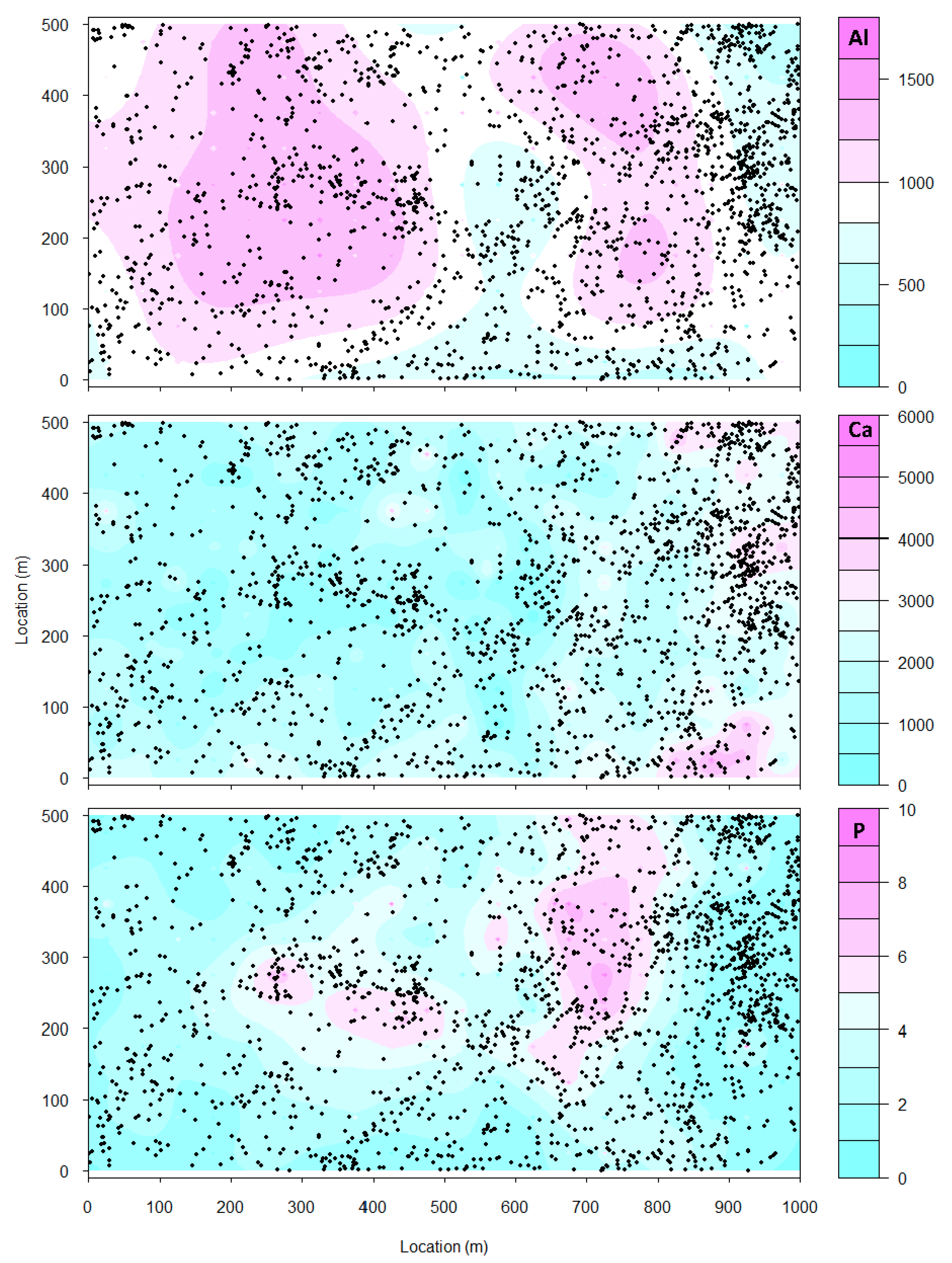
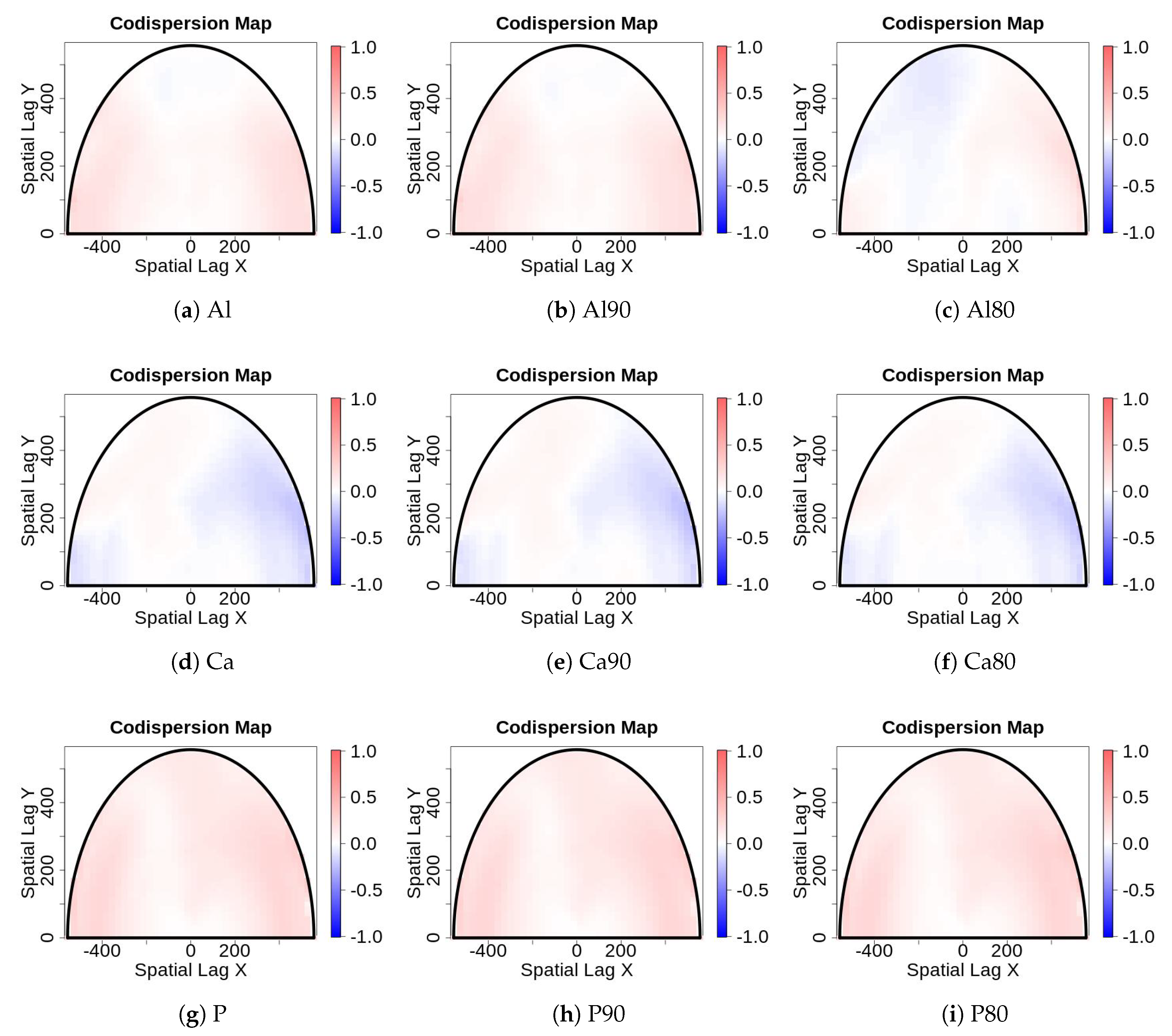
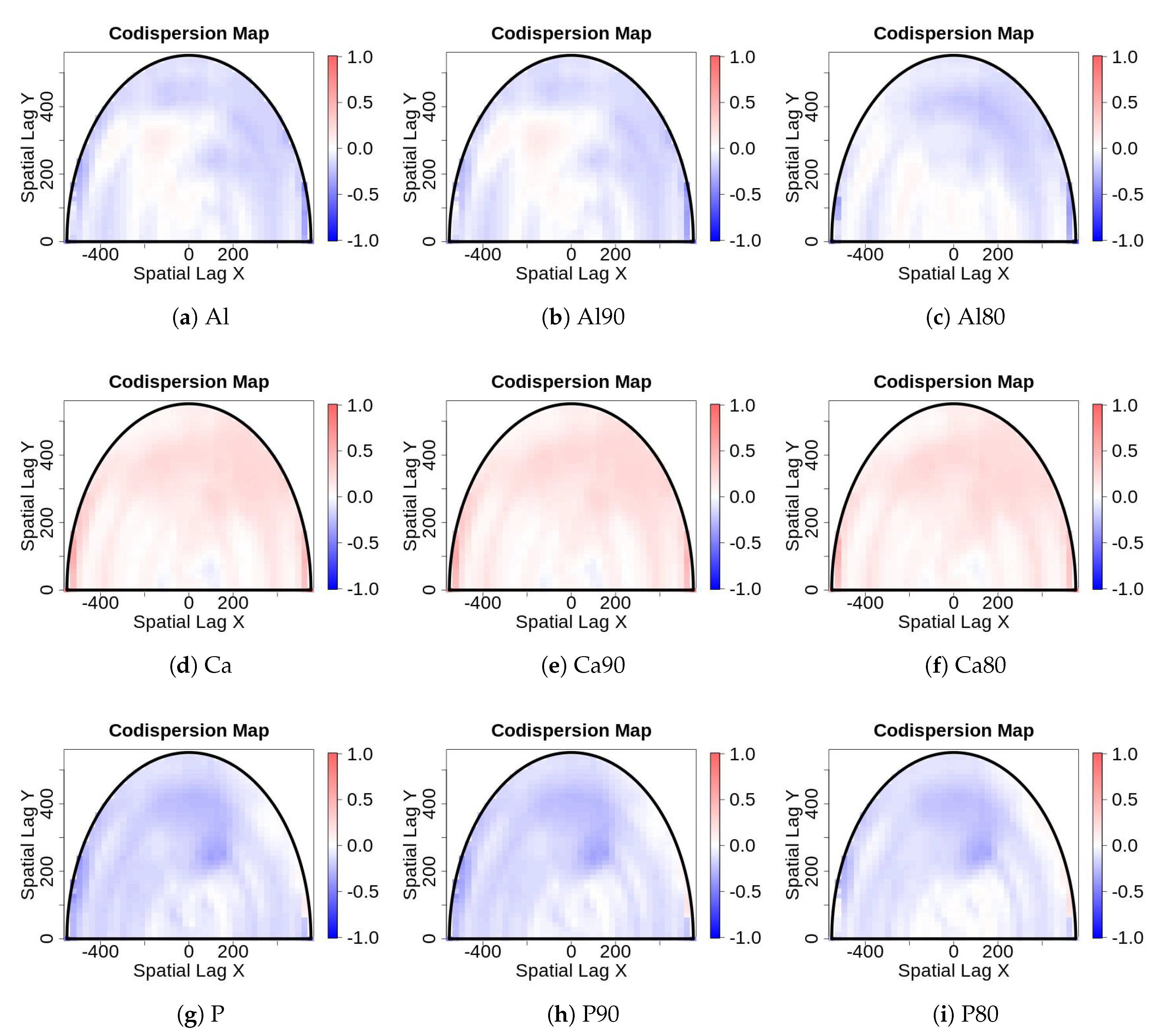
- Sampling error: Values for edaphic or environmental variables at specific locations in space often are sampled from a smoothed (kriged) surface, which itself was generated from a much smaller set of field observations. The actual information in the kriged surface is a function of both the number of observations and the smoothing parameter of the covariance function [18]. For a pair of spatial point processes and (e.g., individual forest trees and soil nutrient concentrations at each tree, respectively), where the number of observed trees (hundreds to thousands) vastly exceeds the number of soil samples (tens), we kriged the soil chemistry variables after thinning (or not) and then calculated the codispersion between the observed tree diameters and the value of the soil-chemistry variable predicted (at each tree location in ) from the kriged surface of soil-chemistry data. The kriged surface was computed either from all the data or from “thinned” soil datasets that contained 90% or 80% of the original soil chemistry data [18]. The sampling error here is error in the predicted values at points on the kriged surface caused by fitting the surface to fewer and fewer points in the “thinned” datasets.To illustrate the effect of this sampling error, we used data from plants and soils collected in the 50-ha forest dynamics plot on Barro Colorado Island, Panamá [19,20,21]. Of the 299 plant species mapped, identified, and measured every five years in this plot, we used six: Alseis blackiana, Oenocarpus mapora, Hirtella triandra, Protium tenuifolium, Poulsenia armata, and Guarea guidonia (Figure 5). The abundances of unique single-stemmed individuals of each of these six species ranged from 993 (Poulsenia armata) to 7928 (Alseis blackiana), and included species that had a range of positive, negative, and weak associations with measured soil variables [22]. Spatial locations and “diameters at breast height” (at 1.3 m aboveground) of individual trees of each species (excluding dead individuals and individuals with more than one stem) were taken from the seventh (2010) semi-decadal census of the plot.Soil samples were collected on a 50-m lattice in 2005 with additional samples taken at finer spatial grains at alternate sampling stations [22]. Soil samples were analyzed for concentrations of 11 elements; we used only data for concentrations of calcium (Ca), phosphorus (P), and aluminium (Al), as these three had the highest loadings on the first three principal axes of a multivariate analysis (NMDS) on the complete soil dataset [22]. We used ordinary kriging in the geoR package [23], version 1.7-5.2, to fit a surface to the data for each soil element and predict its concentration at the location of each tree (Figure 6). Variogram models (exponential, exponential, and wave for Ca, P, and Al, respectively) needed as input for the kriging function were fit to detrended (2nd-order polynomial) data that had been Box–Cox transformed ( = 0.5, 1.0, and 1.0 for Ca, P, and Al, respectively); kriging was done on back-transformed data to which the trend had been added. Nuggets were estimated empirically for Ca and P, but the nugget for Al was fixed (following visual inspection of the empirical variogram) equal to 4000. Alternatively, in order to take into account the spatial heterogeneity, one could perform a test to measure the degree of spatial heterogeneity along the lines given in [24], before applying the kriging interpolation.
3. Results
4. Discussion
5. Conclusions
- (1)
- The codispersion coefficient is robust to small percentages of contamination (less than 15%).
- (2)
- The codispersion coefficient decreases as the percentage of contamination increases no matter the type of noise or direction.
- (3)
- For data collected from large forest plots, the codispersion coefficient and the associated codispersion map provide useful information to describe covariation in the data across complex spatial gradients or patterns.
- (4)
- An imputation algorithm can be used to smoothly fill blocks of missing observations with little impact on the codispersion coefficient.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Image Imputation Algorithm
| Algorithm 1 Approximated AR-2D Image. |
| Input: An original image Z of size . Output: An approximated of size
|
| Algorithm 2 Prediction Algorithm. |
| Input: An image Z with a missing block, and K. Output: Image Z without missing values.
|
References
- Fortin, M.J.; Dale, M. Spatial Analysis: A Guide for Ecologists; Cambridge University Press: Cambridge, UK, 2005; pp. 5–11. [Google Scholar]
- Ellison, A.M.; Gotelli, N.J.; Hsiang, N.; Lavine, M.; Maidman, A. Kernel density estimation of 2-dimensional spatial Poisson point processes from k-tree sampling. J. Agric. Biol. Environ. Stat. 2014, 19, 357–372. [Google Scholar] [CrossRef] [Green Version]
- Vallejos, R.; Osorio, F.; Mancilla, D. The codispersion map: A graphical tool to visualize the association between two spatial processes. Stat. Neerl. 2015, 69, 298–314. [Google Scholar] [CrossRef]
- Buckley, H.L.; Case, B.S.; Ellison, A.M. Using codispersion analysis to characterize spatial patterns in species co-occurrences. Ecology 2016, 97, 32–39. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buckley, H.L.; Case, B.S.; Zimmermann, J.; Thompson, J.; Myers, J.A.; Ellison, A.M. Using codispersion analysis to quantify and understand spatial patterns in species-environment relationships. New Phytol. 2016, 211, 735–749. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Case, B.S.; Buckley, H.L.; Barker Plotkin, A.; Ellison, A.M. Using codispersion analysis to quantify temporal changes in the spatial pattern of forest stand structure. Chil. J. Stat. 2016, 7, 3–15. [Google Scholar]
- Ellison, A.M.; Osterweil, L.J.; Hadley, J.L.; Wise, A.; Boose, E.; Clarke, L.; Foster, D.R.; HAnson, A.; Jensen, D.; Kuzeja, P.; et al. Analytic webs support the synthesis of ecological datasets. Ecology 2006, 87, 1345–1358. [Google Scholar] [CrossRef]
- Matheron, G. Les Variables Régionalisées et leur Estimation; Masson: Paris, France, 1965. [Google Scholar]
- Ojeda, S.; Vallejos, R.; Lamberti, P. Measure of similarity between images based on the codispersion coefficient. J. Electron. Imaging 2012, 21, 023019. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial association–LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Fox, A.J. Outliers in time series. J. R. Stat. Soc. B 1972, 34, 350–363. [Google Scholar]
- Huang, S.; Zhu, J. Removal of salt-and-pepper noise based on compressed sensing. Electron. Lett. 2010, 46, 1198–1199. [Google Scholar] [CrossRef]
- McQuarrie, A.D.; Tsai, C. Outlier detections in autoregressive models. J. Comput. Graph. Stat. 2003, 12, 450–471. [Google Scholar] [CrossRef]
- Gneiting, T.; Kleiber, W.; Schlather, M. Matérn cross-covariance functions for multivariate random fields. J. Am. Stat. Assoc. 2010, 105, 1167–1177. [Google Scholar] [CrossRef]
- Schlather, M.; Malinowski, A.; Oesting, M.; Boecker, D.; Strokorb, K.; Engelke, S.; Martini, J.; Ballani, F.; Moreva, O.; Auel, J.; et al. RandomFields: Simulation and Analysis of Random Fields. R Package Version 3.1.50. 2017. Available online: https://cran.r-project.org/package=RandomFields (accessed on 1 April 2018).
- Allende, H.; Galbiati, J.; Vallejos, R. Robust image modeling on image processing. Pattern Recognit. Lett. 2001, 22, 1219–1231. [Google Scholar] [CrossRef]
- Ojeda, S.; Vallejos, R.; Bustos, O. A new image segmentation algorithm with applications to image inpainting. Comput. Stat. Data Anal. 2010, 54, 2082–2093. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. The Matérn function as a general model for soil variograms. Geoderma 2005, 128, 192–207. [Google Scholar] [CrossRef]
- Condit, R. Tropical Forest Census Plots; Springer: Berlin, Germany, 1998. [Google Scholar]
- Hubbell, S.P.; Condit, R.; Foster, R.B. Barro Colorado Forest Census Plot Data. 2005. Available online: http://ctfs.si.edu/webatlas/datasets/bci (accessed on 18 February 2018).
- Hubbell, S.P.; Foster, R.B.; O’Brien, S.T.; Harms, K.E.; Condit, R.; Wechsler, B.; Wright, S.J.; Loo de Lao, S. Light gap disturbances, recruitment limitation, and tree diversity in a neotropical forest. Science 1998, 283, 554–557. [Google Scholar] [CrossRef]
- John, R.; Dalling, J.W.; Harms, K.E.; Yavitt, J.B.; Stallard, R.F.; Mirabello, M.; Hubbell, S.P.; Valencia, R.; Navarrete, H.; Vallejo, M.; et al. Soil nutrients influence spatial distributions of tropical trees. Proc. Natl. Acad. Sci. USA 2007, 104, 864–869. [Google Scholar] [CrossRef]
- Ribeiro, P.J., Jr.; Diggle, P.J. geoR: A package for geostatistical analysis. R-News 2001, 1, 15–18. [Google Scholar]
- Wang, J.-F.; Zhang, T.-L.; Fu, B.-J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef] [Green Version]
- Vallejos, R.; Mancilla, D.; Acosta, J. Image similarity assessment based on measures of spatial association. J. Math. Imaging Vis. 2016, 56, 77–98. [Google Scholar] [CrossRef]
- Goovaerts, P. Combining Areal and Point Data in Geostatistical Interpolation: Applications to Soil Science and Medical Geography. Math. Geosci. 2010, 42, 535–554. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Acosta, J.; Vallejos, R. Effective sample size for spatial regression processes. Electron. J. Stat. 2018, 12, 3147–3180. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016; Available online: http://www.R-project.org (accessed on 22 March 2018).
- Ver Hoef, J.M.; Peterson, E.E.; Hooten, M.B.; Hanks, E.M.; Fortin, M.J. Spatial autoregressive models for statistical inference from ecological data. Ecol. Monogr. 2018, 88, 36–59. [Google Scholar] [CrossRef] [Green Version]
- Bustos, O.; Ojeda, S.; Vallejos, R. Spatial ARMA models and its applications to image filtering. Braz. J. Prob. Stat. 2009, 23, 141–165. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vallejos, R.; Buckley, H.; Case, B.; Acosta, J.; Ellison, A.M. Sensitivity of Codispersion to Noise and Error in Ecological and Environmental Data. Forests 2018, 9, 679. https://doi.org/10.3390/f9110679
Vallejos R, Buckley H, Case B, Acosta J, Ellison AM. Sensitivity of Codispersion to Noise and Error in Ecological and Environmental Data. Forests. 2018; 9(11):679. https://doi.org/10.3390/f9110679
Chicago/Turabian StyleVallejos, Ronny, Hannah Buckley, Bradley Case, Jonathan Acosta, and Aaron M. Ellison. 2018. "Sensitivity of Codispersion to Noise and Error in Ecological and Environmental Data" Forests 9, no. 11: 679. https://doi.org/10.3390/f9110679
APA StyleVallejos, R., Buckley, H., Case, B., Acosta, J., & Ellison, A. M. (2018). Sensitivity of Codispersion to Noise and Error in Ecological and Environmental Data. Forests, 9(11), 679. https://doi.org/10.3390/f9110679





