Relationships between Tree Vigor Indices and a Tree Classification System Based upon Apparent Stem Defects in Northern Hardwood Stands
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. Tree Sampling
2.3. Tree Vigor Classification
2.4. Vigor Indices
2.4.1. Growth Efficiency Index
2.4.2. Indices Solely Based upon Tree Diameter Measurements
2.5. Statistical Analysis
3. Results
3.1. Relationship between the Growth Efficiency Index and Tree Vigor Classes
3.2. Growth-Based Indices and Changes in Tree Vigor Class
3.3. Predicting the Growth Efficiency Index
4. Discussion
4.1. Relationships between Quantitative and Qualitative Tree Vigor Indices
4.2. Possible Drawbacks of the Growth Efficiency Index
4.3. Estimating the Growth Efficiency Index from State Variables
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Delisle-Boulianne, S.; Fortin, M.; Achim, A.; Pothier, D. Modelling stem selection in northern hardwood stands: Assessing the effects of tree vigour and spatial correlations with a copula approach. Forestry 2014, 87, 607–617. [Google Scholar] [CrossRef]
- Havreljuk, F.; Achim, A.; Auty, D.; Bédard, S.; Pothier, D. Integrating standing value estimations into tree marking guidelines to meet wood supply objectives. Can. J. For. Res. 2014, 44, 750–759. [Google Scholar] [CrossRef]
- Pothier, D.; Fortin, M.; Auty, D.; Delisle-Boulianne, S.; Gagne, L.-V.; Achim, A. Improving tree selection for partial cutting through joint probability modeling of tree vigor and quality. Can. J. For. Res. 2013, 43, 288–298. [Google Scholar] [CrossRef]
- Nyland, R.D. Selection system in northern hardwoods. J. For. 1998, 96, 18–21. [Google Scholar]
- Guillemette, F.; Bédard, S.; Fortin, M. Evaluation of a tree classification system in relation to mortality risk in Québec northern hardwoods. For. Chron. 2008, 84, 886–899. [Google Scholar] [CrossRef]
- Laliberté, J.; Pothier, D.; Achim, A. Adjusting harvest rules for red oak in selection cuts of Canadian northern hardwood forests. Forestry 2016, 89, 402–411. [Google Scholar] [CrossRef]
- Boulet, B.; Landry, G. La Carie des Arbres: Fondements, Diagnostic et Application, 3rd ed.; Les Publications du Québec: Québec, QC, Canada, 2015; p. 372. [Google Scholar]
- Fortin, M.; Bédard, S.; Guillemette, F. Estimation par Simulation Monte Carlo de la Probabilité de Mortalité Quinquennale de L’érable à Sucre, du Bouleau Jaune et du Hêtre à Grandes Feuilles en Peuplements de Feuillus en Fonction de la Classification MSCR; Avis Technique; Gouvernement du Québec, Ministère des Ressources Naturelles et de la Faune, Direction de la Recherche Forestière: Québec, QC, Canada, 2008; p. 11.
- Guillemette, F.; Bédard, S.; Havreljuk, F. Probabilités de Mortalité des Feuillus Selon le Classement de la Priorité de Récolte; Direction de la Recherche Forestière: Québec, QC, Canada, 2015; p. 11. [Google Scholar]
- Hartmann, H.; Beaudet, M.; Messier, C. Using longitudinal survival probabilities to test field vigour estimates in sugar maple (Acer saccharum Marsh.). For. Ecol. Manag. 2008, 256, 1771–1779. [Google Scholar] [CrossRef]
- Waring, R.H.; Thies, W.G.; Muscato, D. Stem growth per unit of leaf area: A measure of tree vigor. For. Sci. 1980, 26, 112–117. [Google Scholar]
- Waring, R.H. Characteristics of trees predisposed to die. Bioscience 1987, 37, 569–574. [Google Scholar] [CrossRef]
- Christiansen, E.; Waring, R.H.; Berryman, A.A. Resistance of conifers to bark beetle attack: Searching for general relationships. For. Ecol. Manag. 1987, 22, 89–106. [Google Scholar] [CrossRef]
- Waring, R.H.; Newman, K.; Bell, J. Efficiency of tree crowns and stemwood production at different canopy leaf densities. Forestry 1981, 54, 129–137. [Google Scholar] [CrossRef]
- Mitchell, R.G.; Waring, R.H.; Pitman, G.B. Thinning lodgepole pine increases tree vigor and resistance to mountain pine beetle. For. Sci. 1983, 29, 204–211. [Google Scholar]
- Waring, R.H.; Pitman, G.B. Modifying lodgepole pine stands to change susceptibility to mountain pine beetle attack. Ecology 1985, 66, 889–897. [Google Scholar] [CrossRef]
- Coops, N.C.; Waring, R.H.; Wulder, M.A.; White, J.C. Prediction and assessment of bark beetle-induced mortality of lodgepole pine using estimates of stand vigor derived from remotely sensed data. Remote Sens. Environ. 2009, 113, 1058–1066. [Google Scholar] [CrossRef]
- Reed, D.D.; Pregitzer, K.S.; Liechty, H.; Burton, A.J.; Mroz, G.D. Productivity and growth efficiency in sugar maple forests. For. Ecol. Manag. 1994, 70, 319–327. [Google Scholar] [CrossRef]
- Coyea, M.R.; Margolis, H.A. The historical reconstruction of growth efficiency and its relationship to tree mortality in balsam fir ecosystems affected by spruce budworm. Can. J. For. Res. 1994, 24, 2208–2221. [Google Scholar] [CrossRef]
- Boivin-Dompierre, S.; Achim, A.; Pothier, D. Functional response of coniferous trees and stands to commercial thinning in eastern Canada. For. Ecol. Manag. 2017, 384, 6–16. [Google Scholar] [CrossRef]
- Pedersen, B.S. Modeling tree mortality in response to short and long-term environmental stresses. Ecol. Model. 1998, 105, 347–351. [Google Scholar] [CrossRef]
- Yao, X.; Titus, S.J.; MacDonald, S.E. A generalized logistic model of individual tree mortality for aspen, white spruce, and lodgepole pine in Alberta mixedwood forests. Can. J. For. Res. 2001, 31, 283–291. [Google Scholar] [CrossRef]
- Bigler, C.; Bugmann, H. Growth-dependent tree mortality models based on tree rings. Can. J. For. Res. 2003, 33, 210–221. [Google Scholar] [CrossRef]
- Duchesne, L.; Ouimet, R.; Morneau, C. Assessment of sugar maple health based on basal area growth pattern. Can. J. For. Res. 2003, 33, 2074–2080. [Google Scholar] [CrossRef]
- Saucier, J.-P.; Grondin, P.; Robitaille, A.; Gosselin, J.; Morneau, C.; Richard, P.J.H.; Brisson, J.; Sirois, L.; Leduc, A.; Morin, H.; et al. Chapitre 4: Écologie forestière. In Manuel de Foresterie; Éditions MultiMondes: Montréal, QC, Canada, 2009; pp. 165–316. [Google Scholar]
- Grondin, P.; Jean, N.; Hotte, D. Intégration de la Végétation et de ses Variables Explicatives à des Fins de Classification et de Cartographie D’unités Homogènes du Québec Meridional; Direction de la Recherche Forestière: Québec, QC, Canada, 2007; p. 62. [Google Scholar]
- Russell, M.B.; Weiskittel, A.R. Maximum and largest crown width equations for 15 tree species in Maine. North. J. Appl. For. 2011, 28, 84–91. [Google Scholar]
- Boulet, B. Défauts Externes et Indices de la Carie des Arbres; Les Publications du Québec: Québec, QC, Canada, 2007; p. 291. [Google Scholar]
- Lambert, M.-C.; Ung, C.-H.; Raulier, F. Canadian national tree aboveground biomass equations. Can. J. For. Res. 2005, 35, 1996–2018. [Google Scholar] [CrossRef]
- Moreau, E.; Bédard, S.; Baral, S.K.; Pothier, D. Evaluating electrical resistivity tomography to estimate sapwood area and leaf area of sugar maple and yellow birch. Ecohydrology 2018, e2014. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Core Team. Nlme: Linear and Nonlinear Mixed Effects Models. R Package Version 3.1-137. 2018. Available online: https://CRAN.R-project.org/package=nlme (accessed on 21 September 2018).
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: New York, NY, USA, 2002; p. 488. [Google Scholar]
- Mazerolle, M.J. Improving data analysis in herpetology: Using Akaike’s information criterion (AIC) to assess the strength of biological hypotheses. Amphibia-Reptilia 2006, 27, 169–180. [Google Scholar] [CrossRef]
- Fawcett, T. ROC Graphs: Notes and Practical Considerations for Researchers; Technical Report HPL-2003-4; HP Laboratories: Palo Alto, CA, USA, 2004. [Google Scholar]
- Maguire, D.A.; Brissette, J.C.; Gu, L.H. Crown structure and growth efficiency of red spruce in uneven-aged, mixed-species stands in Maine. Can. J. For. Res. 1998, 28, 1233–1240. [Google Scholar] [CrossRef]
- Ryan, M.G.; Phillips, N.; Bond, B.J. The hydraulic limitation hypothesis revisited. Plant Cell Environ. 2006, 29, 367–381. [Google Scholar] [CrossRef] [PubMed]
- Seymour, R.S.; Kenefic, L.S. Influence of age on growth efficiency of Tsuga canadensis and Picea rubens trees in mixed-species, multiaged northern conifer stands. Can. J. For. Res. 2002, 32, 2032–2042. [Google Scholar] [CrossRef]
- Power, H.; Havreljuk, P. Predicting hardwood quality and its evolution over time in Quebec’s forests. Forestry 2018, 91, 259–270. [Google Scholar] [CrossRef]
- Petro, F.J.; Calvert, W.W. La Classification des Billes de Bois Francs Destinées au Sciage; Forintek Canada Corp.: Ottawa, ON, Canada, 1990. [Google Scholar]
- Nolet, P.; Hartmann, H.; Bouffard, D.; Doyon, F. Predicted and observed sugar maple mortality in relation to site quality indicators. North. J. Appl. For. 2007, 24, 258–264. [Google Scholar]
- Gauthier, M.-M.; Guillemette, F. Bark type reflects growth potential of yellow birch and sugar maple at the northern limit of their range. Plant Ecol. 2017, 219, 381–390. [Google Scholar] [CrossRef]
- Cecil-Cockwell, M.J.L.; Caspersen, J.P. A simple system for classifying sugar maple vigour and quality. Can. J. For. Res. 2015, 45, 900–909. [Google Scholar] [CrossRef]
- Fortin, D.; Bédard, S.; DeBlois, J.; Meunier, S. Predicting individual tree mortality in northern hardwood stands under uneven-aged management in southern Québec, Canada. Ann. For. Sci. 2008, 65, 205. [Google Scholar] [CrossRef]
- Allen, C.B.; Will, R.E.; Jacobson, M.A. Production efficiency and radiation use efficiency of four tree species receiving irrigation and fertilization. For. Sci. 2005, 51, 556–569. [Google Scholar]
- Binkley, D.; Stape, J.L.; Bauerle, W.L.; Ryan, M.G. Explaining growth of individual trees: Light interception and efficiency of light use by Eucalyptus at four sites in Brazil. For. Ecol. Manag. 2010, 259, 1695–1703. [Google Scholar] [CrossRef]
- Voelker, S.L.; Lachenbruch, B.; Meinzer, F.C.; Kitin, P.; Strauss, S.H. Transgenic poplars with reduced lignin show impaired xylem conductivity, growth efficiency and survival. Plant Cell Environ. 2011, 34, 655–668. [Google Scholar] [CrossRef] [PubMed]
- Lane, C.J.; Reed, D.D.; Mroz, G.D.; Liechty, H.O. Width of sugar maple (Acer saccharum) tree rings as affected by climate. Can. J. For. Res. 1993, 23, 2370–2375. [Google Scholar] [CrossRef]
- Zarnoch, S.J.; Bechtold, W.A.; Stolte, K.W. Using crown condition variables as indicators of forest health. Can. J. For. Res. 2004, 34, 1057–1070. [Google Scholar] [CrossRef]
- Binkley, D.; Stape, J.L.; Ryan, M.G.; Barnard, H.R.; Fownes, J.H. Age-related decline in forest ecosystem growth: An individual-tree, stand-structure hypothesis. Ecosystems 2002, 5, 58–67. [Google Scholar] [CrossRef]
- Clausen, K.E.; Godman, R.M. Bark Characteristics Indicate Age and Growth Rate of Yellow Birch; Research Note NC-75; U.S. Department of Agriculture, Forest Service, North Central Forest Experimental Station: St. Paul, MN, USA, 1969.

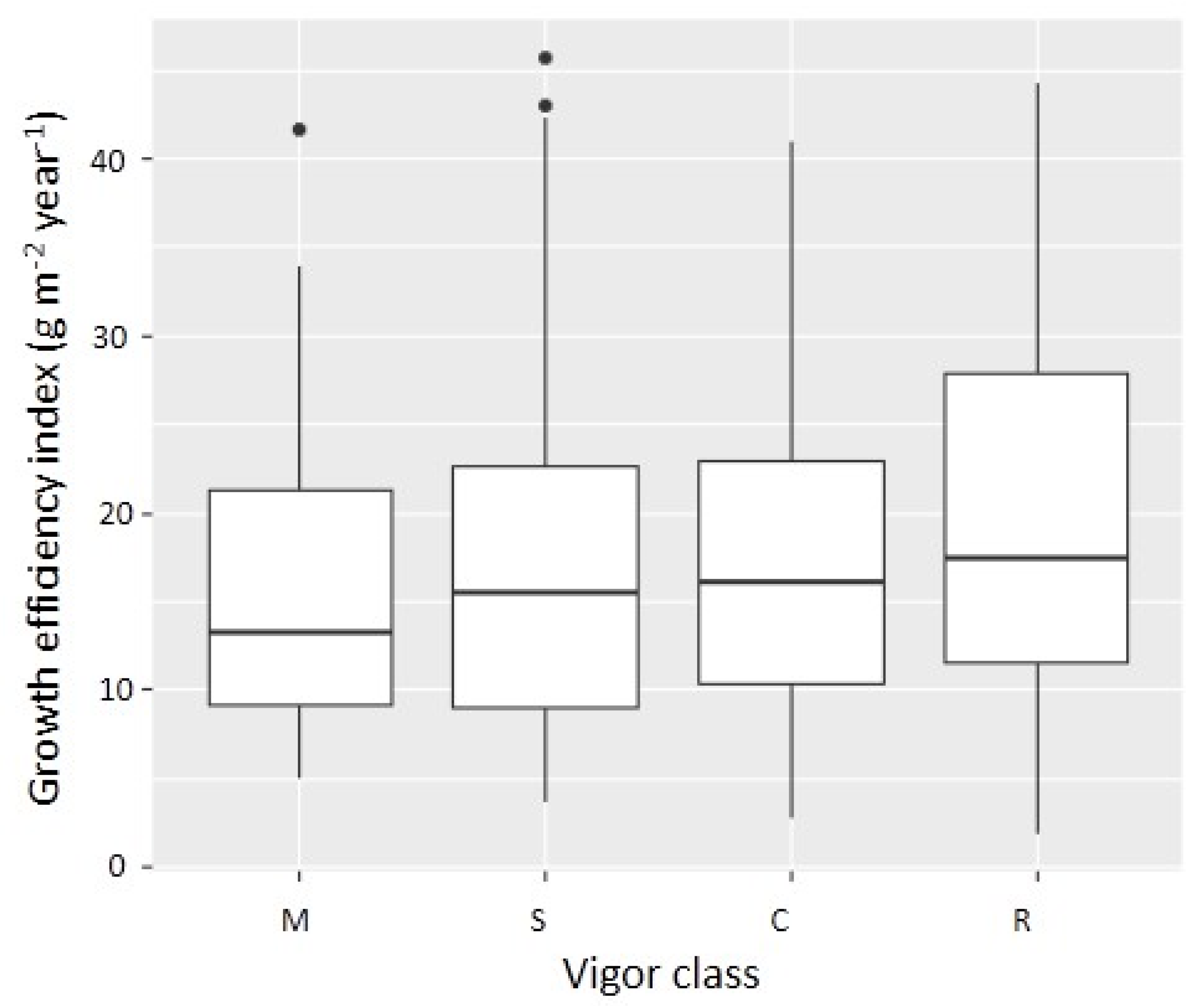
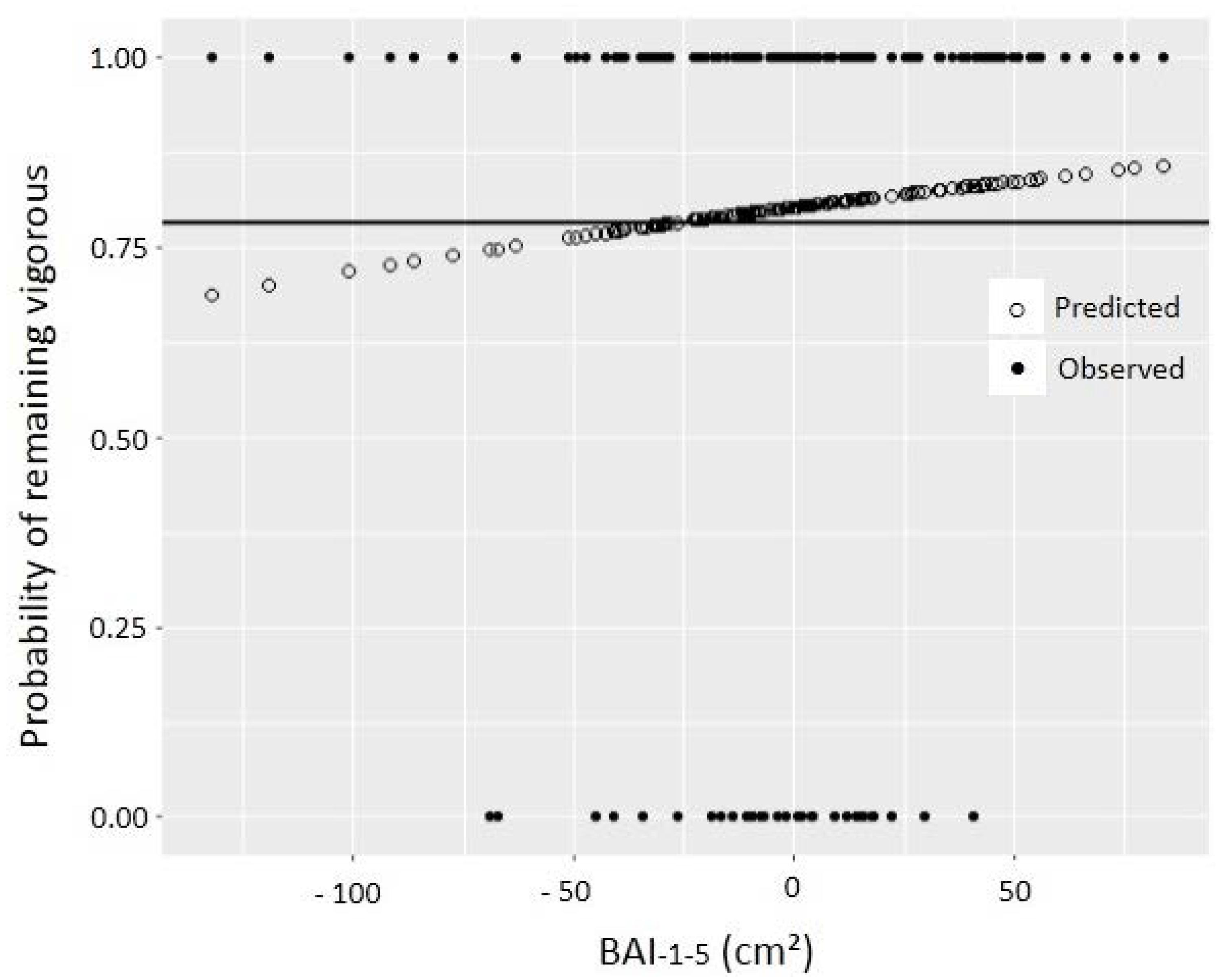
| DBH (cm) | M | S | C | R | Total |
|---|---|---|---|---|---|
| 20–29.9 | 29 | 13 | 39 | 29 | 110 |
| 30–39.9 | 16 | 20 | 28 | 28 | 92 |
| 40–49.9 | 15 | 16 | 21 | 20 | 72 |
| 50–59.9 | 6 | 9 | 7 | 2 | 24 |
| Total | 66 | 58 | 95 | 79 | 298 |
| Growth-Based Index | AIC | Δi | R² | |
|---|---|---|---|---|
| BAI-1-5 | 2232.1 | 0 | 9.0 × 10−1 | 0.35 |
| BAI-1-7 | 2236.5 | 4.5 | 9.6 × 10−2 | 0.34 |
| BAI-1-3 | 2249.3 | 17.3 | 1.6 × 10−4 | 0.31 |
| BAI-1-10 | 2251.0 | 19.9 | 4.2 × 10−5 | 0.31 |
| BAI-1-3/BA-4 | 2268.2 | 36.2 | 1.3 × 10−8 | 0.27 |
| BAI-1-5/BA-6 | 2275.6 | 43.5 | 3.6 × 10−10 | 0.26 |
| First Vigor Evaluation (n = 225) | Second Vigor Evaluation (n = 298) | |||
|---|---|---|---|---|
| Growth-Based Index | F | p-Value | F | p-Value |
| BAI-1-7 | 10.68 | <0.0001 | 5.83 | 0.0007 |
| BAI-1-5 | 9.56 | <0.0001 | 5.83 | 0.0007 |
| BAI-1-10 | 11.63 | <0.0001 | 5.73 | 0.0008 |
| BAI-1-3 | 7.86 | <0.0001 | 4.65 | 0.0034 |
| BAI-1-7/BA-8 | 3.18 | 0.0249 | 5.90 | 0.0006 |
| BAI-1-5/BA-6 | 2.76 | 0.0430 | 5.70 | 0.0008 |
| Predicted = 0 | Predicted = 1 | |
|---|---|---|
| Observed = 0 | 5 | 27 |
| Observed = 1 | 27 | 102 |
| Dependent Variables | Independent Variables | AIC | Δi | R² | |
|---|---|---|---|---|---|
| GE | RH | 2327.5 | 0.0 | 9.5 × 10−1 | 0.05 |
| CSA + RH | 2333.2 | 5.7 | 5.4 × 10−2 | 0.11 | |
| BAI-1-5 | CSA + RH | 2943.9 | 0.0 | 1.0 × 10−1 | 0.39 |
| CSA | 2958.4 | 14.5 | 6.9 × 10−4 | 0.38 | |
| BAI-1-7 | CSA + RH | 3139.9 | 0.0 | 1.0 × 10−1 | 0.39 |
| CSA | 3157.8 | 17.9 | 1.3 × 10−4 | 0.37 | |
| BAI-1-10 | CSA + RH | 3320.1 | 0.0 | 1.0 × 10−1 | 0.37 |
| CSA | 3339.8 | 19.7 | 5.5 × 10−5 | 0.36 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreau, E.; Bédard, S.; Moreau, G.; Pothier, D. Relationships between Tree Vigor Indices and a Tree Classification System Based upon Apparent Stem Defects in Northern Hardwood Stands. Forests 2018, 9, 588. https://doi.org/10.3390/f9100588
Moreau E, Bédard S, Moreau G, Pothier D. Relationships between Tree Vigor Indices and a Tree Classification System Based upon Apparent Stem Defects in Northern Hardwood Stands. Forests. 2018; 9(10):588. https://doi.org/10.3390/f9100588
Chicago/Turabian StyleMoreau, Edouard, Steve Bédard, Guillaume Moreau, and David Pothier. 2018. "Relationships between Tree Vigor Indices and a Tree Classification System Based upon Apparent Stem Defects in Northern Hardwood Stands" Forests 9, no. 10: 588. https://doi.org/10.3390/f9100588
APA StyleMoreau, E., Bédard, S., Moreau, G., & Pothier, D. (2018). Relationships between Tree Vigor Indices and a Tree Classification System Based upon Apparent Stem Defects in Northern Hardwood Stands. Forests, 9(10), 588. https://doi.org/10.3390/f9100588





