The Role of Respiration in Estimation of Net Carbon Cycle: Coupling Soil Carbon Dynamics and Canopy Turnover in a Novel Version of 3D-CMCC Forest Ecosystem Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Model Description
2.3. Model Improvements
2.3.1. Soil Carbon Dynamics
2.3.2. Deciduous Phenology
2.3.3. Evergreen Phenology
- (1)
- Older leaves live in the shaded portions of the canopy, where light transmitted is reduced following Lambert Beer’s exponential decay equation. For this reason, we expect an exponential reduction in absorbed photosynthetically active radiation (APAR);
- (2)
- An age dependent quasi-exponential decay in leaf quantum yield efficiency [53]. These decays impact on the reduction of ;
- (3)
- Nitrogen content in older leaves is often lower than in young ones, because of its transfer from portions of the crown with low productivity to portions more exposed to light [53]. Since maintenance respiration is proportional to nitrogen content, we expect an exponential reduction in ;
- (4)
- was assumed to be constant as in [17] because of the joint effect of reduction in respiration rate and quantum yield efficiency.
2.3.4. Production of Fresh Organic Matter
2.3.5. Optimization
2.3.6. Validation Analysis
3. Results
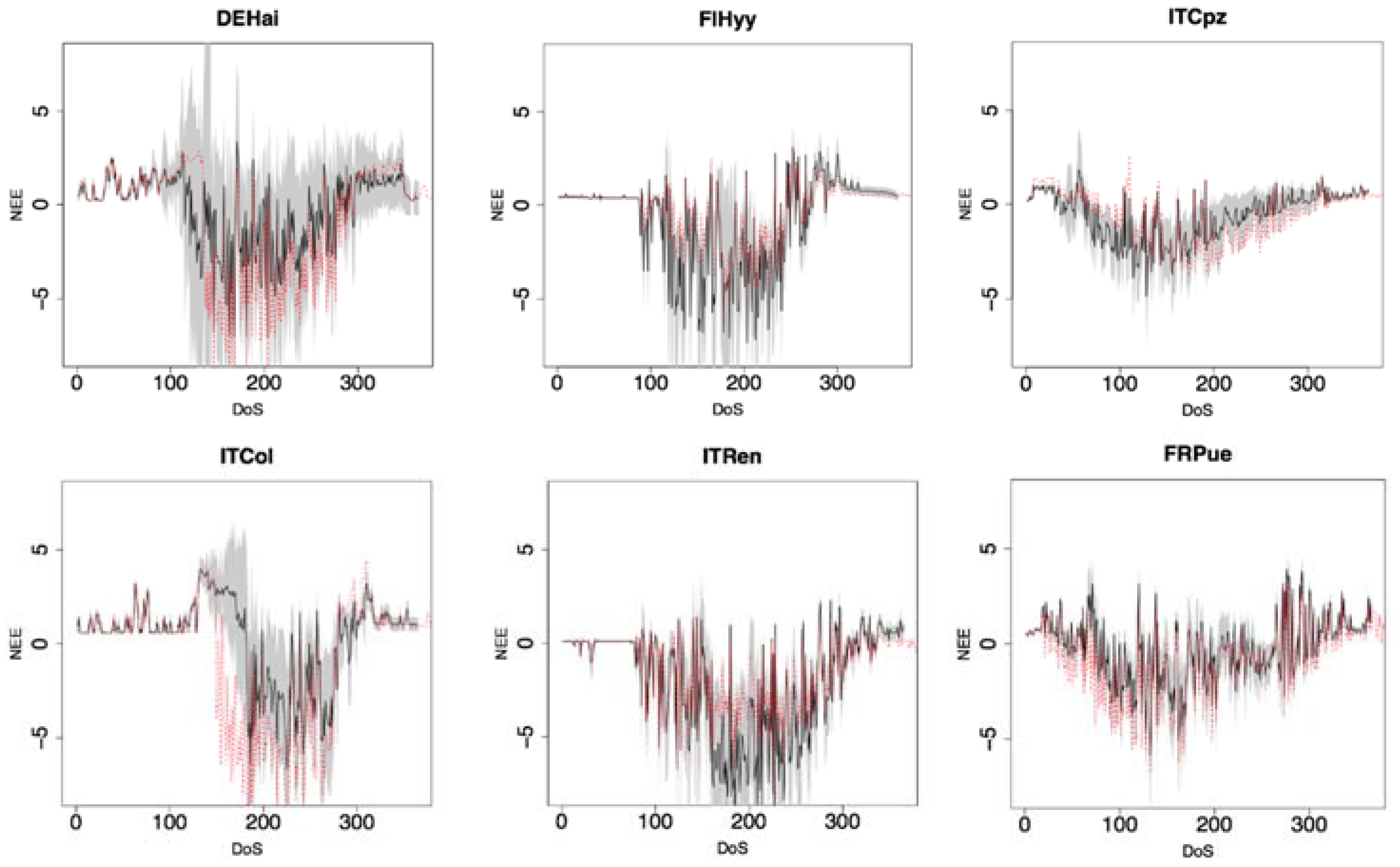
3.1. Evaluation of Daily, Seasonal, and Annual NEE Estimations
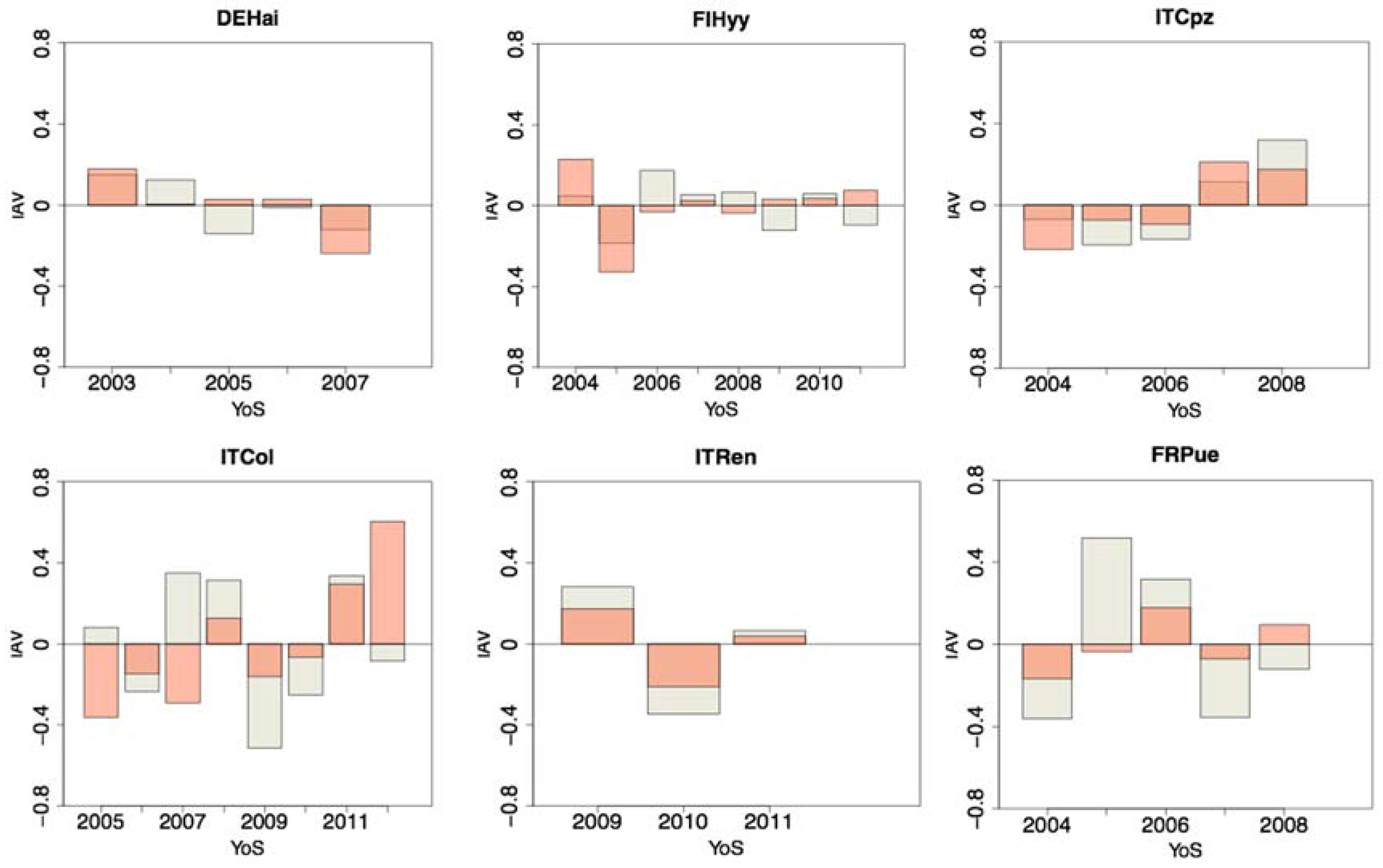
3.2. Anomalies and Parameters Related Uncertainty
3.3. Comparison with the 5.1 Version of 3D-CMCC-FEM
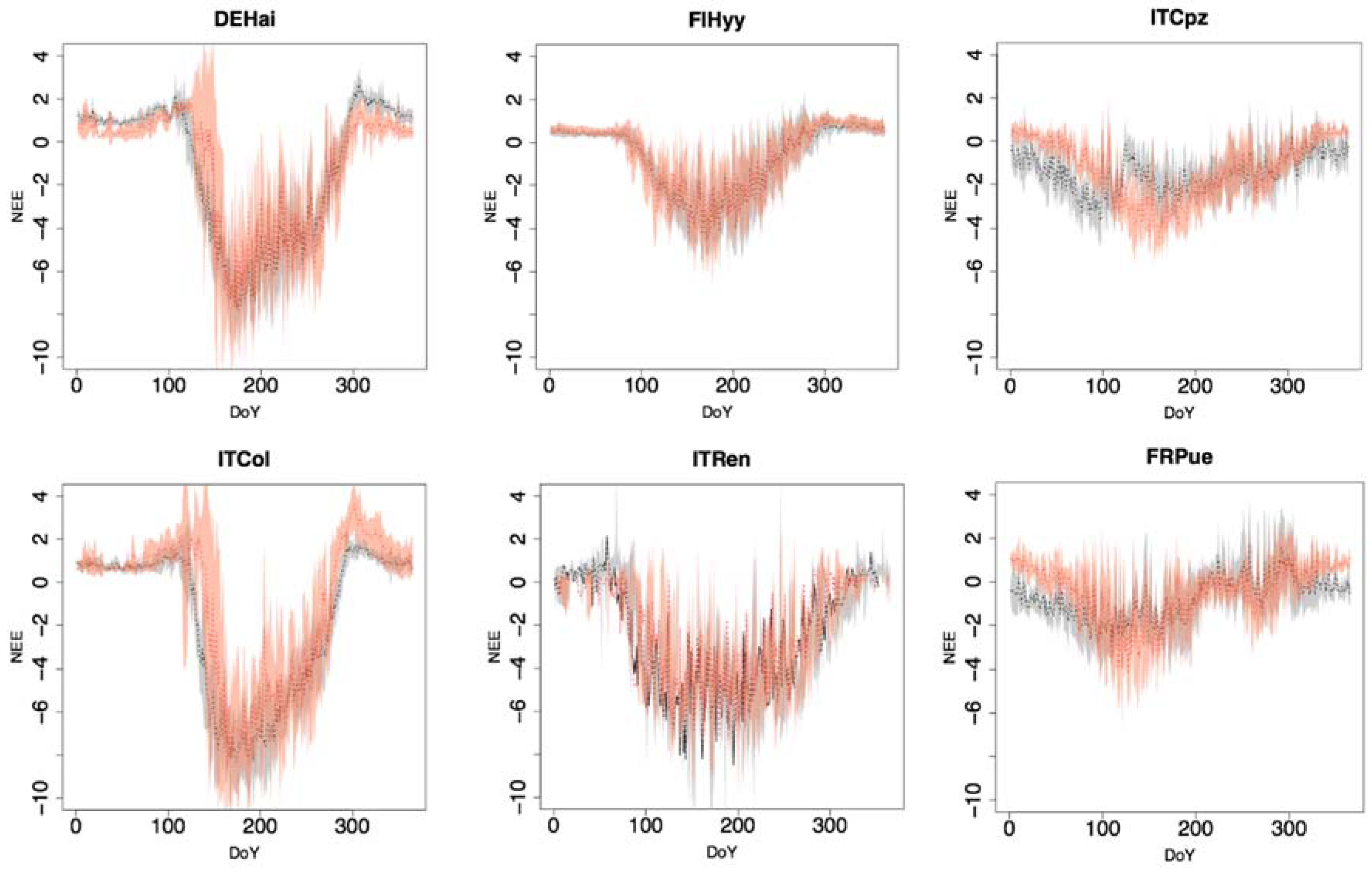
3.4. Daily and Monthly Reco
4. Discussion
4.1. 3D-CMCC-PSM Predictability in Estimating NEE
4.2. 3D-CMCC-PSM Uncertainty in Estimating NEE
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Baldocchi, D.; Ryu, Y.; Keenan, T. Terrestrial Carbon Cycle Variability. F1000Res 2016, 5. [Google Scholar] [CrossRef] [PubMed]
- Göckede, M.; Foken, T.; Aubinet, M.; Aurela, M.; Banza, J.; Bernhofer, C.; Bonnefond, J.M.; Brunet, Y.; Carrara, A.; Clement, R.; et al. Quality control of CarboEurope flux data & ndash; Part 1: Coupling footprint analyses with flux data quality assessment to evaluate sites in forest ecosystems. Biogeosciences 2008, 5, 433–450. [Google Scholar] [CrossRef]
- Xiao, J.; Zhuang, Q.; Law, B.E.; Chen, J.; Baldocchi, D.D.; Cook, D.R.; Oren, R.; Richardson, A.D.; Wharton, S.; Ma, S.; et al. A continuous measure of gross primary production for the conterminous U.S. derived from MODIS and AmeriFlux data. Remote Sens. Environ. 2010, 114, 576–591. [Google Scholar] [CrossRef]
- Tang, X.G.; Liu, D.W.; Song, K.S.; Munger, J.W.; Zhang, B.; Wang, Z.M. A new model of net ecosystem carbon exchange for the deciduous-dominated forest by integrating MODIS and flux data. Ecol. Eng. 2011, 37, 1567–1571. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.D.; Papale, D.; Valentini, R.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1–16. [Google Scholar] [CrossRef]
- Lasslop, G.; Migliavacca, M.; Bohrer, G.; Reichstein, M.; Bahn, M.; Ibrom, A.; Jacobs, C.; Kolari, P.; Papale, D.; Vesala, T.; et al. On the choice of the driving temperature for eddy-covariance carbon dioxide flux partitioning. Biogeosciences 2012, 9, 5243–5259. [Google Scholar] [CrossRef]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycles 1993, 74, 811–841. [Google Scholar] [CrossRef]
- Prince, S.D.; Goward, S.N. Global primary production: A remote sensing approach. J. Biogeogr. 1995, 22, 815–835. [Google Scholar] [CrossRef]
- Mäkelä, A.; Landsberg, J.; Ek, A.R.; Burk, T.E.; Ter-Mikaelian, M.; Agren, G.I.; Oliver, C.D.; Puttonen, P. Process-based models for forest ecosystem management: Current state of the art and challenges for practical implementation. Tree Physiol. 2000, 20, 289–298. [Google Scholar] [CrossRef] [PubMed]
- Yuan, W.P.; Liu, S.G.; Zhou, G.S.; Zhou, G.Y.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. For. Meteorol. 2007, 1433, 189–207. [Google Scholar] [CrossRef]
- Yuan, W.; Cai, W.; Xia, J.; Chen, J.; Liu, S.; Dong, W.; Merbold, L.; Law, B.; Arain, A.; Beringer, J.; et al. Global comparison of light use efficiency models for simulating terrestrial vegetation gross primary production based on the LaThuile database. Agric. For. Meteorol. 2014, 192–193, 108–120. [Google Scholar] [CrossRef]
- Cai, W.W.; Yuan, W.P.; Liang, S.L.; Zhang, X.T.; Dong, W.J.; Xia, J.Z.; Fu, Y.; Chen, Y.; Liu, D.; Zhang, Q. Improved estimations of gross primary production using satellite-derived photosynthetically active radiation. J. Geophys. Res. Biosci. 2014, 119. [Google Scholar] [CrossRef]
- Lacointe, A. Carbon allocation among tree organs. A review of basic processesand representation in functional-structural tree models. Ann. For. Sci. 2000, 57, 521–533. [Google Scholar] [CrossRef]
- Sievänen, R.; Nikinmaa, E.; Nygren, P.; Ozier-Lafontaine, H.; Perttunen, J.; Hakula, H. Components of functional-structural tree models. Ann. For. Sci. 2000, 57, 399–412. [Google Scholar] [CrossRef]
- Lu, M.; Nygren, P.; Perttunen, J.; Pallardy, S.G.; Larsen, D.R. Application of the functional-structural tree model LIGNUM to growth simulation of short-rotation eastern cottonwood. Silva Fenn. 2011, 45, 431–474. [Google Scholar] [CrossRef]
- Nikinmaa, E.; Sievänen, R.; Hölttä, T. Dynamics of leaf gas exchange, xylem and phloem transport, water potential and carbohydrate concentration in a realistic 3-D model tree crown. Ann. Bot. 2014, 114, 653–666. [Google Scholar] [CrossRef] [PubMed]
- Monteith, J.; Moss, C.J. Climate and the efficiency of crop production in Britain. Philos. Trans. R. Soc. Lond. 1977, 281, 277–294. [Google Scholar] [CrossRef]
- Trumbore, S. Carbon respired by terrestrial ecosystems-recent progress and challenges. Glob. Chang. Biol. 2006, 12, 141–153. [Google Scholar] [CrossRef]
- Mitchell, S.; Beven, K.; Freer, J. Multiple sources of predictive uncertainty in modeled estimates of net ecosystem CO2 exchange. Ecol. Model. 2009, 220, 3259–3270. [Google Scholar] [CrossRef]
- Yuan, F.; Arain, M.A.; Barr, A.G.; Black, T.A.; Bourque, C.P.A.; Coursolle, C.; Margolis, H.A.; Mccaughey, J.H.; Wofsy, S.C. Modeling analysis of primary controls on net ecosystem productivity of seven boreal and temperate coniferous forests across a continental transect. Glob. Chang. Biol. 2008, 14, 1765–1784. [Google Scholar] [CrossRef]
- Xu, B.; Yang, Y.; Li, P.; Shen, H.; Fang, J. Global patterns of ecosystem carbon flux in forests: A biometric databased synthesis. Glob. Biogeochem. Cycles 2014, 28, 962–973. [Google Scholar] [CrossRef]
- Zobitz, J.M.; Moore, D.J.P.; Sacks, W.J.; Monson, R.K.; Bowling, D.R.; Schimel, D.S. Integration of process-based soil respiration models with whole-ecosystem CO2 measurements. Ecosystems 2008, 11, 250–269. [Google Scholar] [CrossRef]
- Lloyd, J.; Taylor, J.A. On the temperature dependence of soil respiration. Funct. Ecol. 1994, 8, 315–323. [Google Scholar] [CrossRef]
- Kirschbaum, M.U.F. Soil respiration under prolonged soil warming: Are rate reductions caused by acclimation or substrate loss? Glob. Chang. Biol. 2004, 10, 1870–1877. [Google Scholar] [CrossRef]
- Xu, J.; Chen, J.; Brosofske, K.; Li, Q.; Weintraub, M.; Henderson, R.; Wilske, B.; John, R.; Jensen, R.; Li, H.; et al. Influence of timber harvesting alternatives on forest soil respiration and its biophysical regulatory factors over a 5-year period in the Missouri Ozarks. Ecosystems 2011, 14, 1310–1327. [Google Scholar] [CrossRef]
- Schimel, J.P.; Weintraub, M.N. Soil organic matter does not break itself down the implications of exoenzyme activity on microbial carbon and nitrogen limitation in soil: A theoretical model. Soil Biol. Biochem. 2003, 35, 549–563. [Google Scholar] [CrossRef]
- Tian, H.; Lu, C.; Yang, J.; Banger, K.; Huntzinger, D.N.; Schwalm, C.R.; Michalak, A.M.; Cook, R.; Ciais, P.; Hayes, D.; et al. Global patterns and controls of soil organic carbon dynamics as simulated by multiple terrestrial biosphere models: Current status and future directions. Glob. Biogeochem. Cycles 2015, 29, 775–792. [Google Scholar] [CrossRef] [PubMed]
- Chapin, S., III; McFarland, J.; David McGuire, A.; Euskirchen, E.S.; Ruess, R.W.; Kielland, K. The changing global carbon cycle: Linking plant-soil carbon dynamics to global consequences. J. Ecol. 2009, 97, 840–850. [Google Scholar]
- Hibbard, K.A.; Law, B.E.; Reichstein, M.; Sulzman, J. An analysis of soil respiration across northern hemisphere temperate ecosystems. Biogeochemistry 2005, 73, 29–70. [Google Scholar] [CrossRef]
- Knohl, A.; Schulze, E.D.; Kolle, O.; Buchmann, N. Large carbon uptake by an unmanaged 250-year-old deciduous forest in Central Germany. Agric. For. Meteorol. 2003, 118, 151–167. [Google Scholar] [CrossRef]
- Facelli, J.M.; Pickett, S.T.A. Plant litter: Its dynamics and effects on plant community structure. Bot. Rev. 1991, 57, 1–32. [Google Scholar] [CrossRef]
- Richardson, A.D.; Anderson, R.S.; Arain, M.A.; Barr, A.G.; Bohrer, G.; Chen, G.; Chen, J.M.; Ciais, P.; Davis, K.J.; Desai, A.R.; et al. Terrestrial biosphere models need better representation of vegetation phenology: Results from the North American Carbon Program Site Synthesis. Glob. Chang. Biol. 2012, 18, 566–584. [Google Scholar] [CrossRef]
- Kucharik, C.J.; Barford, C.C.; El Maayar, M.; Wofsy, S.C.; Monson, R.K.; Baldocchi, D.D. A multiyear evaluation of a Dynamic Global Vegetation Model at three AmeriFlux forest sites: Vegetation structure, phenology, soil temperature, and CO2 and H2O vapor exchange. Ecol. Model. 2006, 196, 1–31. [Google Scholar] [CrossRef]
- Ryu, S.R.; Chen, J.; Noormets, A.; Bresee, M.K.; Ollinger, S.V. Comparisons between PnET-Day and eddy covariance based gross ecosystem production in two Northern Wisconsin forests. Agric. For. Meteorol. 2008, 148, 247–256. [Google Scholar] [CrossRef]
- Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
- Collalti, A.; Perugini, L.; Santini, M.; Chiti, T.; Nolè, A.; Matteucci, G.; Valentini, R. A process-based model to simulate growth in forests with complex structure: Evaluation and use of 3D-CMCC Forest Ecosystem Model in a deciduous forest in Central Italy. Ecol. Model. 2014, 272, 362–378. [Google Scholar] [CrossRef]
- Collalti, A.; Marconi, S.; Ibrom, A.; Trotta, C.; Anav, A.; D’andrea, E.; Grünwald, T. Validation of 3D-CMCC Forest Ecosystem Model (v. 5.1) against eddy covariance data for 10 European forest sites. Geosci. Model Dev. 2016, 9, 479–504. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Zhou, X.; Moore, B. A simulation model linking crop growth and soil biogeochemistry for sustainable agriculture. Ecol. Model. 2002, 151, 75–108. [Google Scholar] [CrossRef]
- FLUXNET-Fluxdata. Available online: http://fluxnet.fluxdata.org (accessed on 3 June 2014).
- Papale, D.; Reichstein, M.; Aubinet, M.; Canfora, E.; Bernhofer, C.; Longdoz, B.; Kutsch, W.; Rambal, S.; Valentini, R.; Vesala, T.; et al. Towards a standardized processing of Net Ecosystem Exchange measured with eddy covariance technique: Algorithms and uncertainty estimation. Biogeosciences 2006, 3, 571–583. [Google Scholar] [CrossRef]
- Mencuccini, M.; Bonosi, L. Leaf/sapwood area ratios in Scots pine show acclimation across Europe. Can. J. For. Res. 2001, 31, 442–456. [Google Scholar] [CrossRef]
- Pilegaard, K.; Mikkelsen, T.N.; Beier, C.; Jensen, N.O.; Ambus, P.; Ro-Poulsen, H. Field Measurements of Atmosphere—Biosphere Interactions in a Danish Beech Forest. Boreal Environ. Res. 2003, 8, 315–333. [Google Scholar]
- Landsberg, J.J.; Waring, R.H. A generalised model of forest productivity using simplified concepts of radiation-use efficiency, carbon balance and partitioning. For. Ecol. Manag. 1997, 95, 209–228. [Google Scholar] [CrossRef]
- Molina, J.A.E.; Clapp, C.E.; Shaffer, M.J.; Chichester, F.W.; Larson, W.E. NCSOIL, A Model of Nitrogen and Carbon Transformations in Soil: Description, Calibration, and Behavior1. Soil Sci. Soc. Am. J. 1983, 47, 85. [Google Scholar] [CrossRef]
- Sollins, P.; Homann, P.; Caldwell, B.A. Stabilization and destabilization of soil organic matter: Mechanisms and controls. Geoderma 1996, 74, 65–105. [Google Scholar] [CrossRef]
- Tamon, F.; Kobayashi, K.; Li, C.; Yagi, K.; Hasegawa, T. Revising a Process-based Biogeochemistry Model (DNDC) to Simulate Methane Emission from Rice Paddy Fields under Various Residue Management and Fertilizer. Glob. Chang. 2008, 14, 382–402. [Google Scholar] [CrossRef]
- Coleman, K.; Jenkinson, D.S. “ROTHC-26.3.” A Model for the Turnover of Carbon in Soils, No. November 1999. Available online: http://www.uni-kassel.de/~w_dec/Modellierung/wdec-rothc_manual.pdf (accessed on 1 October 2014).
- Running, S.W.; Raymond Hunt, E., Jr. Generalization of a Forest Ecosystem Process Model for Other Biomes, BIOME-BCG, and an Application for Global-Scale Models; Academic Press, Inc.: London, UK, 1993; pp. 141–158. [Google Scholar]
- Delpierre, N.; Dufrêne, E.; Soudani, K.; Ulrich, E.; Cecchini, S.; Boé, J.; François, C. Modelling Interannual and Spatial Variability of Leaf Senescence for Three Deciduous Tree Species in France. Agric. For. Meteorol. 2009, 149, 938–948. [Google Scholar] [CrossRef]
- Keel, S.G.; Schädel, C. Expanding leaves of mature deciduous forest trees rapidly become autotrophic. Tree Physiol. 2010, 30, 1253–1259. [Google Scholar] [CrossRef] [PubMed]
- Chabot, B.F.; Hicks, D.J. The Ecology of Leaf Life Spans. Ann. Rev. Ecol. Syst. 1982, 13, 229–259. Available online: http://www.jstor.org/stable/2097068 (accessed on 6 October 2015). [CrossRef]
- Tilman, D. Constraints and tradeoffs: Toward a predictive theory of competition and succession. Oikos 1990, 58, 3–15. [Google Scholar] [CrossRef]
- Waring, R.H.; Landsberg, J.J.; Williams, M. Net Primary Production of Forests: A Constant Fraction of Gross primary production? Tree Physiol. 1998, 18, 129–134. [Google Scholar] [CrossRef] [PubMed]
- Praciak, A.; Pasiecznik, N.; Sheil, D.; van Heist, M.; Sassen, M.; Correia, C.S.; Dixon, C.; Fyson, G.; Rushford, K.; Teeling, C. The CABI Encyclopedia of Forest Trees; CABI: Oxfordshire, UK, 2013. [Google Scholar]
- Kuzyakov, Y. Priming effects: Interactions between living and dead organic matter. Soil Biol. Biochem. 2010, 42, 1363–1371. [Google Scholar] [CrossRef]
- Thornton, P. Biome BGC Version 4.2: Theoretical Framework of Biome-BGC; Technical Documentation: Missoula, MT, USA, 2010. [Google Scholar]
- Liang, B.; Lehmann, J.; Sohi, S.P.; Thies, J.E.; O’Neill, B.; Trujillo, L.; Luizão, F.J. Black carbon affects the cycling of non-black carbon in soil. Org. Geochem. 2010, 41, 206–213. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013; Volume 6. [Google Scholar]
- Walther, B.A.; Moore, J.L. The concepts of bias, precision and accuracy, and their use in testing the performance of species richness estimators, with a literature review of estimator performance. Ecography 2005, 28, 815–829. [Google Scholar] [CrossRef]
- Keenan, T.F.; Baker, I.; Barr, A.; Ciais, P.; Davis, K.; Dietze, M.; Dragoni, D.; Gough, C.M.; Grant, R.; Hollinger, D.; et al. Terrestrial Biosphere Model Performance for Inter-Annual Variability of Land-Atmosphere CO2 Exchange. Glob. Chang. Biol. 2012, 18, 1971–1987. [Google Scholar] [CrossRef]
- Taylor, K. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Booth, B.B.B.; Jones, C.D.; Collins, M.; Totterdell, I.J.; Cox, P.M.; Sitch, S.; Huntingford, C.; Betts, R.A.; Harris, G.R.; Lloyd, J. High sensitivity of future global warming to land carbon cycle processes. Environ. Res. Lett. 2012, 7, 024002. [Google Scholar] [CrossRef]
- Zhao, Y.; Ciais, P.; Peylin, P.; Viovy, N.; Longdoz, B.; Bonnefond, J.M.; Rambal, S.; Klumpp, K.; Olioso, A.; Cellier, P.; et al. How errors on meteorological variables impact simulated ecosystem fluxes: A case study for six French sites. Biogeosciences 2012, 9, 2537–2564. [Google Scholar] [CrossRef]
- Doblas-Miranda, E.; Martínez-Vilalta, J.; Lloret, F.; Álvarez, A.; Ávila, A.; Bonet, F.J.; Ferrandis, P. Reassessing global change research priorities in mediterranean terrestrial ecosystems: How far have we come and where do we go from here? Glob. Ecol. Biogeogr. 2015, 24, 25–43. [Google Scholar] [CrossRef]
- Huber-Sanwald, E.; Huenneke, L.F.; Jackson, R.B.; Kinzig, A.; Leemans, R.; Lodge, D.M.; Walker, B.H. Biodiversity global biodiversity scenarios for the year 2100. Science 2000, 287, 1770–1774. [Google Scholar]
- Muraoka, H.; Koizumi, H. Photosynthetic and structural characteristics of canopy and shrub trees in a cool-temperate deciduous broadleaved forest: Implication to the ecosystem carbon gain. Agric. For. Meteorol. 2005, 134, 39–59. [Google Scholar] [CrossRef]
- Kramer, K.; Leinonen, I.; Bartelink, H.H.; Berbigier, P.; Borghetti, M.; Cienciala, E.; Dolman, A.J.; Froer, O.; Gracia, C.; Granier, A.; et al. Evaluation of Six Process-Based Forest Growth Models Using Eddy-Covariance Measurements of CO2 and H2O Fluxes at Six Forest Sites in Europe. Glob. Chang. Biol. 2002, 213–230. [Google Scholar] [CrossRef]
- Keenan, T.; Garcia, R.; Sabate, S.; Gracia, C.A. Process Based Forest Modelling: A Thorough Validation and Future Prospects for Mediterranean Forests in a Changing World. Cuad. Soc. Esp. Cienc. For. 2007, 92, 81–92. [Google Scholar]
- Zhou, W.; Hui, D.; Shen, W. Effects of soil moisture on the temperature sensitivity of soil heterotrophic respiration: A laboratory incubation study. PLoS ONE 2014, 9, e92531. [Google Scholar] [CrossRef] [PubMed]
- Hollinger, D.Y.; Richardson, A.D. Uncertainty in eddy covariance measurements and its application to physiological models. Tree Physiol. 2005, 25, 873–885. [Google Scholar] [CrossRef] [PubMed]
- DeLucia, E.H.; Drake, J.E.; Thomas, R.B.; Gonzalez-Meler, M.A. Forest carbon use efficiency: Is respiration a constant fraction of gross primary production? Glob. Chang. Biol. 2007, 13, 1157–1167. [Google Scholar] [CrossRef]
- Ito, A.; Oikawa, T. Global mapping of terrestrial primary productivity and light-use efficiency with a process-based model. In Global Environmental Change in the Ocean and on Land; TERRAPUB: Tokyo, Japan, 2004; pp. 343–358. [Google Scholar]
- Sabaté, S.; Gracia, C.A.; Sánchez, A. Likely effects of climate change on growth of Quercus ilex, Pinus halepensis, Pinus pinaster, Pinus sylvestris and Fagus sylvatica forests in the Mediterranean region. For. Ecol. Manag. 2002, 162, 23–37. [Google Scholar] [CrossRef]
- Chiti, T.; Papale, D.; Smith, P.; Dalmonech, D.; Matteucci, G.; Yeluripati, J.; Valentini, R. Predicting changes in soil organic carbon in mediterranean and alpine forests during the Kyoto Protocol commitment periods using the CENTURY model. Soil Use Manag. 2010, 26, 475–484. [Google Scholar] [CrossRef]
- Dickinson, C.H. Biology of Plant Litter Decomposition; Elsevier: Amsterdam, The Netherlands, 2012; Volume 2. [Google Scholar]
- Yang, Y.; Zhu, Q.; Peng, C.; Wang, H.; Xue, W.; Lin, G.; Li, S. A novel approach for modelling vegetation distributions and analysing vegetation sensitivity through trait-climate relationships in China. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Zhu, Q.; Peng, C.; Wang, H.; Chen, H. From plant functional types to plant functional traits: A new paradigm in modelling global vegetation dynamics. Prog. Phys. Geogr. 2015, 39, 514–535. [Google Scholar] [CrossRef]
- Messier, J.; McGill, B.J.; Lechowicz, M.J. How do traits vary across ecological scales? A case for trait-based ecology. Ecol. Lett. 2010, 13, 838–848. [Google Scholar] [CrossRef] [PubMed]
- Claussen, M.; Mysak, L.A.; Weaver, A.J.; Crucifix, M.; Fichefet, T.; Loutre, M.-F.; Weber, S.L.; Alcamo, J.; Alexeev, V.A.; Berger, A.; et al. Earth System Models of Intermediate Complexity: Closing the Gap in the Spectrum of Climate System Models. Clim. Dyn. 2002, 18, 579–586. [Google Scholar]
- Lavorel, S.; Díaz, S.; Cornelissen, J.H.C.; Garnier, E.; Harrison, S.P.; McIntyre, S.; Urcelay, C. Plant functional types: Are we getting any closer to the Holy Grail? In Terrestrial Ecosystems in a Changing World; Springer: Berlin/Heidelberg, Germany, 2007; pp. 149–164. [Google Scholar]
- Schaber, J.; Badeck, F.W. Physiology-Based Phenology Models for Forest Tree Species in Germany. Int. J. Biometeorol. 2003, 47, 193–201. [Google Scholar] [CrossRef] [PubMed]
- Linkosalo, T.; Lappalainen, H.K.; Hari, P. A comparison of phenological models of leaf bud burst and flowering of boreal trees using independent observations. Tree Physiol. 2008, 28, 1873–1882. [Google Scholar] [CrossRef] [PubMed]
- Uusitalo, L.; Lehikoinen, A.; Helle, I.; Myrberg, K. An overview of methods to evaluate uncertainty of deterministic models in decision support. Environ. Model. Softw. 2015, 63, 24–31. [Google Scholar] [CrossRef]
- Wythers, K.R.; Reich, P.B.; Bradford, J.B. Incorporating temperature-sensitive Q10 and foliar respiration acclimation algorithms modifies modeled ecosystem responses to global change. J. Geophys. Res. Biogeosci. 2013, 118, 77–90. [Google Scholar] [CrossRef]
- Ryan, M.G.; Gower, S.T.; Hubbard, R.M. Woody Tissue Maintenance Respiration of Four Conifers in Contrasting Climates. Oecologia 1995, 101, 133–140. [Google Scholar] [CrossRef] [PubMed]
- Valentini, R.; Matteucci, G.; Dolman, A.J.; Shulze, E.D.; Rebmann, C.; Moors, E.J.; Granier, A.; Lindroth, A. Respiration as the main determinant of Carbon balance in European forests. Nature 2000, 404, 851–865. [Google Scholar] [CrossRef] [PubMed]
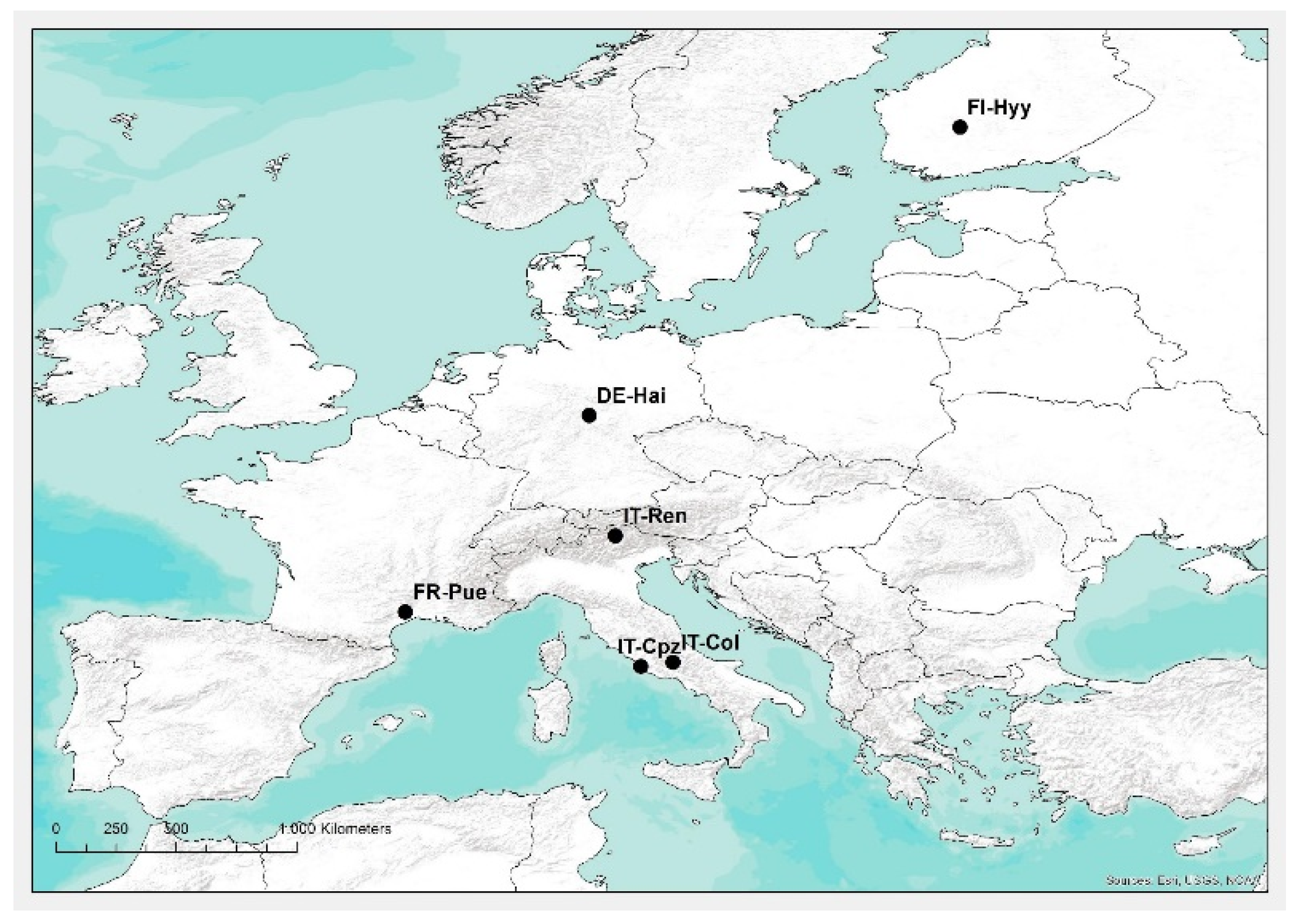

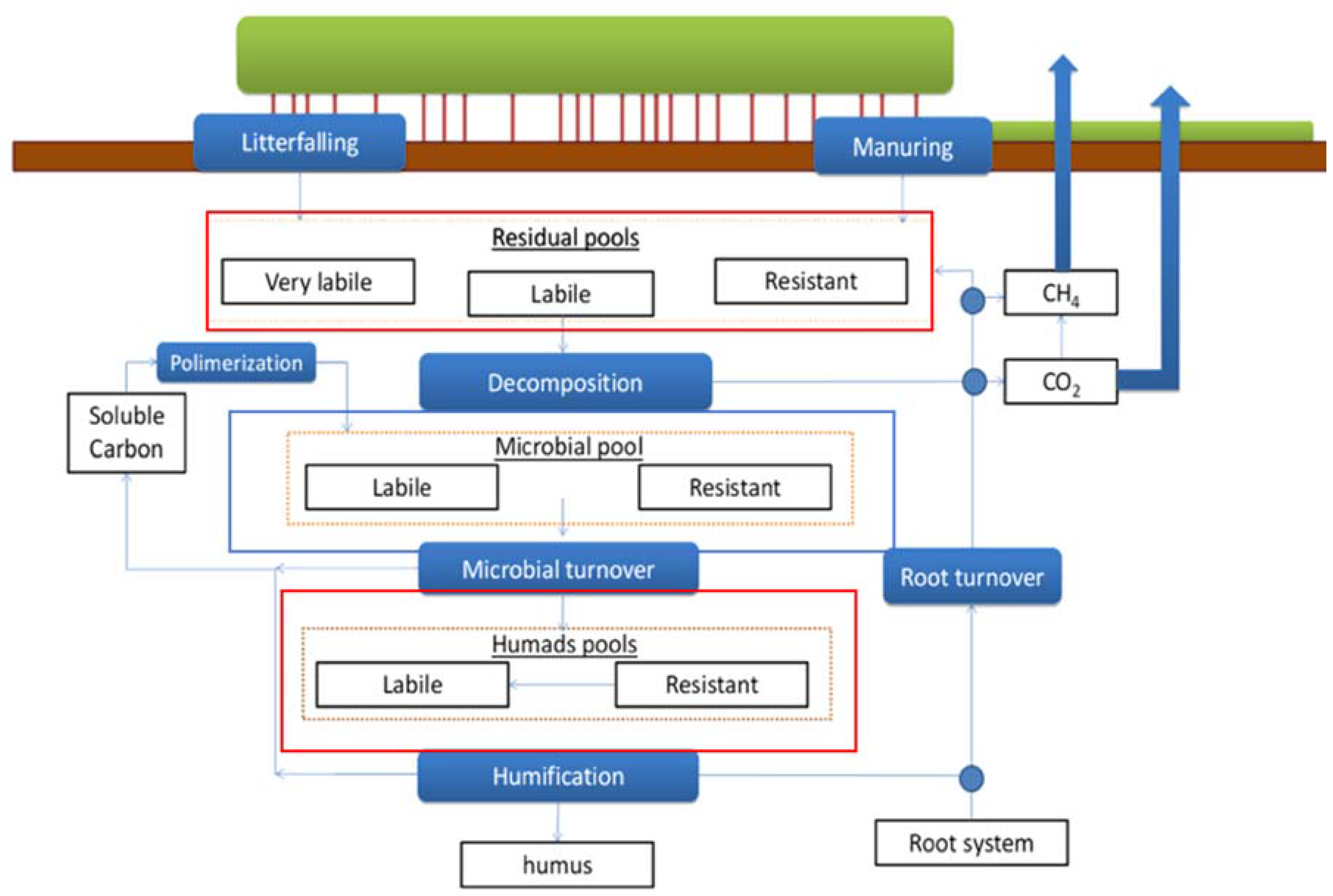
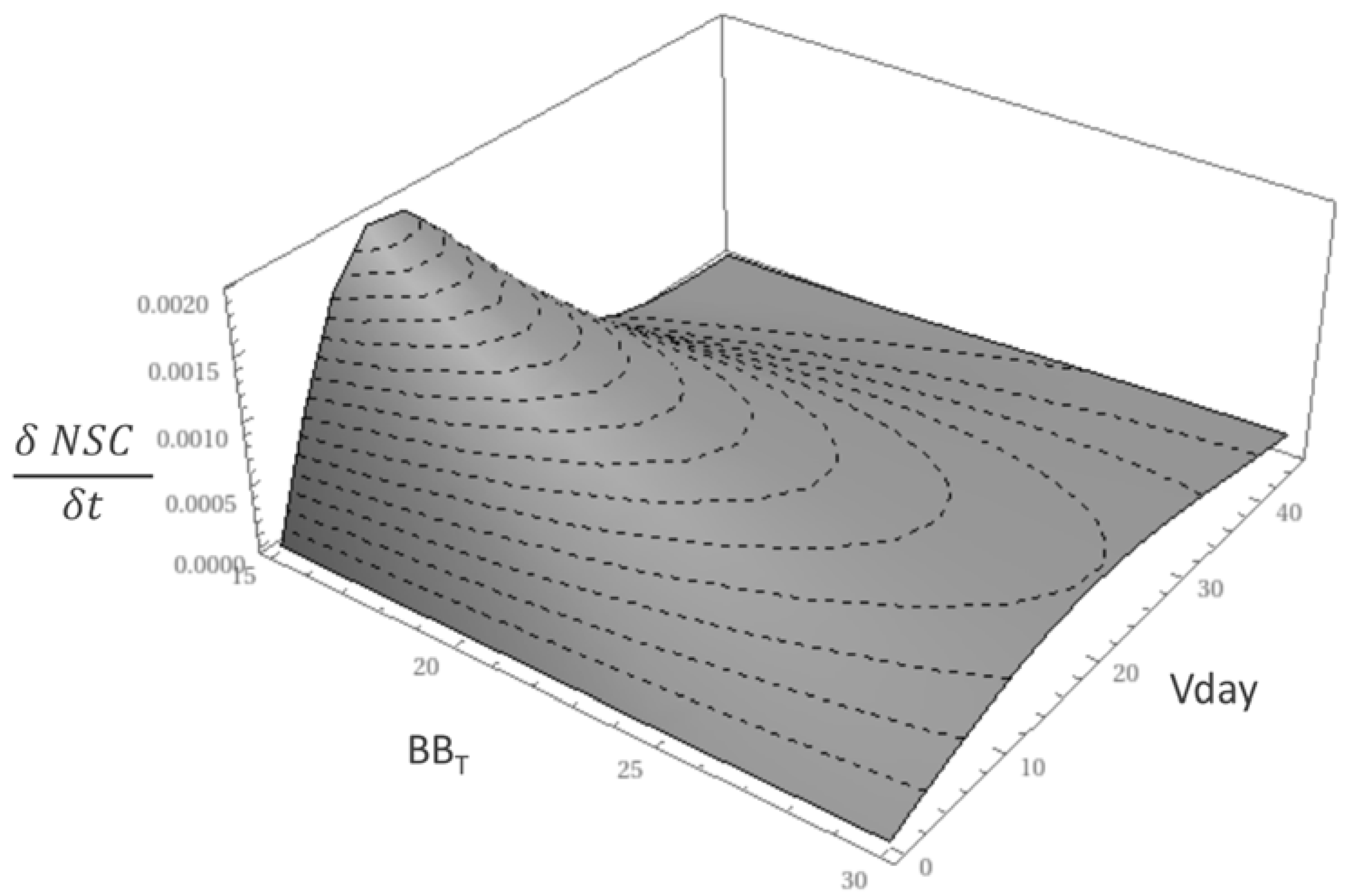
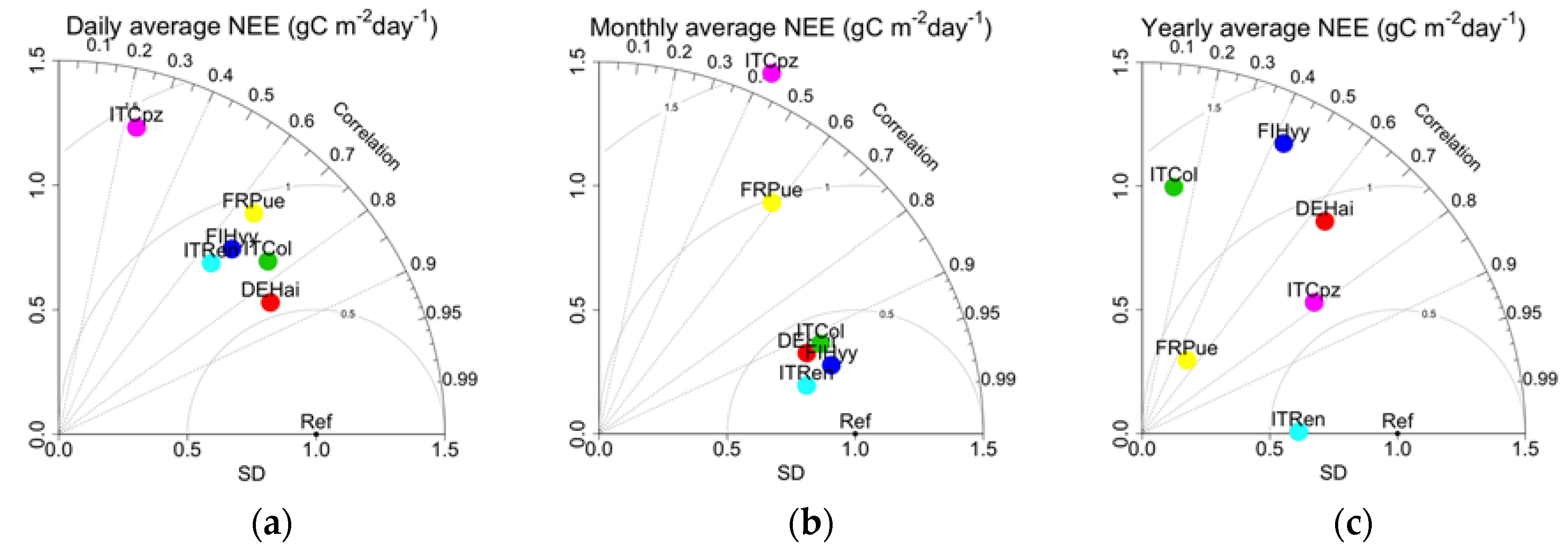

| Site Name | Coords (Lat°/Lon°) | Climate | Species Composition | Mean Annual T (°C) | Mean Annual Prec. (mm year−1) | Mean DBH (cm) | Tree Height (m) | Stand Age (years) | Stand Density (trees ha−1) |
|---|---|---|---|---|---|---|---|---|---|
| Collelongo (ITCol) | 41.8/13.5 | Temperate | Fagus sylvatica L. (DBF) | 6.3 | 1180 | 20.27 | 19.84 | 100 | 900 |
| Hainich (DEHai) | 51.0/10.4 | Temperate | Fagus sylvatica L. (DBF) | 8.3 | 720 | 30.8 | 23.1 | 120 | 334 |
| Hyytiälä (FIHyy) | 61.8/24.2 | Boreal | Pinus sylvestris L. (ENF) | 3.8 | 709 | 10.3 | 6.5 | 39 | 1796 |
| Renon (ITRen) | 46.5/11.4 | Temperate | Picea abies L. (ENF) | 4.7 | 809 | 16.98 | 11.32 | 50 | 767 |
| Castelporziano (ITCpz) | 41.7/12.3 | Mediterranean | Quercus ilex L. (EBF) | 15.6 | 780 | 16 | 12.5 | 45 | 458 |
| Puechabon (FRPue) | 43.7/3.6 | Mediterranean | Quercus ilex L. (EBF) | 13.5 | 883 | 7 | 6 | 59 | 6149 |
| Deciduous | Evergreen | ||
|---|---|---|---|
| Phase | Trigger | Phase | Trigger |
| Bud Burst | GDD threshold | Bud Burst | GDD treshold |
| Leaf Development | PeakLai/2 | PeakLai | Pipe Model |
| PeakLai | Pipe Model | Leaffall | Daylength Treshold |
| Leaffall | Daylength Treshold | ||
| Unvegetative | [49] | ||
| Statistics | Formulation | Use and Ranges |
|---|---|---|
| Pearson Coefficient | Estimation of model’s measure of correlation with EC data [0;1] | |
| Nash Sutcliffe efficiency | Estimation of model’s predictability [−∞;1] | |
| Root Mean Square Error | Estimation of model’s accuracy gC m−2 day−1 [0; ∞] | |
| Mean Absolute Bias | Estimation of model’s bias gC m−2 day−1 [0; ∞] |
| DEHai | ITCol | FIHyy | ITRen | ITCpz | FRPue | Mean | |
|---|---|---|---|---|---|---|---|
| Daily NEE | |||||||
| R | 0.84 | 0.76 | 0.67 | 0.65 | 0.24 | 0.65 | 0.64 |
| NSE | 0.67 | 0.5 | 0.34 | 0.21 | -0.26 | 0.35 | 0.3 |
| RMSE | 1.84 | 2.7 | 1.48 | 2.32 | 1.8 | 1.39 | 1.92 |
| MAB | 0.39 | 0.5 | 0.53 | 0.56 | 1.15 | 0.76 | 0.65 |
| Monthly NEE | |||||||
| R | 0.93 | 0.92 | 0.96 | 0.97 | 0.42 | 0.59 | 0.8 |
| NSE | 0.81 | 0.76 | 0.9 | 0.87 | 0.12 | 0.2 | 0.61 |
| RMSE | 1.15 | 1.58 | 0.45 | 0.72 | 1.24 | 1 | 1.02 |
| MAB | 0.28 | 0.32 | 0.21 | 0.24 | 1.25 | 0.86 | 0.53 |
| R | NSE | RMSE | MAB | |
|---|---|---|---|---|
| DBF | ||||
| MAM | 0.43 | −0.36 | 2.77 | 0.72 |
| JJA | 0.36 | −0.02 | 2.96 | 1.17 |
| SON | 0.82 | 0.58 | 1.9 | 0.58 |
| DJF | 0.2 | −0.93 | 0.7 | 1.58 |
| EBF | ||||
| MAM | 0.65 | 0.28 | 1.83 | 0.62 |
| JJA | 0.11 | −0.92 | 2.76 | 1.01 |
| SON | 0.51 | 0.03 | 1.56 | 0.74 |
| DJF | 0.38 | −1.59 | 0.51 | 0.82 |
| ENF | ||||
| MAM | 0.18 | −0.41 | 1.95 | 1.2 |
| JJA | 0.32 | −0.34 | 1.58 | 1 |
| SON | 0.45 | −0.19 | 1.3 | 0.79 |
| DJF | 0.47 | −6.13 | 1.45 | 1.4 |
| Version | ITRen | FRPue | DEHai | FIHyy | Avg | |
|---|---|---|---|---|---|---|
| Daily | 5.1 | 0.81 | 0.82 | 0.92 | 0.91 | 0.87 |
| R | PSM | 0.88 | 0.64 | 0.93 | 0.91 | 0.85 |
| Monthly | 5.1 | 0.95 | 0.64 | 0.97 | 0.96 | 0.89 |
| R | PSM | 0.96 | 0.84 | 0.98 | 0.96 | 0.94 |
| Daily | 5.1 | 0.61 | −0.54 | 0.84 | 0.87 | 0.45 |
| NSE | PSM | 0.72 | 0.09 | 0.96 | 0.76 | 0.63 |
| Monthly | 5.1 | 0.91 | −0.11 | 0.94 | 0.91 | 0.66 |
| NSE | PSM | 0.91 | 0.56 | 0.98 | 0.92 | 0.84 |
| Daily | 5.1 | 2.09 | 1.52 | 1.85 | 1.56 | 1.76 |
| RMSE | PSM | 1.59 | 1.96 | 1.91 | 1.57 | 1.76 |
| Monthly | 5.1 | 0.97 | 1.01 | 1.07 | 0.91 | 0.99 |
| RMSE | PSM | 0.82 | 1.09 | 0.82 | 0.93 | 0.92 |
| DEHai | ITCol | FIHyy | ITRen | ITCpz | FRPue | Mean | |
|---|---|---|---|---|---|---|---|
| Daily Reco | |||||||
| R | 0.79 | 0.71 | 0.90 | 0.67 | 0.45 | 0.86 | 0.73 |
| NSE | 0.32 | 0.32 | 0.60 | 0.34 | −0.43 | 0.57 | 0.29 |
| RMSE | 1.29 | 1.83 | 1.18 | 1.03 | 1.65 | 0.70 | 1.28 |
| MEB | 0.63 | 1.00 | 0.43 | 0.62 | 0.98 | 0.48 | 0.69 |
| Monthly Reco | |||||||
| R | 0.86 | 0.79 | 0.96 | 0.84 | 0.54 | 0.93 | 0.82 |
| NSE | 0.40 | 0.37 | 0.66 | 0.69 | −0.40 | 0.67 | 0.40 |
| RMSE | 1.10 | 1.67 | 1.04 | 0.64 | 1.49 | 0.54 | 1.08 |
| MEB | 0.60 | 0.99 | 0.41 | 0.50 | 1.04 | 0.43 | 0.66 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marconi, S.; Chiti, T.; Nolè, A.; Valentini, R.; Collalti, A. The Role of Respiration in Estimation of Net Carbon Cycle: Coupling Soil Carbon Dynamics and Canopy Turnover in a Novel Version of 3D-CMCC Forest Ecosystem Model. Forests 2017, 8, 220. https://doi.org/10.3390/f8060220
Marconi S, Chiti T, Nolè A, Valentini R, Collalti A. The Role of Respiration in Estimation of Net Carbon Cycle: Coupling Soil Carbon Dynamics and Canopy Turnover in a Novel Version of 3D-CMCC Forest Ecosystem Model. Forests. 2017; 8(6):220. https://doi.org/10.3390/f8060220
Chicago/Turabian StyleMarconi, Sergio, Tommaso Chiti, Angelo Nolè, Riccardo Valentini, and Alessio Collalti. 2017. "The Role of Respiration in Estimation of Net Carbon Cycle: Coupling Soil Carbon Dynamics and Canopy Turnover in a Novel Version of 3D-CMCC Forest Ecosystem Model" Forests 8, no. 6: 220. https://doi.org/10.3390/f8060220
APA StyleMarconi, S., Chiti, T., Nolè, A., Valentini, R., & Collalti, A. (2017). The Role of Respiration in Estimation of Net Carbon Cycle: Coupling Soil Carbon Dynamics and Canopy Turnover in a Novel Version of 3D-CMCC Forest Ecosystem Model. Forests, 8(6), 220. https://doi.org/10.3390/f8060220







