Spatial Heterogeneity of the Forest Canopy Scales with the Heterogeneity of an Understory Shrub Based on Fractal Analysis
Abstract
:1. Introduction
2. Materials and Methods
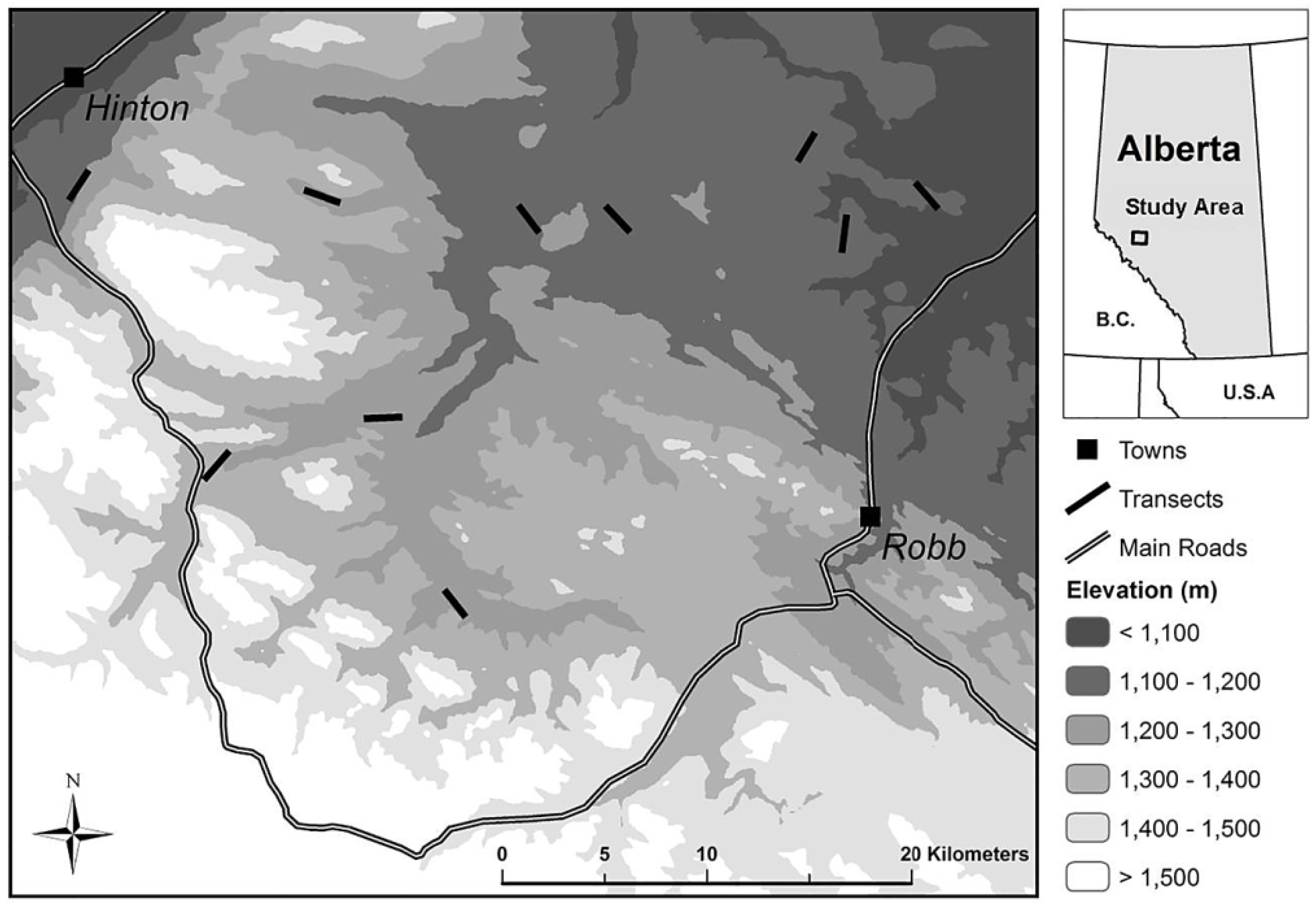
2.1. Study Area
2.2. Site Selection
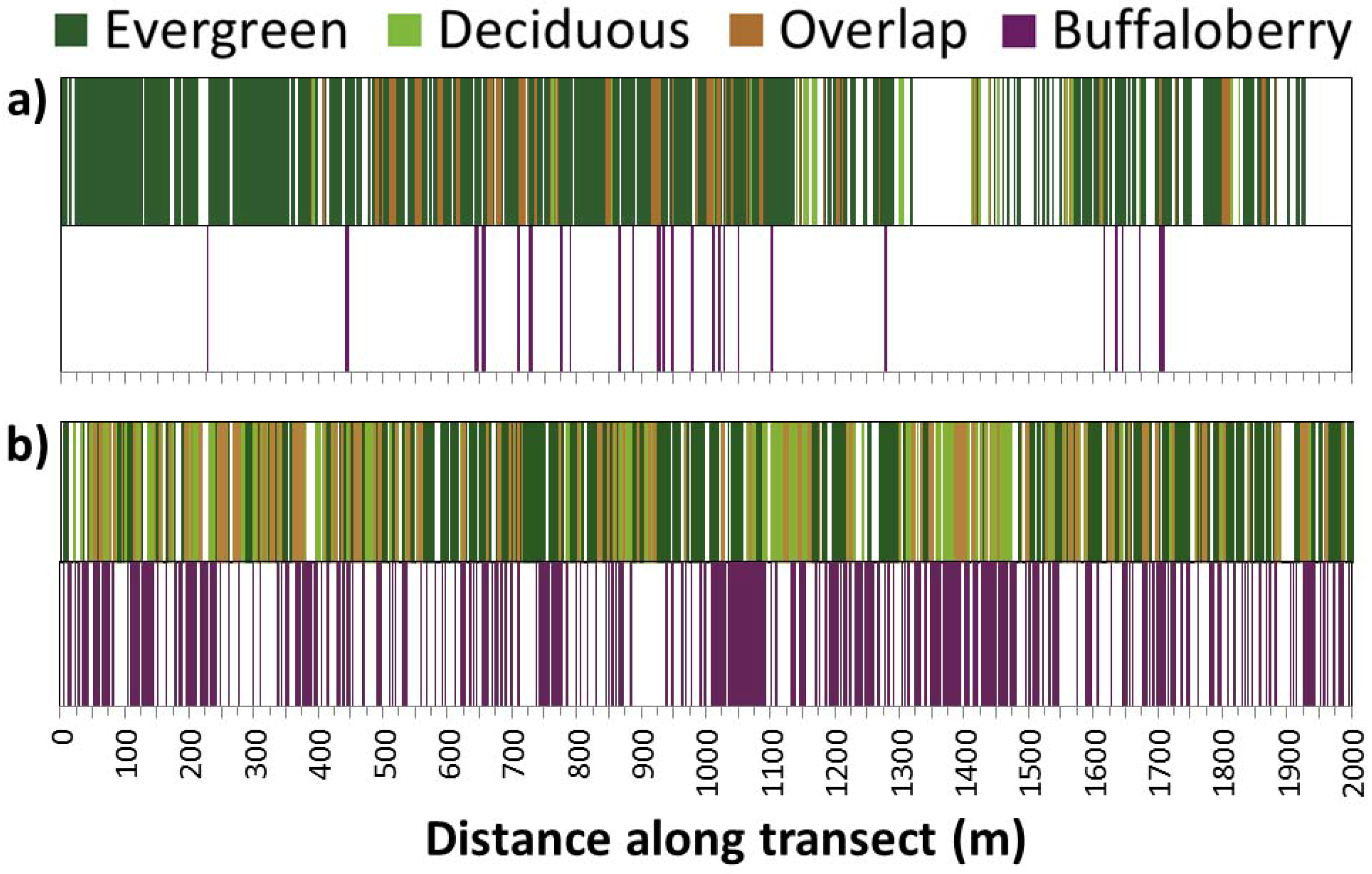
2.3. Field Methods
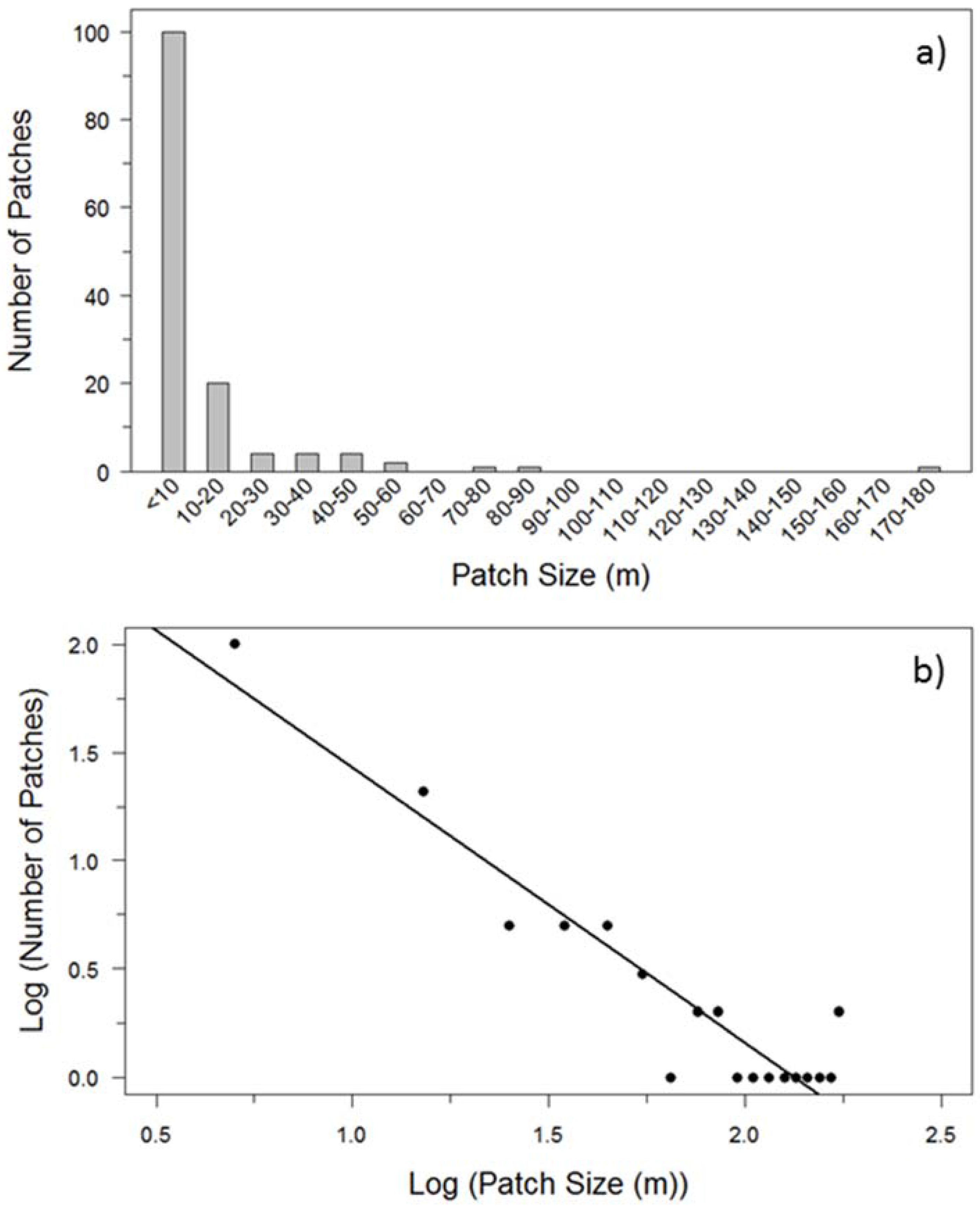
2.4. Patch Size Frequency Distribution
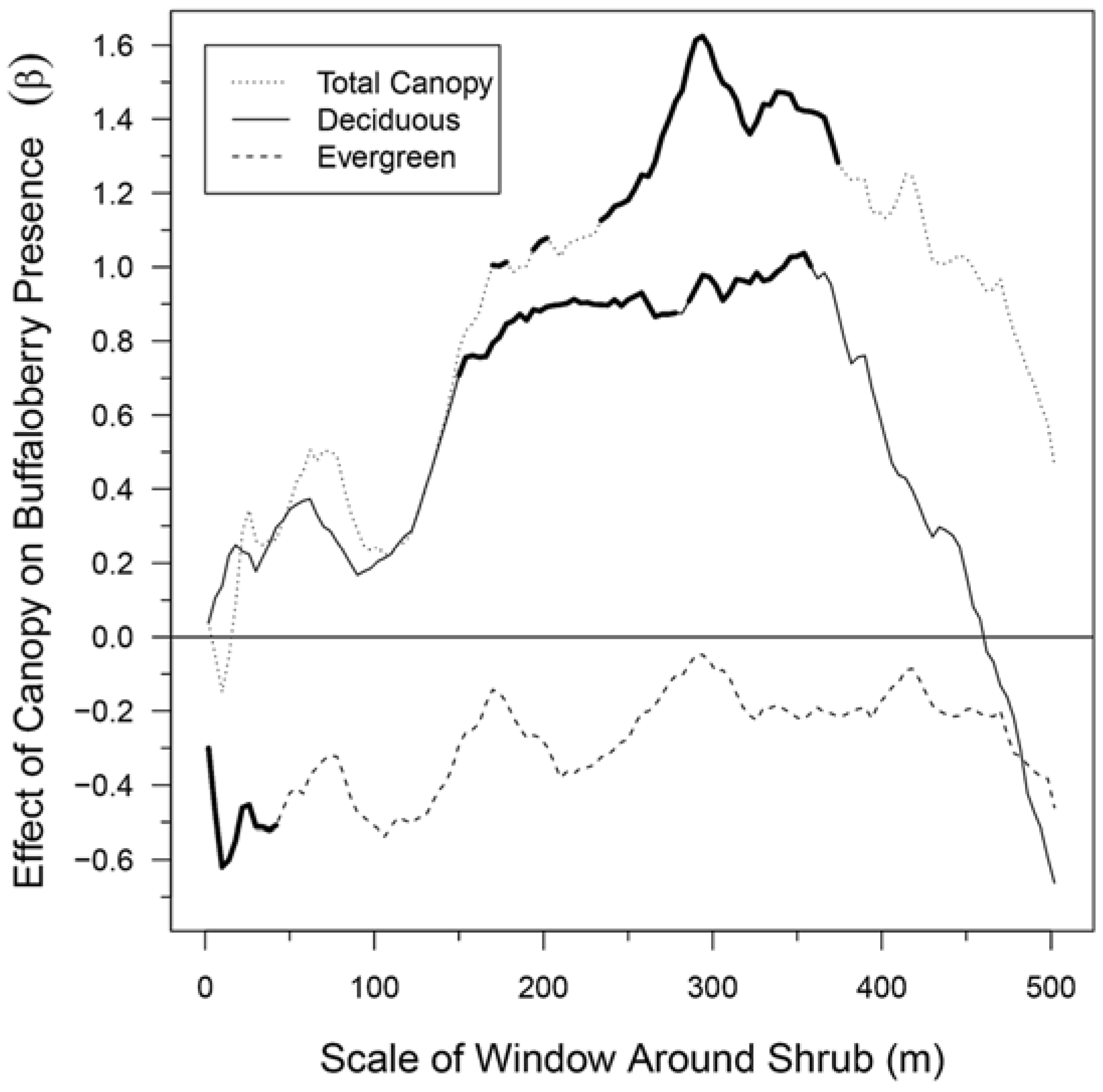
2.5. Effects of Canopy on Buffaloberry Presence across Spatial Scales
2.6. Spatial Heterogeneity of the Forest Canopy and Buffaloberry
3. Results
3.1. Patch Size Frequency Distribution
3.2. Effects of Canopy on Buffaloberry Presence across Spatial Scales
3.3. Spatial Heterogeneity of the Forest Canopy and Buffaloberry
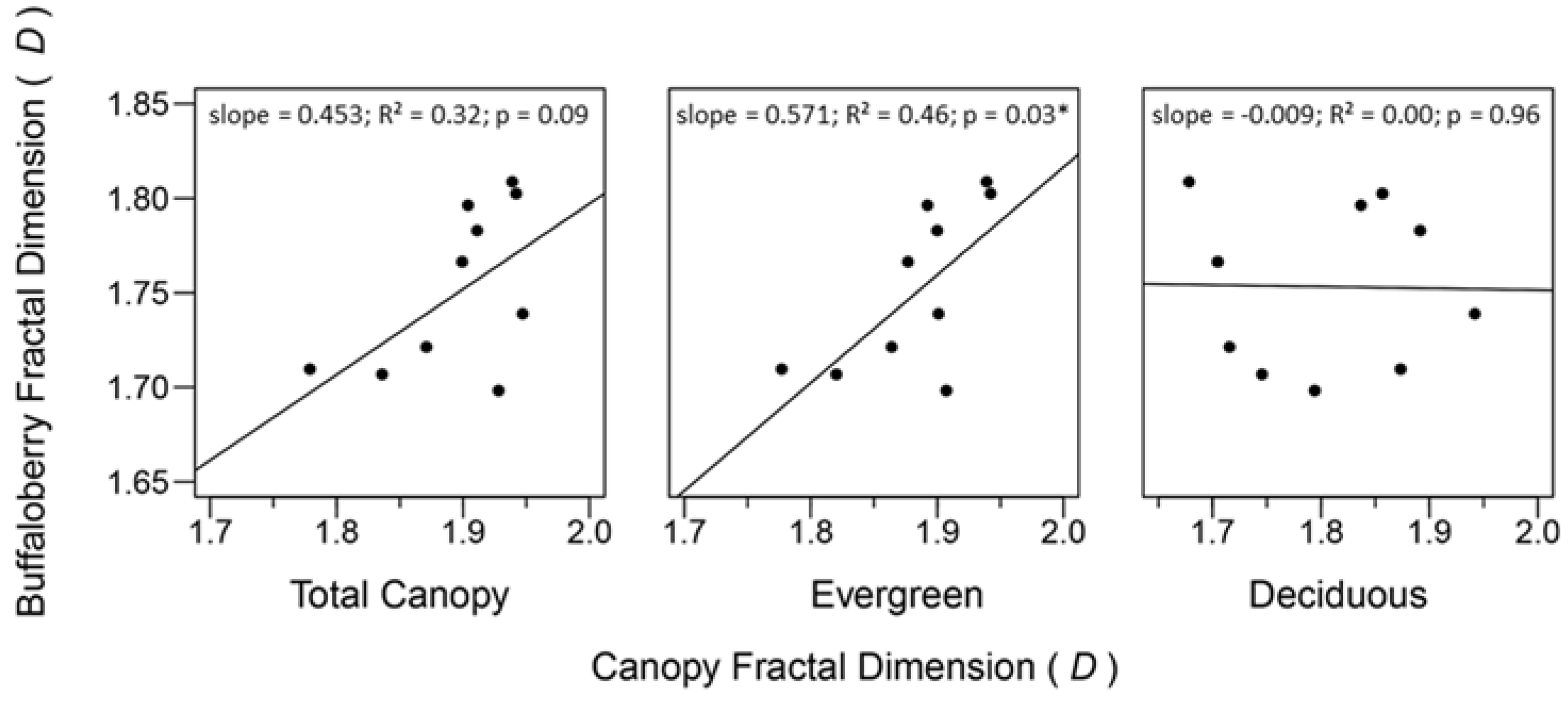
3.4. Relationships between Spatial Heterogeneity of the Forest Canopy and Buffaloberry
4. Discussion
4.1. Effects of Canopy on Buffaloberry Presence across Spatial Scales
4.2. Relationships between Spatial Heterogeneity of the Forest Canopy and Buffaloberry
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Urban, D.L.; O’Neill, R.V.; Shugart, H.H. Landscape ecology. Bioscience 1987, 37, 119–127. [Google Scholar] [CrossRef]
- Kolasa, J.; Rollo, C.D. Introduction: The heterogeneity of heterogeneity: A glossary. In Ecological Heterogeneity; Kolasa, J., Pickett, S.T.A., Eds.; Springer: New York, NY, USA, 1991; pp. 1–23. [Google Scholar]
- Li, H.; Reynolds, J.F. On definition and quantification of heterogeneity. Oikos 1995, 73, 280–284. [Google Scholar] [CrossRef]
- Wiens, J.A. Spatial scaling in ecology. Funct. Ecol. 1989, 3, 385–397. [Google Scholar] [CrossRef]
- Levin, S.A. The problem of pattern and scale in ecology. Ecology 1992, 73, 1943–1967. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman and Company: New York, NY, USA, 1982. [Google Scholar]
- Allen, T.F.H.; Hoekstra, T.W. Toward a Unified Ecology; Columbia University Press: New York, NY, USA, 1992. [Google Scholar]
- Kotliar, N.B.; Wiens, J.A. Multiple scales of patchiness and patch structure: A hierarchical framework for the study of heterogeneity. Oikos 1990, 59, 253–260. [Google Scholar] [CrossRef]
- Watt, A.S. Pattern and process in the plant community. J. Ecol. 1947, 35, 1–22. [Google Scholar] [CrossRef]
- Whittaker, R.H. The design and stability of plant communities. In Unifying Concepts in Ecology; van Dobben, W.H., Lowe-McConnell, R.H., Eds.; Dr. W. Junk B.V. Publishers: The Hague, The Netherlands, 1975; pp. 169–183. [Google Scholar]
- Levin, S.A. Pattern formation in ecological communities. In Spatial Pattern in Plankton Communities; Steele, J.H., Ed.; Plenum Press: New York, NY, USA, 1978; pp. 433–465. [Google Scholar]
- Sousa, W.P. The role of disturbance in natural communities. Annu. Rev. Ecol. Syst. 1984, 15, 353–391. [Google Scholar] [CrossRef]
- Franklin, J.F.; Forman, R.T.T. Creating landscape patterns by forest cutting: Ecological consequences and principles. Landsc. Ecol. 1987, 1, 5–18. [Google Scholar] [CrossRef]
- Kéfi, S.; Rietkerk, M.; Alados, C.L.; Pueyo, Y.; Papanastasis, V.P.; Elaich, A.; de Ruiter, P.C. Spatial vegetation patterns and imminent desertification in Mediterranean arid ecosystems. Nature 2007, 449, 213–217. [Google Scholar] [CrossRef] [PubMed]
- Jennings, S.B.; Brown, N.D.; Sheil, D. Assessing forest canopies and understorey illumination: Canopy closure, canopy cover and other measures. Forestry 1999, 72, 59–74. [Google Scholar] [CrossRef]
- Beatty, S.W. Influence of microtopography and canopy species on spatial patterns of forest understory plants. Ecology 1984, 65, 1406–1419. [Google Scholar] [CrossRef]
- Boettcher, S.E.; Kalisz, P.J. Single-tree influence on soil properties in the mountains of eastern Kentucky. Ecology 1990, 71, 1365–1372. [Google Scholar] [CrossRef]
- Russell, E.W. Soil Conditions and Plant. Growth, 9th ed.; Longmans: London, UK, 1961. [Google Scholar]
- Smith, H. Light quality, photoperception, and plant strategy. Annu. Rev. Plant Physiol. 1982, 33, 481–518. [Google Scholar] [CrossRef]
- Bartels, S.F.; Chen, H.Y.H. Is understory plant species diversity driven by resource quantity or resource heterogeneity? Ecology 2010, 91, 1931–1938. [Google Scholar] [CrossRef] [PubMed]
- Macdonald, S.E.; Fenniak, T.E. Understory plant communities of boreal mixedwood forests in western Canada: Natural patterns and response to variable-retention harvesting. For. Ecol. Manag. 2007, 242, 34–48. [Google Scholar] [CrossRef]
- Pelletier, B.; Fyles, J.W.; Dutilleul, P. Tree species control and spatial structure of forest floor properties in a mixed-species stand. Ecoscience 1999, 6, 79–91. [Google Scholar]
- Kembel, S.W.; Dale, M.R.T. Within-stand spatial structure and relation of boreal canopy and understorey vegetation. J. Veg. Sci. 2006, 17, 783–790. [Google Scholar] [CrossRef]
- Lieffers, V.J.; Stadt, K.J. Growth of understory Picea. glauca, Calamagrostis. canadensis, and Epilobium. angustifolium in relation to overstory light transmission. Can. J. For. Res. 1994, 24, 1193–1198. [Google Scholar] [CrossRef]
- Constabel, A.J.; Lieffers, V.J. Seasonal patterns of light transmission through boreal mixedwood canopies. Can. J. For. Res. 1996, 26, 1008–1014. [Google Scholar] [CrossRef]
- Canham, C.D.; Finzi, A.C.; Pacala, S.W.; Burbank, D.H. Causes and consequences of resource heterogeneity in forests: Interspecific variation in light transmission by canopy trees. Can. J. For. Res. 1994, 24, 337–349. [Google Scholar] [CrossRef]
- Chen, H.Y.H.; Klinka, K.; Kayahara, G.J. Effects of light on growth, crown architecture, and specific leaf area for naturally established Pinus. contorta var. latifolia and Pseudotsuga. menziesii var. glauca saplings. Can. J. For. Res. 1996, 26, 1149–1157. [Google Scholar]
- Messier, C.; Parent, S.; Bergeron, Y. Characterization of understory light environment in closed mixed boreal forests: Effects of overstory and understory vegetation. J. Veg. Sci. 1998, 9, 511–520. [Google Scholar] [CrossRef]
- Lieffers, V.J.; Pinno, B.D.; Stadt, K.J. Light dynamics and free-to-grow standards in aspen-dominated mixedwood forests. For. Chron. 2002, 78, 137–145. [Google Scholar] [CrossRef]
- Lieffers, V.J.; Messier, C.; Stadt, K.J.; Gendron, F.; Comeau, P.G. Predicting and managing light in the understory of boreal forests. Can. J. For. Res. 1999, 29, 796–811. [Google Scholar] [CrossRef]
- Palmer, M.W. Fractal geometry: A tool for describing spatial patterns of plant communities. Vegetatio 1988, 75, 91–102. [Google Scholar] [CrossRef]
- Spies, T.A.; Franklin, J.F. Gap characteristics and vegetation response in coniferous forests of the Pacific Northwest. Ecology 1989, 70, 543–545. [Google Scholar] [CrossRef]
- Klinka, K.; Chen, H.Y.H.; Wang, Q.; de Montigny, L. Forest canopies and their influence on understory vegetation in early-seral stands on West Vancouver Island. Northwest Sci. 1996, 70, 193–200. [Google Scholar]
- Berger, A.L.; Puettmann, K.J. Overstory composition and stand structure influence herbaceous plant diversity in the mixed aspen forest of northern Minnesota. Am. Midl. Nat. 2000, 143, 111–125. [Google Scholar] [CrossRef]
- Svenning, J.-C.; Skov, F. Mesoscale distribution of understorey plants in temperate forest (Kalø, Denmark): The importance of environment and dispersal. Plant Ecol. 2002, 160, 169–185. [Google Scholar] [CrossRef]
- Tewksbury, J.J.; Lloyd, J.D. Positive interactions under nurse-plants: Spatial scale, stress gradients and benefactor size. Oecologia 2001, 127, 425–434. [Google Scholar] [CrossRef]
- Allen, T.F.H.; Starr, T.B. Hierarchy: Perspectives for Ecological Complexity; University of Chicago Press: Chicago, IL, USA, 1982. [Google Scholar]
- Li, B.-L. Fractal geometry applications in description and analysis of patch patterns and patch dynamics. Ecol. Model. 2000, 132, 33–50. [Google Scholar] [CrossRef]
- Brosofske, K.D.; Chen, J.; Crow, T.R.; Saunders, S.C. Vegetation responses to landscape structure at multiple scales across a Northern Wisconsin, USA, pine barrens landscape. Plant Ecol. 1999, 143, 203–218. [Google Scholar] [CrossRef]
- Burrough, P.A. Fractal dimensions of landscapes and other environmental data. Nature 1981, 294, 240–242. [Google Scholar] [CrossRef]
- Frontier, S. Applications of fractal theory to ecology. In Developments in Numerical Ecology; Legendre, P., Legendre, L., Eds.; Springer: Berlin/Heidelberg, Germany, 1987; pp. 335–378. [Google Scholar]
- Milne, B.T. Spatial aggregation and neutral models in fractal landscapes. Am. Nat. 1992, 139, 32–57. [Google Scholar] [CrossRef]
- Milne, B.T. Applications of fractal geometry in wildlife biology. In Wildlife and Landscape Ecology: Effects of Pattern and Scale; Bissonette, J.A., Ed.; Springer: New York, NY, USA, 1997; pp. 32–69. [Google Scholar]
- Brown, J.H.; Gupta, V.K.; Li, B.-L.; Milne, B.T.; Restrepo, C.; West, G.B. The fractal nature of nature: Power laws, ecological complexity and biodiversity. Philos. Trans. R. Soc. B 2002, 357, 619–626. [Google Scholar] [CrossRef] [PubMed]
- Barnsley, M.F. Fractals Everywhere; Academic Press: San Diego, CA, USA, 1988. [Google Scholar]
- Milne, B.T. Lessons from applying fractal models to landscape patterns. In Quantitative Methods in Landscape Ecology; Turner, M.G., Gardner, R.H., Eds.; Springer: New York, NY, USA, 1991; pp. 199–235. [Google Scholar]
- Voss, R.F. Characterization and measurement of random fractals. Phys. Scr. 1986, T13, 27–32. [Google Scholar] [CrossRef]
- Ritchie, M.E.; Wolfe, M.L.; Danvir, R. Predation of artificial sage grouse nests in treated and untreated sagebrush. Gr. Basin Nat. 1994, 54, 122–129. [Google Scholar]
- Ritchie, M.E. Scale, Heterogeneity, and the Structure and Diversity of Ecological Communities; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Olff, H.; Ritchie, M.E. Fragmented nature: Consequences for biodiversity. Landsc. Urban Plan. 2002, 58, 83–92. [Google Scholar] [CrossRef]
- Kenkel, N.C.; Walker, D.J. Fractals in the biological sciences. Coenoses 1996, 11, 77–100. [Google Scholar]
- Krummel, J.R.; Gardner, R.H.; Sugihara, G.; O’Neill, R.V.; Coleman, P.R. Landscape patterns in a disturbed environment. Oikos 1987, 48, 321–324. [Google Scholar] [CrossRef]
- Rex, K.D.; Malanson, G.P. The fractal shape of riparian forest patches. Landsc. Ecol. 1990, 4, 249–258. [Google Scholar] [CrossRef]
- Mladenoff, D.J.; White, M.A.; Pastor, J.; Crow, T.R. Comparing spatial pattern in unaltered old-growth and disturbed forest landscapes. Ecol. Appl. 1993, 3, 294–306. [Google Scholar] [CrossRef] [PubMed]
- Drake, J.B.; Weishampel, J.F. Multifractal analysis of canopy height measures in a longleaf pine savanna. For. Ecol. Manag. 2000, 128, 121–127. [Google Scholar] [CrossRef]
- Parker, G.G.; Russ, M.E. The canopy surface and stand development: Assessing forest canopy structure and complexity with near-surface altimetry. For. Ecol. Manag. 2004, 189, 307–315. [Google Scholar] [CrossRef]
- Morse, D.R.; Lawton, J.H.; Dodson, M.M.; Williamson, M.H. Fractal distribution of vegetation and the distribution of arthropod body lengths. Nature 1985, 314, 731–733. [Google Scholar] [CrossRef]
- Gunnarsson, B. Fractal dimension of plants and body size distribution in spiders. Funct. Ecol. 1992, 6, 636–641. [Google Scholar] [CrossRef]
- Escós, J.; Alados, C.L.; Emlen, J.M. The impact of grazing on plant fractal architecture and fitness of a Mediterranean shrub Anthyllis. cytisoides L. Funct. Ecol. 1997, 11, 66–78. [Google Scholar] [CrossRef]
- Alados, C.L.; Emlen, J.M.; Wachocki, B.; Freeman, D.C. Instability of development and fractal architecture in dryland plants as an index of grazing pressure. J. Arid Environ. 1998, 38, 63–76. [Google Scholar] [CrossRef]
- Humbert, L.; Gagnon, D.; Kneeshaw, D.; Messier, C. A shade tolerance index for common understory species of northeastern North America. Ecol. Indic. 2007, 7, 195–207. [Google Scholar] [CrossRef]
- Stringer, P.W.; La Roi, G.H. The Douglas-fir forests of Banff and Jasper National Parks, Canada. Can. J. Bot. 1970, 48, 1703–1726. [Google Scholar] [CrossRef]
- La Roi, G.H.; Hnatiuk, R.J. The Pinus. contorta forests of Banff and Jasper National Parks: A study in comparative synecology and syntaxonomy. Ecol. Monogr. 1980, 50, 1–29. [Google Scholar] [CrossRef]
- Moss, E.H. Flora of Alberta, 2nd ed.; University of Toronto Press: Toronto, ON, Canada, 1983. [Google Scholar]
- Johnson, K.; Nielsen, S.E. Demographic effects on fruit set in the dioecious shrub Canada buffaloberry (Shepherdia. canadensis). PeerJ 2014, 2, e526. [Google Scholar] [CrossRef] [PubMed]
- Hamer, D. Buffaloberry (Shepherdia. canadensis (L.) Nutt.) fruit production in fire-successional bear feeding sites. J. Range Manag. 1996, 49, 520–529. [Google Scholar] [CrossRef]
- Nielsen, S.E.; Munro, R.H.M.; Bainbridge, E.L.; Stenhouse, G.B.; Boyce, M.S. Grizzly bears and forestry II. distribution of grizzly bear foods in clearcuts of west-central Alberta, Canada. For. Ecol. Manag. 2004, 199, 67–82. [Google Scholar] [CrossRef]
- Achuff, P.L. Natural Regions, Subregions and Natural History Themes of Alberta: A Classification for Protected Areas Management; Alberta Environmental Protection: Edmonton, AB, Canada, 1994. [Google Scholar]
- Udell, R.; Murphy, P.J.; Renaud, D. A 50-Year History of Silviculture on the Hinton Forest 1955–2005: Adaptive Management in Practice; Foothills Research Institute: Hinton, AB, Canada, 2013. [Google Scholar]
- Coops, N.C.; Tompaski, P.; Nijland, W.; Rickbeil, G.J.M.; Nielsen, S.E.; Bater, C.W.; Stadt, J.J. A forest structure habitat index based on airborne laser scanning data. Ecol. Indic. 2016, 67, 346–357. [Google Scholar] [CrossRef]
- ESRI. ArcGIS Desktop: ArcMap Version 10.2.1; Environmental Systems Research Institute: Redlands, CA, USA, 2014. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing, 3.1.2; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Huang, S.; Titus, S.J.; Wiens, D.D. Comparison of nonlinear height-diameter functions for major Alberta tree species. Can. J. For. Res. 1992, 22, 1297–1304. [Google Scholar] [CrossRef]
- Clark, D.B.; Palmer, M.W.; Clark, D.A. Edaphic factors and the landscape-scale distributions of tropical rain forest trees. Ecology 1998, 80, 2662–2675. [Google Scholar] [CrossRef]
- Bates, D.; Mächler, M.; Bolker, B.M.; Walker, S.C. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model. Selection and Inference, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Leduc, A.; Prairie, Y.T.; Bergeron, Y. Fractal dimension estimates of a fragmented landscape: Sources of variability. Landsc. Ecol. 1994, 9, 279–286. [Google Scholar] [CrossRef]
- Taylor, C.C.; Taylor, S.J. Estimating the dimension of a fractal. J. R. Stat. Soc. Ser. B Stat. Methodol. 1991, 53, 353–364. [Google Scholar]
- Halley, J.M.; Hartley, S.; Kallimanis, A.S.; Kunin, W.E.; Lennon, J.J.; Sgardelis, S.P. Uses and abuses of fractal methodology in ecology. Ecol. Lett. 2004, 7, 254–271. [Google Scholar] [CrossRef]
- Kenkel, N.C. Sample size requirements for fractal dimension estimation. Community Ecol. 2013, 14, 144–152. [Google Scholar] [CrossRef]
- Frelich, L.E.; Machado, J.-L.; Reich, P.B. Fine-scale environmental variation and structure of understorey plant communities in two old-growth pine forests. J. Ecol. 2003, 91, 283–293. [Google Scholar] [CrossRef]
- Reich, P.B.; Frelich, L.E.; Voldseth, R.A.; Bakken, P.; Adair, E.C. Understorey diversity in southern boreal forests is regulated by productivity and its indirect impacts on resource availability and heterogeneity. J. Ecol. 2012, 100, 539–545. [Google Scholar] [CrossRef]
- Nielsen, S.E.; Larsen, T.A.; Stenhouse, G.B.; Coogan, S.C.P. Complementary food resources of carnivory and frugivory affect local abundance of an omnivorous carnivore. Oikos 2017, 126, 369–380. [Google Scholar] [CrossRef]
- Nihlgård, B. Pedological influence of spruce planted on former beech forest soils in Scania, south Sweden. Oikos 1971, 22, 302–314. [Google Scholar] [CrossRef]
- Binkley, D.; Valentine, D. Fifty-year biogeochemical effects of green ash, white pine, and Norway spruce in a replicated experiment. For. Ecol. Manag. 1991, 40, 13–25. [Google Scholar] [CrossRef]
- Ste-Marie, C.; Paré, D. Soil, pH and N availability effects on net nitrification in the forest floors of a range of boreal forest stands. Soil Biol. Biochem. 1999, 31, 1579–1589. [Google Scholar] [CrossRef]
- Hobbie, S.E.; Reich, P.B.; Oleksyn, J.; Ogdahl, M.; Zytkowiak, R.; Hale, C.; Karolewski, P. Tree species effects on decomposition and forest floor dynamics in a common garden. Ecology 2006, 87, 2288–2297. [Google Scholar] [CrossRef]
- Ross, M.S.; Flanagan, L.B.; La Roi, G.H. Seasonal and successional changes in light quality and quantity in the understory of boreal forest ecosystems. Can. J. Bot. 1986, 64, 2792–2799. [Google Scholar] [CrossRef]
- Densmore, R.V.; Vander Meer, M.E.; Dunkle, N.G. Native Plant Revegetation Manual for Denali National Park and Preserve; Information and Technology Report USGS/BRD/ITR-2000-0006; US Geological Survey: Anchorage, AK, USA, 2000.
- Chen, J.; Franklin, J.F.; Spies, T.A. Contrasting microclimates among clearcut, edge, and interior of old-growth Douglas-fir forest. Agric. For. Meteorol. 1993, 63, 219–237. [Google Scholar] [CrossRef]
- Pennock, D.J.; van Kessel, C. Clear-cut forest harvest impacts on soil quality indicators in the mixedwood forest of Saskatchewan, Canada. Geoderma 1997, 75, 13–32. [Google Scholar] [CrossRef]
- Dutilleul, P.; Legendre, P. Spatial heterogeneity against heteroscedasticity: An ecological paradigm versus a statistical concept. Oikos 1993, 66, 152–171. [Google Scholar] [CrossRef]
- Li, H.; Reynolds, J.F. A simulation experiment to quantify spatial heterogeneity in categorical maps. Ecology 1994, 75, 2446–2455. [Google Scholar] [CrossRef]
- Malinverno, A. Testing linear models of sea-floor topography. Pure Appl. Geophys. 1989, 131, 139–155. [Google Scholar] [CrossRef]
- Weishampel, J.F.; Blair, J.B.; Dubayah, R.; Clark, D.B.; Knox, R.G. Canopy topography of an old-growth tropical rain forest landscape. Selbyana 2000, 21, 79–87. [Google Scholar]
- Boutet, J.C.; Weishampel, J.F. Spatial pattern analysis of pre- and post-hurricane forest canopy structure in North Carolina, USA. Landsc. Ecol. 2003, 18, 553–559. [Google Scholar] [CrossRef]
- Wiegand, T.; Moloney, K.A. Handbook of Spatial Point-Pattern Analysis in Ecology; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Moeur, M. Characterizing spatial patterns of trees using stem-mapped data. For. Sci. 1993, 39, 756–775. [Google Scholar]
- He, F.; Legendre, P.; LaFrankie, J.V. Distribution patterns of tree species in a Malaysian tropical rain forest. J. Veg. Sci. 1997, 8, 105–114. [Google Scholar]
- Daubechies, I. Othornormal bases of compactly supported wavelets. Commun. Pure Appl. Math. 1988, 41, 909–996. [Google Scholar] [CrossRef]
- Bradshaw, G.A.; Spies, T.A. Characterizing canopy gap structure in forests using wavelet analysis. J. Ecol. 1992, 80, 205–215. [Google Scholar] [CrossRef]
- Kane, V.R.; Gersonde, R.F.; Lutz, J.A.; McGaughey, R.J.; Bakker, J.D.; Franklin, J.F. Patch dynamics and the development of structural and spatial heterogeneity in Pacific Northwest forests. Can. J. For. Res. 2011, 41, 2276–2291. [Google Scholar] [CrossRef]
- Falkowski, M.J.; Smith, A.M.S.; Hudak, A.T.; Gessler, P.E.; Vierling, L.A.; Crookston, N.L. Automated estimation of individual conifer tree height and crown diameter via two-dimensional spatial wavelet analysis of lidar data. Can. J. Remote Sens. 2006, 32, 153–161. [Google Scholar] [CrossRef]
- Strand, E.K.; Smith, A.M.S.; Bunting, S.C.; Vierling, L.A.; Hann, D.B.; Gessler, P.E. Wavelet estimation of plant spatial patterns in multitemporal aerial photography. Int. J. Remote Sens. 2006, 27, 2049–2054. [Google Scholar] [CrossRef]
- McLellan, B.N.; Hovey, F.W. The diet of grizzly bears in the Flathead River drainage of southeastern British Columbia. Can. J. Zool. 1995, 73, 704–712. [Google Scholar] [CrossRef]
- Munro, R.H.M.; Nielsen, S.E.; Price, M.H.; Stenhouse, G.B.; Boyce, M.S. Seasonal and diel patterns of grizzly bear diet and activity in west-central Alberta. J. Mammal. 2006, 87, 1112–1121. [Google Scholar] [CrossRef]
- Wiens, J.A.; Milne, B.T. Scaling of “landscapes” in landscape ecology, or, landscape ecology from a beetle’s perspective. Landsc. Ecol. 1989, 3, 87–96. [Google Scholar] [CrossRef]
- Ritchie, M.E. Scale-dependent foraging and patch choice in fractal environments. Evol. Ecol. 1998, 12, 309–330. [Google Scholar] [CrossRef]
- Ritchie, M.E.; Olff, H. Spatial scaling laws yield a synthetic theory of biodiversity. Nature 1999, 400, 557–560. [Google Scholar] [CrossRef] [PubMed]
- Haskell, J.P.; Ritchie, M.E.; Olff, H. Fractal geometry predicts varying body size scaling relationships for mammal and bird home ranges. Nature 2002, 418, 527–530. [Google Scholar] [CrossRef] [PubMed]
- Sims, D.W.; Southall, E.J.; Humphries, N.E.; Hays, G.C.; Bradshaw, C.J.A.; Pitchford, J.W.; James, A.; Ahmed, M.Z.; Brierley, A.S.; Hindell, M.A.; et al. Scaling laws of marine predator search behaviour. Nature 2008, 451, 1098–1102. [Google Scholar] [CrossRef] [PubMed]
- Levins, R. Evolution in Changing Environments: Some Theoretical Explorations; Princeton University Press: Princeton, NJ, USA, 1968. [Google Scholar]
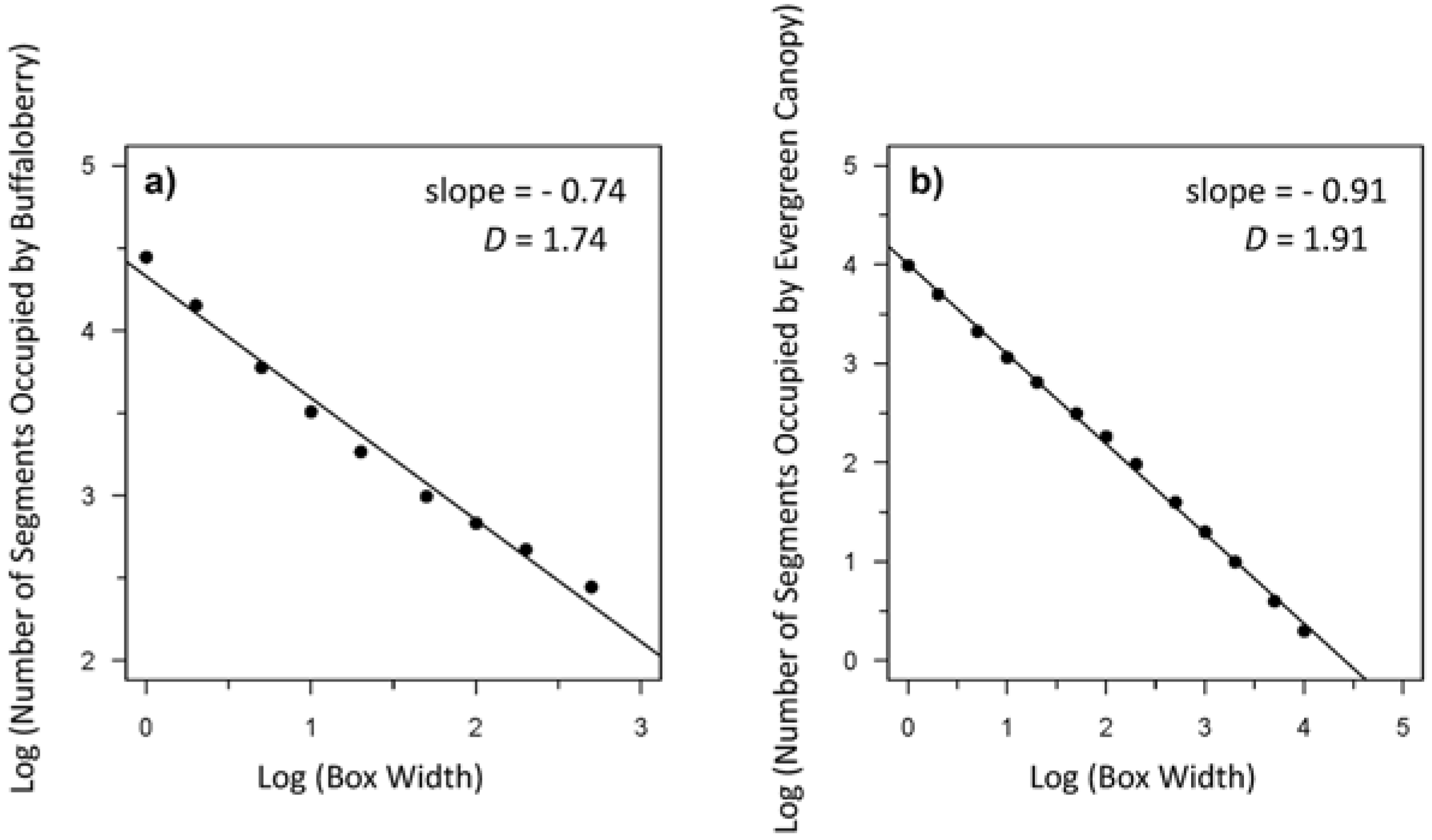
| Intercept Type | Range of Segment or “Box“ Widths (m) | Total Number of Scales |
|---|---|---|
| Buffaloberry | 0.01, 0.02, 0.05, 0.1, 0.2, 0.5, 1, 2, 5 | 9 |
| Total Canopy | 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100, 200, 500, 1000 | 13 |
| Evergreen Canopy | 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100, 200, 500, 1000 | 13 |
| Deciduous Canopy | 0.1, 0.2, 0.5 | 3 |
| Transect | Total | Evergreen | Deciduous | Buffaloberry |
|---|---|---|---|---|
| Number | Canopy (%) | Canopy (%) | Canopy (%) | Shrubs (%) |
| 1 | 69.0 | 49.4 | 32.5 | 14.0 |
| 2 | 26.8 | 24.2 | 3.4 | 0.1 |
| 3 | 35.8 | 34.1 | 2.7 | 0.5 |
| 4 | 57.7 | 49.0 | 13.7 | 0.9 |
| 5 | 46.0 | 41.8 | 5.4 | 0.2 |
| 6 | 43.4 | 37.2 | 9.0 | 0.2 |
| 7 | 51.0 | 46.7 | 8.3 | 2.0 |
| 8 | 59.4 | 59.4 | 0.0 | 0.4 |
| 9 | 62.3 | 62.2 | 0.1 | 1.3 |
| 10 | 18.5 | 18.1 | 0.6 | 0.3 |
| Mean | 47.0 | 42.2 | 7.6 | 2.0 |
| Transect Number | Total Canopy | Evergreen Canopy | Deciduous Canopy | Buffaloberry Shrubs |
|---|---|---|---|---|
| 1 | 1.95 | 1.91 | 1.95 | 1.74 |
| 2 | 1.84 | 1.83 | 1.75 | 1.71 |
| 3 | 1.88 | 1.87 | 1.72 | 1.72 |
| 4 | 1.94 | 1.91 | 1.80 | 1.70 |
| 5 | 1.91 | 1.90 | 1.84 | 1.80 |
| 6 | 1.91 | 1.88 | 1.71 | 1.77 |
| 7 | 1.92 | 1.91 | 1.90 | 1.78 |
| 8 | 1.95 | 1.95 | 1.69 | 1.81 |
| 9 | 1.95 | 1.95 | 1.86 | 1.80 |
| 10 | 1.79 | 1.78 | 1.88 | 1.71 |
| Mean | 1.90 | 1.89 | 1.81 | 1.75 |
| Minimum | 1.79 | 1.78 | 1.69 | 1.70 |
| Maximum | 1.95 | 1.95 | 1.95 | 1.81 |
| Standard Error | 0.02 | 0.02 | 0.03 | 0.01 |
| 95% Confidence Interval | 1.87, 1.94 | 1.86, 1.92 | 1.76, 1.87 | 1.73, 1.78 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Denny, C.K.; Nielsen, S.E. Spatial Heterogeneity of the Forest Canopy Scales with the Heterogeneity of an Understory Shrub Based on Fractal Analysis. Forests 2017, 8, 146. https://doi.org/10.3390/f8050146
Denny CK, Nielsen SE. Spatial Heterogeneity of the Forest Canopy Scales with the Heterogeneity of an Understory Shrub Based on Fractal Analysis. Forests. 2017; 8(5):146. https://doi.org/10.3390/f8050146
Chicago/Turabian StyleDenny, Catherine K., and Scott E. Nielsen. 2017. "Spatial Heterogeneity of the Forest Canopy Scales with the Heterogeneity of an Understory Shrub Based on Fractal Analysis" Forests 8, no. 5: 146. https://doi.org/10.3390/f8050146
APA StyleDenny, C. K., & Nielsen, S. E. (2017). Spatial Heterogeneity of the Forest Canopy Scales with the Heterogeneity of an Understory Shrub Based on Fractal Analysis. Forests, 8(5), 146. https://doi.org/10.3390/f8050146








