The Influence of Monsoon Climate on Latewood Growth of Southwestern Ponderosa Pine
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site and Trees
2.2. Core Collection and Processing
2.2.1. Latewood Ring Width
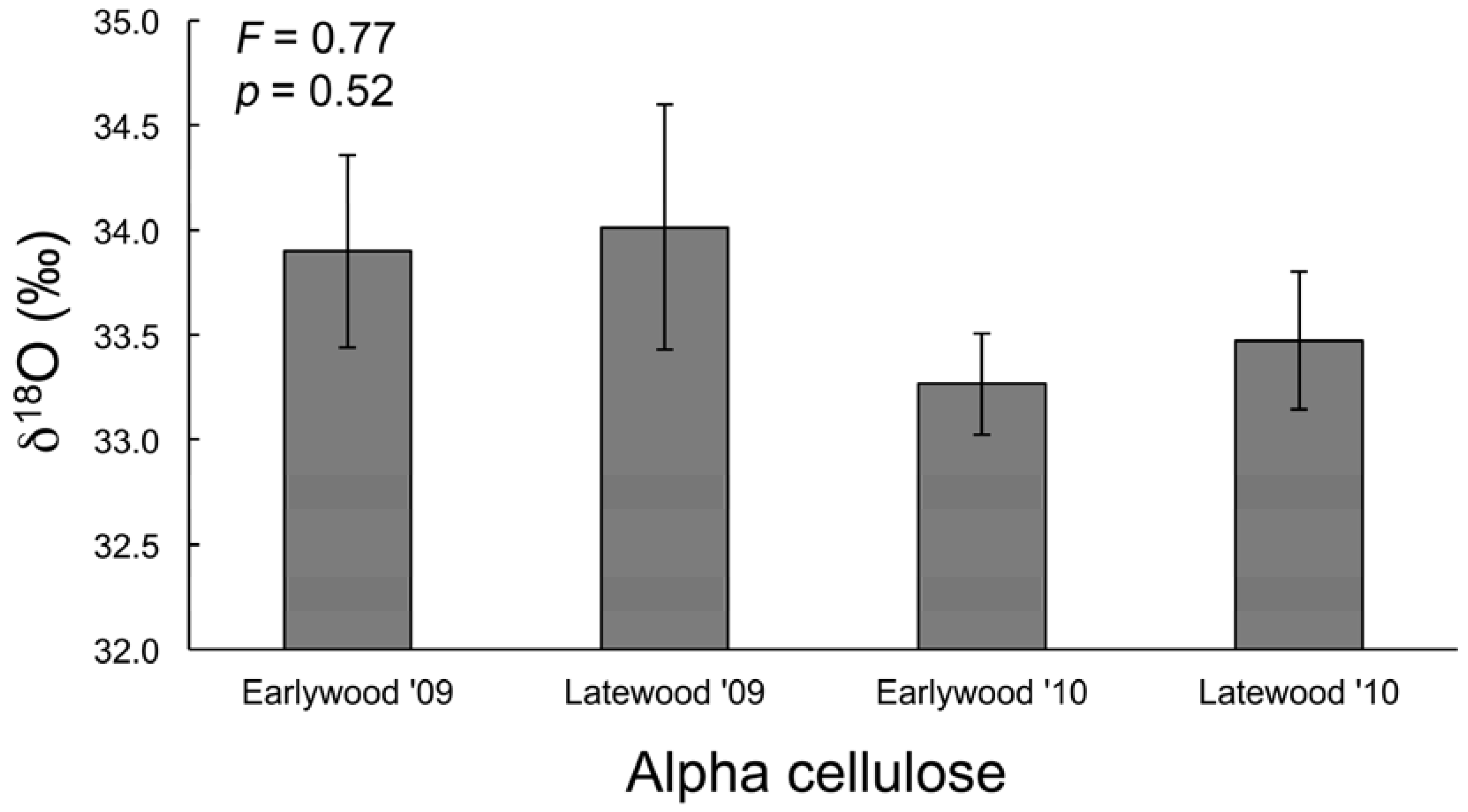
2.2.2. Alpha Cellulose δ18O
2.3. Isotopic Analyses
2.3.1. Precipitation Samples
2.3.2. Soil and Stem Water Samples
2.3.3. Water Sample Analyses
2.3.4. Alpha Cellulose δ18O Samples
2.3.5. Alpha Cellulose δ18O Analyses
2.4. Climate Data
2.5. Data Analysis
3. Results
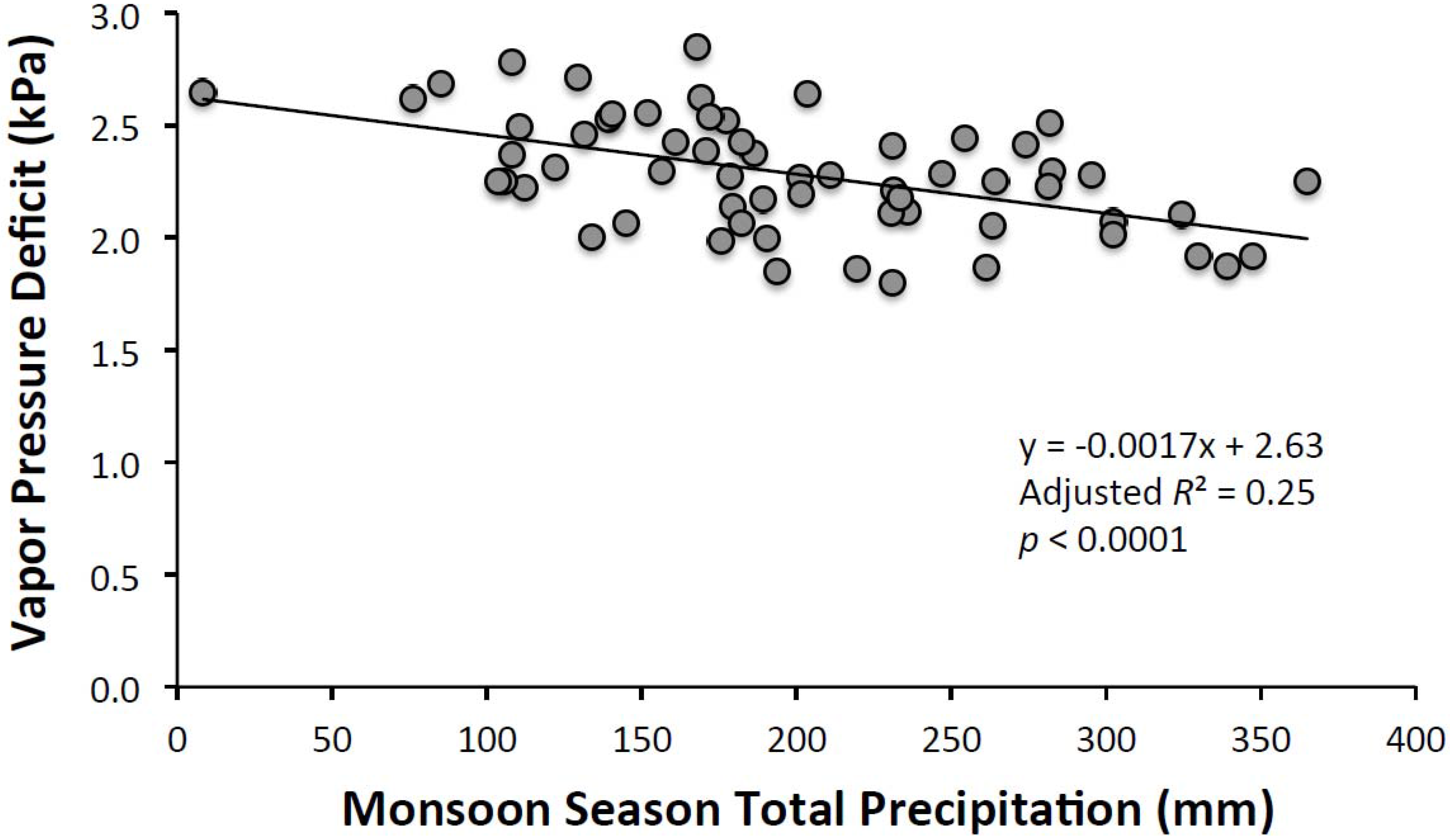
3.1. Climatic Analyses
3.2. Statistical Analyses
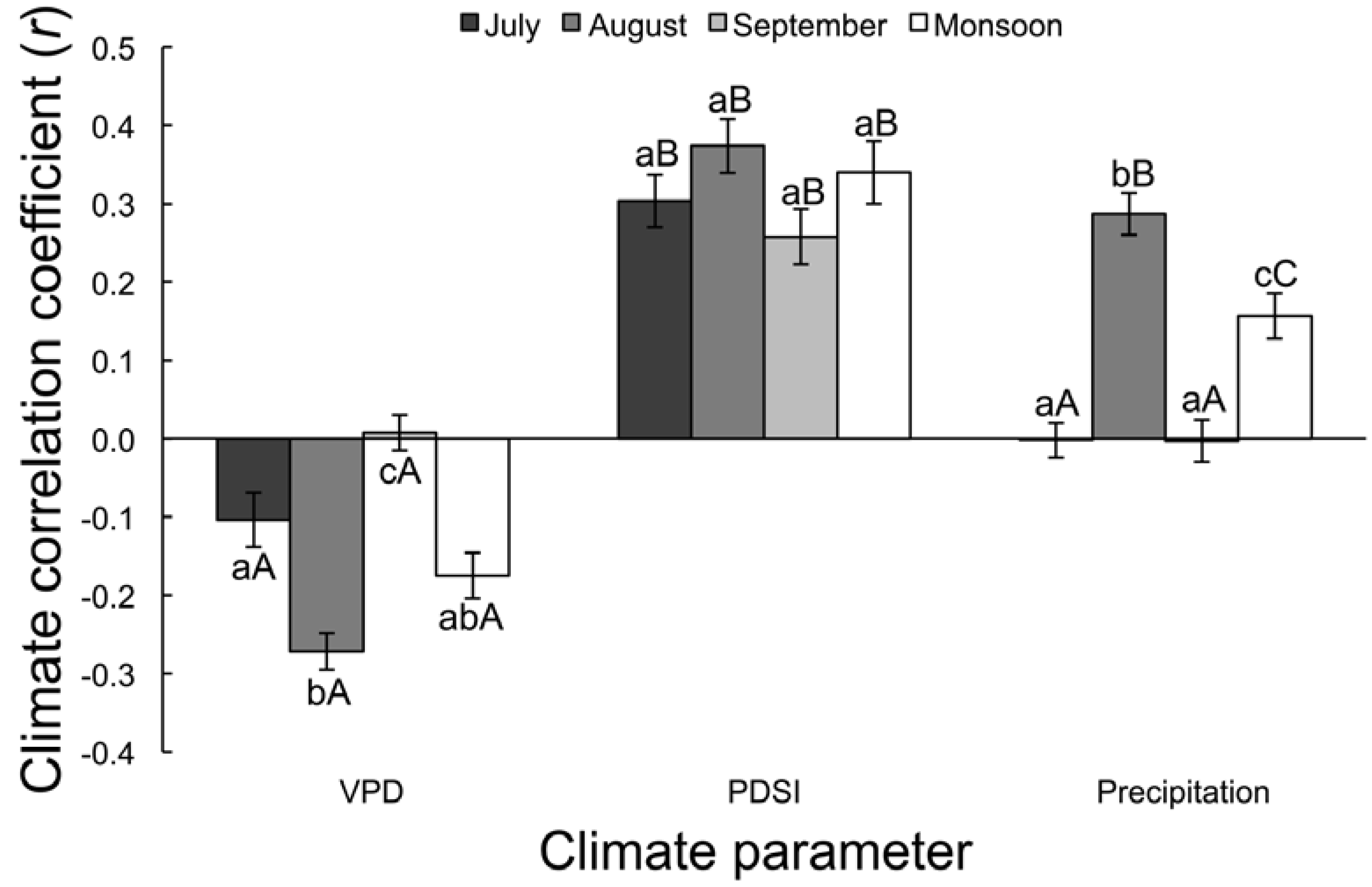
3.2.1. Correlation Analysis
3.2.2. Akaike’s Information Criterion
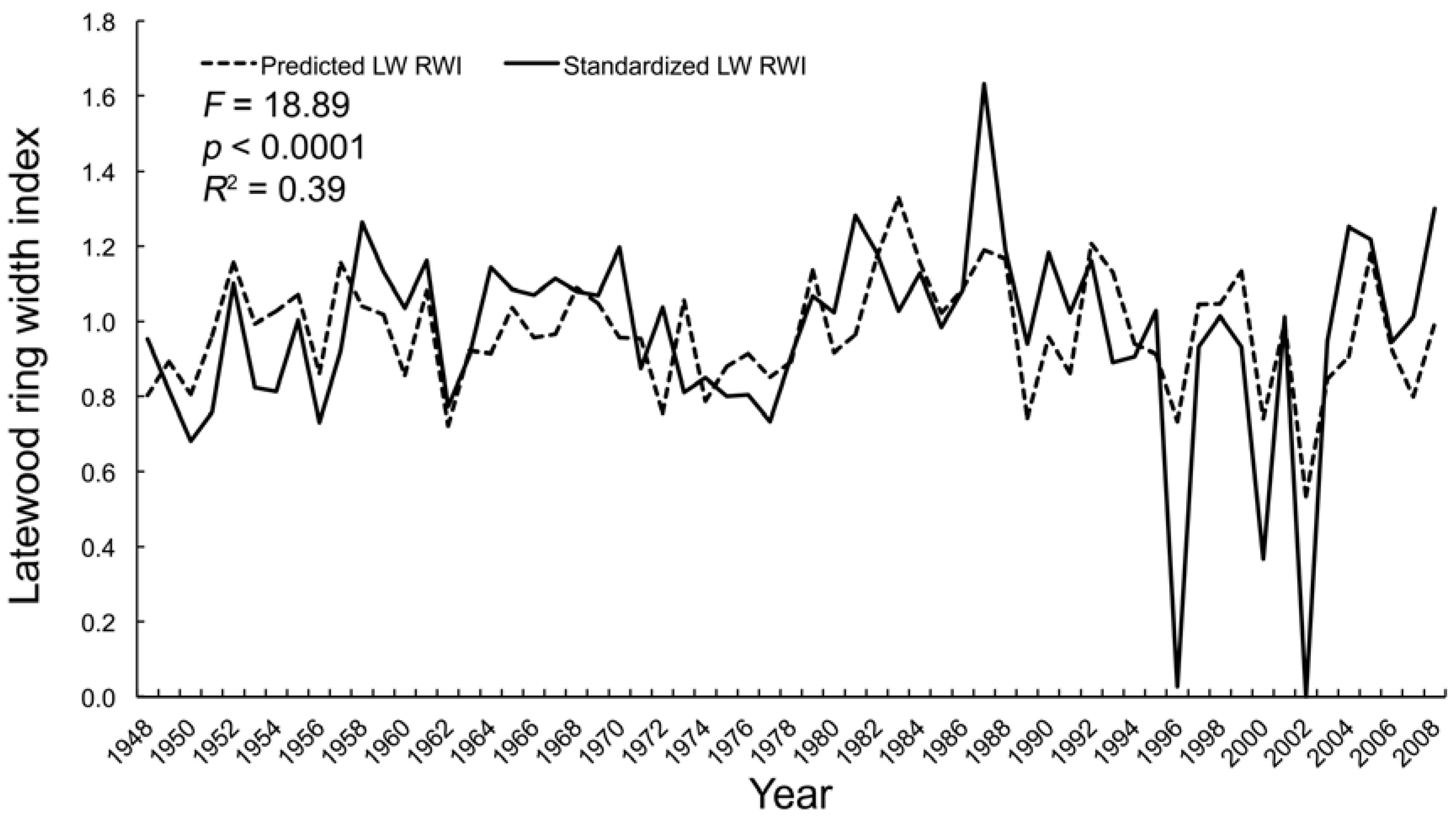
3.2.3. Multivariate Regression
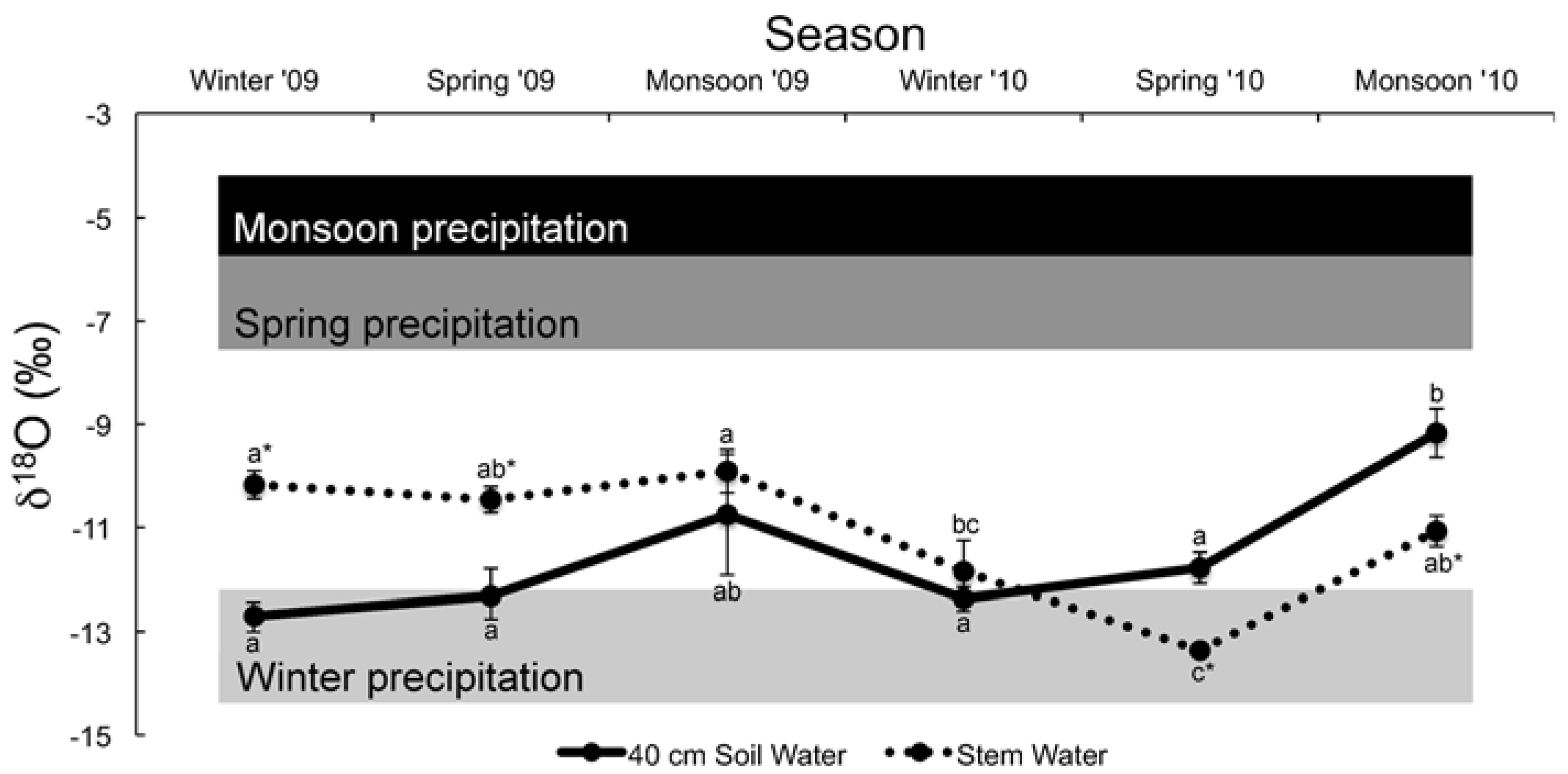
3.3. Water and Cellulose δ18O Analyses
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Van Mantgem, P.; Stephenson, N. Apparent climatically induced increase of tree mortality rates in a temperate forest. Ecol. Lett. 2007, 10, 909–916. [Google Scholar] [CrossRef] [PubMed]
- McDowell, N.; Pockman, W.; Allen, C.; Breshears, D.; Cobb, N.; Kolb, T.; Plaut, J.; Sperry, J.; West, A.; Williams, D. Mechanisms of plant survival and mortality during drought: Why do some plants survive while others succumb to drought? New Phytol. 2008, 178, 719–739. [Google Scholar] [CrossRef] [PubMed]
- Van Mantgem, P.J.; Stephenson, N.L.; Byrne, J.C.; Daniels, L.D.; Franklin, J.F.; Fule, P.Z.; Harmon, M.E.; Larson, A.J.; Smith, J.M.; Taylor, A.H.; et al. Widespread increase of tree mortality rates in the western United States. Science 2009, 323, 521–524. [Google Scholar] [CrossRef] [PubMed]
- Williams, A.P.; Allen, C.D.; Millar, C.I.; Swetnam, T.W.; Michaelsen, J.; Still, C.J.; Leavitt, S.W. Climate change and water in southwestern North America special feature: Forest responses to increasing aridity and warmth in the southwestern United States. Proc. Natl. Acad. Sci. USA 2010, 107, 21289–21294. [Google Scholar] [CrossRef] [PubMed]
- Williams, A.P.; Allen, C.D.; Macalady, A.K.; Griffin, D.; Woodhouse, C.A.; Meko, D.M.; Swetnam, T.W.; Rauscher, S.A.; Seager, R.; Grissino-Mayer, H.D.; et al. Temperature as a potent driver of regional forest drought stress and tree mortality. Nat. Clim. Chang. 2012, 2, 1–6. [Google Scholar] [CrossRef]
- Seager, R.; Vecchi, G.A. Greenhouse warming and the 21st century hydroclimate of southwestern North America. Proc. Natl. Acad. Sci. USA 2010, 107, 21277–21282. [Google Scholar] [CrossRef] [PubMed]
- Seager, R.; Ting, M.; Held, I.; Kushnir, Y.; Lu, J.; Vecchi, G.; Huang, H.; Harnik, N.; Leetmaa, A.; Lau, N. Model projections of an imminent transition to a more arid climate in southwestern North America. Science 2007, 316, 1181–1184. [Google Scholar] [CrossRef] [PubMed]
- Seager, R.; Ting, M.; Li, C.; Naik, N.; Cook, B.; Nakamura, J.; Liu, H. Projections of declining surface-water availability for the southwestern United States. Nat. Clim. Chang. 2012, 3, 482–486. [Google Scholar] [CrossRef]
- Cayan, D.R.; Das, T.; Pierce, D.W.; Barnett, T.P.; Tyree, M.; Gershunov, A. Future dryness in the southwest US and the hydrology of the early 21st century drought. Proc. Natl. Acad. Sci. USA 2010, 107, 21271–21276. [Google Scholar] [CrossRef] [PubMed]
- Swain, S.; Hayhoe, K. CMIP5 projected changes in spring and summer drought and wet conditions over North America. Clim. Dyn. 2014, 44, 2737–2750. [Google Scholar] [CrossRef]
- Knowles, N.; Dettinger, M.D.; Cayan, D.R. Trends in snowfall versus rainfall in the western United States. J. Clim. 2006, 19, 4545–4559. [Google Scholar] [CrossRef]
- Hamlet, A.; Mote, P.; Clark, M.; Lettenmaier, D. Effects of temperature and precipitation variability on snowpack trends in the western United States. J. Clim. 2005, 18, 4545–4561. [Google Scholar] [CrossRef]
- Mote, P.W.; Hamlet, A.F.; Clark, M.P.; Lettenmaier, D.P. Declining mountain snowpack in western North America. Bull. Am. Meteorol. Soc. 2005, 86, 39–49. [Google Scholar] [CrossRef]
- Mote, P.W. Climate-driven variability and trends in mountain snowpack in western North America. J. Clim. 2006, 19, 6209–6219. [Google Scholar] [CrossRef]
- Hu, J.; Moore, D.; Burns, S.; Monson, R. Longer growing seasons lead to less carbon sequestration by a subalpine forest. Glob. Chang. Biol. 2010, 16, 771–783. [Google Scholar] [CrossRef]
- Sheppard, P.R.; Comrie, A.C.; Packin, G.D.; Angersbach, K.; Hughes, M.K. The climate of the US Southwest. Clim. Res. 2002, 21, 219–238. [Google Scholar] [CrossRef]
- Schwinning, S.; Belnap, J.; Bowling, D.; Ehleringer, J. Sensitivity of the Colorado Plateau to change: Climate, ecosystems, and society. Ecol. Soc. 2008, 13, 28. [Google Scholar] [CrossRef]
- Houghton, J.T.; Ding, Y.; Griggs, D.J.; Noguer, M.; van der Linden, P.J.; Dai, X.; Maskell, K. IPCC, 2001: Climate Change 2001: The Scientific Basis; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2001; p. 881. [Google Scholar]
- Kim, J. Precipitation variability associated with the North American Monsoon in the 20th century. Geophys. Res. Lett. 2002, 29, 1650. [Google Scholar] [CrossRef]
- Cook, E.; Woodhouse, C.; Eakin, C.; Meko, D.; Stahle, D. Long-term aridity changes in the western United States. Science 2004, 306, 1015–1018. [Google Scholar] [CrossRef] [PubMed]
- Williams, D.; Ehleringer, J. Intra-and interspecific variation for summer precipitation use in pinyon-juniper woodlands. Ecol. Monogr. 2000, 70, 517–537. [Google Scholar]
- Ehleringer, J.; Dawson, T. Water uptake by plants: Perspectives from stable isotope composition. Plant Cell Environ. 1992, 15, 1073–1082. [Google Scholar] [CrossRef]
- Simpson, E.; Thorud, D.; Friedman, I. Distinguishing seasonal recharge to groundwater by deuterium analysis in southern Arizona. In World Water Balance; UNESCO: Paris, France, 1972; pp. 623–633. [Google Scholar]
- Kerhoulas, L.P.; Kolb, T.E.; Koch, G.W. Tree size, stand density, and the source of water used across seasons by ponderosa pine in northern Arizona. For. Ecol. Manag. 2013, 289, 425–433. [Google Scholar] [CrossRef]
- Dutton, A.; Wilkinson, B.H.; Welker, J.M.; Bowen, G.J.; Lohmann, K.C. Spatial distribution and seasonal variation in 18O/16O of modern precipitation and river water across the conterminous USA. Hydrol. Process. 2005, 19, 4121–4146. [Google Scholar] [CrossRef]
- Tang, K.; Feng, X. The effect of soil hydrology on the oxygen and hydrogen isotopic compositions of plants’ source water. Earth Planet. Sci. Lett. 2001, 185, 355–367. [Google Scholar] [CrossRef]
- Eggemeyer, K.D.; Awada, T.; Harvey, F.E.; Wedin, D.A.; Zhou, X.; Zanner, C.W. Seasonal changes in depth of water uptake for encroaching trees Juniperus virginiana and Pinus ponderosa and two dominant C4 grasses in a semiarid grassland. Tree Physiol. 2008, 29, 157–169. [Google Scholar] [CrossRef] [PubMed]
- Brunel, J.; Walker, G.; Kennett-Smith, A. Field validation of isotopic procedures for determining sources of water used by plants in a semi-arid environment. J. Hydrol. 1995, 167, 351–368. [Google Scholar] [CrossRef]
- Kolb, T.; Hart, S.; Amundson, R. Boxelder water sources and physiology at perennial and ephemeral stream sites in Arizona. Tree Physiol. 1997, 17, 151–160. [Google Scholar] [CrossRef] [PubMed]
- Dawson, T.; Ehleringer, J. Isotopic enrichment of water in the “woody” tissues of plants: Implications for plant water source, water uptake, and other studies which use the stable isotopic composition of cellulose. Geochim. Cosmochim. Acta 1993, 57, 3487–3492. [Google Scholar] [CrossRef]
- Roden, J.; Ehleringer, J. Hydrogen and oxygen isotope ratios of tree ring cellulose for field-grown riparian trees. Oecologia 2000, 123, 481–489. [Google Scholar] [CrossRef] [PubMed]
- McCarroll, D.; Loader, N. Stable isotopes in tree rings. Quat. Sci. Rev. 2004, 23, 771–801. [Google Scholar] [CrossRef]
- Roden, J.; Ehleringer, J. Summer precipitation influences the stable oxygen and carbon isotopic composition of tree-ring cellulose in Pinus ponderosa. Tree Physiol. 2007, 27, 491–501. [Google Scholar] [CrossRef] [PubMed]
- Roden, J.; Lin, G.; Ehleringer, J. A mechanistic model for interpretation of hydrogen and oxygen isotope ratios in tree-ring cellulose. Geochim. Cosmochim. Acta 2000, 64, 21–35. [Google Scholar] [CrossRef]
- Offermann, C.; Ferrio, J.P.; Holst, J.; Grote, R.; Siegwolf, R.; Kayler, Z.; Gessler, A. The long way down—Are carbon and oxygen isotope signals in the tree ring uncoupled from canopy physiological processes? Tree Physiol. 2011, 31, 1088–1102. [Google Scholar] [CrossRef] [PubMed]
- Meko, D.; Baisan, C. Pilot study of latewood-width of conifers as an indicator of variability of summer rainfall in the North American monsoon region. Int. J. Climatol. 2001, 21, 697–708. [Google Scholar] [CrossRef]
- Stahle, D.; Cleaveland, M.; Grissino-Mayer, H.; Griffin, R.; Fye, F.; Therrell, M.; Burnette, D.; Meko, D.; Villanueva Diaz, J. Cool-and warm-season precipitation reconstructions over western New Mexico. J. Clim. 2009, 22, 3729–3750. [Google Scholar] [CrossRef]
- Therrell, M.; Stahle, D.; Cleaveland, M.; Villanueva-Diaz, J. Warm season tree growth and precipitation over Mexico. J. Geophys. Res. 2002, 107, 4205. [Google Scholar] [CrossRef]
- Griffin, D.; Meko, D.M.; Touchan, R.; Leavitt, S.W.; Woodhouse, C.A. Latewood chronology development for summer-moisture reconstruction in the US Southwest. Tree-Ring Res. 2011, 67, 87–101. [Google Scholar] [CrossRef]
- Griffin, D.; Woodhouse, C.A.; Meko, D.M.; Stahle, D.W.; Faulstich, H.L.; Carrillo, C.; Touchan, R.; Castro, C.L.; Leavitt, S.W. North American monsoon precipitation reconstructed from tree-ring latewood. Geophys. Res. Lett. 2013, 40, 954–958. [Google Scholar] [CrossRef]
- Leavitt, S.; Wright, W.; Long, A. Spatial expression of ENSO, drought, and summer monsoon in seasonal δ13C of ponderosa pine tree rings in southern Arizona and New Mexico. J. Geophys. Res.-Atmos. 2002, 107, 4349. [Google Scholar] [CrossRef]
- Leavitt, S.W.; Woodhouse, C.A.; Castro, C.L.; Wright, W.E.; Meko, D.M.; Touchan, R.; Griffin, D.; Ciancarelli, B. The North American monsoon in the U.S. Southwest: Potential for investigation with tree-ring carbon isotopes. Quat. Int. 2011, 235, 101–107. [Google Scholar] [CrossRef]
- Kolb, T.; Dore, S.; Montes-Helu, M. Extreme late-summer drought causes neutral annual carbon balance in southwestern ponderosa pine forests and grasslands. Environ. Res. Lett. 2013, 8, 015015. [Google Scholar] [CrossRef]
- McDowell, N.; Beerling, D.J.; Breshears, D.D.; Fisher, R.A.; Raffa, K.F.; Stitt, M. The interdependence of mechanisms underlying climate-driven vegetation mortality. Trends Ecol. Evol. 2011, 26, 523–532. [Google Scholar] [CrossRef] [PubMed]
- Adams, H.D.; Guardiola-Claramonte, M.; Barron-Gafford, G.A.; Villegas, J.C.; Breshears, D.D.; Zou, C.B.; Troch, P.A.; Huxman, T.E. Temperature sensitivity of drought-induced tree mortality portends increased regional die-off under global-change-type drought. Proc. Natl. Acad. Sci. USA 2009, 106, 7063–7066. [Google Scholar] [CrossRef] [PubMed]
- Eamus, D.; Boulain, N.; Cleverly, J.; Breshears, D.D. Global change-type drought-induced tree mortality: Vapor pressure deficit is more important than temperature per se in causing decline in tree health. Ecol. Evol. 2013, 3, 2711–2729. [Google Scholar] [CrossRef] [PubMed]
- Mast, J.; Fule, P.; Moore, M.; Covington, W.; Waltz, A. Restoration of presettlement age structure of an Arizona ponderosa pine forest. Ecol. Appl. 1999, 9, 228–239. [Google Scholar] [CrossRef]
- Skov, K.; Kolb, T.; Wallin, K. Difference in radial growth response to restoration thinning and burning treatments between young and old ponderosa pine in Arizona. West. J. Appl. For. 2005, 20, 36–43. [Google Scholar]
- Jepson, J. The Tree Climber’s Companion; Beaver Tree Publishing: Longville, MN, USA, 2000. [Google Scholar]
- Kerhoulas, L.P.; Kane, J.M. Sensitivity of ring growth and carbon allocation to climatic variation vary within ponderosa pine trees. Tree Physiol. 2012, 32, 14–23. [Google Scholar] [CrossRef] [PubMed]
- Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree-Ring Bull. 1983, 43, 69–78. [Google Scholar]
- Cook, E.R.; Holmes, R.L. User’s manual for program ARSTAN. In Tree-Ring Chronologies of Western North America: California, Eastern Oregon and Northern Great Basin; Holmes, R.L., Adams, R.K., Fritts, H.C., Eds.; University of Arizona: Tucson, AZ, USA, 1986; pp. 50–56. [Google Scholar]
- Wigley, T.; Briffa, K.; Jones, P. On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J. Clim. Appl. Meteorol. 1984, 23, 201–213. [Google Scholar] [CrossRef]
- Bowen, G.J.; Wassenaar, L.I.; Hobson, K.A. Global application of stable hydrogen and oxygen isotopes to wildlife forensics. Oecologia 2005, 143, 337–348. [Google Scholar] [CrossRef] [PubMed]
- West, A.G.; Goldsmith, G.R.; Brooks, P.D.; Dawson, T.E. Discrepancies between isotope ratio infrared spectroscopy and isotope ratio mass spectrometry for the stable isotope analysis of plant and soil waters. Rapid Commun. Mass Spectrom. 2010, 24, 1948–1954. [Google Scholar] [CrossRef] [PubMed]
- Leavitt, S.; Danzer, S. Method for batch processing small wood samples to holocellulose for stable-carbon isotope analysis. Anal. Chem. 1993, 65, 87–89. [Google Scholar] [CrossRef]
- Sternberg, L.S.L.; DeNiro, M.J.; Savidge, R.A. Oxygen isotope exchange between metabolites and water during biochemical reactions leading to cellulose synthesis. Plant Physiol. 1986, 82, 423–427. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information—Theoretic Approach, 2nd ed.; Springer: New York, NY, USA, 2002; pp. 1–485. [Google Scholar]
- Kolb, T.; Stone, J. Differences in leaf gas exchange and water relations among species and tree sizes in an Arizona pine-oak forest. Tree Physiol. 2000, 20, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Oren, R.; Sperry, J.; Katul, G.; Pataki, D.; Ewers, B.; Phillips, N.; Schafer, K. Survey and synthesis of intra- and interspecific variation in stomatal sensitivity to vapour pressure deficit. Plant Cell Environ. 1999, 22, 1515–1526. [Google Scholar] [CrossRef]
- Szejner, P.; Wright, W.E.; Babst, F.; Belmecheri, S.; Trouet, V.; Leavitt, S.W.; Ehleringer, J.R.; Monson, R.K. Latitudinal gradients in tree-ring stable carbon and oxygen isotopes reveal differential climate influences of the North American Monsoon system. J. Geophys. Res. Biogeosci. 2016, 121, 1978–1991. [Google Scholar] [CrossRef]
- Schwinning, S.; Davis, K.; Richardson, L.; Ehleringer, J. Deuterium enriched irrigation indicates different forms of rain use in shrub/grass species of the Colorado Plateau. Oecologia 2002, 130, 345–355. [Google Scholar] [CrossRef]
- Cook, B.I.; Seager, R. The response of the North American Monsoon to increased greenhouse gas forcing. J. Geophys. Res.-Atmos. 2013, 118, 1690–1699. [Google Scholar] [CrossRef]
| Time | VPD | PDSI | Precipitation | F | p |
|---|---|---|---|---|---|
| July | −0.10 ± 0.03 aA | 0.30 ± 0.03 aB | 0.16 ± 0.03 aA | 47.12 | <0.0001 |
| August | −0.27 ± 0.02 bA | 0.37 ± 0.03 aB | 0.29 ± 0.03 bB | 149.59 | <0.0001 |
| September | 0.01 ± 0.02 cA | 0.26 ± 0.04 aB | 0.16 ± 0.03 aA | 26.00 | <0.0001 |
| Monsoon | −0.17 ± 0.03 abA | 0.34 ± 0.04 aB | 0.16 ± 0.03 cC | 67.98 | <0.0001 |
| F | 17.61 | 1.99 | 28.10 | - | - |
| p | <0.0001 | 0.12 | <0.0001 | - | - |
| Season | Model Parameters | AIC | ∆i | R2 |
|---|---|---|---|---|
| July | PDSI | 1.83 | 0.00 | 0.17 |
| VPD + PDSI | 3.28 | 1.44 | 0.18 | |
| PDSI + Precipitation | 3.78 | 1.95 | 0.17 | |
| VPD + PDSI + Precipitation | 5.23 | 3.39 | 0.18 | |
| VPD | 12.14 | 10.30 | 0.02 | |
| Precipitation | 13.12 | 11.28 | 0.00 | |
| VPD + Precipitation | 13.70 | 11.87 | 0.02 | |
| August | VPD + PDSI + Precipitation | −15.67 | 0.00 | 0.42 |
| VPD + PDSI | −15.36 | 0.31 | 0.39 | |
| PDSI + Precipitation | −12.68 | 2.99 | 0.37 | |
| PDSI | −5.77 | 9.90 | 0.27 | |
| VPD + Precipitation | 0.13 | 15.80 | 0.22 | |
| Precipitation | 1.29 | 16.96 | 0.17 | |
| VPD | 2.72 | 18.40 | 0.16 | |
| September | PDSI | 4.84 | 0.00 | 0.13 |
| VPD + PDSI | 6.29 | 1.45 | 0.14 | |
| PDSI + Precipitation | 6.80 | 1.96 | 0.13 | |
| VPD + PDSI + Precipitation | 7.75 | 2.91 | 0.14 | |
| VPD | 11.93 | 7.09 | 0.02 | |
| Precipitation | 12.56 | 7.72 | 0.01 | |
| VPD + Precipitation | 13.90 | 9.07 | 0.02 | |
| Monsoon | VPD + PDSI | −5.94 | 0.00 | 0.29 |
| VPD + PDSI + Precipitation | −5.47 | 0.47 | 0.31 | |
| PDSI + Precipitation | −4.72 | 1.22 | 0.28 | |
| PDSI | −1.21 | 4.73 | 0.21 | |
| VPD | 7.26 | 13.20 | 0.09 | |
| VPD + Precipitation | 7.49 | 13.43 | 0.12 | |
| Precipitation | 7.59 | 13.53 | 0.09 |
| Model | Time | Model Statistics | Parameters | t Ratio | p |
|---|---|---|---|---|---|
| Multivariate Regression Model Using VPD, PDSI, and Precipitation | July | F = 4.09 | VPD | −0.76 | 0.45 |
| p = 0.01 | PDSI | 3.26 | 0.002 | ||
| R2 = 0.18 | Precipitation | −0.22 | 0.82 | ||
| August | F = 13.55 | VPD | −2.23 | 0.01 | |
| p < 0.0001 | PDSI | 4.40 | <0.0001 | ||
| R2 = 0.42 | Precipitation | 1.46 | 0.15 | ||
| September | F = 3.17 | VPD | −1.02 | 0.31 | |
| p = 0.03 | PDSI | 2.86 | 0.01 | ||
| R2 = 0.14 | Precipitation | −0.73 | 0.47 | ||
| Monsoon | F = 8.52 | VPD | −1.64 | 0.11 | |
| p < 0.0001 | PDSI | 3.98 | 0.0002 | ||
| R2 = 0.31 | Precipitation | 1.19 | 0.24 | ||
| Model after Reverse Order Stepwise Regression | July | F = 11.91 | PDSI | 3.45 | 0.001 |
| p = 0.001 | - | - | - | ||
| R2 = 0.17 | - | - | - | ||
| AIC = 1.83 | - | - | - | ||
| ∆i = 17.19 | - | - | - | ||
| August | F = 18.89 | VPD | −3.50 | 0.001 | |
| p < 0.0001 | PDSI | 4.76 | <0.0001 | ||
| R2 = 0.39 | - | - | - | ||
| AIC = −15.36 | - | - | - | ||
| ∆i = 0.00 | - | - | - | ||
| September | F = 8.58 | PDSI | 2.93 | 0.005 | |
| p = 0.005 | - | - | - | ||
| R2 = 0.13 | - | - | - | ||
| AIC = 4.84 | - | - | - | ||
| ∆i = 20.20 | - | - | - | ||
| Monsoon | F = 11.99 | VPD | −2.62 | 0.01 | |
| p < 0.0001 | PDSI | 4.05 | 0.0002 | ||
| R2 = 0.29 | - | - | - | ||
| AIC = −5.94 | - | - | - | ||
| ∆i = 9.42 | - | - | - |
| Season | Precipitation | 40 cm Soil Water | Stem Water | F | p |
|---|---|---|---|---|---|
| Winter (2009) | −13.29 ± 1.03 aA | −12.70 ± 0.22 aAB | −10.17 ± 0.27 aB | 4.69 | 0.02 |
| Spring (2010) | −6.86 ± 1.23 bA | −12.32 ± 0.53 aB | −10.46 ± 0.25 abB | 11.59 | 0.0002 |
| Monsoon (2010) | −4.90 ± 0.94 bA | −10.75 ± 1.17 abB | −9.91 ± 0.42 aB | 12.33 | <0.0001 |
| Winter (2010) | −13.29 ± 1.03 aA | −12.37 ± 0.23 aA | −11.85 ± 0.60 bcA | 0.54 | 0.59 |
| Spring (2010) | −6.86 ± 1.23 bA | −11.78 ± 0.30 aB | −13.36 ± 0.29 cB | 18.84 | <0.0001 |
| Monsoon (2010) | −4.90 ± 0.94 bA | −9.17 ± 0.47 bB | −11.07 ± 0.30 abB | 17.08 | <0.0001 |
| F | 15.99 | 5.18 | 11.89 | - | - |
| p | <0.0001 | 0.001 | <0.0001 | - | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kerhoulas, L.P.; Kolb, T.E.; Koch, G.W. The Influence of Monsoon Climate on Latewood Growth of Southwestern Ponderosa Pine. Forests 2017, 8, 140. https://doi.org/10.3390/f8050140
Kerhoulas LP, Kolb TE, Koch GW. The Influence of Monsoon Climate on Latewood Growth of Southwestern Ponderosa Pine. Forests. 2017; 8(5):140. https://doi.org/10.3390/f8050140
Chicago/Turabian StyleKerhoulas, Lucy P., Thomas E. Kolb, and George W. Koch. 2017. "The Influence of Monsoon Climate on Latewood Growth of Southwestern Ponderosa Pine" Forests 8, no. 5: 140. https://doi.org/10.3390/f8050140
APA StyleKerhoulas, L. P., Kolb, T. E., & Koch, G. W. (2017). The Influence of Monsoon Climate on Latewood Growth of Southwestern Ponderosa Pine. Forests, 8(5), 140. https://doi.org/10.3390/f8050140






