Using Linear Mixed-Effects Models with Quantile Regression to Simulate the Crown Profile of Planted Pinus sylvestris var. Mongolica Trees
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data Collection
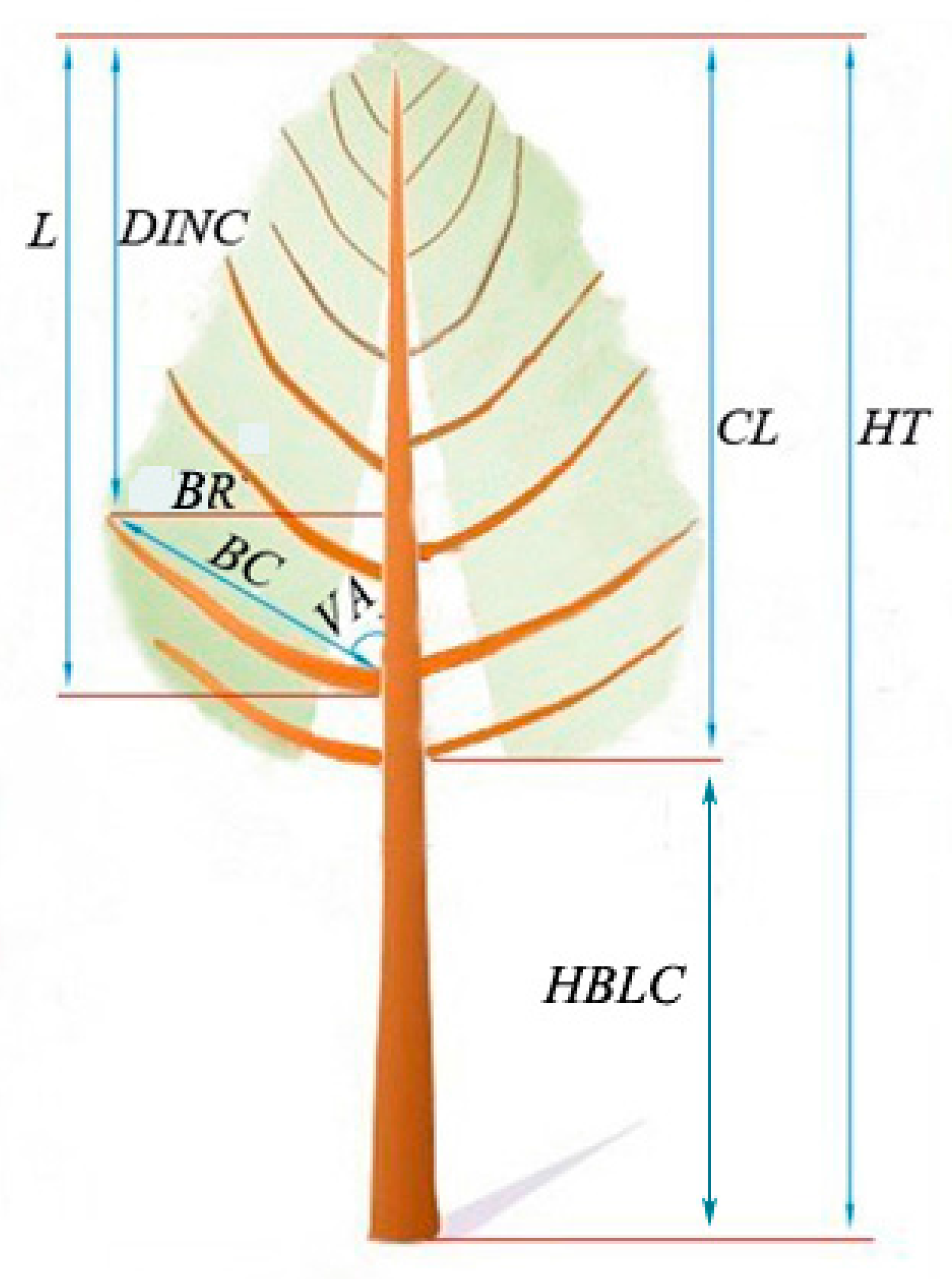
2.2. Data Collection and Analysis
2.3. Model Selection for the Crown Profile
2.4. Quantile Regression for the Mixed-Effects Outer Crown Profile Model
3. Results
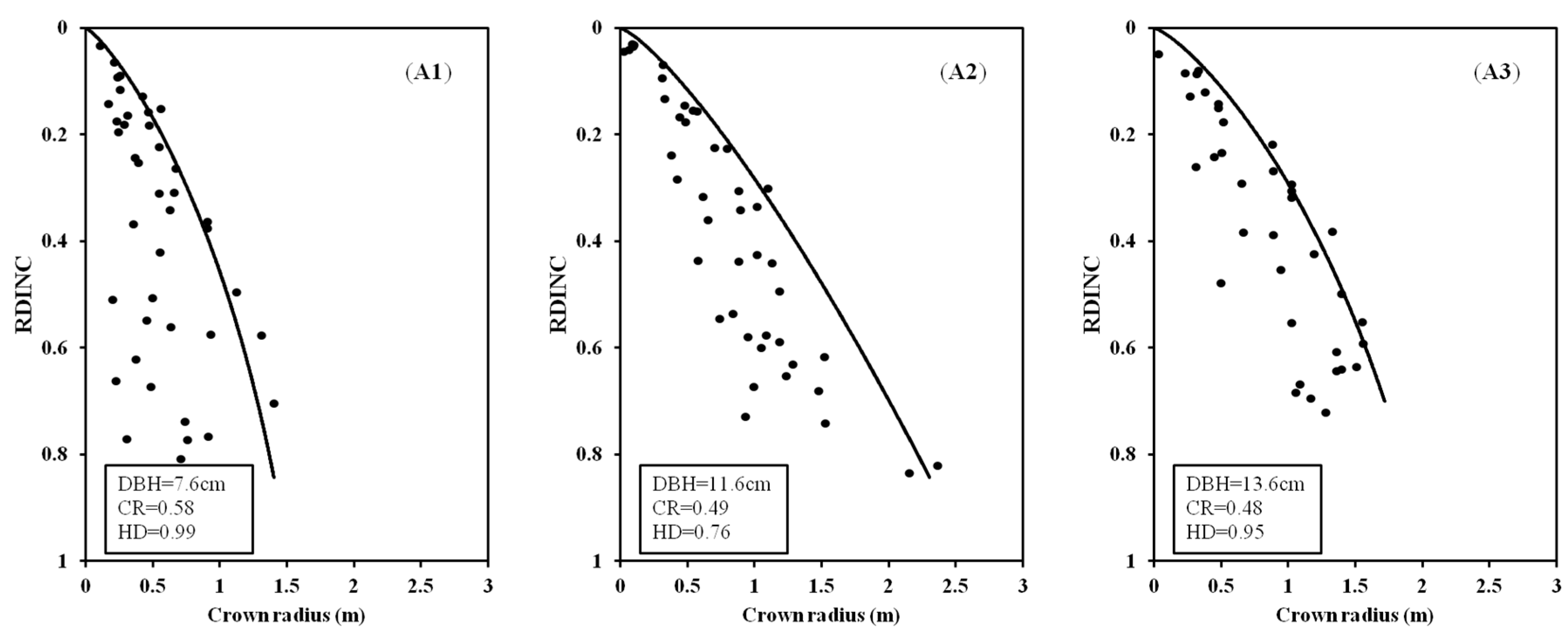
3.1. Best Model Selection for the Crown Profile Model
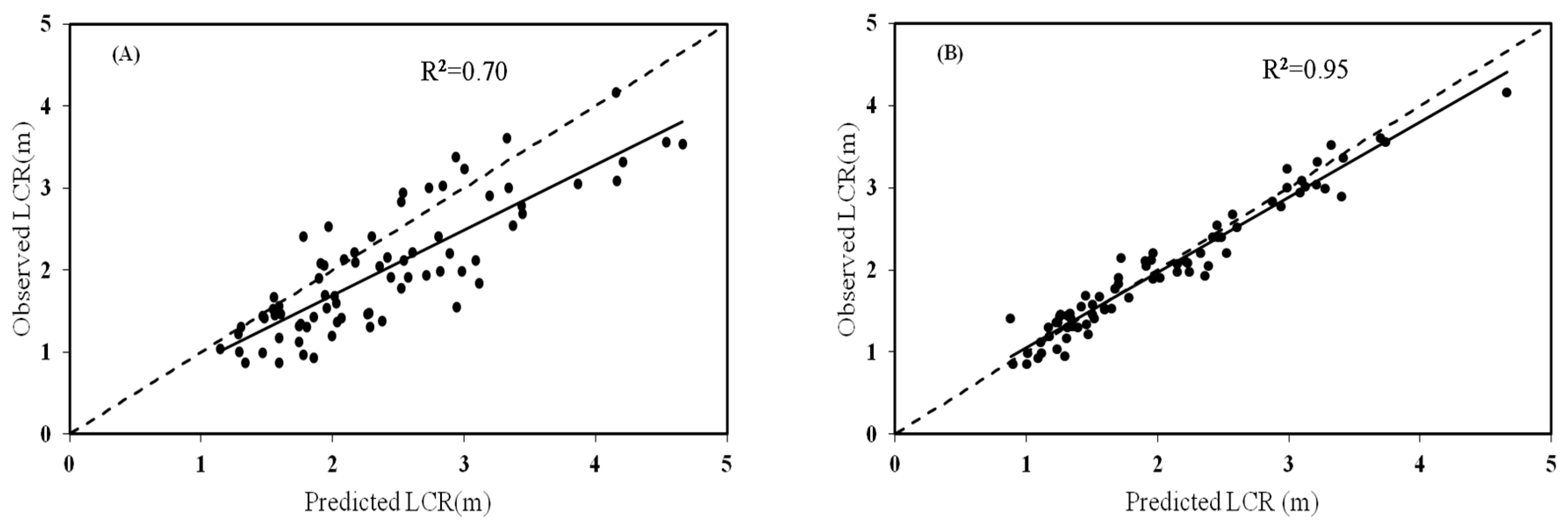
3.2. Quantile Regression for the Linear Mixed-Effects Crown Profile Model
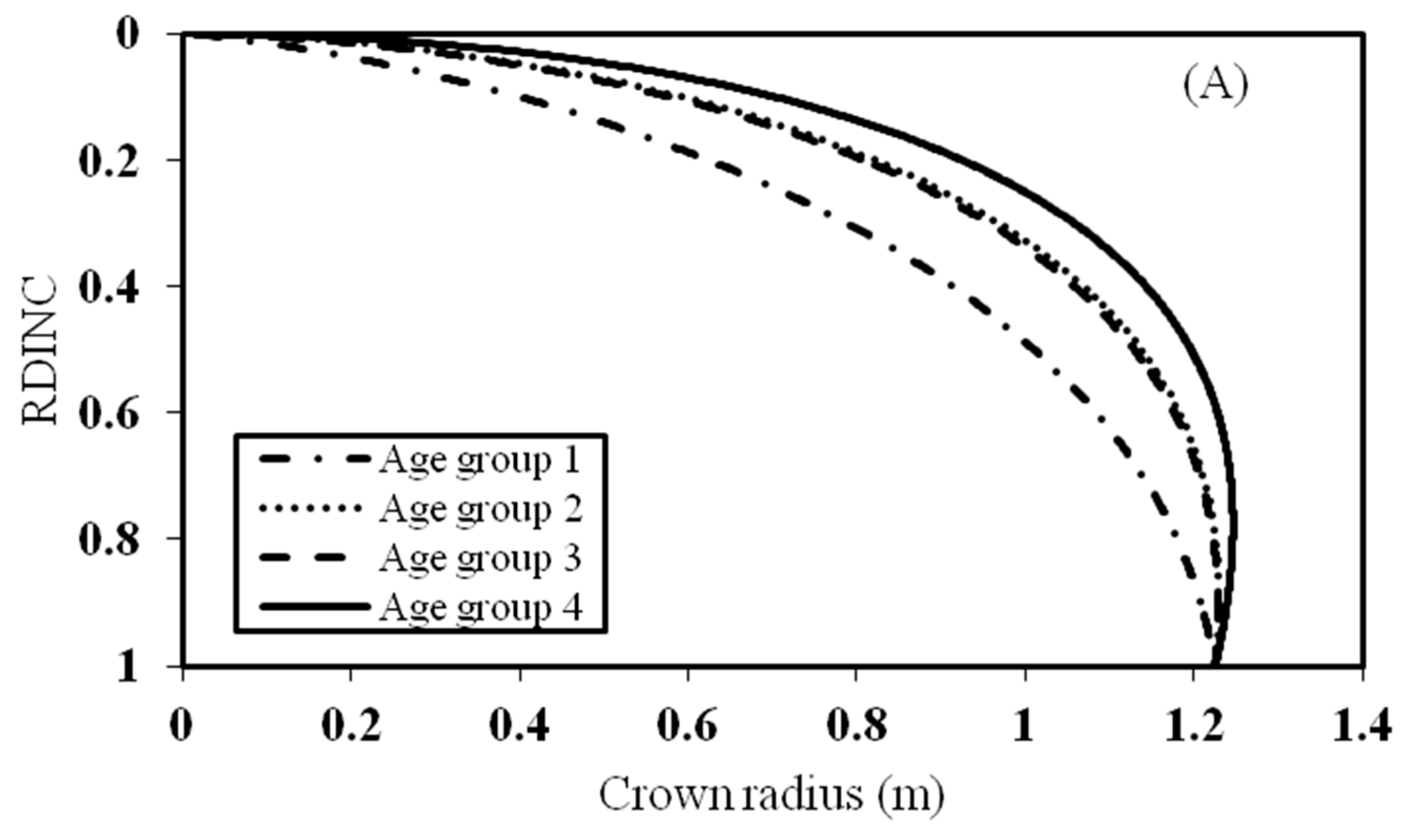
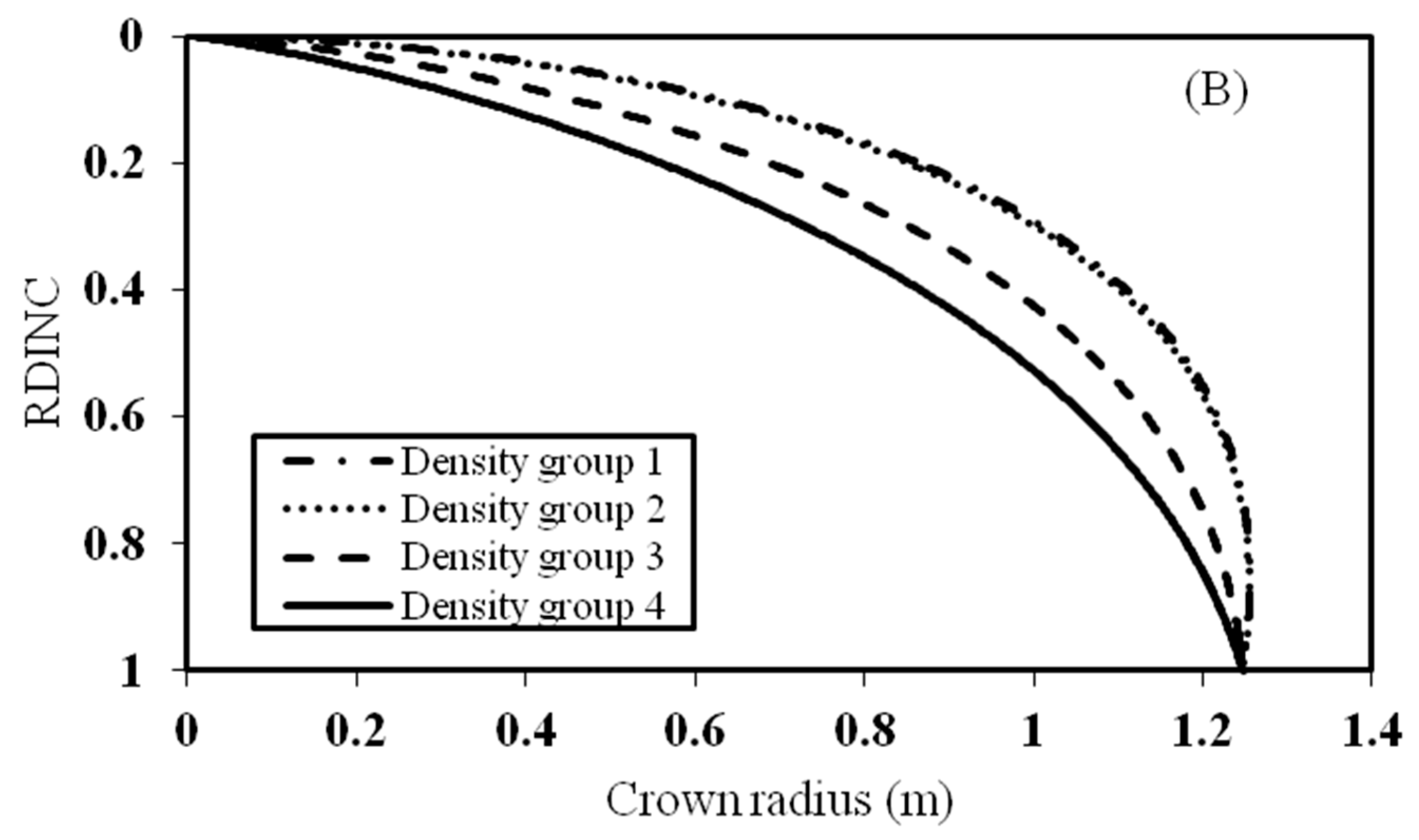
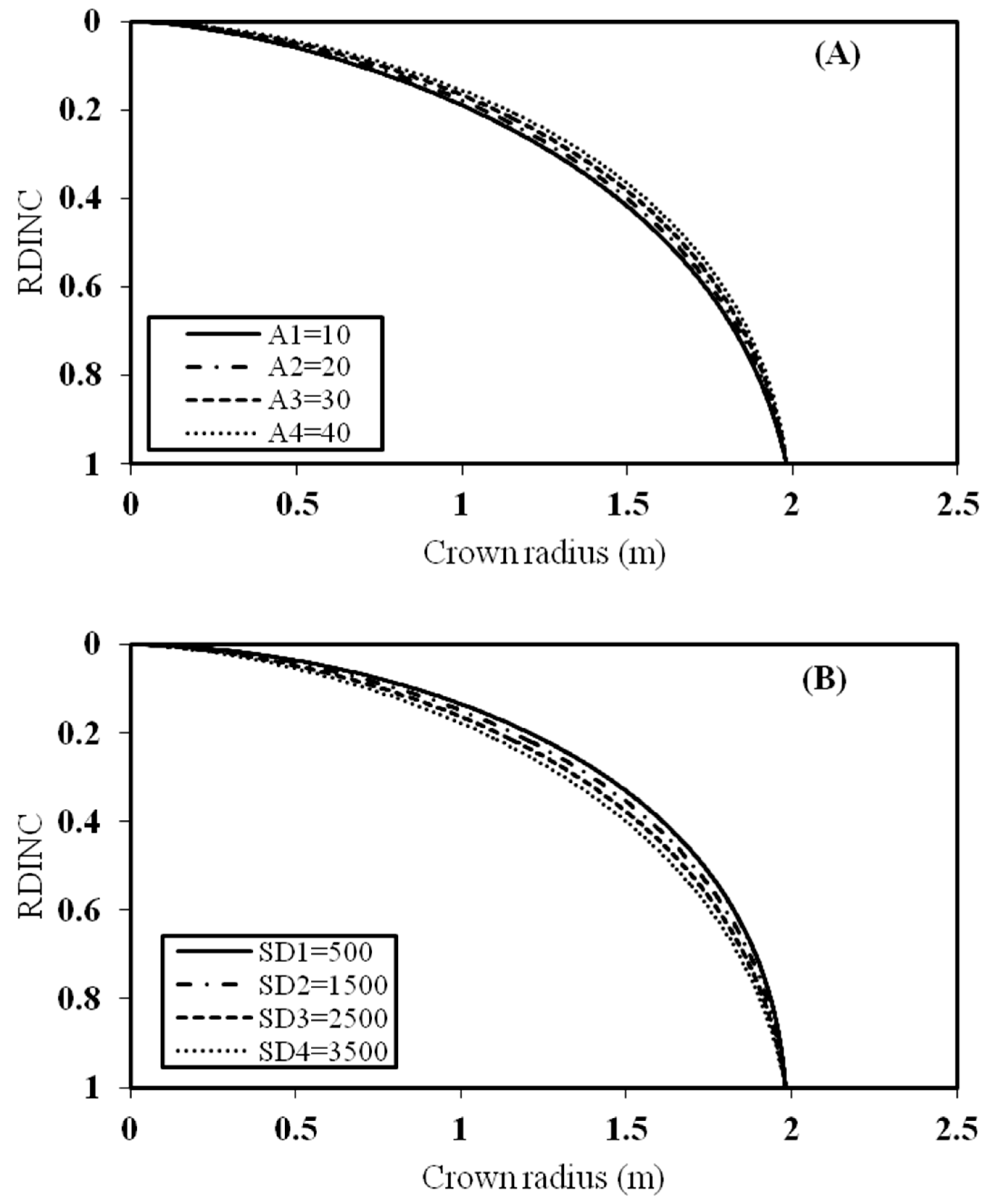
3.3. Effect of Stand Age and Stand Density on the Crown Profile
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hansen, A.J.; Spies, T.A.; Swanson, F.J.; Ohmann, J.L. Conserving biodiversity in managed forests: Lessons from natural forests. BioScience 1991, 41, 382–392. [Google Scholar] [CrossRef]
- Ishii, H.; McDowell, N. Age-related development of crown structure in coastal Douglas-fir trees. For. Ecol. Manag. 2002, 169, 257–270. [Google Scholar] [CrossRef]
- Fichtner, A.; Sturm, K.; Rickert, C.; Oheimb, G.V.; Härdtle, W. Crown size-growth relationships of European beech (Fagus sylvatica L.) are driven by the interplay of disturbance intensity and inter-specific competition. For. Ecol. Manag. 2013, 302, 178–184. [Google Scholar] [CrossRef]
- Mawson, J.C.; Thomas, J.W.; DeGraaf, R.M. Program HTVOL: The Determination of Tree Crown Volume by Layers; Research Paper NE-354; U.S. Department of Agriculture, Forest Service, Northeastern Forest Experiment Station: Philadelphia, PA, USA, 1976.
- Biging, G.S.; Wensel, L.C. Estimation of crown form for six conifer species of northern California. Can. J. For. Res. 1990, 20, 1137–1142. [Google Scholar] [CrossRef]
- Baldwin, V.C., Jr.; Peterson, K.D. Predicting the crown shape of loblolly pine trees. Can. J. For. Res. 1997, 27, 102–107. [Google Scholar] [CrossRef]
- Hann, D.W. An adjustable predictor of crown profile for stand-growth Douglas-fir trees. For. Sci. 1999, 45, 217–225. [Google Scholar]
- Raulier, F.; Ung, C.-H.; Ouellet, D. Influence of social status on crown geometry and volume increment inregular and irregular black spruce stands. Can. J. For. Res. 1996, 26, 1742–1753. [Google Scholar] [CrossRef]
- Crecente-Campo, F.; Marshall, P.; Lemay, V.; Diéguez-Aranda, U. A crown profile model for Pinus radiata D. Don in Northwestern Spain. For. Ecol. Manag. 2009, 257, 2370–2379. [Google Scholar] [CrossRef]
- Crecente-Campo, F.; Álvarez-González, J.G.; Castedo-Dorado, F.; Gómez-García, E.; Diéguez-Aranda, U. Development of crown profile models for Pinus pinaster Ait. and Pinus sylvestris L. in northwestern Spain. Forestry 2013, 86, 481–491. [Google Scholar] [CrossRef]
- Gao, H.L.; Bi, H.Q.; Li, F.R. Modeling conifer crown profiles as nonlinear conditional quantiles: An example with planted Korean pine in northeast China. For. Ecol. Manag. 2007, 398, 101–115. [Google Scholar] [CrossRef]
- Dong, C.; Wu, B.G.; Wang, C.D.; Guo, Y.R.; Han, Y.H. Study on crown profile models for Chinese fir, in Fujian Province and its visualization simulation. Scand. J. Forest. Res. 2016, 31, 1–32. [Google Scholar] [CrossRef]
- Guo, Y.R.; Wu, B.G.; Zheng, X.X.; Zheng, D.X.; Liu, Y.; Dong, C.; Zhang, M.B. Simulation model of crown profile for Chinese fir (Cunninghamia lanceolata) in different age groups. J. Beijing For. Univ. 2015, 37, 40–47. (In Chinese) [Google Scholar]
- Ritchie, M.W.; Hann, D.W. Equations for Predicting Height to Crown Base for Fourteen Tree Species in Southwest Oregon; Research Paper 50; Forest Research Lab., Oregon State University: Corvallis, OR, USA, 1987. [Google Scholar]
- Gao, H.L.; Dong, L.H.; Li, F.R. Modeling Variation in Crown Profile with Tree Status and Cardinal Directions for Planted Larix olgensis Henry Trees in Northeast China. Forests 2017, 8, 139. [Google Scholar]
- Hao, L.; Naiman, D. Quantile Regression. In Statistics for Social Science and Behavorial Sciences; Sage Publications, Inc: London, UK, 2007. [Google Scholar]
- Wackerly, D.D.; Mendenhall, W., III; Scheaffer, R.L. Mathematical Statistics with Applications; Thomson Learning, Inc: Belmont, USA, 2008. [Google Scholar]
- Rao, C.R.; Toutenburg, H.; Shalabh Heumann, C. Linear Models and Generalizations: Least Squares and Alternatives; Springer: Berlin, Germany, 2008. [Google Scholar]
- Koenker, R.; Bassett, G. Regression quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Koenker, R. Quantile Regression; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Koenker, R.; Machado, J.A.F. Goodness of fit and related inference process for quantile regression. J. Am. Stat. Assoc. 1999, 94, 1296–1309. [Google Scholar] [CrossRef]
- Zhang, L.; Bi, H.; Gove, J.H.; Heath, L.S. A comparison of alternative methods for estimating the self-thinning boundary line. Can. J. For. Res. 2005, 35, 1507–1514. [Google Scholar] [CrossRef]
- Cade, B.S.; Noon, B.R. A gentle introduction to quantile regression for ecologists. Front. Ecol. Environ. 2003, 1, 412–420. [Google Scholar]
- Evans, A.M.; Finkral, A.J. A new look at spread rates of exotic diseases in North American forests. For. Sci. 2010, 56, 453–459. [Google Scholar]
- Haile, G.A.; Nguyen, A.N. Determinants of academic attainment in the United States: A quantile regression analysis of test scores. Educ. Econ. 2008, 16, 29–57. [Google Scholar] [CrossRef]
- Austin, P.C.; Schull, M.J. Quantile regression: A statistical tool for out-of hospital research. J. Soc. Acad. Emerg. Med. 2003, 10, 789–797. [Google Scholar] [CrossRef]
- Engle, R.F.; Manganelli, S. CAViaR: Conditional Value at Risk by Quantile Regression; Working Paper No. 7341; National Bureau of Economic Research: Cambridge, UK, 1999. [Google Scholar]
- Machado, J.A.F.; Mata, J. Counterfactual decomposition of changes in wage distributions using quantile regression. J. Appl. Econ. 2005, 20, 445–465. [Google Scholar] [CrossRef]
- Cade, B.S.; Noon, B.R.; Flather, C.H. Quantile regression reveals hidden bias and uncertainty in habitat models. Ecology 2005, 86, 786–800. [Google Scholar] [CrossRef]
- Mehtätalo, L.; Gregoire, T.G.; Burkhart, H.E. Comparing strategies for modeling tree diameter percentiles from remeasured plots. Environmetrics 2008, 19, 529–548. [Google Scholar] [CrossRef]
- Ducey, M.J.; Knapp, R.A. A stand density index for mixed species forests in the northeastern United States. For. Ecol. Manag. 2010, 260, 1613–1622. [Google Scholar] [CrossRef]
- Bohora, S.B.; Cao, Q.V. Prediction of tree diameter growth using quantile regression and mixed-effects models. For. Ecol. Manag. 2014, 319, 62–66. [Google Scholar] [CrossRef]
- Gao, H.L.; Dong, L.H.; Li, F.R. Maximum density-size line for Larix olgensis plantations based on quantile regression. Chin. J. Appl. Ecol. 2016, 27, 3420–3426. (In Chinese) [Google Scholar]
- Fuzi, M.F.M.; Jemain, A.A.; Ismail, N. Bayesian quantile regression model for claim count data. Insur. Math. Econ. 2016, 66, 124–137. [Google Scholar] [CrossRef]
- De-Miguel, S.; Mehtätalo, L.; Shater, Z.; Kraid, B.; Pukkala, T. Evaluating marginal and conditional predictions of taper models in the absence of calibration data. Can. J. For. Res. 2012, 42, 1383–1394. [Google Scholar] [CrossRef]
- Geraci, M.; Bottai, M. Quantile regression for longitudinal data using the asymmetric Laplace distribution. Biostatistics 2007, 8, 140–154. [Google Scholar] [CrossRef] [PubMed]
- Galarza, C.E.; Lachos, V.H. Likelihood based inference for quantile regression in nonlinear mixed effects models. Estadística 2015, 67, 188–189. [Google Scholar]
- Liu, Y.; Bottai, M. Mixed-effects models for conditional quantiles with longitudinal data. Int. J. Biostat. 2009, 5, 28. [Google Scholar] [CrossRef]
- Chen, X.; Tang, N.; Zhou, Y. Quantile regression of longitudinal data with informative observation times. J. Multivar. Anal. 2016, 144, 176–188. [Google Scholar] [CrossRef]
- Marino, M.F.; Farcomeni, A. Linear quantile regression models for longitudinal experiments: An overview. Metron 2015, 73, 229–247. [Google Scholar] [CrossRef]
- Li, C.; Dowling, N.M.; Chappell, R. Quantile regression with a change-point model for longitudinal data: An application to the study of cognitive changes in preclinical Alzheimer’s disease. Biometrics 2015, 71, 625–635. [Google Scholar] [CrossRef] [PubMed]
- Galarza, C.E.; Lachos, V.H. qrLMM: Quantile Regression for Linear Mixed-Effects Models. R Package Version 1.3. 2017. Available online: https://CRAN.R-project.org/package=qrLMM (accessed on 21 March 2017).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017; Available online: https://www.r-project.org/ (accessed on 6 March 2017).
- Marshall, D.D.; Johnson, G.P.; Hann, D.W. Crown profile equations for stand-grown western hemlock trees in northeastern Oregon. Can. J. For. Res. 2003, 33, 2059–2066. [Google Scholar] [CrossRef]
- Pretzsch, H. Canopy space filling and tree crown morphology in mixed-species stands compared with monocultures. For. Ecol. Manag. 2014, 327, 251–264. [Google Scholar] [CrossRef]
- Sotocervantes, J.A.; Lópezsánchez, C.A.; Corralrivas, J.J.; Wehenkel, C.; Álvarez-González, J.G.; Crecente-Campo, F. Development of crown profile model for Pinus cooperi Blanco in the UMAFOR 1008, Durango, Mexico. Revist Chapingo Serie Ciencias Forestales Y Del Ambiente 2016. [Google Scholar] [CrossRef]
- Bianchi, A.; Salvati, N. Asymptotic properties and variance estimators of the M-quantile regression coefficients estimators. Commun. Stat-Theor. Methods 2015, 44, 2416–2429. [Google Scholar] [CrossRef]
- Fu, L.; Sun, H.; Sharma, R.P.; Lei, Y.C.; Zhang, H.R.; Tang, S.Z. Nonlinear mixed-effects crown width models for individual trees of Chinese fir (Cunninghamia lanceolata) in south-central China. For. Ecol. Manag. 2013, 302, 210–220. [Google Scholar] [CrossRef]
- Fu, L.; Sharma, R.P.; Wang, G.; Tang, S.Z. Modeling a system of nonlinear additive crown width models applying seemingly unrelated regression for Prince Rupprecht larch in Northern China. For. Ecol. Manag. 2017, 386, 71–80. [Google Scholar] [CrossRef]
- Sharma, R.P.; Vacek, Z.; Vacek, S. Individual tree crown width models for Norway spruce and European beech in Czech Republic. For. Ecol. Manag. 2016, 366, 208–220. [Google Scholar] [CrossRef]
- Bechtold, W.A. Crown-diameter prediction models for 87 species of stand grown trees in the eastern United States. South. J. Appl. For. 2003, 27, 269–278. [Google Scholar]
- Maguire, D.A.; Hann, D.W. Constructing models for direct prediction of 5-year crown recession in southwestern Oregon Douglas-fir. Can. J. For. Res. 1990, 20, 1044–1052. [Google Scholar] [CrossRef]
- Attocchi, G.; Skovsgaard, J.P. Crown radius of pedunculate oak (Quercus robur L.) depending on stem size, stand density and site productivity. Scand. J. For. Res. 2015, 30, 289–303. [Google Scholar]
- Bechtold, W.A. Largest-crown-width prediction models for 53 species in the western United States. West. J. Appl. For. 2004, 19, 245–251. [Google Scholar]


| Plot Number | Stand Age (Year) | Stand Density (Trees ha−1) | Mean DBH (cm) | Mean Tree Height (m) | Stand Volume (m3 ha−1) | Stand Basal Area (m2 ha−1) | Numbers of Sample Trees |
|---|---|---|---|---|---|---|---|
| 1 | 42 | 385 | 29.1 | 18.2 | 221.9 | 25.81 | 5 |
| 2 | 42 | 650 | 23.6 | 16.9 | 227.2 | 28.86 | 5 |
| 3 | 26 | 783 | 15.2 | 8.6 | 100.1 | 14.99 | 5 |
| 4 | 33 | 1883 | 13.3 | 13.9 | 168.8 | 27.11 | 5 |
| 5 | 18 | 3633 | 8.6 | 5.7 | 117.0 | 22.37 | 5 |
| 6 | 38 | 1025 | 19.1 | 15.4 | 220.4 | 30.33 | 5 |
| 7 | 44 | 1640 | 19.0 | 21.1 | 347.7 | 47.98 | 5 |
| 8 | 33 | 3840 | 10.6 | 9.9 | 163.9 | 28.62 | 5 |
| 9 | 43 | 1100 | 20.1 | 16.5 | 264.3 | 35.73 | 5 |
| 10 | 31 | 2025 | 13.4 | 11.7 | 192.5 | 30.33 | 5 |
| 11 | 46 | 450 | 29.6 | 20.7 | 287.0 | 32.86 | 5 |
| 12 | 38 | 1220 | 19.2 | 16.0 | 267.9 | 36.65 | 5 |
| 13 | 45 | 1217 | 21.0 | 19.5 | 344.0 | 44.36 | 5 |
| 14 | 20 | 3950 | 9.7 | 7.7 | 77.7 | 31.01 | 5 |
| 15 | 12 | 2350 | 7.1 | 4.3 | 36.2 | 9.62 | 6 |
| Statistics | Tree Variables (N = 76) | Branch Variables (N = 3658) | |||||
|---|---|---|---|---|---|---|---|
| DBH (cm) | HT (m) | CL | BL (cm) | BC (cm) | VA (°) | BD (mm) | |
| Mean | 17.9 | 14.3 | 5.4 | 130 | 121 | 47 | 2.02 |
| Std | 7.2 | 5.2 | 1.6 | 88 | 82 | 16 | 1.10 |
| Min | 6.0 | 3.5 | 2.6 | 3 | 3 | 10 | 0.09 |
| Max | 34.5 | 22.5 | 10.9 | 536 | 521 | 150 | 7.16 |
| Crown | Models | Power-Exponential Equation | Modified Kozak Equation | Simple Polynomial Equation |
|---|---|---|---|---|
| Total tree | Ra2 | 0.79 | 0.77 | 0.76 |
| RMSE | 0.3544 | 0.3675 | 0.3722 | |
| AIC | 762 | 835 | 858 | |
| Mean error | 0.0065 | 0.0065 | 0.0079 | |
| Mean absolute error | 0.2579 | 0.2664 | 0.2717 | |
| Light crown | Mean error | 0.0224 | 0.0209 | 0.0206 |
| Mean absolute error | 0.2467 | 0.2511 | 0.2588 | |
| Shade crown | Mean error | −0.1155 | −0.1039 | −0.1357 |
| Mean absolute error | 0.3436 | 0.3835 | 0.3713 bottom boder |
| Dummy Variables | Parameters | a1 | a2 | a30 | a31 | a32 | a33 | a4 | a5 |
|---|---|---|---|---|---|---|---|---|---|
| Stand age | Estimates | 0.3283 | 0.8064 | −0.1450 | −0.4671 | −0.4477 | −0.6057 | 0.4686 | −1.3186 |
| Std | 0.0296 | 0.0768 | 0.1175 | 0.1605 | 0.2065 | 0.1803 | 0.2818 | 0.2936 | |
| Stand density | Estimates | 0.3385 | 0.7571 | −0.4034 | −0.3886 | −0.1364 | 0.1067 | 0.4734 | −1.3342 |
| Std | 0.0296 | 0.0752 | 0.1539 | 0.2087 | 0.1148 | 0.1747 | 0.2752 | 0.2841 |
| Models | R2 | Var(εp) | [E(εp)]2 | MEP | MAEP |
|---|---|---|---|---|---|
| M3 | 0.9380 | 0.2291 | 0.0017 | 0.0388 | 0.1626 |
| q = 0.90 | 0.8789 | 0.2351 | 0.0510 | 0.2280 | 0.2312 |
| q = 0.95 | 0.9342 | 0.2312 | 0.0046 | 0.0668 | 0.1635 |
| q = 0.99 | 0.7987 | 0.3446 | 0.0577 | −0.2400 | 0.3187 |
| q = 0.95 (qrLMM) | 0.9431 | 0.2190 | 0.0026 | −0.0545 | 0.1458 |
| Random Effect | AIC | BIC | HQ | logLike |
|---|---|---|---|---|
| b1 | 1091 | 1130 | 1106 | −537 |
| b2 | 1399 | 1438 | 1414 | −691 |
| b1, b31 | 1064 | 1109 | 1081 | −523 |
| b1, b31, b4 | 1036 | 1104 | 1062 | −504 |
| Parameter | b1 | b2 | b31 | b32 | b33 | b4 | b5 |
|---|---|---|---|---|---|---|---|
| Estimates | 0.4084 | 0.6081 | 0.1240 | −0.0079 | 0.0001 | 1.2039 | −1.6362 |
| Std | 0.0126 | 0.0358 | 0.0783 | 0.0029 | 0.0000 | 0.1353 | 0.1461 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Gao, H.; Li, F. Using Linear Mixed-Effects Models with Quantile Regression to Simulate the Crown Profile of Planted Pinus sylvestris var. Mongolica Trees. Forests 2017, 8, 446. https://doi.org/10.3390/f8110446
Sun Y, Gao H, Li F. Using Linear Mixed-Effects Models with Quantile Regression to Simulate the Crown Profile of Planted Pinus sylvestris var. Mongolica Trees. Forests. 2017; 8(11):446. https://doi.org/10.3390/f8110446
Chicago/Turabian StyleSun, Yunxia, Huilin Gao, and Fengri Li. 2017. "Using Linear Mixed-Effects Models with Quantile Regression to Simulate the Crown Profile of Planted Pinus sylvestris var. Mongolica Trees" Forests 8, no. 11: 446. https://doi.org/10.3390/f8110446
APA StyleSun, Y., Gao, H., & Li, F. (2017). Using Linear Mixed-Effects Models with Quantile Regression to Simulate the Crown Profile of Planted Pinus sylvestris var. Mongolica Trees. Forests, 8(11), 446. https://doi.org/10.3390/f8110446





