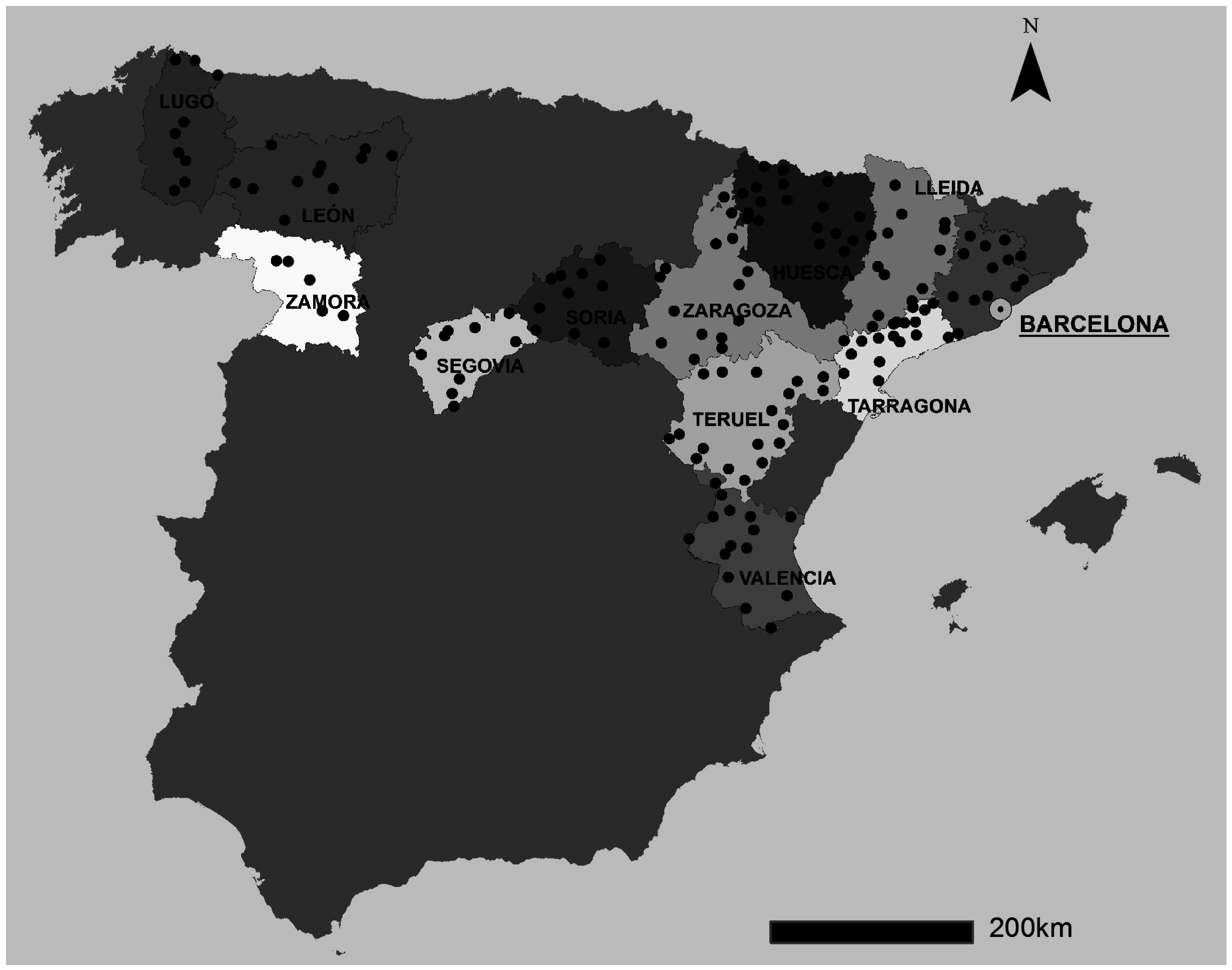
2.2.2. Climate Variables
Climate variables have always been considered to be a decisive vector that, starting from some favorable conditions of vegetation and soil (among other variables), can account for the higher or lower level of picking of saffron milk caps in certain forests. Thus, it is necessary to use weather data, usually measured as a proxy for the temperature and moisture in the soil. This approach has commonly been used to examine different aspects related to mycological harvesting [
41]. Beginning with temperature, the mean weekly temperature (
tmed) and the minimum weekly temperature (
tmin) were used as explanatory variables. To calculate these weekly means, the data relative to the daily maximum and minimum temperatures were noted in order to obtain the means of the weekly maximum and minimum temperatures. In addition to the temperature, another key factor in the fructification of the mycorrhizal fungi is water availability. Rainfall variables include mean weekly rainfall (
rainfm), weekly accumulated rainfall (
rainfw), weekly accumulated rainfall during the summer (
rainfs), and the previous year’s rainfall (
rainfpy). For the first two variables the same methodology as in the case of temperature was followed. The rainfall accumulated only during the summer was taken as a variable,
i.e., a dummy variable whose calculation covers the month of July and the first weeks of August, assigning a value of 1 if it exceeded the mean of the six years studied, and a value of 0 if not. Finally, the previous year’s rainfall has been taken as a dummy variable with the aim of analyzing the existence of certain annual discontinuities in saffron milk cap yields [
23]. It has been defined as a dummy variable with a value of 1 if the previous year’s rainfall was lower than the mean, and with the value of 0 if not. To take into account soil moisture, two variables were used: potential evapotranspiration (
pet) and the difference between accumulated rainfall and potential evapotranspiration (
diff). For the calculation of the weekly mean potential evapotranspiration, the Thornthwaite experiment formula was used [
42].
2.2.4. Statistical Estimation Methodology
A mushroom supply function describes the relationship between mushroom harvesting and mushroom prices. In order to improve the representation of this function and complete a mushroom supply function with all variables that could improve the explanation of this process, we have followed the well-known General-to-Specific method (see [
43,
44] for further developments).
The variable selection process is based on the Hendry method for selection process [
45]. From this, we define a universe with all variables (both explaining variables and the dependent variable (see
Table 1)), which implies the existence of 2
11 possible models.
The most relevant hypothesis to represent mushroom supply is the positive relationship between prices and mushroom picking. Given that this hypothesis is commonly satisfied in mushroom markets, this idea induced us to consider statistical cointegration methods as an adequate estimation technique for mushroom supply. In this model, two variables (such as mushroom price and mushroom harvesting) are said to be cointegrated if a linear combination of them is stationary. So, we start with a very simple supply function, which reflects a cointegrating relationship between mushroom prices and harvesting:
where
lactprt represents the price of mushroom,
lackg is for collected mushroom,
t is for week
t, and
β reflects the incidence of changes of
lactkgt on
lactprt.
Stationarity is when the statistical characteristics of a series such as its mean and variance remain constant, and also that covariance remains finite and constant for all periods across time (see
Appendix for a more detailed explanation of these statistical concepts). In order to test the stationarity between mushroom harvesting and mushroom prices, we calculated the Augmented Dickey–Fuller (ADF), the Phillips–Perron (PP), and the Kwiatkowski–Phillips–Schmidt–Shin (KPSS) tests. Definitions and brief descriptions of the applied tests can be found in the
Appendix.
The concept of cointegration is essential to the understanding of a mushroom supply function because it reflects the intuition that mushroom prices and mushroom harvesting would not drift too far apart from each other over time, even with the existence of external shocks like changes in weather conditions or temporary changes in public regulations on mushroom picking. Cointegration tests, such as the trace test and the eigenvalue test, are applied to test for the existence of a relationship between the two main variables of the mushroom supply function, and are briefly described in the
Appendix. Evidence of cointegration implies the existence of causality between the two variables, at least in one direction. Therefore, we employ vector error correction (VEC) models in order to detect the direction of causality. Although there is a huge amount of literature estimating vector error correction models, there is not so much published research applying this statistical technique to non-timber forest products. One paper investigated the existence of any cointegration relationship and causality effects between price series of non-timber forest products, using VEC models [
46]. These were applied using a price series of non-timber forest products in two markets in the Bankura district, in the state of West Bengal. A main conclusion of the paper is that there exists uniformity of price structure for collectors in almost all markets by different consumers for the same period. It also concludes that village wholesalers serve as the most important marketing agent of sample collectors, and pay the highest price to the collectors in all markets.
Mushroom prices are considered to determine in the Granger sense the size of the mushroom harvest, whenever the value of prices can be predicted more accurately by using past values on harvesting. VEC models are useful because they can distinguish between a long-term and a short-term relationship between variables, and can identify sources of causation that cannot be detected by the usual Granger causality tests. Permanent shocks are identified with long-run changes in the literature (that is, a cointegrating relationship), whereas transitory shocks (error correction term and independent variables in a VEC model) are identified with short-run modifications.
If cointegration is detected between mushroom prices and mushroom harvesting, there is a long-run relationship between them. Furthermore, the short-run dynamics can be described by the error correction model. This is known as the Granger representation theorem. This theorem implies that both mushroom prices and mushroom harvesting may be considered to be generated by two error correction models in the form:
where
lactprt and
lactkgt represent the price of mushrooms and mushroom harvesting, respectively; Δ
lactprt and Δ
lactkgt are the differences in these variables that capture their short-run disturbances (with one week of delay, and with two weeks of delay correspondingly);
rainfm is the variable for the mean weekly rainfall; the
tmed variable is for the mean weekly temperature;
ut and
wt are the serially uncorrelated error terms; and the error correction term (
ECT) is derived from the cointegration relationship and measures the magnitude of the past disequilibrium. In our case, the
ECT is one such as (ln(
lactprt−1)- β ln(
lactkgt−1)). Coefficients for the
ECT in Equation (2.I) is
β1 and coefficient for ECT in Equation (2.II) is
β2. These coefficients represent the deviation of prices and harvesting from the equilibrium in each of the equations so that, if no deviation exists, the
ECT is equal to zero.
This representation allows for causality to emerge in two ways. First, it allows for testing the significance of coefficients β1 and β2. A VEC model is set up for investigating both short- and long- run causality. In Model I (Equation (2)), the joint significance of β12 and β13 indicates that changes in mushroom prices are responding to short-term shocks in harvesting; the joint significance of β14 and β15 indicates that changes in mushroom prices are also determined by the lagged values of these mushroom prices and also by the effects of meteorological variables such as rain (β16) and temperature (β17). In Model II (Equation (2)), the joint significance of β22 and β23 indicates that variations in mushroom harvesting are dependent on short-term shocks in production; the joint significance of β24 and β25 indicates that changes in mushroom harvesting are also determined by the lagged values of differences in mushroom prices. Fluctuations in mushroom picking can also be explained by the effects of meteorological variables such as rain (β26) and temperature (β27).
From this, we could check whether the two sources of causation are jointly significant to test the Granger causality. In the price equation (Model I in Equation (2)), this implies that we test whether both harvesting and market deviations could have a joint influence on pricing. In the harvesting equation (Model II in Equation (2)), this implies that we test whether both prices and market deviations could have an influence on harvesting. This joint test could be an indicator of which variable bears the burden of short-term adjustment following a shock to the system, to re-establish long-term equilibrium.
In the equilibrium, ECTt−1 will be equal to zero. Nevertheless, if some deviation from this path exists in the mushroom market, then each variable should adjust to partially restore the equilibrium relation for the supply of mushrooms. In the estimated supply function, what we should expect is that the value of the ECT is equal to zero (although some random deviations could exist).
In Equation (2), we expect a positive change in mushroom prices to induce a negative change in mushroom harvesting, all other things being equal; that is, β12, β13, β14, β15 ≤ 0. We also expect a positive change in mushroom harvesting to induce a negative change in mushroom prices, all other things being equal; that is, β22, β23, β24, β25 ≤ 0. The expected signs for β16, β17, β26, and β27 are a priori uncertain.
The combined model in the above equation is called a VEC model. In our mushroom supply VEC model, past values of the error correction term (
ECTt−1) help to predict future values of changes in mushroom harvesting (Δ(ln(
lactkgt−1)), Δ(ln(
lactkgt−2)), and changes in mushroom prices (Δln(
lactprt−1) and Δln(
lactkgt−2)). The coefficients of the
ECTt−1 capture the speed of adjustment back towards the cointegrating equilibrium path, and it should be expected that the sign of the coefficient
β should be negative. So, if markets behave properly,
ECT should be equal to zero, and the main consequence of a positive change in production will be a positive change in prices, and
vice versa. Finally, regarding the specification and diagnostic tests, serial correlation, normality, and heteroskedasticity tests are calculated. We have also implemented the VEC Granger causality/block exogeneity Wald test in order to examine the causal effect between mushroom harvesting and mushroom prices. Definitions and brief descriptions of the applied tests can be found in the
Appendix.