Expansion of Protected Areas under Climate Change: An Example of Mountainous Tree Species in Taiwan
Abstract
:1. Introduction
2. Materials and Method
2.1. Study Area and Sampling Data
- (1)
- Alpine vegetation zone (mainly composed of Juniperus squamata forests and scrubs);
- (2)
- Subalpine coniferous forests (Abies zone);
- (3)
- Upper montane coniferous forests (Tsuga-Picea zone).
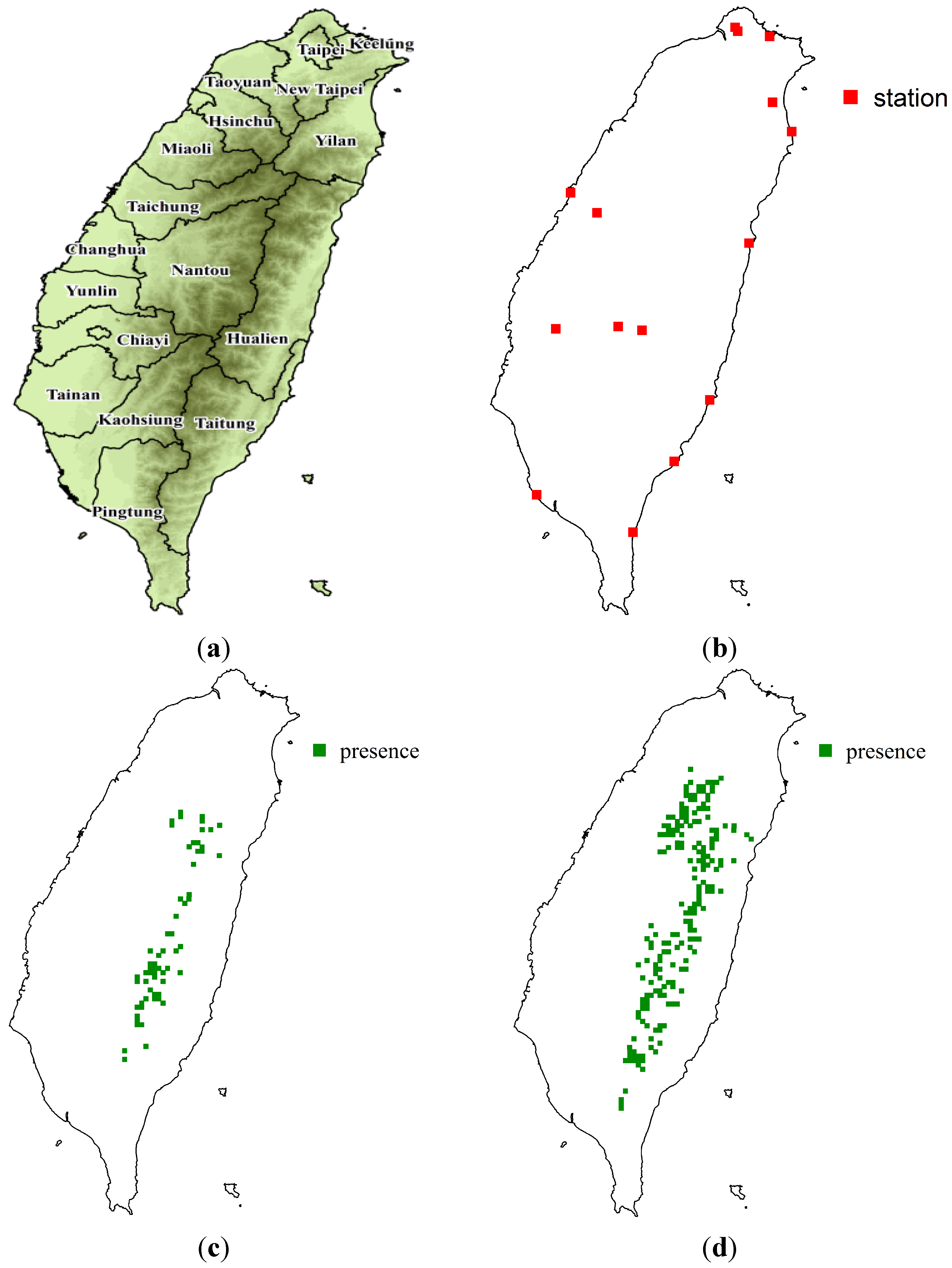
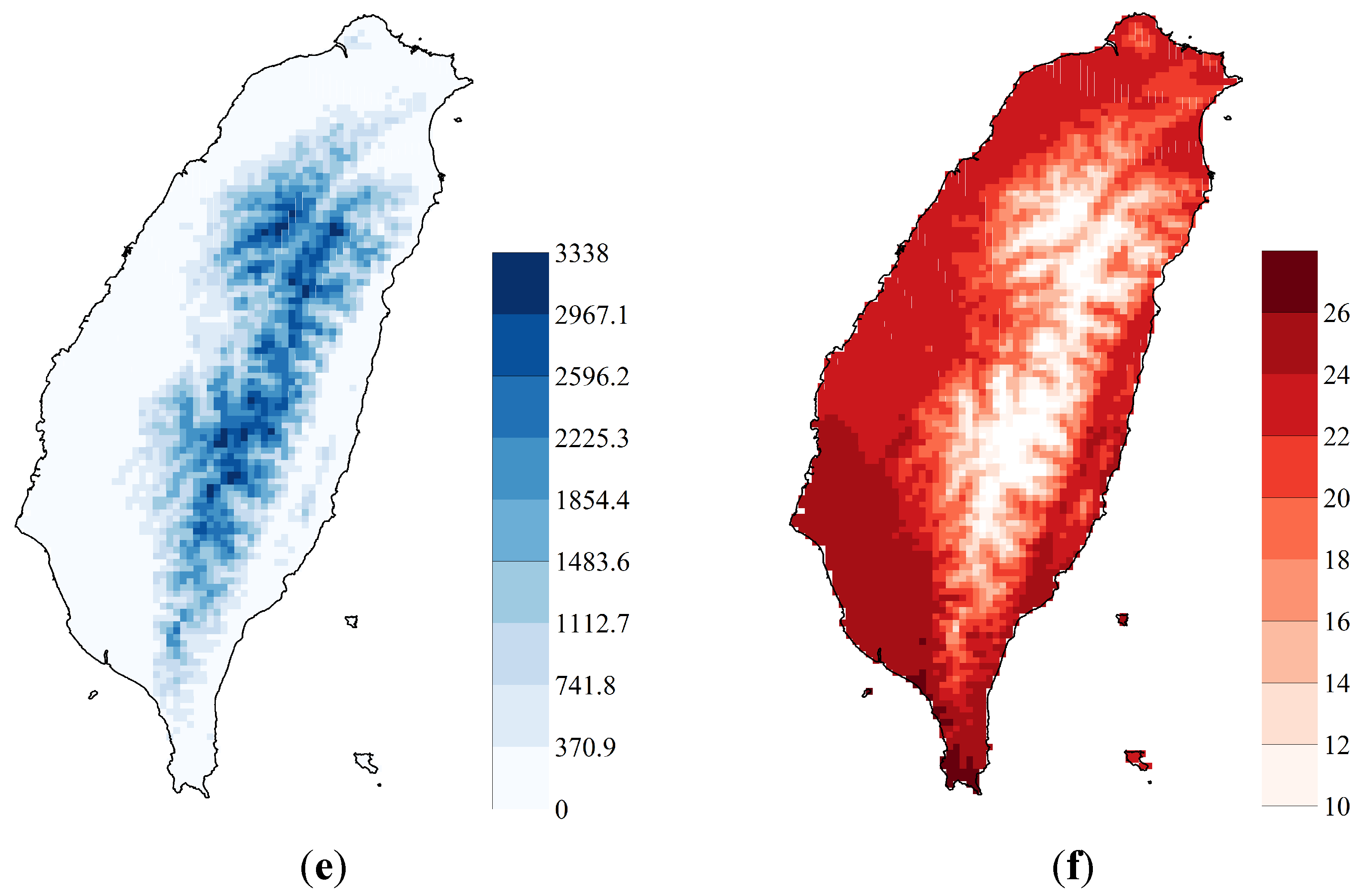
2.2. Maximum Entropy
2.3. The Bootstrapping Method
2.3.1. Evaluating Data and Model Performance
2.3.2. The Confidence Region of SDM Parameters
2.4. Variability Analysis
2.5. Identifying Protected Areas
3. Results and Discussion
3.1. SDM Performance, Focal Species Distribution and Their Shifts in Elevation
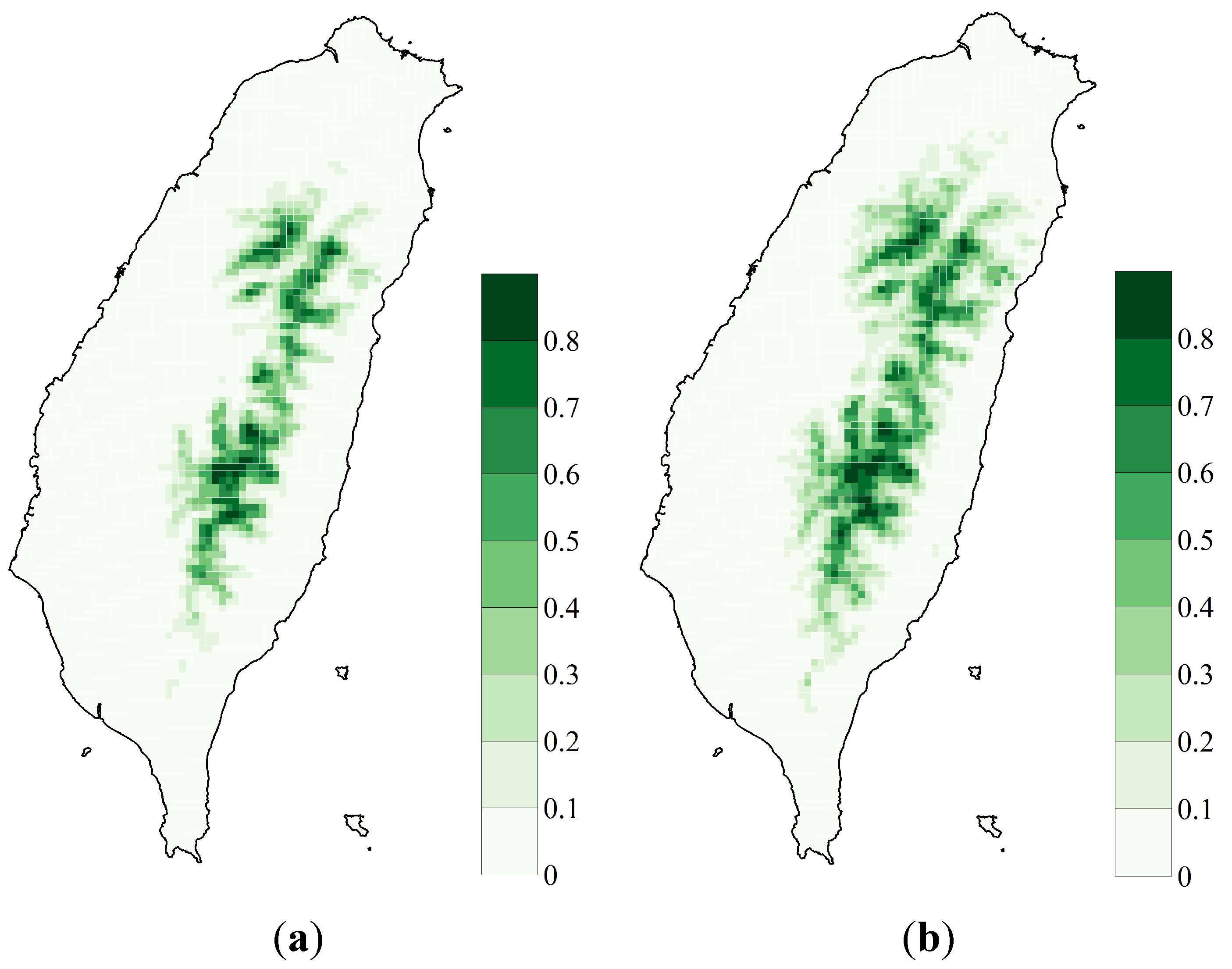
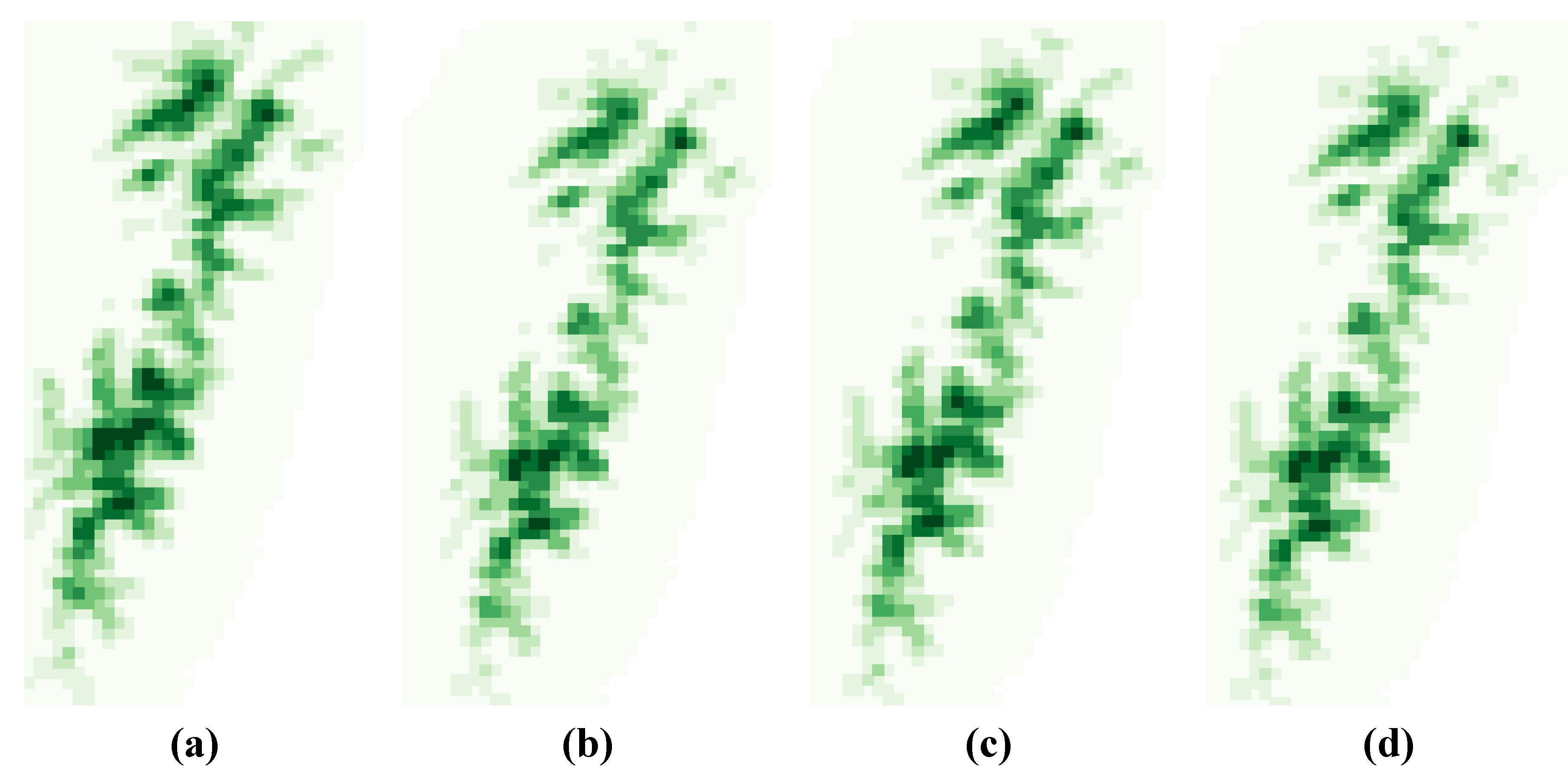
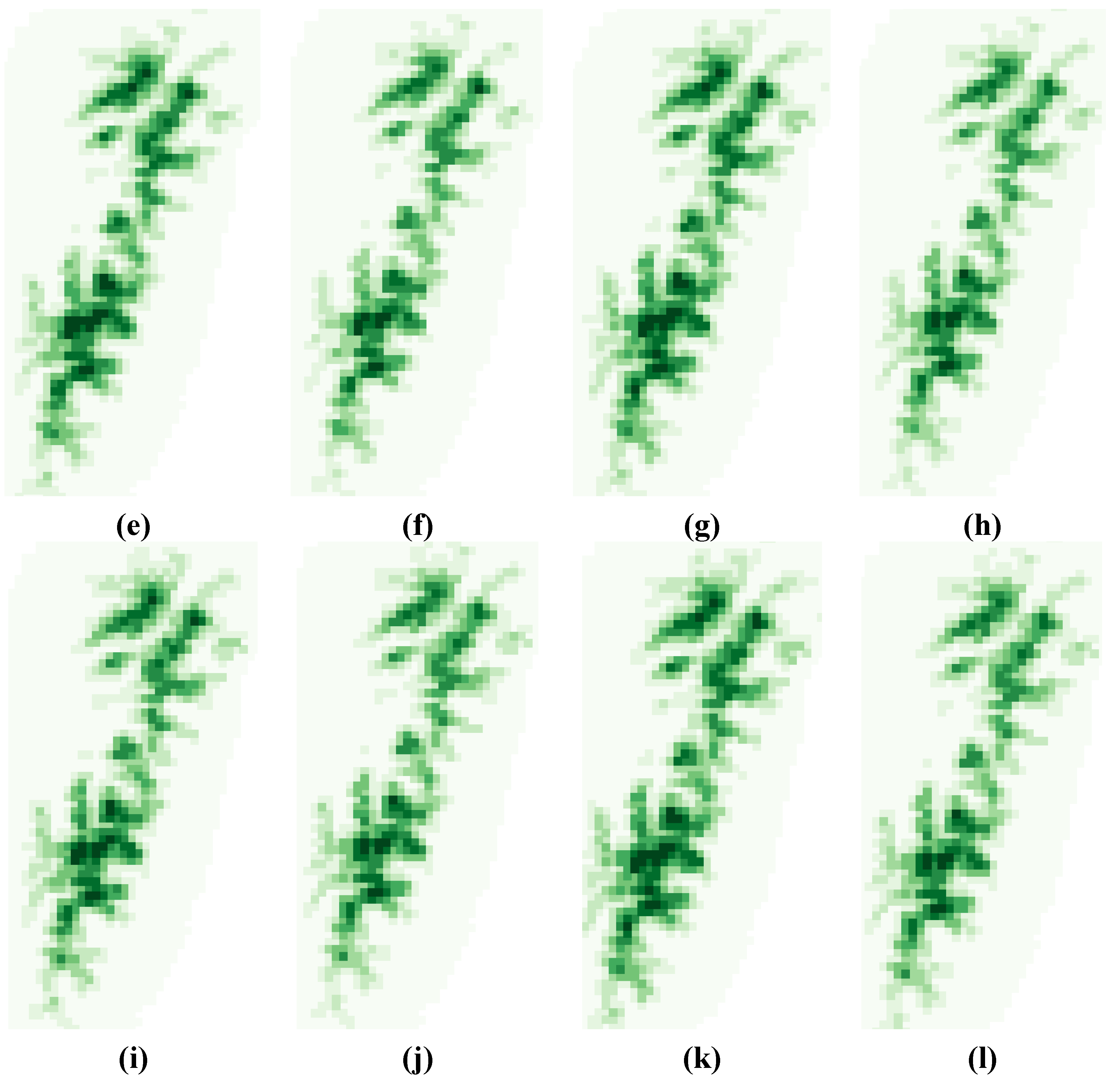

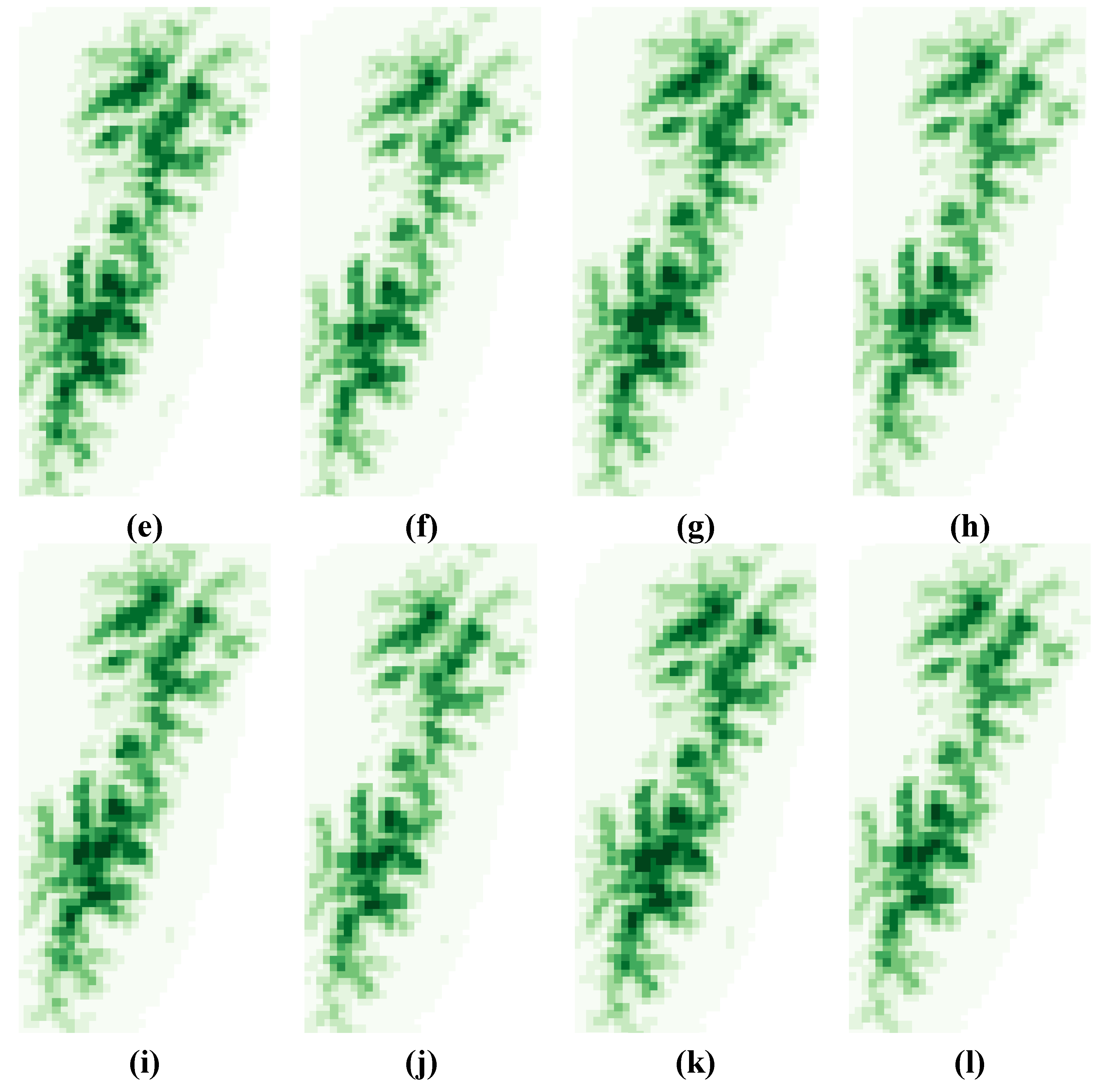
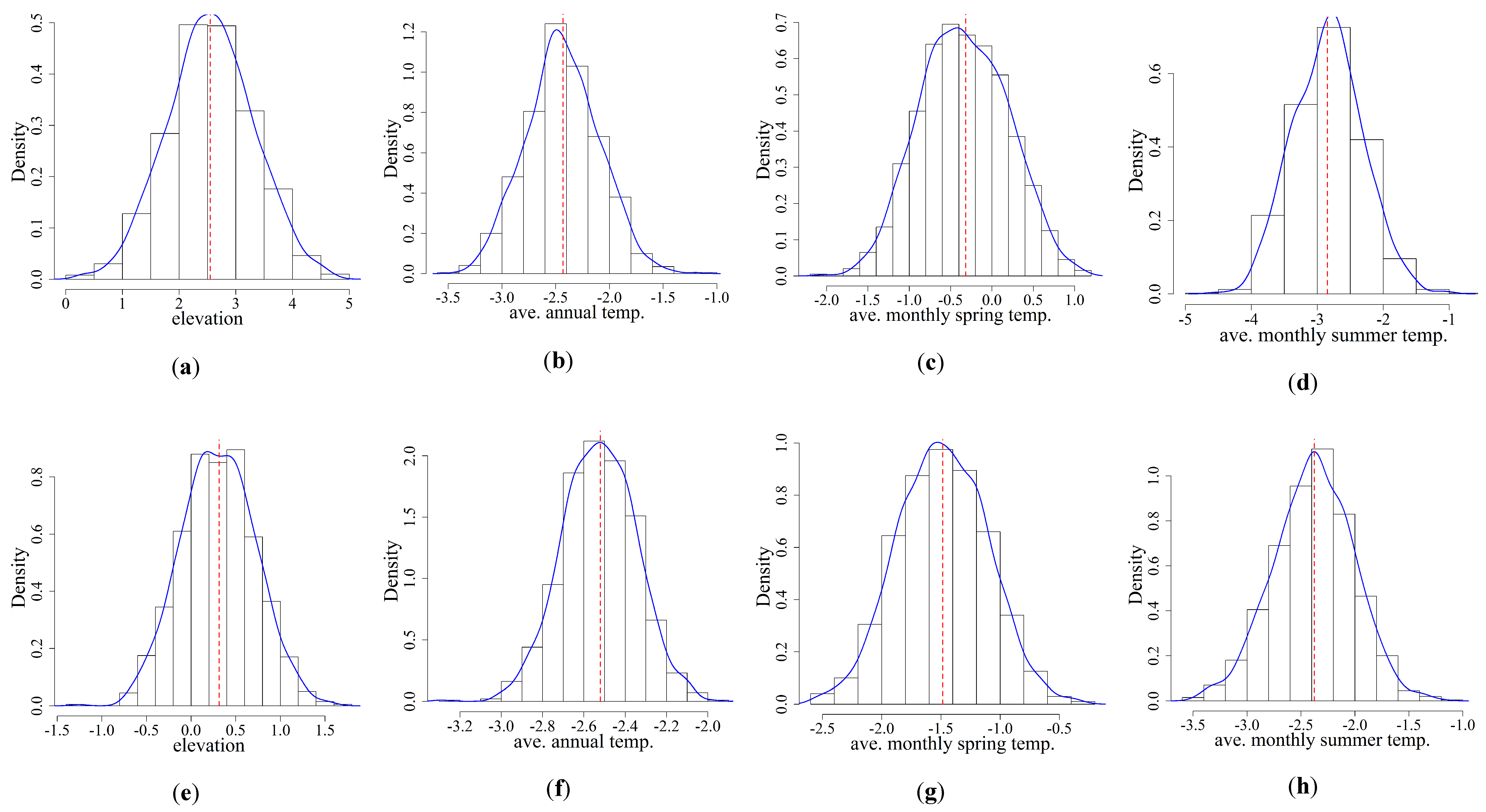
3.2. Variability Analysis
| Scenario | GES | GCM | Change of Average Temperature (°C) | Significant Shift in Elevation of Habitat | |||||
|---|---|---|---|---|---|---|---|---|---|
| Annual | Spring | Summer | Abies | Tsuga | |||||
| Count | Uncertainty | Count | Uncertainty | ||||||
| 1 | B1 | CS | 0.77 | 1.03 | 0.75 | 193 (−) | 0.16 | 489 (+) | 0.25 |
| 2 | GF | 0.88 | 0.76 | 0.93 | 466 (+) | 0.25 | 571 (+) | 0.25 | |
| 3 | MI | 1.02 | 1.22 | 0.93 | 576 (+) | 0.24 | 805 (+) | 0.16 | |
| 4 | MP | −0.03 | −0.06 | −0.2 | 0 (−) | 0.00 | 0 (−) | 0.00 | |
| 5 | MR | 0.34 | 0.17 | 0.59 | 0 (−) | 0.00 | 2 (−) | 0.00 | |
| 6 | A1B | CS | 0.88 | 1.17 | 1.02 | 514 (+) | 0.25 | 722 (+) | 0.20 |
| 7 | GF | 0.84 | 0.52 | 0.82 | 341 (+) | 0.23 | 442 (+) | 0.25 | |
| 8 | MI | 1.09 | 1.08 | 1.07 | 668 (+) | 0.22 | 841 (+) | 0.13 | |
| 9 | MP | −0.03 | −0.06 | −0.2 | 0 (−) | 0.00 | 0 (−) | 0.00 | |
| 10 | MR | 0.38 | 0.33 | 0.67 | 3 (−) | 0.00 | 29 (−) | 0.03 | |
| 11 | A2 | CS | 0.78 | 1.13 | 0.89 | 355 (+) | 0.23 | 589 (+) | 0.24 |
| 12 | GF | 0.67 | 0.69 | 0.79 | 149 (−) | 0.13 | 368 (0) | 0.23 | |
| 13 | MI | 0.91 | 1.29 | 0.91 | 489 (+) | 0.25 | 757 (+) | 0.18 | |
| 14 | MP | −0.03 | −0.06 | −0.2 | 0 (−) | 0.00 | 0 (−) | 0.00 | |
| 15 | MR | 0.35 | 0.31 | 0.51 | 0 (−) | 0.00 | 1 (−) | 0.00 | |
| Source of Uncertainty | Contribution (%) | |
|---|---|---|
| parameters | 67.9 | |
| Abies | GCMs | 31.3 |
| GESs | 0.9 | |
| parameters | 57 | |
| Tsuga | GCMs | 42.8 |
| GESs | 0.2 |
3.3. Local and Global Uncertainties
| Cut-off | Abies | Tsuga | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.7 | 0.75 | 0.8 | 0.85 | 0.9 | 0.95 | 0.7 | 0.75 | 0.8 | 0.85 | 0.9 | 0.95 | ||
| B | 0.43 | 0.58 | 0.65 | 0.7 | 0.78 | 0.9 | 0.43 | 0.58 | 0.65 | 0.7 | 0.78 | 0.9 | |
| s1 | 0.49 | 0.56 | 0.62 | 0.72 | 0.82 | 0.89 | 0.49 | 0.56 | 0.62 | 0.72 | 0.82 | 0.89 | |
| s2 | 0.45 | 0.54 | 0.65 | 0.73 | 0.82 | 0.91 | 0.45 | 0.54 | 0.65 | 0.73 | 0.82 | 0.91 | |
| s3 | 0.47 | 0.62 | 0.66 | 0.73 | 0.83 | 0.91 | 0.47 | 0.62 | 0.66 | 0.73 | 0.83 | 0.91 | |
| s4 | 0.42 | 0.52 | 0.69 | 0.74 | 0.79 | 0.88 | 0.42 | 0.52 | 0.69 | 0.74 | 0.79 | 0.88 | |
| s5 | 0.46 | 0.54 | 0.66 | 0.71 | 0.8 | 0.92 | 0.46 | 0.54 | 0.66 | 0.71 | 0.8 | 0.92 | |
| s6 | 0.45 | 0.51 | 0.67 | 0.72 | 0.84 | 0.91 | 0.45 | 0.51 | 0.67 | 0.72 | 0.84 | 0.91 | |
| s7 | 0.44 | 0.53 | 0.59 | 0.77 | 0.81 | 0.89 | 0.44 | 0.53 | 0.59 | 0.77 | 0.81 | 0.89 | |
| s8 | 0.55 | 0.6 | 0.67 | 0.74 | 0.81 | 0.89 | 0.55 | 0.6 | 0.67 | 0.74 | 0.81 | 0.89 | |
| s9 | 0.42 | 0.52 | 0.69 | 0.74 | 0.79 | 0.88 | 0.42 | 0.52 | 0.69 | 0.74 | 0.79 | 0.88 | |
| s10 | 0.48 | 0.54 | 0.62 | 0.72 | 0.81 | 0.91 | 0.48 | 0.54 | 0.62 | 0.72 | 0.81 | 0.91 | |
| s11 | 0.5 | 0.53 | 0.66 | 0.75 | 0.82 | 0.9 | 0.5 | 0.53 | 0.66 | 0.75 | 0.82 | 0.9 | |
| s12 | 0.47 | 0.53 | 0.62 | 0.74 | 0.86 | 0.91 | 0.47 | 0.53 | 0.62 | 0.74 | 0.86 | 0.91 | |
| s13 | 0.45 | 0.52 | 0.68 | 0.74 | 0.83 | 0.91 | 0.45 | 0.52 | 0.68 | 0.74 | 0.83 | 0.91 | |
| s14 | 0.42 | 0.52 | 0.69 | 0.74 | 0.79 | 0.88 | 0.42 | 0.52 | 0.69 | 0.74 | 0.79 | 0.88 | |
| s15 | 0.46 | 0.56 | 0.64 | 0.7 | 0.82 | 0.9 | 0.46 | 0.56 | 0.64 | 0.7 | 0.82 | 0.9 | |

3.4. Implications for Protected Areas
| Scenario | S | Abies Scons | CP (%) | S | Tsuga Scons | CP (%) |
|---|---|---|---|---|---|---|
| B | 199.7 | 174.2 | 87.2 | 295.3 | 252.8 | 85.6 |
| 145.4 | 161.6 | 90 | 226.2 | 199.6 | 88.2 | |
| s2 | 155.6 | 140.6 | 90.4 | 221.9 | 196.3 | 88.5 |
| s3 | 152.8 | 138.4 | 90.6 | 211.7 | 187.7 | 88.7 |
| s4 | 207.0 | 179.7 | 86.8 | 305.5 | 260.7 | 85.3 |
| s5 | 175.5 | 155.8 | 88.8 | 258.7 | 223.6 | 86.4 |
| s6 | 154.3 | 139.6 | 90.5 | 215.4 | 190.9 | 88.6 |
| s7 | 159.5 | 143.8 | 90.1 | 230.2 | 202.5 | 88 |
| s8 | 149.6 | 136.0 | 90.9 | 209.2 | 185.5 | 88.7 |
| s9 | 207.0 | 179.7 | 86.8 | 305.5 | 260.7 | 85.3 |
| s10 | 172.3 | 153.5 | 89 | 252.0 | 218.3 | 86.7 |
| s11 | 158.2 | 142.7 | 90.2 | 220.8 | 195.4 | 88.5 |
| s12 | 163.0 | 146.4 | 89.8 | 233.3 | 204.8 | 87.8 |
| s13 | 155.1 | 140.2 | 90.4 | 214.1 | 189.8 | 88.6 |
| s14 | 207.0 | 179.7 | 86.8 | 305.5 | 260.7 | 85.3 |
| s15 | 176.7 | 156.7 | 88.7 | 257.7 | 222.8 | 86.5 |
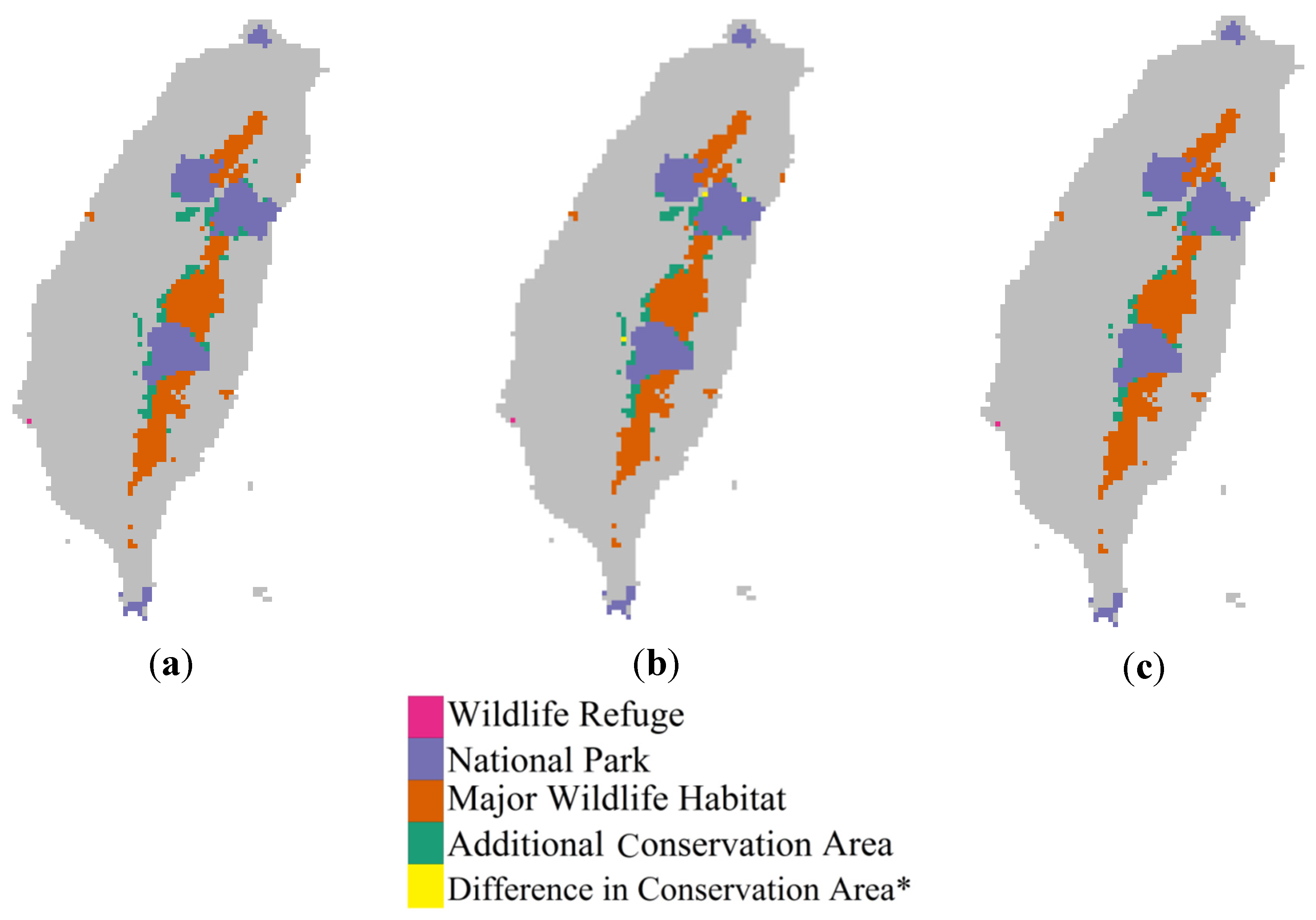
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lindner, M.; Maroschek, M.; Netherer, S.; Kremer, A.; Barbati, A.; Garcia-Gonzalo, J.; Seidl, R.; Delzon, S.; Corona, P.; Kolström, M. Climate change impacts, adaptive capacity, and vulnerability of european forest ecosystems. For. Ecol. Manag. 2010, 259, 698–709. [Google Scholar] [CrossRef]
- Gonzalez, P.; Neilson, R.P.; Lenihan, J.M.; Drapek, R.J. Global patterns in the vulnerability of ecosystems to vegetation shifts due to climate change. Glob. Ecol. Biogeogr. 2010, 19, 755–768. [Google Scholar] [CrossRef]
- Rosenzweig, C.; Karoly, D.; Vicarelli, M.; Neofotis, P.; Wu, Q.; Casassa, G.; Menzel, A.; Root, T.L.; Estrella, N.; Seguin, B. Attributing physical and biological impacts to anthropogenic climate change. Nature 2008, 453, 353–357. [Google Scholar] [CrossRef] [PubMed]
- Parry, M.L. Climate change 2007: Impacts, adaptation and vulnerability: Contribution of working group ii to the fourth assessment report of the intergovernmental panel on climate change; Cambridge University Press: Cambridge, UK, 2007; Vol. 4. [Google Scholar]
- Solomon, S. Climate change 2007: The physical science basis: Working group i contribution to the fourth assessment report of the ipcc; Cambridge University Press: Cambridge, UK, 2007; Vol. 4. [Google Scholar]
- Martin, T.E. Abiotic vs. biotic influences on habitat selection of coexisting species: Climate change impacts? Ecology 2001, 82, 175–188. [Google Scholar] [CrossRef]
- Bykova, O.; Chuine, I.; Morin, X.; Higgins, S.I. Temperature dependence of the reproduction niche and its relevance for plant species distributions. J. Biogeogr. 2012, 39, 2191–2200. [Google Scholar] [CrossRef]
- Guisan, A.; Zimmermann, N.E. Predictive habitat distribution models in ecology. Ecol. Model. 2000, 135, 147–186. [Google Scholar] [CrossRef]
- Randin, C.F.; Engler, R.; Normand, S.; Zappa, M.; Zimmermann, N.E.; Pearman, P.B.; Vittoz, P.; Thuiller, W.; Guisan, A. Climate change and plant distribution: Local models predict high-elevation persistence. Glob. Chang. Biol. 2009, 15, 1557–1569. [Google Scholar] [CrossRef]
- Gehrig-Fasel, J.; Guisan, A.; Zimmermann, N.E. Tree line shifts in the swiss alps: Climate change or land abandonment? J. Veg. Sci. 2007, 18, 571–582. [Google Scholar] [CrossRef]
- Grabherr, G.; Gottfried, M.; Gruber, A.; Pauli, H. Patterns and current changes in alpine plant diversity. In Arctic and Alpine Biodiversity: Patterns, Causes and Ecosystem Consequences; Springer: Heidelberg, Berlin, Germany, 1995; pp. 167–181. [Google Scholar]
- Vittoz, P.; Jutzeler, S.; Guisan, A. Flore alpine et réchauffement climatique: Observation de trois sommets valaisans à travers le 20ème siècle. Bull. Murithienne 2006, 123, 49–59. [Google Scholar]
- Walther, G.R.; Beißner, S.; Burga, C.A. Trends in the upward shift of alpine plants. J. Veg. Sci. 2005, 16, 541–548. [Google Scholar] [CrossRef]
- Erschbamer, B.; Kiebacher, T.; Mallaun, M.; Unterluggauer, P. Short-term signals of climate change along an altitudinal gradient in the south alps. Plant Ecol. 2009, 202, 79–89. [Google Scholar] [CrossRef]
- Klanderud, K.; Birks, H.J.B. Recent increases in species richness and shifts in altitudinal distributions of norwegian mountain plants. Holocene 2003, 13, 1–6. [Google Scholar] [CrossRef]
- Le Roux, P.C.; McGeoch, M.A. Changes in climate extremes, variability and signature on sub-antarctic marion island. Clim. Chang. 2008, 86, 309–329. [Google Scholar] [CrossRef]
- Walther, G.-R.; Post, E.; Convey, P.; Menzel, A.; Parmesan, C.; Beebee, T.J.; Fromentin, J.-M.; Hoegh-Guldberg, O.; Bairlein, F. Ecological responses to recent climate change. Nature 2002, 416, 389–395. [Google Scholar] [CrossRef] [PubMed]
- Felde, V.A.; Kapfer, J.; Grytnes, J.A. Upward shift in elevational plant species ranges in Sikkilsdalen, Central Norway. Ecography 2012, 35, 922–932. [Google Scholar] [CrossRef]
- Hengl, T.; Sierdsema, H.; Radović, A.; Dilo, A. Spatial prediction of species’ distributions from occurrence-only records: Combining point pattern analysis, enfa and regression-kriging. Ecol. Model. 2009, 220, 3499–3511. [Google Scholar] [CrossRef]
- Crossman, N.D.; Bryan, B.A.; Cooke, D.A. An invasive plant and climate change threat index for weed risk management: Integrating habitat distribution pattern and dispersal process. Ecol. Indic. 2011, 11, 183–198. [Google Scholar] [CrossRef]
- Franklin, J.; Davis, F.W.; Ikegami, M.; Syphard, A.D.; Flint, L.E.; Flint, A.L.; Hannah, L. Modeling plant species distributions under future climates: How fine scale do climate projections need to be? Glob. Chang. Biol. 2013, 19, 473–483. [Google Scholar] [CrossRef] [PubMed]
- Araujo, M.B.; Guisan, A. Five (or so) challenges for species distribution modelling. J. Biogeogr. 2006, 33, 1677–1688. [Google Scholar] [CrossRef]
- Diniz-Filho, J.A.F.; Mauricio Bini, L.; Fernando Rangel, T.; Loyola, R.D.; Hof, C.; Nogués-Bravo, D.; Araújo, M.B. Partitioning and mapping uncertainties in ensembles of forecasts of species turnover under climate change. Ecography 2009, 32, 897–906. [Google Scholar] [CrossRef]
- Lawler, J.J. Climate change adaptation strategies for resource management and conservation planning. Ann. N. Y. Acad. Sci. 2009, 1162, 79–98. [Google Scholar] [CrossRef] [PubMed]
- Peterson, A.T.; Ortega-Huerta, M.A.; Bartley, J.; Sánchez-Cordero, V.; Soberón, J.; Buddemeier, R.H.; Stockwell, D.R. Future projections for mexican faunas under global climate change scenarios. Nature 2002, 416, 626–629. [Google Scholar] [CrossRef] [PubMed]
- Guisan, A.; Thuiller, W. Predicting species distribution: Offering more than simple habitat models. Ecol. Lett. 2005, 8, 993–1009. [Google Scholar] [CrossRef]
- Barbet-Massin, M.; Thuiller, W.; Jiguet, F. The fate of european breeding birds under climate, land-use and dispersal scenarios. Glob. Chang. Biol. 2012, 18, 881–890. [Google Scholar] [CrossRef]
- Braunisch, V.; Suchant, R. Predicting species distributions based on incomplete survey data: The trade-off between precision and scale. Ecography 2010, 33, 826–840. [Google Scholar] [CrossRef]
- Broennimann, O.; Fitzpatrick, M.C.; Pearman, P.B.; Petitpierre, B.; Pellissier, L.; Yoccoz, N.G.; Thuiller, W.; Fortin, M.J.; Randin, C.; Zimmermann, N.E. Measuring ecological niche overlap from occurrence and spatial environmental data. Glob. Ecol. Biogeogr. 2012, 21, 481–497. [Google Scholar] [CrossRef]
- Moreno-Rueda, G.; Pleguezuelos, J.M.; Pizarro, M.; Montori, A. Northward shifts of the distributions of spanish reptiles in association with climate change. Conserv. Biol. 2012, 26, 278–283. [Google Scholar] [CrossRef] [PubMed]
- Nazeri, M.; Jusoff, K.; Madani, N.; Mahmud, A.R.; Bahman, A.R.; Kumar, L. Predictive modeling and mapping of malayan sun bear (Helarctos malayanus) distribution using maximum entropy. PLoS One 2012. [Google Scholar] [CrossRef]
- Smith, S.E.; Gregory, R.D.; Anderson, B.J.; Thomas, C.D. The past, present and potential future distributions of cold-adapted bird species. Divers. Distrib. 2013, 19, 352–362. [Google Scholar] [CrossRef]
- Summers, D.M.; Bryan, B.A.; Crossman, N.D.; Meyer, W.S. Species vulnerability to climate change: Impacts on spatial conservation priorities and species representation. Glob. Chang. Biol. 2012, 18, 2335–2348. [Google Scholar] [CrossRef]
- Aitken, S.N.; Yeaman, S.; Holliday, J.A.; Wang, T.; Curtis-McLane, S. Adaptation, migration or extirpation: Climate change outcomes for tree populations. Evolut. Appl. 2008, 1, 95–111. [Google Scholar] [CrossRef]
- Thuiller, W.; Albert, C.; Araújo, M.B.; Berry, P.M.; Cabeza, M.; Guisan, A.; Hickler, T.; Midgley, G.F.; Paterson, J.; Schurr, F.M.; et al. Predicting global change impacts on plant species’ distributions: Future challenges. Perspect. Plant Ecol. Evol. Syst. 2008, 9, 137–152. [Google Scholar] [CrossRef]
- Araújo, M.B.; Cabeza, M.; Thuiller, W.; Hannah, L.; Williams, P.H. Would climate change drive species out of reserves? An assessment of existing reserve-selection methods. Glob. Chang. Biol. 2004, 10, 1618–1626. [Google Scholar] [CrossRef]
- Margules, C.R.; Pressey, R.L. Systematic conservation planning. Nature 2000, 405, 243–253. [Google Scholar] [CrossRef] [PubMed]
- Wenger, S.J.; Som, N.A.; Dauwalter, D.C.; Isaak, D.J.; Neville, H.M.; Luce, C.H.; Dunham, J.B.; Young, M.K.; Fausch, K.D.; Rieman, B.E. Probabilistic accounting of uncertainty in forecasts of species distributions under climate change. Glob. Chang. Biol. 2013, 19, 3343–3354. [Google Scholar] [PubMed]
- Meynard, C.N.; Migeon, A.; Navajas, M. Uncertainties in predicting species distributions under climate change: A case study using Tetranychus evansi (Acari: Tetranychidae), a widespread agricultural pest. PLoS One 2013. [Google Scholar] [CrossRef]
- Logez, M.; Bady, P.; Pont, D. Modelling the habitat requirement of riverine fish species at the european scale: Sensitivity to temperature and precipitation and associated uncertainty. Ecol. Freshw. Fish 2012, 21, 266–282. [Google Scholar] [CrossRef]
- Buisson, L.; Thuiller, W.; Casajus, N.; Lek, S.; Grenouillet, G. Uncertainty in ensemble forecasting of species distribution. Glob. Chang. Biol. 2010, 16, 1145–1157. [Google Scholar] [CrossRef]
- Pearson, R.G.; Thuiller, W.; Araújo, M.B.; Martinez-Meyer, E.; Brotons, L.; McClean, C.; Miles, L.; Segurado, P.; Dawson, T.P.; Lees, D.C. Model-based uncertainty in species range prediction. J. Biogeogr. 2006, 33, 1704–1711. [Google Scholar] [CrossRef]
- Selle, B.; Hannah, M. A bootstrap approach to assess parameter uncertainty in simple catchment models. Environ. Model. Softw. 2010, 25, 919–926. [Google Scholar] [CrossRef]
- Guilhaumon, F.; Gimenez, O.; Gaston, K.J.; Mouillot, D. Taxonomic and regional uncertainty in species-area relationships and the identification of richness hotspots. Proc. Natl. Acad. Sci. 2008, 105, 15458–15463. [Google Scholar] [CrossRef] [PubMed]
- Su, H. Studies on the climate and vegetation types of the natural forests in taiwan (i): Analysis of the variations on climatic factors. Q. J. Chin. For. 1984, 17, 1–14. [Google Scholar]
- Shih, F.-L.; Hwang, S.-Y.; Cheng, Y.-P.; Lee, P.-F.; Lin, T.-P. Uniform genetic diversity, low differentiation, and neutral evolution characterize contemporary refuge populations of taiwan fir (Abies kawakamii, Pinaceae). Am. J. Bot. 2007, 94, 194–202. [Google Scholar] [CrossRef]
- Huang, K.-Y. Evaluation of the topographic sheltering effects on the spatial pattern of taiwan fir using aerial photography and gis. Int. J. Remote Sens. 2002, 23, 2051–2069. [Google Scholar] [CrossRef]
- Taiwan Forest Bureau. The Third Forest Resource and Land Use Inventory in Taiwan; Taiwan Forest Bureau Publications: Taipei, Taiwan, 1995.
- Johns, T.; Gregory, J.; Ingram, W.; Johnson, C.; Jones, A.; Lowe, J.; Mitchell, J.; Roberts, D.; Sexton, D.; Stevenson, D. Anthropogenic climate change for 1860 to 2100 simulated with the HadCM3 model under updated emissions scenarios. Clim. Dyn. 2003, 20, 583–612. [Google Scholar]
- Seo, C.; Thorne, J.H.; Hannah, L.; Thuiller, W. Scale effects in species distribution models: Implications for conservation planning under climate change. Biol. Lett. 2009, 5, 39–43. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-P.; Cheng, B.-Y.; Chu, H.-J.; Chang, T.-K.; Yu, H.-L. Assessing how heavy metal pollution and human activity are related by using logistic regression and kriging methods. Geoderma 2011, 163, 275–282. [Google Scholar] [CrossRef]
- Lin, Y.-P.; Chu, H.-J.; Huang, Y.-L.; Cheng, B.-Y.; Chang, T.-K. Modeling spatial uncertainty of heavy metal content in soil by conditional latin hypercube sampling and geostatistical simulation. Environ. Earth Sci. 2011, 62, 299–311. [Google Scholar] [CrossRef]
- Phillips, S.J.; Dudík, M.; Elith, J.; Graham, C.H.; Lehmann, A.; Leathwick, J.; Ferrier, S. Sample selection bias and presence-only distribution models: Implications for background and pseudo-absence data. Ecol. Appl. 2009, 19, 181–197. [Google Scholar] [CrossRef] [PubMed]
- Dudik, M. Maximum Entropy Density Estimation and Modeling Geographic Distributions of Species; Dissertation Abstracts International; The Faculty of Princeton University: Princeton, NJ, USA, 2007. [Google Scholar]
- Ghosh, S.; Polansky, A.M. Smoothed and Iterated Bootstrap Confidence Regions for Parameter Vectors; Cornell University Library: Ithaca, NY, USA, 2013. [Google Scholar]
- Araújo, M.B.; Pearson, R.G. Equilibrium of species’ distributions with climate. Ecography 2005, 28, 693–695. [Google Scholar] [CrossRef]
- Barry, S.; Elith, J. Error and uncertainty in habitat models. J. Appl. Ecol. 2006, 43, 413–423. [Google Scholar] [CrossRef]
- Guisan, A.; Lehmann, A.; Ferrier, S.; Austin, M.; Overton, J.; Aspinall, R.; Hastie, T. Making better biogeographical predictions of species’ distributions. J. Appl. Ecol. 2006, 43, 386–392. [Google Scholar] [CrossRef]
- Heikkinen, R.K.; Luoto, M.; Araújo, M.B.; Virkkala, R.; Thuiller, W.; Sykes, M.T. Methods and uncertainties in bioclimatic envelope modelling under climate change. Prog. Phys. Geogr. 2006, 30, 751–777. [Google Scholar] [CrossRef]
- Thuiller, W.; Brotons, L.; Araújo, M.B.; Lavorel, S. Effects of restricting environmental range of data to project current and future species distributions. Ecography 2004, 27, 165–172. [Google Scholar] [CrossRef]
- Araújo, M.B.; New, M. Ensemble forecasting of species distributions. Trends Ecol. Evol. 2007, 22, 42–47. [Google Scholar] [CrossRef] [PubMed]
- Goovaerts, P. Geostatistical modelling of uncertainty in soil science. Geoderma 2001, 103, 3–26. [Google Scholar] [CrossRef]
- Goovaerts, P. Medical geography: A promising field of application for geostatistics. Math. Geosci. 2009, 41, 243–264. [Google Scholar] [CrossRef]
- Lin, W.-C.; Lin, Y.-P.; Wang, Y.-C.; Chang, T.-K.; Chiang, L.-C. Assessing and mapping spatial associations among oral cancer mortality rates, concentrations of heavy metals in soil, and land use types based on multiple scale data. Int. J. Environ. Res. Public Health 2014, 11, 2148–2168. [Google Scholar] [CrossRef] [PubMed]
- Arponen, A.; Heikkinen, R.K.; Paloniemi, R.; Pöyry, J.; Similä, J.; Kuussaari, M. Improving conservation planning for semi-natural grasslands: Integrating connectivity into agri-environment schemes. Biol. Conserv. 2013, 160, 234–241. [Google Scholar] [CrossRef]
- Moilanen, A. Landscape zonation, benefit functions and target-based planning: Unifying reserve selection strategies. Biol. Conserv. 2007, 134, 571–579. [Google Scholar] [CrossRef]
- Araújo, M.B.; Alagador, D.; Cabeza, M.; Nogués-Bravo, D.; Thuiller, W. Climate change threatens european conservation areas. Ecol. Lett. 2011, 14, 484–492. [Google Scholar] [CrossRef] [PubMed]
- Stott, P.A.; Kettleborough, J. Origins and estimates of uncertainty in predictions of twenty-first century temperature rise. Nature 2002, 416, 723–726. [Google Scholar] [CrossRef] [PubMed]
- Kerry, R.; Goovaerts, P.; Haining, R.P.; Ceccato, V. Applying geostatistical analysis to crime data: Car-related thefts in the baltic states. Geogr. Anal. 2010, 42, 53–77. [Google Scholar] [CrossRef]
- Hannah, L.; Midgley, G.; Andelman, S.; Araújo, M.; Hughes, G.; Martinez-Meyer, E.; Pearson, R.; Williams, P. Protected area needs in a changing climate. Front. Ecol. Environ. 2007, 5, 131–138. [Google Scholar] [CrossRef]
- Hannah, L.; Midgley, G.; Lovejoy, T.; Bond, W.; Bush, M.; Lovett, J.; Scott, D.; Woodward, F. Conservation of biodiversity in a changing climate. Conserv. Biol. 2002, 16, 264–268. [Google Scholar] [CrossRef]
- Mawdsley, J.R.; O’Malley, R.; Ojima, D.S. A review of climate-change adaptation strategies for wildlife management and biodiversity conservation. Conserv. Biol. 2009, 23, 1080–1089. [Google Scholar] [CrossRef] [PubMed]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, W.-C.; Lin, Y.-P.; Lien, W.-Y.; Wang, Y.-C.; Lin, C.-T.; Chiou, C.-R.; Anthony, J.; Crossman, N.D. Expansion of Protected Areas under Climate Change: An Example of Mountainous Tree Species in Taiwan. Forests 2014, 5, 2882-2904. https://doi.org/10.3390/f5112882
Lin W-C, Lin Y-P, Lien W-Y, Wang Y-C, Lin C-T, Chiou C-R, Anthony J, Crossman ND. Expansion of Protected Areas under Climate Change: An Example of Mountainous Tree Species in Taiwan. Forests. 2014; 5(11):2882-2904. https://doi.org/10.3390/f5112882
Chicago/Turabian StyleLin, Wei-Chih, Yu-Pin Lin, Wan-Yu Lien, Yung-Chieh Wang, Cheng-Tao Lin, Chyi-Rong Chiou, Johnathen Anthony, and Neville D. Crossman. 2014. "Expansion of Protected Areas under Climate Change: An Example of Mountainous Tree Species in Taiwan" Forests 5, no. 11: 2882-2904. https://doi.org/10.3390/f5112882
APA StyleLin, W.-C., Lin, Y.-P., Lien, W.-Y., Wang, Y.-C., Lin, C.-T., Chiou, C.-R., Anthony, J., & Crossman, N. D. (2014). Expansion of Protected Areas under Climate Change: An Example of Mountainous Tree Species in Taiwan. Forests, 5(11), 2882-2904. https://doi.org/10.3390/f5112882







