Modeling Commercial Height in Amazonian Forests: Accuracy of Mixed-Effects Regression Versus Random Forest

Abstract

Accurate estimation of commercial tree height is essential for volumetric predictions in forest management plans, particularly in Amazonian forests with high species diversity. We assessed two predictive approaches for estimating commercial height, using the sum of actual commercial log lengths as the reference metric. The dataset comprised 1745 harvested trees from Annual Production Unit 8 in the Tapajós National Forest. Three commercial volume groups dominated the structural gradient: 46.1% of the trees Group 1 (<6 m³), 36.7% into Group 2 (6–10 m³), and 17.2% into Group 3 (≥10 m³). The Linear Mixed-Effects Model included diameter at breast height (DBH) as a fixed effect and species as a random effect, whereas the Random Forest model used DBH and species as predictors. The mixed-effects model achieved higher accuracy (r = 0.77; RMSE = 2.95 m), while the Random Forest model performed slightly worse (r = 0.73; RMSE = 3.10 m). Species with greater commercial heights exerted a strong influence on both modelling approaches. Principal Component Analysis revealed structural separation among the three volume groups, driven by DBH, commercial height, number of logs, and log volume. The mixed-effects model provided effective framework for predicting commercial height in heterogeneous tropical forests.

1. Introduction

The Amazon Rainforest is the largest contiguous tropical forest on the planet. It regulates atmospheric, hydrological and climatic patterns by influencing evapotranspiration and the carbon cycle, while also maintaining essential ecological processes [1,2,3]. These attributes emphasise the global importance of conserving the forest and the need for evidence-based strategies, such as sustainable forest management, to maintain forest structure and enable the responsible use of wood [4,5]. The planned exploitation can promote natural regeneration and reduce the negative impacts of unregulated extraction [6], while reduced-impact management can protect forest remnants and maintain long-term productivity [7]. In this context, advances in Brazilian forestry and measurement have produced biometric tools that are essential for monitoring and evaluating managed forests [8,9].

Of the biometric variables fundamental to forest structure planning and assessment, tree height is a particularly important attribute in forest science [10]. However, despite its importance, accurately measuring or estimating tree height remains costly and time-consuming in forest inventories [11,12]. However, it is indispensable for calculating volume [13], assessing site quality [13,14] and improving volumetric modelling [15,16]. Additionally, height significantly contributes to the estimation of above-ground biomass and carbon, which are crucial variables in climate change and forest conservation studies [17,18].

Obtaining tree height data in native forests is challenging due to the diversity of understory species and canopy density [10,19]. Heterogeneity in tree growth and the intrinsic characteristics of each species can lead to inaccuracies in field surveys [10]. Even with sophisticated equipment such as hypsometers is available, their efficiency is reduced in native forests, as noted by [14]. Therefore, visual estimations of tree height in practice remain highly imprecise in commercial forest inventories, even with extensive field experience [20]. Refs. [21,22] found that visually estimated commercial height differs by more than 15% from direct measurements of log lengths after felling. Visual estimations of this kind require intensive training, significant field experience and frequent calibration [19,20]. Nevertheless, there is a tendency to underestimate the height of taller trees, which negatively impacts timber volume estimates [14,19,23]. Furthermore, factors such as observer fatigue and mood can also influence the accuracy of height measurements [20,24].

In forest management, various height measurements are used. These include total height, which is the distance from the ground to the top of the tree [25]; dominant height, which is an indicator of stand productivity [20,26] and is calculated using methods such as those of Hart and Assmann [27]; and commercial height, which is the distance from the base to the first branches or the point of greatest timber utility [28]. In forest plantations, the structural homogeneity between diameter at breast height (DBH) and height facilitates accuracy and enables the application of hypsometric equations [14]. Measuring log lengths after felling reduces sampling errors [29,30].

In this context, this study introduces a methodological innovation: using commercial height, determined by cubage (i.e., the actual length of logs measured in the field), as an input variable to evaluate predictive height models. This approach aims to reduce the uncertainty associated with visual height estimations. However, this variable exhibits greater variability in the height-diameter ratio than in total height. This is mainly due to the definition of measurement points, which should be utilized more extensively in the timber industry and vary according to the characteristics of the exploited species. This implies low accuracy when applying traditional regression methods, so more effective methods must be sought to achieve better results.

Traditional regression approaches, whether linear or nonlinear, assume a homogeneous relationship between diameter and height across the population, as well as independence and homoscedasticity of residuals. These assumptions are rarely met in managed Amazonian forests, where trees are hierarchically structured by species, stem quality and operational units, and where commercial height exhibits high variability due to ecological and silvicultural factors. As a result, conventional regression models often fail to adequately represent the complexity of height–diameter relationships when commercial height is derived from actual log lengths, leading to biased estimates and limited generalization capacity.

In this context, Linear Mixed-Effects Models (LMM) provide a statistically coherent framework for modelling commercial height, as they explicitly account for the hierarchical structure of forest data by incorporating random effects associated with species and other grouping factors. By separating population-level trends from group-specific deviations, LMMs allow for the representation of both interspecific and intraspecific variability, improving parameter estimation and predictive reliability under heterogeneous forest conditions [31,32,33]. Complementarily, machine learning algorithms such as Random Forest offer a flexible, non-parametric alternative for height prediction, as they do not require predefined functional forms and are capable of capturing complex nonlinear relationships and interactions among predictor variables. Random Forest models are particularly robust to collinearity, noise and outliers, which are common in operational forest datasets, and have demonstrated strong predictive performance in forest and agricultural sciences [34,35,36]. In this study, Random Forest is used not only as a predictive tool but also as a benchmark to assess the potential gains in accuracy achievable when relaxing the assumptions inherent to parametric models.

This research focuses on two questions. How accurate are predictive frameworks such as mixed-effects regression and Random Forest when estimating commercial height using actual log length as reference? How much do they improve the accuracy and reliability of forest inventories in the Amazon?

Our objective was to develop and compare predictive models for commercial height using field variables measured in the APU under real operational conditions.

2. Materials and Methods

2.1. Study Area

The study was conducted in the TNF (Flona Tapajós), a Sustainable Use Conservation Unit located in western Pará State, Brazil. This protected area spans the municipalities of Santarém, Belterra and Aveiro. Established in 1974, TNF covers approximately 527,000 ha of dense ombrophilous Amazon rainforest, characterized by high biological diversity and substantial relevance for natural resource conservation [37,38]. The forest forms part of Brazil’s National System of Conservation Units and serves as a model for SFM in the Amazon [9].

It was focused on Annual Production Unit 8 (APU 8), located within the Sustainable Forest Management Area at kilometer 67 of the BR-163 highway (Santarém–Cuiabá) (Figure 1). The Tapajós National Forest Mixed Cooperative (Coomflona) holds a non-revenue public forest concession for this area and implements forest management according to the plan approved by the Chico Mendes Institute for Biodiversity Conservation [39].

The regional climate is classified as Am₃ under the Köppen system, following the adaptation proposed by [40] and the updated Amazon climate regionalization developed by [41]. In Belterra, mean annual temperature ranges from 25.5 °C to 27 °C, annual rainfall varies between 2000 mm and 2500 mm, and means relative humidity is about 87% [42].

Vegetation is dominated by dense ombrophilous submontane forest, typical of western Pará [43]. The terrain includes flat to gently undulating surfaces, with elevations between 100 and 200 m. The predominant soils are latosols, argisols and quartzarenic neosols, characterized by medium to clayey textures, low natural fertility and good drainage [39]. The forest contains valuable timber species such as Manilkara huberi, Dinizia excelsa, Mezilaurus itauba, Handroanthus serratifolius and Hymenaea courbaril [44].

Long-term research conducted in Flona Tapajós has contributed significantly to understanding forest dynamics, biodiversity conservation and ecosystem services [9,38,45]. The site has also supported international studies on carbon storage in tropical forests and the socio-environmental sustainability of traditional communities [37,38].

2.2. Database and Analysis

Data were obtained from the forest census inventory and the post-harvest report for APU 8, required under Brazilian forest management regulations. The census inventory provided diameter at breast height (DBH), measured at 1.30 m above ground. The post-harvest report contained detailed information on log length and log volume.

Commercial height was defined as the sum of the lengths of all commercial logs measured after tree felling. Measurements were taken directly in the storage yard using a measuring tape. Diameters at both ends of each log were recorded, and actual log volume was computed using Smalian’s equation:

$$V_{Smalian}=({\displaystyle \frac{g_1+g_2}{2}})L$$

(1)

where V_Smalian = Smalian volume, in m³; g₁ and g₂ = cross-sectional areas of the log ends, in m²; L = log length, in m.

This integration of field data provides robust estimates of harvested-tree yield and supports the evaluation of sustainable forest management practices [9,38]. A total of 2948 commercial trees from 26 species were felled on APU 8. From these, 1745 trees were selected for modeling. Selection was based on a maximum difference of ±20% between inventory-estimated and measured commercial heights, a threshold that reflects the visual nature of pre-harvest height estimates. The sum of measured log lengths was therefore used as the reference commercial height.

We fitted Linear Mixed-Effects Models (LMM) and Random Forest (RF) models to analyze how each method represents the structural variability of this Amazonian forest [31]. Two modeling frameworks were evaluated: a parametric LMM and a non-parametric RF algorithm.

In the LMM, we treated species as random effects. We compared a simpler linear model and a more complex quadratic model using a likelihood ratio test. The test indicated that the quadratic structure significantly improved model fit, so we included both DBH and DBH² as fixed predictors of commercial height. This specification captures the general DBH–height relationship within the observed DBH range while allowing species-specific deviations through the random intercept. The general model is expressed as:

$$H{c}_{ij}=({\beta }_0+b_{0j})+({\beta }_1+b_{1j})DB{H}_{ij}+{\beta }_{2}DB{H}_{ij}^2+{\epsilon }_{ij}$$

(2)

in which $H{c}_{ij}$ is the commercial height (m), $DB{H}_{ij}$ is the diameter at breast height (cm), ${\beta }_0,{ \beta }_1,{ \beta }_2$ are fixed coefficients, $b_{0j}$ and $b_{1j}$ are species-specific random effects, and ${\epsilon }_{ij}$ is the residual error with ${\epsilon }_{ij}\sim N(0,{\sigma }_j^2)$, for i-th tree and j-th species and ${\sigma }_j^2$ being the residual variance adjusted for the j-th species.

The Random Forest model used 70% of the data for training and 30% for validation. Predictor variables included continuous DBH and categorical species. Commercial height was the response variable. Two basic hyperparameters ran the RF model: (a) ntree: number of trees created from the bootstrap samples selection and (b) mtry: number of predictors randomly sampled to gather each node of the trees. After some preliminary tests, we set ntree = 1000 and mtry = 1, a value which corresponds to one-third of the total number of variables, as recommended for regression by [46]. We encoded species using one-hot transformation to allow their inclusion in the model.

We evaluated model performance using the residuals correlation coefficient ($r_{y\widehat{y}}$), Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), Mean Percentage Deviation (MPD%), and Mean Bias (BIAS):

$$r_{y\widehat{y}}={\displaystyle \frac{\sum (Y_I-Y^{-})({\widehat{Y}}_I-{\widehat{Y}}^{-})}{\sqrt{\sum (Y_I-Y^{-}{)}^2\sum ({\widehat{Y}}_I-{\widehat{Y}}^{-}{)}^2}}}$$

(3)

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}\sum (Y_I-{\widehat{Y}}_I{)}^2}$$

(4)

$$MAE={\displaystyle \frac{1}{N}}\sum \mid Y_I-{\widehat{Y}}_I\mid$$

(5)

$$MPD\%={\displaystyle \frac{1}{N}}\sum ({\displaystyle \frac{Y_I-{\widehat{Y}}_I}{Y_I}})\times 100$$

(6)

$$BIAS={\displaystyle \frac{1}{N}}\sum (Y_I-{\widehat{Y}}_I),$$

(7)

in which $y_i$ and ${\widehat{y}}_i$ are observed and predicted commercial heights, respectively, and nis the number of observations.

All analyses were conducted in R (version 4.4.2) [47]. We fitted the Linear Mixed-Effects Model using the nlme package (version 3.1.166) and implemented the Random Forest model and variable importance analyses using the randomForest package (version 4.7.1.2).

It is worth noting that we verified all assumptions of the Linear Mixed-Effects Model (LMM). We assessed residual normality using Q–Q plots, the Shapiro–Wilk test, and visual inspection of skewness and heavy-tail behavior. We evaluated homoscedasticity by inspecting residuals versus fitted values and by examining species-level residual patterns. To address potential collinearity between DBH and DBH², we centered DBH at its overall mean before computing the squared term. We quantified remaining collinearity using the Variance Inflation Factor (VIF), which indicated acceptable levels for all predictors. All model diagnostics showed satisfactory behavior after these adjustments, supporting the suitability of the quadratic LMM within the observed DBH range.

3. Results

The performance statistics obtained during model fitting and validation appear in

Table 1. Performance statistics of the Linear Mixed-Effects Model and the Random Forest model for commercial height estimation.

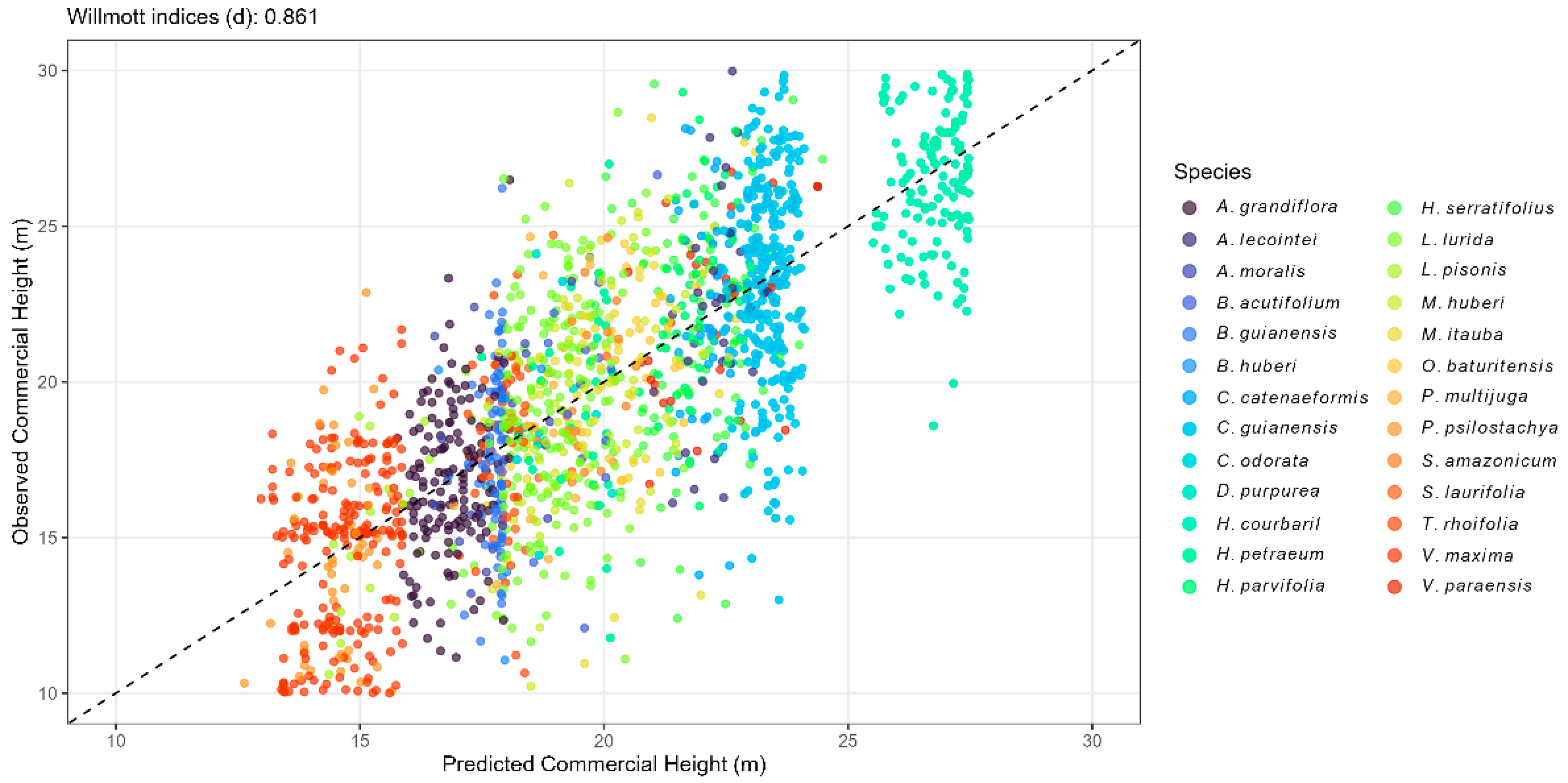
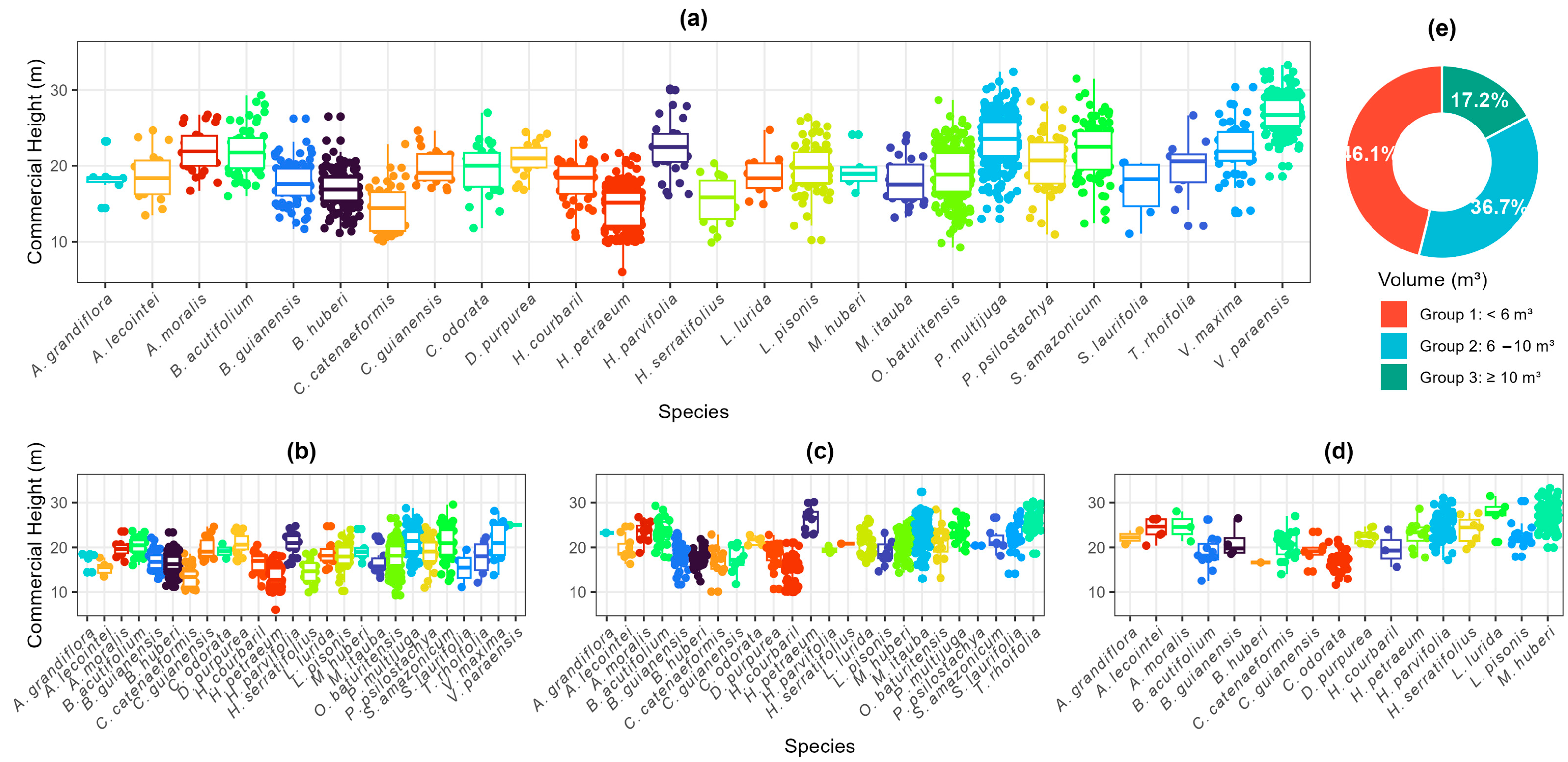
Statistics	Linear Mixed-Effects Model	Random Forest
$r_{y\widehat{y}}$	0.77	0.73
RMSE	2.95	3.10
MAE	2.33	2.44
MPD%	−2.62	−2.76
BIAS	0.002	−0.05

.

The analysis showed that the Linear Mixed-Effects Model surpassed the Random Forest in all performance metrics and demonstrated superior predictive ability for estimating the commercial height of harvested trees in APU 8. The correlation between observed and predicted values reached 0.77 for the mixed-effects model and 0.73 for the Random Forest. This difference indicates that the mixed-effects model captured the natural variability of the data more effectively, especially the structural effects introduced by species and stem quality classes.

Regarding precision, the mixed-effects model produced lower mean errors in both absolute terms (MAE = 2.33) and squared terms (RMSE = 2.95) compared to the Random Forest (MAE = 2.44 and RMSE = 3.10). These results confirm that the mixed-effects model generated predictions that were more stable and closer to the observed measurements. This level of precision is crucial for applications such as harvest planning and timber yield estimation.

The Mean Percentage Deviation (MPD%) showed underestimation in both adjustments, with a lower value for the mixed effects model (−2.62%) and −2.76% for Random Forest. The linear mixed-effects model (LMM), which incorporated species as a random effect, showed a bias of 0.002, indicating no systematic tendency to overestimate or underestimate. Similarly, the Random Forest algorithm produced a bias of –0.05, which is also very close to zero, revealing its robust performance even in the face of high floristic heterogeneity. Thus, both models produced unbiased predictions for commercial height estimation.

The estimated coefficients of the mixed-effects model confirmed a consistent quadratic–linear relationship between the predictor variables and the commercial tree heights in APU 8. The fixed effect associated with DBH was positive (0.142190, standard error 0.0328839), and the coefficient for DBH² was negative (−0.000499, standard error 0.0001653). The positive linear term and the negative quadratic term describe a concave growth curve, in which height increases with DBH but at a decreasing rate as the diameter becomes larger. The complete set of fixed effects appears in

Table 2. Estimated coefficients and standard errors for the fixed effects of the Linear Mixed-Effects Model.

Type of Effect	Group or Variable	Parameter or Levels	Estimate	Standard Error
Fixed Effect	Intercept	${\beta }_0$	11.196970	1.7269491
	DBH	${\beta }_1$	0.142190	0.0328839
	DBH2	${\beta }_2$	−0.000499	0.0001653

.

The results presented in

Table 3. Species-specific random effects and adjusted coefficients estimated by the Linear Mixed-Effects Model.

		Random Effects
Species	Representation	b0 (Rand. Intercept)	b1 (Rand. Slope)	(β0 + b0ⱼ)	(β1 + b1ⱼ)
Alexa grandiflora Ducke	Ag	−1.5227	−0.0127	9.6743	0.1295
Astronium lecointei Ducke	Al	2.7863	0.0062	13.9832	0.1484
Apuleia moralis Spruce ex Benth.	Am	−3.3846	0.0134	7.8124	0.1556
Brosimum acutifolium Huber	Ba	−0.8260	0.0086	10.3709	0.1508
Bagassa guianensis Aubl.	Bg	2.0093	−0.0452	13.2063	0.0970
Buchenavia huberi Ducke	Bh	−1.6343	−0.0034	9.5627	0.1388
Cedrelinga catenaeformis Ducke	Cc	4.6445	−0.0260	15.8414	0.1162
Couratari guianensis Aubl.	Cg	5.1793	−0.0180	16.3763	0.1242
Cedrela odorata L.	Co	−1.2278	0.0043	9.9692	0.1465
Diplotropis purpurea (Rich.) Amshoff	Dp	1.1351	−0.0081	12.3321	0.1340
Hymenaea courbaril L.	Hc	6.7646	−0.0044	17.9616	0.1378
Hymenolobium petraeum Ducke	Hp	−1.2825	0.0010	9.9145	0.1432
Hymenaea parvifolia Huber	Hpa	2.8247	−0.0028	14.0216	0.1394
Handroanthus serratifolius (Vahl) Nichols.	Hs	1.8504	0.0106	13.0473	0.1528
Lecythis lurida (Miers) S.A. Mori	Ll	−1.5838	0.0158	9.6132	0.1580
Lecythis pisonis Cambess.	Lp	−6.0406	0.0235	5.1564	0.1656
Manilkara huberi (Ducke) Chevalier	Mh	−2.2909	0.0280	8.9061	0.1702
Mezilaurus itauba (Meisn.) Taub. ex Mez	Mi	−0.8588	0.0216	10.3381	0.1638
(conclusion) Ocotea baturitensis Vattimo	Ob	3.3957	−0.0149	14.5927	0.1272
Parkia multijuga Benth.	Pm	−1.0481	0.0057	10.1488	0.1479
Pseudopiptadenia psilostachya (Benth.) G.P. Lewis & L. Rico	Pp	−4.3135	−0.0076	6.8834	0.1346
Schizolobium amazonicum Huber ex Ducke	Sam	0.9222	0.0030	12.1192	0.1452
Swartzia laurifolia Benth.	Sl	−0.5173	0.0075	10.6797	0.1497
Trattinnickia rhoifolia Willd.	Tr	0.3874	−0.0256	11.5844	0.1166
Vochysia maxima Ducke	Vm	−5.5428	0.00063	5.6542	0.1428
Vatairea paraensis Ducke	Vp	0.1743	0.0190	11.3713	0.1612

show that the random effects associated with the intercept and the linear slope within species captured the strong structural heterogeneity of the managed forest in APU 8. The model intercept was 11.196970 (standard error 1.7269491), representing the expected commercial height for the baseline DBH condition. This value expresses the central tendency of the dataset, while the random effects revealed species-specific deviations driven by morphological and architectural traits. The residual standard deviation was 3.65 for the intercept, indicating the dispersion of species intercepts around the model intercept, and 0.027 for the linear slope. In addition, the negative correlation (−0.627) between the two shows that species with larger intercepts tend to have smaller slopes, meaning that species reaching greater average heights tend to exhibit lower rates of height increase as DBH enlarges.

The random intercepts and slopes highlighted marked differences among species. H. courbaril, C. guianensis, and C. catenaeformis showed the highest positive coefficients, all above 4, with notable contributions from H. courbaril (6.7646) and C. guianensis (5.1793). These species possess intrinsic structural characteristics that promote the formation of long and straight boles, which are highly valued for industrial timber production. In contrast, species such as L. pisonis (−6.0406), V. maxima (−5.5428), and P. psilostachya (−4.3135) exhibited pronounced negative coefficients. These patterns reflect morphological limitations, including crown expansion, early bifurcation, or stem irregularities, all of which reduce their potential to produce commercially desirable heights, even in individuals with large diameters.

Figure 2 presents the relationship between the observed and predicted commercial heights obtained from the Linear Mixed-Effects Model, together with the Willmott index (d), which quantifies the global agreement between predictions and observations. The Linear Mixed-Effects Model achieved a Willmott index of 0.861, indicating moderate predictive efficiency and showing that the model captures the overall structure of the height–diameter relationship in the dataset. The scatter plot shows a clear positive association between observed and predicted values, demonstrating that the model identifies the general tendency of increasing commercial height with increasing DBH.

However, the wide dispersion of points around the 1:1 line, particularly among trees with low and intermediate commercial heights, reveals substantial prediction uncertainty. This dispersion suggests that the Random Forest model loses precision for individuals that deviate from the central structure of the dataset. The larger spread of points at both extremes of observed height indicates that the model does not fully represent the structural variability among species, nor the effects of bole form and crown architecture on height allocation. This graphical behavior is consistent with the numerical performance metrics, which showed higher RMSE and MAE for the Random Forest compared to the Linear Mixed-Effects Model.

Taken together, the graphical evidence and the Willmott index confirm that, although the Random Forest captures the general trend of commercial height, it underperforms for extreme values and for species with strong architectural differentiation. These limitations reinforce the superior predictive accuracy of the Linear Mixed-Effects Model, which better represents the biological and structural gradients that drive commercial height in heterogeneous tropical forests.

Figure 3 shows the updated distribution of commercial heights across all species and highlights the structural heterogeneity of the managed forest in APU 8. Figure 3a presents species-specific boxplots that display the full variability observed in commercial tree height. These distributions reveal marked differences among species, with some species showing narrow ranges of commercial height and others showing broad dispersion, which reflects contrasting architectural forms, growth strategies, and bole quality.

Figure 3b–d refine this interpretation by presenting commercial height distributions within three commercial volume groups. Figure 3b shows trees with volumes lower than 6 m³, which represent the majority of individuals and show the greatest height dispersion relative to their commercial value. Figure 3c presents trees with intermediate volumes, from 6 to 10 m³, and shows a more concentrated distribution of commercial height, indicating a stronger relationship between height and diameter in this volume range. Figure 3d shows the largest trees, with volumes greater than 10 m³, which display more consistent commercial heights but appear in much lower density.

Figure 3e provides a new quantitative summary of the dataset and shows the proportion of trees in each commercial volume class. Group 1 (<6 m³) represents 46.1% of all individuals. Group 2 (6 to 10 m³) represents 36.7%, and Group 3 (>10 m³) accounts for 17.2%. These precise values were not available in earlier versions of the figure and now provide a clearer understanding of the forest’s structural profile.

The improved figure offers a comprehensive view of how commercial height varies across species and commercial volume groups. It highlights the predominance of smaller-volume trees in the forest and shows how species-specific architecture influences the distribution of commercial height.

Figure 4 presents the updated species-specific curves estimated by the Linear Mixed-Effects Model. Figure 4a overlays the fitted curves on the observed commercial heights for all species, allowing direct comparison between predicted responses and empirical data. The combined visualization highlights the strong structural heterogeneity of the managed forest in APU 8, as each fitted trajectory follows a distinct shape and slope.

Figure 4b displays the fitted curves separately for each species. This representation makes clear that commercial height does not follow a monotonic pattern across species. For several species, such as H. courbaril, C. guianensis, and M. huberi, the model produces steep and consistently increasing curves, indicating substantial gains in commercial height with increasing DBH. In contrast, other species exhibit curves that plateau or even decrease after reaching a maximum point, as observed in V. maxima, P. psilostachya, and L. pisonis.

It is important to clarify that this decreasing pattern does not represent a biological decline in height. Commercial height reflects the sum of merchantable log lengths, which depends on operational criteria such as cutting decisions, bole defects, branching, and standards of log utilization. Because these operational factors can reduce the number or length of usable logs at larger diameters, the commercial height curve may decrease even though total tree height continues to increase biologically. The quadratic form of the model naturally captures this behavior, with the maximum commercial height occurring at the vertex of the curve, which can be obtained analytically from the first derivative.

Overall, the species-specific panels show that each species presents a distinct allometric trajectory shaped by both biological attributes (architecture, crown form, bole taper) and operational factors that define commercial utilization. The mixed-effects model successfully accommodates this variability, confirming its ability to represent species-level structural patterns. This capability strengthens its applicability in forest management, particularly in harvest planning and timber yield estimation, where species differences directly influence commercial volume distribution.

Figure 5 presents the PCA biplot that summarizes the multivariate structure of the dataset and illustrates how trees cluster according to commercial volume classes. The first principal component (PC1), which explains most of the total variability (65.3%), is jointly driven by DBH, commercial height, log volume, and log production (i.e., the number of commercial logs obtained from each tree). Trees positioned on the positive side of PC1 generally have larger diameters, higher log volumes, and greater log production, whereas negative PC1 scores correspond to smaller trees with reduced commercial yield. The second principal component (PC2) captures additional variation that is primarily associated with commercial height. The orientation of the commercial height vector shows a positive contribution to both PC1 and PC2, indicating that taller trees tend to occupy intermediate to high structural positions within the PCA space.

Three distinct clusters appear in accordance with the commercial volume groups. Group 1 (<6 m³), shown in red, lies on the left side of the biplot and includes trees with smaller DBH, fewer commercial logs, and lower commercial heights. Group 2 (6–10 m³), shown in blue, occupies the central region and represents intermediate structural conditions, with moderate values for DBH, commercial height, and log production. Group 3 (≥10 m³), shown in green, appears on the right side of the PCA space and comprises trees with the largest diameters, highest log volumes, and the greatest log production.

The arrangement of individuals along PC1 and PC2 demonstrates that DBH, commercial height, and log production jointly define the main structural gradient of harvested trees in APU 8. The PCA provides a clear visualization of how these variables interact and how they determine the commercial volume classes observed in the forest.

4. Discussion

Previous studies have shown that mixed-effects models perform strongly in forest modeling [48,49,50], particularly when data present hierarchical organization and substantial structural variability [51,52]. The mixed-effects models respond effectively to variation among species and sites without requiring species-specific calibrations [53]. This advantage is especially relevant for tropical forests, where taxonomic diversity and structural heterogeneity create conditions that challenge traditional modeling approaches. The including random effects improves the accuracy of height–diameter equations in uneven-aged forests, a common condition across the Brazilian Amazon [54,55]. These findings align with the results of [56], treating species as a random effect enhances allometric predictions in highly diverse ecosystems.

Although the Random Forest (RF) algorithm showed lower predictive accuracy than the mixed-effects model in this study, it demonstrated robustness and flexibility. When investigating the potential and accuracy of the relationships between metrics derived from LiDAR and forest inventory data for predicting above-ground biomass in Amazonian forests under selective cutting regimes, ref. [57] obtained better results using a Generalized Linear Model (GLM) than with different machine learning techniques, including Random Forest.

Random Forest can handle nonlinear relationships, interactions and multicollinearity, which are frequent characteristics of ecological data [34,58]. In their study of tropical forest, ref. [59] confirmed the effectiveness of the Random Forest algorithm for estimating forest structural parameters using field and remote sensing data in Paragominas, Brazil. Their results support our conclusion that Random Forest can accurately model forest attributes in complex, biodiverse environments. However, there are limitations in predicting extreme values, as demonstrated by the dispersion patterns in Figure 4b of this study.

Ref. [60] provided a comprehensive review of the strengths of this method for ecological applications. Similarly, refs. [61,62] emphasized the predictive advantages of Random Forest in complex settings where parametric assumptions are difficult to meet. In the present study, the algorithm captured the general trend of commercial height, but the dispersion pattern in Figure 2 confirms lower precision at the extremes and reflects its higher RMSE and MAE values.

Interpretability also plays a central role when choosing a predictive approach for forest management. Importantly, when choosing between LMM and Random Forest, consider not only predictive accuracy, but also the interpretability of the model. The machine-learning algorithms often lack transparency regarding the biological and ecological mechanisms involved in predictions [63]. Mixed-effects models, in contrast, provide explicit estimates of fixed and random components, which allow researchers and managers to understand how species and other structural factors influence the modeled attribute [64]. This interpretability is essential for applied forestry, where management decisions depend on understanding not only prediction outcomes but also the underlying ecological processes. Ref. [65] suggested that hybrid modeling strategies may combine the interpretability of statistical models with the flexibility of machine learning, which could lead to even better predictive performance while maintaining ecological transparency.

The decision to center DBH before computing the quadratic term improved both the numerical stability and the interpretability of the mixed-effects model. Centering reduces the collinearity between DBH and DBH², produces more stable coefficient estimates, and ensures that the parameters retain biological meaning. This procedure also prevents unrealistic model behavior, such as implausible intercepts or curvature patterns that can arise when uncentered polynomial terms are used.

Studies in ecological regression demonstrate that centering and rescaling continuous predictors enhance model robustness and improve the interpretation of regression coefficients in both simple and multilevel frameworks [66,67,68]. By incorporating centered DBH, the present study aligns with these best practices and provides species-specific curves that are more coherent and analytically reliable.

The practical implications of these findings for SFM in the Amazon are significant. Accurate predictions of commercial height can enhance forest inventory precision, improve operational planning, and optimize timber yield estimations. This contributes to reducing waste and environmental impacts. Integrating advanced modeling techniques, such as mixed-effects models and machine learning, is a promising way to modernize forest management and ensure exploitation aligns with sustainability objectives.

This methodological approach strengthens the relationship between diameter and commercial height modelled in this study, providing a solid basis for future studies seeking to represent the allometric structure or commercial attributes of heterogeneous tropical forests. However, we recognize that further studies are needed to validate the methodology in environments with different floristic compositions and to improve it for use in other Amazonian environments. Furthermore, future studies should continue to explore techniques such as machine learning, which are capable of handling the complex data structures found in this study.

5. Conclusions

We identified three structural groups among the species, each defined by distinct patterns of stem form, crown architecture and growth strategies. The first group included species with slender individuals and lower commercial heights, which tend to respond more strongly to competition. The second group consisted of species with intermediate structural conformation and a more stable diameter and height relationship. The third group comprised species of larger stature, whose individuals often reach upper canopy positions and exhibit greater commercial height. This grouping showed that the hypsometric structure of the forest depends primarily on interspecific differences rather than on individual variability alone.

The Principal Component Analysis supported this interpretation by demonstrating that DBH, slenderness ratio and total height contributed most to distinguishing species. The organization of species in the factorial plane revealed consistent structural gradients and confirmed that the stand is not homogeneous. These multivariate results indicate that growth allocation strategies and stem morphology explain much of the variation observed in commercial height.

The evaluation of the predictive models emphasized the influence of this structural complexity. The Random Forest model captured the general pattern of increasing height with increasing diameter, but it produced wide dispersion across the species groups and showed higher RMSE and MAE values. Its Willmott index of 0.861 indicated only moderate agreement with observed data and revealed that the model could not represent the structural variability of the stand with sufficient precision.

The Linear Mixed-Effects Model showed better performance because it incorporated variation among species. This model accounted for differences in height allocation and stem form. As a result, it reduced prediction errors and generated more consistent estimates across the full diameter range. Its behavior also agreed with the structural patterns revealed by the cluster analysis and the Principal Component Analysis, which demonstrates that hierarchical models are more suitable for forests with high species diversity and complex structure.

The combined evidence from structural grouping, the multivariate evaluation and the predictive modeling shows that reliable estimation of commercial height in managed Amazonian forests requires explicit representation of interspecific variability. Mixed-effects models provide more accurate estimates for volume calculation, biomass assessment and planning in concession areas. These findings support the use of hierarchical modeling approaches as a priority in continuous forest inventories and in decision-making processes for forest management in the Amazon.