A Statistical Methodology for Evaluating the Potential for Poleward Expansion of Warm Temperate and Subtropical Plants Under Climate Change: A Case Study of South Korean Islands
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.3. Method
3. Methodology: Statistical Analysis
3.1. Mathematical Model
3.2. Parameter Estimation
3.3. Significance Test
3.3.1. Likelihood Ratio Test for the Residuals
3.3.2. Chi-Square Test for Two Times Negative Log-Likelihood Ratio
3.4. Evaluation
3.4.1. Meaning of the Parameters
3.4.2. Direction of Expansion
4. Results
4.1. Mathematical Model
4.2. Parameter Estimation
4.3. Significance Test
4.4. Evaluation
5. Discussion
5.1. Evaluation of the Proposed Methodology
5.2. Functional Range Shifter Stage Analysis for WTS Plant
5.2.1. Similar Patterns Across All Models
5.2.2. A Long Tail in the North: The Role of 35° N
5.2.3. Latitudinal Patterns of the WTS Plant Species Richness Around the 35° N Threshold
5.2.4. Key Species That Require Further Observation and the Need for Classification
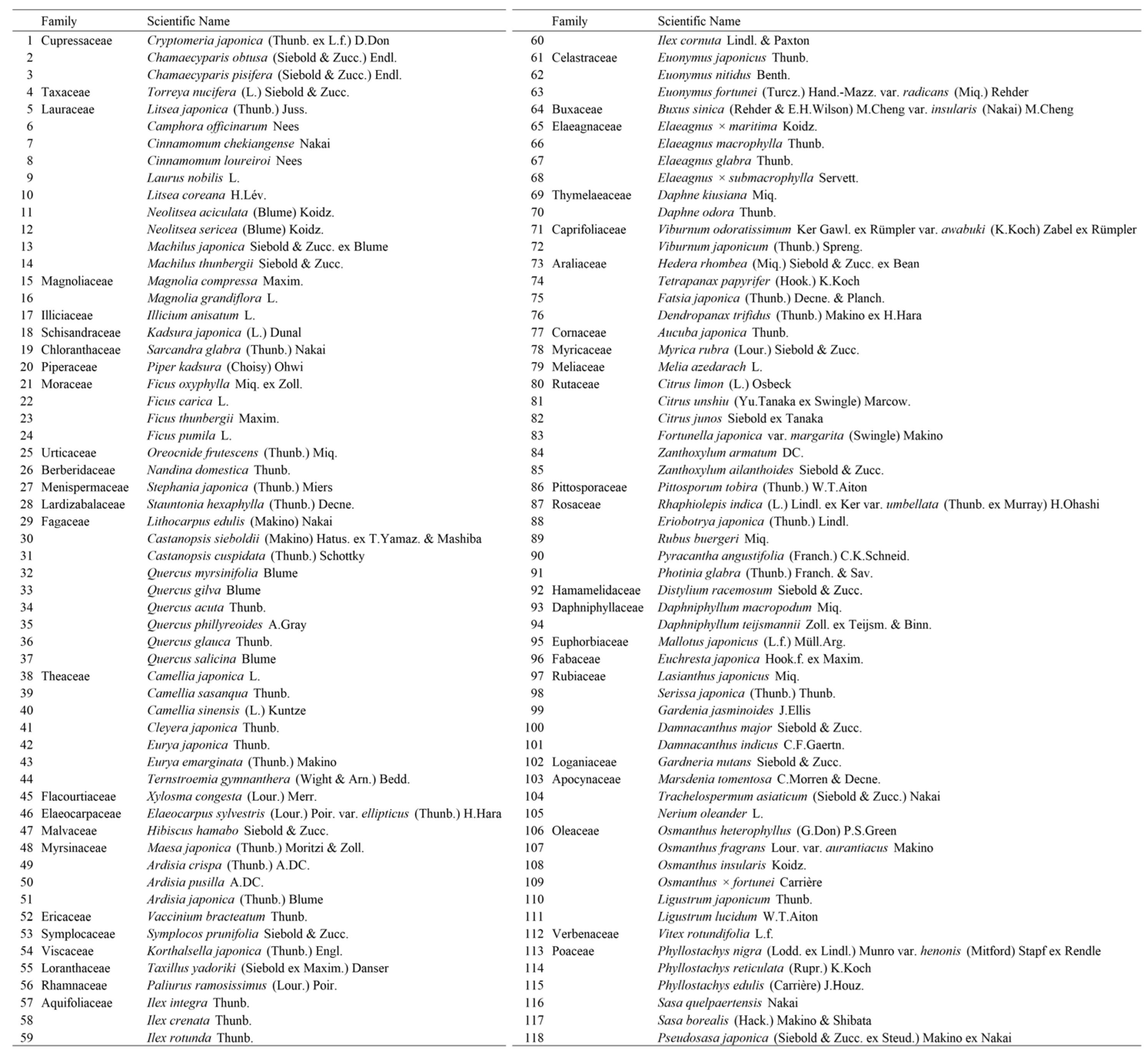
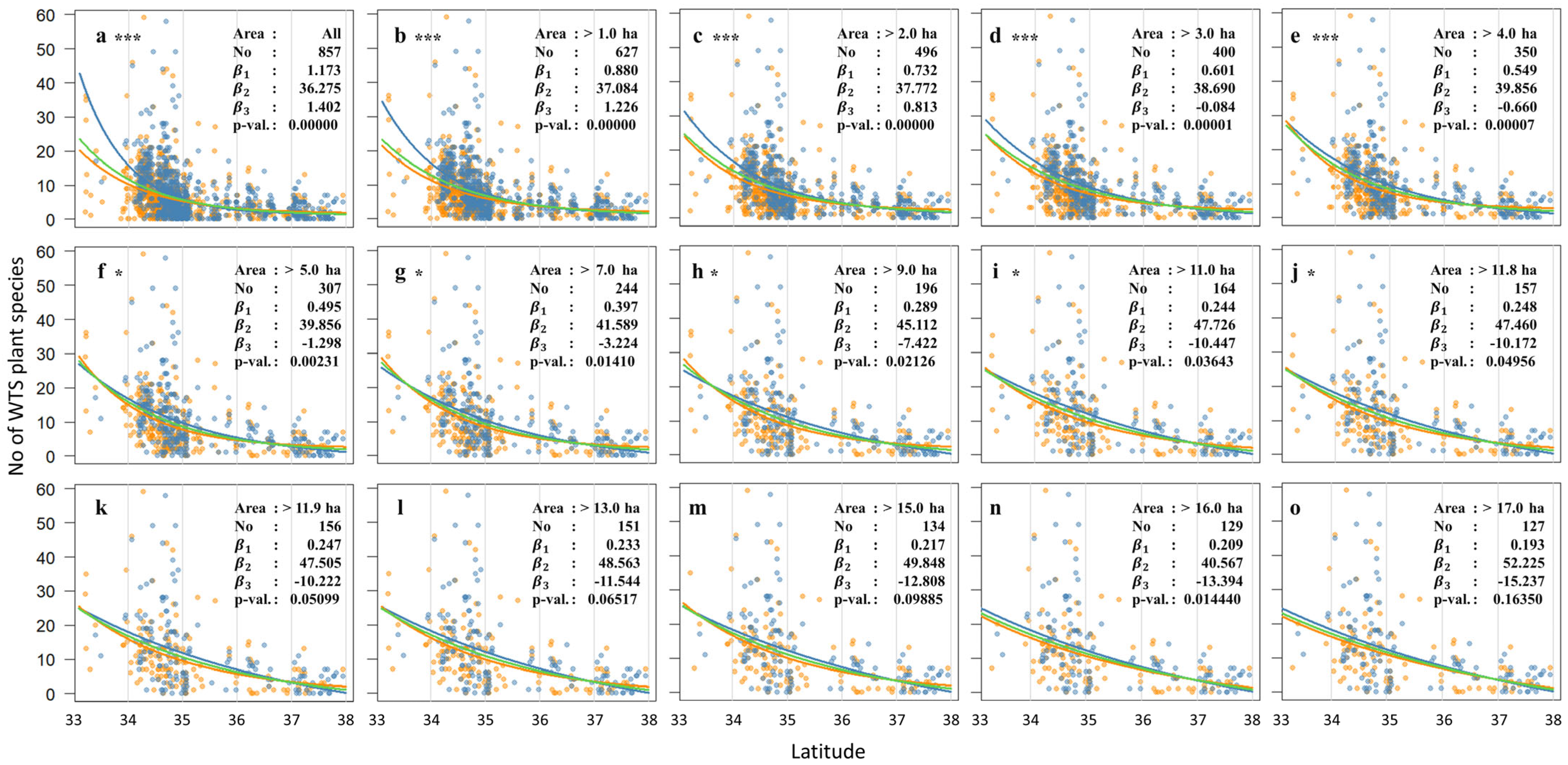
5.2.5. Relationship Between Island Area and Climate-Driven Distribution Shift of WTS Plants
5.3. Global Applicability
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WTS | Warm Temperate and Subtropical |
| df, DF | Degrees of Freedom |
| LR | Likelihood Ratio |
| LRT | Likelihood Ratio Test |
| SM | Simple Model |
| MM | Multi-variable Model |
| FM | Fixed Model |
| TM | Transformed Model |
| SoSM | Sum of Standardized Marginals |
Appendix A
References
- Dong, J.; Xiao, X.; Zhang, G.; Menarguez, M.A.; Choi, C.Y.; Qin, Y.; Luo, P.; Zhang, Y. Northward expansion of paddy rice in northeastern. Geophys. Res. Lett. 2016, 43, 3754–3761. [Google Scholar] [CrossRef]
- Fält-Nardmann, J.J.J.; Tikkanen, O.-P.; Ruohomäki, K.; Otto, L.-F.; Leinonen, R.; Pöyry, J.; Saikkonen, K.; Neuvonenh, S. The recent northward expansion of Lymantria monacha in relation to realized changes in temperatures of different seasons. For. Ecol. Manag. 2018, 427, 96–105. [Google Scholar] [CrossRef]
- Hu, Q.; Han, Z. Northward expansion of desert climate in Central Asia in recent decades. Geophys. Res. Lett. 2022, 49, e2022GL098895. [Google Scholar] [CrossRef]
- Li, H.; Ali, A.; Luo, X.; Liao, K.; Sun, N.; Xu, M.; Sha, L.; He, D.; Du, Y.; Sun, W.; et al. China’s subtropical deciduous plants are more sensitive to climate change than evergreen plants by flowering phenology. Glob. Change Biol. 2024, 30, e17168. [Google Scholar] [CrossRef]
- Viznovych, V.; Zamoroka, A. The northward range shifting of Agapanthiola leucaspis under climate change. J. Vasyl Stefanyk Precarpathian Natl. Univ. 2022, 9, 33–41. [Google Scholar] [CrossRef]
- Sanczuk, P.; Verheyen, K.; Lenoir, J.; Zellweger, F.; Lembrechts, J.J.; Rodríguez-Sánchez, F.; Baeten, L.; Bernhardt-Römermann, M.; De Pauw, K.; De Frenne, P.; et al. Unexpected westward range shifts in European forest plants link to nitrogen deposition. Science 2024, 386, 193–198. [Google Scholar] [CrossRef]
- Ash, J.D.; Givnish, T.J.; Waller, D.M. Tracking lags in historical plant species’ shifts in relation to regional climate change. Glob. Change Biol. 2017, 23, 1305–1315. [Google Scholar] [CrossRef] [PubMed]
- Anderson, C.M.; Jeff Wu, C.F. Dispersion Measures and Analysis for Factorial Directional Data with Replicates. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1996, 45, 47–61. [Google Scholar] [CrossRef]
- Harrison, D.; Kanji, G.K.; Gadsden, R.J. Analysis of variance for circular data. J. Appl. Stat. 1986, 13, 123–138. [Google Scholar] [CrossRef]
- Lehikoinen, A.; Virkkala, R. North by north-west: Climate change and directions of density shifts in birds. Glob. Change Biol. 2016, 22, 1121–1129. [Google Scholar] [CrossRef]
- Watson, G.S.; Williams, E.J. On the Construction of Significance Tests on the Circle and the Sphere. Biometrika 1956, 43, 344–352. [Google Scholar] [CrossRef]
- Banerjee, A.; Dhillon, I.S.; Ghosh, J.; Sra, S. Clustering on the unit hypersphere using von Mises–Fisher distributions. J. Mach. Learn. Res. 2005, 6, 1345–1382. [Google Scholar]
- Mardia, K.V. Statistics of Directional Data; Academic Press: London, UK, 1972. [Google Scholar]
- Mardia, K.V. Statistics of Directional Data. J. R. Stat. Soc. Ser. B (Methodol.) 1975, 37, 349–393. [Google Scholar] [CrossRef]
- Taghia, J.; Ma, Z.; Leijon, A. Bayesian estimation of the von–Mises Fisher mixture model with variational inference. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1701–1715. [Google Scholar] [CrossRef]
- Bagchi, P.; Kadane, J.B. Laplace approximations to posterior moments and marginal distributions on circles, spheres, and cylinders. Can. J. Stat. 1991, 19, 67–77. [Google Scholar] [CrossRef]
- Nuñez-antonio, G.; Gutiérrez-peña, E. A Bayesian Analysis of Directional Data Using the von Mises–Fisher Distribution. Commun. Stat.—Simul. Comput. 2005, 34, 989–999. [Google Scholar] [CrossRef]
- Ravindran, P.; Ghosh, S.K. Bayesian Analysis of Circular Data Using Wrapped Distributions. J. Stat. Theory Pract. 2011, 5, 547–561. [Google Scholar] [CrossRef]
- Bates, D.M.; Watts, D.G. Nonlinear Regression Analysis and Its Applications; John Wiley & Sons: New York, NY, USA, 1988. [Google Scholar]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models, 2nd ed.; Chapman & Hall: London, UK, 1989. [Google Scholar]
- Ritz, C.; Streibig, J.C. Nonlinear Regression with R. Use R! Series; Springer Science+Business Media: New York, NY, USA, 2008. [Google Scholar]
- Cho, Y.C. Climate-induced distribution dynamics and niche adaptation of South Korean endemic plants across the Korean Peninsula. Sci. Rep. 2024, 14, 12345. [Google Scholar] [CrossRef] [PubMed]
- Chung, C. Vegetation response to climate change on Jeju Island, Korea, inferred from pollen record. J. Ecol. Field Biol. 2007, 30, 157–167. [Google Scholar]
- Lim, J.H.; Yoo, S.; Choi, Y.; Jeon, S.W.; Son, Y.; Lee, W.K. Assessing Climate Change Impacts of climate change on forest vegetation and distribution in Korea. Forests 2018, 9, 259. [Google Scholar] [CrossRef]
- Coleman, D.; Keppel, G.; Wardell-Johnson, G. Future climate shifts for vegetation on Australia’s coastal and island regions. Plants 2025, 14, 345. [Google Scholar]
- Veron, S.; Haevermans, T.; Govaerts, R.; Mouchet, M.; Pellens, R. Vulnerability to climate change of islands worldwide and its impact on the tree of life. Sci. Rep. 2019, 9, 14471. [Google Scholar] [CrossRef]
- MacArthur, R.H.; Wilson, E.O. The Theory of Island Biogeography; Princeton University Press: Princeton, NJ, USA, 1967. [Google Scholar]
- Losos, J.B.; Ricklefs, R.E.; MacArthur, R.H. The Theory of Island Biogeography Revisited; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Ministry of Oceans and Fisheries (MOF). Comprehensive Management of Uninhabited Islands: Survey Findings; MOF: Sejong, Republic of Korea, 2025. [Google Scholar]
- Korean Plant Names Index Committee. Checklist of Vascular Plants in Korea. Korea National Arboretum. 2022. Available online: http://www.nature.go.kr/kpni/index.do (accessed on 8 January 2025).
- Uyeki, H. Northern distribution limit of Korean evergreen broadleaved trees. Acta Phytotaxon. Geobot. 1941, 10, 89–93. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014; 151p. [Google Scholar]
- Choi, B.; Kim, J.; Seo, Y.; Yim, E.; Yang, J.; Park, M.; Lee, C.; Yoo, J.; Kim, K.; Yang, H.; et al. Identification of Warm Temperate and Subtropical Evergreen Tree; National Institute of Forest Science: Seoul, Republic of Korea, 2021. [Google Scholar]
- Kang, Y.; Hyun, H.; Song, K. Warm Temperate and Subtropical Plants; National Institute of Forest Science: Seoul, Republic of Korea, 2017; 244p. [Google Scholar]
- Shin, H.; Yoon, J.; Choi, S.; Lee, K.; Park, Y.; Jin, E.; Bae, E.; Han, J. Knowing the Warm Temperate Plants; National Institute of Forest Science: Seoul, Republic of Korea, 2015. [Google Scholar]
- Wilks, S.S. The large-sample distribution of the likelihood ratio for testing composite hypothesis. Ann. Math. Stat. 1938, 9, 60–62. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2025; Available online: https://www.R-project.org/ (accessed on 30 April 2025).
- QGIS Development Team. QGIS Geographic Information System; Open Source Geospatial Foundation Project; QGIS Development Team: Weil am Rhein, Germany, 2024. [Google Scholar]
- Hillebrand, H. On the generality of the latitudinal diversity gradient. Am. Nat. 2004, 163, 192–211. [Google Scholar] [CrossRef]
- Mittelbach, G.G.; Schemske, D.W.; Cornell, H.V.; Allen, A.P.; Brown, J.M.; Bush, M.B.; Harrison, S.P.; Hurlbert, A.H.; Knowlton, N.; Lessios, H.A.; et al. Evolution and the Latitudinal Diversity Gradient: Speciation, Extinction and Biogeography. Ecol. Lett. 2007, 10, 315–331. [Google Scholar] [CrossRef] [PubMed]
- Gratton, S.; Lawless, A.S.; Nichols, N.K. Approximate Gauss-Newton methods for nonlinear least squares problems. SIAM J. Optim. 2007, 18, 106–132. [Google Scholar] [CrossRef]
- Taboga, M. Normal Distribution—Maximum Likelihood Estimation, Lectures on Probability Theory and Mathematical Statistics; Online appendix; Kindle Direct Publishing: Seattle, WA, USA, 2021. [Google Scholar] [CrossRef]
- Crainiceanu, C.M.; Ruppert, D. Likelihood ratio tests for goodness-of-fit of a nonlinear regression model. J. Multivar. Anal. 2004, 91, 35–52. [Google Scholar] [CrossRef]
- Seber, G.A.F.; Wild, C.J. Nonlinear Regression; Wiley-Interscience: Hoboken, NJ, USA, 2003; pp. 34–36. [Google Scholar]
- Huelsenbeck, J.P.; Crandall, K.A. Phylogeny estimation and hypothesis testing using maximum likelihood. Annu. Rev. Ecol. Evol. Syst. 1997, 28, 437–466. [Google Scholar] [CrossRef]
- Pawitan, Y. In All Likelihood: Statistical Modelling and Inference Using Likelihood; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Razali, N.M.; Wah, Y.B. Power comparisons of Shapiro–Wilk, Kolmogorov–Smirnov, Lilliefors and Anderson–Darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- Royston, P. An extension of Shapiro and Wilk’s W test for normality to large samples. Appl. Stat. 1982, 31, 115–124. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall/CRC: New York, NY, USA, 1993. [Google Scholar]
- Møller, A.P.; Jennions, M.D. How much variance can be explained by ecologists and evolutionary biologists? Oecologia 2002, 132, 492–500. [Google Scholar] [CrossRef]
- Symonds, M.R.E.; Moussalli, A. A brief guide to model selection, multimodel inference and model averaging in behavioural ecology using Akaike’s information criterion. Behav. Ecol. Sociobiol. 2011, 65, 13–21. [Google Scholar] [CrossRef]
- Scheffer, M.; Bascompte, J.; Brock, W.A.; Brovkin, V.; Carpenter, S.R.; Dakos, V.; Held, H.; van Nes, E.H.; Rietkerk, M.; Sugihara, G. Early-warning signals for critical transitions. Nature 2009, 461, 53–59. [Google Scholar] [CrossRef] [PubMed]






| Model | DF (C–F) | ||||||
|---|---|---|---|---|---|---|---|
| A. Likelihood Function | B. Parameters | C. Dimension | D. Likelihood Function | E. Parameters | F. Dimension | ||
| SM | 5 | 5 | 5 | ||||
| 5 | |||||||
| MM | 6 | 6 | 6 | ||||
| 6 | |||||||
| FM | 3 | 5 | 1 | ||||
| 3 | |||||||
| TM | 6 | 6 | 6 | ||||
| 6 | |||||||
| Step | Description | Method | Application in This Study | Its Significance |
|---|---|---|---|---|
| 1. Modeling | Develop | island | • Based on MacArthur’s theory, | 1. Theoretical foundation: |
| parameterized | biogeography | log-transformed species richness and distance | Models grounded in island biogeography | |
| model | Theory | yield a linear relationship | 2. Transformability: | |
| • A baseline model is constructed and refined | Adaptable to research objectives | |||
| to include parameters for northward expansion | 3. Model flexibility: | |||
| • Allows nonlinear forms with no constraints | Allows nonlinear or multivariable structures | |||
| 2. Fitting | Estimate | Gauss-Newton, | • Estimates parameters of the nonlinear form | 1. Residuals of nonlinear models typically deviate from |
| model | nls() in R | • Evaluates normality of residuals using Kernel | normality, but island-based model shows near-normal | |
| parameters | Density Estimation (KDE) | residuals. | ||
| 2. Islands are suitable for evaluating the northward | ||||
| expansion of WTS plant species | ||||
| 3. Testing | Significance | Likelihood | • Conducts LRT | 1. LRT is appropriate for nonlinear model. |
| test | Ratio Test | • Applies chi-square test on the −2 log-LR | The F-test, based on the ratio of variances, is not suitable | |
| (LRT), | 2. Degrees of freedom challenges in chi-square distribution | |||
| −2 log-LR, | are addressed flexibly | |||
| Chi-square test | 3. Statistical significance of differences is confirmed | |||
| 4. Evaluating | Determine | Intuitive | • Assess directional shift | 1. Provides a simple indicator to detect directional changes |
| direction of | indicator | in response to significant model differences | 2. Directional logic is embedded in the initial model, | |
| Shifts, if any | (proposed) | supporting interpretation. |
| Dataset | Parameter | Estimate | Std. Error | t Value | Pr (>|t|) | |
|---|---|---|---|---|---|---|
| A_2013 | 1.185348 | 0.1406 | 8.428 | <2 × 10−16 | *** | |
| 36.252680 | 0.2661 | 136.261 | <2 × 10−16 | *** | ||
| 1.758833 | 0.5959 | 2.951 | 0.00325 | ** | ||
| B_2013 | 0.845830 | 0.1507 | 5.612 | 2.73 × 10−8 | *** | |
| 36.544797 | 0.5583 | 65.452 | <2 × 10−16 | *** | ||
| 1.798106 | 0.9074 | 1.982 | 0.0479 | * | ||
| AB_2013 | 0.840041 | 0.0978 | 8.596 | <2 × 10−16 | *** | |
| 36.798868 | 0.3690 | 99.729 | <2 × 10−16 | *** | ||
| 1.431216 | 0.6020 | 2.377 | 0.0175 | * | ||
| −2 log LR | chi-square statistic | 52.35363 | ||||
| degree of freedom | 5 | |||||
| p-value | 0.00000 | *** |
| Dataset | Parameter | Estimate | Std. Error | t Value | Pr (>|t|) | |
|---|---|---|---|---|---|---|
| A_2013 | 1.172858 | 0.12952 | 9.055 | <2 × 10−16 | *** | |
| 36.275370 | 0.25013 | 145.028 | <2 × 10−16 | *** | ||
| 1.401977 | 0.55445 | 2.529 | 0.0116 | * | ||
| 0.000993 | 0.00008 | 12.480 | <2 × 10−16 | *** | ||
| B_2013 | 0.852618 | 0.14701 | 5.800 | 9.46 × 10−9 | *** | |
| 36.526810 | 0.53675 | 68.052 | <2 × 10−16 | *** | ||
| 1.661198 | 0.88093 | 1.886 | 0.597 | |||
| 0.000579 | 0.00010 | 5.949 | 3.99 × 10−9 | *** | ||
| AB_2013 | 0.835776 | 0.09241 | 9.045 | <2 × 10−16 | *** | |
| 36.822240 | 0.35343 | 104.186 | <2 × 10−16 | *** | ||
| 1.135764 | 0.57676 | 1.969 | 0.0491 | * | ||
| 0.000836 | 0.00006 | 13.343 | <2 × 10−16 | *** | ||
| −2 log LR | chi-square statistic | 61.27253 | ||||
| degree of freedom | 6 | |||||
| p-value | 0.00000 | *** |
| Dataset | Parameter | Estimate | Std. Error | t Value | Pr (>|t|) | |
|---|---|---|---|---|---|---|
| A_2013 | 36.995720 | 0.0416 | 889.4 | <2 × 10−16 | *** | |
| B_2013 | 36.633600 | 0.0444 | 825.6 | <2 × 10−16 | *** | |
| AB_2013 | 0.840041 | 0.0978 | 8.596 | <2 × 10−16 | *** | |
| 36.798868 | 0.3690 | 99.729 | <2 × 10−16 | *** | ||
| 1.431216 | 0.6020 | 2.377 | 0.0175 | * | ||
| −2 log LR | chi-square statistic | 39.72759 | ||||
| degree of freedom | 1 | |||||
| p-value | 0.00000 | *** |
| Dataset | Parameter | Estimate | Std. Error | t Value | Pr (>|t|) | |
|---|---|---|---|---|---|---|
| A_2013 | 12.4652 | 1.4306 | 8.713 | <2 × 10−16 | *** | |
| 1.8252 | 0.5009 | 3.644 | 0.000285 | *** | ||
| 34.0050 | 0.1253 | 271.390 | <2 × 10−16 | *** | ||
| 2.9779 | 0.4143 | 7.189 | 1.43 × 10−12 | *** | ||
| B_2013 | 13.6278 | 3.8415 | 3.548 | 0.000411 | *** | |
| 0.4444 | 0.2370 | 1.875 | 0.061146 | . | ||
| 32.9164 | 0.5576 | 59.028 | <2 × 10−16 | *** | ||
| 3.1046 | 0.5955 | 5.214 | 2.34 × 10−7 | *** | ||
| AB_2013 | 12.1126 | 1.1688 | 10.364 | <2 × 10−16 | *** | |
| 0.8372 | 0.1777 | 4.712 | 2.66 × 10−6 | *** | ||
| 33.5619 | 0.1340 | 250.402 | <2 × 10−16 | *** | ||
| 3.0300 | 0.3434 | 8.824 | <2 × 10−16 | *** | ||
| −2 log LR | chi-square statistic | 60.78024 | ||||
| degree of freedom | 6 | |||||
| p-value | 0.00000 | *** |
| Model | AIC | BIC | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | AB | A | B | AB | A | B | AB | A | B | AB | |
| SM | 0.212 | 0.130 | 0.153 | 0.210 | 0.128 | 0.152 | 5598 | 5319 | 10,961 | 5617 | 5338 | 10,983 |
| MM | 0.446 | 0.285 | 0.356 | 0.444 | 0.283 | 0.355 | 5298 | 5158 | 10,500 | 5322 | 5181 | 10,527 |
| FM | 0.212 | 0.130 | 0.153 | 0.210 | 0.128 | 0.152 | 5598 | 5319 | 10,961 | 5617 | 5338 | 10,983 |
| TM | 0.241 | 0.133 | 0.166 | 0.239 | 0.130 | 0.165 | 5567 | 5318 | 10,936 | 5591 | 5342 | 10,963 |
| 35° N | Period | No of Islands | Mean | SD | Mean Difference (A–B) | t Value | Pr (>|t|) | |
|---|---|---|---|---|---|---|---|---|
| North | A_2013 | 312 | 3.55 | 3.48 | −0.70 | −1.245 | 0.107 | |
| B_2013 | 229 | 3.97 | 4.18 | |||||
| South | A_2013 | 545 | 8.61 | 7.96 | 1.23 | 2.888 | 0.002 | ** |
| B_2013 | 603 | 7.35 | 6.73 |
| Group | WTS Plant Species | 2013_A | 2013_B | Difference | |||
|---|---|---|---|---|---|---|---|
| a. Occurrence | b. Ratio | c. Occurrence | d. Ratio | Occurrence (a–c) | Ratio (b–d) | ||
| 1. Established | Elaeagnus macrophylla Thunb. | 407 | 0.62 | 307 | 0.63 | 100 | −0.02 |
| Range Shifters | Euonymus japonicus Thunb. | 370 | 0.54 | 382 | 0.40 | −12 | 0.14 |
| Pseudosasa japonica Makino ex Nakai | 127 | 0.74 | 80 | 0.51 | 47 | 0.23 | |
| 2. Active Range | Machilus thunbergii Siebold & Zucc. | 193 | 0.29 | 191 | 0.21 | 2 | 0.08 |
| Expanders | Neolitsea sericea Koidz. | 147 | 0.26 | 78 | 0.26 | 69 | 0.00 |
| Hedera rhombea Siebold & Zucc. ex Bean | 228 | 0.22 | 238 | 0.19 | −10 | 0.03 | |
| Trachelospermum asiaticum Nakai | 339 | 0.22 | 318 | 0.25 | 21 | −0.03 | |
| Eurya japonica Thunb. | 406 | 0.18 | 448 | 0.14 | −42 | 0.04 | |
| Ardisia japonica (Thunb.) Blume | 229 | 0.16 | 200 | 0.16 | 29 | 0.00 | |
| Pittosporum tobira (Thunb.) W.T.Aiton | 247 | 0.12 | 290 | 0.16 | −43 | −0.04 | |
| Litsea japonica (Thunb.) Juss. | 115 | 0.12 | 129 | 0.09 | −14 | 0.02 | |
| Rhaphiolepis indica var. umbellate | 243 | 0.08 | 228 | 0.10 | 15 | −0.02 | |
| Ligustrum japonicum Thunb. | 263 | 0.07 | 249 | 0.05 | 14 | 0.02 | |
| Ficus oxyphylla Miq. ex Zoll. | 141 | 0.04 | 75 | 0.07 | 66 | −0.03 | |
| Eurya emarginata (Thunb.) Makino | 166 | 0.02 | 169 | 0.01 | −3 | 0.02 | |
| 3. Range-Constrained | The remaining WTS plants, not including Groups 1 and 2 | ||||||
| Species | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, W.; Jung, S.Y. A Statistical Methodology for Evaluating the Potential for Poleward Expansion of Warm Temperate and Subtropical Plants Under Climate Change: A Case Study of South Korean Islands. Forests 2025, 16, 1500. https://doi.org/10.3390/f16091500
Kim W, Jung SY. A Statistical Methodology for Evaluating the Potential for Poleward Expansion of Warm Temperate and Subtropical Plants Under Climate Change: A Case Study of South Korean Islands. Forests. 2025; 16(9):1500. https://doi.org/10.3390/f16091500
Chicago/Turabian StyleKim, Woosung, and Su Young Jung. 2025. "A Statistical Methodology for Evaluating the Potential for Poleward Expansion of Warm Temperate and Subtropical Plants Under Climate Change: A Case Study of South Korean Islands" Forests 16, no. 9: 1500. https://doi.org/10.3390/f16091500
APA StyleKim, W., & Jung, S. Y. (2025). A Statistical Methodology for Evaluating the Potential for Poleward Expansion of Warm Temperate and Subtropical Plants Under Climate Change: A Case Study of South Korean Islands. Forests, 16(9), 1500. https://doi.org/10.3390/f16091500





