Physically Based Canopy Interception Model for a Beech Forest Using Remote Sensing Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Measurements
2.3. Modified Merriam Model
3. Results
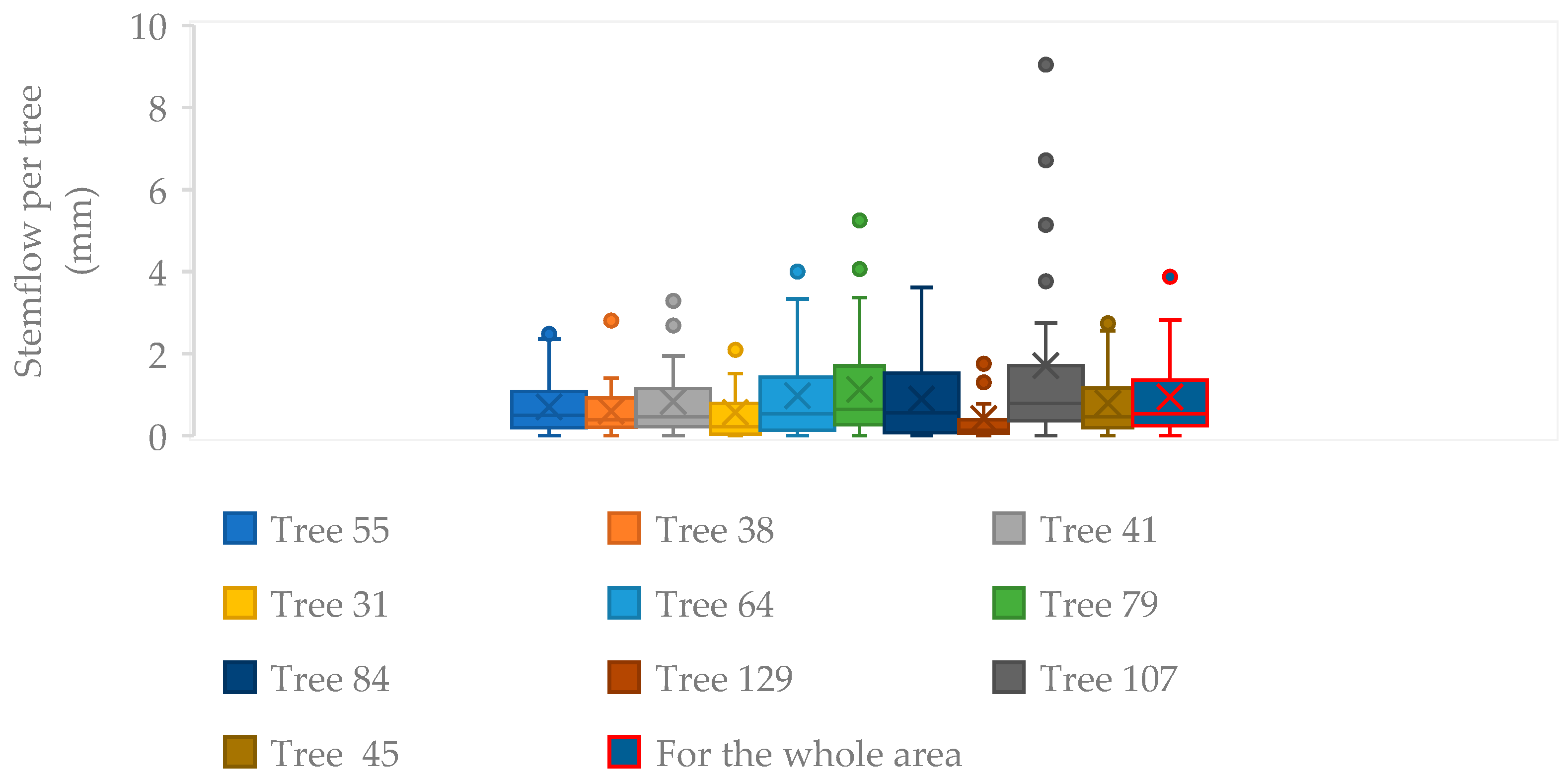
3.1. Measured Interception Values
3.2. Modeled Interception Values
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| precipitation amount [mm] | |
| throughfall [mm] | |
| stemflow [mm] | |
| parameter of the evaporation process during the rainfall event (-) | |
| measured interception [mm] | |
| interception [mm] | |
| maximum storage capacity for a unit surface [mm/m2] | |
| projected leaf area surface [m2/m2] | |
| canopy storage capacity | |
| maximum canopy storage capacity | |
| projected surface area of stems, branches, and twigs above a unit ground area (m2/m2) | |
| maximum storage capacity for a unit surface [mm/m2] | |
| canopy height [m] | |
| canopy density multiplier [-] |
References
- Zhong, F.; Jiang, S.; van Dijk, A.I.J.M.; Ren, L.; Schellekens, J.; Miralles, D.G. Revisiting large-scale interception patterns constrained by a synthesis of global experimental data. Hydrol. Earth Syst. Sci. 2022, 26, 5647–5667. [Google Scholar] [CrossRef]
- Helvey, J.D.; Patric, J.H. Canopy and litter interception of rainfall by hardwoods of eastern United States. Water Resour. Res. 1996, 1, 193–206. [Google Scholar] [CrossRef]
- Valente, F.; David, J.S.; Gash, J.H.C. Modelling interception loss for two sparse eucalypt and pine forests in central Portugal using reformulated Rutter and Gash analytical models. J. Hydrol. 1997, 190, 141–162. [Google Scholar] [CrossRef]
- Tonello, K.C.; Guidelli, A.R.; Salim, J.A.; Corrêa, C.J.P.; Lima, M.T. The dynamics of knowledge about stemflow: A systematic review. Rev. Bras. Ciências Ambient. 2020, 56, 16–27. [Google Scholar] [CrossRef]
- Creed, I.F.; Jones, J.A.; Archer, E.; Claassen, M.; Ellison, D.; McNulty, S.G.; van Noordwijk, M.; Vira, B.; Wei, X.; Bishop, K.; et al. Managing Forests for Both Downstream and Downwind Water. Front. For. Glob. Change 2019, 2, 64. [Google Scholar] [CrossRef]
- Baird, A.J.; Wilby, R.L. (Eds.) Plants and water in terrestrial and aquatic environments. In Eco-Hydrology, 1st ed.; Taylor & Frances: London, UK, 1999. [Google Scholar] [CrossRef]
- Šraj, M.; Brilly, M.; Mikoš, M. Rainfall interception by two deciduous Mediterranean forests of contrasting stature in Slovenia. Agric. For. Meteorol. 2008, 148, 121–134. [Google Scholar] [CrossRef]
- Liang, W.L. Chapter 15: Effects of Stemflow on Soil Water Dynamics in forest Stands. In Forest-Water Interactions (Ecological Studies Book. 240), 1st ed.; Levia, D.F., Carlyle-Moses, D.E., Shin’ichi, I., Michalzik, B., Nanko, K., Tischer, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 34–371. ISBN ISBN-13 978-3030260859. [Google Scholar]
- Gribovszki, Z.; Kalicz, P.; Palocz-Andresen, M.; Szalay, D.; Varga, T. Hydrological role of Central European forests in changing climate—Review. IDOJARAS 2019, 123, 535–550. [Google Scholar] [CrossRef]
- Peck, A.; Mayer, H. Einfluß von Bestandesparametern auf die Verdunstung von Wäldern. Forstw. Cbl. 1996, 115, 1–9. [Google Scholar] [CrossRef]
- Hanchi, A.; Rapp, M. Stemflow determination in forest stands. For. Ecol. Manag. 1997, 97, 231–235. [Google Scholar] [CrossRef]
- van Stan, J.T.; Gordon, D.A. Mini-Review: Stem flow as a Resource Limitation to Near-Stem Soil. Front. Plant Sci. 2018, 9, 248. [Google Scholar] [CrossRef]
- de Mello, C.R.; Li, G.; Yuan, C.; Rodrigues, A.F.; Lima, R.R.; Marcela, C.N.S.T. Deciphering global patterns of forest canopy rainfall interception (FCRI): A synthesis of geographical, forest species, and methodological influences. J. Environ. Manag. 2024, 358, 120879. [Google Scholar] [CrossRef]
- Metzger, J.; Schumacher, J.; Lange, M.; Hildebrandt, A. Neighbourhood and stand structure affect stemflow generation in a heterogeneous deciduous temperate forest. Hydrol. Earth Syst. Sci. 2019, 23, 4433–4452. [Google Scholar] [CrossRef]
- Rutter, A.J.; Morton, A.J. A predictive model of rainfall interception in forests. III. Sensitivity of model to stand parameters and meteorological variables. J. Appl. Ecol. 1977, 14, 567–588. [Google Scholar] [CrossRef]
- Gash, J.; Wright, I.; Lloyd, C.R. Comparative estimates of interception loss from three coniferous forests in Great Britain. J. Hydrol. 1980, 48, 89–105. [Google Scholar] [CrossRef]
- Crockford, R.H.; Richardson, D.P. Partitioning of rainfall into throughfall. stemflow and interception: Effect of forest type, ground cover and climate. Hydrol. Process. 2000, 14, 2903–2920. [Google Scholar] [CrossRef]
- Llorens, P.; Latron, P.R.; Gallart, J.F. Rainfall interception by a Pinus sylvestris forest patch overgrown in a Mediterranean moutainous abandoned area I. Monitoring design and results down to the event scale. J. Hydrol. 1997, 199, 331–345. [Google Scholar] [CrossRef]
- Price, A.G.; Carlyle-Moses, D.E. Measurement and modelling of growing-season canopy water fluxes in a mature mixed deciduous forest stand. northern Ontario. Canada. Agric. For. Meteorol. 2003, 119, 69–85. [Google Scholar] [CrossRef]
- Zabret, K.; Rakovec, J.; Šraj, M. Influence of meteorological variables on rainfall partitioning for deciduous and coniferous tree species in urban area. J. Hydrol. 2018, 558, 29–41. [Google Scholar] [CrossRef]
- Safeeq, M.; Fares, A. Interception losses in three non-native Hawaiian forest stands. Hydrol. Process. 2012, 28, 237–254. [Google Scholar] [CrossRef]
- Gerrits, A.M.J.; Pfister, L.; Savenije, H.H. Spatial and temporal variability of canopy and forest floor interception in a beech forest. Hydrol. Process. 2010, 24, 3011–3025. [Google Scholar] [CrossRef]
- Klamerus-Iwan, A.; Bło’nska, E. Seasonal variability of interception and water wettability of common oak leaves. Ann. For. Res. 2016, 60, 63–73. [Google Scholar] [CrossRef]
- Führer, E. Intercepció meghatározása bükk. kocsánytalan tölgy és lucfenyő erdőben. Vízügyi Közlemények 1992, 74, 281–294. (In Hungarian) [Google Scholar]
- Zabret, K.; Šraj, M. How Characteristics of a Rainfall Event and the Meteorological Conditions Determine the Development of Stemflow: A Case Study of a Birch Tree. Front. For. Glob. Change 2021, 4, 663100. [Google Scholar] [CrossRef]
- Duan, T. The Impact of Leaf Area Index on Rainfall Interception and the Potential to Estimate it Using Sentinel-1 Observations. Master’s Thesis,. Faculty of Geo-Information Science and Earth Observation of the University of Twente, Enschede, The Netherlands, 2017. [Google Scholar]
- Linhoss, A.C.; Siegert, C.M. A comparison of five forest interception models using global sensitivity and uncertainty analysis. J. Hydrol. 2016, 538, 109–116. [Google Scholar] [CrossRef]
- Caudullo, G.; De Rigo, D.; Mauri, A.; Houston Durrant, T.; San-Miguel-Ayanz, J. European Atlas of Forest Tree Species; Caudullo, G., De Rigo, D., Mauri, A., Houston Durrant, T., San-Miguel-Ayanz, J., Eds.; Publications Office of the European Union: Luxembourg, 2016; Available online: https://data.europa.eu/doi/10.2760/776635 (accessed on 12 February 2025).
- Novosadová, K.; Kadlec, J.; Řehořková, Š.; Matoušková, M.; Urban, J.; Pokorný, R. Comparison of Rainfall Partitioning and Estimation of the Utilisation of Available Water in a Monoculture Beech Forest and a Mixed Beech-Oak-Linden Forest. Water 2023, 15, 285. [Google Scholar] [CrossRef]
- Ellenberg, H.; Leuschner, C. Vegetation Mitteleuropas Mit Den Alpen; Ulmer: Stuttgart, Germany, 1996; Volume 1095. [Google Scholar] [CrossRef]
- Bolte, A.; Ammer, C.; Löf, M.; Madsen, P.; Nabuurs, G.J.; Schall, P.; Spathelf, P.; Rock, J. Adaptive forest management in central Europe: Climate change impacts, strategies and integrative concept. Scand. J. For. Res. 2009, 24, 473–482. [Google Scholar] [CrossRef]
- Mátyás, C.; Berki, I.; Bidló, A.; Csóka, G.; Czimber, K.; Führer, E.; Gálos, B.; Gribovszki, Z.; Illés, G.; Hirka, A.; et al. Sustainability of Forest Cover under Climate Change on the Temperate-Continental Xeric Limits. Forests 2018, 9, 489. [Google Scholar] [CrossRef]
- Merriam, R.A. A note on the interception loss equation. J. Geophys. Res. 1960, 65, 3850–3851. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.Y.; Li, W.; Wu, X.C.; Shi, F.Z.; Fang, W.W.; Pei, T.T. Modeling rainfall interception loss by two xerophytic shrubs in the Loess Plateau. Hydrol. Process. 2017, 31, 1926–1937. [Google Scholar] [CrossRef]
- Zheng, J.; Fan, J.; Zhang, F.; Yan, S.; Xiang, Y. Rainfall partitioning into throughfall. stemflow and interception loss by maize canopy on the semi-arid Loess Plateau of China. Agric. Water Manag. 2018, 195, 25–36. [Google Scholar] [CrossRef]
- Calder, I.; Wright, I.; Murdiyarso, D. A study of evaporation from tropical rain forest—West Java. J. Hydrol. 1986, 89, 13–31. [Google Scholar] [CrossRef]
- Calder, I.R. Dependence of rainfall interception on drop size: 1. Development of the two-layer stochastic model. J. Hydrol. 1996, 185, 363–378. [Google Scholar] [CrossRef]
- Rutter, A.; Kershaw, K.; Robins, P.; Morton, A. A predictive model of rainfall interception in forests. 1. Derivation of the model from observations in a plantation of Corsican pine. Agric. Meteorol. 1971, 9, 367–384. [Google Scholar] [CrossRef]
- Van Dijk, A.; Bruijnzeel, L. Modelling rainfall interception by vegetation of variable density using an adapted analytical model. Part 1. Model description. J. Hydrol. 2001, 247, 230–238. [Google Scholar] [CrossRef]
- Návar, J. Modeling rainfall interception components of forests: Extending drip equations. Agric. Forest Meteorol. 2019, 279, 107704. [Google Scholar] [CrossRef]
- Návar, J. Modeling rainfall interception loss components of forests. J. Hydrol. 2020, 584, 124449. [Google Scholar] [CrossRef]
- Acharya, S.; McLaughlin, D.; Kaplan, D.; Cohen, M.J. A proposed method for estimating interception from nearsurface soil moisture response. Hydrol. Earth. Syst. Sci. 2020, 24, 1859–1870. [Google Scholar] [CrossRef]
- Spiecker, H.; Mielikäinen, K.; Köhl, M.; Skovsgaard, J.P. Growth Trends in European Forests: Studies from 12 Countries; European Forest Institute Research Report; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Muzylo, A.; Llorens, P.; Valente, F.; Keizer, J.J.; Domingo, F.; Gash, J.H.C. A review of rainfall interception modelling. J. Hydrol. 2009, 370, 191–206. [Google Scholar] [CrossRef]
- Dövényi, Z. (Ed.) Magyarország Kistájainak Katasztere; MTA Földrajztudományi Kutatóintézet: Budapest, Hungary, 2010; pp. 345–353. [Google Scholar]
- Gribovszki, Z.; Kalicz, P.; Kucsara, M. Streamflow Characteristics of Two Forested Catchments in Sopron Hills. Acta Silv. Lign. Hung. 2006, 2, 81–92. [Google Scholar] [CrossRef]
- Deguchi, A.; Hattori, S.; Park, H. The influence of seasonal changes in canopy structure on interception loss: Application of the revised Gash model. J. Hydrol. 2006, 318, 80–102. [Google Scholar] [CrossRef]
- Causton, D.R. Biometrical, structural and physiological relationships among tree parts. In Attributes of Trees as Crop Plants; Cannel, M.G.R., Jackson, J.E., Eds.; Inst. Terrestrial Ecology: Huntingdon, UK, 1985; pp. 137–159. [Google Scholar]
- Federer, C.A.; Lash, D. BROOK: A Hydrologic Simulation Model for Eastern Forests; Water Resources Research Center Research Report; University of New Hampshire: Durham, UK, 1978; Volume 19. [Google Scholar]
- Federer, C.A. BROOK 90: A Simulation Model for Evaporation, Soil Water, and Streamflow. 2002. Available online: http://www.ecoshift.net/brook/brook90.htm (accessed on 21 April 2025).
- Myneni, R.; Knyazikhin, Y.; Park, T. MOD15A2H MODIS Leaf Area Index/FPAR 8-Day L4 Global 500m SIN Grid V006; NASA EOSDIS Land Processes DAAC: Sioux Falls, South Dakota, 2015. [Google Scholar] [CrossRef]
- Kucsara, M.; Gribovszki, Z. Az intercepció vizsgálata és számszerűsítése csapadékeseményhez kötött modellel. In Agrárklíma: Az Előrevetített Klímaváltozás Hatáselemzése és az Alkalmazkodás Lehetősége; Bidló, A., Király, A., Mátyás, C., Eds.; Nyugat-Magyarországi Egyetem Kiadó: Sopron, Hungary, 2014; pp. 25–27. ISBN 978-963-334-204-6. (In Hungarian) [Google Scholar]
- Kucsara, M. Csapadék és Lefolyás Erdészeti Kisvízgyűjtőn. Ph.D. Thesis. University of Sopron, Sopron, Hungary, 1996. (In Hungarian). [Google Scholar]
- Chen, K.; Dorado Liñán, I.; Akhmetzyanov, L.; Gea-Izquierdo, G.; Zlatanov, T.; Menzel, A. Climate drivers and NAO influence on beech growth at marginal sites across the Mediterranean. Clim. Res. 2015, 66, 229–242. [Google Scholar] [CrossRef]
- Kulla, L.; Roessiger, J.; Bošeľa, M.; Kucbel, S.; Murgaš, V.; Vencurik, J.; Pittner, J.; Jaloviar, P.; Šumichrast, L.; Saniga, M. Changing patterns of natural dynamics in old-growth European beech (Fagus sylvatica L.) forests can inspire forest management in Central Europe. For. Ecol. Manag. 2023, 529, 120633. [Google Scholar] [CrossRef]
- Střelcová, K.; Matejka, F.; Kučera, J. Beech stand transpiration assessment—Two methodical approaches. Ekologia 2004, 22, 147–162. [Google Scholar]
- Gossner, M.M.; Vitasse, Y.; Queloz, V.; Wohlgemuth, T. Laubfall im Sommer als Indiz für späteres Buchensterben. Wald Und Holz 2022, 9, 10–13. [Google Scholar]
- Obladen, N.; Dechering, P.; Skiadaresis, G.; Tegel, W.; Keßler, J.; Höllerl, S.; Kaps, S.; Hertel, M.; Dulamsuren, C.; Seifert, T.; et al. Tree mortality of European beech and Norway spruce induced by 2018-2019 hot droughts in central Germany. Agric. For. Meteorol. 2021, 307, 108482. [Google Scholar] [CrossRef]
- Frei, E.R.; Gossner, M.M.; Vitasse, Y.; Queloz, V.; Dubach, V.; Gessler, A.; Ginzler, C.; Hagedorn, F.; Meusburger, K.; Moor, M.; et al. European beech dieback after premature leaf senescence during the 2018 drought in northern Switzerland. Plant Biol. 2022, 24, 1132–1145. [Google Scholar] [CrossRef]
- Ma, C.; Li, X.; Luo, Y.; Shao, M.; Jia, X. The modelling of rainfall interception in growing and dormant seasons for a pine plantation and a black locust plantation in semi-arid Northwest China. J. Hydrol. 2019, 577, 123849. [Google Scholar] [CrossRef]
- Rodrigues, A.F.; Mello, C.R.; Nehren, U.; Ribeiro, J.P.C.; Mantovani, V.A.; Mello, J.M. Modeling canopy interception under drought conditions: The relevance of evaporation and extra sources of energy. J. Environ. Manag. 2021, 292, 112710. [Google Scholar] [CrossRef] [PubMed]
- Augusto, L.; Ranger, J.; Binkley, D.; Rothe, A. Impact of several common tree species of European temperate forests on soil fertility. Ann. For. Sci. 2002, 59, 233–253. [Google Scholar] [CrossRef]
- Neal, C.; Robson, A.J.; Bhardwaj, C.L.; Conway, T.; Jefery, H.A.; Meal, M.; Ryland, G.P.; Smith, C.J.; Walls, J. Relationships between precipitation. stemflow and throughfall for a lowland beech plantation. Black wood. Hampshire. southern England: Interception at a forest edge and the effects of storm damage. J. Hydrol. 1993, 146, 221–233. [Google Scholar] [CrossRef]
- Peck, A.K. Hydrometeorologische Und Mikroklimatische. Kennzeichen von Buchenwäldern. Ph.D. Thesis, University of Freiburg, Freiburg, Germany, 2004. (In Germany). [Google Scholar]
- Staelens, J.; Schrijver, A.D.; Verheyen, K.; Verhoest, N. Rainfall partitioning into throughfall, stemflow, and interception within a single beech (Fagus sylvatica L.) canopy: Influence of foliation, rain event characteristics, and meteorology. Hydrol. Process. 2008, 22, 33–45. [Google Scholar] [CrossRef]
- Granier, A.; Biron, P.; Lemoine, D. Water balance. transpiration and canopy conductance in two beech stands. Agric. For. Meteorol. 2000, 100, 291–308. [Google Scholar] [CrossRef]
- Tarazona, T.; Santa Regina, I.; Calvo, R. Interception. throughfall and stemflow in two forests of the” Sierra de la Demanda” in the Province of Burgos. Pirineos 1996, 147–148, 27–40. [Google Scholar] [CrossRef]
- Aussenac, G.; Boulangeat, C. Interception des précipitations et évapotranspiration réelle dans des peuplements de feuillu (Fagus silvatica L.) et de résineux (Pseudotsuga menziesii (Mirb) Franco). Ann. Sci. For. 1980, 37, 91–107. [Google Scholar] [CrossRef]
- Giacomin, A.; Trucchi, P. Rainfall interception in a beech coppice (Acquerino, Italy). J. Hydrol. 1992, 137, 141–147. [Google Scholar] [CrossRef]
- Ahmadi, M.T.; Attarod, P.; Bayramzadeh, V. The role of rainfall size in canopy interception loss: An observational study in a typical beech forest. Middle East J. Sci. Res. 2013, 13, 876–882. [Google Scholar] [CrossRef]











| Precipitation Category | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 |
|---|---|---|---|---|---|---|
| 0–0.5 mm | 54 | 43 | 22 | 21 | 44 | 55 |
| 0.51–1.0 mm | 22 | 15 | 20 | 20 | 15 | 27 |
| 1.01–2.0 mm | 24 | 19 | 22 | 21 | 18 | 22 |
| 2.01–5.0 mm | 29 | 29 | 29 | 23 | 28 | 22 |
| 5.01–10.0 mm | 25 | 30 | 16 | 24 | 17 | 20 |
| 10.01–20.0 mm | 13 | 19 | 21 | 13 | 11 | 12 |
| 20.01< mm | 5 | 5 | 7 | 7 | 7 | 5 |
| Interception/Precipitation | ||||||
|---|---|---|---|---|---|---|
| Precipitation Category | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 |
| 0–0.5 mm | 0.77 | 0.78 | 0.83 | 0.74 | 0.83 | 0.81 |
| 0.51–1.0 mm | 0.72 | 0.47 | 0.61 | 0.59 | 0.56 | 0.60 |
| 1.01–2.0 mm | 0.39 | 0.40 | 0.38 | 0.54 | 0.51 | 0.51 |
| 2.01–5.0 mm | 0.27 | 0.23 | 0.30 | 0.33 | 0.29 | 0.31 |
| 5.01–10.0 mm | 0.19 | 0.18 | 0.18 | 0.23 | 0.17 | 0.25 |
| 10.01–20.0 mm | 0.14 | 0.12 | 0.16 | 0.17 | 0.12 | 0.17 |
| 20.01< mm | 0.10 | 0.10 | 0.11 | 0.11 | 0.12 | 0.10 |
| Precipitation Categories | I | P | I | P | I | P |
|---|---|---|---|---|---|---|
| Dormancy (4 November–9 May) | Growing Season (10 May–3 November) | 2017–2022 | ||||
| 0–0.5 mm | 17.50 | 25.68 | 22.22 | 23.36 | 39.72 | 49.04 |
| 0.51–1.0 mm | 15.68 | 41.93 | 34.66 | 41.44 | 50.35 | 83.37 |
| 1.01–2.0 mm | 27.74 | 97.40 | 54.95 | 84.66 | 82.70 | 182.05 |
| 2.01–5.0 mm | 39.92 | 257.95 | 116.34 | 267.63 | 156.26 | 525.59 |
| 5.01–10.0 mm | 39.99 | 388.44 | 150.78 | 530.71 | 190.77 | 919.15 |
| 10.01–20.0 mm | 35.93 | 401.12 | 151.87 | 813.48 | 187.80 | 1214.60 |
| 20.01< mm | 9.84 | 178.79 | 121.23 | 1002.65 | 131.07 | 1181.44 |
| I sums [mm] | 186.62 | 652.05 | 838.67 | |||
| P sums [mm] | 1391.31 | 2763.93 | 4155.24 | |||
| I/P ratio (dynamic storage capacity) | 0.13 | 0.24 | 0.20 | |||
| I/P ratio (constant storage capacity) | 0.42 | 0.30 | 0.34 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zagyvai-Kiss, K.A.; Gribovszki, Z.; Kalicz, P.; Zabret, K.; Szilágyi, J.; Herceg, A. Physically Based Canopy Interception Model for a Beech Forest Using Remote Sensing Data. Forests 2025, 16, 1469. https://doi.org/10.3390/f16091469
Zagyvai-Kiss KA, Gribovszki Z, Kalicz P, Zabret K, Szilágyi J, Herceg A. Physically Based Canopy Interception Model for a Beech Forest Using Remote Sensing Data. Forests. 2025; 16(9):1469. https://doi.org/10.3390/f16091469
Chicago/Turabian StyleZagyvai-Kiss, Katalin Anita, Zoltán Gribovszki, Péter Kalicz, Katarina Zabret, József Szilágyi, and András Herceg. 2025. "Physically Based Canopy Interception Model for a Beech Forest Using Remote Sensing Data" Forests 16, no. 9: 1469. https://doi.org/10.3390/f16091469
APA StyleZagyvai-Kiss, K. A., Gribovszki, Z., Kalicz, P., Zabret, K., Szilágyi, J., & Herceg, A. (2025). Physically Based Canopy Interception Model for a Beech Forest Using Remote Sensing Data. Forests, 16(9), 1469. https://doi.org/10.3390/f16091469








