The Impact of the Number of Sensors on Stress Wave Velocity in 2D Acoustic Tomography of Araucaria cunninghamii Sweet
1
Forest Products Utilization Division, Taiwan Forestry Research Institute, Taipei 10066, Taiwan
2
Department of Forestry and Natural Resources, National Ilan University, Yilan 26047, Taiwan
3
Chiayi Research Center, Taiwan Forestry Research Institute, Chiayi 60081, Taiwan
*
Author to whom correspondence should be addressed.
Forests 2025, 16(9), 1439; https://doi.org/10.3390/f16091439
Submission received: 18 August 2025
/
Revised: 5 September 2025
/
Accepted: 6 September 2025
/
Published: 9 September 2025
(This article belongs to the Section Forest Health)
Abstract
This study investigated the effect of the number of sensors (8, 12, 16, and 20) on the measurement results of stress wave velocity in two-dimensional acoustic tomography of Hoop pine (Araucaria cunninghamii Sweet) trees and evaluated the method’s accuracy and operational efficiency in tree health diagnostics. Tests were conducted on five sample trees, two of which were confirmed to have internal damage using the drilling resistance method. The results showed that increasing the number of sensors improved image resolution and information completeness. However, differences in the average stress wave velocities among sensor configurations were not statistically significant (p ≥ 0.05), indicating limited overall velocity variation. In healthy trees, stress wave velocities measured with different sensor quantities (e.g., eight vs. twenty) exhibited weak linear correlations (R2 = 0.06–0.58), reflecting a relatively uniform internal structure. In contrast, damaged trees showed strong consistency in velocity results (R2 = 0.82–0.91, p < 0.01), with both minimum and average velocities being significantly lower than those in healthy trees. These findings demonstrate that acoustic tomography can effectively identify internal tree defects. Notably, even with only eight sensors, decay and cavities can still be accurately detected, which significantly enhances field inspection efficiency and reduces costs, thereby showing strong potential for practical applications.
1. Introduction
Tree risk assessment aims to evaluate the structural stability of trees and serves as a critical foundation for subsequent management decisions. A widely used approach in such assessments is Visual Tree Assessment (VTA), which involves systematic evaluations based on observable external symptoms [1,2]. However, the internal condition of a tree often cannot be reliably inferred from its outward appearance alone, necessitating the use of non-destructive testing (NDT) or Minimally Invasive Technologies (MITs) to overcome the limitations of VTA and to provide more detailed structural insights. These advanced diagnostic methods have thus become essential tools in comprehensive tree risk evaluation.
Among the available advanced techniques, acoustic tomography and resistance drilling have been widely adopted for assessing internal tree structures with minimal damage [3,4]. Acoustic tomography works by transmitting stress waves through the tree trunk to detect internal decay and cavities, reconstructing a visualized two-dimensional cross-sectional image [5]. This technique has proven effective for diagnosing decay in urban trees [6], although its image accuracy may still be influenced by multiple factors. In contrast, resistance drilling—while invasive—is considered only minimally due to its design, and it provides continuous resistance data that can aid in interpreting acoustic images and understanding internal wood structure [7,8,9]. When used together, these two techniques offer a more holistic understanding of tree health and contribute to enhancing safety in both urban and rural environments.
In the application of two-dimensional acoustic tomography, the number of sensors (transducers) plays a crucial role in determining image quality and diagnostic reliability. If varying sensor quantities affect stress wave velocity (V) measurements, this can directly influence image interpretation and subsequent assessments. In field practice, especially when inspecting large-diameter trees, limitations in time and labor often restrict the number of sensors that can be deployed. Thus, whether increasing the number of sensors enhances image accuracy and interpretability is a question of both scientific and practical importance. This study explores whether different numbers of sensors result in significant variations in the acoustic images of the same trunk cross-section and whether these variations affect the spatial distribution and variability of stress wave velocity values.
Previous studies have suggested that increasing sensor quantity can enhance image resolution and diagnostic performance. Most existing research has used between eight and twelve sensors for detecting internal decay and cavities, with a focus on evaluating image accuracy [10,11,12]. Other studies have examined how sensor placement and number influence acoustic imaging outcomes [13,14]. However, research remains limited on how sensor quantity affects the numerical variation, spatial distribution, and inter-configuration correlation of stress wave velocity values, particularly in distinguishing between healthy and decayed regions. For example, a study comparing 12 and 24 sensors found that the velocity threshold values used for detecting decay varied depending on the number of sensors employed [15]. If both acoustic images and stress wave velocities are influenced by sensor quantity, it may be necessary to dynamically adjust the threshold values used for damage detection.
Therefore, this study aims to investigate the impact of sensor quantity on the distribution of stress wave velocity (V) in 2D acoustic tomography images. The specific objectives are to (1) analyze image differences across various sensor quantities; (2) assess the spatial distribution and variability of V values; (3) examine correlations of V values between different sensor configurations; and (4) compare V values between healthy and damaged regions. The findings are expected to provide a valuable reference for interpreting acoustic tomography images and for assessing the extent of internal trunk damage in practical applications.
2. Materials and Methods
2.1. Experimental Materials
This study was conducted at the Gongguan Campus of National Taiwan Normal University, located in the Wenshan District of Taipei City, Taiwan. Hoop pine (Araucaria cunninghamii Sweet) trees were examined during the period of March 2025. Trees growing along the roadside were selected as the research subjects. To ensure effective detection of the internal condition of tree trunks, sample trees with a diameter at breast height (DBH) greater than 70 cm were chosen for analysis. The estimated age of the sampled trees, based on visible annual growth rings, is between 47 and 51 years, determined using an increment corer to extract core samples. A total of five qualified trees were selected for subsequent acoustic tomography and resistance drilling tests.
2.2. Experimental Methods
This study aimed to investigate the effect of different numbers of sensors on the two-dimensional (2D) acoustic tomographic imaging of stress wave velocity in the trunks of Araucaria cunninghamii. Resistance drilling was also employed to assist in evaluating the internal wood condition. The experimental procedure consisted of two major parts: acoustic tomography and resistance drilling tests.
2.3. Acoustic Tomography
A Fakopp 3D Acoustic Tomograph (Fakopp Enterprise Ltd., Sopron, Hungary; version 6.5 [16]) was used to perform acoustic scanning on the five sample trees to construct 2D images of stress wave velocity across trunk cross-sections. The equipment was operated and the software was used in accordance with the user manual [16,17]. The system measured the transmission time and velocity of stress waves along various paths across the tree trunk cross-section to obtain raw data for image reconstruction.
During testing, sensors were evenly distributed around the trunk in a horizontal plane at a height of 30 cm above ground. Each sample tree was scanned using 8, 12, 16, and 20 sensors, respectively. ArborSonic 3D software (v5.3.164; Fakopp Enterprise Ltd.) was used to generate the tomographic images. Stress wave data were collected by repeatedly tapping each sensor to ensure a complete data matrix. The generated stress wave frequency ranged between 35 and 40 kHz. This method of generating mechanical stress waves helped improve the consistency and reliability of data collection for subsequent analysis. The software automatically calculated stress wave velocities and produced 2D tomographic images showing lateral distributions of wave speeds. The acoustic tomography procedure is illustrated in Figure 1.
2.4. Resistance Drilling Test
To further assess the internal wood condition of the sample trees and validate the acoustic tomographic interpretations regarding regions of differing wave velocities, resistance drilling tests were conducted on the five Araucaria cunninghamii trees with no apparent external defects. A RESI PD500 resistance drill (IML, Kennesaw, GA, USA) was used for the testing.
On the cross-section of each tree, radial drillings were conducted in four directions—east, south, west, and north—extending from the bark toward the center. During the drilling process, the device recorded variations in drilling resistance, producing resistance amplitude profiles. The drill bit specifications were as follows: a cylindrical drill bit with a tip diameter of 3.0 mm, a shaft diameter of 1.5 mm, and made of stainless steel with a special coating. The drill bit features a sharp conical tip designed for efficient penetration.
The RESI PD500 had a maximum drilling depth of 500 mm and a resolution of 0.1 mm, providing data on drilling depth with a 1:1 scale to ensure measurement accuracy. The test parameters were set as follows: one resistance amplitude value was recorded every 0.1 mm, the feed rate was 100 cm/min, and the drill rotation speed was 2500 RPM. The resulting profiles were used to assess wood soundness and identify potential decay or hollow zones, serving as a reference for interpreting the acoustic tomography images.
3. Results
3.1. Drilling Resistance Amplitude Analysis
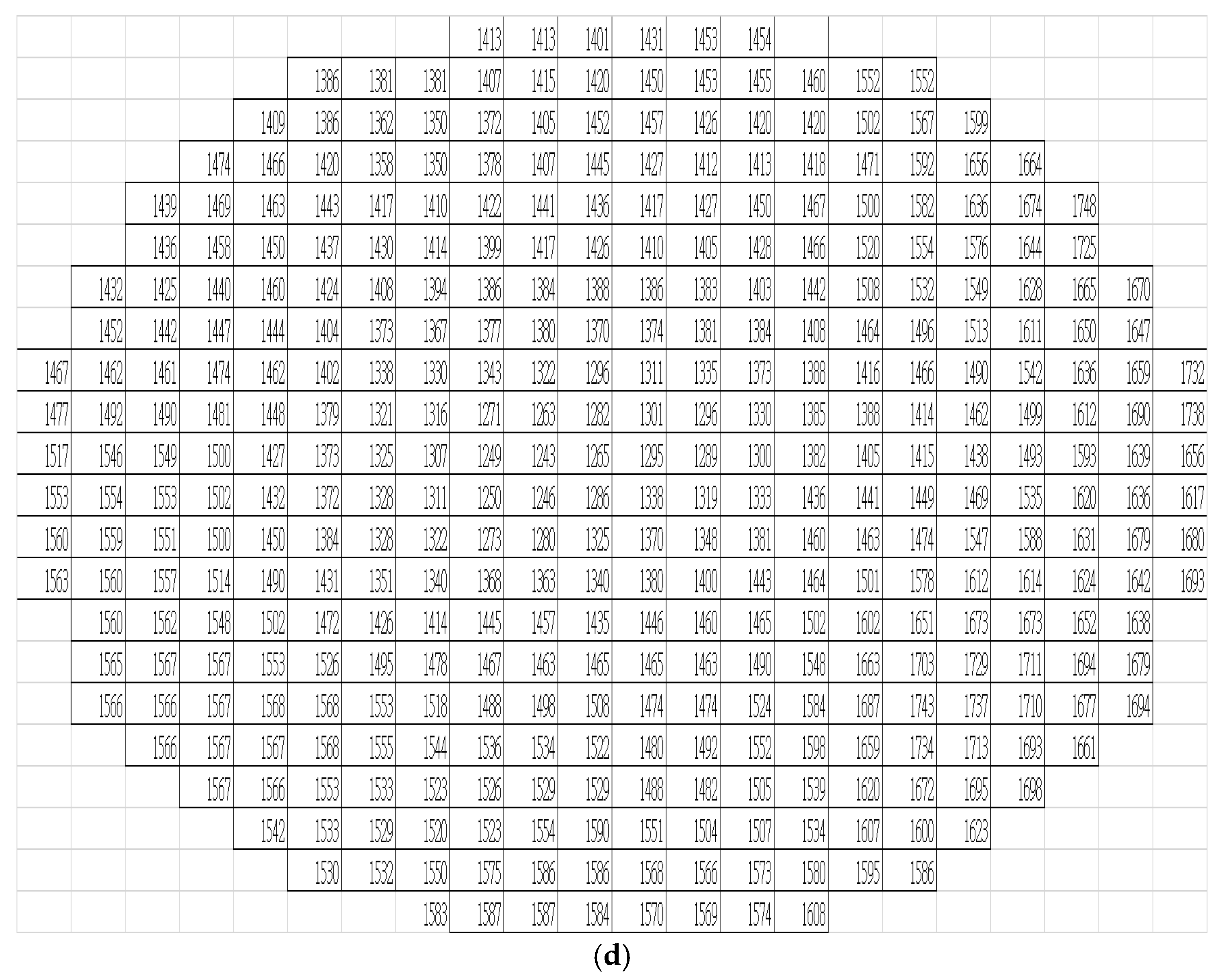
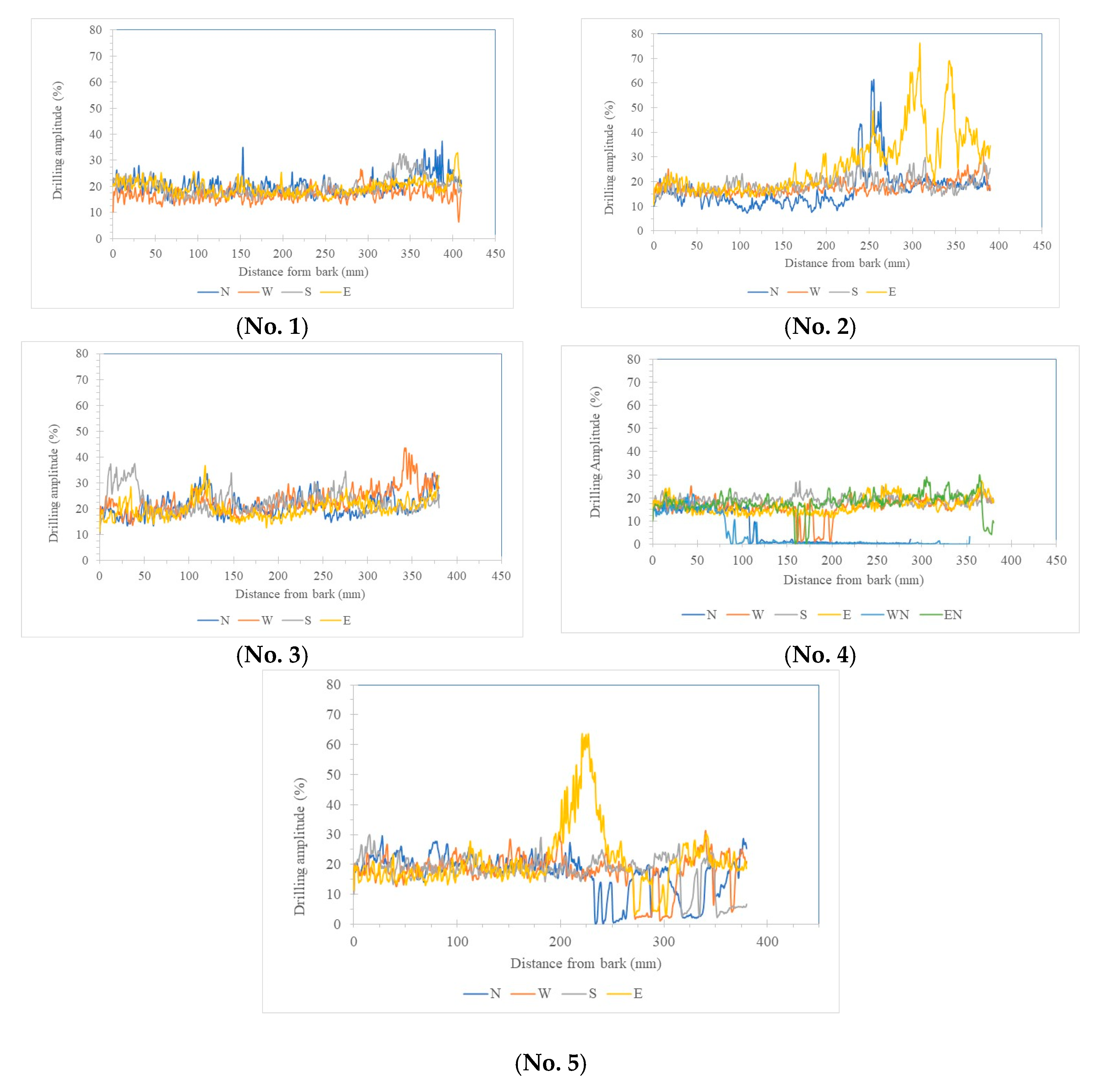
This study employed a minimally invasive resistance drilling technique to evaluate the internal wood structure of tree trunks by analyzing the amplitude variation curves recorded during drilling. This technique allowed the spatial identification of both sound and defective regions and served as a reference for subsequent comparisons with stress wave velocity images generated under different sensor configurations. Five sample trees were tested, with radial drillings conducted in four directions (north, south, east, and west) on each tree. Each drilling path extended from the bark to the central axis, and resistance amplitude data were recorded throughout the process (Figure 2).
The measured data showed that sound wood generally exhibited higher drilling resistance amplitudes compared to areas with structural defects, such as decay or cavities. A threshold was set at 70% of the amplitude value for sound wood. Based on this criterion, the results indicated that Tree No. 4 and Tree No. 5 exhibited localized amplitude values below the threshold, confirming the presence of internal defects. Specifically, Tree No. 4 had a defective area concentrated on the northern cross-section, covering 13.3% (damage area) of the total area and showing an asymmetrical distribution. Tree No. 5 exhibited defects near the central axis, occupying 9.4% of the cross-sectional area.
In contrast, the average amplitudes (Table 1) in all four directions of the sound trees (Tree No. 1, 2, and 3) ranged from 16.9% to 27.1%, significantly higher than the 4.1%–19.2% range observed in the defective trees. These ranges did not overlap, indicating that the selected threshold effectively distinguished structural integrity differences.
In the subsequent analytical stage, the damaged areas identified through resistance drilling were used as fixed references for grid-based numerical analysis of the stress wave velocity images. This approach verified the effect of different sensor numbers on the accuracy of interpreting two-dimensional tomographic images, while minimizing bias from subjective interpretation. Notably, the applicability of the amplitude threshold may be influenced by species-specific properties and environmental factors (e.g., wood moisture content). Future research is recommended to incorporate species-specific calibration models and integrate high-resolution tomographic imaging technologies to enhance the accuracy of defect volume estimation.
3.2. Stress Wave Velocity 2D Tomographic Image Analysis
According to Table 2, this study conducted two-dimensional tomographic analyses of stress wave velocity on five sample trees using eight, twelve, sixteen, and twenty sensors, respectively, to investigate the impact of the number of sensors on the interpretation of internal trunk cross-sectional structures. Overall, the maximum stress wave velocity ranged from 1605 m/s to 2404 m/s, the minimum velocity from 828 m/s to 1396 m/s, and the average velocity from 1216 m/s to 1840 m/s, reflecting differences in internal structure among the sample trees.
A closer look at the healthy trees (Tree No. 1, 2, and 3) showed maximum velocities ranging from 1744 to 2342 m/s, minimum velocities from 970 to 1396 m/s, and average velocities from 1435 to 1840 m/s. In contrast, the defective trees (Tree No. 4 and 5) showed maximum velocities from 1605 to 2404 m/s, minimum velocities from 828 to 1102 m/s, and average velocities from 1216 to 1651 m/s. Although the maximum velocities were comparable between the two groups, the minimum and average velocities were consistently lower in defective trees, indicating reduced structural integrity. A t-test analysis confirmed that the minimum stress wave velocities of the defective trees were significantly lower than those of the healthy trees (p < 0.05), supporting the use of minimum velocity as a potential indicator of internal deterioration.
Regarding sensor quantity, increasing the number of sensors from eight to twenty generally led to more stable velocity readings across most sample trees, with a noticeable decrease in minimum velocity values. This result indicates that increasing the sensor count improves image resolution and enhances the ability to detect localized anomalies. Notably, the number of sensors had a significant influence on minimum velocity, highlighting its importance in revealing potential structural defects.
A comparison between tomographic images and drilling resistance amplitude analysis showed visible decay and cavities in the cross-sections of Tree No. 4 and 5, consistent with their stress wave velocity performance. Tree No. 4 exhibited an average minimum velocity of 876 m/s, and for Tree No. 5, this value was 975.5 m/s, both markedly lower than that of healthy trees such as Tree No. 1 (1179.8 m/s) and Tree No. 3 (1181.8 m/s), reinforcing the diagnostic value of stress wave velocity in detecting internal abnormalities.
Overall, regardless of tree health condition, increasing the number of sensors consistently resulted in lower minimum velocity values, reflecting enhanced sensitivity to localized wave propagation delays due to higher resolution. Therefore, in practical applications, when using stress wave velocity as a diagnostic reference, it is important to account for the influence of the number of sensors on velocity readings and apply standardization or calibration procedures to improve diagnostic accuracy and consistency.
In summary, the results of this study support the use of stress wave velocity as an effective indicator of tree health. They also confirm that internal damage such as decay and cavities significantly affects wave propagation characteristics. Proper adjustment of sensor configuration and analysis parameters can improve the accuracy of image interpretation and enhance the feasibility of practical application.
3.3. Effect of the Number of Sensors on Stress Wave Velocity
As shown in Table 3, this study conducted two-dimensional stress wave tomography on five sample trees using eight, twelve, sixteen, and twenty sensors. The resulting images from each test were processed into grids ranging from 384 to 421 cells, followed by one-way analysis of variance (ANOVA) and Tukey’s post hoc tests to examine the effect of the number of sensors on stress wave velocity values. The analysis revealed that, for most sample trees, the average stress wave velocity varied significantly with different numbers of sensors (p < 0.05), indicating that changes in the number of sensors influenced the velocity values presented in the images.
Among the healthy sample trees (Tree No. 1, 2, and 3), stress wave velocity generally showed a decreasing trend. Specifically, when eight sensors were used, the average velocity ranged from 1644.4 to 1796.5 m/s; with twelve sensors, from 1585.8 to 1633.8 m/s; with sixteen sensors, from 1581.6 to 1712.4 m/s; and with twenty sensors, from 1549.4 to 1624.1 m/s. These results indicate a consistent pattern in which an increase in the number of sensors corresponded to a decrease in stress wave velocity in this group.
A similar trend was observed in the defective trees (Tree No. 4 and 5). When using eight sensors, the average velocity ranged from 1490.2 to 1494.9 m/s; with twelve sensors, from 1423.3 to 1436.3 m/s; with sixteen sensors, from 1336.2 to 1403.7 m/s; and with twenty sensors, from 1299.3 to 1395.3 m/s. Overall, the stress wave velocities in the defective trees were lower than those in the healthy trees, and the degree of velocity reduction with an increase in the number of sensors was more pronounced.
Taken together, these results demonstrate that the number of sensors had a clear influence on the stress wave velocities obtained from the tomographic images, regardless of tree condition. As the number of sensors increased, stress wave velocity generally decreased, suggesting that measurement results were affected by sensor configuration. This effect should be carefully considered during data analysis and practical application. Selecting an appropriate sensor configuration based on diagnostic purposes and required resolution will help improve the interpretability and consistency of the measurement data.
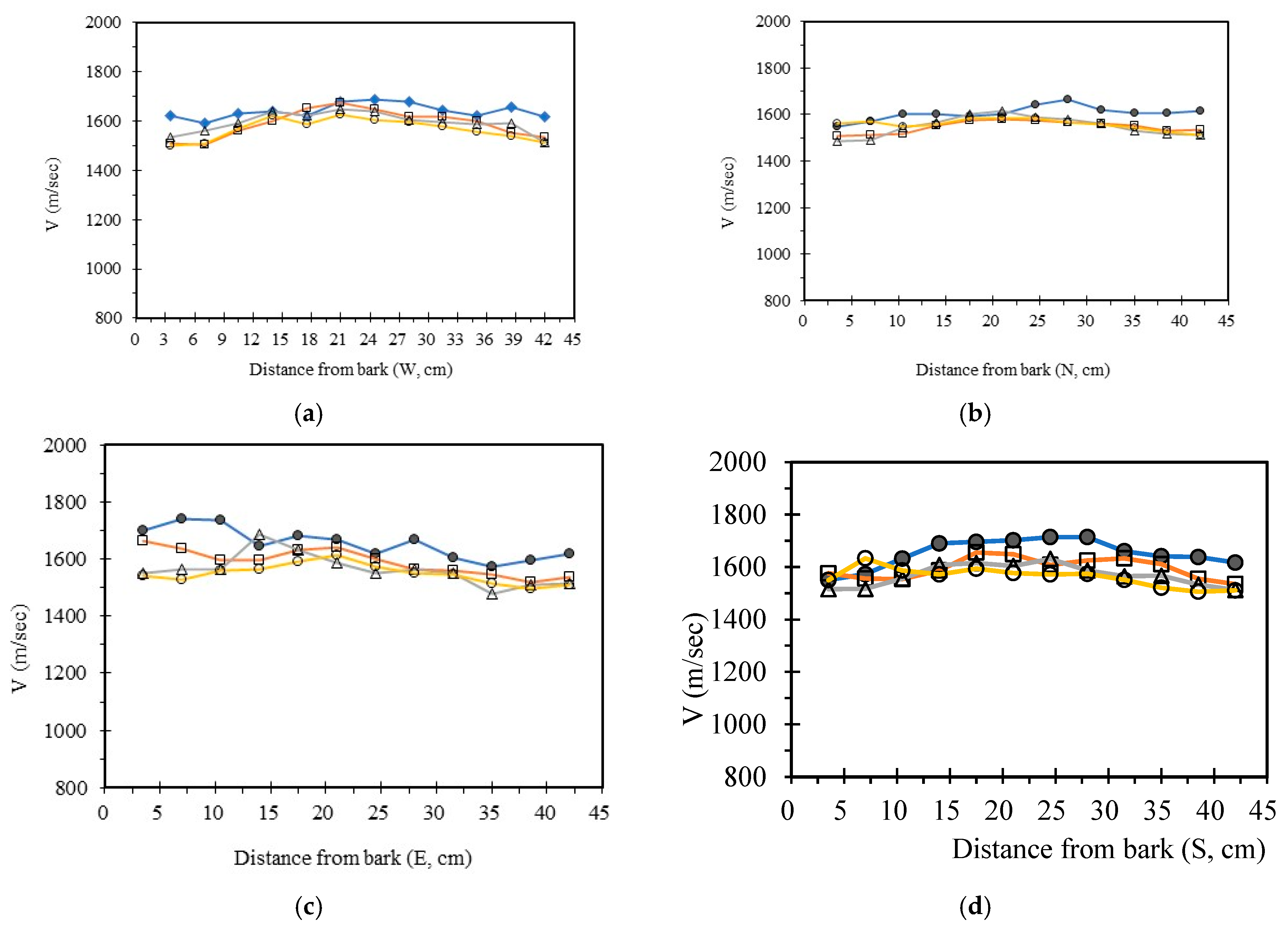
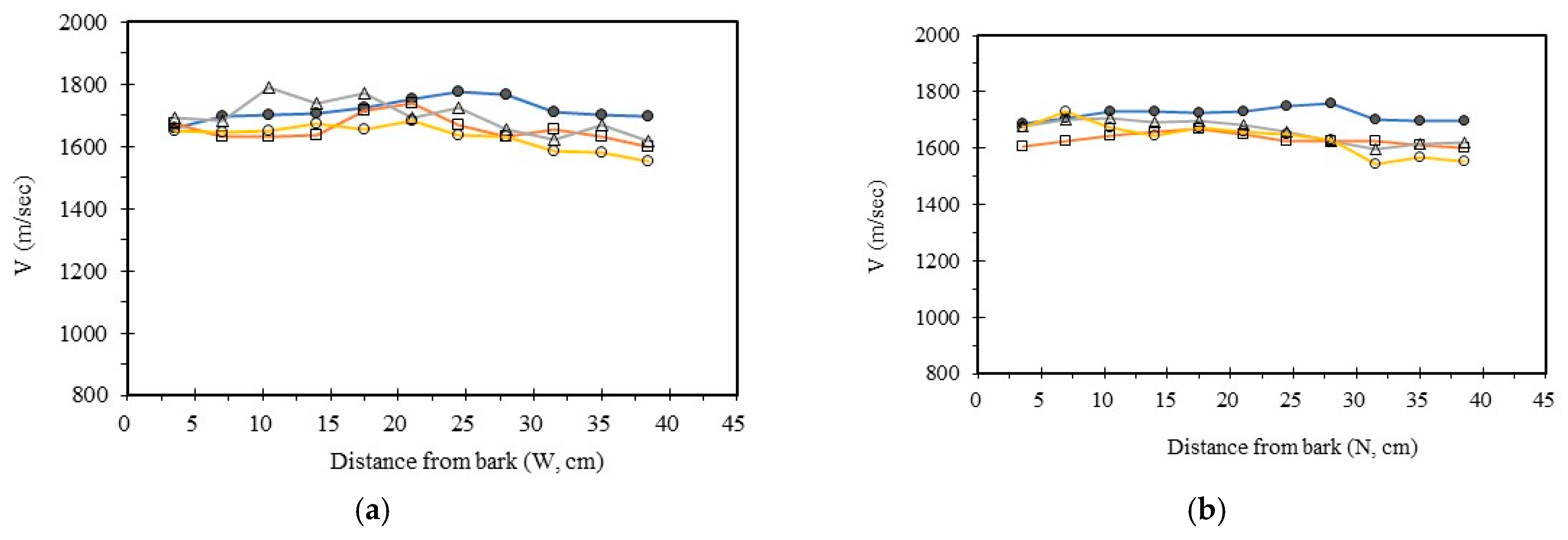
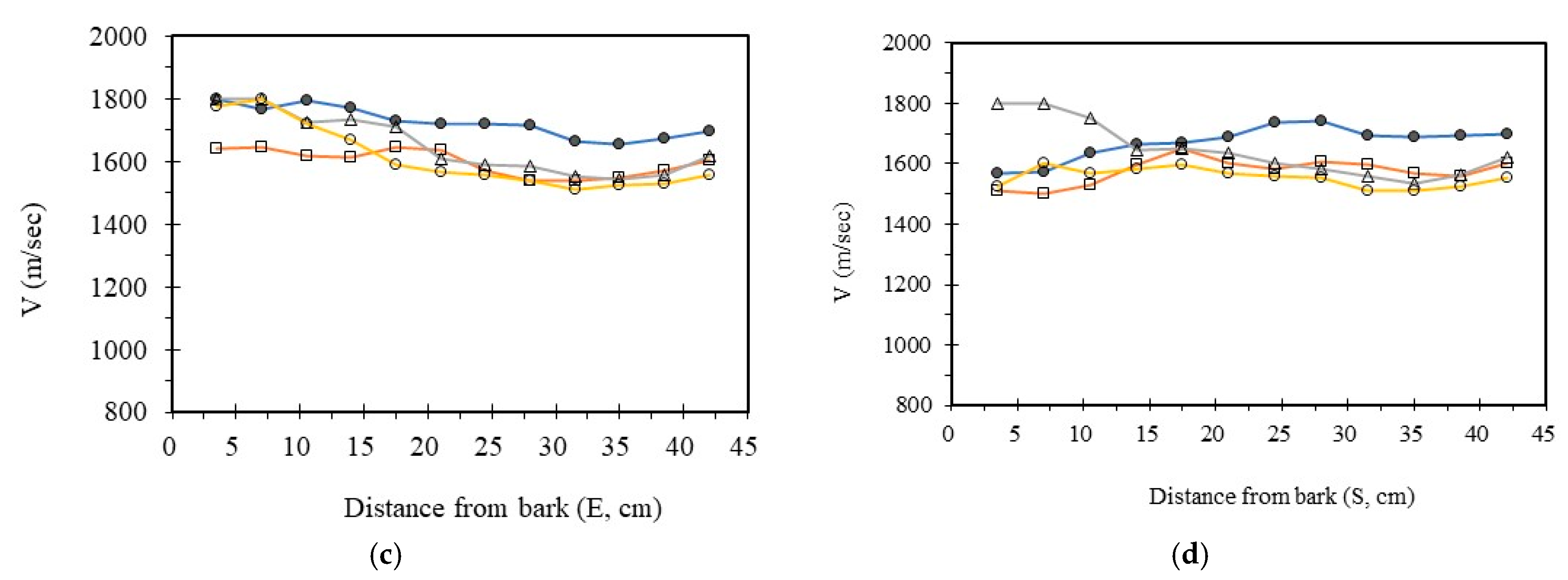
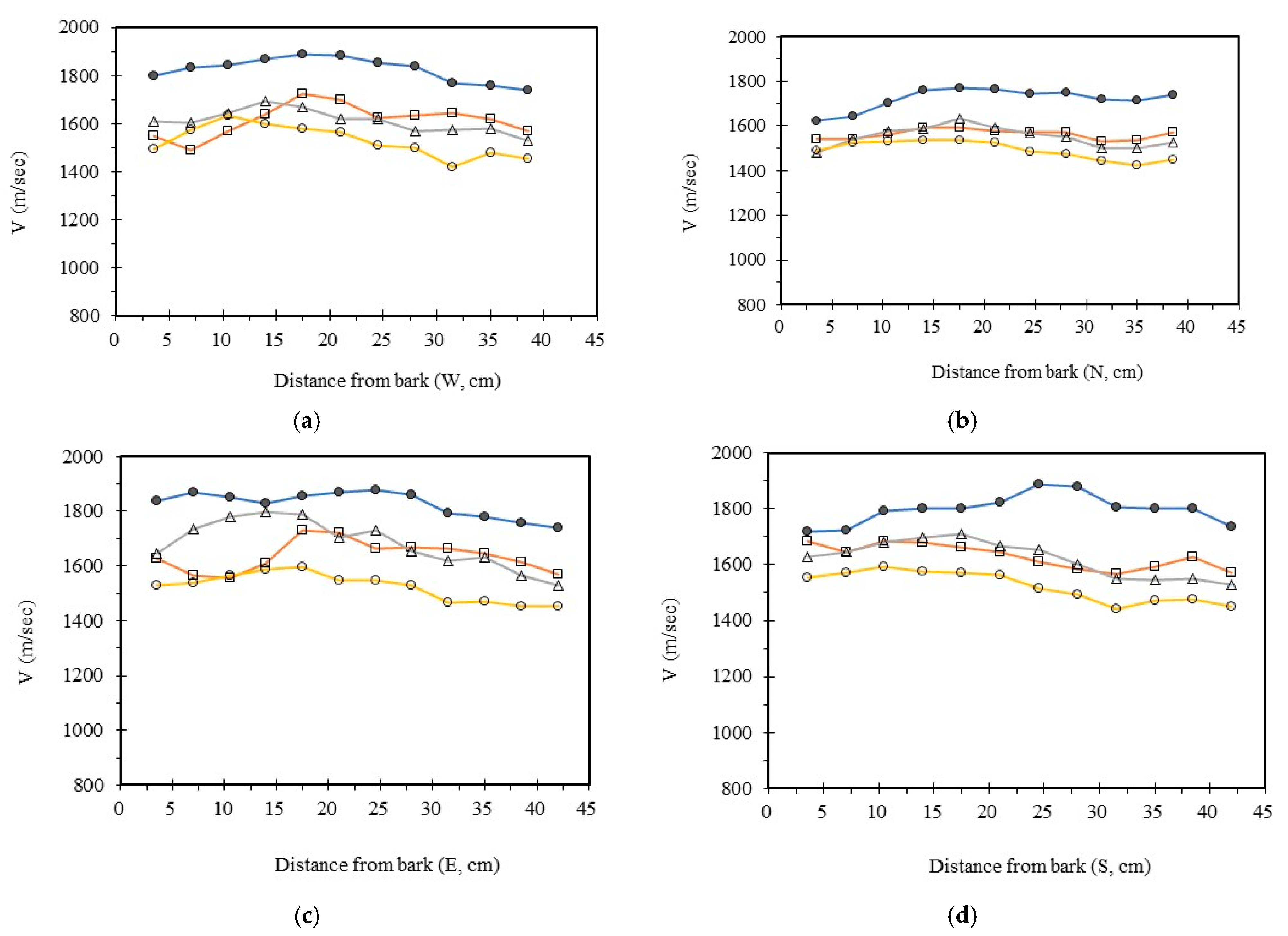
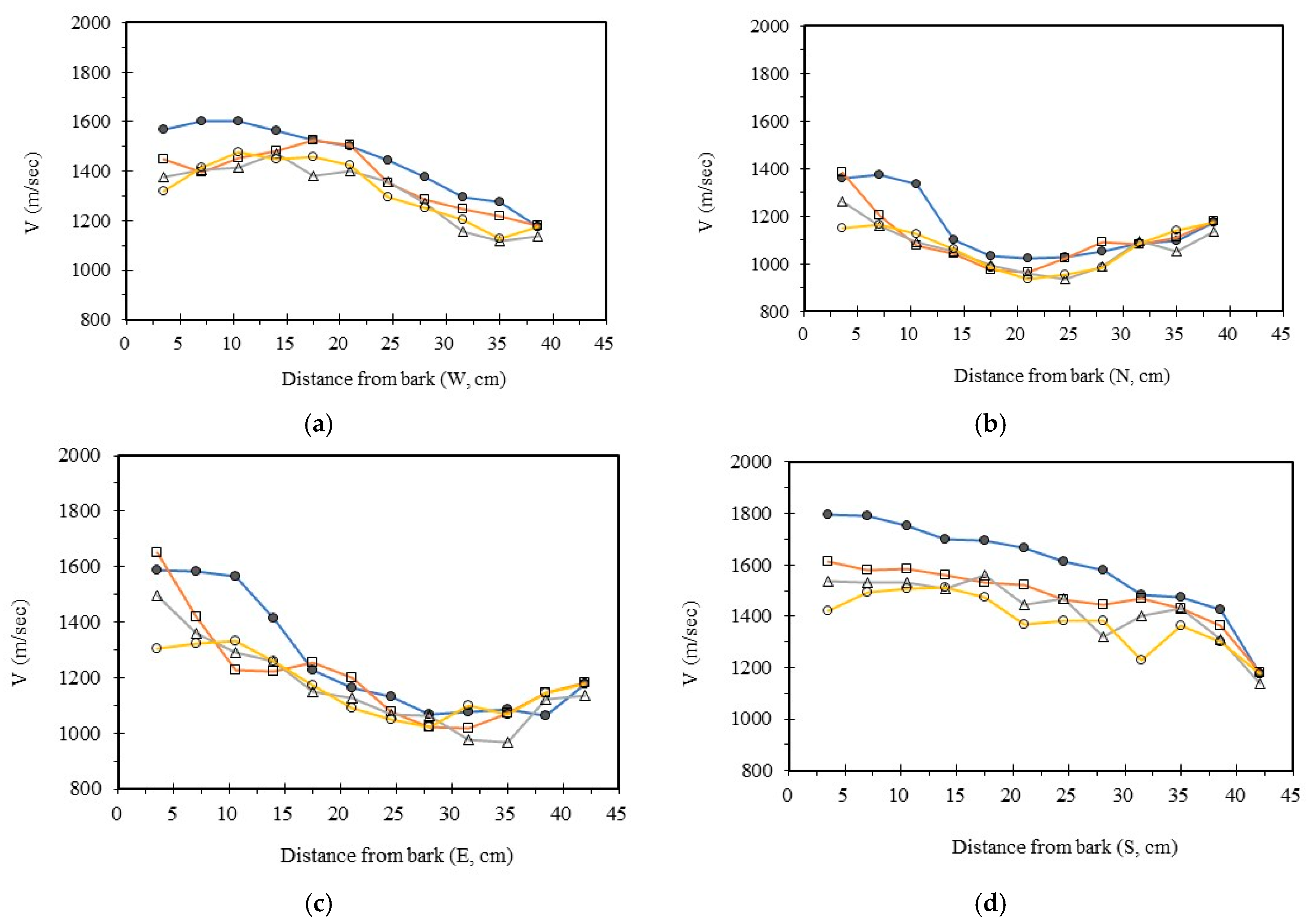
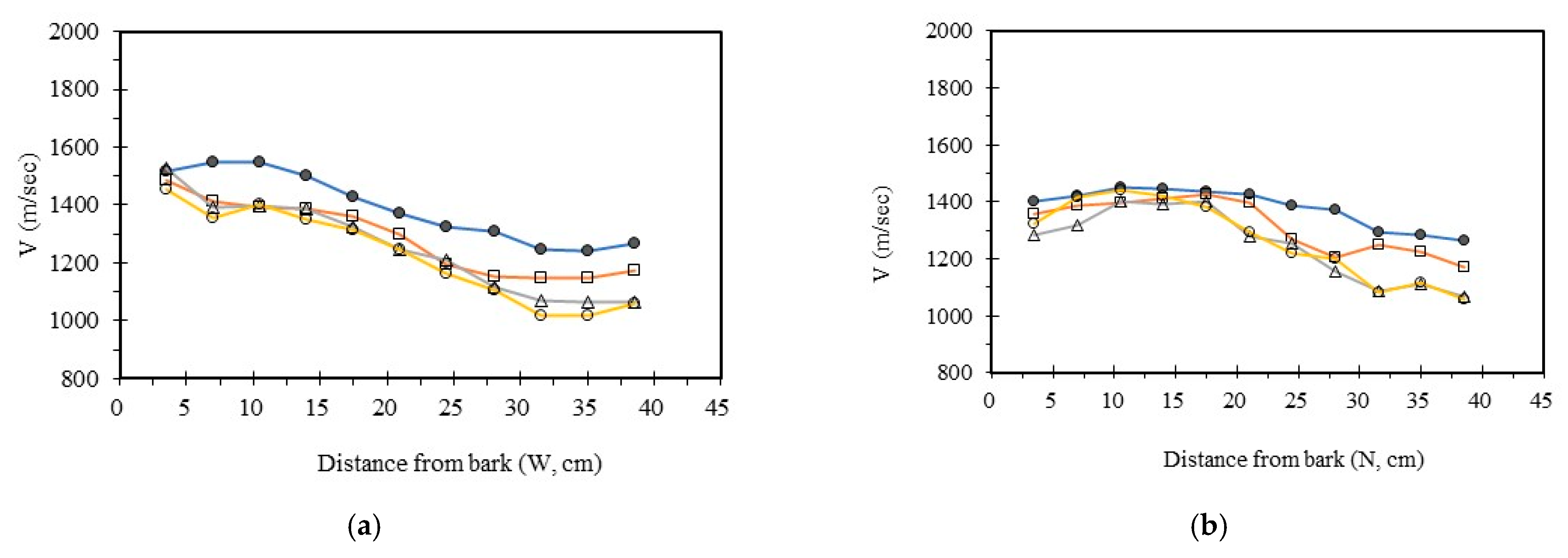
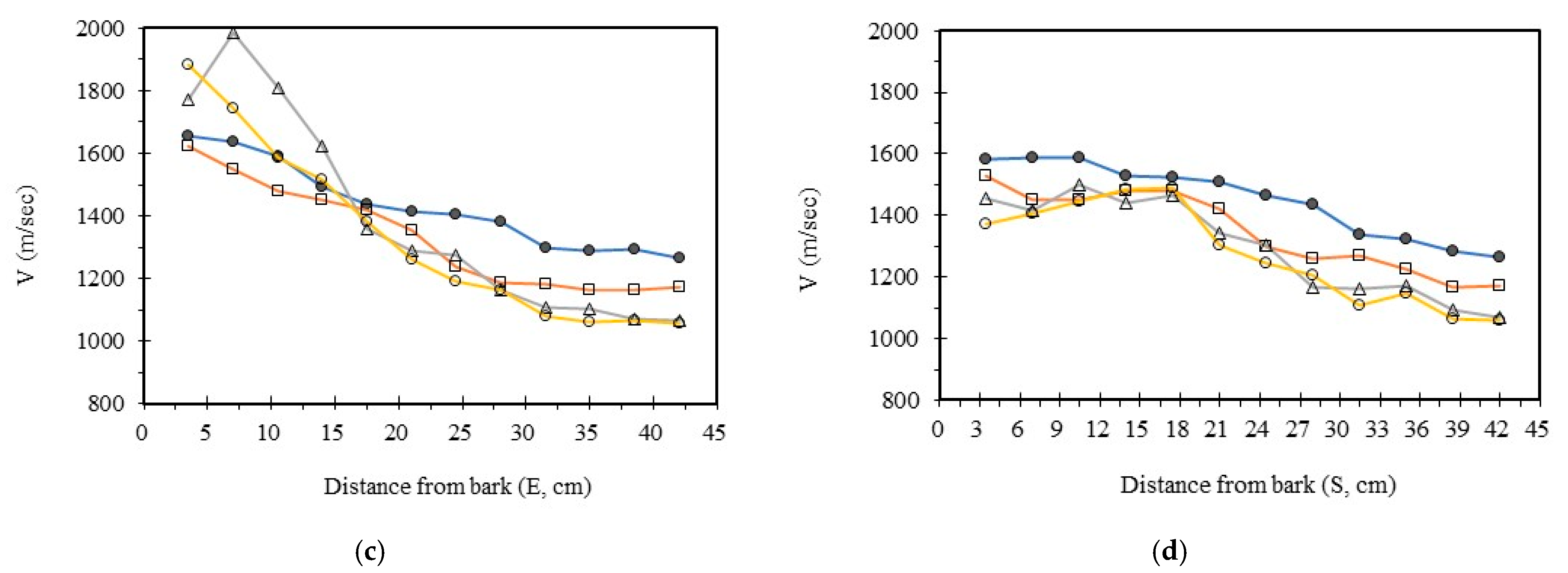
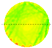
3.4. Analysis Radial Variation Analysis
In this study, five sample trees were examined using varying numbers of sensors to perform two-dimensional stress wave tomography. The resulting images were processed into grids, with each cell measuring 3.5 × 3.5 cm, allowing for the extraction of stress wave velocity values from the bark to the center of the trunk at 3.5 cm intervals. Based on the collected data, radial variation curves of stress wave velocity were plotted (Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7), illustrating the patterns of radial change in each tree.
From the imaging results, two distinct types of radial variation characteristics were identified. Sample Trees 1, 2, and 3 exhibited stress wave velocity ranges approximately between 1400 and 1800 m/s, while Trees 4 and 5 showed broader velocity ranges, from about 1000 to 2000 m/s. Notable differences in the distribution patterns of stress wave velocities were observed among the different trees.
Further examination of the radial variation patterns revealed diverse trends in Trees 1 to 3, including irregular fluctuations, initial increases followed by decreases, gradual declines, and gradual increases in velocity. In contrast, Trees 4 and 5 primarily exhibited a decreasing velocity trend from the outer bark inward, or a decline followed by a slight increase near the trunk center. Additionally, comparisons of tomographic images generated using different numbers of sensors (eight, twelve, sixteen, and twenty) showed that the radial variation trends in Trees 1 to 3 were more dispersed, whereas Trees 4 and 5 presented relatively consistent variation patterns. These findings indicate that sensor configuration had a measurable impact on image quality and consistency.
Notably, regardless of tree condition, the visual presentation of stress wave velocity images tended to stabilize as the number of sensors increased, following a trend of “8 sensors > 12 sensors > 16 sensors > 20 sensors” in terms of velocity distribution variability. This phenomenon suggests that increasing the number of sensors contributes to improved resolution, greater stability in velocity measurements, and enhanced ability to detect internal structural variations within the trunk.
3.5. Linear Regression Analysis
According to the results presented in Table 4, the linear regression analyses of 2D stress wave velocity images derived from different sensor combinations showed notable differences among individual trees. For healthy trees (Trees 1, 2, and 3), the coefficient of determination (R2) values were generally low, ranging from 0.06 to 0.58, indicating low consistency in the velocity values measured between different sensor combinations, with more dispersed data distributions. Nevertheless, some sensor combinations still exhibited relatively high and statistically significant R2 values. For instance, Tree 1 had an R2 of 0.49 for the “12 vs. 8” sensor combination, Tree 2 showed an R2 of 0.52 in the “20 vs. 16” combination, and Tree 3 reached 0.58 in the same combination.
In contrast, decayed or hollow trees (Trees 4 and 5) exhibited highly significant linear relationships (p < 0.01) across all sensor combinations, with R2 values ranging from 0.82 to 0.91, demonstrating that the trends in velocity variation between sensor combinations were highly consistent, reflecting the predictable stress wave differences caused by internal deterioration. Overall, the comparison showed that in healthy trees with intact internal structures, velocity values measured from different sensor combinations were more variable, resulting in weaker correlations in regression outcomes, and some combinations did not reach statistical significance. Conversely, in decayed or hollow trees, damage was more concentrated, leading to more consistent velocity variation trends across sensor combinations, and therefore higher R2 values and significance. These findings indicate that analyzing the linear correlation and R2 values of velocity measurements between different sensor combinations can serve as a valuable reference for assessing the internal condition of trees.
Additionally, regression results presented in Table 4 demonstrated that for decayed or hollow trees, even with a limited number of sensors (e.g., eight), the velocity trends measured were still effective in predicting the imaging outcomes obtained from larger sensor configurations (e.g., twelve, sixteen, or twenty sensors). Therefore, in practical applications where the goal is to detect decay or hollowness, employing only eight sensors may be sufficient for effective measurement, enhancing operational efficiency while balancing accuracy and time costs.
In summary, the linear correlation and R2 values of velocity results between different sensor combinations not only effectively reflect the internal structural condition of trees but also serve as important references for developing on-site inspection strategies.
3.6. Stress Wave Velocity Analysis of Sound and Damaged Areas
According to the drilling resistance test results for Trees 4 and 5, decayed and hollow areas were detected within the trunks of both trees. When the drilling resistance amplitude dropped below 70% of the original amplitude, the area was classified as decayed or hollow. Based on this criterion, the trunks were divided into sound and damaged regions for comparative analysis with the 2D stress wave images. Through image grid processing, stress wave velocities at each location were obtained, and the average stress wave velocities for the sound and damaged regions were calculated accordingly, as shown in Table 5.
Under different sensor combination conditions, the average stress wave velocity in the sound regions of Tree 4 ranged from 1336.8 to 1553.2 m/s, while that in the damaged regions ranged from 1017.3 to 1055.2 m/s (13.3% damage ratio). For Tree 5, the velocity in the sound regions ranged from 1420.9 to 1506.9 m/s, and in the damaged regions, it ranged from 1105.9 to 1309.3 m/s (9.4% damage ratio). Overall, the stress wave velocities in sound areas were significantly higher than those in damaged areas, indicating a clear positive correlation between wood structural integrity and stress wave propagation velocity.
In addition, when using eight, twelve, sixteen, and twenty sensors for detection, both the sound and damaged regions showed a slight decreasing trend in average stress wave velocity as the number of sensors increased. However, a one-way ANOVA test revealed that the differences among the sensor configurations were not statistically significant (p ≥ 0.05).
4. Discussion
4.1. Integration of Detection Techniques
This study employed two-dimensional acoustic tomography in combination with resistance micro-drilling for cross-validation. The results indicated that both methods are capable of detecting internal decay and cavities within tree trunks. Resistance drilling provides detailed information on the depth of decay and variations in wood density, which helps explain the anomalies observed in acoustic images. The innovation of this study lies in the integration of these two techniques, forming a new, and more comprehensive, method for tree health diagnosis that is not commonly found in the existing literature. Acoustic tomography, by contrast, offers advantages such as being rapid and non-destructive (or minimally invasive), making it a suitable tool for preliminary inspections. The combination of these two methods effectively enhances diagnostic accuracy and operational efficiency. Specifically, the resistance drilling data served as a crucial ground truth to validate the acoustic tomography results, particularly in identifying the precise location and extent of internal decay.
The relevant literature also suggests that integrating multiple non-destructive testing techniques can improve overall diagnostic reliability and provide a more robust assessment of tree health [18], and that acoustic tomography should be used alongside other methods to compensate for its limitations—a viewpoint supported by the results of this study [15]. Furthermore, Dudkiewicz and Durlak [19] successfully identified decayed regions in large-diameter trunks using acoustic tomography, with a noticeable decrease in acoustic velocity, which is consistent with our findings. However, our study further demonstrates the benefit of supplementing this with resistance drilling, which provides a quantitative measure of the extent and severity of the decay, moving beyond simple detection.
4.2. The Impact of the Number of Sensors on Imaging Quality
This study also analyzed the effect of the number of sensors on image quality. The results showed that increasing the number of sensors from eight to twenty led to slight improvements in image resolution and the stability of acoustic velocities. This finding underscores a critical trade-off between data resolution and operational efficiency. Another innovation of this study is the systematic evaluation of the impact of sensor numbers on image quality, which is often described qualitatively in previous studies.
However, the differences in measured velocities between various sensor configurations did not reach statistical significance (p ≥ 0.05), indicating that the benefits of increasing the number of sensors are limited to a certain range. This observation is particularly important because it suggests that adding more sensors may not necessarily yield a proportional increase in diagnostic accuracy, especially when considering the practical constraints of fieldwork. Notably, in damaged trees, there was a strong linear correlation between results obtained from different sensor combinations (R2 > 0.82), indicating that even with only eight sensors, the system remains a practical and effective choice for decay detection. This strong correlation serves as a form of “ground truth” validation, suggesting that a simpler, more efficient setup (eight sensors) can provide highly reliable data, particularly in high-risk scenarios where swift and accurate initial assessment is crucial.
Other studies have similarly noted that while the number of sensors affects imaging accuracy, the benefits diminish beyond a certain threshold [10,14]. Maurer et al. [20] emphasized that dense sensor configurations must be paired with appropriate algorithms to achieve optimal results. Liu and Li [21] also highlighted the crucial role of acoustic propagation models in ensuring accurate velocity measurements, which aligns with the observations of this study regarding sensor configuration stability.
4.3. The Relationship Between Acoustic Velocity and Tree Health
The spatial distribution of acoustic velocity serves as an indicator of tree health. The results indicated that healthy trees exhibit greater variability in acoustic velocity across radial directions and weaker linear regression relationships, indicating uniform internal structures without significant defects. In contrast, damaged trees, due to internal decay or cavities, showed more consistent trends in acoustic velocity and significant regression relationships, indicating the influence of damaged areas on wave propagation. This finding offers a new perspective on the relationship between acoustic velocity and tree health, emphasizing the potential application of acoustic measurements in monitoring tree health. This study quantifies these trends, thereby transforming previous qualitative observations into statistically significant indicators that enhance the scientific rigor of the diagnosis.
This phenomenon aligns with observations by [12,13], which suggest that decreases in acoustic velocity serve as indicators of decay. Li et al. [22] pointed out that acoustic tomography can effectively map internal wood defects, with acoustic shadow distributions highly consistent with actual physical characteristics. However, its ability to detect early-stage decay is relatively limited. Consequently, detection performance may be poorer in cases where decayed regions have low density and small size. This study found that velocities in decayed zones (1017–1309 m/s) were significantly lower than those in sound areas, and that image resolution improved with an increased number of sensors, further supporting this finding.
Our findings also confirm finding in the prior literature, according to which acoustic tomography may either underestimate or overestimate the extent of decay. For example, these techniques may underestimate internal decay in the center of the trunk while overestimating decay in the outer trunk. Research has emphasized the impact of cross-sectional geometry on the accuracy of acoustic tomography [11,23,24,25], where deviations from a circular profile typically lead to reduced accuracy. Additionally, the number of sensors used can also affect measurement accuracy [26]. The simplified circular geometry used in this study may therefore explain some of the observed inaccuracies. For certain equipment, accuracy also depends on the number of intersections in the sound wave propagation path. The center of the trunk has more intersections; thus, the accuracy in the outer cross-section is often lower. In comparison, detecting decay in the center of the trunk may be more appropriate than detecting decay in the outer regions [27].
Furthermore, using hardness mapping and acoustic tomography to detect decay in the heartwood area of the trunk indicates that acoustic tomography may underestimate the area of decay [28]. The frequency of stress waves is influenced by various factors, including wood material, applied sensors, and geometric shapes, such as the distance between the source and receiver [12]. When evaluating structural defects in the trunk, the presence of internal cracks or annular fissures may lead to an overestimation of defect areas, which is often due to inappropriate distances between probes affecting the accuracy of stress wave measurements. Therefore, the accuracy of tomography is highly dependent on the correct setting of these parameters to avoid misrepresenting the size and extent of structural defects. Defect or decay areas can only be detected when they occupy more than 2.8% to 5% of the cross-sectional area [12]. To better assess the internal condition and decay of trees, it is recommended to combine other more effective methods, such as using more probe sensors to improve resolution. Acoustic tomography only reflects the acoustic characteristics of the measured cross-section and not the actual internal condition. Therefore, performing drilling resistance tests guided by the information provided by tomography can more accurately distinguish decayed wood from the fissures indicated by tomography [18]. Drilling resistance technology or using incremental drillers for core sampling to determine the location and nature of defects can improve the accuracy of the information. Finally, severe wood decay can reduce stress wave velocity to 70% of the characteristic values of healthy wood, indicating a significant decline in strength [29]. If the stress wave velocity (Fakopp) drops below 90% to 85% of the average velocity, cavities or decay may be present. When the relative velocity decreases to 0%, 5%, 10%, 15%, 20%, 30%, 40%, 50%, and >50%, the estimated areas of decay are 0%, 0%, 0%, 0% to 10%, 10% to 20%, 10% to 20%, 20% to 40%, 30% to 50%, and >50%, respectively [16]. As the stress wave velocity decreases, the area and extent of decay and cavities become more severe [12].
4.4. Limitations of Acoustic Tomography
In discussing the application of acoustic tomography, this study must explicitly state that a major limitation is the sample size. Since the focus of this research was to investigate the effect of different numbers of sensors on stress wave velocity detection, we selected five trees of the same species (Hoop pine, Araucaria cunninghamii Sweet) from a single location to ensure highly consistent experimental conditions. The small sample size, along with the single location and species, limits the generalizability of the findings, and the conclusions cannot be fully extrapolated to other tree species or different growing environments. Nevertheless, under these specific controlled conditions, this study successfully established the relationship between the number of sensors and the detection results. To address these limitations, future research should expand the sample size to include a wider range of tree species and growing environments, which will be essential to further validate and strengthen the findings of this study.
Although the concentrated distribution of acoustic velocity can serve as a basis for identifying damage, this study also found that image reconstruction has limitations in depicting the shapes of decay or crack boundaries. This limitation reminds us that, despite the potential of acoustic tomography, results should be interpreted cautiously in applications. Some reconstructions may result in overestimations or underestimations due to algorithmic constraints, especially in cases where decay and cracks coexist, which we observed in our analysis. This issue corresponds with the “velocity overlap” and “image misinterpretation” problems reported by [11,15]. Proto et al. [30] successfully identified ring cracks in chestnut trees (Castanea sativa) and noted that multi-path measurements could significantly improve localization accuracy, consistent with our findings that increasing the number of sensors (from 8 to 20) enhances image resolution and decay detection capability.
The accuracy of stress wave measurements is influenced by numerous factors beyond just the number of sensors, including the wood’s inherent physical properties and microstructure. These factors, such as density, moisture content, grain angle, and microfibril angle, directly affect wave propagation speed. Specifically, studies have found a high negative correlation between annual ring width and longitudinal wave velocity, indicating that smaller and more regular annual rings result in higher stress wave velocities. This finding provides a new direction for future research to explore the intricate relationship between wood properties and acoustic performance. As an anisotropic material, a tree’s elastic constants differ in radial, tangential, and longitudinal directions, leading to varying stress wave velocities [31]. The velocity of stress waves propagating across a log’s cross-section is also affected by the tangential angle [32]. Furthermore, factors such as the number and planar distribution of sensors are critical for improving image fitting and reducing error rates [33]. The wood species, moisture content, signal frequency, and the presence of cracks also significantly influence the velocity and thus the detection accuracy [34]. This complex interplay of factors highlights the need for a comprehensive approach to stress wave detection, where the sensor configuration and the physical properties of the wood are considered together to avoid misrepresenting the size and extent of structural defects. For instance, the presence of internal cracks or annular fissures may lead to an overestimation of defect areas, often due to inappropriate distances between probes [12]. Ultimately, to better assess the internal condition of a tree, it is recommended to combine acoustic tomography with other more effective methods. This integration ensures that the final diagnosis moves beyond a simple acoustic reading to a validated assessment of tree health, as discussed in previous sections.
4.5. Importance and Development
In summary, this study verified that acoustic tomography and resistance micro-drilling offer complementary advantages in diagnosing tree health. Despite the inherent limitations of this study, influenced by various factors such as tree species, sample size, moisture content, wood grain, and decay, which may affect the test results, these factors do not diminish the value and importance of this research. The innovation of this study lies not only in the integration of techniques but also in the in-depth exploration of their applicability across different tree species and environmental conditions, providing valuable references for future research. As a coniferous species, the low wood density of Hoop pine provides an important case study whose test methods and results can serve as a foundational reference for future applications involving similar tree species or wood materials. By appropriately configuring the number of sensors and integrating diverse detection techniques, diagnostic accuracy and operational efficiency can be significantly improved.
The experimental results also demonstrated that with an increased number of sensors, the sensitivity and resolution of acoustic tomography for detecting localized decay noticeably increased. However, it is crucial to note that the lowest acoustic velocity values observed under high-resolution imaging conditions may not accurately reflect an actual decline in wood strength. Instead, they indicate the system’s enhanced ability to detect previously unrecognized micro-defective areas due to improved resolution. This inference aligns with the findings of Arciniegas et al. [35] and Liu and Li [21], who suggested that high-frequency sensing and adaptive signal processing can enhance imaging quality. Li et al. [36] and Sharapov et al. [37] also indicated that drilling amplitude can be used to distinguish between healthy and damaged zones, further supporting the feasibility of using variations in acoustic velocity for diagnostic purposes.
Moving forward, future studies are recommended to expand the sample scope by including a broader range of tree species, different diameter classes, and diverse environmental conditions to establish a representative acoustic parameter database. Additionally, the integration of three-dimensional imaging technologies, machine learning algorithms, and various non-destructive testing tools should be explored to enhance diagnostic precision and support the development of intelligent systems. Special attention should be given to the relationship between variations in acoustic velocity and different types of damage, in order to develop practical threshold values—either fixed or adaptive—as indicators for early decay detection, thereby promoting the scientific and standardized assessment of urban tree risk.
5. Conclusions
This study investigated the effects of varying numbers of sensors (eight, twelve, sixteen, and twenty) on the distribution of acoustic wave velocity in 2D acoustic tomography of Hoop pine (Araucaria cunninghamii Sweet) trees and examined their applicability for internal health assessment. The key findings and their implications are summarized as follows:
1. Increasing the number of sensors improved the resolution of the imaging grid, enhancing the system’s ability to detect smaller defects. However, no statistically significant differences were found in the average acoustic wave velocities across different sensor configurations (p ≥ 0.05), indicating that velocity measurements remained stable regardless of sensor count.
2. Healthy trees exhibited higher acoustic wave velocities with greater spatial heterogeneity, reflecting a relatively uniform internal structure. In contrast, decayed or hollow trees showed a decreasing velocity trend from the bark to the center (or a central rebound), suggesting that damaged areas created identifiable and quantifiable interference patterns in wave propagation.
3. Healthy trees displayed lower correlations in acoustic velocity measurements across different sensor configurations (R2 range: 0.06–0.58), whereas defective trees showed strong and consistent linear relationships (R2 = 0.82–0.91, p < 0.01). This finding confirms that the measurements accurately reflect internal deterioration and underscores the reliability of the method for assessing tree health. Additionally, acoustic wave velocities in defective areas were significantly lower than those in sound regions (p < 0.05), further validating the feasibility of using acoustic tomography to detect structural defects.
4. A critical finding is that even with fewer sensors (e.g., eight), a reasonable level of defect identification was maintained. This configuration proved effective for rapid on-site assessments, balancing operational efficiency with cost-effectiveness. For future applications, it is recommended to adjust the number of sensors based on diagnostic objectives and desired image resolution, thereby optimizing the practical value of this non-destructive evaluation technique.
Author Contributions
P.-H.P. and P.-H.L. contributed to the preparation of experimental materials, conducted the experiments, and analyzed the data. C.-J.L. proposed the research idea and the experimental framework and wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Taiwan Forestry Research Institute and National Taiwan Normal University Tree Inspection Project [No. 114GT744A01 and No. 1133756013].
Data Availability Statement
The tree detection dataset used in this study is confidential but can be made available by the corresponding author upon reasonable request after the article is published online.
Conflicts of Interest
The authors declare that there are no competing interests.
References
- Linhares, C.S.F.; Gonçalves, R.; Martins, L.M.; Knapic, S. Structural stability of urban trees using visual and instrumental techniques: A review. Forests 2021, 12, 1752. [Google Scholar] [CrossRef]
- Nocetti, M.; Brunetti, M. Advancements in wood quality assessment: Standing tree visual evaluation—A review. Forests 2024, 15, 943. [Google Scholar] [CrossRef]
- Lin, C.J.; Lin, P.H.; Chang, C.Y.; Gong, Q.Z. Detection of Ganoderma australe decay in three Acacia confusa trees: A case study. In Arboriculture & Urban Forestry; International Society of Arboriculture: Atlanta, GA, USA, 2025; pp. 1–14. [Google Scholar] [CrossRef]
- Lin, C.J.; Peng, P.H.; Cheng, C.Y. Tree risk assessment of date palms with aerial roots using minimally invasive technologies. Forests 2025, 16, 558. [Google Scholar] [CrossRef]
- Ishaq, I.; Alias, M.S.; Kadir, J.; Kasawani, I. Detection of basal stem rot disease at oil palm plantations using sonic tomography. J. Sustain. Sci. Manag. 2014, 9, 52–57. [Google Scholar]
- Son, J.; Kim, S.; Shin, J.; Lee, G.; Kim, H. Reliability of nondestructive sonic tomography for detection of defects in old Zelkova serrata (Thunb.) Makino trees. For. Sci. Technol. 2021, 17, 110–118. [Google Scholar] [CrossRef]
- Downes, G.M.; Lausberg, M.; Potts, B.M.; Pilbeam, D.L.; Bird, M.; Bradshaw, B. Application of the IML Resistograph to the infield assessment of basic density in plantation eucalypts. Aust. For. 2018, 81, 177–185. [Google Scholar] [CrossRef]
- Fundova, I.; Funda, T.; Wu, H.X. Non-destructive wood density assessment of Scots pine (Pinus sylvestris L.) using resistograph and Pilodyn. PLoS ONE 2018, 13, e0204518. [Google Scholar] [CrossRef]
- Sharapov, E.; Brischke, C.; Militz, H.; Smirnova, E. Effects of white rot and brown rot on the drilling resistance measurements in wood. Holzforschung 2018, 72, 905–913. [Google Scholar] [CrossRef]
- Gilbert, E.A.; Smiley, E.T. Picus sonic tomography for the quantification of decay in white oak (Quercus alba) and hickory (Carya spp.). J. Arboric. 2004, 30, 277–281. [Google Scholar]
- Wang, X.; Wiedenbeck, J.; Liang, S. Acoustic tomography for decay detection in black cherry trees. Wood Fiber Sci. 2009, 41, 127–137. [Google Scholar]
- Ostrovsky, R.; Kobza, M.; Jan Gažo, J. Extensively damaged trees tested with acoustic tomography considering tree stability in urban greenery. Trees 2017, 31, 1015–1023. [Google Scholar] [CrossRef]
- Liang, S.; Fu, F. Effect of sensor number and distribution on accuracy rate of wood defect detection with stress wave tomography. Wood Res. 2014, 59, 521–532. [Google Scholar]
- Divos, F.; Divos, P. Resolution of stress wave based acoustic tomography. In Proceedings of the 14th International Symposium on Nondestructive Testing of Wood, Eberswalde, Germany, 2–4 May 2005. [Google Scholar]
- Espinosa, L.; Arciniegas, A.; Cortes, Y.; Prieto, F.; Brancheriau, L. Automatic segmentation of acoustic tomography images for the measurement of wood decay. In Wood Science and Technology; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Fakopp Enterprise Bt. FAKOPP Manual for the ArborSonic 3D Acoustic Tomography; User’s Manual v6.5; Fakopp Enterprise Bt.: Agfalva, Hungary, 2020; 63p, Available online: https://files.fakopp.com/upload/manuals/Manual.en-USv6.2.3.pdf (accessed on 7 March 2025).
- Michael, M.L.; Cheong, S.Y.; Janaun, J.; Phin, C.K.; Dayou, J. A short report on application of acoustic tomography for basal stem rot disease severity assessment in oil palm. Planter 2021, 97, 465–476. [Google Scholar] [CrossRef]
- Wang, X.; Allison, R.B. Decay Detection in Red Oak Trees Using a Combination of Visual Inspection, Acoustic Testing, and Resistance Microdrilling; Arboriculture & Urban Forestry: Atlanta, GA, USA, 2008; Volume 34, pp. 1–4. [Google Scholar]
- Dudkiewicz, M.; Durlak, W. Sustainable management of very large trees with the use of acoustic tomography. Sustainability 2021, 13, 12315. [Google Scholar] [CrossRef]
- Maurer, H.; Schubert, S.I.; Bächle, F.; Clauss, S.; Gsell, D.; Dual, J.; Niemz, P. A simple anisotropy correction procedure for acoustic wood tomography. Holzforschung 2006, 60, 567–573. [Google Scholar] [CrossRef]
- Liu, L.; Li, G. Acoustic tomography based on hybrid wave propagation model for tree decay detection. Comput. Electron. Agric. 2018, 151, 276–285. [Google Scholar] [CrossRef]
- Li, L.; Wang, X.; Wang, L.; Allison, R.B. Acoustic tomography in relation to 2D ultrasonic velocity and hardness mappings. Wood Sci. Technol. 2012, 46, 551–561. [Google Scholar] [CrossRef]
- Wang, X.; Allison, R.B.; Wang, L.; Ross, R.J. Acoustic Tomography for Decay Detection in Red Oak Trees; US Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2007; FPL-RP-642; 7p. [Google Scholar] [CrossRef]
- Soge, A.O.; Popoola, O.I.; Adetoyinbo, A.A. Detection of wood decay and cavities in living trees: A review. Can. J. For. Res. 2020, 51, 937–947. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Li, Z.; Wen, J.; Tan, X. A review of research on tree risk assessment methods. Forests 2022, 13, 1556. [Google Scholar] [CrossRef]
- Rabe, C.; Ferner, D.; Fink, S.; Schwarze, F.W.M.R. Detection of decay in trees with stress waves and interpretation of acoustic tomograms. Arboric. J. 2004, 28, 3–19. [Google Scholar] [CrossRef]
- Deflorio, G.; Fink, S.; Schwarze, F.W.M.R. Detection of incipient decay in tree stems with sonic tomography after wounding and fungal inoculation. Wood Sci. Technol. 2008, 42, 117–132. [Google Scholar] [CrossRef]
- Liang, S.; Wang, X.; Wiedenbeck, J.; Cai, Z.; Fu, F. Evaluation of acoustic tomography for tree decay detection. In Proceedings of the 15 International Symposium on Nondestructive Testing of Wood, Duluth, MN, USA, 10–12 September 2007; Ross, R.J., Wang, X., Brashaw, B.K., Eds.; Forest Products Society: Madison, WI, USA, 2008; pp. 49–54. Available online: https://www.nrs.fs.usda.gov/pubs/jrnl/2008/nrs_2008_liang_001.pdf (accessed on 18 March 2025).
- Bethge, K.; Mattheck, C.; Hunger, E. Equipment for detection and evaluation of incipient decay in trees. Arboric. J. 1996, 20, 13–37. [Google Scholar] [CrossRef]
- Proto, A.R.; Cataldo, M.F.; Costa, C.; Papandrea, S.F.; Zimbalatti, G. A tomographic approach to assessing the possibility of ring shake presence in standing chestnut trees. Eur. J. Wood Wood Prod. 2020, 8, 1137–1148. [Google Scholar] [CrossRef]
- Wang, L.H.; Wang, Y.; Xu, H.D. Effects of Tangential Angles on Stress Wave Propagation Velocities in Log’s Cross Sections. Sci. Silvae Sin. 2011, 47, 139–142. [Google Scholar]
- Wang, L.H.; Xu, H.D.; Yan, Z.X.; Lü, J.X.; Yang, X.C.; Zhou, C.L. Effects of Sensor Quantity and Planar Distribution on Testing Results of Log Defects Based on Stress Wave. Sci. Silvae Sin. 2008, 44, 115–121. [Google Scholar]
- Bucur, V. A Review on Acoustics of Wood as a Tool for Quality Assessment. Forests 2023, 14, 1545. [Google Scholar] [CrossRef]
- El-Hadad, A.; Brodie, G.; Ahmed, H. Effect of physical and mechanical properties on propagation characteristics of stress waves in wood. Open J. Acoust. 2018, 8, 1–13. [Google Scholar]
- Arciniegas, A.; Prieto, F.; Brancheriau, L.; Lasaygues, P. Literature review of acoustic and ultrasonic tomography in standing trees. Trees 2014, 28, 1559–1567. [Google Scholar] [CrossRef]
- Li, G.; Wang, X.; Feng, H.; Wiedenbeck, J.; Ross, R.J. Analysis of wave velocity patterns in black cherry trees and its effect on internal decay detection. Comput. Electron. Agric. 2014, 104, 32–39. [Google Scholar] [CrossRef]
- Sharapov, E.; Brischke, C.; Militz, H. Assessment of preservative-treated wooden poles using drilling-resistance measurements. Forests 2020, 11, 20. [Google Scholar] [CrossRef]
Figure 1.
Sonic tomography testing of a tree using the Fakopp Stress Wave Tomography system (8 sensors, Tree No. 5). (a) Photograph showing the external appearance of the tree trunk. (b) Sensor arrangement, sonic measurement paths, and reconstructed stress wave velocity tomogram displayed in a green–yellow–red color scale (1883–1492–1102 m/s): green indicates sound wood, yellow indicates slightly degraded wood, and red indicates severely decayed or hollow wood. (c) Schematic diagram of the stress wave velocity tomogram shown in grayscale (from highest to lowest velocity). (d) Corresponding stress wave velocity grid map, with each grid cell representing a 35 × 35 mm area.
Figure 1.
Sonic tomography testing of a tree using the Fakopp Stress Wave Tomography system (8 sensors, Tree No. 5). (a) Photograph showing the external appearance of the tree trunk. (b) Sensor arrangement, sonic measurement paths, and reconstructed stress wave velocity tomogram displayed in a green–yellow–red color scale (1883–1492–1102 m/s): green indicates sound wood, yellow indicates slightly degraded wood, and red indicates severely decayed or hollow wood. (c) Schematic diagram of the stress wave velocity tomogram shown in grayscale (from highest to lowest velocity). (d) Corresponding stress wave velocity grid map, with each grid cell representing a 35 × 35 mm area.
Figure 2.
Drilling amplitude profiles across four orientations (N, W, S, E) from bark to trunk center in sampled living trees.
Figure 2.
Drilling amplitude profiles across four orientations (N, W, S, E) from bark to trunk center in sampled living trees.
Figure 3.
Variation trend of stress wave velocity from bark to pith (radial direction) in the 2D acoustic tomography of Tree No. 1. Note 1: W, western; N, northern; E, eastern; S, southern orientation. Note 2: ●, 8 sensors; □, 12 sensors; △, 16 sensors; ○, 20 sensors. Note 3: 2D acoustic tomography with different sensor quantities, as detailed in Table 2. Note 4: The (a), (b), (c), and (d) present the variation of stress wave velocity at the western, northern, eastern, and southern regions in the 2D tomography, respectively.
Figure 3.
Variation trend of stress wave velocity from bark to pith (radial direction) in the 2D acoustic tomography of Tree No. 1. Note 1: W, western; N, northern; E, eastern; S, southern orientation. Note 2: ●, 8 sensors; □, 12 sensors; △, 16 sensors; ○, 20 sensors. Note 3: 2D acoustic tomography with different sensor quantities, as detailed in Table 2. Note 4: The (a), (b), (c), and (d) present the variation of stress wave velocity at the western, northern, eastern, and southern regions in the 2D tomography, respectively.
Figure 4.
Variation trend of stress wave velocity from bark to pith (radial direction) in the 2D acoustic tomography of Tree No. 2. Note 1: W, western; N, northern; E, eastern; S, southern orientation. Note 2: ●, 8 sensors; □, 12 sensors; △, 16 sensors; ○, 20 sensors. Note 3: 2D acoustic tomography with different sensor quantities, as detailed in Table 2. Note 4: The (a), (b), (c), and (d) present the variation of stress wave velocity at the western, northern, eastern, and southern regions in the 2D tomography, respectively.
Figure 4.
Variation trend of stress wave velocity from bark to pith (radial direction) in the 2D acoustic tomography of Tree No. 2. Note 1: W, western; N, northern; E, eastern; S, southern orientation. Note 2: ●, 8 sensors; □, 12 sensors; △, 16 sensors; ○, 20 sensors. Note 3: 2D acoustic tomography with different sensor quantities, as detailed in Table 2. Note 4: The (a), (b), (c), and (d) present the variation of stress wave velocity at the western, northern, eastern, and southern regions in the 2D tomography, respectively.
Figure 5.
Variation trend of stress wave velocity from bark to pith (Radial Direction) in the 2D acoustic tomography of Tree No. 3. Note 1: W, western; N, northern; E, eastern; S, southern orientation. Note 2: ●, 8 sensors; □, 12 sensors; △, 16 sensors; ○, 20 sensors. Note 3: 2D acoustic tomography with different sensor quantities, as detailed in Table 2. Note 4: The (a), (b), (c), and (d) present the variation of stress wave velocity at the western, northern, eastern, and southern regions in the 2D tomography, respectively.
Figure 5.
Variation trend of stress wave velocity from bark to pith (Radial Direction) in the 2D acoustic tomography of Tree No. 3. Note 1: W, western; N, northern; E, eastern; S, southern orientation. Note 2: ●, 8 sensors; □, 12 sensors; △, 16 sensors; ○, 20 sensors. Note 3: 2D acoustic tomography with different sensor quantities, as detailed in Table 2. Note 4: The (a), (b), (c), and (d) present the variation of stress wave velocity at the western, northern, eastern, and southern regions in the 2D tomography, respectively.
Figure 6.
Variation trend of stress wave velocity from bark to pith (Radial Direction) in the 2D acoustic tomography of Tree No. 4. Note 1: W, western; N, northern; E, eastern; S, southern orientation. Note 2: ●, 8 sensors; □, 12 sensors; △, 16 sensors; ○, 20 sensors. Note 3: 2D acoustic tomography with different sensor quantities, as detailed in Table 2. Note 4: The (a), (b), (c), and (d) present the variation of stress wave velocity at the western, northern, eastern, and southern regions in the 2D tomography, respectively.
Figure 6.
Variation trend of stress wave velocity from bark to pith (Radial Direction) in the 2D acoustic tomography of Tree No. 4. Note 1: W, western; N, northern; E, eastern; S, southern orientation. Note 2: ●, 8 sensors; □, 12 sensors; △, 16 sensors; ○, 20 sensors. Note 3: 2D acoustic tomography with different sensor quantities, as detailed in Table 2. Note 4: The (a), (b), (c), and (d) present the variation of stress wave velocity at the western, northern, eastern, and southern regions in the 2D tomography, respectively.
Figure 7.
Variation trend of stress wave velocity from bark to pith (radial direction) in the 2D acoustic tomography of Tree No. 5. Note 1: W, western; N, northern; E, eastern; S, southern orientation. Note 2: ●, 8 sensors; □, 12 sensors; △, 16 sensors; ○, 20 sensors. Note 3: 2D acoustic tomography with different sensor quantities, as detailed in Table 2. Note 4: The (a), (b), (c), and (d) present the variation of stress wave velocity at the western, northern, eastern, and southern regions in the 2D tomography, respectively.
Figure 7.
Variation trend of stress wave velocity from bark to pith (radial direction) in the 2D acoustic tomography of Tree No. 5. Note 1: W, western; N, northern; E, eastern; S, southern orientation. Note 2: ●, 8 sensors; □, 12 sensors; △, 16 sensors; ○, 20 sensors. Note 3: 2D acoustic tomography with different sensor quantities, as detailed in Table 2. Note 4: The (a), (b), (c), and (d) present the variation of stress wave velocity at the western, northern, eastern, and southern regions in the 2D tomography, respectively.
Table 1.
Average drilling amplitude at four orientations (N, W, S, E) in sampled trees (unit: %).
| Position | N | W | S | E | WN | EN |
|---|---|---|---|---|---|---|
| No. 1 | ||||||
| Average | 20.3 | 16.9 | 19.9 | 19.5 | X | X |
| SD | 3.4 | 2.3 | 3.5 | 2.7 | ||
| No. 2 | ||||||
| Average | 16.9 | 17.9 | 18.8 | 27.1 | X | X |
| SD | 7.9 | 2.9 | 3.1 | 12.5 | ||
| No. 3 | ||||||
| Average | 21.0 | 23.1 | 22.5 | 20.1 | X | X |
| SD | 4.0 | 4.9 | 4.4 | 3.6 | ||
| No. 4 | ||||||
| Average | 6.4 | 16.3 | 19.2 | 16.6 | 4.1 | 18.0 |
| SD | 7.3 | 4.1 | 1.8 | 3.3 | 6.5 | 4.1 |
| No. 5 | ||||||
| Average | 16.9 | 17.9 | 17.8 | 21.3 | X | X |
| SD | 6.6 | 5.7 | 5.4 | 10.0 | ||
SD, standard deviation. X, not tested.
Table 2.
Maximum, minimum, and average stress wave velocity of 2D acoustic tomography (m/s).
| Sampled Tree | Diameter of 2D (cm) | Numbers of Sensors | V (m/s) | 2D | ||
|---|---|---|---|---|---|---|
| Vmax | Vmin | Vmean | ||||
| No. 1 | 82.2 | 8 | 1793 | 1319 | 1556 |  |
| 12 | 1744 | 1126 | 1435 |  | ||
| 16 | 1841 | 1183 | 1512 |  | ||
| 20 | 1883 | 1091 | 1487 |  | ||
| Average | 1815.3 | 1179.8 | 1497.5 | |||
| SD | 60.1 | 100.3 | 50.5 | |||
| No. 2 | 78.7 | 8 | 2342 | 1338 | 1840 |  |
| 12 | 1830 | 1123 | 1476 |  | ||
| 16 | 2251 | 970 | 1610 |  | ||
| 20 | 2031 | 981 | 1506 |  | ||
| Average | 2113.5 | 1103.0 | 1608.0 | |||
| SD | 229.7 | 171.5 | 165.0 | |||
| No. 3 | 76.4 | 8 | 1992 | 1396 | 1694 |  |
| 12 | 1894 | 1154 | 1524 |  | ||
| 16 | 1853 | 1207 | 1530 |  | ||
| 20 | 1768 | 970 | 1369 |  | ||
| Average | 1876.8 | 1181.8 | 1529.3 | |||
| SD | 93.0 | 175.3 | 132.7 | |||
| No. 4 | 76.4 | 8 | 1894 | 946 | 1420 |  |
| 12 | 2404 | 873 | 1638 |  | ||
| 16 | 2055 | 857 | 1456 |  | ||
| 20 | 1605 | 828 | 1216 |  | ||
| Average | 1989.5 | 876.0 | 1432.5 | |||
| SD | 333.2 | 50.2 | 173.0 | |||
| No. 5 | 76.4 | 8 | 1883 | 1102 | 1492 |  |
| 12 | 1904 | 998 | 1451 |  | ||
| 16 | 2384 | 918 | 1651 |  | ||
| 20 | 2204 | 884 | 1544 |  | ||
| Average | 2093.8 | 975.5 | 1534.5 | |||
| SD | 242.8 | 96.9 | 86.5 | |||
Note 1: Vmax, maximum stress wave velocity; Vmean, mean stress wave velocity; Vmin, minimum stress wave velocity; SD, standard deviation. Note 2: stress wave velocity tomography using a green–yellow–red color scale (Vmax–Vmean–Vmin). Green represents the highest velocity, yellow indicates medium velocity, and red denotes the lowest velocity.
Table 3.
Average stress wave velocity of 2D acoustic tomographies with different numbers of sensors after gridding (m/s).
Table 3.
Average stress wave velocity of 2D acoustic tomographies with different numbers of sensors after gridding (m/s).
| Numbers of Sensors | 8 | 12 | 16 | 20 |
|---|---|---|---|---|
| No.1 (n = 421) | ||||
| Average | 1644.4 a | 1585.8 b | 1581.6 b | 1565.7 c |
| SD | 56.3 | 64.1 | 58.6 | 52.0 |
| No.2 (n = 384) | ||||
| Average | 1740.1 a | 1614.8 c | 1712.4 b | 1624.1 c |
| SD | 101.8 | 71.9 | 124.6 | 76.2 |
| No.3 (n = 384) | ||||
| Average | 1796.5 a | 1633.8 b | 1659.3 c | 1549.4 d |
| SD | 71.3 | 77.6 | 77.5 | 48.8 |
| No.4 (n = 384) | ||||
| Average | 1494.9 a | 1436.3 b | 1336.2 c | 1299.3 c |
| SD | 230.1 | 268.7 | 195.5 | 172.9 |
| No.5 (n = 384) | ||||
| Average | 1490.2 a | 1423.3 b | 1403.7 bc | 1395.3 c |
| SD | 111.4 | 121.5 | 184.4 | 162.4 |
In the given column, different letters (such as a, b, c, d) indicate significant differences (p ≤ 0.05), as determined by the ANOVA Tukey test. SD, standard deviation.
Table 4.
Coefficients of linear regression formulas (Y = AX + B) for the correlation between stress wave velocities from different numbers of sensors in 2D acoustic tomography.
Table 4.
Coefficients of linear regression formulas (Y = AX + B) for the correlation between stress wave velocities from different numbers of sensors in 2D acoustic tomography.
| Coefficients | R2 | F Value | p Value | ||||
|---|---|---|---|---|---|---|---|
| Y | X | A | B | ||||
| No. 1 | 12 sensors | 8 sensors | 0.71 | 422 | 0.49 | 44.7 ** | <0.001 |
| 16 sensors | 8 sensors | 0.58 | 616 | 0.33 | 22.6 ** | <0.001 | |
| 20 sensors | 8 sensors | 0.18 | 1268 | 0.06 | 2.8 -- | 0.10 | |
| 16 sensors | 12 sensors | 0.69 | 480 | 0.47 | 40.6 ** | <0.001 | |
| 20 sensors | 12 sensors | 0.41 | 905 | 0.31 | 21.1 ** | <0.001 | |
| 20 sensors | 16 sensors | 0.45 | 857 | 0.37 | 27.2 ** | <0.001 | |
| No. 2 | 12 sensors | 8 sensors | 0.62 | 550 | 0.37 | 25.8 ** | <0.001 |
| 16 sensors | 8 sensors | 0.09 | 1506 | <0.01 | 0.15 -- | 0.7 | |
| 20 sensors | 8 sensors | 0.81 | 224 | 0.29 | 18.4 ** | <0.001 | |
| 16 sensors | 12 sensors | 0.44 | 956 | 0.08 | 3.8 -- | 0.06 | |
| 20 sensors | 12 sensors | 0.86 | 220 | 0.35 | 23.5 ** | <0.001 | |
| 20 sensors | 16 sensors | 0.67 | 488 | 0.52 | 47.6 ** | <0.001 | |
| No. 3 | 12 sensors | 8 sensors | 0.41 | 882 | 0.21 | 11.9 ** | 0.001 |
| 16 sensors | 8 sensors | 0.81 | 167 | 0.44 | 34.9 ** | <0.001 | |
| 20 sensors | 8 sensors | 0.37 | 846 | 0.20 | 11.0 ** | 0.002 | |
| 16 sensors | 12 sensors | 0.75 | 414 | 0.29 | 18.3 ** | <0.001 | |
| 20 sensors | 12 sensors | 0.38 | 904 | 0.16 | 8.5 ** | 0.006 | |
| 20 sensors | 16 sensors | 0.52 | 670 | 0.58 | 61.1 ** | <0.001 | |
| No. 4 | 12 sensors | 8 sensors | 0.76 | 248 | 0.87 | 286 ** | <0.001 |
| 16 sensors | 8 sensors | 0.74 | 230 | 0.92 | 483 ** | <0.001 | |
| 20 sensors | 8 sensors | 0.63 | 373 | 0.87 | 300 ** | <0.001 | |
| 16 sensors | 12 sensors | 0.92 | 65 | 0.93 | 610 ** | <0.001 | |
| 20 sensors | 12 sensors | 0.75 | 266 | 0.83 | 213 ** | <0.001 | |
| 20 sensors | 16 sensors | 0.82 | 241 | 0.89 | 340 ** | <0.001 | |
| No. 5 | 12 sensors | 8 sensors | 1.05 | −168 | 0.87 | 289 ** | <0.001 |
| 16 sensors | 8 sensors | 1.65 | −1037 | 0.82 | 202 ** | <0.001 | |
| 20 sensors | 8 sensors | 1.55 | −913 | 0.84 | 230 ** | <0.001 | |
| 16 sensors | 12 sensors | 1.45 | −624 | 0.82 | 195 ** | <0.001 | |
| 20 sensors | 12 sensors | 1.41 | −586 | 0.89 | 355 ** | <0.001 | |
| 20 sensors | 16 sensors | 0.89 | 126 | 0.91 | 462 ** | <0.001 | |
R2, Coefficient of determination; ** p < 0.01; -- p ≧ 0.05.
Table 5.
Average stress wave velocity in healthy and damaged zones using 2D acoustic tomography with different numbers of sensors post-gridding (Unit: m/s).
Table 5.
Average stress wave velocity in healthy and damaged zones using 2D acoustic tomography with different numbers of sensors post-gridding (Unit: m/s).
| Numbers of Sensors | 8 | 12 | 16 | 20 |
|---|---|---|---|---|
| No.4 | ||||
| Health zones (n = 333) | ||||
| Average | 1553.2 | 1448.1 | 1378.2 | 1336.8 |
| SD | 174.7 | 241.9 | 166.2 | 145.5 |
| Damaged zones (n = 51) | ||||
| Average | 1055.2 | 1046.0 | 1019.6 | 1017.3 |
| SD | 48.9 | 52.8 | 65.8 | 92.0 |
| No.5 | ||||
| Health zones (n = 348) | ||||
| Average | 1506.9 | 1442.9 | 1430.0 | 1420.9 |
| SD | 101.7 | 107.8 | 171.6 | 144.4 |
| Damaged zones (n = 36) | ||||
| Average | 1309.3 | 1206.2 | 1119.8 | 1105.9 |
| SD | 44.2 | 39.3 | 48.2 | 58.8 |
SD, standard deviation.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
MDPI and ACS Style
Lin, C.-J.; Peng, P.-H.; Lin, P.-H. The Impact of the Number of Sensors on Stress Wave Velocity in 2D Acoustic Tomography of Araucaria cunninghamii Sweet. Forests 2025, 16, 1439. https://doi.org/10.3390/f16091439
AMA Style
Lin C-J, Peng P-H, Lin P-H. The Impact of the Number of Sensors on Stress Wave Velocity in 2D Acoustic Tomography of Araucaria cunninghamii Sweet. Forests. 2025; 16(9):1439. https://doi.org/10.3390/f16091439
Chicago/Turabian StyleLin, Cheng-Jung, Ping-Hsun Peng, and Po-Heng Lin. 2025. "The Impact of the Number of Sensors on Stress Wave Velocity in 2D Acoustic Tomography of Araucaria cunninghamii Sweet" Forests 16, no. 9: 1439. https://doi.org/10.3390/f16091439
APA StyleLin, C.-J., Peng, P.-H., & Lin, P.-H. (2025). The Impact of the Number of Sensors on Stress Wave Velocity in 2D Acoustic Tomography of Araucaria cunninghamii Sweet. Forests, 16(9), 1439. https://doi.org/10.3390/f16091439
Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.
