Next Article in Journal
Soil Carbon Sequestration by Biological Crusts in Photovoltaic Power Stations: Southern Tengger Desert and Artemisia ordosica Shrubland Restoration
Previous Article in Journal
Saving the Near Extinct Harbison Hawthorn (Crataegus harbisonii): An Ex Situ Approach for Woody Plant Species Conservation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 16
Issue 9
10.3390/f16091395
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Towards the Identification of Candidate Genes for Pollen Morphological Traits in Rubus L. Using Association Mapping

by
Jan Bocianowski
1,* and
Agnieszka Leśniewska-Bocianowska
2
1
Department of Mathematical and Statistical Methods, Poznań University of Life Sciences, Wojska Polskiego 28, 60-637 Poznań, Poland
2
Department of Pathophysiology of Ageing and Civilization Diseases, Poznan University of Medical Sciences, Święcickiego 4, 60-781 Poznań, Poland
*
Author to whom correspondence should be addressed.
Forests 2025, 16(9), 1395; https://doi.org/10.3390/f16091395
Submission received: 25 July 2025 / Revised: 27 August 2025 / Accepted: 30 August 2025 / Published: 1 September 2025
(This article belongs to the Section Genetics and Molecular Biology)
Browse Figures
Review Reports Versions Notes

Abstract

Rubus L. species display considerable morphological and genetic variability. Traditional taxonomic methods, which rely primarily on the observation of external characters, are often insufficient to resolve this complexity. Consequently, molecular biology tools are being increasingly employed. This study aimed to identify markers associated with candidate genes responsible for four selected pollen morphological traits—namely, the length of the polar axis, length of the ectoaperture, distance between the apices of two ectocolpi, and equatorial diameter—using association mapping. Based on the available literature, this is the first report of association mapping used to identify candidate genes for pollen morphological traits in Rubus L. Sixteen Rubus species and the complete set of possible markers (65534) were analyzed. Association mapping enabled the identification of 44 markers that are statistically significantly associated with all four morphological traits under consideration. The ten markers with the highest total LOD value for four pollen morphological traits allowed the distinction of six species: Rubus bifrons, Rubus caesius, Rubus idaeus, Rubus radula, Rubus saxatilis, and Rubus scissus. The results demonstrate that the proposed comprehensive approach of analyzing all possible markers may serve as an effective tool for detecting markers linked to genes controlling important traits, not only in Rubus species but potentially in other taxa as well.

1. Introduction

The genus Rubus L., belonging to the family Rosaceae, comprises hundreds of species, including well-known raspberries and blackberries. These species exhibit remarkable morphological and genetic variability [1,2]. Phenomena such as apomixis (asexual reproduction without fertilization), polyploidy (the presence of multiple sets of chromosomes), and frequent hybridization make traditional taxonomic methods based mainly on observations of external characters insufficient and may lead to erroneous conclusions [3]. Consequently, researchers are increasingly employing molecular biology tools, which enable more precise determination of phylogenetic relationships and allow for the verification of taxonomic classifications [4,5]. Moreover, molecular markers facilitate the selection process in breeding programs [6,7,8].
One of the areas in which modern research methods, including molecular biology, can be applied is the analysis of floral pollen [9,10]. Morphological characteristics of pollen grains, such as their shape, size, surface ornamentation, and the thickness of the cell wall (exine), are commonly used in taxonomic and palynological studies [11,12]. However, these traits may be influenced by environmental factors and may not fully reflect the underlying genetic variability within a species [13,14]. Therefore, combining morphological analysis of pollen with molecular approaches provides a much more comprehensive understanding of the variability of a given taxon [15].
Molecular markers, such as Inter Simple Sequence Repeats (ISSRs) and Simple Sequence Repeats (SSRs, also known as microsatellites), enable the assessment of DNA variation among individuals or populations. Molecular markers are independent of environmental influences, exhibit consistency across different plant tissues, and enable precise assessment of allelic frequencies [16]. As such, they constitute a reliable tool for genetic analysis. Molecular markers are indispensable in contemporary genetic research and plant breeding programs, as they facilitate the detection of genetic diversity at the DNA level with high resolution [17]. They offer several significant advantages, including resistance to environmental variability, high reproducibility, the ability to detect fine-scale genetic variation, and suitability for high-throughput analysis. An ideal molecular marker should (i) accurately reflect underlying genetic diversity, (ii) demonstrate high reliability and reproducibility, (iii) provide comprehensive genomic coverage and be representative of the entire genome, (iv) be cost-effective, rapid, and technically straightforward, and (v) be compatible with bioinformatics tools and data analysis platforms [7]. Although the development of a single marker system that fully meets all these criteria remains challenging, various marker types can be strategically selected and combined to address specific research objectives. The application of molecular markers in research on Rubus enables not only a more detailed understanding of phylogenetic relationships among species but also an assessment of genetic variability within a single species, a variability that is not always evident at the morphological level, yet is crucial, for example, for biodiversity conservation [14,18]. In the case of the genus Rubus, where morphology is often misleading due to frequent hybridization and environmental variation, the use of molecular markers is particularly valuable [13,19].
Studies combining pollen analysis with molecular markers demonstrate that there is a correlation between pollen traits and the genetic profiles of species [20,21]. For example, differences in pollen size and surface ornamentation often correspond to genetic variation detected using SSR markers [22]. In certain cases, morphological characteristics may indicate the hybrid origin of a given individual, which can subsequently be confirmed through DNA analysis [23]. Conversely, molecular analysis can also aid in identifying cases of apomixis, when individuals with identical genotypes exhibit morphological differences resulting from environmental influences [24,25].
The application of molecular markers in pollen research of Rubus species not only enhances the understanding of their variability but also facilitates their classification, the conservation of genetic resources, and potentially their utilization in plant breeding [26,27]. The integration of morphological and genetic data is particularly important for taxa that are difficult to distinguish based solely on external traits. Molecular markers are valuable tools for the identification of candidate genes, especially when combined with QTL mapping to validate loci associated with quantitative traits [28]. The combination of these methods has helped to overcome their individual limitations [29]. As an alternative to conventional breeding methods, precise genetic engineering based on genome editing technologies may play a pivotal role in accessing and utilizing genetic resources. There is information in the literature on molecular markers of raspberry pollen traits [30,31,32], but this is limited to specific marker observations. In this study, we present the possibility of analysis conducted on all theoretically possible markers.
The aim of the present study was to identify markers associated with candidate genes responsible for four selected pollen morphological traits (length of the polar axis, length of the ectoaperture, distance between the apices of two ectocolpi, and equatorial diameter) in Rubus L. (Rosaceae) using association mapping based on all theoretically possible markers obtainable in the experiment. The proposed approach, which involves analysis of all possible binary combinations—representing every theoretically attainable molecular marker—facilitates complex and time-consuming analyses. Moreover, it offers the potential to reduce the costs associated with the development of molecular markers. These four specific traits were chosen for study because, according to the literature, they best characterize Rubus pollen. To our knowledge, this is the first report of association mapping to identify candidate genes for pollen morphological traits in Rubus L.

2. Materials and Methods

2.1. Plant Material

Phenotypic data were obtained from Lechowicz et al. [33]. Sixteen species of Rubus L. (Rosaceae) were included in the analysis: Rubus bifrons (species no. 1), Rubus caesius (no. 2), Rubus constrictus (no. 3), Rubus divaricatus (no. 4), Rubus gracilis (no. 5), Rubus henrici-egonis (no. 6), Rubus idaeus (no. 7), Rubus nessensis (no. 8), Rubus opacus (no. 9), Rubus plicatus (no. 10), Rubus praecox (no. 11), Rubus radula (no. 12), Rubus saxatilis (no. 13), Rubus scissus (no. 14), Rubus sprengelii (no. 15), and Rubus sulcatus (no. 16) (Table A1). The origin of each species was treated as a replicate. Four quantitative traits characterizing pollen morphology were selected for analysis: length of the polar axis (P), length of the ectoaperture (Le), the distance between the apices of two ectocolpi (d), and equatorial diameter (E). These four specific traits were chosen for study because, according to the literature, they best characterize Rubus pollen.

2.2. Genotypic Observations

All theoretically possible markers were treated as genotype observations. This approach corresponds to the scenario in which all possible binary (0–1) patterns are generated through DArTseq technology. For 16 genotypes, the total number of such binary configurations is 216 = 65,536. The extreme configurations 0000000000000000 and 1111111111111111 represent monomorphic cases. Only configurations corresponding to polymorphic cases were retained for further analysis; hence, the final number of marker observations was 216 − 2 = 65,534. To facilitate the interpretation of specific markers, binary values were converted to decimal notation. Examples of conversions between binary and decimal representations are provided in Appendix B, Formula (A1), and Table A2.

2.3. Statistical Methods

The conformity of the empirical distributions of four analyzed morphological pollen traits with the normal distribution was assessed using the Shapiro–Wilk W-test [34]. Homogeneity of variances was evaluated using Bartlett’s test. A multivariate analysis of variance (MANOVA) was carried out to determine the effects of species on all four of the observed traits jointly. Next, one-way analyses of variance (ANOVA) were conducted to assess the effect of species on each trait individually. Arithmetic means and standard deviations were calculated for each trait. Additionally, Fisher’s least significant differences (LSDs) test was estimated at a significance level of α = 0.05, and homogeneous groups were identified based on these LSD values. Relationships between the examined traits were evaluated using Pearson correlation coefficients calculated from species mean values. Multivariate methods were also applied for further analysis. Canonical variate analysis was employed to facilitate the multivariate assessment of interspecific similarity by reducing the dimensionality of the trait space with minimal information loss [35]. This enabled graphical visualization of variation among species based on all observed traits. Mahalanobis distance was used as a measure of multivariate similarity among species [36], and its statistical significance was determined using the critical value Dα, referred to as the least significant distance [37].
Association mapping was conducted based on species mean trait values and the generated marker data, using a mixed linear model (MLM) approach. This model incorporated population structure inferred via eigenanalysis and modeled as random effects [38,39]. All statistical analyses and result visualizations were carried out using GenStat 23.1 software [40], specifically employing the QSASSOCIATION procedure. This procedure implements a mixed-model marker–trait association analysis (also known as linkage disequilibrium mapping) for data obtained from a single-trait trial. To control for false-positive associations due to population structure and relatedness, the model included a genetic relatedness correction. The RELATIONSHIPMODEL = eigenanalysis option was used, which identifies major principal components from the marker matrix to account for population stratification [41]. The scores of the significant principal components were incorporated as covariates in the MLM, providing an approximation of the genetic variance–covariance structure via a kinship matrix. The statistical significance of marker–trait associations was evaluated using p-values adjusted for multiple testing using the Benjamini–Hochberg false discovery rate correction method.

3. Results

3.1. Phenotyping

The number of observations per species varied, ranging from two (for R. constrictus and R. opacus) to five (for R. bifrons, R. caesius, R. gracilis, R. henrici-egonis, R. idaeus, R. nessensis, R. plicatus, R. radula, R. saxatilis, R. sprengelii, and R. sulcatus) (Table 1). In each case, measurements were made from 30 mature, randomly selected, properly developed pollen grains using light microscopy (LM), measuring a total of 2100 pollen grains.
The empirical distributions of all four pollen morphology traits conformed to the normal distribution (Figure 1, Table 1). Bartlett’s test confirmed the homogeneity of variances across all four traits (Table 1).
The results of the multivariate analysis of variance (MANOVA) indicated that the species differed significantly when all four pollen morphology traits were considered jointly (Wilks’ λ = 0.0973; F60,201 = 2.74; p < 0.0001). The results of the univariate analyses of variance (ANOVA) further confirmed that the main effect of species was significant for each of the four traits individually (Table 1). The mean length of the polar axis ranged from 21.71 µm in R. divaricatus to 25.43 µm in R. bifrons, with an overall mean of 23.59 µm (Table 1). Based on this trait, species were grouped into five statistically homogeneous clusters. The coefficient of variation (CV) for the mean polar axis length among species was 4.57%, representing the lowest variability among the traits analyzed. The mean length of the ectoaperture varied from 18.09 µm in R. opacus to 21.50 µm in R. bifrons, with an overall mean of 19.94 µm (Table 1). Species formed six homogeneous groups based on this trait. The coefficient of variation for ectoaperture length was 4.77%. The mean distance between the apices of two ectocolpi ranged from 2.009 µm in R. divaricatus to 3.719 µm in R. caesius, with an overall mean of 2.93 µm (Table 1). Five homogeneous species groups were identified based on this trait. The coefficient of variation, 4.57%, was the highest among all four traits examined. The equatorial diameter ranged from 17.74 µm in R. opacus to 21.65 µm in R. caesius, with an overall mean of 20.47 µm (Table 1). Based on equatorial diameter, four homogeneous species groups were distinguished. The coefficient of variation for this trait was 5.201%.
An almost perfect correlation was observed between the length of the polar axis (P) and the length of the ectoaperture (Le), with a Pearson correlation coefficient of 0.99 (Figure 2). Statistically significant correlations were also found between P and equatorial diameter (E) (r = 0.80), Le and E (r = 0.83), as well as between E and the distance between the apices of two ectocolpi (d) (r = 0.55) (Figure 2). Only two correlation coefficients were not statistically significant: those between P and d (r = 0.22) and between Le and d (r = 0.23) (Figure 2).
Given that individual traits form distinct homogeneous groups and contribute unequally to the overall multivariate variability among the studied species, multivariate analyses were conducted. The results of the canonical variate analysis (CVA), illustrating the distribution of the 16 Rubus species in the space defined by the first two canonical variates, are presented in Figure 3. In this plot, the coordinates of each point represent the species’ scores on the first and second canonical variates, respectively. The first two canonical variates together accounted for 82.32% of the total interspecific variability (Figure 3). The distance between the apices of two ectocolpi exhibited the strongest significant positive linear association with the first canonical variate (r = 0.7013, p = 0.0025), while the length of the polar axis showed a significant negative association (r = –0.5131, p = 0.0421). The second canonical variate was significantly negatively correlated with all four analyzed traits: length of the polar axis (r = –0.8147, p < 0.001), length of the ectoaperture (r = –0.8328, p < 0.001), the distance between the apices of two ectocolpi (r = –0.7175, p = 0.0018), and equatorial diameter (r = –0.8481, p < 0.001).
The greatest multivariate divergence, as measured by the Mahalanobis distance, was observed between R. bifrons and R. idaeus (4.291) (Table S1, Figure 3). In contrast, the highest similarity based on the combined variation of the four traits was found between R. praecox and R. sulcatus, with a Mahalanobis distance of 0.502 (Table S1, Figure 3).
The distribution of the 16 Rubus species within the space defined by the first two canonical variates revealed a clear separation into four distinct groups. The first group comprised four species, R. bifrons, R. gracilis, R. nessensis, and R. radula, characterized by the highest values for both the length of the polar axis (P) and the length of the ectoaperture (Le). The second group included R. divaricatus, R. henrici-egonis, and R. opacus, which exhibited the lowest values across all four analyzed traits. The third group consisted of five species, R. caesius, R. idaeus, R. plicatus, R. saxatilis, and R. scissus, distinguished by the highest values for the distance between the apices of two ectocolpi (d). The fourth group comprised the remaining four species, R. constrictus, R. praecox, R. sprengelii, and R. sulcatus, which displayed intermediate (average) values for all four traits (Figure 3).

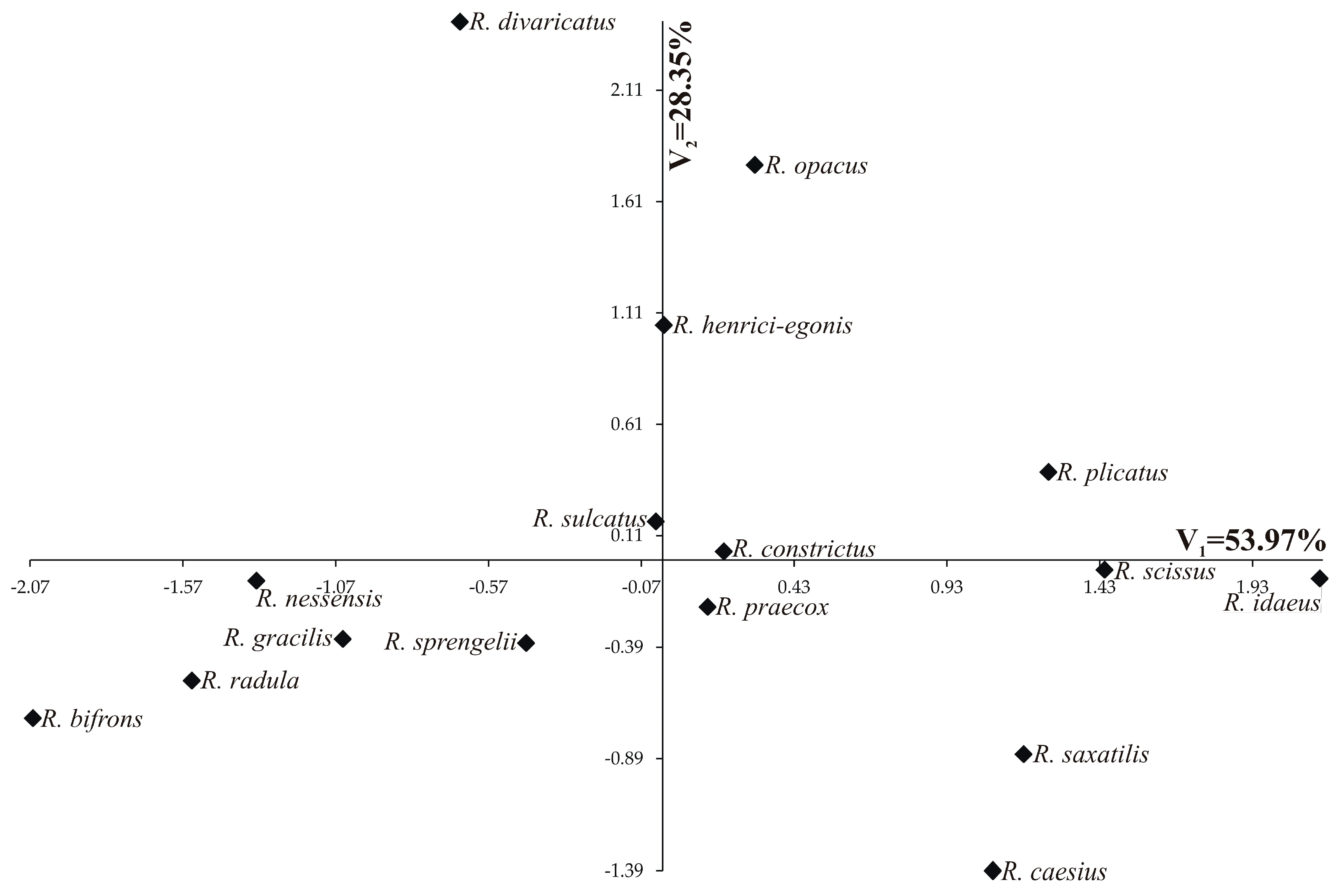
3.2. Association Mapping

Association mapping identified 8320 markers that were statistically significant at the 0.05 level with at least one of the four studied traits (Table 2).
The length of the polar axis was determined by 3346 markers (Table 2, Figure 4A), and this was the trait for which the largest number of statistically significant markers were detected. The length of the ectoaperture was influenced by 3340 markers (Table 2, Figure 4B), and the distance between the apices of two ectocolpi by 3342 markers (Table 2, Figure 4C). The smallest number of markers (2882) determining the observed traits was for equatorial diameter (Table 2, Figure 4D).
The absolute effects of individual statistically significant markers ranged from 1.040 to 2.131 for the length of the polar axis, from 0.916 to 1.989 for the length of the ectoaperture, from 0.400 to 0.980 for the distance between the apices of two ectocolpi, and from 1.025 to 2.905 for the equatorial diameter (Table 2). The proportion of phenotypic variance explained by each marker varied from 19.4% to 63.6% for the length of the polar axis (markers 5832 and 59703), from 19.4% to 65.0% for the length of the ectoaperture (markers 5824 and 59711), from 19.4% to 60.4% for the distance between apices of two ectocolpi (markers 16972 and 48563), and from 19.4% to 70.8% for equatorial diameter (markers 4224 and 61311) (Table 2). The highest LOD scores ranged from 3.62 (for the distance between apices of two ectocolpi) to 4.57 (for equatorial diameter) (Table 2, Figure 4).
A total of 44 markers were simultaneously statistically significant (p < 0.05, LOD > 1.30) for all four morphological traits of Rubus L. (Rosaceae) pollen (Table 3). The effects of the individual markers exhibited consistent directions across all traits. The proportion of variation explained by these common significant markers ranged from 19.50% (for markers m [5509] = 0001010110000101 and m [60026] = 1110101001111010) to 46.90% (for markers m [5248] = 0001010010000000 and m [60287] = 1110101101111111) for the length of the polar axis; from 20.40% (for markers m [13443] = 0011010010000011 and m [52092] = 1100101101111100) to 51.80% (for markers m [5248] = 0001010010000000 and m [60287] = 1110101101111111) for the length of the ectoaperture; from 19.40% (for markers m [13761] = 0011010111000001 and m [51774] = 1100101000111110) to 35.70% (for markers m [5504] = 0001010110000000 and m [60031] = 1110101001111111) for the distance between the apices of two ectocolpi; and from 25.00% (for markers m [7361] = 0001110011000001 and m [58174] = 1110001100111110) to 70.80% (for markers m [4224] = 0001000010000000 and m [61311] = 1110111110111111) for the equatorial diameter (Table 3).
Particularly noteworthy is the observation that identical results (apart from the opposite sign of the effect) were obtained for ‘twin’ markers, i.e., markers that have an inverted 0–1 binary pattern. For example, markers m [13761] = 0011010111000001 and m [51774] = 1100101000111110 yielded identical values for one of the traits, namely the length of the polar axis (P): the proportion of explained variation, p-value, and LOD score were 24.0%, 0.03105, and 1.51, respectively, for both markers (Table 3). However, the effects were −1.136 and 1.136 for m [13761] and m [51774], respectively (Table 3). This indicates that, in subsequent stages of breeding work, it should be sufficient to employ only one of these ‘twin’ markers.

4. Discussion

Assessing biodiversity without accounting for genetic variability may result in an incomplete evaluation [42]. Analyses based solely on agronomic or morphological traits risk underestimating the true diversity of local populations, as phenotypic plasticity can obscure underlying genetic variation, particularly in environments strongly influenced by climatic factors [43]. In the absence of genetic analyses, it is challenging to determine whether local populations are genuinely distinct or if gene flow contributes to their homogeneity. This has important implications for conservation and valorization efforts. A comprehensive understanding of genetic diversity and intraspecific relationships within plant species is crucial for the development of effective conservation and breeding strategies [44,45]. Molecular markers are indispensable tools for the identification and characterization of plant species and hybrids, as well as for assessing the status of natural populations threatened by disease and genetic contamination [46,47,48]. In the present study, phenotypic variability was observed for all four morphological traits of Rubus pollen under investigation. This variability was evident both at the level of individual traits (Table 1) and in multivariate analyses using Mahalanobis distances (Table S1) and canonical variable analysis (Figure 3). The distribution of the studied Rubus species in the space defined by the first two canonical variables is particularly noteworthy, as the information loss resulting from reducing the similarity/dissimilarity structure to two dimensions (a plane) is only 17.68% (Figure 3).
Molecular markers are highly valuable for practical applications, such as the breeding of new cultivars, including raspberries and blackberries. They enable the identification of genetic traits responsible for disease resistance [49], fruit flavor [50], and yield performance [7]. This allows for more targeted and efficient breeding efforts, which is significant not only for scientific research but also for agriculture and the food industry [51,52]. Molecular markers constitute an indispensable tool in studies of Rubus L. species [53,54]. They facilitate a deeper understanding of the complex genetic relationships within this plant group, support accurate species identification, and aid in breeding and conservation efforts. Given the challenges associated with classifying plants with such high variability as Rubus, modern molecular techniques are not only beneficial but essential.
The molecular markers most commonly used in studies of the genus Rubus include SSR [18,55,56,57,58], SNP [19,59,60], and AFLP markers [61,62,63]. The application of these markers enables, among other things, the assessment of relatedness among species or individuals [19], the identification of hybrids [55], the confirmation of the taxonomic status of ambiguous systematic units [19,54], and the analysis of genetic diversity within wild and cultivated populations [56].
Numerous studies have demonstrated that molecular markers effectively support species identification and the assessment of intraspecific variability within the genus Rubus. Huang et al. [54] elucidated the global phylogenetic relationships within Rubus, incorporating an extensive sampling of Chinese endemic species, and accordingly revised the infrageneric classification based on combined morphological and molecular evidence. Sochor and Manning [55] investigated evolutionary patterns and mechanisms in South African blackberries using three types of molecular markers: plastid DNA sequences, nuclear DNA sequences, and nuclear microsatellites. The analysis of SSR markers enabled the assessment of genetic diversity and population structure in wild Korean black raspberry (Rubus coreanus Miq.) [56]. AFLP markers were used to construct a genetic linkage map for black raspberry (Rubus occidentalis) and red raspberry (R. idaeus) based on interspecific progeny [63]. The application of SNP markers has made it possible, among other findings, to confirm the polyphyly of several traditionally circumscribed subgenera, sections, and subsections within Rubus, and to identify 19 well-supported clades that are molecularly, morphologically, and geographically distinct [19]. In addition, SSR markers were used to determine the genetic similarity and to characterize a collection of 21 R. ellipticus accessions from different regions of India [18].
When combined with morphological analyses (e.g., pollen studies), molecular markers also make it possible to verify whether external traits are consistent with genetic data, which is invaluable for taxa that are difficult to classify unambiguously [15].
Molecular markers are an indispensable component of contemporary research on the taxonomy, phylogeny, and genetic variability of the genus Rubus. By overcoming the limitations of traditional morphology-based methods, they provide robust insights into plant genetic structure. Their application is valuable not only in fundamental science but also in breeding programs, conservation biology, and the identification of morphologically cryptic species. In the context of accelerating environmental change and the increasing homogenization of cultivated germplasm, the judicious use of molecular markers will be pivotal to future Rubus research and practice. The results obtained here confirm the utility of molecular markers as an auxiliary tool for classifying and analyzing variability within this genus. They enable the detection of hidden diversity that often remains invisible to morphological assessment. Association mapping pinpointed 44 markers linked to candidate genes that jointly determine the four Rubus pollen traits examined. Because many loci occur in “twin” pairs (opposite 0/1 allele configurations), the set of informative markers should be reduced to 22 for subsequent research stages. Importantly, each significant marker showed an allelic effect of the same sign across all four pollen traits. The ten markers with the highest total LOD value for four pollen morphological traits allowed the distinction of six species: R. bifrons, R. caesius, R. idaeus, R. radula, R. saxatilis, and R. scissus (Figure 5). Figure 5 further presents the association mapping scheme for identifying candidate genes for the four considered morphological traits of Rubus L. pollen and the most significant results obtained for 16 species. Three statistically significant loci warrant particular attention—m [5248] = 0001010010000000, m [4224] = 0001000010000000, and m [5249] = 0001010010000001 (or, after inversion of the 0/1 coding, m [60287] = 1110101101111111, m [61311] = 1110111101111111, and m [60286] = 1110101101111110)—as they exhibited the highest cumulative LOD values (Table 3). In the face of climate change and ongoing biodiversity loss, these markers may serve as molecular-genetic tools that support the conservation of wild Rubus species, many of which inhabit ecologically valuable sites. Association mapping is a tool very often used to analyze marker-trait relationships for different species.

5. Conclusions

Molecular markers play a pivotal role in the study of genetic variability within the genus Rubus. Based on the available literature, this is the first report of association mapping used to identify candidate genes for pollen morphological traits in Rubus L. The results of this study demonstrated that molecular markers are effective and reliable tools for evaluating morphological traits among Rubus genotypes. The ten markers with the highest total LOD value for four pollen morphological traits allowed the distinction of six species: R. bifrons, R. caesius, R. idaeus, R. radula, R. saxatilis, and R. scissus. Notably, six markers m [5248] = 0001010010000000, m [4224] = 0001000010000000, m [5249] = 0001010010000001, m [60287] = 1110101101111111, m [61311] = 1110111101111111, and m [60286] = 1110101101111110 exhibited particularly high cumulative LOD scores, reflecting their strong discriminatory power. In summary, the findings suggest that these markers are highly useful for the characterization of genetic resources, diversity assessment, and inference of phylogenetic relationships within the genus Rubus. The approach presented here—based on analyzing all possible binary marker combinations—can be applied broadly to other species. It offers a means to streamline the otherwise complex and time-consuming process of association mapping, while also reducing the costs associated with developing molecular markers. Moreover, selected molecular markers that significantly determine the observed traits can be used to select genotypes characterized by the most favorable parameters determining the pollen structure.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/f16091395/s1, Table S1: Mahalanobis distances between 16 Rubus species were calculated based on four observed traits.

Author Contributions

Conceptualization, J.B. and A.L.-B.; methodology, J.B. and A.L.-B.; software, J.B.; validation, J.B. and A.L.-B.; formal analysis, J.B.; investigation, J.B. and A.L.-B.; resources, J.B. and A.L.-B.; data curation, J.B. and A.L.-B.; writing—original draft preparation, J.B. and A.L.-B.; writing—review and editing, J.B. and A.L.-B.; visualization, J.B.; supervision, J.B. and A.L.-B.; project administration, J.B.; funding acquisition, J.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

All phenotypic data on Rubus L. (Rosaceae) pollen morphology are included in the manuscript and presented in Table A1 in Appendix A. Data for all possible 65,534 theoretical markers were generated and stored in a binary system according to the method described in Appendix B.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
ISSRInter Simple Sequence Repeats
SSRSimple Sequence Repeats
DNADeoxyribonucleic acid
QTLQuantitative Trait Loci
MANOVAMultivariate analysis of variance
ANOVAAnalysis of variance
LSDLeast significant difference
s.d.Standard deviation
PLength of the polar axis
LeLength of the ectoaperture
dThe distance between the apices of two ectocolpi
EEquatorial diameter
LODThe limit of detection
SNPSingle-nucleotide polymorphism
AFLPAmplified fragment length polymorphism

Appendix A

Table A1. Data on four quantitative traits characterizing pollen morphology were used for analysis [33].
Table A1. Data on four quantitative traits characterizing pollen morphology were used for analysis [33].
No.SpeciesP 1Le 2d 3E 4No.SpeciesPLedE
1Rubus bifrons25.5321.222.36021.409Rubus opacus20.5417.732.14716.88
1Rubus bifrons24.8420.892.96821.549Rubus opacus22.9618.463.06118.61
1Rubus bifrons26.6922.982.84222.3610Rubus plicatus23.1119.752.63821.30
1Rubus bifrons24.7821.092.58021.3510Rubus plicatus21.1518.362.83318.97
1Rubus bifrons25.3321.312.53121.0110Rubus plicatus24.2919.743.13821.79
2Rubus caesius21.8918.262.34718.3910Rubus plicatus23.4619.333.33321.25
2Rubus caesius26.1522.383.85022.9210Rubus plicatus22.7019.303.65321.95
2Rubus caesius25.7221.753.77022.9711Rubus praecox24.2920.702.81121.67
2Rubus caesius25.5821.034.55321.7711Rubus praecox22.2718.873.38419.53
2Rubus caesius23.6819.834.07522.2211Rubus praecox23.0419.782.70020.44
3Rubus constrictus23.8920.103.28321.3211Rubus praecox25.3621.772.97921.90
3Rubus constrictus23.4619.712.73420.1812Rubus radula26.7623.152.42822.14
4Rubus divaricatus22.3419.151.83418.9312Rubus radula23.6320.092.62020.58
4Rubus divaricatus21.0117.702.06616.8112Rubus radula25.6321.293.15321.84
4Rubus divaricatus21.7618.172.08819.2712Rubus radula24.2719.983.32421.11
4Rubus divaricatus21.7218.192.04719.1512Rubus radula25.0521.252.15321.82
5Rubus gracilis25.6321.653.09822.0813Rubus saxatilis24.4821.573.66920.31
5Rubus gracilis23.7020.332.58120.7013Rubus saxatilis24.1220.003.42120.86
5Rubus gracilis24.6921.413.00021.4313Rubus saxatilis22.6319.243.34520.83
5Rubus gracilis22.7419.292.44218.2313Rubus saxatilis22.2218.803.54419.77
5Rubus gracilis25.4621.232.72021.3013Rubus saxatilis22.5419.153.23919.37
6Rubus henrici-egonis22.6718.842.26618.6414Rubus scissus22.7319.182.59720.94
6Rubus henrici-egonis24.4220.873.72222.5314Rubus scissus23.2919.803.52921.68
6Rubus henrici-egonis22.4218.912.15119.1314Rubus scissus24.3620.643.57621.13
6Rubus henrici-egonis21.2317.922.28818.9115Rubus sprengelii24.8021.153.22221.08
6Rubus henrici-egonis22.7019.262.61419.1215Rubus sprengelii23.5019.752.77420.72
7Rubus idaeus22.1619.233.44420.1315Rubus sprengelii24.7420.912.70719.92
7Rubus idaeus24.6220.324.05322.4615Rubus sprengelii24.2220.522.99721.00
7Rubus idaeus22.8119.153.07619.4315Rubus sprengelii23.5820.452.90020.93
7Rubus idaeus21.3918.393.32119.5116Rubus sulcatus24.3420.413.01121.65
7Rubus idaeus22.5219.123.54220.7716Rubus sulcatus22.4619.312.69618.37
8Rubus nessensis23.1019.602.54919.0016Rubus sulcatus23.1019.552.78021.33
8Rubus nessensis24.0020.263.07020.1116Rubus sulcatus23.0919.382.92720.66
8Rubus nessensis25.6321.342.59720.8016Rubus sulcatus24.6621.382.73421.42
8Rubus nessensis24.9020.822.98720.63
8Rubus nessensis24.3120.342.44019.79
1 P—length of the polar axis, 2 Le—length of the ectoaperture, 3 d—the distance between apices of two ectocolpi, 4 E—equatorial diameter.

Appendix B

Example of converting a number from binary (11001112) to decimal (10310):
  =   1   +     1   +     0   +   0   +   1   +   1   +   1   =   64   +   32   +   40   +   0   +   4   +   2     +   1   =  
Table A2. Example of converting a number from decimal (10310) to binary (11001112).
Table A2. Example of converting a number from decimal (10310) to binary (11001112).
Integer from Division by 2Residual from Division by 2Direction of Writing Digits in Binary Number Notation
103 ↑
511
251
121
60
30
11
01

References

  1. Wu, W.; Wang, L.; Huang, W.; Zhang, X.; Li, Y.; Guo, W. A high-quality genome assembly reveals adaptations underlying glossy, wax-coated leaves in the heat-tolerant wild raspberry Rubus leucanthus. DNA Res. 2024, 31, dsae024. [Google Scholar] [CrossRef]
  2. Zhang, L.; Huang, C.; Zhang, G.; Zhang, C.; Zhao, Y.; Huang, J.; Guo, J.; Cheng, L.; Zhang, T.; Ma, H. Nuclear phylogenomics of angiosperms and evolutionary implications. Diversity 2025, 17, 136. [Google Scholar] [CrossRef]
  3. Meng, Q.; Manghwar, H.; Hu, W. Study on Supergenus Rubus L.: Edible, Medicinal, and Phylogenetic Characterization. Plants 2022, 11, 1211. [Google Scholar] [CrossRef]
  4. Shi, Y.; Chen, Z.; Jiang, J.; Wu, W.; Xin, Y.; Zeng, W. Assembly and comparative analysis of the complete mitogenome of Rubus chingii var. suavissimus, an exceptional berry plant possessing sweet leaves. Front. Plant Sci. 2024, 15, 1504687. [Google Scholar] [CrossRef]
  5. Gaskin, J. Recent contributions of molecular population genetic and phylogenetic studies to classic biological control of weeds. BioControl 2024, 69, 353–360. [Google Scholar] [CrossRef]
  6. Eathington, S.R.; Crosbie, T.M.; Edwards, M.D.; Reiter, R.S.; Bull, J.K. Molecular markers in a commercial breeding program. Crop Sci. 2007, 47, S-154–S-163. [Google Scholar] [CrossRef]
  7. Kumar, R.; Das, S.P.; Choudhury, B.U.; Kumar, A.; Prakash, N.R.; Verma, R.; Chakraborti, M.; Devi, A.G.; Bhattacharjee, B.; Das, R.; et al. Advances in genomic tools for plant breeding: Harnessing DNA molecular markers, genomic selection, and genome editing. Biol. Res. 2024, 57, 80. [Google Scholar] [CrossRef]
  8. da Silva, A.V.; Prado, M.; Campos, G.R.; Borges, K.L.R.; Yassue, R.M.; Husein, G.; Sposito, M.B.; Amorim, L.; Crossa, J.; Fritsche-Neto, R. Comparing strategies for genomic predictions in interspecific biparental populations: A case study with the Rubus genus. Euphytica 2024, 220, 146. [Google Scholar] [CrossRef]
  9. Abdullah, M.; Ahmad, M.; Ullah, Z.; Khan, A.; Ahmad, S.; Shah, H.; Ullah, A.; Farah, M.A.; Emmanuel, O.; Iqbal, R.; et al. Palynological diversity in the Rosaceae flora of Northern Khyber Pakhtunkhwa, Pakistan. Genet. Resour. Crop Evol. 2024, 72, 4361–4379. [Google Scholar] [CrossRef]
  10. Hayrapetyan, A.; Asatryan, M.; Sonyan, H.; Balayan, K.; Beketovski, D. Pollen morphological study of some species of the genus Rubus L.(Rosaceae) of the flora of Armenia. Hacquetia 2025, 24, 67–82. [Google Scholar] [CrossRef]
  11. Lechowicz, K.; Wrońska-Pilarek, D.; Bocianowski, J.; Maliński, T. Pollen morphology of Polish species from the genus Rubus L.(Rosaceae) and its systematic importance. PLoS ONE 2020, 15, e0221607. [Google Scholar] [CrossRef]
  12. Purgina, C.; Ulrich, S.; Weber, M.; Grímsson, F. Morphological and Ultrastructural Features of Selected Epidendroideae Pollen Dispersal Units and New Insights into Their Chemical Nature. Plants 2024, 13, 1114. [Google Scholar] [CrossRef] [PubMed]
  13. Mimura, M.; Suga, M. Ambiguous species boundaries: Hybridization and morphological variation in two closely related Rubus species along altitudinal gradients. Ecol. Evol. 2020, 10, 7476–7486. [Google Scholar] [CrossRef] [PubMed]
  14. Zhou, Z.; Liu, F.; Xu, Y.; Hu, W. Genetic Diversity Analysis and Core Germplasm Construction of Rubus chingii Hu. Plants 2024, 13, 618. [Google Scholar] [CrossRef]
  15. Zaman, W.; Ayaz, A.; Park, S. Integrating morphological and molecular data in plant taxonomy. Pak. J. Bot. 2025, 57, 1453–1466. [Google Scholar] [CrossRef]
  16. Agarwal, M.; Shrivastava, N.; Padh, H. Advances in molecular marker techniques and their applications in plant sciences. Plant Cell Rep. 2008, 27, 617–631. [Google Scholar] [CrossRef]
  17. Hayward, A.C.; Tollenaere, R.; Dalton-Morgan, J.; Batley, J. Molecular Marker Applications in Plants. In Plant Genotyping. Methods in Molecular Biology; Batley, J., Ed.; Humana Press: New York, NY, USA, 2015; Volume 1245. [Google Scholar] [CrossRef]
  18. Sharma, S.; Kaur, R.; Kumar, K.; Kumar, D.; Solanke, A.K.U. Genetic variability in Rubus ellipticus collections assessed by morphological traits and EST-SSR markers. J. Plant Biochem. Biotechnol. 2021, 30, 37–55. [Google Scholar] [CrossRef]
  19. Gao, X.-F.; Xiong, X.-H.; Boufford, D.E.; Gao, Y.-D.; Xu, B.; Zhang, C. Phylogeny of the Diploid Species of Rubus (Rosaceae). Genes 2023, 14, 1152. [Google Scholar] [CrossRef]
  20. Galeano, E.; Bousquet, J.; Thomas, B.R. SNP-based analysis reveals unexpected features of genetic diversity, parental contributions and pollen contamination in a white spruce breeding program. Sci. Rep. 2021, 11, 4990. [Google Scholar] [CrossRef] [PubMed]
  21. Wang, X.; Chen, Y.; Hu, Y.; Zhou, J.; Chen, L.; Lu, X. Systematic review of the characteristic markers in honey of various botanical, geographic, and entomological origins. ACS Food Sci. Technol. 2022, 2, 206–220. [Google Scholar] [CrossRef]
  22. Zhu, X.; Wu, Y.; Zhou, J.; Lin, J.; Chen, X. Morphological, palynological and transcriptomic-based SSR assessment of peony varieties adaptive in the Jiangnan region. Sci. Hortic. 2023, 310, 111771. [Google Scholar] [CrossRef]
  23. Luo, J.; Zheng, X.; Xin, Q.; Liu, M.; Zhang, J.; Chen, W.; Chen, C.; Zhang, C.; Wan, G.; Xia, C.; et al. Glycyrrhiza plastid paternal inheritance and a new DNA barcode provide new strategies for molecular identification of three medicinal licorice hybrid complexes. BMC Plant Biol. 2025, 25, 885. [Google Scholar] [CrossRef] [PubMed]
  24. Karunarathne, P.; Reutemann, A.V.; James, J.E.; Zhou, Q.; Sassone, A.; Rose, L.E.; Hojsgaard, D. Navigating the challenges in apomixis population genetics: Insights from past, present, and future perspectives. Crit. Rev. Plant Sci. 2025, 1–32. [Google Scholar] [CrossRef]
  25. Šarhanová, P.; Majeský, Ľ.; Sochor, M. A novel strategy to study apomixis, automixis, and autogamy in plants. Plant Reprod. 2024, 37, 379–392. [Google Scholar] [CrossRef]
  26. Nybom, H.; Lācis, G. Recent large-scale genotyping and phenotyping of plant genetic resources of vegetatively propagated crops. Plants 2021, 10, 415. [Google Scholar] [CrossRef] [PubMed]
  27. Amiteye, S. Basic concepts and methodologies of DNA marker systems in plant molecular breeding. Heliyon 2021, 7, e08093. [Google Scholar] [CrossRef] [PubMed]
  28. Korte, A.; Farlow, A. The advantages and limitations of trait analysis with GWAS: A review. Plant Methods 2013, 9, 29. [Google Scholar] [CrossRef]
  29. Brachi, B.; Faure, N.; Horton, M.; Flahauw, E.; Vazquez, A.; Nordborg, M.; Bergelson, J.; Cuguen, J.; Roux, F. Linkage and association mapping of Arabidopsis thaliana flowering time in nature. PLoS Genet. 2010, 6, e1000940.1. [Google Scholar] [CrossRef]
  30. Leoni, V.; Panseri, S.; Giupponi, L.; Pavlovic, R.; Gianoncelli, C.; Coatti, G.; Beretta, G.; Giorgi, A. Phytochemical profiling of red raspberry (Rubus idaeus L.) honey and investigation of compounds related to its pollen occurrence. J. Sci. Food Agric. 2024, 104, 5391–5406. [Google Scholar] [CrossRef]
  31. Kostryco, M.; Chwil, M. Structure of anther epidermis and endothecium, production of pollen, and content of selected nutrients in pollen grains from six Rubus idaeus L. cultivars. Agronomy 2021, 11, 1723. [Google Scholar] [CrossRef]
  32. Leoni, V.; Giupponi, L.; Pavlovic, R.; Gianoncelli, C.; Cecati, F.; Ranzato, E.; Martinotti, S.; Pedrali, D.; Giorgi, A.; Panseri, S. Multidisciplinary analysis of Italian Alpine wildflower honey reveals criticalities, diversity and value. Sci. Rep. 2021, 11, 19316. [Google Scholar] [CrossRef]
  33. Lechowicz, K.; Bocianowski, J.; Wrońska-Pilarek, D. Pollen Morphological Inter- and Intraspecific Variability in Selected Species of Rubus L. (Rosaceae). Forests 2022, 13, 1946. [Google Scholar] [CrossRef]
  34. Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
  35. Rencher, A.C. Interpretation of canonical discriminant functions, canonical variates, and principal components. Am. Stat. 1992, 46, 217–225. [Google Scholar] [CrossRef]
  36. Seidler-Łożykowska, K.; Bocianowski, J. Evaluation of variability of morphological traits of selected caraway (Carum carvi L.) genotypes. Ind. Crops Prod. 2012, 35, 140–145. [Google Scholar] [CrossRef]
  37. Mahalanobis, P.C. On the generalized distance in statistics. Proc. Natl. Inst. Sci. India 1936, 12, 49–55. [Google Scholar]
  38. van Eeuwijk, F.A.; Bink, M.C.A.M.; Chenu, K.; Chapman, S.C. Detection and use of QTL for complex traits in multiple environments. Curr. Opin. Plant Biol. 2010, 13, 193–205. [Google Scholar] [CrossRef] [PubMed]
  39. Malosetti, M.; Ribaut, J.-M.; van Eeuwijk, F.A. The statistical analysis of multi-environment data: Modeling genotype-by-environment interaction and its genetic basis. Front. Physiol. 2013, 4, 44. [Google Scholar] [CrossRef]
  40. VSN International. VSN International Genstat for Windows, 23rd ed.; VSN International: Hemel Hempstead, UK, 2023. [Google Scholar]
  41. Patterson, N.; Price, A.L.; Reich, D. Population structure and eigenanalysis. PLoS Genet. 2006, 2, e190. [Google Scholar] [CrossRef] [PubMed]
  42. Hoban, S.; Archer, F.I.; Bertola, L.D.; Bragg, J.G.; Breed, M.F.; Bruford, M.W.; Coleman, M.A.; Ekblom, R.; Funk, W.C.; Grueber, C.E.; et al. Global genetic diversity status and trends: Towards a suite of Essential Biodiversity Variables (EBVs) for genetic composition. Biol. Rev. 2022, 97, 1511–1538. [Google Scholar] [CrossRef]
  43. Schneider, H.M. Characterization, costs, cues and future perspectives of phenotypic plasticity. Ann. Bot. 2022, 130, 131–148. [Google Scholar] [CrossRef] [PubMed]
  44. Eren, B.; Keskin, B.; Demirel, F.; Demirel, S.; Türkoğlu, A.; Yilmaz, A.; Haliloğlu, K. Assessment of genetic diversity and population structure in local alfalfa genotypes using iPBS molecular markers. Genet. Resour. Crop Evol. 2023, 70, 617–628. [Google Scholar] [CrossRef]
  45. Demirel, S.; Demirel, F. Molecular identification and population structure of emmer and einkorn wheat lines with different ploidy levels using SSR markers. Genet. Resour. Crop Evol. 2024, 71, 363–372. [Google Scholar] [CrossRef]
  46. Palaz, E.B.; Demirel, F.; Adali, S.; Demirel, S.; Yilmaz, A. Genetic relationships of salep orchid species and gene flow among Serapias vomeracea × Anacamptis morio hybrids. Plant Biotechnol. Rep. 2023, 17, 315–327. [Google Scholar] [CrossRef]
  47. Demirel, S.; Pehluvan, M.; Aslantaş, R. Evaluation of genetic diversity and population structure of peach (Prunus persica L.) genotypes using inter-simple sequence repeat (ISSR) markers. Genet. Resour. Crop Evol. 2024, 71, 1301–1312. [Google Scholar] [CrossRef]
  48. Orman, E.; Çakar, D.; Alkan, M.; Özer, G.; Güler, E.; Gündoğdu, M. Genetic diversity and population structure of Turkish European chestnut (Castanea sativa) genotypes assessed using start codon targeted polymorphism (SCoT) markers. Genet. Resour. Crop Evol. 2025, 72, 6507–6519. [Google Scholar] [CrossRef]
  49. Paudel, D.; Parrish, S.B.; Peng, Z.; Parajuli, S.; Deng, Z. A chromosome-scale and haplotype-resolved genome assembly of tetraploid blackberry (Rubus L. subgenus Rubus Watson). Hortic. Res. 2025, 12, uhaf052. [Google Scholar] [CrossRef]
  50. De Mori, G.; Cipriani, G. Marker-assisted selection in breeding for fruit trait improvement: A review. Int. J. Mol. Sci. 2023, 24, 8984. [Google Scholar] [CrossRef]
  51. Sun, L.; Lai, M.; Ghouri, F.; Nawaz, M.A.; Ali, F.; Baloch, F.S.; Nadeem, M.A.; Aasim, M.; Shahid, M.Q. Modern Plant Breeding Techniques in Crop Improvement and Genetic Diversity: From Molecular Markers and Gene Editing to Artificial Intelligence—A Critical Review. Plants 2024, 13, 2676. [Google Scholar] [CrossRef]
  52. Song, L.; Wang, R.; Yang, X.; Zhang, A.; Liu, D. Molecular Markers and Their Applications in Marker-Assisted Selection (MAS) in Bread Wheat (Triticum aestivum L.). Agriculture 2023, 13, 642. [Google Scholar] [CrossRef]
  53. Moreno–Medina, B.L.; Casierra–Posada, F. Molecular characterization of a species in the genus Rubus in Boyacá, Colombia. Rev. Bras. Frutic. 2021, 43, e-713. [Google Scholar] [CrossRef]
  54. Huang, T.-R.; Chen, J.-H.; Hummer, K.E.; Alice, L.A.; Wang, W.-H.; He, Y.; Yu, S.-X.; Yang, M.-F.; Chai, T.-Y.; Zhu, X.-Y.; et al. Phylogeny of Rubus (Rosaceae): Integrating molecular and morphological evidence into an infrageneric revision. Taxon 2023, 72, 278–306. [Google Scholar] [CrossRef]
  55. Sochor, M.; Manning, J.C. Evolutionary patterns in South African brambles (Rubus L.)—new insights from molecular markers. Bothalia 2023, 53, a8. [Google Scholar] [CrossRef]
  56. Han, S.K.; Shin, H.; Lee, J.W.; Hong, K.N.; Ahn, J.Y. Genetic diversity and population relationships in wild Korean black raspberry (Rubus coreanus Miq.) based on microsatellite markers: Establishing a fruit tree breeding strategy. Hortic. Environ. Biotechnol. 2024, 65, 293–302. [Google Scholar] [CrossRef]
  57. Ward, J.A.; Bhangoo, J.; Fernández-Fernández, F.; Moore, P.; Swanson, J.D.; Viola, R.; Velasco, R.; Bassil, N.; Weber, C.A.; Sargent, D.J. Saturated linkage map construction in Rubus idaeus using genotyping by sequencing and genome-independent imputation. BMC Genom. 2013, 14, 2. [Google Scholar] [CrossRef]
  58. Pinczinger, D.; von Reth, M.; Hanke, M.V.; Flachowsky, H. Self-incompatibility of raspberry cultivars assessed by SSR markers. Sci. Hortic. 2021, 288, 110384. [Google Scholar] [CrossRef]
  59. Ryu, J.; Kim, W.J.; Im, J.; Kim, S.H.; Lee, K.S.; Jo, H.J.; Kim, E.Y.; Kang, S.Y.; Lee, J.H.; Ha, B.K. Genotyping-by-sequencing based single nucleotide polymorphisms enabled Kompetitive Allele Specific PCR marker development in mutant Rubus genotypes. Electron. J. Biotechnol. 2018, 35, 57–62. [Google Scholar] [CrossRef]
  60. Bushakra, J.M.; Bryant, D.W.; Dossett, M.; Vining, K.J.; VanBuren, R.; Gilmore, B.S.; Lee, J.; Mockler, T.C.; Finn, C.E.; Bassil, N.V. A genetic linkage map of black raspberry (Rubus occidentalis) and the mapping of Ag4 conferring resistance to the aphid Amphorophora agathonica. Theor. Appl. Genet. 2015, 128, 1631–1646. [Google Scholar] [CrossRef]
  61. Kollmann, J.; Steinger, T.; Roy, B.A. Evidence of sexuality in European Rubus (Rosaceae) species based on AFLP and allozyme analysis. Am. J. Bot. 2000, 87, 1592–1598. [Google Scholar] [CrossRef]
  62. Graham, J.; Smith, K.; MacKenzie, K.; Jorgenson, L.; Hackett, C.; Powell, W. The construction of a genetic linkage map of red raspberry (Rubus idaeus subsp. idaeus) based on AFLPs, genomic-SSR and EST-SSR markers. Theor. Appl. Genet. 2004, 109, 740–749. [Google Scholar] [CrossRef]
  63. Bushakra, J.M.; Stephens, M.J.; Atmadjaja, A.N.; Lewers, K.S.; Symonds, V.V.; Udall, J.A.; Chagné, D.; Buck, E.J.; Gardiner, S.E. Construction of black (Rubus occidentalis) and red (R. idaeus) raspberry linkage maps and their comparison to the genomes of strawberry, apple, and peach. Theor. Appl. Genet. 2012, 125, 311–327. [Google Scholar] [CrossRef]
Forests 16 01395 g001
Figure 1. The empirical distribution of observations of the four traits.
Figure 1. The empirical distribution of observations of the four traits.
Forests 16 01395 g001
Forests 16 01395 g002
Figure 2. Heatmap showing the correlation coefficients between all pairs of observed traits. P—length of the polar axis, Le—length of the ectoaperture, d—the distance between apices of two ectocolpi, E—equatorial diameter; * p < 0.05; *** p < 0.001.
Figure 2. Heatmap showing the correlation coefficients between all pairs of observed traits. P—length of the polar axis, Le—length of the ectoaperture, d—the distance between apices of two ectocolpi, E—equatorial diameter; * p < 0.05; *** p < 0.001.
Forests 16 01395 g002
Forests 16 01395 g003
Figure 3. Distribution of 16 Rubus species in the space of the first two canonical variables: V1 and V2.
Figure 3. Distribution of 16 Rubus species in the space of the first two canonical variables: V1 and V2.
Forests 16 01395 g003
Forests 16 01395 g004
Figure 4. Manhattan plot for: length of the polar axis (A), length of the ectoaperture (B), the distance between apices of two ectocolpi (C), and equatorial diameter (D). The yellow line indicates significance at the 0.05 level (LOD = 1.30), the blue line at the 0.01 level (LOD = 2.0), and the red line at the 0.001 level (LOD = 3.0). The statistical significance of marker–trait associations was evaluated using p-values adjusted for multiple testing using the Benjamini–Hochberg false discovery rate correction method.
Figure 4. Manhattan plot for: length of the polar axis (A), length of the ectoaperture (B), the distance between apices of two ectocolpi (C), and equatorial diameter (D). The yellow line indicates significance at the 0.05 level (LOD = 1.30), the blue line at the 0.01 level (LOD = 2.0), and the red line at the 0.001 level (LOD = 3.0). The statistical significance of marker–trait associations was evaluated using p-values adjusted for multiple testing using the Benjamini–Hochberg false discovery rate correction method.
Forests 16 01395 g004
Forests 16 01395 g005
Figure 5. Association mapping scheme for identifying candidate genes for four pollen morphological traits in Rubus L., and the most significant results obtained for 16 species.
Figure 5. Association mapping scheme for identifying candidate genes for four pollen morphological traits in Rubus L., and the most significant results obtained for 16 species.
Forests 16 01395 g005
Table 1. Mean values and standard deviations, values of the F test statistic from the analysis of variance, as well as results of the Shapiro–Wilk W-test for normality and Bartlett test for the length of the polar axis (P), length of the ectoaperture (Le), the distance between apices of two ectocolpi (d), and equatorial diameter (E).
Table 1. Mean values and standard deviations, values of the F test statistic from the analysis of variance, as well as results of the Shapiro–Wilk W-test for normality and Bartlett test for the length of the polar axis (P), length of the ectoaperture (Le), the distance between apices of two ectocolpi (d), and equatorial diameter (E).
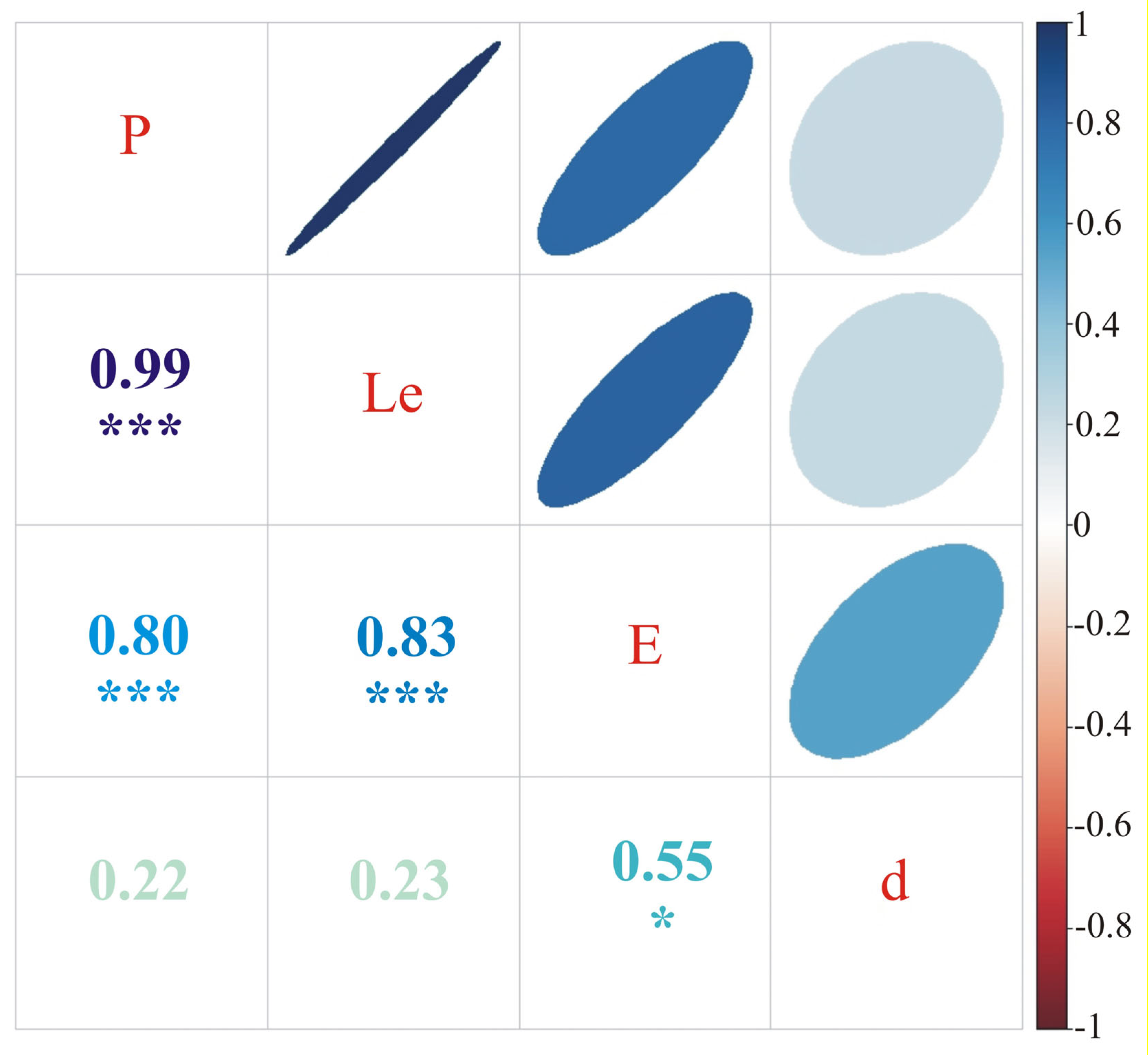
SpeciesReplP 1Le 2d 3E 4
Mean s.d.Mean s.d.Mean s.d.Mean s.d.
Rubus bifrons525.43a0.77121.5a0.84342.656de0.245421.53ab0.502
Rubus caesius524.6abc1.78920.65abcd1.6383.719a0.825321.65a1.892
Rubus constrictus223.68abcd0.30419.91abcde0.27583.008bcd0.388220.75ab0.806
Rubus divaricatus421.71e0.54518.3ef0.60872.009e0.117718.54cd1.162
Rubus gracilis524.44abcd1.2220.78abc0.9722.768cd0.276720.75ab1.491
Rubus henrici-egonis522.69de1.1419.16def1.07662.608de0.64619.67bc1.613
Rubus idaeus522.7de1.19819.24cdef0.69133.487ab0.361120.46ab1.242
Rubus nessensis524.39abcd0.95120.47abcd0.65142.729d0.281220.07abc0.72
Rubus opacus221.75e1.71118.09f0.51622.604de0.646317.74d1.223
Rubus plicatus522.94cde1.1619.3cdef0.56583.119abcd0.401421.05ab1.203
Rubus praecox423.74abcd1.36420.28abcd1.24292.969bcd0.299820.88ab1.108
Rubus radula525.07ab1.21321.15ab1.27692.736d0.491921.5ab0.638
Rubus saxatilis523.2cde1.02519.75bcde1.10653.444abc0.168120.23abc0.655
Rubus scissus323.46bcde0.82819.87bcde0.73283.234abcd0.552221.25ab0.384
Rubus sprengelii524.17abcd0.61720.56abcd0.53392.92bcd0.202620.73ab0.472
Rubus sulcatus523.53bcde0.9320.01abcd0.88532.83bcd0.13420.69ab1.346
LSD0.05 1.869 1.61 0.6935 1.914
F-ANOVA 3.91 *** 3.9 *** 4.49 *** 2.9 **
Shapiro–Wilk test for normalityW-test0.987 0.982 0.986 0.969
p-value0.658 0.41 0.626 0.066
Bartlett testχ29.51 12.02 16.99 17.7
p-value0.849 0.677 0.329 0.279
1 P—length of the polar axis, 2 Le—length of the ectoaperture, 3 d—the distance between apices of two ectocolpi, 4 E—equatorial diameter; ** p < 0.01; *** p < 0.001; LSD—Fisher’s least significant difference; a–e—in columns, means followed by the same letters are not significantly different; s.d.—standard deviation.
Table 2. Characteristics of molecular markers significantly associated with selected morphological traits of Rubus L. (Rosaceae) pollen (significant associations selected at p < 0.05 with Benjamini–Hochberg multiple testing correction).
Table 2. Characteristics of molecular markers significantly associated with selected morphological traits of Rubus L. (Rosaceae) pollen (significant associations selected at p < 0.05 with Benjamini–Hochberg multiple testing correction).
CharacteristicsP 1LedE
The number of significant markers3346334033422882
Effect (absolute value)Min1.0400.9160.4001.025
Max2.1311.9890.9802.905
The percentage of variation explainedMin19.419.419.419.4
Max63.665.160.470.8
LODMin1.301.301.301.30
Max3.884.013.624.57
1 P—length of the polar axis, Le—length of the ectoaperture, d—the distance between apices of two ectocolpi, E—equatorial diameter.
Table 3. Forty-four markers were statistically significant (p < 0.05) simultaneously for all four considered morphological traits of Rubus L. (Rosaceae) pollen.
Table 3. Forty-four markers were statistically significant (p < 0.05) simultaneously for all four considered morphological traits of Rubus L. (Rosaceae) pollen.
MarkerPLedE
EffectPerc 1p-ValueLODEffectPercp-ValueLODEffectPercp-ValueLODEffectPercp-ValueLOD
m [4224]=0001000010000000−2.13141.60.004162.38−1.98947.70.001842.74−0.7129.50.017421.76−2.65870.80.000034.57
m [4225] = 0001000010000001−1.55629.10.018211.74−1.430.70.015181.82−0.5523.40.033021.48−1.81943.70.003172.50
m [5248] = 0001010010000000−1.90246.90.002052.69−1.74751.80.001013.00−0.64134.40.010012.00−2.23769.80.000034.46
m [5249] = 0001010010000001−1.56638.00.006532.19−1.39739.20.005592.25−0.55331.00.014771.83−1.74550.50.001232.91
m [5250] = 0001010010000010−1.35426.60.023811.62−1.21427.90.020691.68−0.52326.90.022921.64−1.73149.50.001422.85
m [5251] = 0001010010000011−1.223.20.033841.47−1.0422.30.037121.43−0.48526.40.024211.62−1.44738.20.006342.20
m [5280] = 0001010010100000−1.49634.00.010411.98−1.30633.40.011231.95−0.50724.80.028541.54−1.67946.20.002272.64
m [5281] = 0001010010100001−1.32429.80.016731.78−1.1227.00.022671.64−0.47124.50.029641.53−1.40235.40.008842.05
m [5504] = 0001010110000000−1.2823.00.034521.46−1.24229.50.017331.76−0.58735.70.008542.07−1.95264.90.000104.00
m [5505] = 0001010110000001−1.13620.00.046641.33−1.06423.70.032141.49−0.54134.60.009812.01−1.6451.10.001112.95
m [5509] = 0001010110000101−1.07719.50.049201.31−0.99322.20.037691.42−0.41419.50.049251.31−1.29532.50.012421.91
m [5568] = 0001010111000000−1.30728.90.018601.73−1.27136.80.007502.12−0.45622.60.036091.44−1.53443.80.003112.51
m [5569] = 0001010111000001−1.21526.80.023221.63−1.14731.90.013231.88−0.44423.60.032461.49−1.34835.80.008482.07
m [5601] = 0001010111100001−1.1223.10.034071.47−1.00624.40.029861.52−0.41320.70.043621.36−1.17827.30.022051.66
m [7296] = 0001110010000000−1.26222.10.037751.42−1.13923.70.032271.49−0.57433.80.010671.97−1.72549.10.001502.82
m [7360] = 0001110011000000−1.29128.00.020491.69−1.18130.80.015001.82−0.44521.10.041971.38−1.33531.50.013911.86
m [7361] = 0001110011000001−1.226.00.025361.60−1.06426.50.023941.62−0.43422.20.037661.42−1.16625.00.028101.55
m [13440] = 0011010010000000−1.51835.20.009052.04−1.43141.50.004212.38−0.49323.20.033911.47−1.72449.10.001512.82
m [13441] = 0011010010000001−1.34330.90.014881.83−1.22934.00.010461.98−0.45922.90.034771.46−1.44137.90.006622.18
m [13442] = 0011010010000010−1.15821.10.041931.38−1.06924.00.031201.51−0.43319.60.048841.31−1.42837.10.007292.14
m [13443] = 0011010010000011−1.07819.60.048871.31−0.96220.40.045201.34−0.42320.70.043721.36−1.25129.90.016661.78
m [13761] = 0011010111000001−1.13624.00.031051.51−1.10130.70.015251.82−0.40319.40.049981.30−1.21229.30.017691.75
m [51774] = 11001010001111101.13624.00.031051.511.10130.70.015251.820.40319.40.049981.301.21229.30.017691.75
m [52092] = 11001011011111001.07819.60.048871.310.96220.40.045201.340.42320.70.043721.361.25129.90.016661.78
m [52093] = 11001011011111011.15821.10.041931.381.06924.00.031201.510.43319.60.048841.311.42837.10.007292.14
m [52094] = 11001011011111101.34330.90.014881.831.22934.00.010461.980.45922.90.034771.461.44137.90.006622.18
m [52095] = 11001011011111111.51835.20.009052.041.43141.50.004212.380.49323.20.033911.471.72449.10.001512.82
m [58174] = 11100011001111101.226.00.025361.601.06426.50.023941.620.43422.20.037661.421.16625.00.028101.55
m [58175] = 11100011001111111.29128.00.020491.691.18130.80.015001.820.44521.10.041971.381.33531.50.013911.86
m [58239] = 11100011011111111.26222.10.037751.421.13923.70.032271.490.57433.80.010671.971.72549.10.001502.82
m [59934] = 11101010000111101.1223.10.034071.471.00624.40.029861.520.41320.70.043621.361.17827.30.022051.66
m [59966] = 11101010001111101.21526.80.023221.631.14731.90.013231.880.44423.60.032461.491.34835.80.008482.07
m [59967] = 11101010001111111.30728.90.018601.731.27136.80.007502.120.45622.60.036091.441.53443.80.003112.51
m [60026] = 11101010011110101.07719.50.049201.310.99322.20.037691.420.41419.50.049251.311.29532.50.012421.91
m [60030] = 11101010011111101.13620.00.046641.331.06423.70.032141.490.54134.60.009812.011.6451.10.001112.95
m [60031] = 11101010011111111.2823.00.034521.461.24229.50.017331.760.58735.70.008542.071.95264.90.000104.00
m [60254] = 11101011010111101.32429.80.016731.781.1227.00.022671.640.47124.50.029641.531.40235.40.008842.05
m [60255] = 11101011010111111.49634.00.010411.981.30633.40.011231.950.50724.80.028541.541.67946.20.002272.64
m [60284] = 11101011011111001.223.20.033841.471.0422.30.037121.430.48526.40.024211.621.44738.20.006342.20
m [60285] = 11101011011111011.35426.60.023811.621.21427.90.020691.680.52326.90.022921.641.73149.50.001422.85
m [60286] = 11101011011111101.56638.00.006532.191.39739.20.005592.250.55331.00.014771.831.74550.50.001232.91
m [60287] = 11101011011111111.90246.90.002052.691.74751.80.001013.000.64134.40.010012.002.23769.80.000034.46
m [61310] = 11101111011111101.55629.10.018211.741.430.70.015181.820.5523.40.033021.481.81943.70.003172.50
m [61311] = 11101111011111112.13141.60.004162.381.98947.70.001842.740.7129.50.017421.762.65870.80.000034.57
1 The percentage of variation explained by individual markers.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Bocianowski, J.; Leśniewska-Bocianowska, A. Towards the Identification of Candidate Genes for Pollen Morphological Traits in Rubus L. Using Association Mapping. Forests 2025, 16, 1395. https://doi.org/10.3390/f16091395

AMA Style

Bocianowski J, Leśniewska-Bocianowska A. Towards the Identification of Candidate Genes for Pollen Morphological Traits in Rubus L. Using Association Mapping. Forests. 2025; 16(9):1395. https://doi.org/10.3390/f16091395

Chicago/Turabian Style

Bocianowski, Jan, and Agnieszka Leśniewska-Bocianowska. 2025. "Towards the Identification of Candidate Genes for Pollen Morphological Traits in Rubus L. Using Association Mapping" Forests 16, no. 9: 1395. https://doi.org/10.3390/f16091395

APA Style

Bocianowski, J., & Leśniewska-Bocianowska, A. (2025). Towards the Identification of Candidate Genes for Pollen Morphological Traits in Rubus L. Using Association Mapping. Forests, 16(9), 1395. https://doi.org/10.3390/f16091395

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop