Modeling Urban-Vegetation Aboveground Carbon by Integrating Spectral–Textural Features with Tree Height and Canopy Cover Ratio Using Machine Learning
Abstract
1. Introduction
1.1. The Value and Complexity of Estimating Urban-Vegetation Aboveground Carbon Storage (AGC)
1.2. Progress and Limitations of Estimating Urban-Vegetation ACG by Remote Sensing (RS)
1.2.1. Traditional RS Estimation
1.2.2. Multimodal RS Estimation
1.2.3. Advanced Algorithm Model
1.3. Objectives and Innovations of This Study
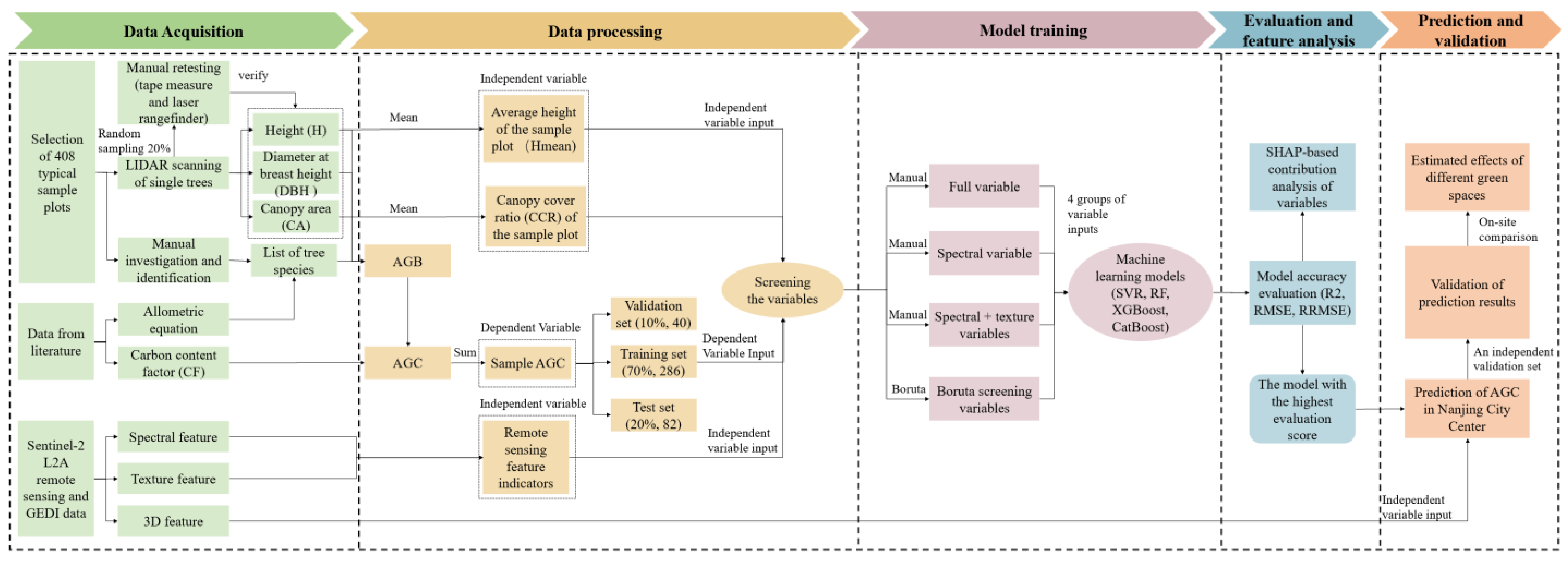
2. Data and Methods
2.1. Data Acquisition
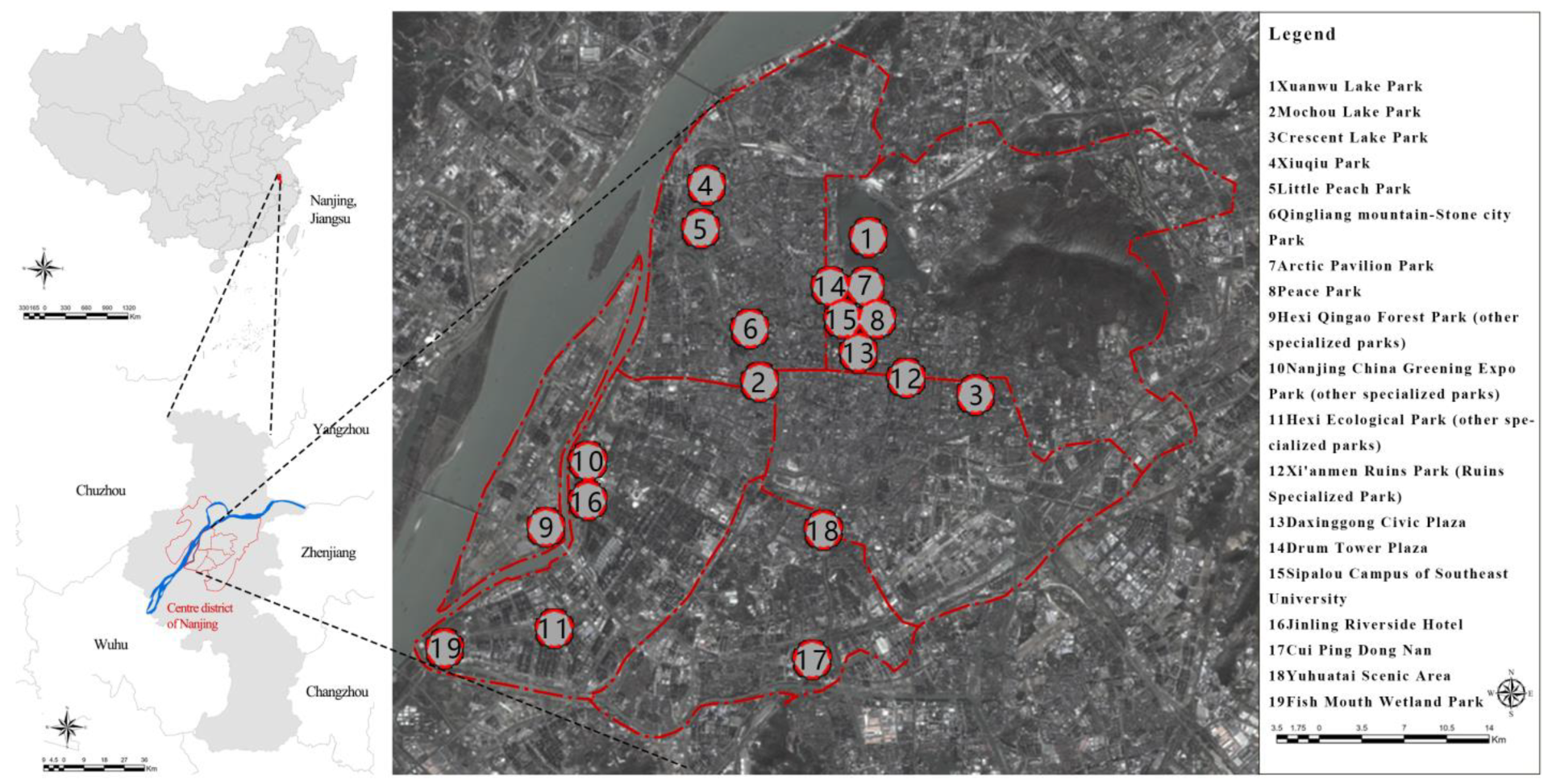
2.1.1. Study Area and Sampling Strategy
2.1.2. Remote Sensing Data
2.1.3. Data from the Literature
2.2. Data Processing
2.2.1. and CCR of Sample Plots
2.2.2. AGC for Single Trees and Sample Plots
- (1)
- Biomass estimation
- (2)
- AGC estimation
2.2.3. Remote Sensing Feature Extraction
- (1)
- Spectral and Texture Features
- (2)
- Tree height and Canopy cover ratio data for prediction
- (a)
- Tree height (H)
- (b)
- Canopy cover ratio (CCR)
2.2.4. Data Alignment and Consistency Analysis
2.2.5. Sample Separation Before Training
2.3. Model Training
2.3.1. Feature-Variable Screening
2.3.2. Four Machine Learning Algorithms
2.4. Evaluation and Feature Analysis
2.4.1. Model Accuracy Test
2.4.2. Shapley Additivity (SHAP)
2.5. Prediction and Validation
3. Results
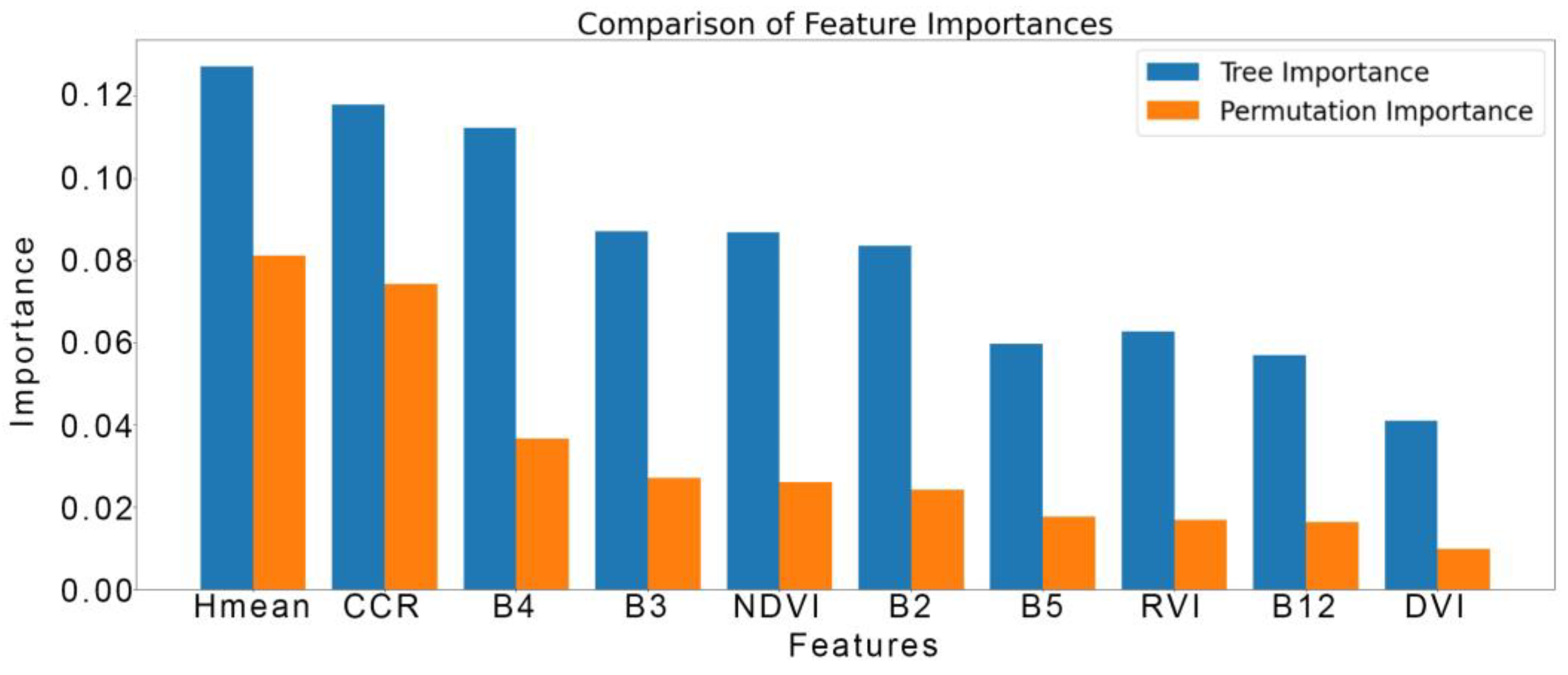
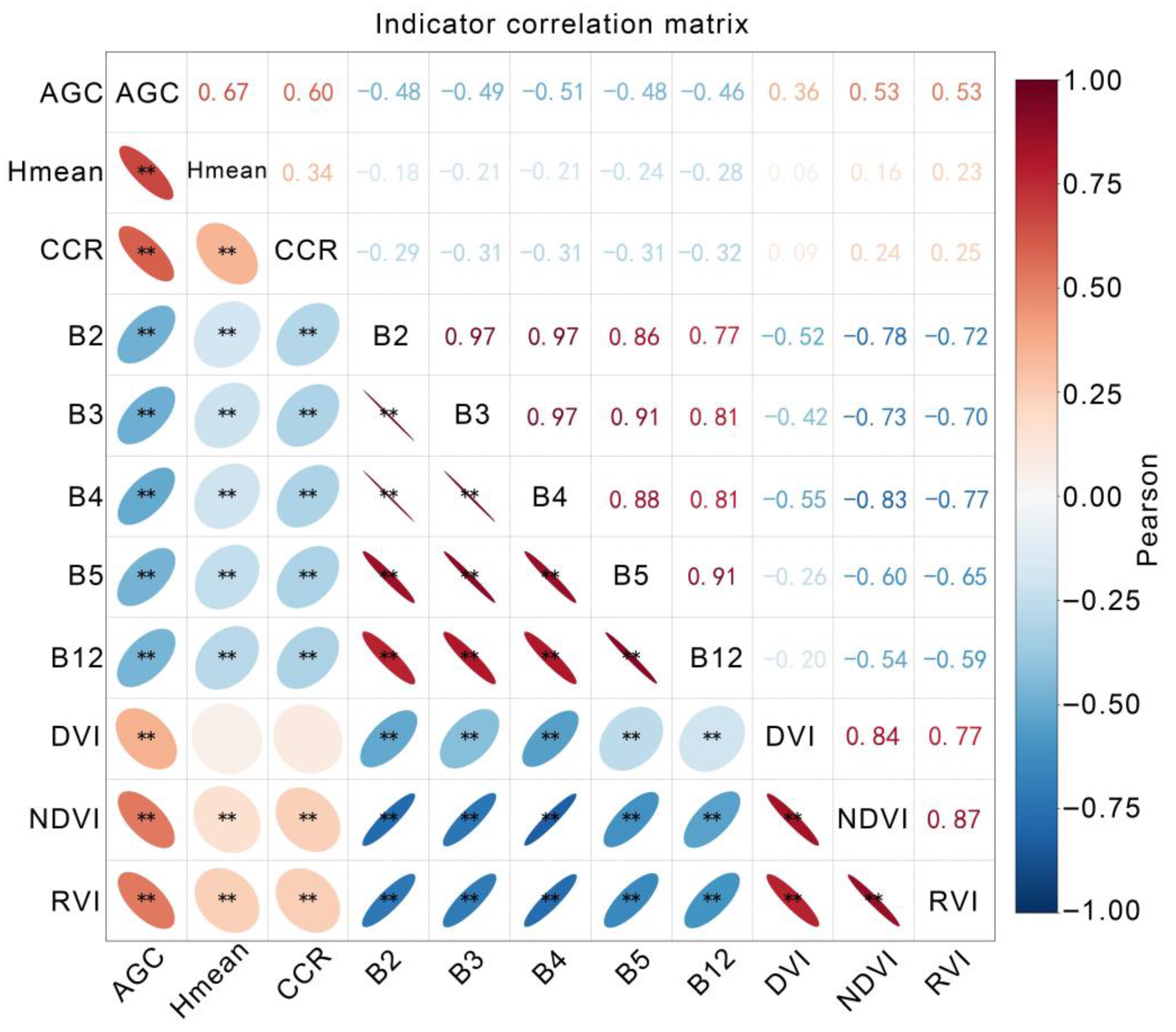
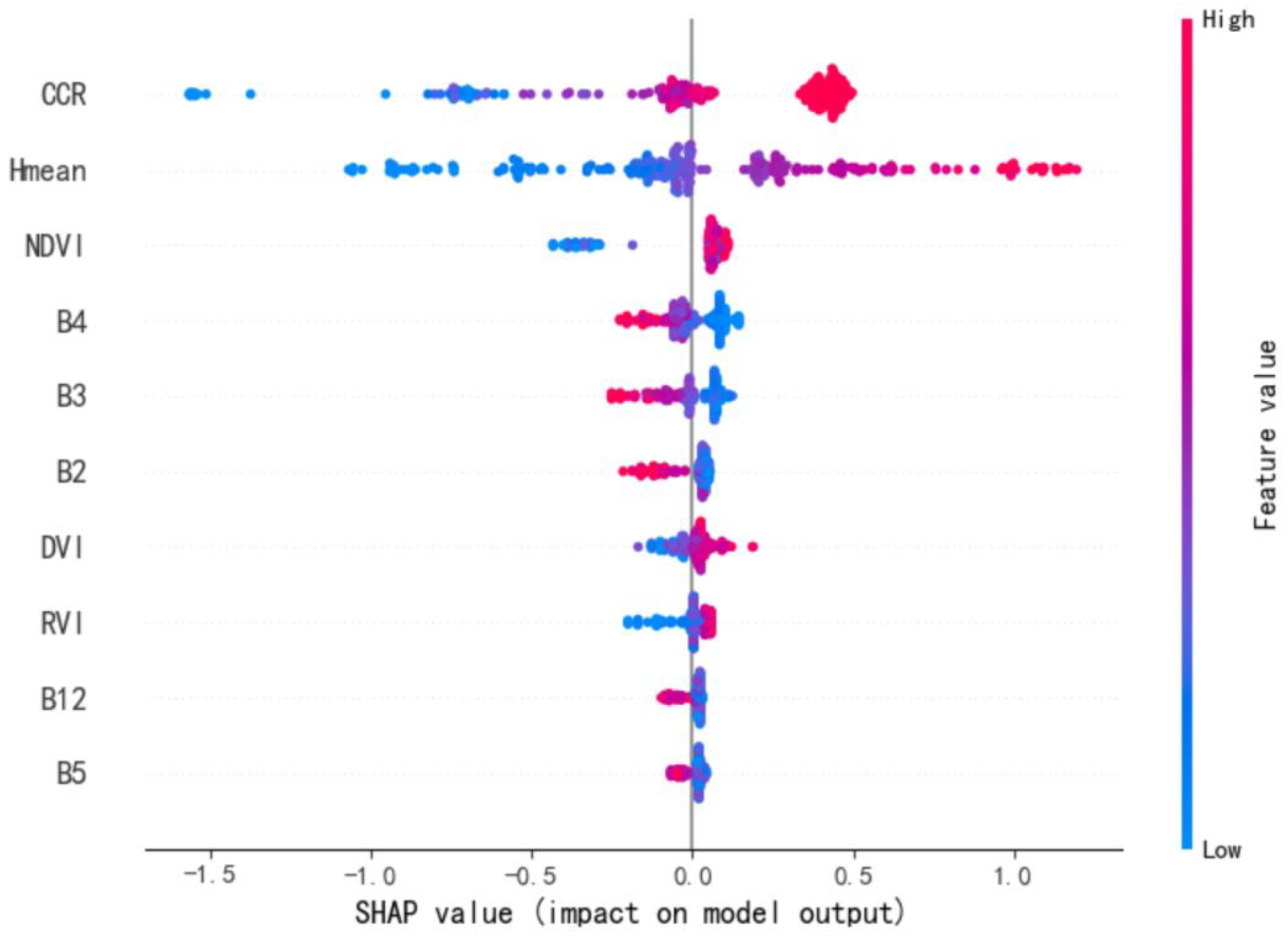
3.1. Feature Importance and Relevance
3.2. Model Accuracy Comparison
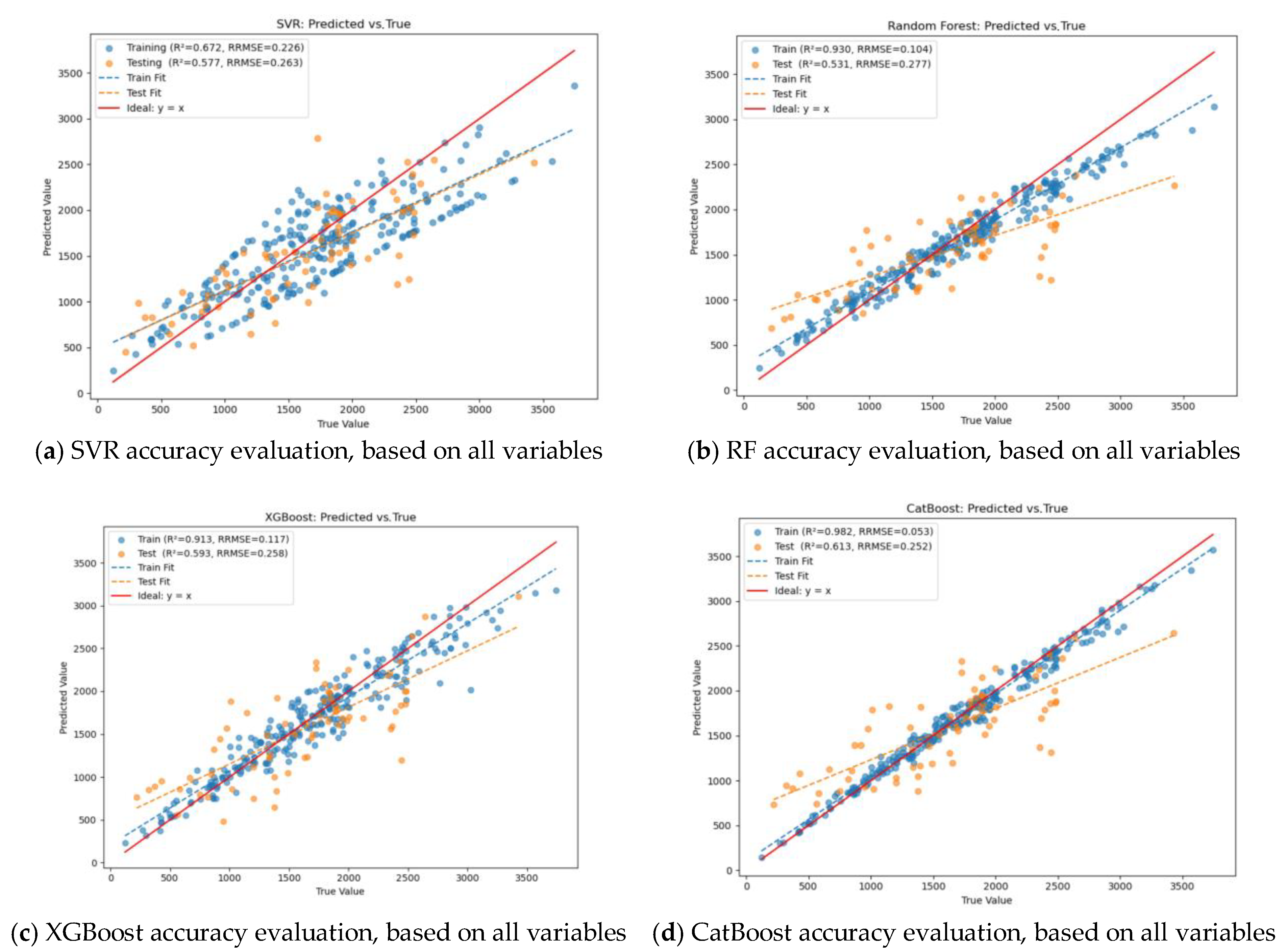
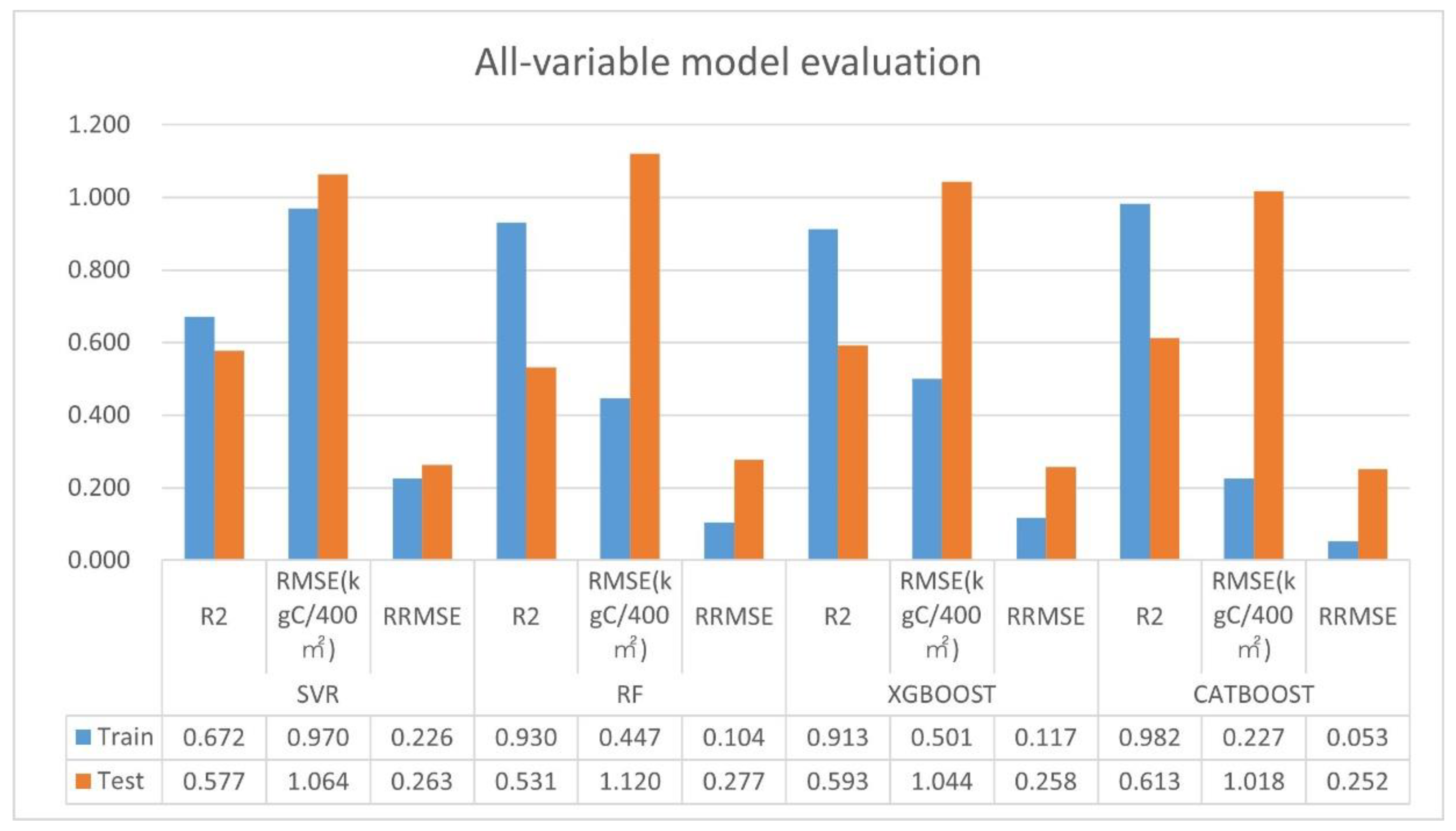
3.2.1. All-Variable Model
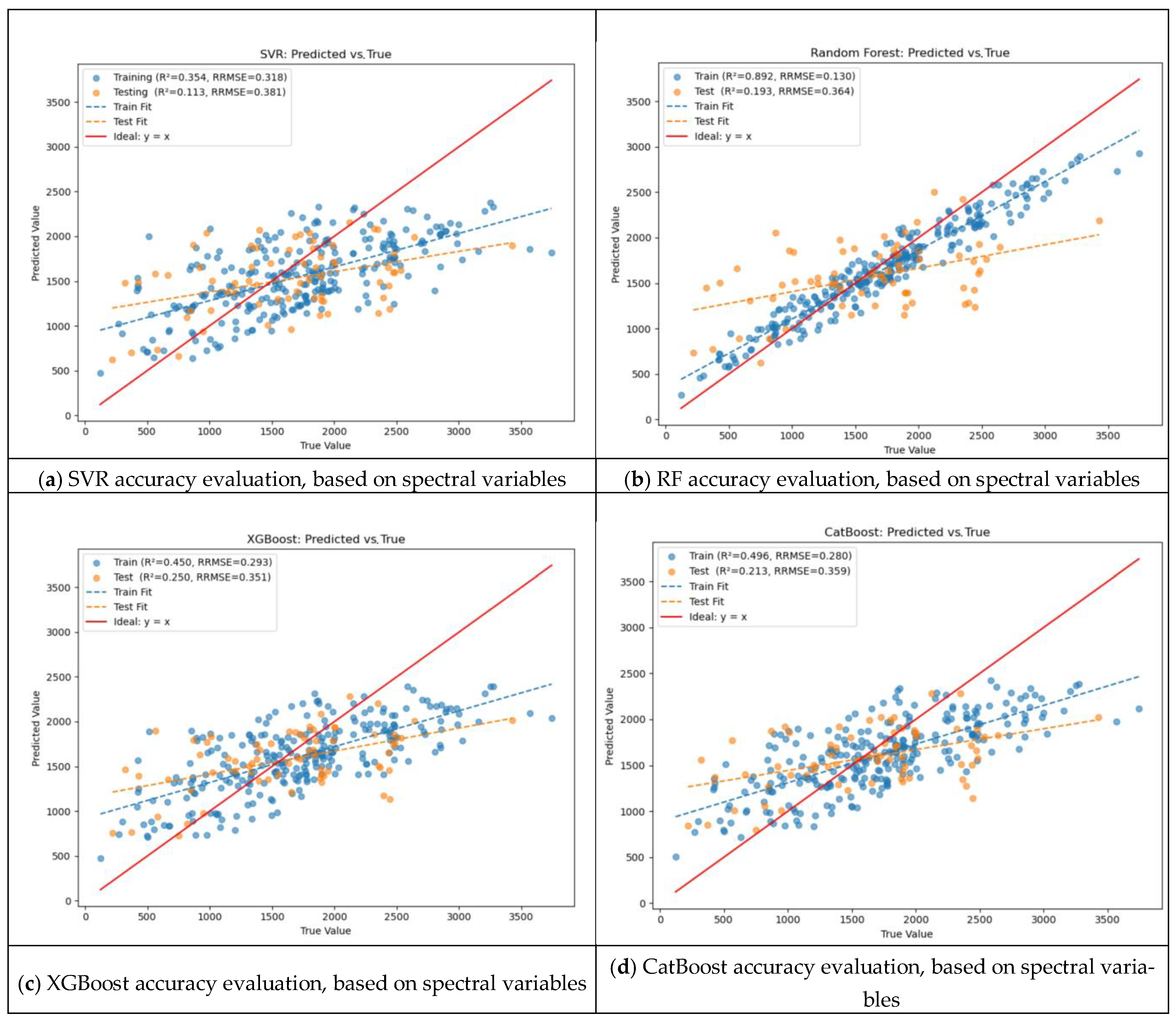
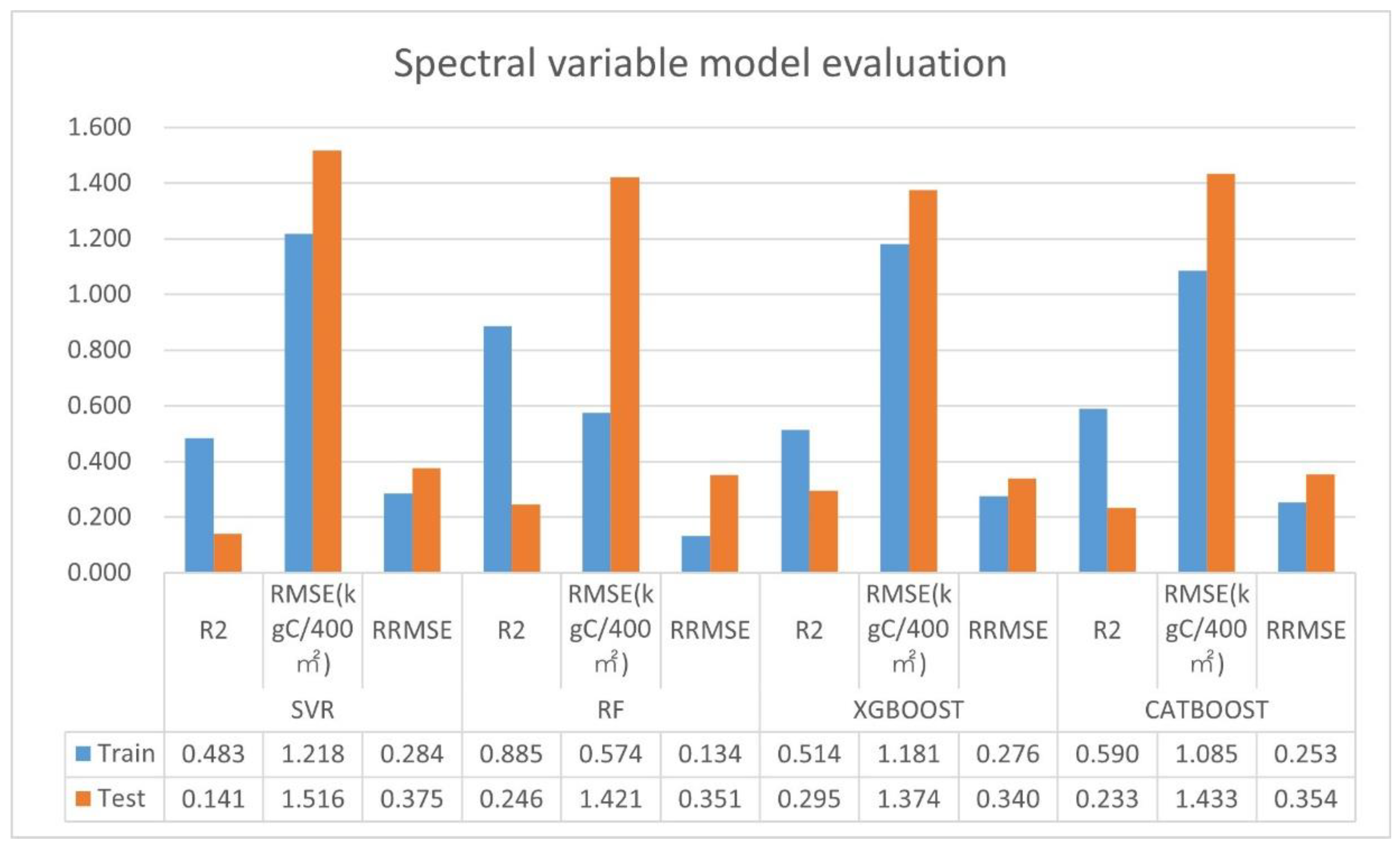
3.2.2. Spectral Variable Model
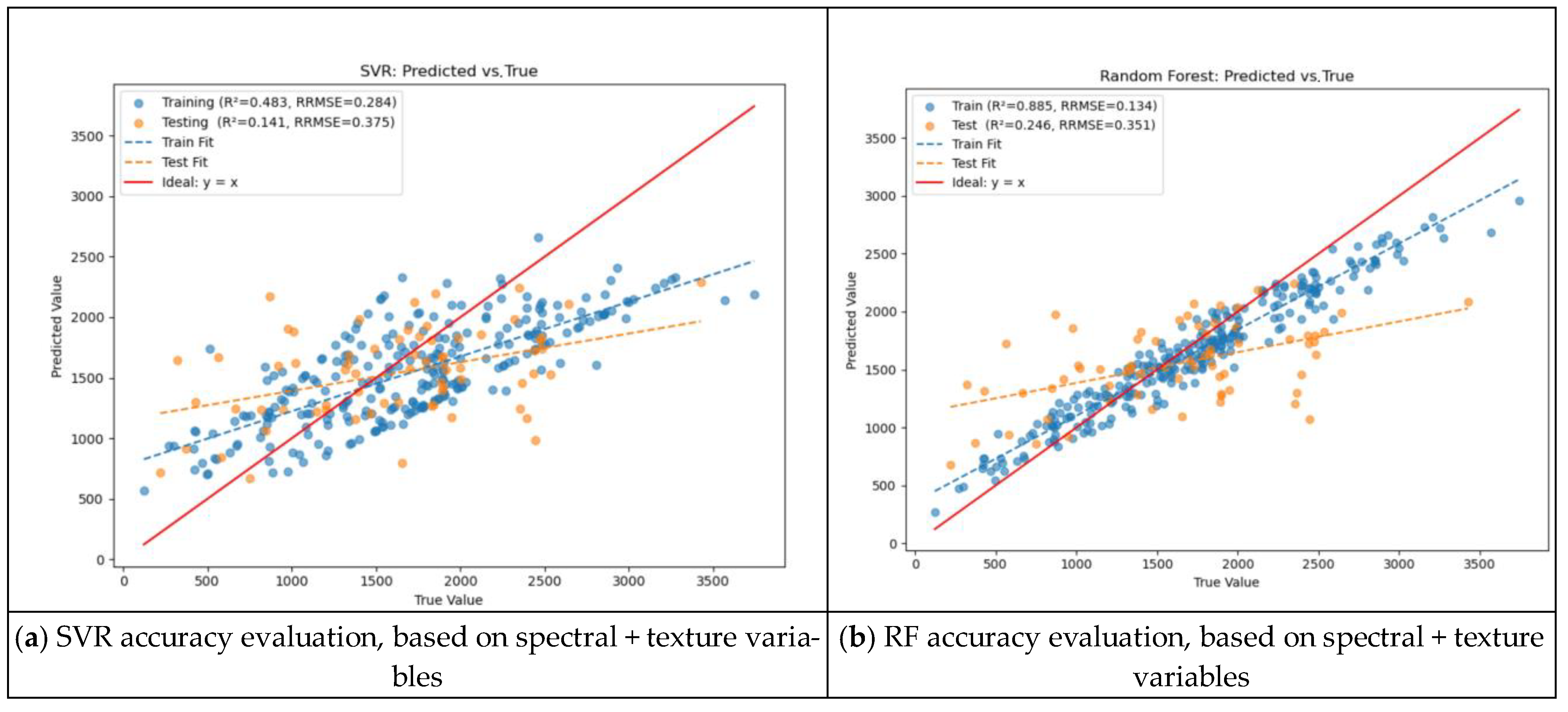
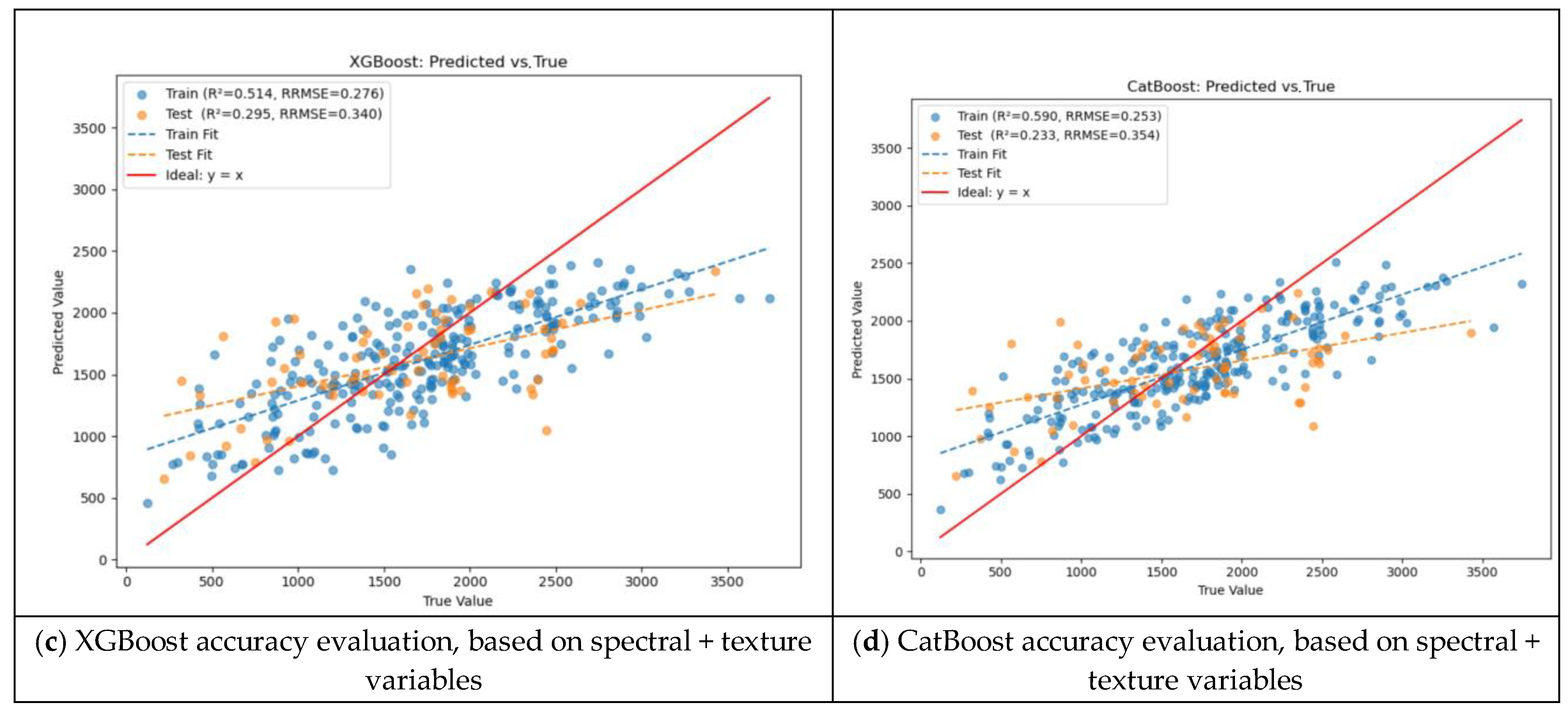
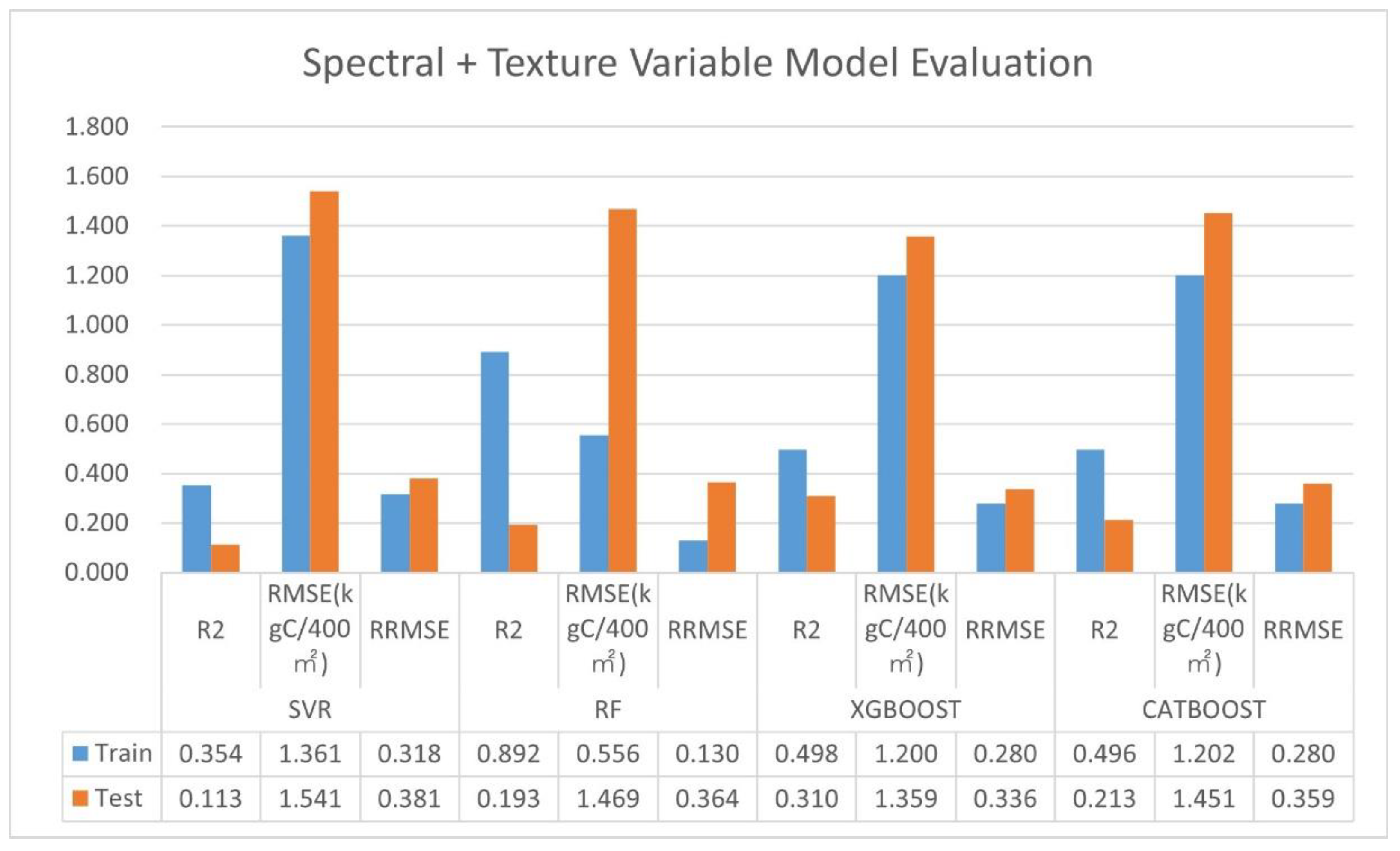
3.2.3. Spectral + Texture Variable Model
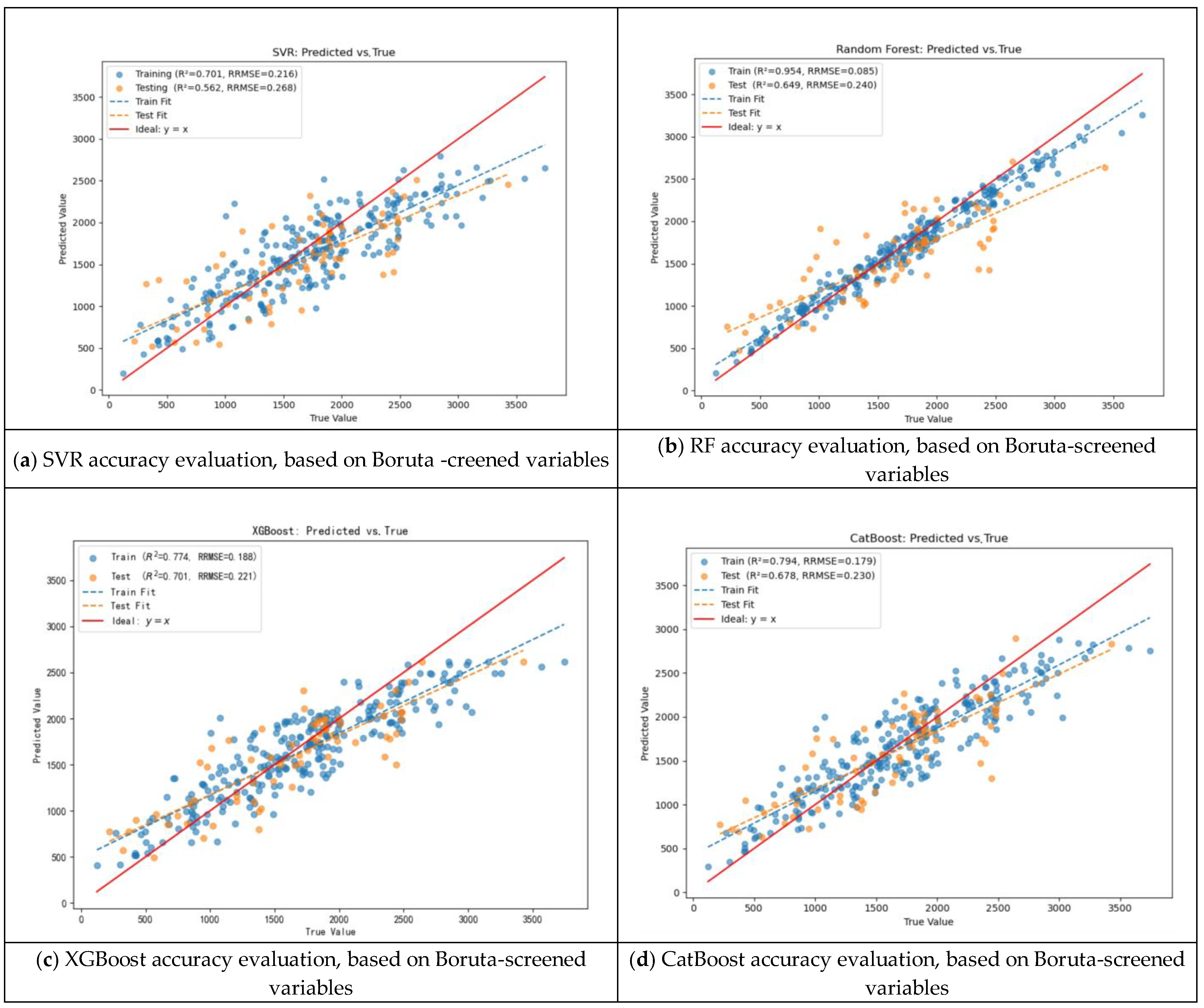
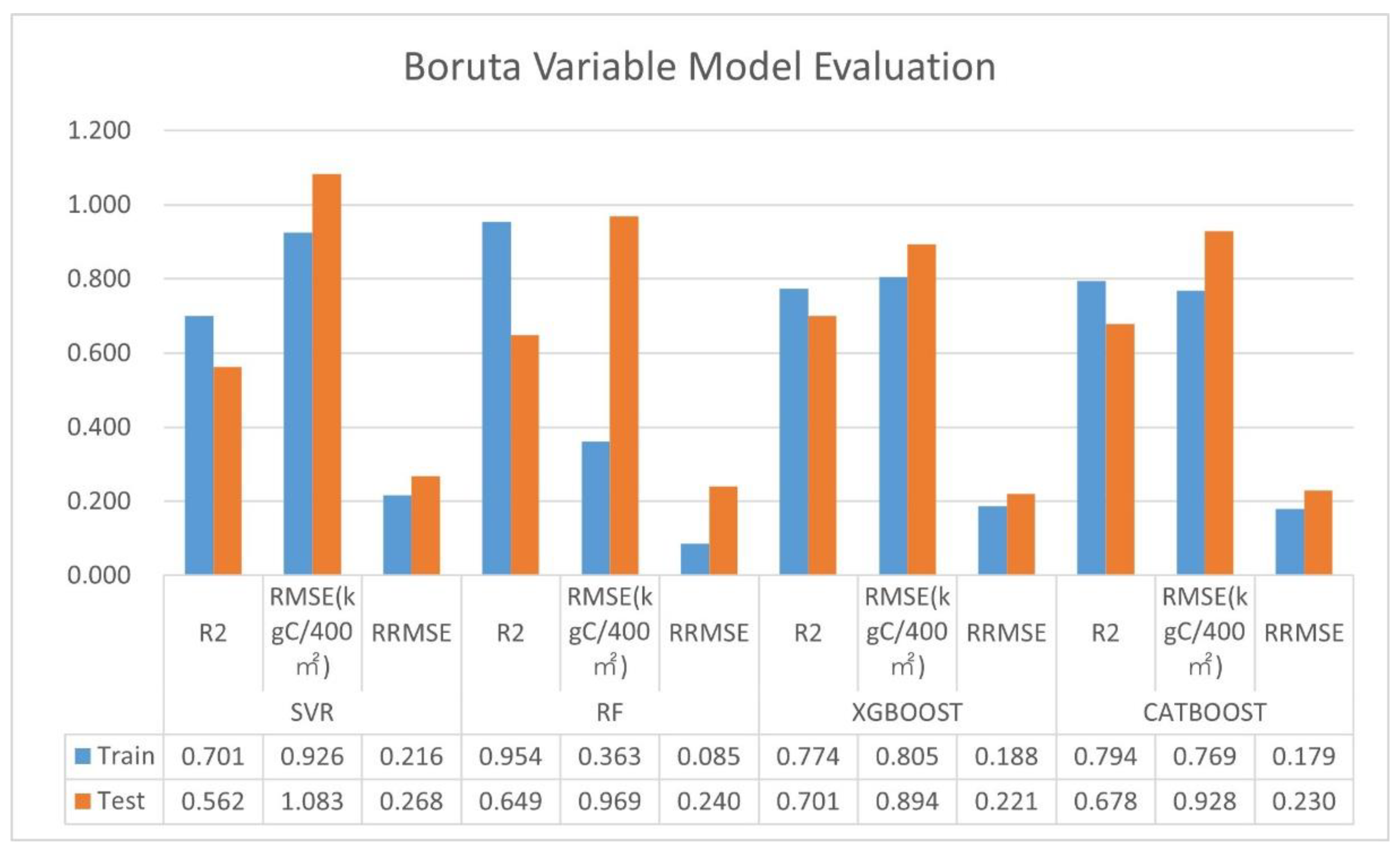
3.2.4. Boruta Screened-Variable Model
3.2.5. The Optimal Model
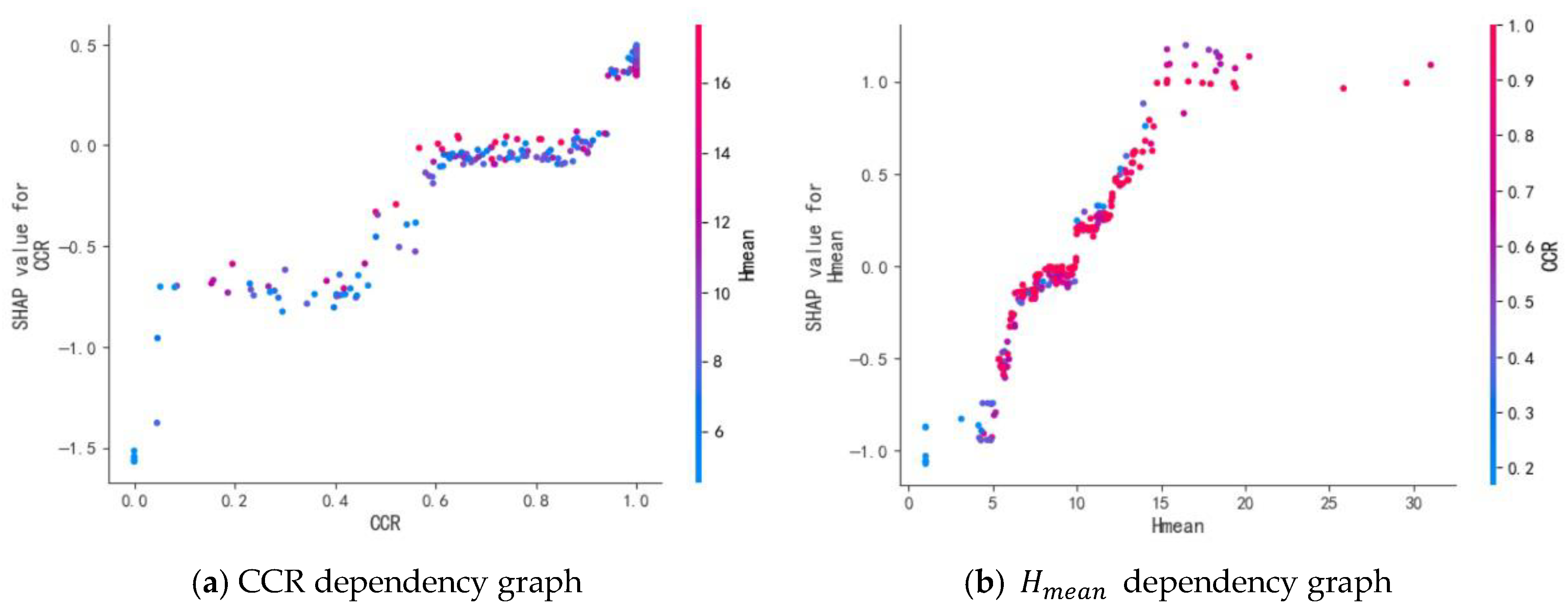
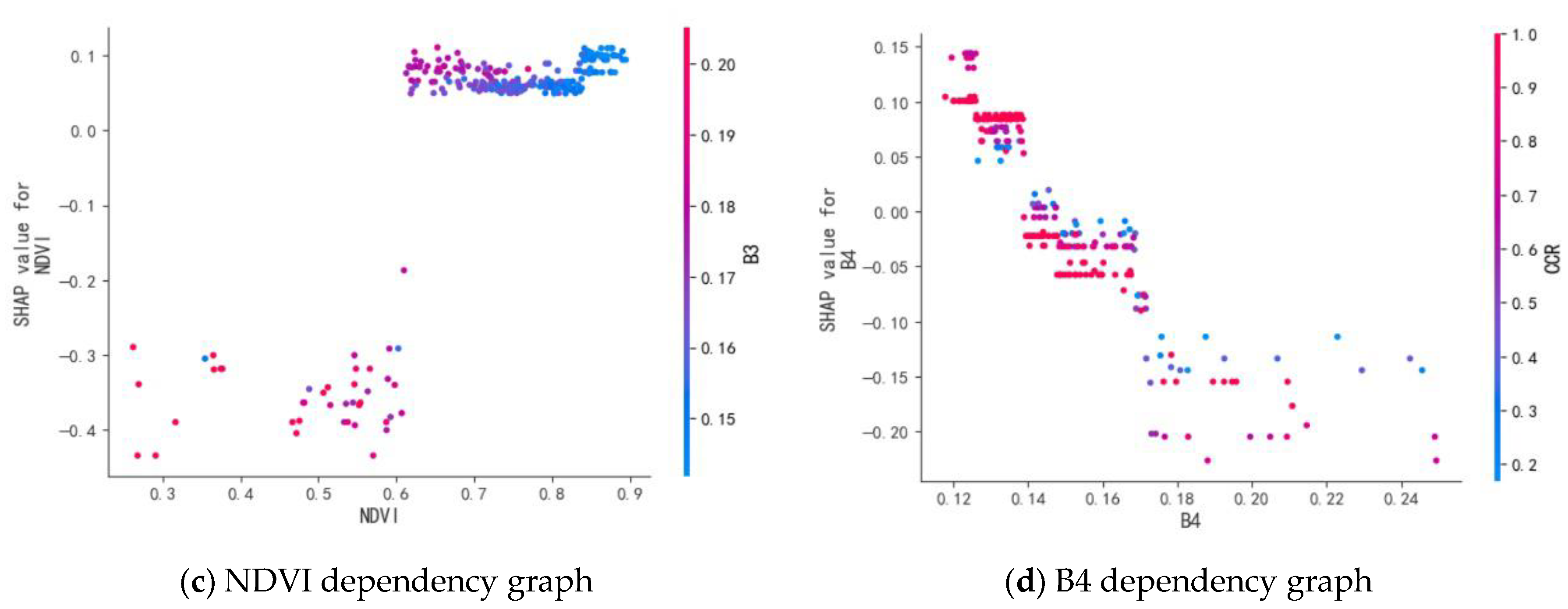
3.3. Assessment of the Contribution of Variables
3.4. Model Applications
4. Discussion
4.1. Interpretability of the Model
4.2. Estimated Effects of Different Green Spaces
4.3. Research Limitations and Perspectives
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Type of Green Space | Name of Green Space | No. | Number of Communities | |
|---|---|---|---|---|
| Park green space | Comprehensive Park (waterfront) | Xuanwu Lake Park | 1 | 60 |
| Mochou Lake Park | 2 | 30 | ||
| Crescent Lake Park | 3 | 20 | ||
| Xiuqiu Park | 4 | 20 | ||
| Little Peach Park | 5 | 20 | ||
| Comprehensive Park (Mountain) | Qingliang mountain—Stone city Park | 6 | 30 | |
| Arctic Pavilion Park | 7 | 20 | ||
| Neighborhood park | Peace Park | 8 | 10 | |
| Specialty park | Hexi Qingao Forest Park (other specialized parks) | 9 | 30 | |
| Nanjing China Greening Expo Park (other specialized parks) | 10 | 35 | ||
| Hexi Ecological Park (other specialized parks) | 11 | 30 | ||
| Xi’anmen Ruins Park (Specialized ruins park) | 12 | 15 | ||
| Plaza green space | Daxinggong Civic Plaza | 13 | 5 | |
| Drum Tower Plaza | 14 | 10 | ||
| Affiliated green space | Campus | Sipalou Campus of Southeast University | 15 | 15 |
| Commercial | Jinling Riverside Hotel | 16 | 15 | |
| Residential | Cui Ping Dong Nan | 17 | 20 | |
| Regional green space | Scenic | Yuhuatai Scenic Area | 18 | 20 |
| Wetlands | Fish Mouth Wetland Park | 19 | 30 | |
| No. | Community Type | Canopy Level | Quantities | |
|---|---|---|---|---|
| 1 | pure forest community | evergreen broadleaf | Single layer | 16 |
| 2 | evergreen conifers | Single layer | 5 | |
| 3 | deciduous broadleaf | Single layer | 20 | |
| 4 | deciduous conifers | Single layer | 5 | |
| 5 | mixed forest community | mixed evergreen and deciduous broadleaves | Single layer | 11 |
| 6 | Multilayer | 200 | ||
| 7 | mixed evergreen and deciduous conifers | Single level | 2 | |
| 8 | evergreen and deciduous mixed conifers and broadleaves | Multilayer | 81 | |
| 9 | deciduous mixed conifer | Multilayer | 19 | |
| 10 | evergreen mixed conifer | Multilayer | 6 | |
| 11 | No tree communities | Lawns, Ground Covers and Shrubs | Crownless | 10 |
| Total | 375 | |||
| Species | (kg) | Branch Biomass (kg) | Leaf Biomass (kg) | Bark Biomass (kg) | Aboveground Biomass (AGB) (kg) | Modeling Area |
|---|---|---|---|---|---|---|
| Cupressus funebris | / | / | / | / | Jiangsu [87] | |
| Pinus thunbergii | / | / | / | / | Anhui [87] | |
| Pinus massoniana | / | / | / | / | | Zhejiang [88] |
| Cunninghamia lanceolata | / | / | / | / | | Zhejiang [88] |
| Cryptomeria fortunei | Jiangsu [87] | |||||
| Metasequoia glyptostroboides | Jiangsu [87] | |||||
| Cinnamomum camphora | / | / | / | / | Shanghai [87] | |
| Robinia pseudoacacia | Jiangsu [87] | |||||
| Elaeocarpus decipiens | / | / | / | / | Shanghai [87] | |
| Quercus spp. | Henan [87] | |||||
| Ulmus spp. | Liaoning [87] | |||||
| Ligustrum lucidum | / | / | / | / | Shanghai [87] | |
| Magnolia grandiflora | / | / | / | / | Shanghai [87] | |
| Hard broadleaf species | / | / | / | / | Zhejiang [88] | |
| Populus spp. | / | Jiangsu [87] | ||||
| Paulownia spp. | Anhui [87] | |||||
| Koelreuteria bipinnata | / | / | / | / | Shanghai [87] | |
| Liriodendron chinense | / | / | / | / | Shanghai [87] | |
| Soft broadleaf species/Softwood broadleaves | / | / | / | / | Zhejiang [88] | |
| Eucommia ulmoides | / | Henan [87] | ||||
| Ginkgo biloba | / | / | / | / | Shanghai [87] | |
| Mixed broadleaf species | / | / | / | / | Guizhou [87] | |
| Phyllostachys edulis | / | / | / | / | Shanghai [87] | |
| Prunus persica (D = ground diameter) | / | / | / | / | Shanghai [87] | |
| Shrub cluster Shrub layer | / | / | / | / | Zhejiang [88] | |
| Conifers | / | / | / | / | National [87] | |
| Broadleaves | / | / | / | / | National [87] |
| Tree Species | CF | Tree Species | CF |
|---|---|---|---|
| Pinus sylvestris var. mongolica | 0.486 [89] | Betula platyphylla | 0.506 [89] |
| Pinus yunnanensis | 0.508 [89] | Eucalyptus spp. | 0.525 [89] |
| Pinus kesiya var. langbianensis | 0.501 [89] | Firmiana simplex | 0.423 [89] |
| Pinus elliottii | 0.474 [89] | Platanus × acerifolia | 0.441 [89] |
| Pinus massoniana | 0.525 [89] | Acer spp. | 0.45 [89] |
| Larix gmelinii | 0.489 [89] | Ginkgo biloba | 0.447 [89] |
| Pinus hwangshanensis | 0.506 [89] | Sapindus mukorossi | 0.435 [89] |
| Pinus taeda | 0.511 [89] | Koelreuteria paniculata | 0.424 [89] |
| Pinus armandii | 0.523 [89] | Celtis sinensis | 0.422 [89] |
| Pinus densata | 0.501 [89] | Liquidambar formosana | 0.418 [89] |
| Pinus koraiensis | 0.511 [89] | Bischofia polycarpa | 0.436 [89] |
| Pinus thunbergii | 0.515 [89] | Schima superba | 0.471 [89] |
| Pinus tabuliformis | 0.517 [89] | Michelia chapensis | 0.443 [89] |
| Pinus densiflora | 0.515 [89] | Alnus trabeculosa | 0.45 [89] |
| Cedrus deodara | 0.454 [89] | Populus tomentosa | 0.471 [89] |
| Quercus spp. | 0.48 [89] | Populus spp. | 0.43 [89] |
| Betula spp. | 0.487 [89] | Salix matsudana | 0.432 [89] |
| Picea spp. | 0.49 [89] | Salix spp. | 0.465 [89] |
| Abies spp. | 0.496 [89] | Ulmus spp. | 0.421 [89] |
| Cryptomeria fortunei | 0.514 [89] | Sophora japonica | 0.444 [89] |
| Metasequoia glyptostroboides | 0.439 [89] | Robinia spp. | 0.502 [89] |
| Cunninghamia lanceolata | 0.446 [89] | Prunus salicina | 0.44 [89] |
| Sabina chinensis | 0.45 [89] | Prunus spp. | 0.46 [89] |
| Cunninghamia lanceolata | 0.499 [89] | Prunus armeniaca | 0.43 [89] |
| Cupressus spp. | 0.485 [89] | Pyrus spp. | 0.46 [89] |
| Tilia spp. | 0.475 [89] | Syringa spp. | 0.43 [89] |
| Machilus pingii | 0.485 [89] | Malus spp. | 0.45 [89] |
| Cinnamomum spp. | 0.434 [89] | Forsythia spp. | 0.43 [89] |
| Magnolia spp. | 0.434 [89] | Broadleaf species | 0.48 [89] |
| Osmanthus fragrans | 0.434 [89] | Coniferous species | 0.489 [89] |
| Fraxinus chinensis | 0.488 [89] |
| Type | Name | Calculation Models or Descriptions | Remarks |
|---|---|---|---|
| Spectral feature | Coastal | Band1 | |
| Blue | Band2 | ||
| Green | Band3 | ||
| Red | Band4 | ||
| Red-edge1 | Band5 | ||
| Red-edge2 | Band6 | ||
| Red-edge3 | Band7 | ||
| NIR1 | Band8 | ||
| NIR2 | Band8A | ||
| Swir1 | Band9 | ||
| Swir2 | Band11 | ||
| Swir3 | Band12 | ||
| DVI | NIR-R | ||
| NDVI | |||
| EVI | |||
| RVI | |||
| Texture feature | Mean | There are five window sizes for texture feature extraction: 3 × 3, 5 × 5, 7 × 7, 9 × 9, 11 × 11 | |
| Variance | |||
| Homogeneity | |||
| Contrast | |||
| Dissimilarity | |||
| Entropy | |||
| Second moment | |||
| Correlation | |||
| 3D feature | Average of tree heights within a 20 m grid | ||
| CCR | Percentage of canopy area within a 20 m grid |
References
- Ge, J.; Wang, Y.; Zhou, D.; Gu, Z.; Meng, X. Effects of urban vegetation on microclimate and building energy demand in winter: An evaluation using coupled simulations. Sust. Cities Soc. 2024, 102, 105199. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, N.; Wang, X. Development of a modified thermal humidity index and its application to human thermal comfort of urban vegetation patches. Ecosyst. Health Sustain. 2022, 8, 2130095. [Google Scholar] [CrossRef]
- Diener, A.; Mudu, P. How can vegetation protect us from air pollution? A critical review on green spaces’ mitigation abilities for air-borne particles from a public health perspective-with implications for urban planning. Sci. Total Environ. 2021, 796, 148605. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Cai, J.; Xu, Y.; Liu, Y.; Yao, M. Carbon sinks in urban public green spaces under carbon neutrality: A bibliometric analysis and systematic literature review. Urban For. Urban Green. 2023, 86, 128037. [Google Scholar] [CrossRef]
- Stroud, S.; Peacock, J.; Hassall, C. Vegetation-based ecosystem service delivery in urban landscapes: A systematic review. Basic Appl. Ecol. 2022, 61, 82–101. [Google Scholar] [CrossRef]
- Ma, J.; Li, X.; Baoquan, J.; Liu, X.; Li, T.; Zhang, W.; Liu, W. Spatial variation analysis of urban forest vegetation carbon storage and sequestration in built-up areas of Beijing based on i-Tree Eco and Kriging. Urban For. Urban Green. 2021, 66, 127413. [Google Scholar] [CrossRef]
- Liu, C.; Liu, Z.; Xie, B.; Liang, Y.; Li, X.; Zhou, K. Decoupling the effect of climate and land-use changes on carbon sequestration of vegetation in Mideast Hunan Province, China. Forests 2021, 12, 1573. [Google Scholar] [CrossRef]
- Zhang, Y.; Shao, Z. Assessing of urban vegetation biomass in combination with LiDAR and high-resolution remote sensing images. Int. J. Remote Sens. 2021, 42, 964–985. [Google Scholar] [CrossRef]
- Sonti, N.F.; Groffman, P.M.; Nowak, D.J.; Henning, J.G.; Avolio, M.L.; Rosi, E.J. Urban net primary production: Concepts, field methods, and Baltimore, Maryland, USA case study. Ecol. Appl. 2022, 32, e2562. [Google Scholar] [CrossRef]
- Yang, K.; Zhou, P.; Wu, J.; Yao, Q.; Yang, Z.; Wang, X.; Wen, Y. Carbon stock inversion study of a carbon peaking pilot urban combining machine learning and Landsat images. Ecol. Indic. 2024, 159, 111657. [Google Scholar] [CrossRef]
- Zhao, M.; He, Z.; Du, J.; Chen, L.; Lin, P.; Fang, S. Assessing the effects of ecological engineering on carbon storage by linking the CA-Markov and InVEST models. Ecol. Indic. 2019, 98, 29–38. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Zhu, E.; Wu, H.; Feng, D. Carbon storage estimation and strategy optimization under low carbon objectives for urban attached green spaces. Sci. Total Environ. 2024, 923, 171507. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zhang, G.; Zhong, Q.; Xing, L.; Du, H. Prediction of urban forest aboveground carbon using machine learning based on landsat 8 and Sentinel-2: A case study of Shanghai, China. Remote Sens. 2023, 15, 284. [Google Scholar] [CrossRef]
- Pregitzer, C.C.; Hanna, C.; Charlop-Powers, S.; Bradford, M.A. Estimating carbon storage in urban forests of New York City. Urban Ecosyst. 2022, 25, 617–631. [Google Scholar] [CrossRef]
- Kinnunen, A.; Talvitie, I.; Ottelin, J.; Heinonen, J.; Junnila, S. Carbon sequestration and storage potential of urban residential environment—A review. Sust. Cities Soc. 2022, 84, 104027. [Google Scholar] [CrossRef]
- Jaman, S.; Zhang, X.; Islam, F. Carbon storage and tree diversity in the urban vegetation of Dhaka city, Bangladesh: A study based on intensive field investigation. Arboric. J. 2020, 42, 76–92. [Google Scholar] [CrossRef]
- Gao, X.; Huang, R.; Li, J.; Wang, C.; Lan, T.; Li, Q.; Deng, O.; Tao, Q.; Zeng, M. Temperature induces soil organic carbon mineralization in urban park green spaces, Chengdu, southwestern China: Effects of planting years and vegetation types. Urban For. Urban Green. 2020, 54, 126761. [Google Scholar] [CrossRef]
- Schimel, D.; Schneider, F.D.; Carbon, J.; Participants, E. Flux towers in the sky: Global ecology from space. New Phytol. 2019, 224, 570–584. [Google Scholar] [CrossRef]
- Amoatey, P.; Sulaiman, H.; Kwarteng, A.; Al-Reasi, H.A. Above-ground carbon dynamics in different arid urban green spaces. Environ. Earth Sci. 2018, 77, 431. [Google Scholar] [CrossRef]
- Myeong, S.; Nowak, D.J.; Duggin, M.J. A temporal analysis of urban forest carbon storage using remote sensing. Remote Sens. Environ. 2006, 101, 277–282. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, D.; Cao, Y.; Zhang, L.; Peng, H.; Wang, K.; Xie, H.; Wang, C. An integrated remote sensing and model approach for assessing forest carbon fluxes in China. Sci. Total Environ. 2022, 811, 152480. [Google Scholar] [CrossRef]
- Thurner, M.; Beer, C.; Santoro, M.; Carvalhais, N.; Wutzler, T.; Schepaschenko, D.; Shvidenko, A.; Kompter, E.; Ahrens, B.; Levick, S.R.; et al. Carbon stock and density of northern boreal and temperate forests. Glob. Ecol. Biogeogr. 2014, 23, 297–310. [Google Scholar] [CrossRef]
- Liu, A.; Cheng, X.; Chen, Z. Performance evaluation of GEDI and ICESat-2 laser altimeter data for terrain and canopy height retrievals. Remote Sens. Environ. 2021, 264, 112571. [Google Scholar] [CrossRef]
- Zacharias, J. Addressing global climate change with big data-driven urban planning policy. Int. J. E-Plan. Res. (IJEPR) 2021, 10, 1–16. [Google Scholar] [CrossRef]
- Tian, H.; Xie, C.; Zhong, M.; Ye, Y.; Zhou, R.; Zhao, D. Urban tree carbon storage estimation using unmanned aerial vehicles remote sensing. Urban For. Urban Green. 2025, 107, 128755. [Google Scholar] [CrossRef]
- Liu, X.; Pei, F.; Wen, Y.; Li, X.; Wang, S.; Wu, C.; Cai, Y.; Wu, J.; Chen, J.; Feng, K.; et al. Global urban expansion offsets climate-driven increases in terrestrial net primary productivity. Nat. Commun. 2019, 10, 5558. [Google Scholar] [CrossRef] [PubMed]
- Song, Q.; Albrecht, C.M.; Xiong, Z.; Zhu, X.X. Biomass estimation and uncertainty quantification from tree height. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2023, 16, 4833–4845. [Google Scholar] [CrossRef]
- Tanase, M.A.; Mihai, M.C.; Miguel, S.; Cantero, A.; Tijerín, J.; Ruiz-Benito, P.; Domingo, D.I.O.; García-Martín, A.; Aponte, C.; Lamelas, M.I.A.T. Long-term annual estimation of forest above ground biomass, canopy cover, and height from airborne and spaceborne sensors synergies in the Iberian Peninsula. Environ. Res. 2024, 259, 119432. [Google Scholar] [CrossRef]
- Kamoske, A.G.; Dahlin, K.M.; Serbin, S.P.; Stark, S.C. Leaf traits and canopy structure together explain canopy functional diversity: An airborne remote sensing approach. Ecol. Appl. 2021, 31, e02230. [Google Scholar] [CrossRef]
- Malambo, L.; Popescu, S.C. Assessing the agreement of ICESat-2 terrain and canopy height with airborne lidar over US ecozones. Remote Sens. Environ. 2021, 266, 112711. [Google Scholar] [CrossRef]
- Liu, S.; Brandt, M.; Nord-Larsen, T.; Chave, J.; Reiner, F.; Lang, N.; Tong, X.; Ciais, P.; Igel, C.; Pascual, A.; et al. The overlooked contribution of trees outside forests to tree cover and woody biomass across Europe. Sci. Adv. 2023, 9, eadh4097. [Google Scholar] [CrossRef]
- Dorado-Roda, I.A.N.; Pascual, A.A.N.; Godinho, S.; Silva, C.A.; Botequim, B.; Rodríguez-Gonzálvez, P.; González-Ferreiro, E.; Guerra-Hernández, J. Assessing the accuracy of GEDI data for canopy height and aboveground biomass estimates in Mediterranean forests. Remote Sens. 2021, 13, 2279. [Google Scholar] [CrossRef]
- Zhuang, Q.; Shao, Z.; Gong, J.; Li, D.; Huang, X.; Zhang, Y.; Xu, X.; Dang, C.; Chen, J.; Altan, O.; et al. Modeling carbon storage in urban vegetation: Progress, challenges, and opportunities. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103058. [Google Scholar] [CrossRef]
- Zhao, Y.; Wu, B.; Shu, S.; Yang, L.; Wu, J.; Yu, B. Evaluation of ICESat-2 ATL03/08 surface heights in urban environments using airborne LiDAR point cloud data. IEEE Geosci. Remote Sens. Lett. 2021, 19, 7002905. [Google Scholar] [CrossRef]
- Shettles, M.; Hilker, T.; Temesgen, H. Examination of uncertainty in per unit area estimates of aboveground biomass using terrestrial LiDAR and ground data. Can. J. For. Res. 2016, 46, 706–715. [Google Scholar] [CrossRef]
- Shen, G.; Wang, Z.; Liu, C.; Han, Y. Mapping aboveground biomass and carbon in Shanghai’s urban forest using Landsat ETM+ and inventory data. Urban For. Urban Green. 2020, 51, 126655. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O. Evaluating the utility of the medium-spatial resolution Landsat 8 multispectral sensor in quantifying aboveground biomass in uMgeni catchment, South Africa. ISPRS-J. Photogramm. Remote Sens. 2015, 101, 36–46. [Google Scholar] [CrossRef]
- Griffiths, P.; Nendel, C.; Pickert, J.U.R.; Hostert, P. Towards national-scale characterization of grassland use intensity from integrated Sentinel-2 and Landsat time series. Remote Sens. Environ. 2020, 238, 111124. [Google Scholar] [CrossRef]
- Dong, L.; Du, H.; Mao, F.; Han, N.; Li, X.; Zhou, G.; Zhu, D.; Zheng, J.; Zhang, M.; Xing, L.; et al. Very high resolution remote sensing imagery classification using a fusion of random forest and deep learning technique—Subtropical area for example. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 13, 113–128. [Google Scholar] [CrossRef]
- Dang, A.T.N.; Nandy, S.; Srinet, R.; Luong, N.V.; Ghosh, S.; Kumar, A.S. Forest aboveground biomass estimation using machine learning regression algorithm in Yok Don National Park, Vietnam. Ecol. Inform. 2019, 50, 24–32. [Google Scholar] [CrossRef]
- Ou, Q.X.; Li, H.K.; Lei, X.D.; Yang, Y. Difference analysis in estimating biomass conversion and expansion factors of masson pine in Fujian Province, China based on national forest inventory data: A comparison of three decision tree models of ensemble learning. Ying Yong Sheng Tai Xue Bao J. Appl. Ecol. 2018, 29, 2007–2016. [Google Scholar]
- Cheng, F.; Ou, G.; Wang, M.; Liu, C. Remote sensing estimation of forest carbon stock based on machine learning algorithms. Forests 2024, 15, 681. [Google Scholar] [CrossRef]
- Pham, T.D.; Yokoya, N.; Xia, J.; Ha, N.T.; Le, N.N.; Nguyen, T.T.T.; Dao, T.H.; Vu, T.T.P.; Pham, T.D.; Takeuchi, W. Comparison of machine learning methods for estimating mangrove above-ground biomass using multiple source remote sensing data in the red river delta biosphere reserve, Vietnam. Remote Sens. 2020, 12, 1334. [Google Scholar] [CrossRef]
- Bui, Q.; Pham, Q.; Pham, V.; Tran, V.; Nguyen, D.; Nguyen, Q.; Nguyen, H.; Do, N.T.; Vu, V. Hybrid machine learning models for aboveground biomass estimations. Ecol. Inform. 2024, 79, 102421. [Google Scholar] [CrossRef]
- Gašparović, M.; Dobrinić, D. Comparative assessment of machine learning methods for urban vegetation mapping using multitemporal sentinel-1 imagery. Remote Sens. 2020, 12, 1952. [Google Scholar] [CrossRef]
- Wei, S.; Lin, Y.; Wan, L.; Lin, G.; Zhang, Y.; Zhang, H. Developing a grid-based association rules mining approach to quantify the impacts of urbanization on the spatial extent of mangroves in China. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102431. [Google Scholar] [CrossRef]
- Yu, X.; Lu, D.; Jiang, X.; Li, G.; Chen, Y.; Li, D.; Chen, E. Examining the roles of spectral, spatial, and topographic features in improving land-cover and forest classifications in a subtropical region. Remote Sens. 2020, 12, 2907. [Google Scholar] [CrossRef]
- Ye, Q.; Yu, S.; Liu, J.; Zhao, Q.; Zhao, Z. Aboveground biomass estimation of black locust planted forests with aspect variable using machine learning regression algorithms. Ecol. Indic. 2021, 129, 107948. [Google Scholar] [CrossRef]
- Nanjing Municipal Bureau of Statistics. Nanjing Statistical Yearbook; Nanjing Municipal Bureau of Statistics: Nanjing, China, 2021.
- Yang, K.; Sun, W.; Luo, Y.; Zhao, L. Impact of urban expansion on vegetation: The case of China (2000–2018). J. Environ. Manag. 2021, 291, 112598. [Google Scholar] [CrossRef]
- Nowak, D.J.; Walton, J.T.; Stevens, J.C.; Crane, D.E.; Hoehn, R.E. Effect of plot and sample size on timing and precision of urban forest assessments. Aboricult. Urban For. 2008, 34, 386–390. [Google Scholar] [CrossRef]
- Dai, X.; Yang, G.; Liu, D.; Wan, R. Vegetation carbon sequestration mapping in herbaceous wetlands by using a MODIS EVI time-series data set: A case in Poyang lake wetland, China. Remote Sens. 2020, 12, 3000. [Google Scholar] [CrossRef]
- Baniya, B.; Tang, Q.; Huang, Z.; Sun, S.; Techato, K. Spatial and temporal variation of NDVI in response to climate change and the implication for carbon dynamics in Nepal. Forests 2018, 9, 329. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K. Computer classification of reservoir sandstones. IEEE Trans. Geosci. Electron. 1973, 11, 171–177. [Google Scholar] [CrossRef]
- Zhou, B.; Gao, S.; Yin, Y.; Zhong, Y. Enhancing active fire detection in Sentinel 2 imagery using GLCM texture features in random forest models. Sci. Rep. 2024, 14, 31076. [Google Scholar] [CrossRef]
- Numbisi, F.N.; Van Coillie, F.M.; De Wulf, R. Delineation of cocoa agroforests using multiseason sentinel-1 SAR images: A low grey level range reduces uncertainties in GLCM texture-based mapping. ISPRS Int. J. Geo-Inf. 2019, 8, 179. [Google Scholar] [CrossRef]
- Bijlsma, R.J. The characterization of natural vegetation using first-order and texture measurements in digitized, colour-infrared photography. Int. J. Remote Sens. 1993, 14, 1547–1562. [Google Scholar] [CrossRef]
- Lang, N.; Jetz, W.; Schindler, K.; Wegner, J.D. A high-resolution canopy height model of the Earth. Nat. Ecol. Evol. 2023, 7, 1778–1789. [Google Scholar] [CrossRef]
- Shi, Q.; Liu, M.; Marinoni, A.; Liu, X. UGS-1m: Fine-grained urban green space mapping of 34 major cities in China based on the deep learning framework. Earth Syst. Sci. Data Discuss. 2022, 15, 555–577. [Google Scholar] [CrossRef]
- Li, X.; Du, H.; Mao, F.; Zhou, G.; Chen, L.; Xing, L.; Fan, W.; Xu, X.; Liu, Y.; Cui, L.; et al. Estimating bamboo forest aboveground biomass using EnKF-assimilated MODIS LAI spatiotemporal data and machine learning algorithms. Agric. For. Meteorol. 2018, 256, 445–457. [Google Scholar] [CrossRef]
- Paja, W.; Wrzesień, M.; Niemiec, R.; Rudnicki, W.R. Application of all relevant feature selection for failure analysis of parameter-induced simulation crashes in climate models. Geosci. Model Dev. Discuss. 2015, 8, 5419–5435. [Google Scholar] [CrossRef]
- Ahady, A.B.; Kaplan, G. Classification comparison of Landsat-8 and Sentinel-2 data in Google Earth Engine, study case of the city of Kabul. Int. J. Eng. Geosci. 2022, 7, 24–31. [Google Scholar] [CrossRef]
- Vincenzi, S.; Zucchetta, M.; Franzoi, P.; Pellizzato, M.; Pranovi, F.; De Leo, G.A.; Torricelli, P. Application of a Random Forest algorithm to predict spatial distribution of the potential yield of Ruditapes philippinarum in the Venice lagoon, Italy. Ecol. Model. 2011, 222, 1471–1478. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Li, M.; Liu, Z. Influence of variable selection and forest type on forest aboveground biomass estimation using machine learning algorithms. Forests 2019, 10, 1073. [Google Scholar] [CrossRef]
- Hancock, J.T.; Khoshgoftaar, T.M. CatBoost for big data: An interdisciplinary review. J. Big Data 2020, 7, 94. [Google Scholar] [CrossRef] [PubMed]
- Yunjiao, J.; Man, H.; Mingyang, L.; Xiangyang, Z. Remote sensing based estimation of forest aboveground biomass at county level. J. Southwest For. Univ. 2015, 35, 53–59. [Google Scholar]
- Lundberg, S.M.; Lee, S. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Hakkal, S.; Ait Lahcen, A. XGBoost to enhance learner performance prediction. Comput. Educ. Artif. Intell. 2024, 7, 100254. [Google Scholar] [CrossRef]
- Tamayo-Vera, D.; Wang, X.; Mesbah, M. A review of machine learning techniques in agroclimatic studies. Agriculture 2024, 14, 481. [Google Scholar] [CrossRef]
- Uniyal, S.; Purohit, S.; Chaurasia, K.; Rao, S.S.; Amminedu, E. Quantification of carbon sequestration by urban forest using Landsat 8 OLI and machine learning algorithms in Jodhpur, India. Urban For. Urban Green. 2022, 67, 127445. [Google Scholar] [CrossRef]
- Mngadi, M.; Odindi, J.; Mutanga, O. The utility of sentinel-2 spectral data in quantifying above-ground carbon stock in an urban reforested landscape. Remote Sens. 2021, 13, 4281. [Google Scholar] [CrossRef]
- Sheridan, R.P.; Wang, W.M.; Liaw, A.; Ma, J.; Gifford, E.M. Extreme gradient boosting as a method for quantitative structure--activity relationships. J. Chem. Inf. Model. 2016, 56, 2353–2360. [Google Scholar] [CrossRef]
- Aguilar, C.; Zinnert, J.C.; Polo, M.I.A.J.; Young, D.R. NDVI as an indicator for changes in water availability to woody vegetation. Ecol. Indic. 2012, 23, 290–300. [Google Scholar] [CrossRef]
- Ardila, J.P.; Tolpekin, V.A.; Bijker, W.; Stein, A. Markov-random-field-based super-resolution mapping for identification of urban trees in VHR images. ISPRS-J. Photogramm. Remote Sens. 2011, 66, 762–775. [Google Scholar] [CrossRef]
- Lee, Y.; Son, B.; Im, J.; Zhen, Z.; Quackenbush, L.J. Two-step carbon storage estimation in urban human settlements using airborne LiDAR and Sentinel-2 data based on machine learning. Urban For. Urban Green. 2024, 94, 128239. [Google Scholar] [CrossRef]
- Nesbitt, L.; Meitner, M.J.; Girling, C.; Sheppard, S.R.; Lu, Y. Who has access to urban vegetation? A spatial analysis of distributional green equity in 10 US cities. Landsc. Urban Plan. 2019, 181, 51–79. [Google Scholar] [CrossRef]
- De La Iglesia Martinez, A.; Labib, S.M. Demystifying normalized difference vegetation index (NDVI) for greenness exposure assessments and policy interventions in urban greening. Environ. Res. 2023, 220, 115155. [Google Scholar] [CrossRef]
- Timilsina, S.; Aryal, J.; Kirkpatrick, J.B. Mapping urban tree cover changes using object-based convolution neural network (OB-CNN). Remote Sens. 2020, 12, 3017. [Google Scholar] [CrossRef]
- Tian, L.; Qu, Y.; Qi, J. Estimation of forest LAI using discrete airborne LiDAR: A review. Remote Sens. 2021, 13, 2408. [Google Scholar] [CrossRef]
- Jin, J.; Yang, J. Effects of sampling approaches on quantifying urban forest structure. Landsc. Urban Plan. 2020, 195, 103722. [Google Scholar] [CrossRef]
- Monteiro, M.V.; Levanič, T.; Doick, K.J. Growth rates of common urban trees in five cities in Great Britain: A dendrochronological evaluation with an emphasis on the impact of climate. Urban For. Urban Green. 2017, 22, 11–23. [Google Scholar] [CrossRef]
- Sjöman, H.; Nielsen, A.B.; Oprea, A. Trees for urban environments in northern parts of Central Europe--a dendroecological study in north-east Romania and Republic of Moldavia. Urban Ecosyst. 2012, 15, 267–281. [Google Scholar] [CrossRef]
- Nowak, D.J. Atmospheric carbon dioxide reduction by Chicago’s urban forest. In Chicago’S Urban Forest Ecosystem: Results of the Chicago Urban Forest Climate Project; USDA: Washington, DC, USA, 1994; pp. 83–94. [Google Scholar]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The Global Ecosystem Dynamics Investigation: High-resolution laser ranging of the Earth’s forests and topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Wu, S.; Chen, B.; Song, Y.; An, J.; Lin, C.; Gong, P. Shade watch: Mapping citywide shade dynamics through ray tracing and LiDAR data in Hong Kong’s complex 3-D built environment. Sust. Cities Soc. 2025, 118, 106011. [Google Scholar] [CrossRef]
- Yuan, Y.; Guo, W.; Tang, S.; Zhang, J. Effects of patterns of urban green-blue landscape on carbon sequestration using XGBoost-SHAP model. J. Clean. Prod. 2024, 476, 143640. [Google Scholar] [CrossRef]
- LY/T 2253-2014; Guidelines for Measuring and Monitoring Afforestation Project Carbon Sinks. State Forestry Administration: Beijing, China, 2014.
- DB33/T 2416-2021; Technical Regulations for Carbon Sink Measurement and Monitoring of Urban Greening. Zhejiang Provincial Market Supervision Administration: Hangzhou, China, 2021.
- Urban Green Space Carbon Sink Measurement and Monitoring Technical Standard (Draft for Comments); Chinese Society of Landscape Architecture: Beijing, China, 2025.
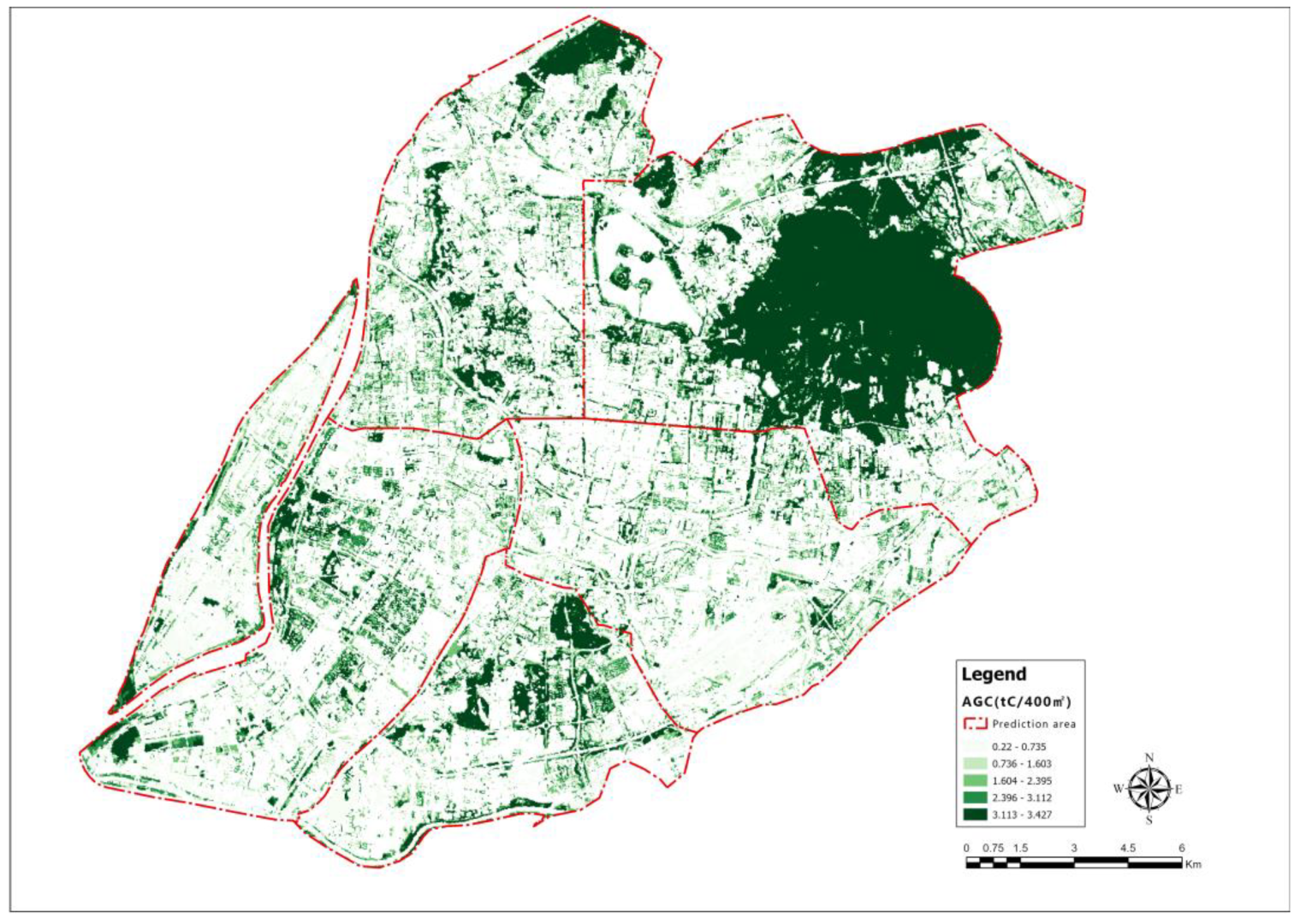
| Type of Green Space | (a) Satellite RGB Imagery | (b) Estimated Results |
|---|---|---|
| Parks |  | 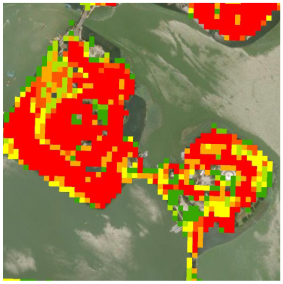 |
| Roads |  | 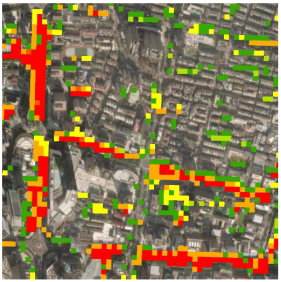 |
| Residential |  |  |
| Campus |  |  |
| Legend |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Cheng, Y.; Cao, Y. Modeling Urban-Vegetation Aboveground Carbon by Integrating Spectral–Textural Features with Tree Height and Canopy Cover Ratio Using Machine Learning. Forests 2025, 16, 1381. https://doi.org/10.3390/f16091381
Fang Y, Cheng Y, Cao Y. Modeling Urban-Vegetation Aboveground Carbon by Integrating Spectral–Textural Features with Tree Height and Canopy Cover Ratio Using Machine Learning. Forests. 2025; 16(9):1381. https://doi.org/10.3390/f16091381
Chicago/Turabian StyleFang, Yuhao, Yuning Cheng, and Yilun Cao. 2025. "Modeling Urban-Vegetation Aboveground Carbon by Integrating Spectral–Textural Features with Tree Height and Canopy Cover Ratio Using Machine Learning" Forests 16, no. 9: 1381. https://doi.org/10.3390/f16091381
APA StyleFang, Y., Cheng, Y., & Cao, Y. (2025). Modeling Urban-Vegetation Aboveground Carbon by Integrating Spectral–Textural Features with Tree Height and Canopy Cover Ratio Using Machine Learning. Forests, 16(9), 1381. https://doi.org/10.3390/f16091381






