Abstract
Carbon sinks are of great significance for mitigating the greenhouse effect and climate change. However, only a few carbon sink measurement methods are suitable for small-scale research, such as at the city-region scale. Methods that can accurately distinguish the high–low gradients of forest carbon sinks within small-scale areas have not yet been established. To fill this gap, we used a tree allometric growth model—the i-Tree Eco model—and applied it to Tai’an, which is a National Forest City in China. By using indicator conversion methods, we innovatively combined the China Forest Resources Inventory Geographic Information Database with i-Tree Eco. The results showed that i-Tree Eco successfully estimated the carbon sinks provided by urban–rural forests (in 2019)—the total carbon storage in Tai’an forest was 5,828,165.90 t; the average carbon storage per hectare was 37.19 tC·ha−1; the total carbon sequestration was 936,789.03 tC·yr−1; and the annual carbon sequestration was, on average, 5.97 tC·ha−1·yr−1. Our method improved the spatial resolution of carbon sequestration and storage compared to the commonly used InVEST model, from about 350 m × 350 m to 195 m × 195 m. Compared to the traditional IPCC method, the i-Tree Eco model provided greater accuracy and timeliness in small-scale carbon sequestration measurements, eliminating the need to wait for the next forest inventory to be published. Our method yielded results that covered the entire city region and better reflected the spatial heterogeneity of carbon sinks. We conclude that the innovative application of the i-Tree Eco model to urban–rural-scale carbon sink measurements provides stronger technical support for urban green space planning, as well as data guidance, in relation to local carbon mitigation strategies.
1. Introduction
Forest and grassland carbon sinks are the primary sources of regional carbon sinks; however, among the widely used methods, the precision of their statistical measurements remains relatively low. Carbon sinks refer to biological or artificial procedures, actions, and mechanisms that take away CO2 from the atmosphere [1]; they are essential components in achieving carbon neutrality and mitigating global climate change [2]. Due to their importance, the quantity and distribution of carbon sinks have become key research areas across various disciplines [1]. Among the two major types of carbon sinks, ecosystem carbon sinks are safer, more stable, and more efficient than artificial ones [3]. Terrestrial forest [4], grassland [5], wetland [4], and cultivated land [6] are the four major carbon sinks in ecosystems. Therefore, forest and grassland carbon sinks are important components that researchers must focus on when studying regional carbon sink distributions. For example, larger forests in many Finnish municipalities compensate for carbon emissions from cropland, mires, and waterbodies (which can be calculated using the LUONNIKAS calculation tool) [7]. It can be seen that the importance of forest carbon sinks is very prominent and there is a need to strengthen the body of research in relation to them.
On the other hand, small-scale, detailed carbon sink inventories are more conducive to implementing regional carbon strategies. To support urban planning, land use, and forest management policies, small-scale data on various carbon sinks are required [7,8]. The development of local carbon mitigation strategies requires detailed carbon sink data. Therefore, the need to address the methodological gap in small-scale carbon sink inventories has become apparent [9].
In current research, carbon sink measurements are primarily based on regional- or national-scale methods. Only a few models have been developed for small-scale carbon sink estimation, including sample plot inventory–sample marking tree analysis, tree allometric equations, CITYgreen, InVEST, CENTURY, IBIS, and LPJ-GUESS. The sample plot inventory method is suitable for fine-scale studies but is labor-intensive and error-prone [10,11]. CITYgreen and i-Tree Eco are the only empirical models that support plant or forest sub-compartment-level estimations, effectively capturing spatial heterogeneity [10,12]. However, the results of CITYgreen lead to some uncertainty and the model involves high costs [12,13,14,15].
Process-based models like InVEST lack sufficient spatial resolution and ignore natural tree growth [10], while LPJ-GUESS requires complex parameters and high labor inputs, limiting its application [16]. CENTURY and IBIS are generally not suited for fine-scale urban forest studies [17].
The i-Tree Eco model is a tree allometric growth model that is more comprehensive and accurate than other models [10,18], estimating carbon sinks using diverse forest characteristics and incorporating meteorological conditions. Unlike other commonly used methods, it avoids forest inventory comparisons, reducing labor and cost while improving accuracy.
Despite its advantages, i-Tree Eco’s reliance on local forest surveys restricts its broader use due to high data acquisition costs [19,20]. Airborne radar remote sensing has been introduced to address this; however, it still remains expensive and technically demanding [8,21,22]. Therefore, there is an urgent need to develop high-resolution, easily applicable, and low-cost carbon sink measurement methods that are suitable for small-scale studies.
To tackle these challenges, this study integrates China’s Forest Resources Inventory database into i-Tree Eco through indicator conversion, enabling citywide (a type of small-scale) carbon sink mapping in Tai’an (a National Forest City in China). The i-Tree Eco model was accessed at https://www.itreetools.org/i-tree-tools-download (accessed on 1 May 2023). Additionally, our improved estimation process is easily applicable and low-cost, leading to results with a high spatial resolution. This way, to a certain extent, the drawback of high data acquisition costs in the i-Tree Eco model has been overcome.
The i-Tree Eco model, which is relatively new in relation to the application of citywide carbon sink estimation and can effectively differentiate between high and low gradients of forest carbon sinks, aims to complement other commonly used carbon sink models in terms of improving accuracy, spatial resolution, and applicability. We applied this model in Tai’an City, with the help of China’s Forest Resources Inventory database, to assess its suitability for fine-scale forest carbon sink measurement at the citywide level. Our core hypothesis is as follows: the i-Tree Eco model is suitable for this application. In summary, this study’s innovation is reflected in three key aspects. First, theoretically, the proposed i-Tree Eco model addresses the gap in applying fine-scale, application-prone, and high-resolution forest carbon sink measurement methods in urban contexts. Second, in terms of model advantages, we have developed and validated the model’s accuracy. Compared to the commonly used models, this method offers better resolution in relation to carbon density and spatial heterogeneity. Lastly, from a technical perspective, the improved data import process enhances the method’s applicability for small-scale carbon sink studies, reducing research labor intensity.
2. Literature Review
2.1. Carbon Sink Estimation Methods
Seven methods are currently used for small-scale carbon sink estimation. We focused on carbon sink estimation methods that are applicable at the small scale in order to provide support for green space planning in cities, as well as for local carbon mitigation strategies. The current carbon sink estimation methods that may be suitable for small-scale studies are listed in Table 1. Among these, sample plot inventory–sample marking tree analysis is suitable for small-scale studies; however, the required forest inventory investigation consumes considerable manpower and material resources, which limits its usability [10,11].

Table 1.
Advantages and disadvantages of current carbon sink estimation models.
Notably, the i-Tree Eco and CITYgreen models stand out for their advantages. Among the various empirical models, only the i-Tree Eco and CITYgreen models can complete calculations at the plant or forest sub-compartment scale and are easy to use [10,12]. Carbon sink calculations at such small scales better demonstrate the spatial heterogeneity of carbon density. Therefore, they provide basic data for the spatial analysis of carbon sinks within cities [10,12]. These two methods have a significant advantage in terms of result information content [10,12,13,14,15].
However, the differences between static and dynamic models—such as in their attributes and empirical parameters—lead to uncertainty in the carbon sink results. Among the mechanism model classes, various static models differ with respect to principles, structures, and attributes, resulting in great uncertainties in the assessment of carbon sinks; the errors involved in the models eventually accumulate in the carbon sink calculation results [11]. In various dynamic models, complex biochemical processes involved in carbon sink formation have been simplified into several key driving factors. Key attributes rely on empirical settings that reduce the estimation accuracy [11]. The applicable scales of mechanism model classes are at least regional (except for the LPJ-GUESS model) and are generally not suitable for small-scale studies.
In practice, different models offer varying advantages. However, the plot inventory–sample tree analysis method leads to large errors in carbon sequestration estimation and is costly [11]; the InVEST method lacks sufficient spatial resolution [10]; the CITYgreen model presents uncertain results and is also costly [12,13,14,15]; the LPJ-GUESS model is difficult to widely apply due to parameter acquisition challenges and high labor costs [16]; and other methods are not suitable for small-scale studies [17]. Based on these factors, we chose the i-Tree Eco model for our study. It is ideal for small-scale (forest) carbon sink estimation and offers detailed estimates of forest carbon sinks, making efficient use of official forest inventory data.
2.2. New Applications of the i-Tree Eco Model for Carbon Sink Estimation
The i-Tree Eco model was developed in the early 21st century and has become widely referenced in urban carbon sink research. The i-Tree Eco [25] model (we used the i-Tree Eco v6.0.32 in this study) is a flexible software application that was developed by the Forest Service of the United States Department of Agriculture in 2006 [26]. It uses data collected from individual trees, complete forest inventories, and sample plots to quantify the forest structure, environmental effects, and ecosystem service values [27]. Information on tree species, tree morphological characteristics, air pollution, and meteorological data is required. In this study, the ecosystem service value included carbon storage and sequestration as two carbon sink indicators. The i-Tree series has grown to cover trees in diverse settings such as urban areas and rural regions [28] and has been validated by many case studies worldwide [29]. In urban research, scholars use i-Tree Eco to determine the models of urban green growth [30]; evaluate one particular ecosystem service, like carbon storage [29] or air quality improvement [31]; estimate the ecosystem services provided by urban parks [32]; or compare different urban green designs concerning ecosystem service provision [33]. The timeline of the development of i-Tree Eco for carbon sink estimation is as shown in Figure 1.
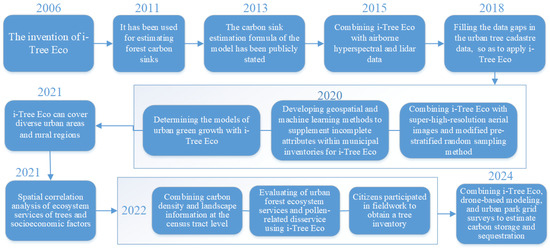
Figure 1.
Timeline of the development of i-Tree Eco for carbon sink estimation [8,20,21,22,26,28,30,34,35,36,37,38,39].
In recent years, various innovative applications and method optimizations have been established for i-Tree Eco in urban studies (Table 2).

Table 2.
Innovative applications and method optimizations of i-Tree Eco in urban studies.
Additionally, the i-Tree Eco model is highly suitable for precise forest carbon sink research. The i-Tree Eco model is based on tree species and tree morphological characteristics [25,27]. The model calculation program includes the allometric growth formulae of the trees [18]. Factors, such as crown characteristics and light competition, are also considered by the model algorithm to calculate the annual carbon sequestration and storage of each tree [18]. The calculation results have a high spatial resolution. Annual carbon sequestration can be directly estimated based on the forest resource inventory [26]. Carbon storage in interval years does not need to be compared to obtain annual carbon sequestration [18], which reduces the data requirements. The model avoids large errors in measuring the increment in the tree height and DBH by measuring trees in intervals of years [11]. Therefore, there is no need to wait for the next forest resource inventory to calculate forest carbon sequestration for the current year, which helps improve the timeliness of research.
Moreover, compared to the commonly used methods, the i-Tree Eco model is more comprehensive and efficient [10,18]. Forest carbon storage and sequestration are not averaged; instead, they depend on factors like forest type, tree species, forest age, and volume [18,27]. The heterogeneity of forest characteristics becomes more pronounced at smaller spatial scales. Unlike the commonly used models such as InVEST, i-Tree Eco estimates carbon sinks based on a variety of forest factors. Furthermore, i-Tree Eco emphasizes carbon sequestration resulting from natural tree growth, which is an aspect that other models, such as InVEST, do not take into account. In comparison with plot inventory–sample tree analysis and biomass conversion factor methods, i-Tree Eco does not require comparisons of forest resource inventories between survey years and does not rely on tables. This enables quicker carbon storage/sequestration calculations while saving both labor and resources. Additionally, i-Tree Eco accounts for meteorological conditions and canopy features, which significantly improves estimation accuracy.
Building on this, we sought to introduce new data sources to expand the i-Tree Eco model’s applicability and accessibility. Among the new applications of i-Tree Eco listed in the table above, many projects use local forest inventories as basic data. However, because of the huge cost of human resources in forest inventories, many researchers can only apply their local forest surveys to several communities or parks [19,20]. As a result, their applications are limited. Continuous carbon sink distribution patterns were not observed and the extensive research requirements for the spatial analysis of small-scale carbon sinks cannot be met. To solve this issue, remote sensing observation data from airborne radars have been introduced in some studies [8,21,22]. However, the interpretation of radar images may result in certain errors. Furthermore, the airborne remote sensing method consumes considerable human and material resources and requires high technical expertise, which limits its accessibility. Therefore, we introduced a new data source for i-Tree Eco to reduce the cost of the method and extend its application and accessibility. Based on the China Forest Resources Inventory database and several indicator conversions, we used i-Tree Eco to estimate the forest carbon sink distribution at a small scale (taking Tai’an in Shandong Province, China, as an example).
3. Methodology
3.1. Estimation Models
3.1.1. i-Tree Eco Model
i-Tree Eco is based on a database of species-specific allometric equations [35]. We used the i-Tree Eco v6.0.32 (USDA Forest Service, Washington, DC, USA) in this study. The carbon sink estimation equations are as follows (different formulas are used depending on the data and tree species):
where β1 and β2 are coefficients specific to species, DBH is measured 1.37 m above the ground, HEIGHT denotes the total tree height, and σ2 represents the variance of model errors, which is utilized to correct the transformation bias when predictions are back-transformed from the logarithmic scale to the original scale [41]. The estimated biomass of the whole tree (comprising both above-ground and below-ground biomass) is multiplied by 0.5 for conversion to carbon storage [42].
Biomass = exp(β1 + β2 × LN(DBH) + σ2/2)
Biomass = exp(β1 + β2 × LN(DBH2 × HEIGHT) + σ2/2)
Biomass = β1 × (DBHβ2)
Biomass = β1 × ((DBH2 × HEIGHT)β2)
Based on the Tai’an Forest Resources Inventory database from 2019, the data were converted and input into an attribute table. First, the data year was entered into the i-Tree Eco model software (2019). Second, the data type was entered into a complete inventory. Third, the location was entered, i.e., Jinan, Shandong Province (Jinan is the closest optional address to Tai’an); we chose to use 2019 meteorological data from the Mount Tai weather station, which is in Tai’an. Fourth, the tree species, tree DBH, crown size (including height to live top, height to crown, crown width, and percent crown missing), total tree height, and land use were input. With respect to the attribute “crown health”, we selected to input “dieback”. The above-mentioned input indicators include all attributes the i-Tree Eco software requires or strongly recommends.
Because the input attributes required by i-Tree Eco could not all be found in the Tai’an Forest Resources Inventory database, similar indicators included in the Tai’an Forest Resources Inventory database were converted so that they could be as close as possible to the input attributes required by i-Tree Eco. In previous studies, to supplement incomplete attributes within existing municipal inventories, Cimburova, Z. and Barton, D.N. developed geospatial and machine learning methods that follow attribute definitions in accordance with the i-Tree Eco Field Guide [22]. A similar input attribute transformation was used by Scholz, T. et al. [36] in German urban forest research. Therefore, we can also perform some indicator conversions, provided that the conversion processes are reasonable.
In addition, i-Tree Eco (complete inventory mode) can be used as a carbon sink calculation method for a single tree. However, each item in the Tai’an Forest Resources Inventory database represents a woodland patch in which each tree species is located, providing indicators, such as tree species, average tree height, average DBH, and the overall crown health condition of the woodland patch. Therefore, the “number of trees per hectare” index BCZS and the woodland patch area in the Tai’an Forest Resources Inventory database were used to convert the carbon sink of a single tree evaluated using i-Tree Eco into the total carbon sink of all trees in that woodland patch. The total carbon sink was derived from the average carbon sink per tree. The formula is as follows:
The total carbon sink of all trees in a woodland patch = carbon sink of a representative tree (the species of this tree is the dominant species in this woodland patch; its height is the average height of all trees in this woodland patch; its DBH is the average DBH of all trees in this woodland patch; and its crown health condition is consistent with the overall crown health condition in this woodland patch) × BZCS × area (in hectares)
BCZS is the number of trees per hectare within this woodland patch; this is a survey indicator included in the Tai’an Forest Resources Inventory database.
Our indicator conversion methods include the following (Figure 2 illustrates where the relevant indicators are located on the tree):
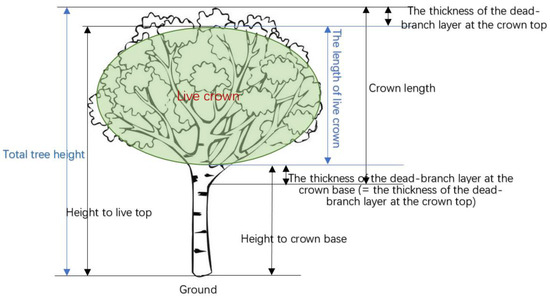
Figure 2.
Side view of a tree (with relevant indicators).
- 1.
- The ZHDJ indicator (“disaster level”) in the Tai’an Forest Resources Inventory database corresponds to the dieback indicator (required by i-Tree Eco). Their correspondence is shown in Table 3.
 Table 3. Correspondence between the “disaster level” ZHDJ indicator and the dieback indicator, as derived from [43]. NAFT refers to the number of affected forest trees. The dieback indicator is set to be equal to the average tree damage severity.
Table 3. Correspondence between the “disaster level” ZHDJ indicator and the dieback indicator, as derived from [43]. NAFT refers to the number of affected forest trees. The dieback indicator is set to be equal to the average tree damage severity. - 2.
- The formula for height to live top is as follows:Height to live top = Total tree height − Total tree height × CR × (Dieback/100)
CR: Crown ratio = (Crown length/Total tree height)
- 3.
- The formula for height to crown base is as follows:Height to crown base = Total tree height − Total tree height × CR × (1 − Dieback/100)
- 4.
- The formula for crown width is as follows:BCZS is the number of trees per hectare. BCZS and “canopy density” are survey indicators included in the Tai’an Forest Resources Inventory database.
- 5.
- The formula for percent crown missing is as follows:Percent crown missing = 39.6 × (1 + Dieback/100)
The coefficient “39.6” is from Ref. [44].
- 6.
- The “canopy density” indicator in the Tai’an Forest Resources Inventory database corresponds to the crown light exposure indicator. Their correspondence is shown in Table 4.
 Table 4. Correspondence between the “canopy density” indicator and the crown light exposure indicator, as derived from [45].
Table 4. Correspondence between the “canopy density” indicator and the crown light exposure indicator, as derived from [45].
- Regarding the correlation between canopy density and canopy lighting conditions, reference was made to previous research on forests in the areas of low mountains and hills of the Yangtze River Basin [45].
The derivation of the indicator conversion (Equations (A1)–(A6)) is shown in the Appendix A. The key variables input into i-Tree Eco for carbon sink estimation are listed in Table 5.

Table 5.
Key variables of the i-Tree Eco model.
The flowchart of this study is shown in Figure 3.
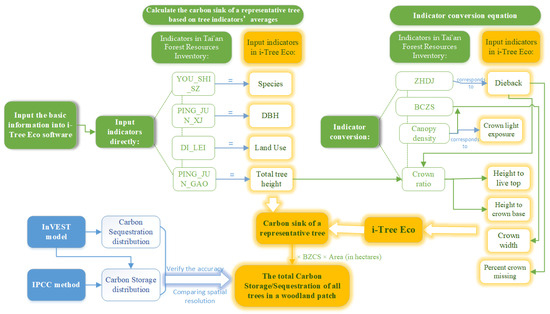
Figure 3.
Flowchart integrating the Tai’an Forest Resources Inventory data with i-Tree Eco in this study.
3.1.2. InVEST Model
This method serves as a comparison and supplement; it uses land use maps to estimate carbon sinks. We used InVEST 3.9.2 x64 (Stanford Woods Institute for the Environment, Palo Alto, CA, USA). The estimated results include carbon storage and carbon sequestration.
The “Carbon Storage and Sequestration” module in the InVEST model and the current Tai’an land use map were utilized as the current LULC (land use and land cover). The Tai’an land use map of the next phase was employed as the future LULC.
Carbon pool values are input parameters that are required by the InVEST model. The carbon pool values represent the carbon content of each hectare of various types of land, including the carbon in the above-ground part, the carbon in the below-ground part, soil carbon, and carbon in dead organic matter. The carbon pool values in this study were adopted from the average of the carbon pool values in Shandong Province and the neighboring provinces of Shandong (the data are from previous studies, as shown in Appendix B). Shandong Province is where our study area Tai’an is located. We input Table 6 into the InVEST model to derive the carbon storage and carbon sequestration distributions for Tai’an (Table 6; see Appendix B for the derivation process).

Table 6.
Input carbon pool values (tC·ha−1).
All land use types in our data sources corresponded to the six land use types in the InVEST model—cropland, woodland, grassland, water area, built-up land, and unused land. These categories were used to obtain the three-phase LULC data of Tai’an in 2009, 2017, and 2019. The LULC data were input into the InVEST 3.13.0-workbench software to estimate carbon sinks. The resolution of the LC data used is approximately 350 m × 350 m.
3.1.3. IPCC Forest Carbon Storage Calculation Method
Forest carbon storage was calculated according to the 2006 IPCC (Intergovernmental Panel on Climate Change) on Climate Change Guidelines for National Greenhouse Gas Inventories.
where
C: the total carbon in biomass;
A: area of the land;
V: timber volume;
BCEF: the biomass conversion coefficient that converts the timber volume to above-ground biomass;
R: the ratio of subsurface biomass to above-ground biomass;
CF: the carbon content of dry matter;
D: wood basic density;
BEF: biomass expansion factor;
i: Ecological zone i;
j: Climate domain j.
We primarily performed this calculated based on the “living tree stock per hectare” and “tree species” attributes in the Tai’an Forest Resources Inventory database. We set the “standing stock volume of living trees per hectare” to V.
Our study area belonged to the TeDC temperate continental forest.
- CF: temperate broadleaf forest—0.48; temperate coniferous forest—0.51 [46].
- BCEFs: The BCEFs values for hard broadleaf, pine, and other coniferous species were the average BCEFs recommended by the 2006 IPCC Guidelines for National Greenhouse Gas Inventories. The BCEFs value of soft broadleaf trees refers to the biomass expansion factor (BEF = 1.586) and basic wood density (D = 0.443) of soft broadleaf species in the temperate broadleaf forests of Heilongjiang Province, China [47]. Based on multiplying BEF and D, the BCEF of soft broadleaf species was 0.7026.
- R: R was set according to the value recommended by the 2006 IPCC Guidelines for National Greenhouse Gas Inventories and based on the tree species and size of the above-ground biomass.
3.2. Study Area and Data Acquisition
3.2.1. Study Area
Tai’an City is located in Shandong Province, China, covering an area of 7762 km2. Its location is shown in Figure 4. Tai’an had a population of 5,635,000 in 2019; it is rich in forest resources and is known as China’s “National Forest City”. By the end of 2020, Tai’an City’s forest area was 200,316 ha, the forest coverage was 25.81%, and the total standing stock volume of living trees was 10.81 million m3. Tai’an City had 1189.80 ha of new afforestation between 2021 and 2022 [48]. The forest resource inventory and land use data of Tai’an meet the needs of carbon sink research. Therefore, Tai’an was selected as the study area. The carbon sink function of the forest should be significant, the total carbon sink and carbon density in the municipality should be relatively high, and the spatial heterogeneity of carbon sinks should be evident. The capability of different models to demonstrate the spatial heterogeneity of carbon sinks was tested using this area as a case study.
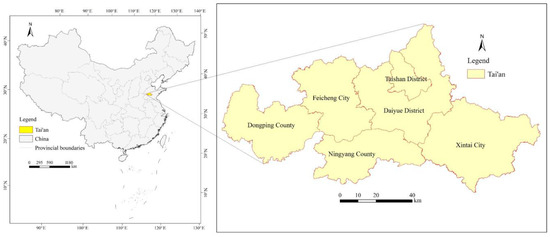
Figure 4.
Location of Tai’an.
3.2.2. Data Sources
- 1.
- Land use data
We used Tai’an’s Second National Land Survey data (2009), Tai’an’s Second National Land Survey—Change Survey data (2017), and Tai’an’s Third National Land Survey data (end of 2019) in this study. All the land use data are sourced from the Tai’an Municipal Bureau of Natural Resources and Planning.
- 2.
- Forest resources inventory data
Data were obtained from the Tai’an Forest Resources Inventory Geographic Information Database (2019). The database is based on the technical method of China’s forest resource inventory, which is a combination of forest subcompartment mapping and subcompartment surveys promulgated by the China National Forestry Administration and operated by the Tai’an Forestry Department. China Forest Resources Inventory data comply with unified national survey standards and cover the whole territory. Therefore, these high-quality data were suitable for our research. The mean tree height was 10.00 m and the average DBH was 11.46 cm. The data included 52 tree species, dominated by Populus tomentosa, Robinia pseudoacacia, and Platycladus orientalis.
The Tai’an Forest Resources Inventory database includes 42,682 woodland patches. After excluding invalid data that lacked tree height or DBH information, 41,031 items of valid data were obtained (accounting for 96.13% of all data), representing 41,031 woodland patches. These items represent the patches of inventory plots. Each sample plot was divided into several patches of different shapes according to the dominant tree species. We matched all 52 tree species to predefined species in the i-Tree database. The meteorological data we used were obtained from the 2019 Mount Tai Weather Station in the i-Tree Eco software.
3.3. Methods of Statistical Analysis
We used correlation analysis, linear regression models, and one-way ANOVA (F-test) for statistical analysis. The statistical analysis software used was IBM SPSS Statistics 23 (IBM, Armonk, NY, USA).
4. Results
4.1. Carbon Storage
First, we utilized the InVEST model to estimate carbon storage in Tai’an City based on a land use map. The carbon storage density in Tai’an in 2009 was 0.86 tC·ha−1, while the total carbon storage was 664,407.37 t. In 2017, the carbon storage density in Tai’an was 0.86 tC·ha−1 and the total carbon storage was 663,631.19 t. In 2019, the carbon storage density in Tai’an City was 0.95 tC·ha−1 and the total carbon storage was 735,039.46 t. The model estimation results covered the entire city. The minimum carbon storage density was always 0.21 tC·ha−1, while the maximum was always 1.54 tC·ha−1. The resolution effect of the obtained carbon storage map is shown in Figure 5d; the resolution is approximately 350 m × 350 m. Except for a few locations, the carbon storage density was uniform in the Mount Tai Nature Reserve (1.54 tC·ha−1).
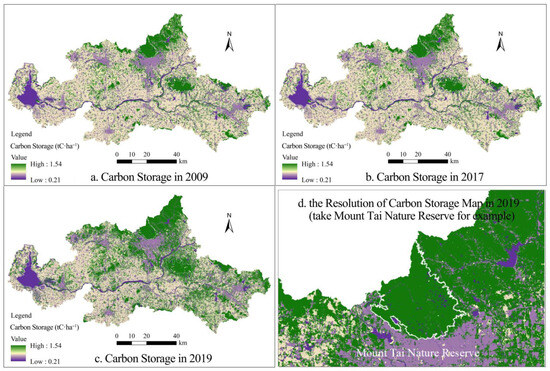
Figure 5.
InVEST: Tai’an carbon storage. Notes: (a–d) show the carbon storage distribution obtained using the InVEST model. (a–c) are based on Tai’an’s Second National Land Survey data (2009), Tai’an’s Second National Land Survey—Change Survey data (2017), and Tai’an’s Third National Land Survey data (end of 2019), respectively. The figures demonstrate the distribution and changes in carbon storage throughout Tai’an in 2009, 2017, and 2019. (d) shows a localized, enlarged, and detailed view of (c) in order to illustrate the distribution of carbon storage in and around Mount Tai Nature Reserve. (d) highlights the clarity of the carbon storage distribution maps obtained by combining land use data with the carbon sink estimation method of the InVEST model, allowing the resolution of the InVEST method for estimating carbon sinks to be visualized.
Second, we used the IPCC method to calculate the carbon storage in Tai’an City in 2019. We obtained a total of 6,897,473.91 t of carbon in Tai’an’s forest carbon storage; the average carbon storage density was 44.89 tC·ha−1; and the standard deviation was 31.60 tC·ha−1. The calculation results covered all forestlands in Tai’an. The resolution effect of the carbon storage map is shown in Figure 6; the resolution is approximately 195 m × 195 m. In the Mount Tai Nature Reserve, the carbon storage density can be roughly divided into four levels.
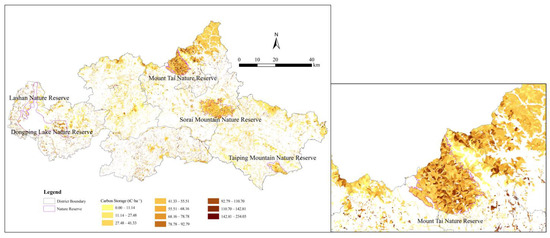
Figure 6.
IPCC method: forest carbon storage in Tai’an in 2019 (unit: tC·ha−1). Note: This Figure shows the distribution of carbon storage in Tai’an City in 2019 obtained using the IPCC method, based on the Tai’an Forest Resources Inventory Geographic Information Database (2019). It demonstrates the distribution of carbon storage within the city’s woodlands. The figure on the right is a localized, enlarged, and detailed view of the figure on the left, showing the distribution of carbon storage in and around Mount Tai Nature Reserve. The figure on the right highlights the clarity of the carbon storage map obtained by combining the forest resources inventory with the IPCC method of estimating carbon sinks, allowing the resolution of the IPCC method for estimating carbon sinks to be visualized.
Third, we employed the i-Tree Eco model to estimate the carbon storage of Tai’an City in 2019 based on the Tai’an Forest Resources Inventory database. The total carbon storage in Tai’an was determined to be 5,828,165.90 t; the average carbon storage per hectare was 37.19 tC·ha−1; and the standard deviation was 45.64 tC·ha−1. The resolution effect of the carbon storage map is shown in Figure 7; the resolution is approximately 195 m × 195 m. In the Mount Tai Nature Reserve, the carbon storage density can be roughly divided into five levels. The carbon density at the edge is lower than that in the core area. Patches with high carbon density are scattered in the core area of the reserve and are concentrated in the northwest–southeast direction. As seen in Figure 8, the district with the highest total carbon storage was Daiyue District (according to the results of both methods), while the district with the lowest total carbon storage was Taishan District (according to the IPCC method) or Ningyang County (according to the i-Tree Eco method). The i-Tree Eco model has a higher resolution with respect to measuring carbon storage than the InVEST model (the resolution is improved from 350 m × 350 m to 195 m × 195 m) and can visually display gradual changes in relation to forest carbon storage density. The InVEST model calculates forest carbon storage based on the average carbon storage density of forest land in Shandong Province. However, in the National Forest City Tai’an, Mount Tai and four other nature reserves have long-standing forest protection policies. As a result, the trees in these areas have remained unharvested for years, allowing them to sequester a large amount of carbon in their biomass. Consequently, the forest carbon storage density in Tai’an is higher than the provincial average in Shandong Province; the latter is represented using the InVEST model.
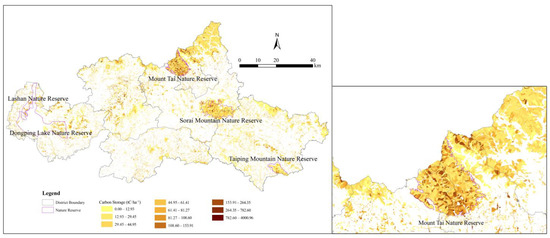
Figure 7.
i-Tree Eco: forest carbon storage in Tai’an in 2019 (unit: tC·ha−1). Note: This Figure shows the distribution of carbon storage in Tai’an City in 2019 obtained using the i-Tree Eco method. It is based on the Tai’an Forest Resources Inventory Geographic Information Database (2019) and demonstrates the distribution of carbon storage within the city’s woodlands. The figure on the right is a localized, enlarged, and detailed view of the figure on the left, showing details of the distribution of carbon storage in and around Mount Tai Nature Reserve. The figure on the right shows the clarity of the carbon storage map obtained by combining the forest resources inventory with the i-Tree Eco model for carbon sink estimation, which allows the resolution of the i-Tree Eco model to estimate carbon sinks to be visualized.
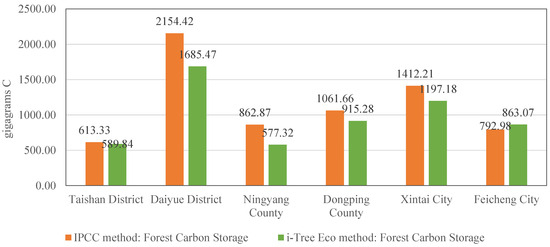
Figure 8.
Forest carbon storage in Tai‘an’s districts and counties in 2019 using the IPCC method and the i-Tree Eco method.
4.2. Carbon Sequestration
First, we used the InVEST model to calculate carbon sequestration in Tai’an City based on Tai’an land use maps for 2009, 2017, and 2019. The average carbon sequestration from 2009 to 2017 was −0.001 tC·ha−1 and the carbon sequestration totaled −776.18 t. This means that the total carbon storage decreased. Tai’an’s average carbon sequestration from 2017 to 2019 was 0.09 tC·ha−1 and the carbon sequestration totaled 71,408.27 t (substantial carbon sequestration may be caused by improvements in land survey technology). The model calculation results covered the entire city.
The resolution effect of the carbon sequestration map from 2017 to 2019 is shown in Figure 9c; the resolution is approximately 350 m × 350 m. Except for a few locations (red and green spots on the map), carbon sequestration was uniform (yellow in the map) in the Mount Tai Nature Reserve.
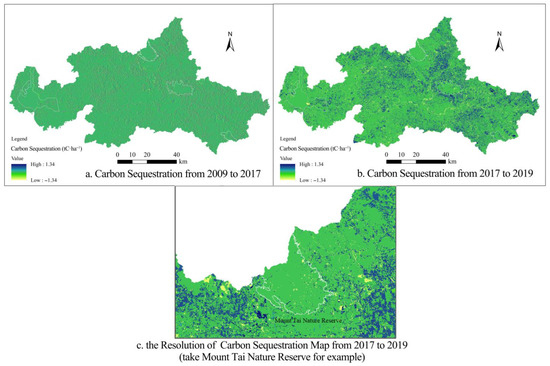
Figure 9.
InVEST: carbon sequestration in Tai’an. Note: (a–c)show the distribution of carbon sequestration obtained using the InVEST model. (a,b) are based on the land use change between Tai’an’s Second National Land Survey data (2009) and Tai’an’s Second National Land Survey—Change Survey data (2017), as well as between Tai’an’s Second National Land Survey—Change Survey data (2017) and Tai’an’s Third National Land Survey data (end of 2019). (a,b) show the distribution of carbon sequestration in Tai’an for the years 2009–2017 and 2017–2019, respectively, showing the distribution of carbon sequestration throughout the city during the two periods. This part of the carbon sequestration is caused by land use change. (c) shows a localized, enlarged, and detailed view of (b) to demonstrate the details of the distribution of carbon sequestration in and around Mount Tai Nature Reserve. (c) shows the clarity of the carbon sequestration maps obtained by combining land use change data with the carbon sink estimation method of the InVEST model, allowing the resolution of the InVEST method for estimating carbon sinks to be visualized.
Second, we applied the i-Tree Eco model to estimate annual forest carbon sequestration in 2019 based on the Tai’an Forest Resources Inventory database.
The estimated total carbon sequestration in Tai’an (2019) was 936,789.03 tC·yr−1; the annual carbon sequestration in Tai’an was, on average, 5.97 tC·ha−1·yr−1; and the standard deviation was 4.11 tC·ha−1·yr−1. The estimation results of the i-Tree Eco model covered all forested land. The forest carbon sequestrations in Tai ‘an’s different districts and counties are shown in Table 7. The district with the highest total carbon sequestration was Daiyue District, at 290,100.30 tC·yr−1. The district with the lowest total carbon sequestration was Taishan District, at 68,556.02 tC·yr−1. The resolution effect of the carbon sequestration map is shown in Figure 10; the resolution is approximately 195 m × 195 m. In the Mount Tai Nature Reserve, carbon sequestration per hectare can be roughly divided into six levels. Carbon sequestration at the edge of the reserve is lower than that in the core. Patches with a high carbon sequestration density were scattered throughout the core area and were particularly concentrated in the northwest–southeast direction. The i-Tree Eco carbon sequestration measurement had a higher resolution than the InVEST model. The i-Tree Eco model can visually display gradual changes in the forest carbon sequestration density and is a more refined carbon sink estimation model. The two approaches focus on different components of carbon sinks. The InVEST model estimates the carbon sequestration due to land use change, while the i-Tree Eco model calculates the carbon sequestered by tree growth. That is why the carbon sequestration values obtained by the two models are different. Because the two models calculate different components of carbon sinks, their calculation results can complement each other. The results of the two models can be cross-referenced and provide a multifaceted reference for the measurement of local carbon sinks.

Table 7.
Forest carbon sequestration in Tai ‘an’s districts and counties in 2019 using the i-Tree Eco method.
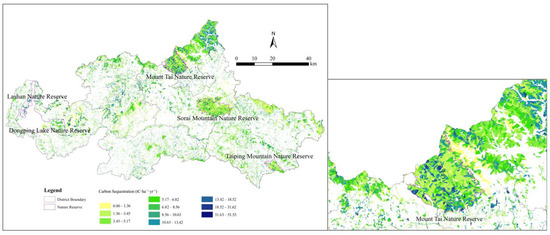
Figure 10.
i-Tree Eco: annual carbon sequestration of forests in Tai’an in 2019. Note: This Figure shows the distribution of carbon sequestration in Tai’an City in 2019 obtained using the i-Tree Eco method. It is based on the Tai’an Forest Resources Inventory Geographic Information Database (2019), demonstrating the distribution of carbon sequestration across the city’s forests. This part of carbon sequestration is caused by CO2 uptake by existing tree growth. The figure on the right is a localized, enlarged, and detailed view of the figure on the left, showing details of the distribution of carbon sequestration in and around Mount Tai Nature Reserve. The figure on the right highlights the clarity of the carbon sequestration map obtained by combining forest resources inventory data with the i-Tree Eco model. The resolution of the i-Tree Eco model for estimating carbon sinks can be visualized.
4.3. Spatial Resolution Advantages of the i-Tree Eco Model
We compared the spatial resolution of the carbon sink maps obtained using i-Tree Eco and the commonly used InVEST model. A sampling band was constructed to observe the differences between the two maps. As shown in Figure 11, the sampling band ran from the northeast to the southwest of Tai’an City, passing through the Daiyue District, Taishan District, Feicheng City, and Ningyang County, especially through the Mount Tai Nature Reserve. The sampling band traverses the area where the results of our new methodology are distributed. The sampling band contained one sampling point every 50 m in order to comprehensively test the resolution of the Tai’an carbon sink map.
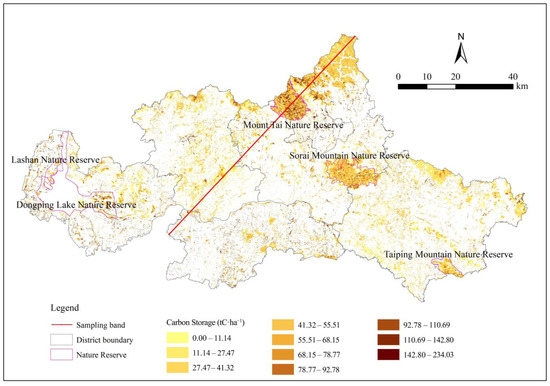
Figure 11.
Schematic diagram of the sampling band location.
i-Tree Eco demonstrated a gradient difference in forest carbon storage. Based on the carbon storage distribution maps calculated using the InVEST, IPCC, and i-Tree Eco methods, the carbon storage density of the sampling band was extracted. InVEST calculation of carbon storage density sampling band values is shown in Figure 12. IPCC method calculation of carbon storage density sampling band values is shown in Figure 13. i-Tree Eco calculation of carbon storage density sampling band values is shown in Figure 14. The comparison showed that the carbon storage density obtained with the InVEST model can only be divided into four main levels; this is because the InVEST model is based on the average carbon storage values of six land use types and can only present six values at most. The carbon storage density values acquired using the IPCC method and i-Tree Eco revealed differences between peak-to-valley values and better demonstrated the gradient change in the carbon storage density.
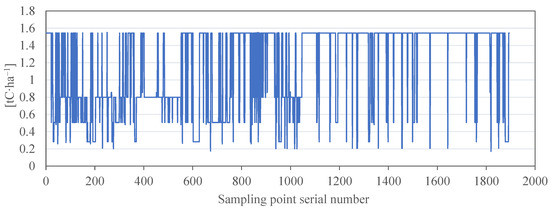
Figure 12.
InVEST calculation of carbon storage density sampling band values of 2019. Note: The figure shows the series of values taken from the intersection of the sampling band with the distribution map of carbon storage density in Tai’an City in 2019, which were obtained using the InVEST method.
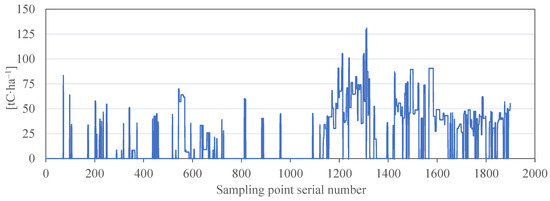
Figure 13.
IPCC method calculation of carbon storage density sampling band values of 2019. Note: The figure shows the series of values taken from the intersection of the sampling band with the distribution map of carbon storage density in Tai’an City in 2019, which were obtained using the IPCC method.
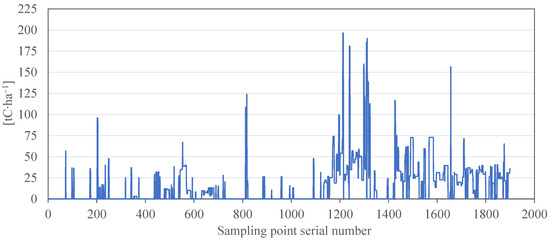
Figure 14.
i-Tree Eco calculation of carbon storage density sampling band values for 2019. Note: The figure shows the series of values taken from the intersection of the sampling band with the distribution map of carbon storage density in Tai’an City in 2019, which were obtained using the i-Tree Eco method.
Based on the comparison of i-Tree Eco and InVEST, the i-Tree Eco model demonstrated a higher temporal and spatial resolution for estimating carbon sequestration and was more appropriate for small-scale carbon sink research. Values of the sampling band calculated using InVEST for the carbon sequestration density are shown in Figure 15. Values of the sampling band calculated using i-Tree Eco for the carbon sequestration density are shown in Figure 16. Based on the carbon sequestration per hectare calculated using InVEST and i-Tree Eco, the carbon sequestration density obtained using InVEST fluctuated within ±2 tC·ha−1, and a gradient change could not be observed. The distribution of the peak-to-valley values of carbon sequestration obtained using i-Tree Eco was pronounced and better reflected the gradient changes in carbon sequestration density across different locations.
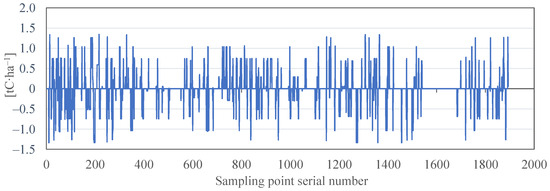
Figure 15.
Values of the sampling band calculated using InVEST for the carbon sequestration density from 2009 to 2017. Note: The figure shows the series of values taken from the intersection of the sampling band with the distribution map of carbon sequestration density in Tai’an City between 2009 and 2017, which were obtained using the InVEST method.
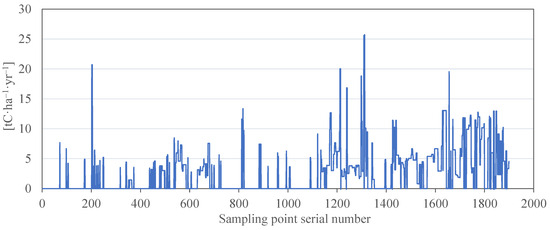
Figure 16.
Values of the sampling band calculated using i-Tree Eco for the carbon sequestration density in 2019. Note: The figure shows the series of values taken from the intersection of the sampling band with the distribution map of carbon sequestration density in Tai’an City in 2019, which were obtained using the i-Tree Eco method.
4.4. Verification of the Accuracy of i-Tree Eco Model Results
As we innovatively combined China Forest Resources Inventory data with the i-Tree Eco model to calculate forest carbon sinks on a citywide scale, the results may have been over- or underestimated. Therefore, we applied the classic IPCC method to the carbon storage results to verify the accuracy of i-Tree Eco. Here, we used SPSS software to conduct multiple statistical analyses.
4.4.1. Correlation Analysis of Carbon Storage Obtained Using the Two Methods
We first conducted a correlation analysis between the carbon storage calculated using the i-Tree Eco model and that calculated using the IPCC method. The results were utilized to preliminarily verify whether the carbon storage of the two methods was similar and served as the basis for further statistical analysis. Because the carbon storage estimated using the IPCC method and i-Tree Eco did not follow a normal distribution, the Pearson correlation coefficient was not appropriate; therefore, we used the Spearman correlation coefficient for the analysis. The analysis results showed that the Spearman correlation coefficient reached 0.968 and the correlation was significant at the 0.01 level (two-tailed). Hence, the correlation between the carbon storage based on the two methods was determined to be significant. This serves as the first step in validating the similarity between the i-Tree Eco model’s carbon storage and that calculated using the IPCC method.
4.4.2. Attempt to Use Carbon Storage Based on the IPCC Method to Correct i-Tree Eco
We constructed a linear regression model to approximately convert the carbon storage obtained using i-Tree Eco into the IPCC-based carbon storage in order to verify the newly applied carbon sink model using the classic method. We used SPSS software to establish a unary linear regression model based on the carbon storage data obtained using the two methods, as well as performing a validity test. It should be noted that we first excluded data from either method where the carbon storage value was 0 (a result of missing data for relevant indicators). In addition, 20 extreme values from the i-Tree Eco carbon storage dataset were removed. After that, we built the regression model to prevent the effect of outliers on the model’s accuracy. We used an over-origin regression (no-intercept model), as carbon storage from the i-Tree Eco model should also be 0 when the IPCC-estimated carbon storage is 0. The validity of the model was tested using one-way ANOVA (F-test). Table 8 presents the regression model coefficients.

Table 8.
Regression model coefficients a,b.
We obtained the following regression equation:
where y is the carbon storage obtained using the IPCC method; x is the carbon storage obtained using the i-Tree Eco method.
y = 1.002x
As shown in Table 9, according to the validity test, the correlation coefficient of the regression model was 0.905, the coefficient of determination (R2) reached 0.820, and the adjusted R2 was also 0.820. All three coefficients are relatively high, indicating the good fit of the regression model. In the one-way ANOVA (F-test), at the 0.05 confidence level, the p-value was <0.05, indicating that carbon storage estimated using i-Tree Eco has a statistically significant impact on carbon storage based on the IPCC method. Moreover, the test for the regression coefficient (B) of the independent variable is shown in Table 8, with a p-value < 0.05 at the 0.05 confidence level. This indicates that the regression coefficient (B) of the independent variable was also statistically significant. We also generated a standardized residual histogram and a P–P plot to verify that the residual roughly followed a normal distribution, thereby satisfying the assumptions for establishing a linear regression model. Our regression model passed statistical validation, indicating that our forest carbon storage estimation method, based on the China Forest Resources Inventory database and the i-Tree Eco model, is effective. Additionally, since B = 1.002, which is very close to 1, if the carbon storage obtained using the i-Tree Eco method is converted to the carbon storage obtained using the IPCC method using this linear regression equation (Equation (12)), the pre- and post-conversion values would be nearly identical. Therefore, there is essentially no need for conversion. This further suggests that the carbon storage estimated using the i-Tree Eco method is approximately equivalent to that estimated using the IPCC method (i.e., the conventional approach).

Table 9.
Model summary c,d.
5. Discussion
First, compared with other studies, our estimated carbon sequestration rate in the Tai’an Forest was within a reasonable range. By using the i-Tree Eco model, we determined the total forest carbon sequestration in Tai’an City in 2019 and the average forest carbon sequestration per hectare to be 936,789.03 tC·yr−1 and 5.97 tC·ha−1·yr−1, respectively. The carbon sequestration rate of forest ecosystems in Guizhou Province in 2019 was 3.922 tC·ha−1·yr−1 [49], while the carbon sequestration rate of forest stands in the Xiaoxing’an Mountains ranged from 0.4 to 2.8 tC·ha–1·yr−1 [50]. According to 22 previous forest carbon sink studies, the carbon sequestration rate of newly planted forests ranges from 0.04 to 7.52 tC·ha−1·yr−1 [51]. Hou, L. et al. (2009) and Zhao, Y. (2023) studied the annual carbon sequestration of Pinus tabuliformis in a forest area of the Qinling Mountains [52,53]. Their measurements of organic carbon sequestration in the arbor layer were 7.81 tC·ha−1·yr−1 and 10.45 tC·ha−1·yr−1, respectively [52,53]. Zhao, Y. (2023) also determined that the annual carbon sequestration of the arbor layer of the Quercus aliena var. acutiserrata forest in this area was 8.57 tC·ha−1·yr−1 [53]. Ding, J. et al. (2017) calculated the annual carbon sequestration rate of each tree species in common economic forests (apple, peach, apricot, cherry, pear, jujube, and walnut) in Beijing, which ranged from 6.73 to 13.80 tC·ha−1·yr−1 [54]. Sun, M. et al. (2020) estimated the carbon sequestration rate in the arbor layer of Robinia pseudoacacia and Quercus wutaishanica forests in the loess hilly area of Shaanxi Province to be between 4.83 and 5.85 tC·ha−1·yr−1, respectively [55]. The forest carbon sequestration rate in Tai’an (our research) was higher than that in Guizhou Province, the Xiaoxing’an Mountains (in Heilongjiang Province), and the loess hilly area (in Shaanxi Province) and lower than that in the Qinling Mountains and the common economic forests of Beijing. It also falls within the empirical range summarized by Liu, B.J. et al. [51]. Our estimation of Tai’an forest’s carbon sequestration is within a reasonable range and is not significantly different from results reported in other provinces in China. This indicates that i-Tree Eco is reasonable and effective for estimating forest carbon sequestration.
Second, not all indicators required by i-Tree Eco exactly matched the tree attributes in the Tai’an Forest Resources Inventory database. Therefore, the relevant attributes in the database were converted into the indicators required for i-Tree Eco. These indicator conversions cannot guarantee absolute accuracy; thus, they affect the estimation accuracy of carbon storage and carbon sequestration. Furthermore, there is a possibility of over- or underestimation to a certain extent. Possible errors introduced by indicator conversions include the following:
- In Table 3, “dieback” may not be completely consistent with “average tree damage severity”. This discrepancy may affect the accuracy of dieback parameter settings.
- No exact figure exists for the crown ratio of coniferous and broad-leaved forests in Tai’an; therefore, we can only refer to corresponding data in North China and Northeast China. In Equations (6) and (7), the crown ratio influences the setting of both “Height to Live Top” and “Height to Crown Base”.
- In Appendix A.2, regarding “Height to Live Top”, we assumed that the ratio of the thickness of the dead-branch layer at the crown top to the crown length ≈ the ratio of the number of dead branches in the crown to the number of all branches (i.e., dieback). However, this assumption may not be accurate in practice. Although “centripetal dieback” is common, there are also trees where dieback mainly occurs in the inner crown area, and the dead-branch layer at the crown top or bottom may not be prominent. This introduces some error, which is also present in the derivation of “Height to Crown Base” (Equation (7)).
- In Appendix A.4, to calculate “Crown Width”, it is necessary to make four assumptions, However, in practice, these ideal assumptions may not hold. For Assumption ➀ (please refer to Appendix A.4), it is unlikely that crown overlap is entirely absent. Some canopy areas are shaded twice by the crowns of two neighboring trees. Such overlapping areas should be included in the crown coverage area of both trees, rather than assigned to only one, leading to an underestimation of total crown coverage. Since Assumption ➁ (please refer to Appendix A.4) cannot be fully realized, the projected crown coverage of each tree is unlikely to be completely closed. Therefore, the estimated crown size and crown width are also likely underestimated.
- Regarding the constant “39.6” in Equation (9), due to the lack of data on the “percent crown missing” indicator in China, we relied on the reference value obtained from Massachusetts, USA—39.6. This substitution may introduce a certain degree of error.
- The correspondence table of crown light exposure converted from canopy density (Table 4) cannot be completely accurate due to the influences of multiple factors. In Table A2, the correspondence between canopy density and relative light intensity (%) is also based on limited references. Although we considered two primary forest types—coniferous (represented by Pinus massoniana) and broadleaf (represented by Cinnamomum camphora)—to reduce error, the gradient mapping between canopy density and relative light intensity may still lack precision. However, Table 4 and Table A2 both reflect the general pattern, showing positive correlations between canopy density, relative light intensity, and crown light exposure.
Future research is needed to address the above-mentioned limitations and improve the new “Forest Resources Inventory Database–i-Tree Eco Carbon Sink Estimation Method”.
6. Application Outlook
By using the i-Tree Eco model with a high spatial resolution to calculate carbon storage and carbon sequestration across Tai’an City, we are able to provide more detailed data on the distribution of carbon sinks and reveal variations in carbon storage and sequestration density within woodlands. Such high-precision carbon sink data can offer robust support for urban planning and policymaking—especially for initiatives related to green space and ecological planning—ensuring that policies and plans are more closely aligned with actual local conditions, thereby improving their effectiveness in implementation.
For instance, in urban green space planning, high-resolution carbon sink data can support the optimization of green space layout and landscape structure, the selection of tree species for planting, the development of management strategies, and the calculation of the ecological benefits of forests, as well as their conversion into economic value.
In ecological and environmental protection planning, high-precision carbon sink data can be used to accurately identify ecologically degraded areas, guide the scientific selection of restoration species, and serve as a foundational tool for building a carbon sink unit network. It can help in unlocking the carbon sink potential in a hierarchical manner, dynamically adjusting forestry management strategies and translating the ecological value of carbon sinks into economic benefits. Additionally, such data can be used for the breakdown and evaluation of progress toward carbon peaking and carbon neutrality goals, the assessment of ecological equity, and as quantitative evidence for compliance with international carbon reduction agreements, such as the Paris Agreement.
For the delineation of the ecological protection red line—a core element of China’s National Land Spatial Planning—high-resolution carbon sink data can assist in accurately identifying high-value carbon sink areas, assessing carbon stock baselines, predicting carbon sink potential, and optimizing the pattern of ecological space. It can further support the construction of carbon sink corridors, the control of development intensity gradients, the prioritization of degraded ecosystem restoration, the dynamic monitoring of carbon sink losses, and the quantitative assessment of ecological restoration effectiveness. Such data also provide scientific support for ecological compensation mechanisms and enhance coordination between carbon peaking, neutrality targets, and related policies.
7. Conclusions
We introduced a new carbon sink estimation method that combined the i-Tree Eco model and the China Forest Resources Inventory. Our approach enables the calculation of both forest carbon sequestration and storage in Tai’an. Thus, it can address the limitations of the commonly used InVEST model, which overlooks annual forest carbon sequestration. It also enhances the spatial resolution of small-scale carbon sink estimations (improving it from 350 m × 350 m to 195 m × 195 m).
Statistical tests showed that the carbon storage calculation results were valid. Similarly, the forest carbon sequestration data produced using this method provided a foundation for the spatial analysis of urban carbon sinks. Compared with the commonly used carbon sink estimation methods (e.g., the IPCC method and InVEST model), our method has the advantage of capturing spatial gradient variations in both carbon storage and sequestration. The i-Tree Eco model estimates forest carbon sequestration with relatively higher temporal and spatial resolutions, which is especially valuable for small-scale (e.g., city-level) carbon sink research. Therefore, this carbon sink estimation method can be used to complement and improve the commonly used approaches. It helps fill the gap in citywide applications of small-scale forest carbon sink estimation methods that require high spatial resolution and precision.
Author Contributions
Conceptualization, Y.-X.L. and W.-X.Z.; methodology, Y.-X.L. and W.-X.Z.; software, Y.-X.L. and P.H.; validation, Y.-X.L.; formal analysis, Y.-X.L.; investigation, Y.-X.L.; resources, W.-X.Z.; data curation, Y.-X.L.; writing—original draft preparation, Y.-X.L.; writing—review and editing, W.M., W.-X.Z. and Y.-X.L.; visualization, Y.-X.L.; supervision, W.-X.Z.; project administration, W.-X.Z.; funding acquisition, W.-X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
National Key R&D Program of China (2023YFC3205600): Green Watershed Evaluation Index System and Method.
Data Availability Statement
The datasets presented in this article are not readily available because according to the regulations of the Tai’an Forestry Bureau and the Bureau of Natural Resources, the raw datasets used in this article are confidential. Requests to access the datasets should be directed to Tai ‘an Forestry Bureau and the Bureau of Natural Resources.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A. Indicator Conversion Method for the i-Tree Eco Model
Appendix A.1
Dieback refers to the “estimated percentage of the crown composed of dead branches”. We correlated dieback with the “disaster level index” ZHDJ in the Tai’an Forest Resources Inventory database. The “disaster level index” ZHDJ was categorized into four levels—0, 1, 2, and 3. These four disaster levels corresponded, in turn, to the severity of tree damage and to the percentage of dieback.
First, according to the local Chinese standard from Sichuan Province, “Technical Procedures for the Evaluation and Protection of Ancient Cypresses”, a dieback of ≤5% is considered a characteristic of a healthy tree [56]. Therefore, we set the base dieback value at 5%. Based on this, and with reference to the “Forest Disaster Rating Standard” in the Operating Rules of Forest Resources Inventory of Shandong Province, we used the median percentage of affected trees in the “Rating Standard” as the average level of disaster severity; in turn, we set the average disaster severity of the trees to equal dieback. We slightly adjusted the median upward, where appropriate, based on the descriptions of tree damage in the “Rating Standard” and the assumption that healthy trees have a base dieback value of 5%.
Appendix A.2
Height to live top = Total tree height − Total tree height × CR × (Dieback/100)
CR: Crown ratio = (Crown length/Total tree height)
The equation of crown ratio is from Refs. [57,58].
Figure 2 illustrates where the relevant indicators are located on the tree. The “height to live top” represents the vertical distance from the ground to the topmost branches and leaves of the tree’s live crown; therefore, it is equal to the height of the live crown top. We can determine the “height to live top” by subtracting the thickness of the dead-branch layer at the crown top from the “total tree height”. The thickness of the dead-branch layer at the crown top is considered equal to the thickness of the layer of dieback branches. Here, we assumed that the ratio of the thickness of the dead-branch layer at the crown top to the total crown length ≈ the ratio of the number of dead branches to the total number of branches within the crown (i.e., dieback). This assumption is based on the fact that dieback—specifically centripetal dieback—is a common phenomenon in a tree’s life cycle. A thin layer of dead branches at the top of the crown is particularly common in trees affected by pests, diseases, drought, or aging [59]. Based on this assumption, the thickness of the dead-branch layer at the crown top can be calculated as follows: Crown length × (Dieback/100). And Crown length = Total tree height × Crown ratio (CR).

Table A1.
Correspondence between forest type and CR.
Table A1.
Correspondence between forest type and CR.
| Forest Type | CR | |
|---|---|---|
| Coniferous Trees | 0.5 [60] | |
| Broad-leaved trees | Natural forest | 0.5 [61] |
| Planted forest | 0.6 [61] | |
Appendix A.3
Height to crown base = Total tree height − Total tree height × CR × (1 − Dieback/100)
“Height to crown base” refers to the “height from the ground to the base of the live crown”. It can be calculated by subtracting the crown length from the total tree height and adding the thickness of the dead-branch layer at the base of the crown. Here, we assume that the thickness of the dead-branch layer at the crown base = the thickness of the dead-branch layer at the crown top. This assumption is based on the fact that the bottom of the crown may also be subject to dieback due to prolonged shading, and this may be exacerbated by pests, diseases, drought, or waterlogging. Therefore, we set the following: the thickness of the dead-branch layer at the crown base, as a proportion of the crown length, = the thickness of the dead-branch layer at the crown top, as a proportion of the crown length ≈ the number of dead branches in the crown as a proportion of the number of all branches (i.e., dieback). According to the formula for “Height to Live Top”, the thickness of the dead-branch layer at the crown top = the thickness of the dead-branch layer at the crown base = Crown length × (Dieback/100). Summarizing the above formulas, we conclude that Height to crown base = Total tree height − Total tree height × CR × (1 − Dieback/100).
Dieback is considered in both the “Height to live top” and “Height to crown base” equations to avoid underestimating the impact of diseases, pests, drought, or waterlogging on tree crowns, as well as to account for the potential overestimation of crown ratio (CR in Table A1). However, due to limited reference data for CR in China’s forests, currently we can only use the crown ratio preset in Table A1.
Appendix A.4
We derived crown width from the “canopy density” indicator in the Tai’an Forest Resource Inventory database, as canopy density is the indicator most closely related to crown width among those included in the Tai’an Forest Resource Inventory database. Canopy density—also referred to as canopy cover—is the ratio of the projected area of the forest canopy to the area of the forest floor [62,63]. To derive crown width from canopy density, we sampled a woodland plot and analyzed it using a projection (overhead) view (Figure A1). We distributed the total canopy projection area of the plot equally among all trees in the plot, estimating each tree’s crown width by assuming that each tree’s crown coverage equals its crown size. This method is based on the following ideal assumptions: ➀ No crown overlap exists between the upper canopies of trees. ➁ The vertical projection of each tree’s crown coverage is completely closed. In other words, within the crown coverage [64], the ground is entirely shaded by the crown, with no sunlight penetration. Sunlight penetration occurs only between tree crowns, not within them. ➂ The crown projection of each tree is circular. ➃ Crown diameter (i.e., crown width) was averaged for each tree.
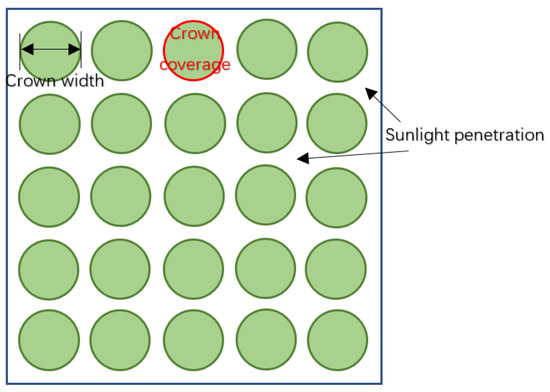
Figure A1.
Schematic overhead projection of a woodland plot.
As shown in Figure A1, according to the definition of canopy density,
total canopy projection of the plot = plot area × canopy density.
At the same time, since crown overlap is assumed to be nonexistent, the total canopy projection area of the plot = the sum of the crown coverages of all the trees within it. Therefore, the following holds true:
If the plot area =1 hectare, the
Number of trees = average number of trees per hectare “BCZS” (BCZS is a survey indicator included in the Tai’an Forest Resources Inventory database).
If both equations are combined, Equation (A3) can be obtained.
If the plot size is larger or smaller than 1 hectare, the number of trees will increase or decrease proportionally, in accordance with BCZS. In Equation (A3), plot size is divided by the number of trees. If both the plot size and the number of trees change in the same proportion, the ratio remains constant. Therefore, Equation (A3) is unaffected. Therefore, we can set the plot size = 1 hectare.
Appendix A.5
Percent crown missing = 39.6 × (1 + Dieback/100)
Percent crown missing refers to the “percentage of the crown volume that is not occupied by branches and leaves”.
The value 39.6 in Equation (A6) originates from the average “percent crown missing” of unpruned trees reported in [44]. Here, we assumed that the average “percent crown missing” of 39.6 for unpruned trees was the standard reference for healthy trees. Since this is the only study, both in China and internationally, that has published empirical data on percent crown missing, we currently rely on this Massachusetts-based data as the standard value.
We used the standard value of 39.6 as a benchmark for healthy trees. Dieback was then used to represent the health status of the tree crowns. Because dead branches lose their leaves, this reduces the crown volume occupied by foliage. Therefore, we assumed that the higher the dieback, the greater the “percent crown missing”. The two values should be positively correlated, as both describe proportions within the crown and represent similar indicators. Based on this assumption, we set the standard value of percent crown missing at 39.6, and calculated percent crown missing as increasing proportionally with dieback (by multiplying the two values). Therefore, Equation (A6) was obtained.
Appendix A.6
Crown light exposure refers to the “number of sides of the tree receiving sunlight from above,” with a maximum value of 5.
In [45], the gradient relationship between canopy density and relative light intensity (%) of a Pinus massoniana forest in low mountains and hills in the central and upper reaches of the Yangtze River was established (Table A2). On this basis, we also referred to the classification of canopy density and canopy light conditions in other related studies [65]. Finally, we used relative light intensity as a mediating variable and assigned crown light exposure values based on canopy density, as shown in Table A2 and Table 4. “Relative light intensity” refers to the ratio of light intensity in a forest area to the light intensity in a reference area (usually the top of the canopy or an open space outside the forest).

Table A2.
Correspondence between canopy density and relative light intensity (%). Data for this table were obtained from [45].
Table A2.
Correspondence between canopy density and relative light intensity (%). Data for this table were obtained from [45].
| Canopy Density [45] | Relative Light Intensity | ||||||
|---|---|---|---|---|---|---|---|
| Sampled in April (%) [45] | Sampled in May (%) [45] | Sampled in July (%) [45] | Sampled in August (%) [45] | Sampled in October (%) [45] | April, May, July, August, and October Averages (%) | Average Relative Light Intensity in April, May, July, August, and October ≈ Fraction | |
| 0.9 | 20 | 22 | 21 | 23 | 19, 19 | 21.25 | 1/5 |
| 0.8 | 33 | 34 | 38 | 38 | 15, 15 | 31.25 | 1/5 |
| 0.7 | 40 | 40 | 52 | 53 | 20, 35 | 43.13 | 2/5 |
| 0.6 | 57 | 47 | 61 | 62 | 27, 35 | 50.25 | 2/5 |
| 0.5 | 60 | 59 | 87 | 87 | 49, 42 | 69.63 | 3/5 |
Note: the bold text indicates emphasis.
The research area lies in the middle and upper reaches of the Yangtze River and has a mid-subtropical humid monsoon climate [45]. March marks the beginning of leaf growth, April is when full leaf expansion occurs [66], and late October is when leaf fall begins. Subsequently, with the arrival of winter, only evergreen trees retain their foliage, while deciduous trees suspend photosynthesis since their leaves fall. Because forest carbon sequestration focuses on spring and summer, when photosynthesis is most active, the average relative light intensity from April to October was used. We first calculated the average relative light intensity from April to October and then converted that value to the closest fraction with a denominator of 5 (as long as the average was at least no less than that fraction). We then used the numerator of that fraction as the crown light exposure. We set it this way because relative light intensity and crown light exposure are analogous indicators that represent the amount of sunlight received by the crown. The definition of “relative light intensity” can actually be interpreted as the proportion of the five sides of the crown that receive sunlight. The maximum relative light intensity of 100%, which occurs in open areas, corresponds to full sunlight on all five sides of the crown and thus a crown light exposure value of 5. Therefore, we converted 100% relative light intensity to 5/5 (equivalent to 5 of the 5 total sides of the crown receive sunlight); this corresponds to the maximum value of 5 for crown light exposure. By analogy, we converted 20% relative light intensity to 1/5 (1 out of a total of 5 sides of the canopy receives sunlight), which corresponded to a crown light exposure of 1. We converted 40% relative light intensity to 2/5, which then corresponded to a crown light exposure of 2. We converted 60% relative light intensity to 3/5, which then corresponded to a crown light exposure of 3. Finally, we converted 80% relative light intensity to 4/5, which then corresponded to a crown light exposure of 4.
Regarding the base value of canopy density, we assumed a relative light intensity of 100% when canopy density is 0 and crown light exposure is 5. Based on the canopy density classifications in Table A2, we used relative light intensity as a mediating variable to convert canopy density classes to crown light exposure values, as shown in Table 4.
Appendix B. Carbon Pool Parameters for the InVEST Model
We referred to a study on carbon sinks in Beijing by He, C. et al. (2016) [67]; a study on carbon sinks in the Yellow River Basin by Xu, C. et al. (2023) [68]; a study on carbon sinks in the Beijing–Tianjin–Hebei region by He, Y. et al. (2022) [69]; a study on carbon sinks in the Su-Xi-Chang Region by Fu, Q. et al. (2019) [70]; a study on carbon sinks in the Yellow River Basin by Wang, J. et al. (2022) [71]; a study on carbon sinks in the Beijing–Tianjin–Hebei region by Wang, C. et al. (2019) [72]; a study on carbon sinks in Shandong by Piao, S.L. et al. (2004) [73]; a study on carbon sinks in the Nanjing Metropolitan Area by Tao, Y. et al. (2023) [74]; and a study on carbon sinks in Rizhao, Shandong Province, by Cong, W.C. et al. (2018) [75]. We calculated the average carbon pool parameters from these sources for use as input parameters in the InVEST model.
When selecting these nine references, our primary consideration was the geographic proximity of the study areas to Tai’an, ensuring that the carbon pool parameters would be relevant and applicable. In addition, we selected an equal number of references from provinces north and south of Shandong to minimize bias. Thus, when calculating the average carbon pool parameters, we reduced the potential errors caused by geographic differences outside of Shandong Province. Before finalizing the nine references mentioned above, we screened several other studies whose carbon pool parameters were excluded because they were either unreasonably high or low.
To calculate the average carbon pool parameters from the nine selected studies, we first removed the highest and lowest values, before calculating the arithmetic mean of the remaining data. This approach was used to reduce the error in the parameter setting. This is equivalent to assigning carbon pool parameters to Tai’an according to the overall conditions of the carbon sinks in the Shandong Province.
References
- Li, Z. Calculation of Terrestrial Carbon Sink Capacity in Dongying City, Shandong Province. In Proceedings of the 2nd International Conference on Energy and Environmental Protection (ICEEP 2013), Guilin, China, 20–21 April 2013. [Google Scholar]
- Wang, Z.R.; Xiao, J.Y. Study on the Statistics Measurement of Carbon Sink. J. Xi’an Univ. Financ. Econ. 2013, 26, 48–51. [Google Scholar]
- Pacala, S.W.; Hurtt, G.C.; Baker, D.; Peylin, P.; Houghton, R.A.; Birdsey, R.A.; Heath, L.; Sundquist, E.T.; Stallard, R.F.; Ciais, P.; et al. Consistent land- and atmosphere-based US carbon sink estimates. Science 2001, 292, 2316–2320. [Google Scholar] [CrossRef] [PubMed]
- Fang, J.Y.; Guo, Z.D.; Piao, S.L.; Chen, A.P. Estimation of carbon sink of terrestrial vegetation in China from 1981 to 2000. Sci. China Ser. D Earth Sci. 2007, 37, 804–812. [Google Scholar]
- Liu, X.H.; Yan, Y.J.; Liu, W.; Huang, Z.B. System Construction and the Function Improvement of Ecological Carbon Sink in Coal Mining Areas Under the Carbon Neutral Strategy. Environ. Sci. 2022, 43, 2237–2240+2242–2250. [Google Scholar]
- Han, B.; Wang, X.K.; Lu, F.; Duan, X.N.; Ouyang, Z.Y. Soil carbon sequestration and its potential by cropland ecosystems in China. Acta Ecol. Sin. 2008, 28, 612–619. [Google Scholar]
- Vanhala, P.; Bergström, I.; Haaspuro, T.; Kortelainen, P.; Holmberg, M.; Forsius, M. Boreal forests can have a remarkable role in reducing greenhouse gas emissions locally: Land use-related and anthropogenic greenhouse gas emissions and sinks at the municipal level. Sci. Total Environ. 2016, 557, 51–57. [Google Scholar] [CrossRef]
- Lin, J.; Ma, Q.; Ju, Y.; Zhang, H.S.; Wang, Q.; Huang, B. Relationships between urbanization, tree morphology, and carbon density: An integration of remote sensing, allometric models, and field survey. Urban For. Urban Green. 2022, 76, 127725. [Google Scholar] [CrossRef]
- Mohareb, E.A. Quantifying the Transition to Low-Carbon Cities. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2012. [Google Scholar]
- Zhang, G.L.; Xing, L.Q.; Zhang, L.; Zhong, Q.C.; Yi, Y. Summary on the Monitoring Methods of Carbon Sequestration in Urban Green Space. Landsc. Archit. Acad. J. 2022, 39, 4–9. [Google Scholar]
- Liu, K.; Zhang, H.; Kong, L.H.; Qiao, Y.J.; Hu, M.T. An overview of terrestrial ecosystem carbon sink assessment methods towards achieving carbon neutrality in China. Acta Ecol. Sin. 2023, 43, 4294–4307. [Google Scholar] [CrossRef]
- Zhang, L.P. A Study on Ecological Benefits of Green Spaces in Downtown Shanghai Based on CITY Green Model. Master’s Thesis, Nanjing Forestry University, Nanjing, China, 1 June 2011. [Google Scholar]
- Yang, H.J.; Shao, Q.Q.; Chen, Z.Q.; Zhang, S. Summary of Estimation Methods of Carbon Storage in Forests. Geo-Inf. Sci. 2007, 9, 5–12. [Google Scholar]
- Tan, Y.F.; Qie, G.P.; Wang, M.Z.; Wang, G.X.; Peng, Y.G.; Luo, C.Q.; Sun, H.; Lin, H. Comparison of Landsat 8 images based city forest carbon modeling for Shenzhen built-up area. J. Cent. South Univ. For. Technol. 2014, 34, 140–144. [Google Scholar]
- Du, Q.; Duan, W.J.; Luo, S.F. Application of CITYgreen model on carbon storage calculation of plantations. J. Cent. South Univ. For. Technol. 2016, 36, 103–107+112. [Google Scholar]
- Zhang, B. Based on the LPJ-GUESS Model, the Carbon Cycle Process in the Permafrost Area Around the Arctic Is Simulated. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 1 April 2022. [Google Scholar]
- Xie, X.Y.; Li, A.N.; Jin, H.A. The simulation models of the forest carbon cycle on a large scale: A review. Acta Ecol. Sin. 2018, 38, 41–54. [Google Scholar] [CrossRef]
- Nowak, D.J. Understanding i-Tree: Summary of programs and methods. In General Technical Reports NRS-200; Department of Agriculture, Forest Service, Northern Research Station: Madison, WI, USA, 2020; p. 100. [Google Scholar]
- Pace, R.; Biber, P.; Pretzsch, H.; Grote, R. Modeling Ecosystem Services for Park Trees: Sensitivity of i-Tree Eco Simulations to Light Exposure and Tree Species Classification. Forests 2018, 9, 89. [Google Scholar] [CrossRef]
- Prigioniero, A.; Paura, B.; Zuzolo, D.; Tartaglia, M.; Postiglione, A.; Scarano, P.; Bellenger, S.; Capuano, A.; Serpe, E.; Sciarrillo, R.; et al. Holistic tool for ecosystem services and disservices assessment in the urban forests of the Real Bosco di Capodimonte, Naples. Sci. Rep. 2022, 12, 16413. [Google Scholar] [CrossRef]
- Alonzo, M.G. Urban Forest Ecosystem Analysis Using Fused Airborne Hyperspectral and Lidar Data. Ph.D. Thesis, University of California, Santa Barbara, CA, USA, 1 September 2015. [Google Scholar]
- Cimburova, Z.; Barton, D.N. The potential of geospatial analysis and Bayesian networks to enable i-Tree Eco assessment of existing tree inventories. Urban For. Urban Green. 2020, 55, 126801. [Google Scholar] [CrossRef]
- Feng, X.H.; Cheng, R.M.; Xiao, W.F.; Wang, R.L.; Wang, X.R.; Liu, Z.B. Productivity and Carbon Dynamic of the Masson Pine Stands in Jigongshan Region Based on LPJ-GUESS Model. Sci. Silvae Sin. 2013, 49, 7–15. [Google Scholar]
- Liu, R.G.; Li, N.; Su, H.X.; Sang, W.G. Simulation and Analysis on Future Carbon Balance of Three Deciduous Forests in Beijing Mountain Area, Warm Temperate Zone of China. Chin. J. Plant Ecol. 2009, 33, 516–534. [Google Scholar]
- i-Tree Eco. Available online: https://www.itreetools.org/tools/i-tree-eco (accessed on 1 May 2023).
- Rossi, L.; Menconi, M.E.; Grohmann, D.; Brunori, A.; Nowak, D.J. Urban Planning Insights from Tree Inventories and Their Regulating Ecosystem Services Assessment. Sustainability 2022, 14, 1684. [Google Scholar] [CrossRef]
- i-Tree Eco v6 Overview. Available online: https://www.itreetools.org/tools/i-tree-eco#i-Tree%20Eco%20V6%20Overview (accessed on 15 May 2023).
- Nowak, D.J. Understanding i-Tree; U.S. Department of Agriculture, Forest Service, Northern Research Station: Madison, WI, USA, 2021.
- Fox, W.; Dwivedi, P.; Lowe, R.C.; Welch, S.; Fuller, M. Estimating Carbon Stock of Live Trees Located on the Main Campus of the University of Georgia. J. For. 2020, 118, 457–465. [Google Scholar] [CrossRef]
- Berland, A. Urban tree growth models for two nearby cities show notable differences. Urban Ecosyst. 2020, 23, 1253–1261. [Google Scholar] [CrossRef]
- Riondato, E.; Pilla, F.; Basu, A.S.; Basu, B. Investigating the effect of trees on urban quality in Dublin by combining air monitoring with i-Tree Eco model. Sustain. Cities Soc. 2020, 61, 102356. [Google Scholar] [CrossRef]
- Yarnvudhi, A.; Leksungnoen, N.; Tor-Ngern, P.; Premashthira, A.; Thinkampheang, S.; Hermhuk, S. Evaluation of Regulating and Provisioning Services Provided by a Park Designed to Be Resilient to Climate Change in Bangkok, Thailand. Sustainability 2021, 13, 13624. [Google Scholar] [CrossRef]
- Zanzi, A.; Andreotti, F.; Vaglia, V.; Alali, S.; Orlando, F.; Bocchi, S. Forecasting Agroforestry Ecosystem Services Provision in Urban Regeneration Projects: Experiences and Perspectives from Milan. Sustainability 2021, 13, 2434. [Google Scholar] [CrossRef]
- Martin, N.A. A 100% Tree Inventory Using i-Tree Eco Protocol: A Case Study at Auburn University, Alabama. Master’s Thesis, Auburn University, Auburn, AL, USA, 9 May 2011. [Google Scholar]
- Nowak, D.J.; Greenfield, E.J.; Hoehn, R.E.; Lapoint, E. Carbon storage and sequestration by trees in urban and community areas of the United States. Environ. Pollut. 2013, 178, 229–236. [Google Scholar] [CrossRef]
- Scholz, T.; Hof, A.; Schmitt, T. Cooling Effects and Regulating Ecosystem Services Provided by Urban Trees-Novel Analysis Approaches Using Urban Tree Cadastre Data. Sustainability 2018, 10, 712. [Google Scholar] [CrossRef]
- Song, P.H.; Kim, G.; Mayer, A.; He, R.Z.; Tian, G.H. Assessing the Ecosystem Services of Various Types of Urban Green Spaces Based on i-Tree Eco. Sustainability 2020, 12, 1630. [Google Scholar] [CrossRef]
- Moody, R.; Geron, N.; Healy, M.; Rogan, J.; Martin, D. Modeling the spatial distribution of the current and future ecosystem services of urban tree planting in Chicopee and Fall River, Massachusetts. Urban For. Urban Green. 2021, 66, 127403. [Google Scholar] [CrossRef]
- Kim, J.; Kang, Y.; Kim, D.; Son, S.; Kim, E.J. Carbon Storage and Sequestration Analysis by Urban Park Grid Using i-Tree Eco and Drone-Based Modeling. Forests 2024, 15, 683. [Google Scholar] [CrossRef]
- Koricho, H.H.; Seboka, A.D.; Fufa, F.; Gebreyesus, T.; Song, S.X. Study on the ecosystem services of urban forests: Implications for climate change mitigation in the case of Adama City of Oromiya Regional Sate, Ethiopia. Urban Ecosyst. 2022, 25, 575–584. [Google Scholar] [CrossRef]
- Nowak, D.J. Estimating leaf area and leaf biomass of open-grown deciduous urban trees. For. Sci. 1996, 42, 504–507. [Google Scholar] [CrossRef]
- Nowak, D.J.; Crane, D.E. Carbon storage and sequestration by urban trees in the USA. Environ. Pollut. 2002, 116, 381–389. [Google Scholar] [CrossRef]
- Shandong Territorial and Spatial Planning Institute, China. Shandong Province 2021 Forest and Grass Ecological Comprehensive (Map Spot) Monitoring Operation Rules; Shandong Territorial and Spatial Planning Institute, China: Jinan, China, 2021; pp. 44–45. [Google Scholar]
- Suttle, R.; Kane, B.; Bloniarz, D. Comparing the Structure, Function, Value, and Risk of Managed and Unmanaged Trees along Rights-of-Way and Streets in Massachusetts. Forests 2022, 13, 1602. [Google Scholar] [CrossRef]
- Zhang, J. Effects of Various Canopy Densities on the Understory Vegetation Development and Decomposition of Pinus massoniana Foliar Litter in the Pinus Massoniana Plantations. Ph.D. Thesis, Sichuan Agricultural University, Ya’an, China, 1 May 2018. [Google Scholar]
- Aalde, H.; Gonzalez, P.; Gytarsky, M.; Krug, T.; Kurz, W.A.; Ogle, S.; Raison, J.; Schoene, D.; Ravindranath, N.H.; Elhassan, N.G.; et al. Chapter 4 Forest land. Volume 4 Agriculture, forestry and other land uses. In 2006 IPCC Guidelines for National Greenhouse Gas Inventories; Institute for Global Environmental Strategies (IGES), Japan: Hayama, Japan, 2003; p. 46. [Google Scholar]
- Li, G.C.; Wang, W.F. Discussion on key technologies of carbon sequestration afforestation project in Heilongjiang Province. Prot. For. Sci. Technol. 2017, 1, 107–108. [Google Scholar] [CrossRef]
- Tai’an Municipal Bureau of Statistics; National Bureau of Statistics Tai’an investigation team. Tai’an City People’s Government 2020 Annual National Economic and Social Development Statistical Communique; Tai’an City Government Office: Tai’an, China, 2021; pp. 4–5.
- Liu, S.J. The annual carbon sequestration in Guizhou forest ecosystem is 30.23 million tons. In Guizhou Daily; Guizhou Daily Press: Guiyang, China, 2021. [Google Scholar]
- Hu, H.Q.; Luo, B.Z.; Wei, S.J.; Wei, S.W.; Sun, L.; Luo, S.S.; Ma, H.B. Biomass carbon density and carbon sequestration capacity in seven typical forest types of the Xiaoxing’an Mountains, China. Chin. J. Plant Ecol. 2015, 39, 140–158. [Google Scholar]
- Liu, B.J.; Lu, F.; Wang, X.K.; Liu, W.W. Greenhouse gas emissions, carbon leakage and net carbon sequestration from afforestation and forest management: A review. Chin. J. Appl. Ecol. 2017, 28, 673–688. [Google Scholar] [CrossRef]
- Hou, L. Carbon Balance in Natural Secondary Pinus Tabulaeformis Forest at Huoditang Forest Zone in the Qinling Mountains. Ph.D. Thesis, Northwest A&F University, Shaanxi, China, 1 April 2009. [Google Scholar]
- Zhao, Y. Carbon Balance of Pinus tabulaeformis Forests and Quercus aliena var. acuteserrata Forests at Huoditang Forest Region in the Qinling Mountains. Master’s Thesis, Northwest A&F University, Shaanxi, China, 23 May 2023. [Google Scholar]
- Ding, J.; Li, S.N.; Lu, S.W.; Shi, Y.Y.; Zhao, Y.G.; Yang, X.B.; Chen, B. Water Utilization and Carbon Sequestration and Oxygen Release Functions of Common Economic Forests in Beijing. Jiangsu Agric. Sci. 2017, 45, 130–133. [Google Scholar]
- Sun, M.M.; Song, B.L.; Shi, W.Y.; Yamanaka, N.; Li, G.Q.; Du, S. Characteristics of Carbon Sink in Black Locust Plantation and Oak Natural Secondary Forest in Loess Hilly Region. Res. Soil Water Conserv. 2020, 27, 55–61. [Google Scholar]
- Li, H.C.; Wang, W.J.; Ma, W.B.; Tang, T.Y.; Hu, J.J.; Liu, G.; Zhang, F.H.; Qiu, Q.C.; Li, Y.Q.; Fei, Y.X.; et al. Technical Procedures for the Evaluation and Protection of Ancient Cypresses; Sichuan Provincial Administration for Market Regulation: Chengdu, China, 2024; p. 3. [Google Scholar]
- Ou, J.D.; Wu, Z.Z.; Kang, Y.W. Path Analysis between Canopy Characteristics and Growth, Form Quality of Cunninghamia konishii. J. Northeast. For. Univ. 2018, 46, 8–11+40. [Google Scholar]
- Monleon, V.J.; Azuma, D.; Gedney, D. Equations for predicting uncompacted crown ratio based on compacted crown ratio and tree attributes. West. J. Appl. For. 2004, 19, 260–267. [Google Scholar] [CrossRef]
- Li, Y.Y.; Huang, X.; Liu, X.Q. Garden Plants and the Construction of Ecological Human Settlement Environment; Jilin Publishing Group Co., Ltd.: Changchun, China, 2022; p. 26. [Google Scholar]
- Guo, X.Y.; Sun, Y.J.; Ouyang, X.Z. Modeling Crown Ratio in Even-Aged Stands of Larix olgensis. In Proceedings of the 16th Annual Meeting of the China Association for Science and Technology—11 Academic Symposium on Technological Innovation in Forest Cultivation and Development of Characteristic Resource Industry, Kunming, Yunnan, 24 May 2014. [Google Scholar]
- Zheng, C.H. Building of Growth Models for Quercus Variabilis Blume in North China. Ph.D. Thesis, Beijing Forestry University, Beijing, China, 1 April 2015. [Google Scholar]
- Bai, Y.Q.; Hao, W.K.; Jiang, Y.Y.; Lang, K.J. Forest Measuremens; Northeast Forestry University Press: Harbin, China, 1987; p. 102. [Google Scholar]
- Meng, X.Y. Forest Measuremens; China Forestry Publishing House: Beijing, China, 1996; p. 120. [Google Scholar]
- Zhan, Z.N. Crown Coverage. In Encyclopedia of China Agriculture; China Agricultural Encyclopedia Editorial Department, Ed.; China Agriculture Press: Beijing, China, 1989; p. 614. [Google Scholar]
- Chen, Q.H. Study of Cinnamomum Camphora Communities in Changsha City Parks Based on Realistic Ecological Niches. Master’s Thesis, Central South University of Forestry & Technology, Changsha, China, 1 June 2022. [Google Scholar]
- Hu, S.P.; Deng, Z.Q.; Lei, X.H. Analysis of climatic conditions of oil tea growth in Jinping County. Mod. Agric. Sci. Technol. 2011, 11, 308+311. [Google Scholar]
- He, C.Y.; Zhang, D.; Huang, Q.X.; Zhao, Y.Y. Assessing the potential impacts of urban expansion on regional carbon storage by linking the LUSD-urban and InVEST models. Environ. Model. Softw. 2016, 75, 44–58. [Google Scholar] [CrossRef]
- Xu, C.L.; Zhang, Q.B.; Yu, Q.; Wang, J.P.; Wang, F.; Qiu, S.; Ai, M.S.; Zhao, J.K. Effects of land use/cover change on carbon storage between 2000 and 2040 in the Yellow River Basin, China. Ecol. Indic. 2023, 151, 110345. [Google Scholar] [CrossRef]
- He, Y.T.; Xia, C.Y.; Shao, Z.; Zhao, J. The Spatiotemporal Evolution and Prediction of Carbon Storage: A Case Study of Urban Agglomeration in China’s Beijing-Tianjin-Hebei Region. Land 2022, 11, 858. [Google Scholar] [CrossRef]
- Fu, Q.; Xu, L.L.; Zheng, H.Y.; Chen, J.H. Spatiotemporal Dynamics of Carbon Storage in Response to Urbanization: A Case Study in the Su-Xi-Chang Region, China. Processes 2019, 7, 836. [Google Scholar] [CrossRef]
- Wang, J.F.; Li, L.F.; Li, Q.; Wang, S.; Liu, X.L.; Li, Y. The Spatiotemporal Evolution and Prediction of Carbon Storage in the Yellow River Basin Based on the Major Function-Oriented Zone Planning. Sustainability 2022, 14, 7963. [Google Scholar] [CrossRef]
- Wang, C.; Zhan, J.Y.; Chu, X.; Liu, W.; Zhang, F. Variation in ecosystem services with rapid urbanization: A study of carbon sequestration in the Beijing-Tianjin-Hebei region, China. Phys. Chem. Earth 2019, 110, 195–202. [Google Scholar] [CrossRef]
- Piao, S.L.; Fang, J.Y.; He, J.S.; Xiao, Y. Spatial Distribution of Grassland Biomass in China. Acta Phytoecol. Sin. 2004, 28, 491–498. [Google Scholar]
- Tao, Y.; Tian, L.; Wang, C.; Dai, W. Dynamic simulation of land use and land cover and its effect on carbon storage in the Nanjing metropolitan circle under different development scenarios. Front. Ecol. Evol. 2023, 11, 1102015. [Google Scholar] [CrossRef]
- Cong, W.C.; Sun, X.Y. A study on Carbon Sequestration Capacity Based on GIS and InVEST Model in Rizhao City. Bull. Soil Water Conserv. 2018, 38, 200–205. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).