A Simple Model to Predict the Temporal Nitrogen Saturation Point of a Jack Pine (Pinus banksiana L.) Forest
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.2. High-Exposure Site
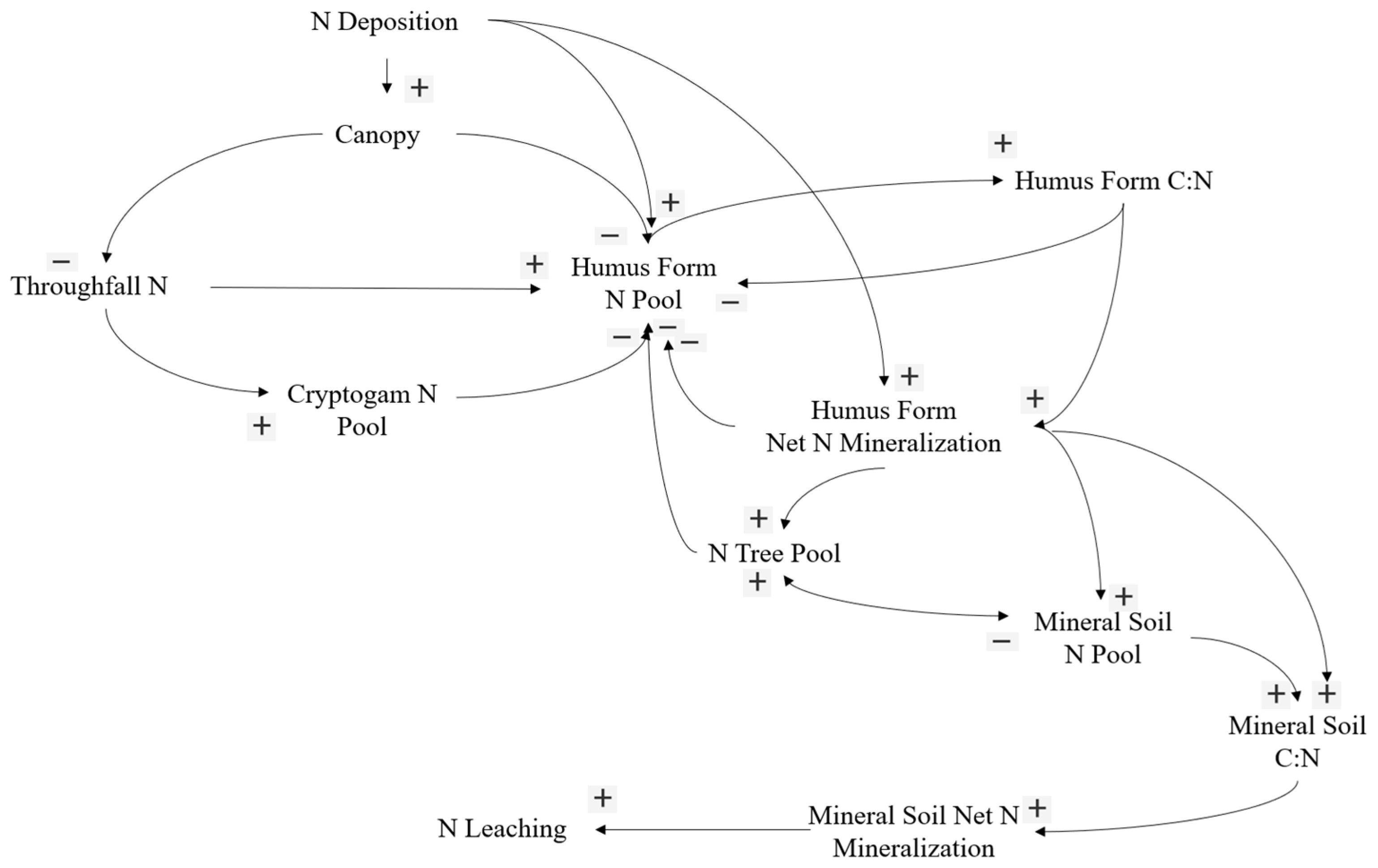
2.3. Simple Model
2.4. Model Calculations
2.5. Statistical Analysis
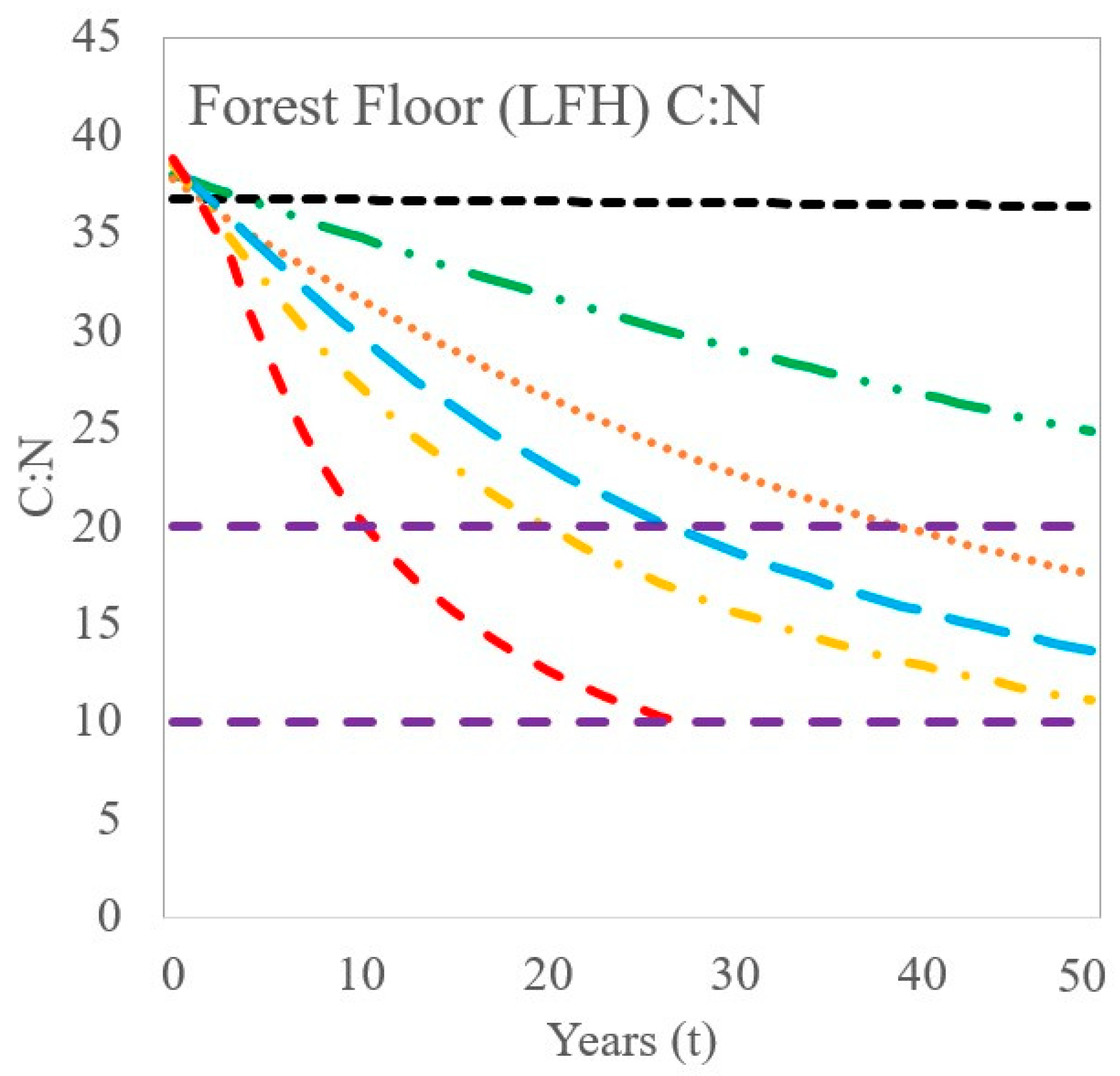
3. Results
3.1. Modeling Change in the Nitrogen Pool of Cryptogams
3.2. Comparing the Experimental Site with the In Situ High-Nitrogen-Exposure Site
4. Discussion
4.1. Modeled Response to Elevated Nitrogen Deposition
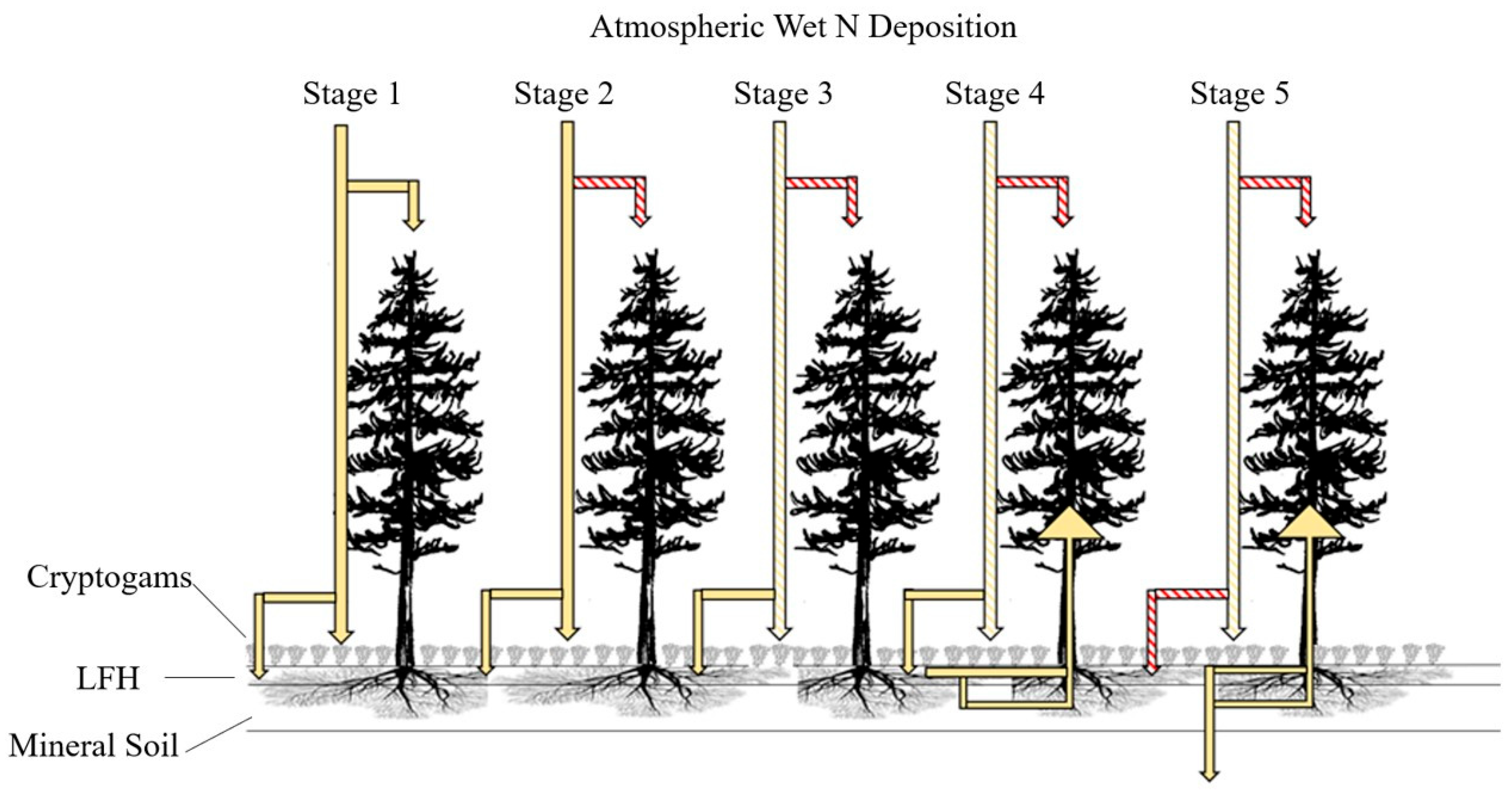
4.2. Conceptual Model of Nitrogen in Jack Pine Forests
4.3. High-Exposure vs. Experimental Site
4.4. Critical Loads of N for Jack Pine Forests
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aber, J.; McDowell, W.; Nadelhoffer, K.; Magill, A.; Bernston, G.; Kamakea, M.; McNulty, S.; Currie, W.; Rustad, L.; Fernandez, I. Nitrogen saturation in temperate forest ecosystems: Hypotheses revisited. BioScience 1998, 48, 921–934. [Google Scholar] [CrossRef]
- Soons, M.B.; Hefting, M.M.; Dorland, E.; Lamers, L.P.M.; Versteeg, C.; Bobbink, R. Nitrogen effects on plant species richness in herbaceous communities are more widespread and stronger than those of phosphorus. Biol. Conserv. 2017, 212, 390–397. [Google Scholar] [CrossRef]
- Chandler, J.W.; Dale, J.E. Nitrogen deficiency and fertilization effects on needle growth and photosynthesis in Sitka spruce (Picea sitchensis). Tree Physiol. 1995, 15, 813–817. [Google Scholar] [CrossRef]
- Boussadia, O.; Steppe, K.; Zgallai, H.; Hadj, B.E.; Braham, M.; Lemeur, R.; Van Labeke, M.C. Effects of nitrogen deficiency on leaf photosynthesis, carbohydrate status and biomass production in two olive cultivars ‘Meski’ and ‘Koroneiki’. Sci. Hortic. 2010, 123, 336–342. [Google Scholar] [CrossRef]
- Bobbink, R.; Hicks, K.; Galloway, J.; Spranger, T.; Alkemade, R.; Ashmore, M.; Bustamante, M.; Cinderby, S.; Davidson, E.; Dentener, F.; et al. Global assessment of nitrogen deposition effects on terrestrial plant diversity: A synthesis. Ecol. Appl. 2010, 20, 30–59. [Google Scholar] [CrossRef] [PubMed]
- Schulte-Uebbing, L.; de Vries, W. Global-scale impacts of nitrogen deposition on tree carbon sequestration in tropical, temperate, and boreal forests: A meta-analysis. Glob. Change Biol. 2018, 24, e416–e431. [Google Scholar] [CrossRef] [PubMed]
- Nadelhoffer, K.J. The potential effects of nitrogen deposition on fine-root production in forest ecosystems. New Phytol. 2000, 147, 131–139. [Google Scholar] [CrossRef]
- McDonough, A.M.; Watmough, S.A.; Bird, A.W. Biogeochemcial responses to multiyear above-canopy applications of nitrogen at a jack pine (Pinus banksiana) forest in northern Alberta, Canada. Can. J. For. Res. 2023, 53, 1–13. [Google Scholar] [CrossRef]
- Lovett, G.M.; Goodale, C.L. A new conceptual model of nitrogen saturation based on experimental nitrogen addition to an oak forest. Ecosystems 2011, 14, 615–631. [Google Scholar] [CrossRef]
- Gaige, E.; Dail, D.B.; Hollinger, D.Y.; Davidson, E.A.; Gernandez, I.J.; Sievering, H.; White, A.; Halteman, W. Changes in canopy processes following whole-forest canopy nitrogen fertilization of a mature spruce-hemlock forest. Ecosystems 2007, 10, 1133–1147. [Google Scholar] [CrossRef]
- Cosby, B.J.; Ferrier, R.C.; Jenkins, A.; Wright, R.F. Modelling the effects of acid deposition: Refinements, adjustments and inclusion of nitrogen dynamics in the MAGIC model. Hydrol. Earth Syst. Sci. 2001, 5, 499–517. [Google Scholar] [CrossRef]
- Posch, M.; Reinds, G.J. A very simple dynamic soil acidification model for scenario analyses and target load calculations. Environ. Model. Softw. 2009, 24, 329–340. [Google Scholar] [CrossRef]
- Evens, C.D.; Caporn, S.J.M.; Carroll, J.A.; Pilkington, M.G.; Wilson, D.B.; Ray, N.; Cresswell, N. Modelling nitrogen saturation and carbon accumulation in heathland soils under elevated nitrogen deposition. Environ. Pollut. 2006, 143, 468–478. [Google Scholar] [CrossRef] [PubMed]
- de Vries, W.; Posch, M.; Kamari, J. Modeling Time Patterns of Forest Soil Acidification for Various Deposition Scenarios. In Regional Acidification Models; Kamari, J., Brakke, D.F., Jenkins, A., Norton, S.A., Wright, R.F., Eds.; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar] [CrossRef]
- Chen, L.; Driscoll, C.T. A two-layer model to simulate variations in surface water chemistry draining a northern forest watershed. Water Resour. Res. 2005, 41, W09425. [Google Scholar] [CrossRef]
- Belyazid, S. Dynamic Modelling of Biogeochemical Processes in Forest Ecosystems. Ph.D. Thesis, Department of Chemical Engineering, Lund University, Lund, Sweden, 2006. [Google Scholar]
- Le Roux, X.; Schmid, B.; Poly, F.; Barnard, R.L.; Niklaus, P.A.; Guillaumaud, N.; Habekost, M.; Oelmann, Y.; Pilippot, L.; Salles, J.F.; et al. Soil environmental conditions and microbial build-up mediate the effects of plant diversity on soil nitrifying and denitrifying enzyme activities in temperate grasslands. PLoS ONE 2013, 8, e61069. [Google Scholar] [CrossRef] [PubMed]
- Hawkes, C.V.; Wren, I.F.; Herman, D.J.; Firestone, M.K. Plant invasion alters nitrogen cycling by modifying the soil nitrifying community. Ecol. Lett. 2005, 8, 976–985. [Google Scholar] [CrossRef] [PubMed]
- Bird, A.; Watmough, S.A.; Carson, M.A.; Basiliko, N.; McDonough, A.M. Nitrogen retention of terricolous lichens in a northern Alberta jack pine forest. Ecosystems 2019, 22, 1308–1324. [Google Scholar] [CrossRef]
- Ste-Marie, C.; Pare, D. Soil, pH and N availability effects on net nitrification in the forest floor of a range of boreal forest stands. Soil Biol. Biochem. 1999, 31, 1579–1589. [Google Scholar] [CrossRef]
- McDonough, A.M.; Watmough, S.A. Interactive effects of precipitation and above canopynitrogen deposition on understorey plants in a jack pine (Pinus banksiana) forest in northern Alberta, Canada. Sci. Total Environ. 2023, 855, 158706. [Google Scholar] [CrossRef] [PubMed]
- Crowley, K.F.; Lovett, G.M. Effects of nitrogen deposition on nitrate leaching from forests of the northeastern United States will change with tree species composition. Can. J. For. Res. 2017, 47, 997–1009. [Google Scholar] [CrossRef]
- MacDonald, J.A.; Dise, N.B.; Matzner, E.; Armbruster, M.; Gundersen, P.; Forsius, M. Nitrogen input together with ecosystem nitrogen enrichment predict nitrate leaching from European Forests. Glob. Change Biol. 2002, 8, 1028–1033. [Google Scholar] [CrossRef]
- Gundersen, P.; Emmet, B.A.; Kjonaas, O.J.; Koopsman, C.J.; Tietema, A. Impact of nitrogen deposition on nitrogen cycling in a forest: A synthesis of NITREX data. For. Ecol. Manag. 1998, 101, 37–56. [Google Scholar] [CrossRef]
- Fenn, M.E.; Bytnerowicz, A.; Schilling, S.L.; Ross, C.S. Atmospheric deposition of nitrogen, sulphur and base cations in jack pine stands in the Athabasca Oil Sands Region, Alberta, Canada. Environ. Pollut. 2015, 196, 497–510. [Google Scholar] [CrossRef] [PubMed]
- Watmough, S.A.; Koseva, I.; Landre, A. A comparison of tension and zero-tension lysimeter and PRSTM probes for measuring soil water chemistry in sandy boreal soils in the Athabasca Oil Sands Region, Canada. Water Air Soil Pollut. 2013, 224, 1663–1672. [Google Scholar] [CrossRef]
- Watmough, S.A.; Bird, A.; McDonough, A.M.; Grimm, E. Forest fertilization associated with oil sands emissions. Ecosystems 2019, 22, 1–14. [Google Scholar] [CrossRef]
- Proemse, B.; Mayer, B.; Fenn, M.E.; Ross, C.S. A multi-isotope approach for estimating industrial contributions to atmospheric nitrogen deposition in the Athabasca oil sands region in Alberta, Canada. Environ. Pollut. 2013, 182, 80–91. [Google Scholar] [CrossRef] [PubMed]
- Melong, N. Early Responses of Understorey Vegetation After One Year of Above Canopy Nitrogen Additions in a Jack Pine Stand in Northern Alberta. Master’s Thesis, Trent University, Peterborough, ON, Canada, 2014; 135p. [Google Scholar]
- Harmens, H.; Norris, D.A.; Cooper, D.M.; Mills, G.; Steinnes, E.; Kubin, E.; Thoni, L.; Aboal, J.R.; Alber, R.; Carballeira, A.; et al. Nitrogen concentrations in mosses indicate the spatial distribution of atmospheric nitrogen deposition in Europe. Environ. Pollut. 2011, 159, 2852–2860. [Google Scholar] [CrossRef] [PubMed]
- Osler, G.H.R.; Sommerkorn, M. Toward a complete soil C and N cycle: Incorporating the soil fauna. Ecology 2007, 88, 1611–1621. [Google Scholar] [CrossRef] [PubMed]
- Manzoni, S.; Jackson, R.B.; Trofymow, J.A.; Porporato, A. The global stoichiometry of litter nitrogen mineralization. Science 2008, 321, 684–686. [Google Scholar] [CrossRef] [PubMed]
- Aitkenhead, J.A.; McDowell, W.H. Soil C:N ratio as a predictor of annual riverine DOC flux at local and global scales. Glob. Biogeochem. Cycles 2000, 14, 127–138. [Google Scholar] [CrossRef]
- Weetman, G.F.; Fournier, R.M. Ten-year growth and nutrition effects of straw treatment and of repeated fertilization on jack pine. Can. J. For. Res. 1984, 14, 416–423. [Google Scholar] [CrossRef]
- Prescott, C.E.; Kishchuk, B.E.; Weetman, G.F. Long-term effects of repeated N fertilization and straw application in a jack pine forest. 3. Nitrogen availability in the forest floor. Can. J. For. Res. 1995, 25, 1991–1996. [Google Scholar] [CrossRef]
- Weetman, G.F.; Dallaire, L.C.; Fournier, R. Long-term effects of repeated N fertilization and straw application in a jack pine forest. 1. Twenty-two-year growth response. Can. J. For. Res. 1995, 25, 1978–1983. [Google Scholar] [CrossRef]
- Burns, R.M.; Honkala, B.H. Silvics of North America. 1990. Available online: https://www.srs.fs.usda.gov/pubs/misc/ag_654/volume_1/pinus/banksiana.htm (accessed on 1 July 2016).
- Lambert, M.-C.; Ung, C.-H.; Raulier, F. Canadian national tree aboveground biomass equations. Can. J. For. Res. 2005, 35, 1996–2018. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2025; Available online: https://www.R-project.org/ (accessed on 1 May 2020).
- Laxton, D.L.; Watmough, S.A.; Aherne, J.; Straker, J. An assessment of nitrogen saturation in Pinus banksiana plots in the Athabasca Oil Sands Region, Alberta. J. Limnol. 2010, 69, 171. [Google Scholar] [CrossRef]
- Horb, E.C.; Wentworth, G.R.; Maker, P.A.; Liggio, J.; Hayden, K.; Boutzis, E.I.; Beausoleil, D.L.; Hazewinkel, R.O.; Mahaffey, A.C.; Sayanda, D.; et al. A decadal synthesis of atmospheric emissions, ambient air quality, and deposition in the oil sands region. Integr. Environ. Assess. Manag. 2021, 18, 333–360. [Google Scholar] [CrossRef] [PubMed]
- Wieder, R.K.; Vitt, D.H.; Burke-Scoll, M.; Scott, K.D.; House, M.; Vile, M.A. Nitrogen and sulphur deposition and the growth of Sphagnum fuscum in bogs of the Athabasca Oil Sands Region, Alberta. J. Limnol. 2010, 69, 161–170. [Google Scholar] [CrossRef]
- Berg, B.; Matzner, E. Effect of N deposition on decomposition of pant litter and soil organic matter in forest ecosystems. Environ. Rev. 1997, 5, 1–25. [Google Scholar] [CrossRef]
- Santaniello, F.; Djupstrom, L.B.; Ranius, T.; Weslien, J.; Rudolphi, J.; Thor, G. Large portion of wood dependent lichens in boreal pine forest are confined to old hard wood. Biodivers. Conserv. 2017, 26, 1295–1310. [Google Scholar] [CrossRef]
- Boudreault, C.; Drapeau, P.; Bouchard, M.; St-Laurent, M.-H.; Imbeau, L.; Bergeron, Y. Contrasting responses of epiphytic and terricolous lichens to variations in forest characteristics in northern boreal ecosystems. Can. J. For. Res. 2015, 45, 595–606. [Google Scholar] [CrossRef]
- Lang, S.I.; Cornelissen, J.H.C.; Klahn, T.; Logtestijn, R.S.P.; Broekman, R.; Schweikert, W.; Aerts, R. An experimental comparison of chemical traits and litter decomposition rates in a diverse range of subarctic bryophyte, lichen and vascular plant species. J. Ecol. 2009, 87, 886–900. [Google Scholar] [CrossRef]
- van Diepen, L.T.A.; Lilleskov, E.A.; Pregitzer, K.S.; Miller, R.M. Decline of arbuscular mycorrhiza fungi in northern hardwood forests exposed to chronic nitrogen additions. New Phytol. 2007, 176, 175–183. [Google Scholar] [CrossRef] [PubMed]
- Treseder, K.K. A meta-analysis of mycorrhizal responses to nitrogen, phosphorus, and atmospheric CO2 in field studies. New Phytol. 2004, 164, 347–355. [Google Scholar] [CrossRef] [PubMed]
- Caldwell, T.G.; Johnson, D.W.; Miller, W.W.; Qualls, R.G. Forest floor carbon and nitrogen losses due to prescription fire. Soil Sci. Soc. Am. J. 2002, 66, 262–267. [Google Scholar] [CrossRef]
- DeBell, D.S.; Ralston, C.W. Release of nitrogen by burning light forest fuels. Soil Sci. Soc. Am. J. 1970, 34, 936–938. [Google Scholar] [CrossRef]
- Wieder, R.K.; Vile, M.A.; Scott, K.D.; Albright, C.M.; McMillen, K.J.; Vitt, D.H.; Fenn, M.E. Differential effects of high atmospheric N and S deposition on bog and plant/lichen tissue and porewater chemistry across the Athabasca Oil Sands Region. Environ. Sci. Technol. 2016, 50, 12630–12640. [Google Scholar] [CrossRef] [PubMed]
- Cleavitt, N.L.; Hinds, J.W.; Poirot, R.L.; Geiser, L.H.; Dibble, A.; Leon, B.; Perron, R.; Pardo, L.H. Epiphytic macrolichen communities correspond to patterns of sulfur and nitrogen deposition in the northeastern United States. Bryol. 2015, 118, 304–324. [Google Scholar] [CrossRef]
- Nilsson, J.; Grennfelt, P. Critical Loads for Sulphur and Nitrogen; Nordic Council of Ministers: Copenhagen, Denmark, 1988; Report No. 1988; p. 15. [Google Scholar]




| Species | Treatment (kg ha−1 yr−1) | Ct | k | C0 |
|---|---|---|---|---|
| Cladonia mitis Sandst. | 0 | 0.39 | 0.00 | 0.42 |
| 5 | 0.42 | 0.01 | 0.38 | |
| 10 | 0.61 | 0.10 | 0.39 | |
| 15 | 0.81 | 0.11 | 0.38 | |
| 20 | 0.87 | 0.13 | 0.37 | |
| 25 | 1.06 | 0.17 | 0.39 | |
| Cladonia stellaris Opiz. | 0 | 0.41 | 0.00 | 0.46 |
| 5 | 0.50 | 0.02 | 0.39 | |
| 10 | 0.69 | 0.07 | 0.41 | |
| 15 | 0.68 | 0.07 | 0.4 | |
| 20 | 0.84 | 0.11 | 0.42 | |
| 25 | 0.95 | 0.13 | 0.43 | |
| Pluerozium schreberi | 0 | 0.82 | 0.02 | 0.73 |
| (Brid.) Mitt. | 5 | 0.81 | 0.03 | 0.68 |
| 10 | 0.97 | 0.07 | 0.68 | |
| 15 | 1.23 | 0.14 | 0.68 | |
| 20 | 1.32 | 0.16 | 0.67 | |
| 25 | 1.39 | 0.18 | 0.67 | |
| Pinus banksiana Lamb. | 0 | 0.89 | 0.00 | 0.89 |
| 5 | 2.30 | 0.02 | 0.89 | |
| 10 | 2.30 | 0.03 | 0.89 | |
| 15 | 2.30 | 0.04 | 0.89 | |
| 20 | 2.30 | 0.05 | 0.89 | |
| 25 | 2.30 | 0.09 | 0.89 | |
| Jack Pine Bole Diameter (cm) | All | 20 | 0.02 | 0.20 |
| Parameter | High-Exposure Site | 25 kg N ha−1 yr−1 | 15 kg N ha−1 yr−1 | Control |
|---|---|---|---|---|
| Throughfall (kg N ha−1 yr−1) | 12–26 | 25 | 15 | 2.5 |
| Vegetation N% | ||||
| Jack Pine Needles (Growth Year 1) | 1.0 (±0.1) | 1.0 (±0.1) | 1.0 (±0.1) | 1.0 (±0.2) |
| Jack Pine Growth Needles (Year 2) | 1.17 (±0.1) | 1.0 (±0.1) | 1.0 (±0.1) | 0.9 (±0.2) |
| Jack Pine Growth Needles (Year 3) | 1.0 (±0.1) | 0.9 (±0.1) | 0.8 (±0.1) | 0.8 (±0.0) |
| Arctostaphylos uva-ursi L. | 1.0 (±0.1) | 0.7 (±0.1) | 0.8 (±0.1) | 0.8 (±0.1) |
| Vaccinium vitis-idaea L. | 1.0 (±0.1) | 1.0 (±0.1) | 1.1 (±0.0) | 0.9 (±0.0) |
| Vaccinium myrtilloides Michx. | 1.6 (±0.1) | 1.9 (±0.1) | 1.8 (±0.1) | 1.9 (±0.1) |
| Evernia mesomorpha Nyl. | 2.1 (±0.1) | 1.2 (±0.0) | 1.2 (±0.1) | 0.9 (±0.1) |
| Hypogymnia physodes L. | 2.1 (±0.1) | 0.9 (±0.2) | 1.1 (±0.1) | 0.8 (±0.1) |
| Cladonia mitis Sandst | 0.7 (±0.2) | 1.1 (±0.1) | 0.8 (±0.0) | 0.4 (±0.0) |
| Cladonia stellaris Opiz. | 0.6 (±0.1) | 1.0 (±0.1) | 0.7 (±0.1) | 0.4 (±0.1) |
| Pleurozium schreberi (Brid.) Mitt | 0.9 (±0.24) | 1.4 (±0.3) | 1.2 (±0.1) | 0.8 (±0.1) |
| Soil | ||||
| LFH N% | 0.8 (±0.2) | 0.6 (±0.1) | 0.8 (±0.2) | 0.6 (±0.1) |
| LFH C:N | 34.6 (±7.01) | 32.7 (±3.1) | 37.3 (±2.5) | 41.7 (±5.6) |
| Ae N% | 0.1 (±0.0) | 0.03 (±0.02) | 0.04 (±0.01) | 0.02 (±0.01) |
| Ae C:N | 38.4 (±6.2) | 38.0 (±7.8) | 35.3 (±14) | 41.5 (±12.2) |
| NO3− Leaching (kg N ha−1) | <1 | <1 | <1 | <1 |
| Parameter | High-Exposure Site | 25 kg N ha−1 yr−1 | 15 kg N ha−1 yr−1 | Control |
|---|---|---|---|---|
| Vascular Ground Vegetation (% Cover) | ||||
| Amelanchier alnifolia Nutt. | 1.5 (±1.9) | 0.03 (±0.13) | 0.02 (±0.09) | 0.02 (±0.1) |
| Arctostaphylos uva-ursi L. | 33.7 (±22) | 4 (±6) | 4.5 (±7) | 5.8 (±6.9) |
| Galium boreale L. | 0.25 (±0.40) | 0 (±0) | 0 (±0) | 0 (±0) |
| Geocaulon lividum Rich. | 1.2 (±1) | 0 (±0) | 0 (±0) | 0 (±0) |
| Maianthemum canadense Desf. | 10.4 (±8.57) | 0.36 (±1.14) | 0.21 (±0.6) | 0.34 (±2.1) |
| Melampyrum lineare Desr. | 2.3 (±1.5) | 0.03 (±0.02) | 0 (±0) | 0 (±0) |
| Oryzopsis asperifolia Michx. | 10.2 (±11.6) | 0.02 (±0.1) | 0 (±0) | 0.03 (±0.1) |
| Solidago simplex Kunth. | 0.67 (±1.6) | 0 (±0) | 0 (±0) | 0 (±0) |
| Vaccinium myrtilloides Michx. | 3.5 (±2.7) | 5.2 (±4.6) | 3.4 (±3.8) | 2.6 (±2.1) |
| Vaccinium vitis-idaea L. | 1.71 (±1.1) | 0.4 (±1) | 0.2 (±0.3) | 2.8 (±2.7) |
| Total Cover | 53 (±52.8) | 10 (±1) | 8.3 (±7.4) | 13.9 (±14) |
| Mean Species Richness | 8 (±1) | 3 (±1) | 2 (±1) | 4 (±1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McDonough, A.M.; Watmough, S.A. A Simple Model to Predict the Temporal Nitrogen Saturation Point of a Jack Pine (Pinus banksiana L.) Forest. Forests 2025, 16, 1195. https://doi.org/10.3390/f16071195
McDonough AM, Watmough SA. A Simple Model to Predict the Temporal Nitrogen Saturation Point of a Jack Pine (Pinus banksiana L.) Forest. Forests. 2025; 16(7):1195. https://doi.org/10.3390/f16071195
Chicago/Turabian StyleMcDonough, Andrew M., and Shaun A. Watmough. 2025. "A Simple Model to Predict the Temporal Nitrogen Saturation Point of a Jack Pine (Pinus banksiana L.) Forest" Forests 16, no. 7: 1195. https://doi.org/10.3390/f16071195
APA StyleMcDonough, A. M., & Watmough, S. A. (2025). A Simple Model to Predict the Temporal Nitrogen Saturation Point of a Jack Pine (Pinus banksiana L.) Forest. Forests, 16(7), 1195. https://doi.org/10.3390/f16071195






