Abstract
In the case of forest inventory, heterogeneous areas are particularly challenging due to variability in vegetation structure. This is especially true in Galicia (northwest Spain), where land is highly fragmented, complicating the planning and management of single-species plantations such as Pinus radiata. This study proposes a cost-effective strategy using open-access tools and data to characterize and estimate wood volume in these plantations. Two stratification approaches—classical and cluster-based—were compared to a modeling method based on Principal Component Analysis (PCA). Data came from open-access national LiDAR point clouds, acquired using manned aerial vehicles under the Spanish National Aerial Orthophoto Plan (PNOA). Moreover, two volume estimation methods were applied: one from the Xunta de Galicia (XdG) and another from Spain’s central administration (4IFN). A Generalized Linear Model (GLM) was also fitted using PCA-derived variables with logarithmic transformation. The results show that although overall volume estimates are similar across methods, cluster-based stratification yielded significantly lower absolute errors per hectare (XdG: 28.04 m3/ha vs. 44.07 m3/ha; 4IFN: 25.64 m3/ha vs. 38.22 m3/ha), improving accuracy by 7% over classical stratification. Moreover, it does not require precise field parcel locations, unlike PCA modeling. Both official volume estimation methods tended to overestimate stock by about 10% compared to PCA. These results confirm that clustering offers a practical, low-cost alternative that improves estimation accuracy by up to 18 m3/ha in fragmented forest landscapes.
1. Introduction
From an environmental perspective, forests provide a wide array of ecosystem services [1]. They play a crucial role in soil protection, mitigating erosion [2], participate in the water cycle [3], and provide a haven for biodiversity, hosting approximately 80% of the planet’s terrestrial biodiversity [4]. To make informed decisions and ensure the conservation and management of forests, it is essential to obtain updated, accurate, and dynamic information about forest cover. To that end, national forest inventories based on field studies [5] are instrumental in understanding the structure and functioning of forest ecosystems, enabling the planning, management, and conservation of these vital natural resources [6]. However, the requirement and demand for forest cover information exceeds the scope and design of most existing forest inventories [7], especially in structurally heterogeneous or fragmented landscapes (Figure A1). To address this limitation, it is essential to optimize these inventories, improving both their accuracy and cost-effectiveness. In this sense, stratification methods play a crucial role, as they allow dividing forest stands into more homogeneous units, facilitating more reliable estimates with less sampling effort [8]. One common approach is classical stratification, which divides forest areas into predefined, homogeneous strata based on expert knowledge and field data, such as tree species, age classes, or site conditions [9]. However, this approach can be limited by the accuracy and availability of such prior information. More recently, data-driven stratification methods, such as cluster analysis applied to remote sensing data like Light Detection and Ranging (LiDAR), have emerged [10]. These techniques identify groups or strata directly from patterns in the data, allowing a more objective and potentially more precise division of forest stands, especially in heterogeneous or fragmented landscapes [11].
On the other hand, recent advances in remote sensing have considerably improved forest cover mapping at various scales, from small plots [12,13] to regional [14,15], national [16,17] and global levels [18,19]. In this context, aerial imagery [20], satellite data [21], and radar [22] and drone-based technologies [23] have been used primarily for mapping and monitoring forest areas and vegetation. However, for accurate estimation of standing timber volume, LiDAR technology, both terrestrial (TLS) and airborne (ALS), has established itself as the most effective tool due to its ability to capture the three-dimensional structure of the canopy [24]. TLS allows for very detailed plot-level characterization, although its coverage and operability are limited [25]. For its part, ALS offers wider and more consistent coverage, which makes it especially appropriate for regional-scale analyses and forest management planning [26]. In this regard, it has been shown that the use of LiDAR data provides accurate estimates of regeneration [27], density [28], species composition [29], and canopy height [30]. However, although LiDAR has proven its applicability for directly measuring structural variables (such as tree height) and modeling others (for example, aboveground biomass), its accuracy is largely conditioned by flight specifications, particularly point density [31]. Nevertheless, some authors argue that plot size has a greater effect than LiDAR point density and emphasize that plots with a minimum area of 500 to 600 m2 are needed to estimate volume, biomass, and basal area, and 300 to 400 m2 for canopy cover [32].
To address the challenges, various approaches have been explored that combine LiDAR data with other remote sensing datasets [31]. In addition, many nations have started or are currently engaged in comprehensive LiDAR data collection efforts. The Spanish National Aerial Orthophoto Plan (PNOA) LiDAR projects in a case in point. The PNOA provides free of charge data from airborne LiDAR sensors (also known as Airborne Laser Scanning—ALS), acquired using manned aerial vehicles equipped with LEICA ALS60 sensors, which provide a point density of 0.5 points/m2. The incorporation of LiDAR sensors into the PNOA was driven by the need to obtain more accurate digital terrain models, particularly in areas with complex topography and varied forest structure. But its possibilities go much further, with the potential to map land cover [33], estimate fuel properties [34], and analyze structural and biomass characteristics [35].
In the context of Galicia, the study area of this research, forest management planning is regulated by Decree 52/2014, which establishes the legal framework for sustainable forestry practices in the region [36]. This decree makes stratified forest inventories mandatory for approved management plans and sets specific requirements for the precision of dasometric estimates. In particular, it requires relative sampling errors of no more than 20% for the total area and 40% for each stratum, supported by a fiducial probability of 0.95. Compliance with these criteria is overseen by the regional forestry authority, and failure to meet them may result in delays or rejections of forest management plans. These legal requirements are especially relevant given Galicia’s prominent role in Spain’s forestry sector [37]. The region accounts for 8% of the country’s forest cover [38], with a total area of 2,040,754 hectares—about 1.5 million of which are forested. These forests are composed of 28% coniferous, 51% broadleaved, and 21% mixed stands [39]. Under this premise, our study focuses on innovation and the need to demonstrate that the use of PNOA-LiDAR data makes for faster, more accurate stratification of forest stands, using groupings as strata in inventory processes. This methodology helps significantly to improve accuracy and reduce errors, in contrast with traditional stratification, which relies heavily on detailed knowledge by managers. Factors such as age, quality, cover, density, or orography are taken into account to divide the forest into management units with homogeneous characteristics. In addition, the information provided by LiDAR is expected to minimize uncertainties arising from gaps in managers’ knowledge of forest data. In the framework of this research, comparisons of errors will be run between the traditional inventory approach with traditional stratification and the approach based on clusters generated from LiDAR data by the k-means algorithm. Discrepancies in the calculation of forest stocks in cubic meters will also be assessed compared to a LiDAR inventory, whose superior accuracy is recognized. This study is essential to promote sustainable forest management and informed decision-making in the important setting of the autonomous community of Galicia.
2. Materials and Methods
2.1. Study Area
This study was carried out in Galicia (north-western Spain) (Figure 1). This region has a surface area of 29,575 km2 and a population of almost three million people [40]. The population is widely dispersed, making travel and services such as water provision difficult. Most of the population is concentrated along the coast, leaving a growing demographic vacuum in much of the interior of the region [41]. According to the Köppen–Geiger classification, Galicia has two types of climates: Csb (Mediterranean–Oceanic climate) and Csa (Mediterranean climate) [42]. Csb is characterized by a seasonal maximum of precipitation in winter and a minimum in summer, while the Csa (typical of the north coast of Spain) has a warm, temperate climate which is extremely humid, with hot summers [43]. According to the Climate Data Store, for the climatic period from 1979 to 2018, the average annual temperature in Galicia was 12.34 °C, and the average annual precipitation was 1276.17 mm. The maximum temperature during the warmest month was 23.74 °C, while the minimum during the coldest month was 8.74 °C. The predominant soils lie on granitic rock and acid schist, have a loam or sandy loam texture, and are well drained [44]. The dominant tree species in the area are the genera Pinus, Eucalyptus, and various hardwoods. These woodlands are mainly plantations rather than semi-natural forests. Forestry management and the forestry industry account for 12% of the final agricultural output of Galicia’s rural economy, compared to 3.5% in Spain as a whole [45]. It is estimated that there are around 162,000 ha under forest cover, with an average parcel size of between 1.5 and 2.0 ha.
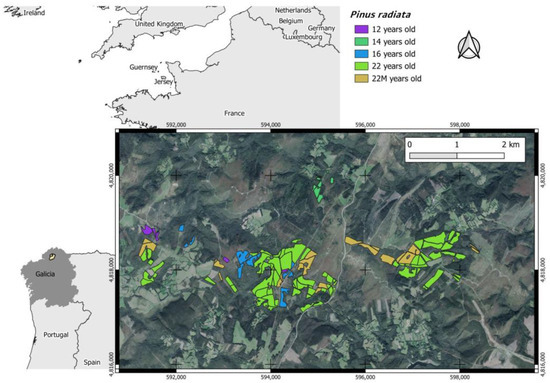
Figure 1.
Parcel distribution analyzed in Galicia (NW Spain). Coordinate system ETRS89/UTM zone 29 N.
A total of 40 randomly distributed parcels were studied (Table A1), located in the municipalities of As Somozas and As Pontes de García Rodríguez. The parcels were checked to ensure that they adequately captured the variability of the forest stand. This study focuses on Pinus radiata, as it is the most widespread species in the area, covering a total of 231.95 ha (Table 1).

Table 1.
Surface areas covered by Pinus radiata. The first column shows the ages of the stands.
The strata of Pinus radiata obtained by forest managers are defined according to age and quality. This information is collected from ground truth based on managers’ knowledge of the forest and the planting dates of each stand (Table A2). Other species also found on the parcels, albeit to a lesser extent, are Eucalyptus globulus (0.29 ha), Eucalyptus nitens (10.73 ha), Betula celtiberica (16.18 ha), and hardwoods (57.46 ha). There are also cleared parcels (28.63 ha), tracks (12.17 ha), firebreaks (1.49 ha), enclaves (47.21 ha), unproductive areas (15.63 ha), and power lines (7.86 ha). A total of 118 different polygons have been created on the basis of belonging to different strata or having boundaries defined by tracks, enclaves, or firebreaks.
2.2. PNOA-LiDAR Data
PNOA-LiDAR data were processed in common for the cluster stratification and the calculation of the Principal Component Analysis model (LiDAR inventory), which was used to predict and validate the stratification (Figure 2).
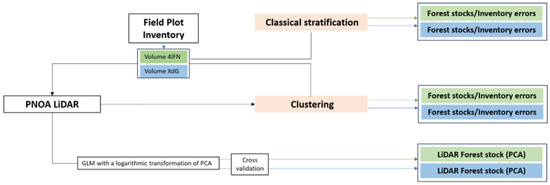
Figure 2.
Outline of the applied methodology.
LiDAR data from PNOA were provided by the Instituto de Estudios del Territorito de la Xunta de Galicia [46]. A total of 11 files covering 2.0 × 2.0 km were acquired in 2015. They were cropped with FUSION software (version 4.20) (Figure 3), using the “PolyClipData” command. By default, this produces a number of files containing all vector points (*shp). These files contain the totality of returns but contain errors due to extraneous elements on the surface. These returns, which generally refer to a height well above the ground, may cause variations in the statistical analysis of the point cloud. Using the “Catalog” command incorporated in the FUSION software, reports describing various characteristics of this LiDAR dataset were produced. These provide information about the internal quality of the point cloud, degree of coverage, return, and density of the points. This command provides both alphanumeric and visual information. To obtain these figures, the lower limit was set at 0.5 returns per unit area (m2) and the upper limit at 1.0 m2.

Figure 3.
(A) LiDAR point cloud on DEM surface. (B) Obtaining the ground surface from the points previously selected as belonging to the ground. The surface is shown together with the LiDAR information of all returns. The gray surface corresponds to the Digital Elevation Model (DEM), generated from the points classified as ground (in blue). These ground points define the terrain surface, over which all LiDAR returns are displayed. The rest of the point cloud is color-coded according to the height above ground: lower vegetation is shown in green tones, while higher canopy structures appear in yellow to red tones, allowing for a detailed visualization of vertical forest structure.
The “Intensity Image” command was used to obtain an image of intensities. The return of the intensities is related to the rate of loss of laser energy detected in the receiver due to the reflection of a given coverage. Using this tool, an image was obtained that reflects the coverage at the time of data capture, thus certifying through the use of orthophotos that there was no change in the structure of the forest stand.
The true altitude of the ground needs to be known to obtain the reference elevation for measuring heights. To that end, the algorithm studied by Kraus & Pfeifer [47] was applied using the GroundFilter tool (FUSION software). This command filters the returns of the point cloud, identifying those that are at ground level. The default coefficients of the weight function have been shown to produce optimal results for high-density point clouds (>4 returns/m2) [47]. In this study, with low-density point clouds, coefficient values were tested, and those that provided the best adjustment were selected. This adjustment was made using a shadow model in the Digital Elevation Model (DEM). A cell size of 1.0 m was used, since using a larger size without altimetric information (density 0.5 points/m2) would have increased the irregularities of the terrain. This methodology was carried out using the “GridSurfaceCreate” command of the FUSION software.
The Digital Surface Model (DSM) was then applied using the FUSION software developed by the Forest Service of the U.S. Department of Agriculture. By default, the algorithm used assigns the elevation of the highest point of each pixel to the center of the pixel. A smoothing switch was used to consider the heights falling on the pixels every 3.0 × 3.0 m. The MDS model and the DEM together provide a description of forest structure variables.
The canopy height distribution of Pinus radiata stands was assessed using key descriptive statistics. The results indicated a normal distribution, with all 118 analyzed polygons showing values within the expected range for the species and no detectable anomalies. The maxima were located by consulting GIS, and the validity of the data was checked by visual checks against orthophotography.
Firstly, the forest stand was described, and the basic information for its management was obtained. The statistical variables were collected in cells covering the whole territory, and the metrics describing the forest stand were stored in each cell. Then the territory was divided into square cells with a square base. Conveniently, the area of these cells is the same as the area of the sample parcels. The choice of grid cell size is mainly determined by the size of the field parcel, as it is important for the area of the field parcel and the grid cell to be as similar as possible [48,49]. Larger grid cells (and larger inventory parcels) will also contain a larger number of laser pulses and are more likely to have a more uniform distribution of pulses [49]. The total area covered by the point cloud is 706.86 m2, and each subdivided section of the study area measures 26.5 m2. It is important for the pixel size for which the statistics are calculated to be similar to the parcel size so that a comparative analysis of the statistics can be made. The size of the field parcels is conditioned by the density of the PNOA-LiDAR data points. In this case, the initial information is of low density, so the statistics need to be collected in sufficiently large areas. If the size of the field parcel were decreased, a low number of returns would be obtained, and the statistical analyses would be less reliable.
The GridMetrics command of the FUSION software was applied. A file containing the same number of rows as there are cells in the working grid was obtained. Each row corresponds to the metric data of the point cloud. The metrics obtained describe and serve to analyze the forest stand of the study area. A total of 35,178 points were obtained, with 74 statistics for each one. These points are referenced as the center of 26.5 × 26.5 m parcels. Those cells that did not contain Pinus radiata were then eliminated, giving a total of 4650 available parcels.
Stratified sampling entails subdividing the forest into homogeneous groups and then performing simple random sampling within each stratum. This “pre-stratification” achieves a variance within each stratum that is smaller than the total overall variance of the entire population [8]. It provides an opportunity to reduce sampling intensity because part of the overall variance is explained by the strata. The stratification that exists is based on the type of species, the age of the stands, the height, and slight differences in qualities (Table 1). A comparison was made with the data produced by the management company (Table 1) and those obtained from LiDAR data processing.
Stratification using the cluster generation process is an example of unsupervised learning. The data were grouped according to certain rules without predicting values as in regression. The elements were grouped by k-means and divided into k-clusters, thus determining the optimal number of clusters into which it is possible or recommended to divide the population (Figure A2). To that end, the LiDAR data most relevant to forest structure and characteristics were used. These are the same data used in the following sections to carry out the LiDAR inventory. The LiDAR metrics of interest used as input data for creating and searching clusters are listed in Table A3. These metrics were chosen for their ability to capture key features of forest structure, such as density, height, and biomass distribution, which are critical for understanding the forest environment [50,51]. The clustering process was carried out directly using these LiDAR metrics, ensuring that the grouping was based on variables with direct forestry relevance. This approach allowed for an effective stratification of the study area, facilitating subsequent analyses related to LiDAR-based inventory and forest resource estimation.
2.3. Field Inventory Planning
The field parcels are used for three purposes: to carry out a stock calculation based on Classical Stratification, a Cluster Stratification, and a stock calculation based on a LiDAR inventory.
A total of 40 circular parcels with a radius of 15 m were randomly distributed throughout the study area. The fieldwork was carried out in June 2017. In each parcel, the diameter at breast height and heights of all trees were measured (the minimum inventory diameter considered was 7.5 cm). The circular shape was chosen because it was easy to stake out, i.e., only the location of the parcel center needed to be obtained. In choosing the parcel size, the significance of the LiDAR statistics was taken into consideration. Analyzing the density values in the field, a radius of 15 m was considered. In addition, the 706.86 m2 area of each parcel also included about 300 returns (0.5 pulses/m2 density). The parcels should represent the age variability of the vegetation in the study area. The estimation models must capture all the variability if they are to correctly represent the sample. The parcels were arranged randomly, with each being identified via QGIS and its coordinates calculated. LiDAR point clouds were created for each parcel. A buffer was created by QGIS with the location of the parcels (Figure A3), then a 15 m radius shapefile of parcels was created for each parcel. The ClipData command of the FUSION software was used to match the generated point clouds with the field parcels. Finally, all the parcels were cut, and 40-point clouds were obtained (1 for each parcel).
Two different equations were used, both with double entry: one was provided by Diéguez-Aranda et al. [52] and developed by the Xunta de Galicia (XdG) (regional government), and the other by Dirección General de Medio Natural y Política Forestal [53], a department of the central Spanish government (4IFN). The IFN is a decennial project that provides information on the forestry situation in Spain at the provincial, regional, and national levels. One of its objectives is to know the volumes and growth of forest species. It is based on a network of permanent parcels on which different data on forest cover and dendrometric parameters of forest species are taken. One of the results published in this document is a set of cubic rates applicable in different parts of Spain. On the other hand, Diéguez-Aranda et al. [52] published a set of tools oriented to sustainable forest management in the autonomous community of Galicia. Among the products made available by these authors are production tables, dynamic growth models, and individual tree stocking equations for the main production species in Galicia. The data for the construction of these models also comes from a network of permanent parcels of the Sustainable Forest Management Unit of the University of Santiago de Compostela.
The center of each inventory parcel was obtained using GPS since ALS point clouds need to be clipped based on the area occupied by each inventory parcel, with its geo-position being taken at its center. Two types of devices were used to locate the centers depending on their availability at the relevant time: a handheld GPS device (Stonex S7G GNSS) and a Stonex S700A GNSS receiver with 700 channels. Both devices were designed in Italy and assembled in the People’s Republic of China (P.R.C.) by Stonex Srl (Viale dell’Industria, 53, 20037 Paderno Dugnano, Milan, Italy), and are capable of receiving real-time differential signals from continuously operating reference stations. Only position accuracies below one meter were considered, as this is more than sufficient for the size of the inventory parcel. Large parcels are not affected by position errors of less than 5 m, although small errors in the geo-position of small parcels may induce substantial biases [54].
The considerable variability of forests requires their classification into homogeneous classes. This stratification can be carried out according to many different criteria, such as the specific composition of vegetation, the fraction of tree cover and age, seeking to form homogeneous units of vegetation to use as the basis for deciding on the sampling for calculating stocks through stratified sampling and thus enabling the number of inventory parcels to be reduced. In stratified inventories, samples are taken within each stratum, and stocks and levels of desired variables are estimated for each stratum and for the entire forest. In this study, the stands are divided by age and quality based on the knowledge held by forest managers (Table 1).
Clustering can be either a supervised or an unsupervised learning method, where objects are grouped based on inherent similarity by quantitatively comparing their characteristics [55]. Translating this technique to forestry as a tool for stratifying vegetation formations involves automatically grouping stands after exploring their metrics using an algorithm. These metrics were scaled so as to normalize the scale of the data. The optimal number of clusters was then determined using RStudio’s NbClust library (RStudio version 2023.06.2+561 “Mountain Hydrangea”) and found to be 3, so the Pinus radiata population was divided into three homogeneous groups: Cluster 1, which covered a total of 42.91 ha, cluster 2 with 96.77 ha and cluster 3 with 90.52 ha (Figure 4). The final result of k-means clustering is sensitive to the initial random assignments, so we specified a nstart = 25, which means that “R” tries 25 different initial random assignments and then selects the best results.
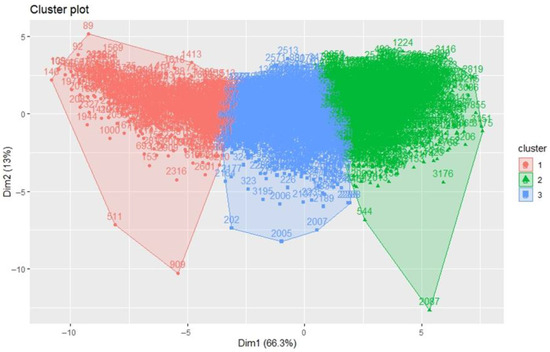
Figure 4.
Spatial positioning of the three clusters. The observations (3278 tessellations) are represented by a point, and principal components are used if there are more than 2 variables (in our case 19 LiDAR measurements). Data points are located according to the first principal components that describe most of the variance.
Errors in the estimation of the variables are assimilated into the goodness-of-fit obtained in the regression used to predict these variables. The error was estimated considering the variation in the volumes. To that end, the standard sampling error (Sxj) was calculated using the commonly applied formula in forest inventories [56], given by Equation (1). Since the sampling ratio in our case is n/N ≤ 0.05, the finite population correction (FPC) is typically omitted, as the differences in results are minimal.
where, Sj = standard deviation in stratum j, n = number of parcels in stratum j, Nj = number of parcels of 15 m radius that could be assembled on the surface of stratum j, nj = number of parcels in each stratum.
The error Sxstr, which is the weighted standard error of the sample mean, was thus calculated (Equation (2)).
where Pj is the weight of stratum j based on the manager’s data, for stratum j, Sxj is the standard error of the mean of stratum j, and m is the number of strata.
The absolute error was calculated as (Equation (3)):
where t is the value of the t-Student distribution (for a fixed error with a 95% confidence probability and n − 1 degrees of freedom).
From the absolute error, it is possible to calculate the relative error, which is given by Equation (4).
where Vj is the average mean volume of wood in stratum j expressed in m3/ha.
In addition, the weighted average volume for all strata was calculated as follows (Equation (5)):
2.4. LiDAR Forest Stock Estimation Using GLM with PCA-Derived Components
Estimates made through classical stratification and cluster-based stratification will be compared against a global volume prediction using LiDAR metrics. An area-based approach will be used, considering stand-level attributes rather than individual tree-level attributes for volume estimation. In this study, a single stratum (Pinus radiata) was defined, and other variables such as season, canopy cover fraction, height, and density were not separately assessed. Instead, these factors were captured through the LiDAR-derived metrics included in the model, which effectively represent the variability in forest structure. The LiDAR metrics used in the model included height distribution metrics such as percentiles of height (H25, H50, H75, and H95), mean height (Hmean), maximum height (Hmax), and height variance (Hvariance), as well as canopy cover and density metrics like canopy density (CDM3, CDM5, CDM7, and CDM8) and the percentage of first returns (PRO4, PROM). These metrics capture essential characteristics of forest structure, including vertical distribution and canopy density.
To model the forest inventory data, we selected a GLM with a Gamma distribution and a logarithmic link function, as it provides a good fit for the continuous and positively skewed nature of the response variable (wood volume). The choice of GLM was based on its flexibility in modeling different types of response variables from the exponential family, allowing a more accurate representation of the data structure. In this case, GLM with a logarithmic transformation of the principal components was used (Equation (6)). This methodology was chosen because it yielded the best results in the study area.
where E[V] is the expected value of the volume for both models (4IFN and XdG), PC1, PC2, and PC3 are the first three principal components used as predictors, β0 is the intercept, and β1, β2, and β3 are the coefficients associated with each principal component.
Principal Component Analysis (PCA) enables all variables to be reduced to a smaller number of principal components, which explain a significant portion of the data’s variability [57]. Each dimension or principal component produced by PCA is a linear combination of the original variables, and they are also uncorrelated with each other. Many machine-learning algorithms are sensitive to the scale and variance of data measurement, so when predictors are not standardized, those measured on a larger scale or with more variance tend to dominate the model. To address this issue, data-centering and normalization techniques were employed. The utilization of PCA thus serves to reduce multicollinearity, as it constructs a set of linear combinations of all predictors (i.e., principal components) instead of selecting a subset of predictors [58]. For modeling purposes, the first three principal components were selected, as they accounted for the majority of the variance in the dataset while maintaining model interpretability. Additionally, model assumptions were checked, and full diagnostic procedures were conducted on the resulting GLM to ensure its validity and reliability. The PCA in this study was conducted using R and RStudio, specifically employing the caret package (Classification And Regression Training), which is a useful tool for data preparation (scaling, imputation, and variable selection), splitting data into training and testing sets, training predictive models, and evaluating their performance through cross-validation and error metrics. Additionally, the performance package was used to apply the check_model() function for visualizing and assessing model assumptions. This analysis was applied to all LiDAR data.
The model was validated by k-fold cross-validation [59], which provided Relative Mean Squared Error (RMSE), R2, and Mean Absolute Error (MAE) values. This is an iterative process that consists of randomly dividing data into k groups of approximately the same size. k − 1 groups are used to train the model, and the remaining group is used for validation; in this case, k = 10. This process is repeated k times using a different group in each iteration.
3. Results
3.1. Stock Calculation and Inventory Errors: Classical and Clustering-Based Stratification
To the best of our knowledge, this article is the first analysis of the potential of PNOA-LiDAR technology for reducing the need for field sampling in forest inventories in the Autonomous Community of Galicia. Specifically, for the generation of clusters using PNOA-LiDAR data to assess the volume of these parcels, it is estimated that the sampling effort can be reduced by as much as 41% [8]. The errors were calculated both within each stratum and for the whole forest (Table 2). The values obtained were 26.08 m3/ha or 22.66 m3/ha, depending on the model used (XdG and 4IFN, respectively). Both the Ea (XdG = 44.07 m3/ha or 4IFN = 38.22 m3/ha) and E (%) (XdG = 21.59% or 4IFN = 20.55%) are within the tolerable range. Furthermore, M is the volume-weighted mean for all strata (XdG = 204.11 m3/ha or 4IFN = 190.89 m3/ha).

Table 2.
Inventory errors in timber volumes according to XdG and 4IFN rates based on classical strata.
The same calculations were performed for the clusters (Table 3), resulting in figures of 16.62 m3/ha or 15.19 m3/ha, depending on the rate used (XdG and 4IFN, respectively). Again, both Ea (XdG = 28.04 m3/ha or 4IFN = 25.64 m3/ha) and E(%) (XdG = 13.67% or 4IFN = 13.38) are within the tolerable range established by Decree 52/2014 [36]. Furthermore, M is the volume-weighted average for all strata (XdG = 205.16 m3/ha or 4IFN = 191.62 m3/ha). A comparison of the errors obtained with the classical stratification processes (Table 2) and with stratification by means of clusters (Table 3) leads to the conclusion that the latter process reduces the errors at the stratum and forest level in a generalized manner. This makes it a quick way of stratifying the forest with no need for interpretation or in-depth knowledge of the forest stands. This reduces inventory effort (resulting in a substantial reduction in costs) and gives better results.

Table 3.
Inventory errors in timber volumes according to XdG and 4IFN rates based on clusters.
The number of cubic meters of timber obtained in the forest was calculated via classical stratification and clusters (Table 4). The overall timber stocks do not show significant variations at the overall forest level. The two cubing methodologies (XdG and 4IFN) provide results with only very small differences between them.

Table 4.
Strata-based stock calculation.
In general, the error rate with classical stratification is around 20%, while for stratification using clusters it falls to 13% (Table 5). This result falls within the range (8%–16%) obtained by Georgakis et al. [11] who evaluated different clustering algorithms for the stratification of an irregular coniferous forest in central Greece, using different variables and a number of clusters.

Table 5.
Inventory errors at the hillside level.
3.2. LiDAR Forest Stock: Prediction and Validation
In general, the PCA-based model shows high R2 values and performs well for the independent variable under study, i.e., volume. The GLM provides R2 levels of 0.90 for the XdG methodology and 0.90 for 4IFN. These models were validated using the k-fold cross-validation method (k = 10), which gives an RMSE value of 3.06, an R2 of 0.91, and an MAE of 2.35 for the XdG methodology and a RMSE value of 2.46, an R2 of 0.91, and an MAE of 1.92 for 4IFN. These low RMSE values are especially notable given that the LiDAR data used had a point density of just 0.5 pts/m2, demonstrating the model’s robustness and the potential for cost-effective implementation using open-access resources. Moreover, volume accuracy is within the ranges found in other similar studies (e.g., Fernández-Landa et al. [60]; Gónzalez Ferreiro et al. [61], even considering studies with specific LiDAR flights and field parcels. Furthermore, various studies have pointed out that predictions in parcel-level LiDAR Forest inventories in temperate forests are better when models are fitted independently for different species in the study area [62,63], with the GLM for the genus Pinus being one of the best-performing (Nord-Larsen & Schumacher, 2012 [62]). The suitability of LiDAR for stock estimation was also corroborated at larger scales and in this case, using a Random Forest model, [64] obtained R2 values above 0.9 for models applicable to poplar and pine.
The four principal components explain almost 95% of the variability (Figure A4). PC1 accounts for 66.4% of the variability and is positively correlated with different measurements studied. PC2 accounts for 13% and has a moderately positive correlation, especially with the measurements Hcv, Hiq, and Hvariance. PC3 is associated with Entropy, CDM3, PRO4, and PROM and accounts for 8.1% of the variance. PC4 is associated with Hkurtosis and explains 5.7% of the variance (Figure 5). Given the limited additional variance explained by PC4, only the first three components were retained in order to keep the model simple and efficient.
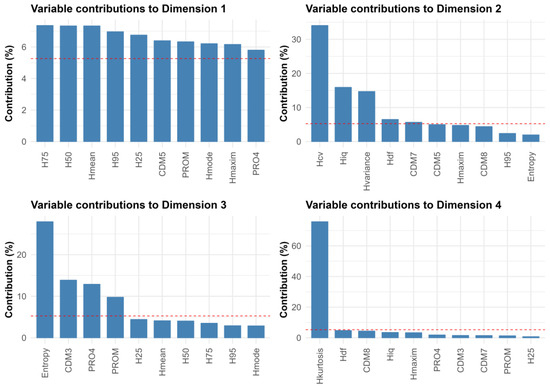
Figure 5.
Contribution of each variable to the various dimensions (DIM). For a given component, a variable with a contribution greater than the set threshold can be considered important in contributing to the relevant component.
The predicted volume of wood for the entire forest is 42,501.63 m3 for the XdG methodology and 39,974.31 m3 for 4IFC. Comparing these results with classical stratification (XdG = 47,342.28 m3, 4IFN = 44,276.39 m3) and cluster-based stratification (XdG = 47,228.67 m3, 4IFN = 44,111.87 m3), it is observed that LiDAR data underestimate the volume by 10%. It is observed that the lowest sampling error for volume estimation is obtained when the regression is performed on pixels of the same size as the field sampling parcel [48]. To minimize the error in the total forest volume, it is necessary to maximize the range of application of the regression [65].
4. Discussion
This study presents a methodology based on the generation of clusters from PNOA-LiDAR data to stratify forested areas, which proves to be a fast, efficient solution. This approach enables us to dispense with conventional stratification, which requires a deeper knowledge of the forest area. It is also considered more appropriate and realistic than the use of subjective parameters. Note that it is an automatic stratification that does not depend on the interpretation of aerial images and thus facilitates the work involved and reduces the time required. Moreover, the methodology developed thus facilitates compliance with Decree 52/2014 [36] which regulates the general instructions for the planning and management of forests in Galicia. This reduction in errors enables the calculation of stocks to be improved, in general, and makes for a description of forest stands that is much more in line with reality.
To facilitate the clustering process, PCA was selected as the dimensionality reduction technique for processing the LiDAR-derived metrics. This choice was based on a comparative evaluation with other common methods, such as t-distributed Stochastic Neighbor Embedding (t-SNE) and Uniform Manifold Approximation and Projection (UMAP). While t-SNE and UMAP are powerful nonlinear techniques that are effective at preserving local structure and visualizing high-dimensional data, they are less suitable for clustering tasks in operational settings [66,67]. For instance, t-SNE does not preserve global distances and is sensitive to parameter tuning, making it unstable for large-scale stratification [66]. UMAP, although more robust and faster than t-SNE, still introduces distortions in distance metrics that can interfere with unsupervised clustering [67]. In contrast, PCA is a linear and interpretable method that retains global variance structure and reduces collinearity, offering computational efficiency and reproducibility [68]. These characteristics make PCA particularly suitable for large-area forest inventory applications where scalability, simplicity, and consistency are essential.
The ultimate goal of an inventory is to obtain information about the timber stocks in the forest. The most realistic value for assessing the differences in stock calculations between traditional inventory strata and strata based on clusters is considered to be obtained via LiDAR inventory. It is widely acknowledged that the most accurate stock predictions are provided by this method. As mentioned above, the total volume of timber in cubic meters according to the LiDAR inventory is estimated at 42,801.62 m3 or 39,974.31 m3 when adjusted based on inventory parcel results using various models. In this study, the positions of inventory parcels were not altered to compare different methodologies. However, it should be noted that if one methodology is chosen over the other for stock calculation, the inventory parcels will need to be repositioned to achieve a more accurate stock assessment (classical stratification vs. cluster stratification).
Cluster-based stratification offers an effective way to leverage LiDAR information in cases where conducting a full LiDAR inventory of the forest stand is not feasible. In order to conduct a LiDAR inventory, precise knowledge of field parcel locations is essential. However, conventional GPS devices often lack the necessary accuracy under dense forest canopies. This limitation arises because most geo-positioning tools used by forest managers are not designed to achieve the spatial precision required to accurately align field plots with LiDAR point clouds [54,69]. As a result, geolocation errors can lead to biased volume estimates and reduced model reliability [69]. These limitations tend to affect PCA-based models more significantly, as they rely on precise geolocation to extract continuous variables from LiDAR data at the plot level [70]. Inaccurate plot positioning introduces noise into the principal components, which may reduce the predictive performance of the resulting models. In contrast, cluster-based stratification is less sensitive to GPS inaccuracies because it groups plots based on structural and dasometric similarities, rather than requiring exact spatial alignment [71]. On the other hand, it is also vital to consider the edge effect when employing inventory parcels for LiDAR inventories [54,72]. Forest managers often position inventory parcels within stands without sufficient geometric precision. This introduces additional variance that can lead to underestimation or overestimation of forest attributes, which complicates the extrapolation of the sample data to the entire forest stand [72]. Moreover, in many instances, the inventory parcel sizes may not be compatible with the available LiDAR data [73]. The link between inventory parcel size and LiDAR pulse density is crucial. When plot size is not well matched to LiDAR pulse density, smaller plots can generate sparse data that reduces statistical robustness, while increasing plot size to compensate for this increases operational costs and limits the feasibility of the inventory in practice.
It should also be noted that the results obtained show a significant gain in terms of inventory error when using cluster-based stratification techniques compared to traditional inventory. Using the same number of parcels in both methodologies, the error was 7% lower in the case of the cluster method, thus comfortably meeting the requirements of the legislation. This indicates that even with a significant reduction in the number of inventory parcels, the error would be within the margins set both at the stratum level (40%) and for the whole area (20%). Clustering also avoids a certain degree of subjectivity that exists within the technical criteria for defining the strata, solving the stratification problem in a quantitative way.
Despite the advantages offered by the use of LiDAR data and cluster-based stratification, it is important to acknowledge certain limitations. First, the accuracy of LiDAR-derived information can be primarily affected by vegetation structure, especially by factors such as canopy vegetation density and height, where occlusion can reduce point density in the lower layers [74]. In addition, technical limitations of the sensors, such as beam divergence and scanning angle, can introduce noise and distortions in the point cloud [75]. On the other hand, the use of clustering algorithms such as k-means largely depends on parameter selection and data normalization, which can affect the resulting stratification [76]. Another source of uncertainty lies in the spatial mismatch between inventory plots and LiDAR data, especially in fragmented landscapes like Galicia, where smallholdings and irregular geometries predominate [77].
Finally, although cluster-based stratification can reduce sampling effort, field validation remains essential to ensure that the identified strata accurately reflect real structural differences within the forest. These considerations are crucial when interpreting results and applying this methodology in operational forest management. From a practical standpoint, clustering techniques allow forest stands to be segmented according to structural typologies identified in advance. This enables more representative and efficient inventory plot design, as the selected plots better capture the structural variability of the forest. Consequently, it lays a solid foundation for complementing traditional inventory methods, reducing both time and costs without compromising the quality of the collected information. Additionally, forest managers should carefully consider the number of clusters, the choice of clustering algorithm, and the auxiliary variables used, as these factors significantly affect the reliability of design-based direct estimates and the effectiveness of model-based small-area estimation approaches [11].
Furthermore, in many scenarios, LiDAR stratification may require more inventory parcels than traditional stratification due to the high level of fragmentation of the forest area in Galicia. Specifically, official land register information indicates that 162,188 ha of forest is estimated to stand in land register parcels of less than 0.5 ha. This represents close to 40% of the surface area covered by the main productive tree species in Galicia. According to Harrel et al. [78] at least 10 to 20 inventory parcels per estimated parameter (covariate) would be needed. This could significantly impact inventory costs in comparison to traditional stratification methods.
5. Conclusions
Developing forest inventories using LiDAR data poses significant challenges, especially due to the high costs, extensive fieldwork, and precision GPS requirements typically involved. To address these limitations, this study compared classical and cluster-based stratification methods, along with a PCA-based modeling approach, using low-density, open-access LiDAR data. Among these, the proposed cluster-based stratification method stands out for its ability to delineate structurally homogeneous stand types without relying on historical information or precise parcel geolocation. This makes it especially well-suited for smallholder forests and regions with limited resources, where traditional GPS-dependent inventories may be infeasible or cost-prohibitive. Although overall wood volume estimates were comparable across methods, the cluster-based approach achieved lower absolute errors per hectare and satisfied the legal accuracy standards set by Decree 52/2014. By reducing field effort and enhancing operational feasibility, this methodology offers a practical, low-cost solution for sustainable forest inventory and planning.
Author Contributions
Conceptualization, A.L.-A., H.L. and X.Á.; methodology, A.L.-A.; software, A.L.-A.; validation, A.L.-A.; formal analysis, A.L.-A.; investigation, A.L.-A. and C.A.-A.; resources, H.L. and X.Á.; data curation, A.L.-A.; writing—original draft preparation, A.L.-A. and C.A.-A.; writing—review and editing, H.L., C.A.-A. and X.Á.; visualization, A.L.-A. and C.A.-A.; project administration, H.L. and X.Á.; funding acquisition, H.L. and X.Á. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Project 4Map4Health, ERA-Net CHIST-ERA (2019)—PCI2020-120705-2 funded by MCIN/AEI/10.13039/501100011033 and the European Union “NextGenerationEU”/PRTR” (H. Lorenzo) and by Grant ACACIA-SAT (PID2022-138374OA-I00) funded by MICIU/AEI/10.13039/501100011033/and ERDF, EU (C. Acuña and X. Álvarez). Funding for the open access charge was provided by Universidade de Vigo/CISUG.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to thank the staff of ASEFOR S.L. for their administrative and technical support. Special thanks to Carlos Peco Costas and Elena Seoane Martínez for his assistance during the review period. We would also like to thank Chris Pellow for proofreading the English and for helpful comments.
Conflicts of Interest
The authors have declared that no competing interests exist.
Abbreviations
The following abbreviations are used in this manuscript:
| ALS | Airbone Laser Scanning |
| DEM | Digital Elevation Model |
| DSM | Digital Surface Model |
| GIS | Geographic Information System |
| GLM | Generalized Linear Model |
| IFN | Inventario Forestal Nacional |
| LiDAR | Light Detection and Ranging |
| MAE | Mean Absolute Error |
| PCA | Principal Component Analysis |
| PNOA | Spanish National Aerial Ortophoto Plan |
| RMSE | Relative Mean Squared Error |
| TLS | Terrestrial Laser Scanning |
| XdG | Xunta de Galicia |
Appendix A
Appendix A.1
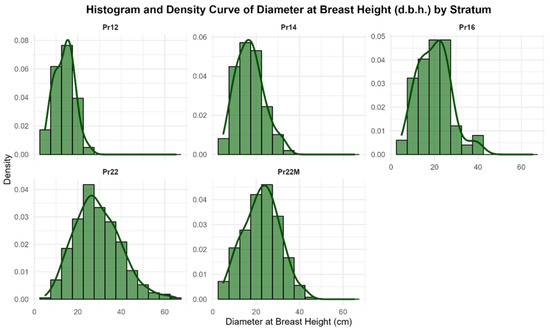
Figure A1.
Histogram of diameter at breast height (d.b.h.) distribution (cm) by forest stratum. The figure illustrates the structural variability among strata based on tree diameter frequencies collected in inventory plots.

Table A1.
Number of sample parcels that are located on each stratum or on each cluster.
Table A1.
Number of sample parcels that are located on each stratum or on each cluster.
| Stratum | N° of Plots | Cluster | N° of Plots |
| Pr12 | 2 | 1 | 9 |
| Pr14 | 2 | 2 | 17 |
| Pr16 | 2 | 3 | 14 |
| Pr22 | 27 | ||
| Pr22M | 7 | ||
| Total | 40 | 40 |
Appendix A.2
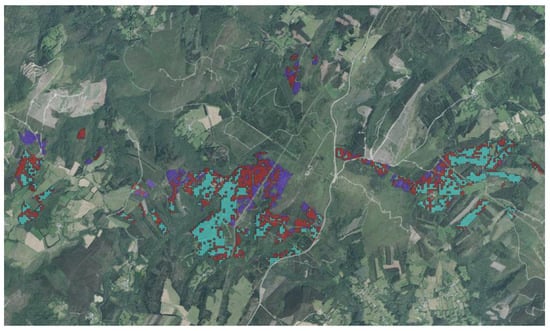
Figure A2.
Location of the different clusters, new mass stratification based on k-means. Each color represents one of the resulting homogeneous groups: Purple: Cluster 1, Light blue: Cluster 2, Red: Cluster 3.

Table A2.
Identification, location, volumes and number of trees obtained from the inventory parcels, plus the stratum and cluster where each parcel is located.
Table A2.
Identification, location, volumes and number of trees obtained from the inventory parcels, plus the stratum and cluster where each parcel is located.
| Parcel | Coordinate X | Coordinate Y | XdG [1] (m3/ha) | 4IFN [1] (m3/ha) | No. of Trees | Stratum | Cluster | Avg. d.b.h. per Stratum (cm) |
|---|---|---|---|---|---|---|---|---|
| 1 | 591,309.7 | 4,818,314 | 293.28 | 268.31 | 38 | Pr22 [2] | 2 | 29.1 |
| 2 | 593,853.7 | 4,817,692 | 313.36 | 283.72 | 32 | Pr22 | 2 | 29.1 |
| 3 | 594,132.3 | 4,817,878 | 227.31 | 206.96 | 19 | Pr22 | 2 | 29.1 |
| 4 | 594,299.4 | 4,818,145 | 296.52 | 272.69 | 17 | Pr22 | 2 | 29.1 |
| 5 | 594,645.4 | 4,817,658 | 334.83 | 303.82 | 33 | Pr22 | 2 | 29.1 |
| 6 | 594,706.2 | 4,817,185 | 281.27 | 257.10 | 29 | Pr22 | 2 | 29.1 |
| 7 | 596,827.5 | 4,818,178 | 241.90 | 220.30 | 27 | Pr22M | 3 | 22.6 |
| 8 | 597,400 | 4,817,769 | 317.63 | 291.14 | 35 | Pr22 | 2 | 29.1 |
| 9 | 597,459.2 | 4,818,519 | 316.58 | 287.87 | 36 | Pr22 | 2 | 29.1 |
| 10 | 597,744.1 | 4,818,504 | 429.23 | 394.87 | 24 | Pr22 | 2 | 29.1 |
| 11 | 596,153 | 4,818,417 | 268.15 | 250.31 | 53 | Pr22M | 2 | 22.6 |
| 12 | 594,098.8 | 4,818,196 | 414.46 | 378.42 | 40 | Pr22 | 2 | 29.1 |
| 13 | 593,845.8 | 4,818,246 | 330.62 | 301.61 | 23 | Pr22 | 2 | 29.1 |
| 14 | 593,753.1 | 4,817,289 | 477.16 | 434.60 | 31 | Pr22 | 2 | 29.1 |
| 15 | 596,830.5 | 4,817,915 | 171.59 | 159.17 | 13 | Pr22 | 3 | 29.1 |
| 16 | 597,876.9 | 4,818,638 | 223.17 | 203.78 | 15 | Pr22 | 2 | 29.1 |
| 17 | 598,004.7 | 4,818,281 | 418.74 | 380.31 | 40 | Pr22 | 2 | 29.1 |
| 18 | 594,429.3 | 4,818,411 | 67.36 | 70.42 | 32 | Pr22 | 1 | 29.1 |
| 19 | 594,406.4 | 4,818,060 | 97.91 | 92.77 | 20 | Pr22 | 3 | 29.1 |
| 20 | 595,055.8 | 4,817,667 | 125.95 | 121.74 | 36 | Pr22M | 3 | 22.6 |
| 21 | 594,848 | 4,817,513 | 77.56 | 71.46 | 7 | Pr22 | 3 | 29.1 |
| 22 | 597,020.9 | 4,818,409 | 75.25 | 83.02 | 44 | Pr22M | 1 | 22.6 |
| 23 | 591,441.5 | 4,818,509 | 215.63 | 198.46 | 32 | Pr22M | 3 | 22.6 |
| 24 | 593,116.6 | 4,817,783 | 132.24 | 124.64 | 31 | Pr22 | 3 | 29.1 |
| 25 | 593,655.2 | 4,817,594 | 165.35 | 150.06 | 20 | Pr22 | 2 | 29.1 |
| 26 | 597,017.3 | 4,818,204 | 275.08 | 253.82 | 38 | Pr22 | 3 | 29.1 |
| 27 | 597,124.1 | 4,818,551 | 196.01 | 182.04 | 27 | Pr22 | 2 | 29.1 |
| 28 | 594,817 | 4,818,121 | 63.12 | 67.0 | 31 | Pr22M | 1 | 22.6 |
| 29 | 591,373.8 | 4,818,784 | 27.69 | 43.58 | 46 | Pr12 | 1 | 13.8 |
| 30 | 596,514.9 | 4,818,205 | 31.74 | 39.38 | 29 | Pr22M | 1 | 22.6 |
| 31 | 592,114.6 | 4,818,894 | 161.55 | 154.50 | 39 | Pr16 | 3 | 19.8 |
| 32 | 594,983.7 | 4,819,637 | 129.25 | 126.03 | 40 | Pr14 | 3 | 17.2 |
| 33 | 594,552.4 | 4,818,310 | 217.68 | 201.08 | 32 | Pr22 | 3 | 29.1 |
| 34 | 593,307.2 | 4,818,302 | 90.59 | 102.43 | 60 | Pr16 | 1 | 19.8 |
| 35 | 595,053.4 | 4,819,532 | 59.25 | 74.67 | 58 | Pr14 | 1 | 17.2 |
| 36 | 594,633.3 | 4,818,418 | 82.58 | 79.98 | 23 | Pr22 | 1 | 29.1 |
| 37 | 594,289.4 | 4,818,259 | 96.39 | 91.12 | 22 | Pr22 | 3 | 29.1 |
| 38 | 595,243.4 | 4,817,808 | 204.56 | 205.59 | 77 | Pr22 | 3 | 29.1 |
| 39 | 594,024.7 | 4,817,357 | 102.18 | 93.33 | 12 | Pr22 | 3 | 29.1 |
| 40 | 591,373 | 4,818,890 | 25.18 | 36.68 | 35 | Pr12 | 1 | 13.8 |
[1] Volume estimated in the field according to diameter and height via the two cubing rates (XdG and 4IFN). [2] Note: Pr = Pinus radiata.
Appendix A.3
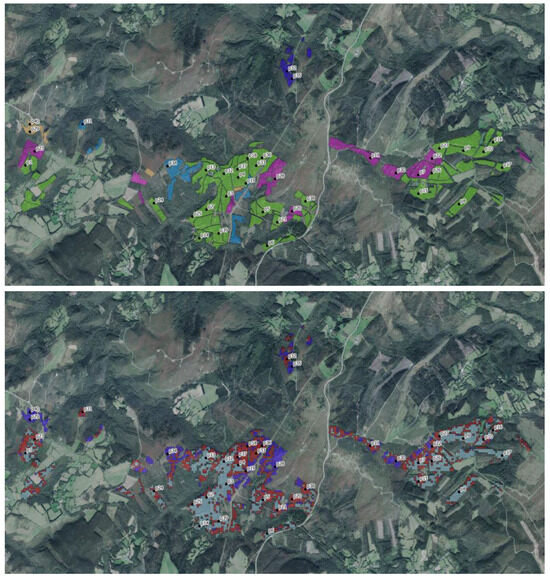
Figure A3.
Location of the inventory parcels on the different classical strata and on the clusters into which the forest mass was divided. Top panel (silvicultural strata): Green: Pr22, Magenta: Pr22M, Light blue: Pr16, Dark blue: Pr14, Light brown: Pr12. Bottom panel (unsupervised classification clusters): Purple: Cluster 1, Light blue: Cluster 2, Red: Cluster 3.

Table A3.
Metrics used to obtain and train the prediction model.
Table A3.
Metrics used to obtain and train the prediction model.
| LiDAR Metrics | Metrics | Units | Abbrev. | Description |
|---|---|---|---|---|
| Height distribution metrics | Percentile heights | m | H25, H50, H75, H95 | The percentiles of the height distributions (25th, 50th, 75th, 95th) |
| Mean heights | m | Hmean | The mean height above 3 m of all points | |
| Maximum heights | m | Hmaxim | The maximum height of all points above 3 m | |
| Mode | m | Hmode | The mode height above 3 m | |
| Coefficient of variation in heights | Coefficient, ratio | Hcv | Coefficient of variation in heights, defined as the ratio between the standard deviation and the mean of the heights | |
| Kurtosis of heights | m | Hkurtosis | The kurtosis of the heights of all points above 3 m | |
| Interquantile distance of heights | m | Hiq | The Interquartile distance of the heights of all points above 3 m | |
| Variance of heights | m | Hvariance | The variance of the heights of all points above 3 m | |
| Height distribution factor ((mean-min)/(max-min)) | Coefficient, ratio | Hdf | Canopy Relief Ratio ((mean-min)/(max-min)) | |
| Canopy and density distribution metrics | Canopy density metrics | % | CDM3, CDM5, CDM7 CDM8 | Each tessera is divided into 10 equal parts by calculating the cumulative proportions of LiDAR returns |
| Percentage of first returns over 4 m | % | PRO4 | (number of first returns above 4 meters)/(total number of first returns) | |
| Percentage of first returns over the mean | % | PROM | (number of first returns above the mean height)/(total number of first returns) | |
| Entropy | Vertical Complexity Index | Entropy | Fixed normalization of the entropy function. where HB is the total number of height bins and pi is the proportional abundance of LiDAR returns in height bin i |
Appendix A.4
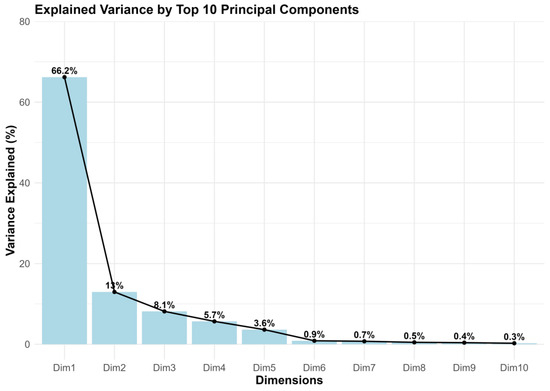
Figure A4.
Representation of the eigenvalues ordered from highest to lowest.
References
- Felipe-Lucia, M.R.; Soliveres, S.; Penone, C.; Manning, P.; van der Plas, F.; Boch, S.; Prati, D.; Ammer, C.; Schall, P.; Gossner, M.M.; et al. Multiple forest attributes underpin the supply of multiple ecosystem services. Nat. Commun. 2018, 9, 4839. [Google Scholar] [CrossRef] [PubMed]
- RSyrbe, U.; Schorcht, M.; Grunewald, K.; Meinel, G. Indicators for a nationwide monitoring of ecosystem services in Germany exemplified by the mitigation of soil erosion by water. Ecol. Indic. 2018, 94, 46–54. [Google Scholar] [CrossRef]
- Ojea, E.; Martin-Ortega, J.; Chiabai, A. Defining and classifying ecosystem services for economic valuation: The case of forest water services. Environ. Sci. Policy 2012, 19, 1–15. [Google Scholar] [CrossRef]
- Poudel, B.S. Ecological solutions to prevent future pandemics like COVID-19. Banko Janakari 2020, 30, 1–2. [Google Scholar] [CrossRef]
- Tomppo, E.; Gschwantner, T.; Lawrence, M.; McRoberts, R.E.; Gabler, K.; Schadauer, K.; Vidal, C.; Lanz, A.; Ståhl, G.; Cienciala, E. National forest inventories. Pathw. Common Report. Eur. Sci. Found. 2010, 1, 541–553. [Google Scholar]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote sensing technologies for enhancing forest inventories: A review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Alam, M.B.; Shahi, C.; Pulkki, R. Economic impact of enhanced forest inventory information and merchandizing yards in the forest product industry supply chain. Socioecon. Plann. Sci. 2014, 48, 189–197. [Google Scholar] [CrossRef]
- Papa, D.d.A.; de Almeida, D.R.A.; Silva, C.A.; Figueiredo, E.O.; Stark, S.C.; Valbuena, R.; Rodriguez, L.C.E.; Oliveira, M.V.N.D. Evaluating tropical forest classification and field sampling stratification from lidar to reduce effort and enable landscape monitoring. For. Ecol. Manag. 2020, 457, 117634. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Gobakken, T.; Næsset, E. Post-stratified estimation of forest area and growing stock volume using lidar-based stratifications. Remote Sens. Environ. 2012, 125, 157–166. [Google Scholar] [CrossRef]
- Chen, W.; Hu, X.; Chen, W.; Hong, Y.; Yang, M. Airborne LiDAR Remote Sensing for Individual Tree Forest Inventory Using Trunk Detection-Aided Mean Shift Clustering Techniques. Remote. Sens. 2018, 10, 1078. [Google Scholar] [CrossRef]
- Georgakis, A.; Gatziolis, D.; Stamatellos, G. A Primer on Clustering of Forest Management Units for Reliable Design-Based Direct Estimates and Model-Based Small Area Estimation. Forests 2023, 14, 1994. [Google Scholar] [CrossRef]
- Schumacher, J.; Rattay, M.; Kirchhöfer, M.; Adler, P.; Kändler, G. Combination of Multi-Temporal Sentinel 2 Images and Aerial Image Based Canopy Height Models for Timber Volume Modelling. Forests 2019, 10, 746. [Google Scholar] [CrossRef]
- Morell-Monzó, S.; Estornell, J.; Sebastiá-Frasquet, M.-T. Comparison of Sentinel-2 and high-resolution imagery for mapping land abandonment in fragmented areas. Remote. Sens. 2020, 12, 2062. [Google Scholar] [CrossRef]
- Wang, Z.; Ginzler, C.; Waser, L.T. A novel method to assess short-term forest cover changes based on digital surface models from image-based point clouds. For. Int. J. For. Res. 2015, 88, 429–440. [Google Scholar] [CrossRef]
- Barakat, A.; Khellouk, R.; El Jazouli, A.; Touhami, F.; Nadem, S. Monitoring of forest cover dynamics in eastern area of Béni-Mellal Province using ASTER and Sentinel-2A multispectral data. Geol. Ecol. Landscapes 2018, 2, 203–215. [Google Scholar] [CrossRef]
- Matasci, G.; Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W.; Zald, H.S.J. Large-area mapping of Canadian boreal forest cover, height, biomass and other structural attributes using Landsat composites and lidar plots. Remote Sens. Environ. 2018, 209, 90–106. [Google Scholar] [CrossRef]
- Jia, T.; Li, Y.; Shi, W.; Zhu, L. Deriving a forest cover map in Kyrgyzstan using a hybrid fusion strategy. Remote. Sens. 2019, 11, 2325. [Google Scholar] [CrossRef]
- Tang, H.; Armston, J.; Hancock, S.; Marselis, S.; Goetz, S.; Dubayah, R. Characterizing global forest canopy cover distribution using spaceborne lidar. Remote. Sens. Environ. 2019, 231, 111262. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef]
- Ganz, S.; Adler, P.; Kändler, G. Forest Cover Mapping Based on a Combination of Aerial Images and Sentinel-2 Satellite Data Compared to National Forest Inventory Data. Forests 2020, 11, 1322. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Wendt, D.G.; Nelson, M.D.; Hansen, M.H. Using a land cover classification based on satellite imagery to improve the precision of forest inventory area estimates. Remote Sens. Environ. 2002, 81, 36–44. [Google Scholar] [CrossRef]
- Hyyppa, J.; Pulliainen, J.; Hallikainen, M.; Saatsi, A. Radar-derived standwise forest inventory. IEEE Trans. Geosci. Remote. Sens. 1997, 35, 392–404. [Google Scholar] [CrossRef]
- Kotivuori, E.; Kukkonen, M.; Mehtätalo, L.; Maltamo, M.; Korhonen, L.; Packalen, P. Forest inventories for small areas using drone imagery without in-situ field measurements. Remote. Sens. Environ. 2020, 237, 111404. [Google Scholar] [CrossRef]
- Alvites, C.; Marchetti, M.; Lasserre, B.; Santopuoli, G. LiDAR as a Tool for Assessing Timber Assortments: A Systematic Literature Review. Remote. Sens. 2022, 14, 4466. [Google Scholar] [CrossRef]
- Newnham, G.J.; Armston, J.D.; Calders, K.; Disney, M.I.; Lovell, J.L.; Schaaf, C.B.; Strahler, A.H.; Danson, F.M. Terrestrial Laser Scanning for Plot-Scale Forest Measurement. Curr. For. Rep. 2015, 1, 239–251. [Google Scholar] [CrossRef]
- Buchalová, D.; Hofierka, J.; Šupinský, J.; Kaňuk, J. Estimating Subcanopy Solar Radiation Using Point Clouds and GIS-Based Solar Radiation Models. Remote. Sens. 2025, 17, 328. [Google Scholar] [CrossRef]
- Hill, R.A.; Broughton, R.K. Mapping the understorey of deciduous woodland from leaf-on and leaf-off airborne LiDAR data: A case study in lowland Britain. ISPRS J. Photogramm. Remote Sens. 2009, 64, 223–233. [Google Scholar] [CrossRef]
- Chamberlain, C.P.; Meador, A.J.S.; Thode, A.E. Airborne lidar provides reliable estimates of canopy base height and canopy bulk density in southwestern ponderosa pine forests. For. Ecol. Manag. 2021, 481, 118695. [Google Scholar] [CrossRef]
- Alards-Tomalin, J.; Stott, L.; Standish, J.; Parlow, M. Seeing the Forest Through the Trees: Assessing Urban Forest Values Using a Combination of LiDAR, Timber Species Identifier, i-Tree Eco and GPS Ground Surveys. In Ecocities Now; Springer: Berlin/Heidelberg, Germany, 2020; pp. 149–160. [Google Scholar]
- Zhu, X.; Wang, C.; Nie, S.; Pan, F.; Xi, X.; Hu, Z. Mapping forest height using photon-counting LiDAR data and Landsat 8 OLI data: A case study in Virginia and North Carolina, USA. Ecol. Indic. 2020, 114, 106287. [Google Scholar] [CrossRef]
- Tijerín-Triviño, J.; Moreno-Fernández, D.; Zavala, M.A. Astigarraga, and M. García. Identifying forest structural types along an aridity gradient in peninsular Spain: Integrating low-density LiDAR, forest inventory, and aridity index. Remote Sens. 2022, 14, 235. [Google Scholar] [CrossRef]
- Ruiz, L.A.; Hermosilla, T.; Mauro, F.; Godino, M. Analysis of the Influence of Plot Size and LiDAR Density on Forest Structure Attribute Estimates. Forests 2014, 5, 936–951. [Google Scholar] [CrossRef]
- Fragoso-Campón, L.; Quirós, E.; Mora, J.; Gallego, J.A.G.; Durán-Barroso, P. Overstory-understory land cover mapping at the watershed scale: Accuracy enhancement by multitemporal remote sensing analysis and LiDAR. Environ. Sci. Pollut. Res. 2020, 27, 75–88. [Google Scholar] [CrossRef] [PubMed]
- González-Ferreiro, E.; Diéguez-Aranda, U.; Crecente-Campo, F.; Barreiro-Fernández, L.; Miranda, D.; Castedo-Dorado, F. Modelling canopy fuel variables for Pinus radiata D. Don in NW Spain with low-density LiDAR data. Int. J. Wildl. Fire 2014, 23, 350–362. [Google Scholar] [CrossRef]
- Pascual, A.; Guerra-Hernández, J. An integrated assessment of carbon emissions from forest fires beyond impacts on aboveground biomass. A showcase using airborne lidar and GEDI data over a megafire in Spain. J. Environ. Manag. 2023, 345, 118709. [Google Scholar] [CrossRef] [PubMed]
- Xunta de Galicia. DECRETO 52/2014, de 16 de Abril, Por el Que se Regulan las Instrucciones Generales de Ordenación y de Gestión de Montes de Galicia. Diario Oficial de Galicia. Available online: https://www.xunta.gal/dog/Publicados/2014/20140508/AnuncioG0165-250414-0003_es.html (accessed on 1 March 2024).
- Bastida, M.; García, A.V.; Taín, M.Á.V. A New Life for Forest Resources: The Commons as a Driver for Economic Sustainable Development—A Case Study from Galicia. Land 2021, 10, 99. [Google Scholar] [CrossRef]
- Valdés, C.M.M.; Sánchez, L.G. Tercer Inventario Forestal Nacional 1997–2006: La Transformación Histórica del Paisaje Forestal en Galicia. 2ª ed.; Ministerio de Medio Ambiente, Dirección General de Conservación de la Naturaleza: Madrid; Stonex Srl: Paderno Dugnano (MI), Italia, 2002; 159p, (Galicia: Lugo). [Google Scholar]
- MITECO. Anuario de Esadística Forestal 2020. Available online: https://www.miteco.gob.es/es/biodiversidad/estadisticas/forestal_anuarios_todos.aspx (accessed on 1 March 2024).
- de Galicia, X. Institulo Galego de Estadística. Available online: https://www.ige.gal/web/index.jsp?idioma=es (accessed on 1 March 2024).
- Alonso, C.A. River Ecosystem Assessment: Towards Water Security and Environmental Governance. Universidade de Vigo. 2023. Available online: https://www.investigo.biblioteca.uvigo.es/xmlui/handle/11093/4710 (accessed on 1 March 2024).
- Guitián, M.R.; Rego, P.R. Clasificaciones climáticas aplicadas a Galicia: Revisión desde una perspectiva biogeográfica. Recur. Rurais 2007, 3, 31–53. [Google Scholar]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- FAO. Guidelines for Soil Description, 3rd ed.; Food and Agriculture Organization: Rome, Italy, 1990. [Google Scholar]
- Marey-Pérez, M.F.; Rodríguez-Vicente, V. Factors determining forest management by farmers in northwest Spain: Application of discriminant analysis. For. Policy Econ. 2011, 13, 318–327. [Google Scholar] [CrossRef]
- Xunta de Galicia. Información Xeográfica de Galicia; Instituto Geográfico Nacional, Ministerio de Transportes y Movilidad Sostenible. 2025. Available online: https://centrodedescargas.cnig.es/CentroDescargas/home (accessed on 6 July 2025).
- Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Magnussen, S.; Boudewyn, P. Derivations of stand heights from airborne laser scanner data with canopy-based quantile estimators. Can. J. For. Res. 1998, 28, 1016–1031. [Google Scholar] [CrossRef]
- Næsset, E. Determination of mean tree height of forest stands by digital photogrammetry. Scand. J. For. Res. 2002, 17, 446–459. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Innes, J.L.; Dai, J.; Ruan, H.; She, G. Tree species classification in subtropical forests using small-footprint full-waveform LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 39–51. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, T.; Skidmore, A.K.; Holzwarth, S.; Heiden, U.; Heurich, M. Mapping individual silver fir trees using hyperspectral and LiDAR data in a Central European mixed forest. Int. J. Appl. Earth Obs. Geoinf. 2021, 98, 102311. [Google Scholar] [CrossRef]
- Diéguez-Aranda, U.; Alboreca, A.R.; Castedo-Dorado, F.; González, J.Á.; Barrio-Anta, M.; Crecente-Campo, F.; González-González, J.M.; Cruzado, C.P.; Rodríguez-Soalleiro, R.; López-Sánchez, A.; et al. Herramientas selvícolas para la gestión forestal sostenible en Galicia. Forestry 2009, 82, 1–16. [Google Scholar]
- Dirección General de Medio Natural y Política Forestal. Cuarto Inventario Forestal Nacional; Ministerio para la Transición Ecológica y el Reto Demográfico: Madrid, Spain, 2011.
- Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of LiDAR-derived estimates of forest stand biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Saxena, A.; Prasad, M.; Gupta, A.; Bharill, N.; Patel, O.P.; Tiwari, A.; Er, M.J.; Ding, W.; Lin, C.-T. A review of clustering techniques and developments. Neurocomputing 2017, 267, 664–681. [Google Scholar] [CrossRef]
- Molina, J.M.G.; Nicolau, M.P.; Grau, P.V. Manual de Ordenación por Rodales: Gestión Multifoncional de los Espacios Forestales; Centre Tecnològic Forestal de Catalunya, 2ª ed. 2006; Available online: https://www.researchgate.net/publication/264536504_Manual_de_ordenacion_por_rodales_gestion_multifuncional_de_los_espacios_forestales (accessed on 6 July 2025).
- Salem, N.; Hussein, S. Data dimensional reduction and principal components analysis. Procedia Comput. Sci. 2019, 163, 292–299. [Google Scholar] [CrossRef]
- Shendryk, Y.; Sofonia, J.; Garrard, R.; Rist, Y.; Skocaj, D.; Thorburn, P. Fine-scale prediction of biomass and leaf nitrogen content in sugarcane using UAV LiDAR and multispectral imaging. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102177. [Google Scholar] [CrossRef]
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-validation. Encycl. Database Syst. 2009, 5, 532–538. [Google Scholar]
- Fernández-Landa, A.; Fernández-Moya, J.; Tomé, J.L.; Algeet-Abarquero, N.; Guillén-Climent, M.L.; Vallejo, R.; Sandoval, V.; Marchamalo, M. High resolution forest inventory of pure and mixed stands at regional level combining National Forest Inventory field plots, Landsat, and low density lidar. Int. J. Remote Sens. 2018, 39, 4830–4844. [Google Scholar] [CrossRef]
- González-Ferreiro, E.; Diéguez-Aranda, U.; Miranda, D. Estimation of stand variables in Pinus radiata D. Don plantations using different LiDAR pulse densities. Forestry 2012, 85, 281–292. [Google Scholar] [CrossRef]
- Nord-Larsen, T.; Schumacher, J. Estimation of forest resources from a country wide laser scanning survey and national forest inventory data. Remote Sens. Environ. 2012, 119, 148–157. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T. Estimation of above-and below-ground biomass across regions of the boreal forest zone using airborne laser. Remote Sens. Environ. 2008, 112, 3079–3090. [Google Scholar] [CrossRef]
- Niu, X.; Jiang, N.; Hou, K.; Yin, Y. Estimating Forest Stock Volume Based on Airborne Lidar Data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.—ISPRS Arch. 2024, 48, 535–540. [Google Scholar] [CrossRef]
- Maltamo, M.; Bollandsås, O.M.; Næsset, E.; Gobakken, T.; Packalén, P. Different plot selection strategies for field training data in ALS-assisted forest inventory. Forestry 2010, 84, 23–31. [Google Scholar] [CrossRef]
- Devassy, B.M.; George, S.; Nussbaum, P. Unsupervised Clustering of Hyperspectral Paper Data Using t-SNE. J. Imaging 2020, 6, 29. [Google Scholar] [CrossRef]
- Milošević, D.; Medeiros, A.S.; Piperac, M.S.; Cvijanović, D.; Soininen, J.; Milosavljević, A.; Predić, B. The application of Uniform Manifold Approximation and Projection (UMAP) for unconstrained ordination and classification of biological indicators in aquatic ecology. Sci. Total Environ. 2022, 815, 152365. [Google Scholar] [CrossRef]
- Wang, M.; Gao, G.; Huang, H.; Heidari, A.A.; Zhang, Q.; Chen, H.; Tang, W. A Principal Component Analysis-Boosted Dynamic Gaussian Mixture Clustering Model for Ignition Factors of Brazil’s Rainforests. IEEE Access 2021, 9, 145748–145762. [Google Scholar] [CrossRef]
- Gobakken, T.; Næsset, E. Assessing effects of positioning errors and sample plot size on biophysical stand properties derived from airborne laser scanner data. Can. J. For. Res. 2009, 39, 1036–1052. [Google Scholar] [CrossRef]
- Bueso, D.; Piles, M.; Camps-Valls, G. Nonlinear PCA for Spatio-Temporal Analysis of Earth Observation Data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5752–5763. [Google Scholar] [CrossRef]
- De Cáceres, M.; Martín-Alcón, S.; González-Olabarria, J.R.; Coll, L. A general method for the classification of forest stands using species composition and vertical and horizontal structure. Ann. For. Sci. 2019, 76, 40. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Campbell, M.J.; Dennison, P.E.; Hudak, A.T.; Parham, L.M.; Butler, B.W. Quantifying understory vegetation density using small-footprint airborne lidar. Remote Sens. Environ. 2018, 215, 330–342. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Béland, M.; Caspersen, J.; Achim, A. A mathematical framework to describe the effect of beam incidence angle on metrics derived from airborne LiDAR: The case of forest canopies approaching turbid medium behaviour. Remote Sens. Environ. 2018, 209, 824–834. [Google Scholar] [CrossRef]
- Wongoutong, C. The impact of neglecting feature scaling in k-means clustering. PLoS ONE 2024, 19, e0310839. [Google Scholar] [CrossRef] [PubMed]
- Corbelle-Rico, E.; López-Iglesias, E. Farmland Abandonment and Afforestation—Socioeconomic and Biophysical Patterns of Land Use Change at the Municipal Level in Galicia, Northwest Spain. Land 2024, 13, 1394. [Google Scholar] [CrossRef]
- Harrell, F.E. Regression modeling strategies. Bios 2017, 330, 14. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).