The Influence of Thermal Modification, Moisture Content, Frequency, and Vibration Direction Plane on the Damping of Spruce Wood (Picea abies) as Determined by the Wavelet Transform Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Specimen Preparation
2.2. Vibration Measurements
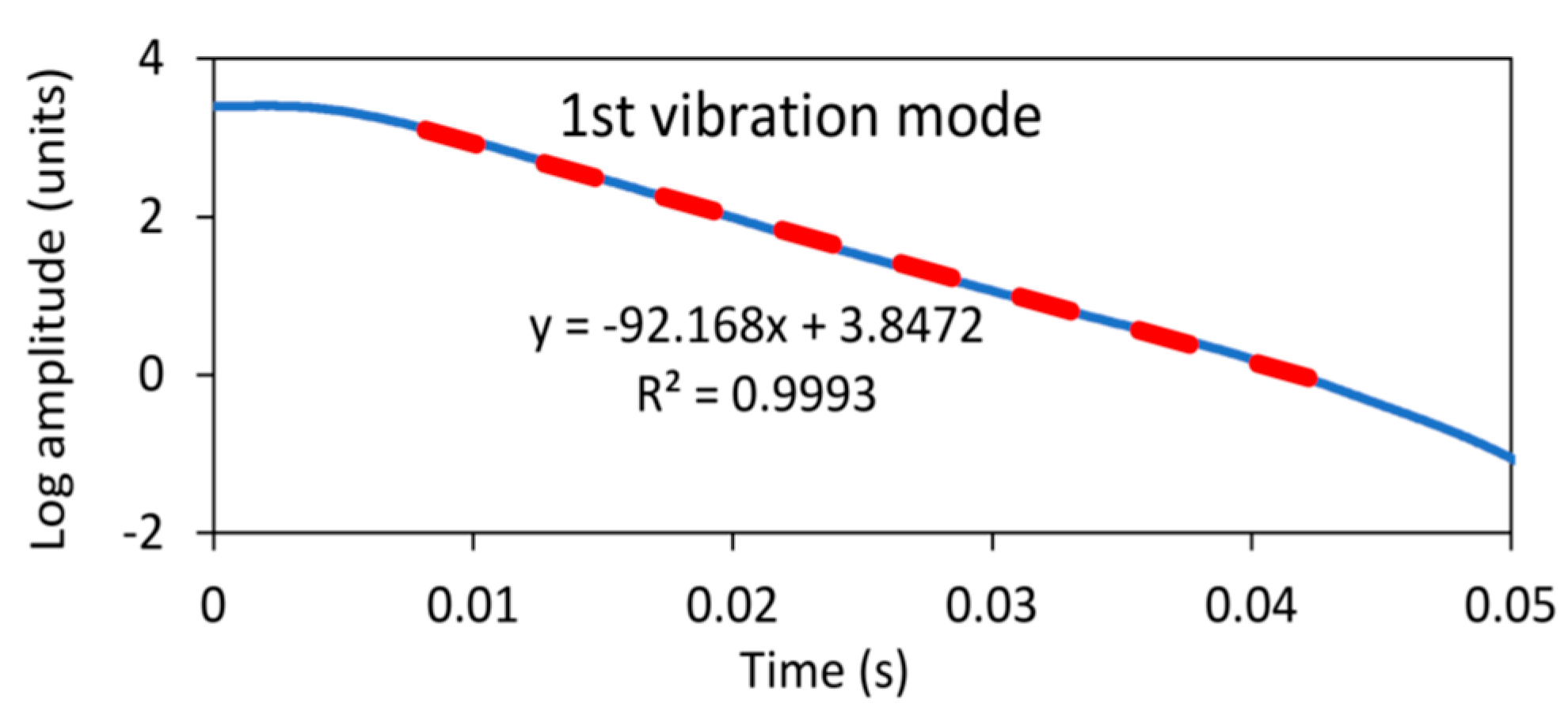
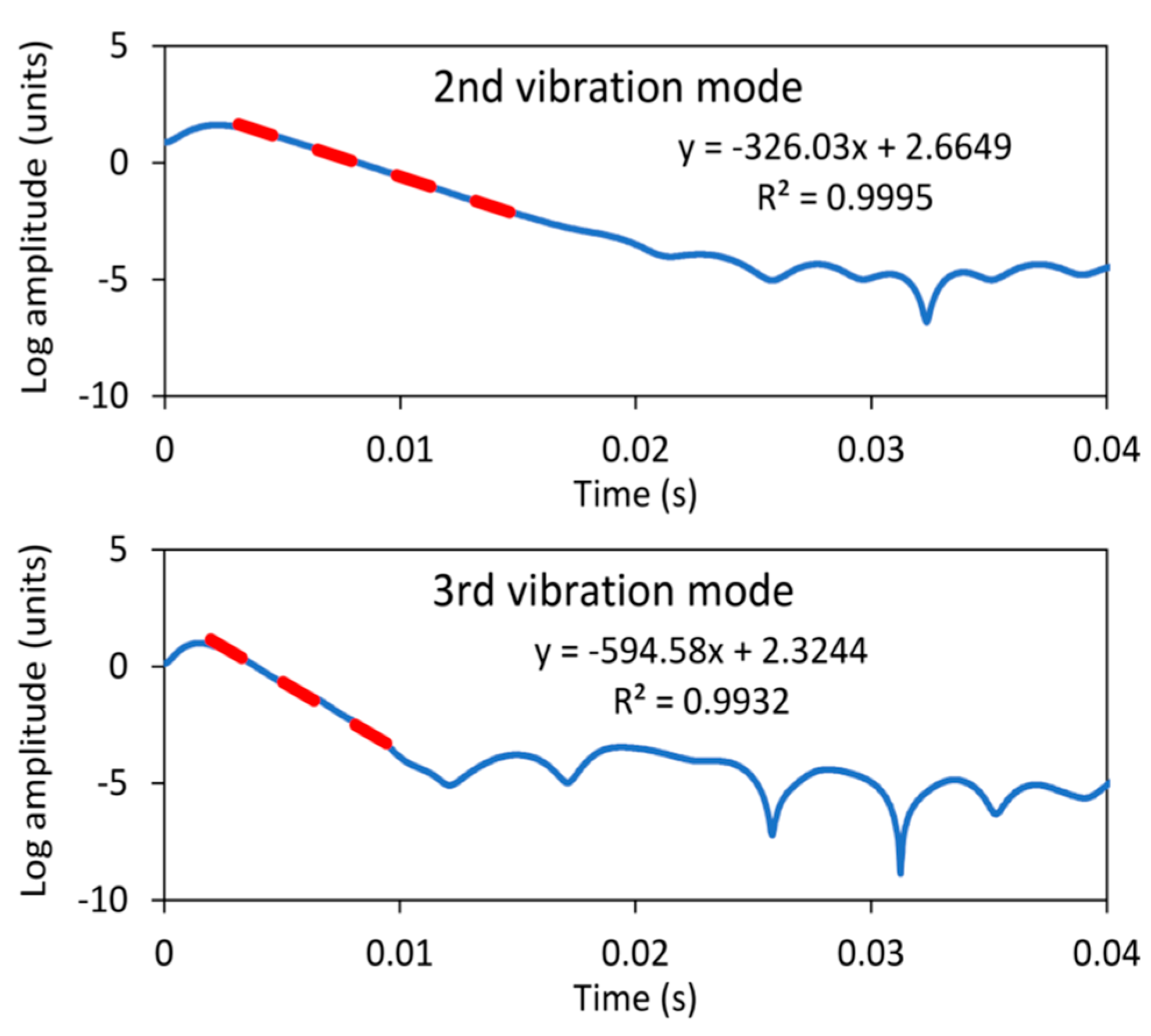
2.3. Damping Determination
2.4. Statistical Analysis
3. Results and Discussion
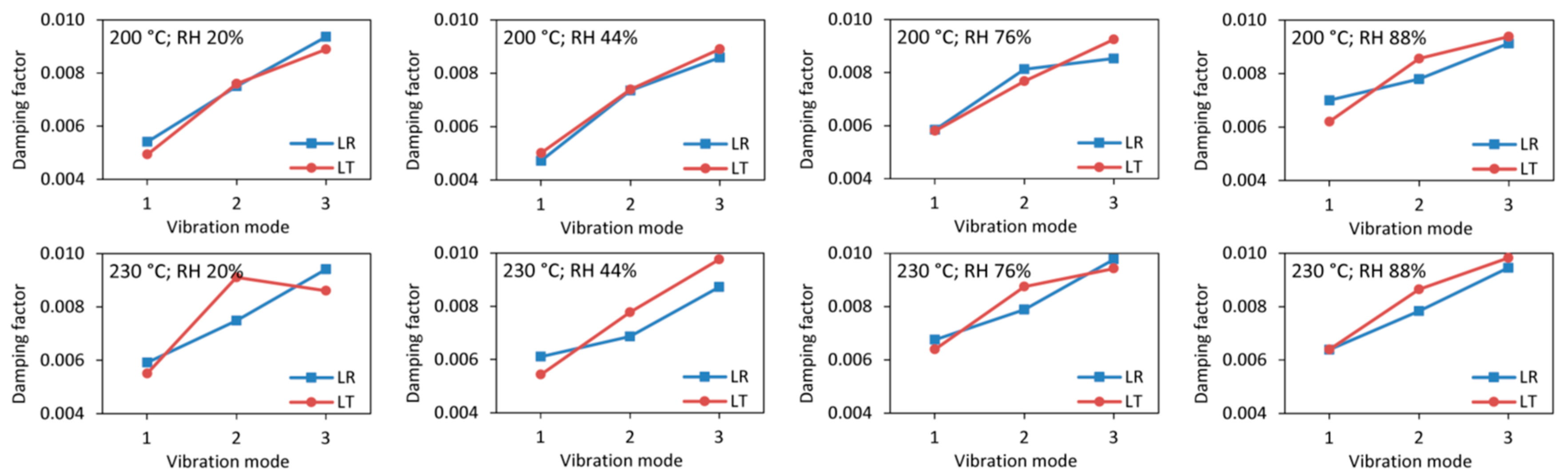
3.1. Damping Values
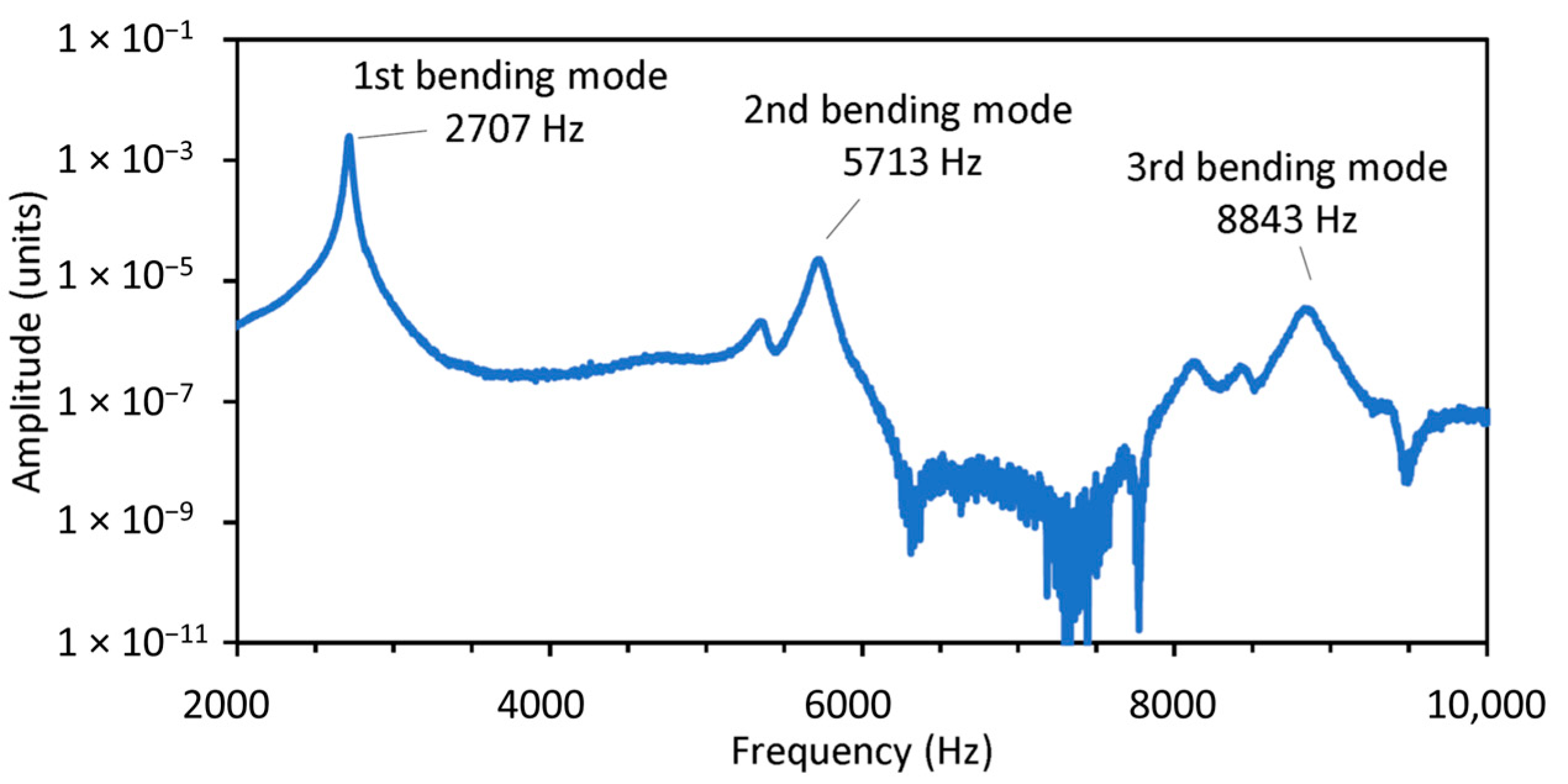
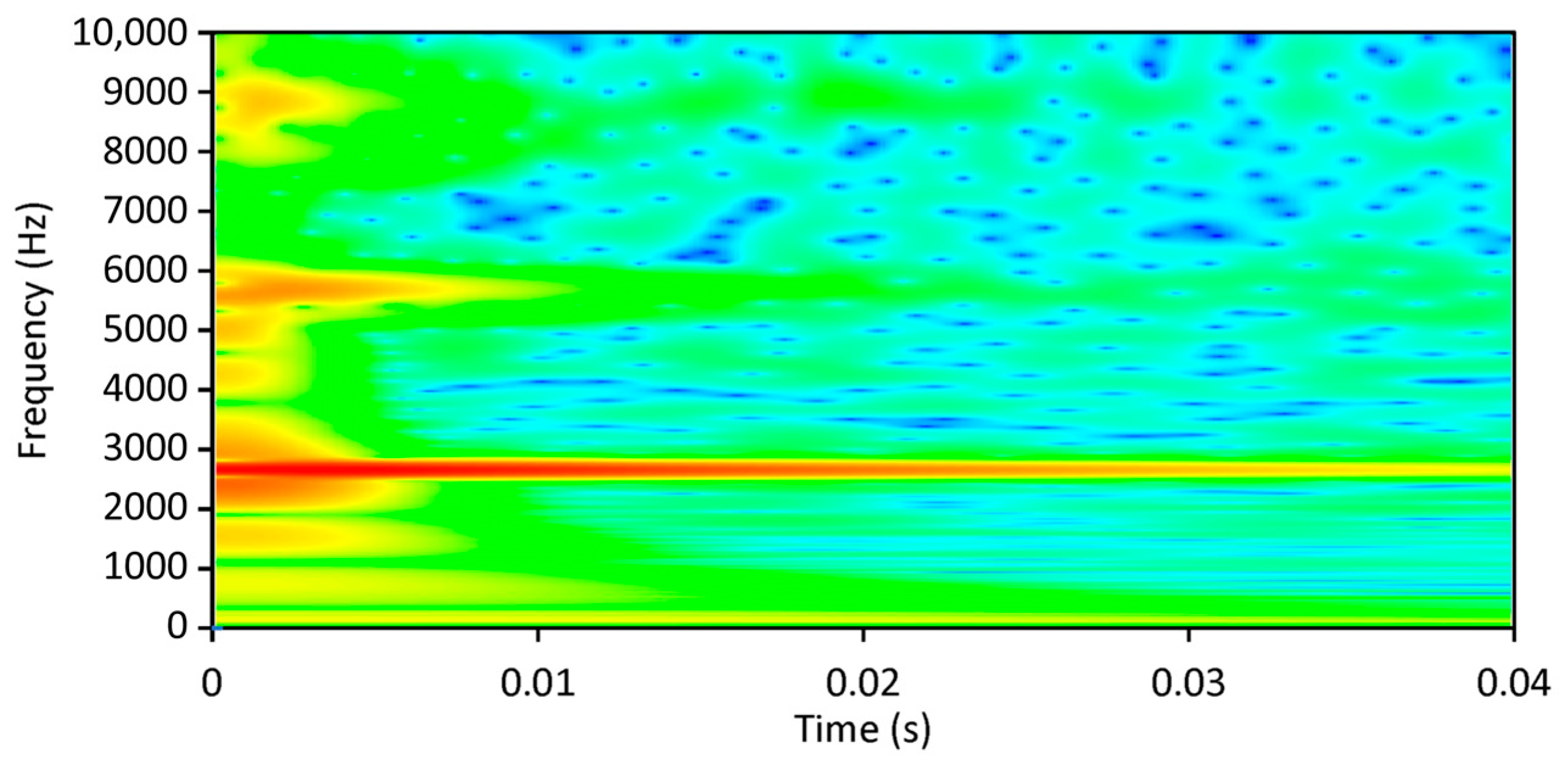
3.2. WT Damping Identification Process
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Tiemann, A.; Zhang, T.; Gauthier, T.; Hsu, K.; Mahamid, M.; Moniruzzaman, P.K.; Ozevin, D. Nondestructive assessment of cross-laminated timber using non-contact transverse vibration and ultrasonic testing. Eur. J. Wood Wood Prod. 2021, 79, 335–347. [Google Scholar] [CrossRef]
- Brémaud, I. Acoustical properties of wood in string instruments soundboards and tuned idiophones: Biological and cultural diversity. J. Acoust. Soc. Am. 2012, 131, 807–818. [Google Scholar] [CrossRef] [PubMed]
- Brémaud, I.; El Kaïm, Y.; Guibal, D.; Minato, K.; Thibaut, B.; Gril, J. Characterisation and categorisation of the diversity in viscoelastic vibrational properties between 98 wood types. Ann. For. Sci. 2012, 69, 373–386. [Google Scholar] [CrossRef]
- Brémaud, I.; Gril, J. Moisture content dependence of anisotropic vibrational properties of wood at quasi equilibrium: Analytical review and multi-trajectories experiments. Holzforschung 2021, 75, 313–327. [Google Scholar] [CrossRef]
- Ahmed, S.A.; Adamopoulos, S. Acoustic properties of modified wood under different humid conditions and their relevance for musical instruments. Appl. Acoust. 2018, 140, 92–99. [Google Scholar] [CrossRef]
- Obataya, E.; Norimoto, M.; Gril, J. The effects of adsorbed water on dynamic mechanical properties of wood. Polymer 1998, 39, 3059–3064. [Google Scholar] [CrossRef]
- Yano, H.; Minato, K. Improvement of the acoustic and hygroscopic properties of wood by a chemical treatment and application to the violin parts. J. Acoust. Soc. Am. 1992, 92, 1222–1227. [Google Scholar] [CrossRef]
- Ono, T.; Norimoto, M. Study on young’s modulus and internal friction of wood in relation to the evaluation of wood for musical instruments. Jpn. J. Appl. Phys. 1983, 22, 611–614. [Google Scholar] [CrossRef]
- Kollmann, F.; Krech, H. Dynamic measurement of damping capacity and elastic properties of wood. Eur. J. Wood Wood Prod. 1960, 18, 41–54. [Google Scholar] [CrossRef]
- Wegst, U.G.K. Wood for sound. Am. J. Bot. 2006, 93, 1439–1448. [Google Scholar] [CrossRef]
- Merhar, M.; Humar, M. The influence of wood modification on transfer function of a violin bridge. Drv. Ind. 2020, 71, 163–169. [Google Scholar] [CrossRef]
- Sproßmann, R.; Zauer, M.; Wagenführ, A. Characterization of acoustic and mechanical properties of common tropical woods used in classical guitars. Results Phys. 2017, 7, 1737–1742. [Google Scholar] [CrossRef]
- Gurău, L.; Timar, M.C.; Coșereanu, C.; Cosnita, M.; Stanciu, M.D. Aging of Wood for Musical Instruments: Analysis of Changes in Color, Surface Morphology, Chemical, and Physical-Acoustical Properties during UV and Thermal Exposure. Polymers 2023, 15, 1794. [Google Scholar] [CrossRef] [PubMed]
- Thomson, W.T.; Dahleh, M.D. Theory of Vibration with Applications, 5th ed.; Prentice Hall: New York, NY, USA, 1998; p. 524. [Google Scholar]
- Bekhta, P.; Niemz, P. Effect of high temperature on the change in color, dimensional stability and mechanical properties of spruce wood. Holzforschung 2003, 57, 539–546. [Google Scholar] [CrossRef]
- Tjeerdsma, B.F.; Boonstra, M.; Pizzi, A.; Tekely, P.; Militz, H. Characterisation of thermally modified wood: Molecular reasons for wood performance improvement. Eur. J. Wood Wood Prod. 1998, 56, 149–153. [Google Scholar] [CrossRef]
- Andor, T.; Lagaňa, R. Selected properties of thermally treated ash wood. Acta Fac. Xylologiae 2018, 60, 51–60. [Google Scholar] [CrossRef]
- Kurul, F.; Görgün, H.V. Effect of Thermal Modification on Some Physical and Mechanical Properties of Yellow Poplar (Liriodendron tulipifera). Drewno 2022, 65, 1–11. [Google Scholar] [CrossRef]
- Molinski, W.; Roszyk, E.; Jablonski, A.; Puszynski, J.; Cegiela, J. Mechanical parameters of thermally modified ash wood determined on compression in tangential direction. Maderas Cienc. Tecnol. 2018, 20, 267–276. [Google Scholar] [CrossRef]
- Nhacila, F.; Sitoe, E.; Uetimane, E.; Manhica, A.; Egas, A.; Möttönen, V. Effects of thermal modification on physical and mechanical properties of Mozambican Brachystegia spiciformis and Julbernardia globiflora wood. Eur. J. Wood Wood Prod. 2020, 78, 871–878. [Google Scholar] [CrossRef]
- Roszyk, E.; Stachowska, E.; Majka, J.; Mania, P.; Broda, M. Moisture-dependent strength properties of thermally-modified Fraxinus excelsior wood in compression. Materials 2020, 13, 1647. [Google Scholar] [CrossRef]
- Wang, X.; Chen, X.; Xie, X.; Wu, Y.; Zhao, L.; Li, Y.; Wang, S. Effects of thermal modification on the physical, chemical and micromechanical properties of Masson pine wood (Pinus massoniana Lamb.). Holzforschung 2018, 72, 1063–1070. [Google Scholar] [CrossRef]
- Merhar, M.; Pitti, R.M.; Argensse, T. Mode I fracture properties of thermally-modified spruce wood (Picea abies) at different moisture contents. Wood Mat. Sci. Eng. 2023, 18, 2093–2103. [Google Scholar] [CrossRef]
- Zauer, M.; Kowalewski, A.; Sproßmann, R.; Stonjek, H.; Wagenführ, A. Thermal modification of European beech at relatively mild temperatures for the use in electric bass guitars. Eur. J. Wood Wood Prod. 2016, 74, 43–48. [Google Scholar] [CrossRef]
- Mania, P.; Skrodzka, E. Modal parameters of resonant spruce wood (Picea abies L.) after thermal treatment. J. King Saud. Univ. Sci. 2020, 32, 1152–1156. [Google Scholar] [CrossRef]
- Danihelová, A.; Vidholdová, Z.; Gergeľ, T.; Spišiaková Kružlicová, L.; Pástor, M. Thermal Modification of Spruce and Maple Wood for Special Wood Products. Polymers 2022, 14, 2813. [Google Scholar] [CrossRef]
- Buchelt, B.; Krüger, R.; Wagenführ, A. The vibrational properties of native and thermally modified wood in dependence on its moisture content. Eur. J. Wood Wood Prod. 2023, 81, 947–956. [Google Scholar] [CrossRef]
- Thybring, E.E.; Fredriksson, M. Wood modification as a tool to understand moisture in wood. Forests 2021, 12, 372. [Google Scholar] [CrossRef]
- Stanciu, M.D.; Sova, D.; Savin, A.; Ilias, N.; Gorbacheva, G.A. Physical and mechanical properties of ammonia-treated black locust wood. Polymers 2020, 12, 377. [Google Scholar] [CrossRef] [PubMed]
- Tian, F.; Xu, X. Dynamical mechanical behaviors of rubber-filled wood fiber composites with urea formaldehyde resin. J. Bioresour. Bioprod. 2022, 7, 320–327. [Google Scholar] [CrossRef]
- Mihalcica, M.; Stanciu, M.D.; Teodorescu, H.D.; Iftimie, N. Evaluation of viscous-elastic properties of resonance maple wood. Int. J. Mod. Manuf. Technol. 2022, 14, 145–150. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, J.; Wang, Z.; Hua, F.; He, S.; Lu, B.; Wang, X.; Zhang, X.; Leng, W. Microstructural and Thermo-Mechanical Characterization of Furfurylated Douglas Fir. Polymers 2022, 14, 4641. [Google Scholar] [CrossRef]
- Lunguleasa, A.; Spirchez, C. Influence of Thermal Treatment on Properties of Ash Wood. Forests 2025, 16, 155. [Google Scholar] [CrossRef]
- Dong, H.; Hasanagić, R.; Fathi, L.; Bahmani, M.; Kržišnik, D.; Keržič, E.; Humar, M. Selected Mechanical and Physical Properties of Thermally Modified Wood after Field Exposure Tests. Forests 2023, 14, 1006. [Google Scholar] [CrossRef]
- Piersol, A.; Paez, T. Harris’ Shock and Vibration Handbook, 6th ed.; McGraw Hill: New York, NY, USA, 2009. [Google Scholar]
- Staszewski, W.J. Identification of damping in MDOF systems using time-scale decomposition. J. Sound Vib. 1997, 203, 283–305. [Google Scholar] [CrossRef]
- Hamdi, S.E.; Sbartaï, Z.M.; Elachachi, S.M. Performance assessment of modal parameters identification methods for timber structures evaluation: Numerical modeling and case study. Wood Sci. Technol. 2021, 55, 1593–1618. [Google Scholar] [CrossRef]
- Ruzzene, M.; Fasana, A.; Garibaldi, L.; Piombo, B. Natural frequencies and dampings identification using wavelet transform: Application to real data. Mech. Syst. Signal Process. 1997, 11, 207–218. [Google Scholar] [CrossRef]
- Tomac, I.; Slavič, J. Morlet-wave-based modal identification in the time domain. Mech. Syst. Signal Process. 2023, 192, 110243. [Google Scholar] [CrossRef]
- Chandra, N.H.; Sekhar, A.S. Nonlinear damping identification in rotors using wavelet transform. Mech. Mach. Theory 2016, 100, 170–183. [Google Scholar] [CrossRef]
- Merhar, M. Identification of Damping of Spruce Wood (Picea abies) under Various Levels of Moisture Content Using Time-Scale Decomposition. Polymers 2024, 16, 1313. [Google Scholar] [CrossRef]
- Chen, S.L.; Liu, J.J.; Lai, H.C. Wavelet analysis for identification of damping ratios and natural frequencies. J. Sound Vib. 2009, 323, 130–147. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, W.; Zhang, G.; Xu, H.; Du, Y. Identification of structural parameters from free vibration data using Gabor wavelet transform. Mech. Syst. Signal Process. 2021, 147, 107122. [Google Scholar] [CrossRef]
- Ashory, M.R.; Khatibi, M.M.; Jafari, M.; Malekjafarian, A. Determination of mode shapes using wavelet transform of free vibration data. Arch. Appl. Mech. 2013, 83, 907–921. [Google Scholar] [CrossRef]
- Slavič, J.; Simonovski, I.; Boltežar, M. Damping identification using a continuous wavelet transform: Application to real data. J. Sound Vib. 2003, 262, 291–307. [Google Scholar] [CrossRef]
- Li, M.; Wang, M.; Ding, R.; Deng, T.; Fang, S.; Lai, F.; Luoi, R. Study of acoustic emission propagation characteristics and energy attenuation of surface transverse wave and internal longitudinal wave of wood. Wood Sci. Technol. 2021, 55, 1619–1637. [Google Scholar] [CrossRef]
- Rep, G.; Pohleven, F.; Kosmerl, S. Development of the industrial kiln for thermal wood modification by a procedure with an initial vacuum and commercialisation of modified Silvapro wood. In Proceedings of the 6th European Conference on Wood Modification, Ljubljana, Slovenia, 16–18 September 2012; pp. 11–17. [Google Scholar]
- Chui, C.K. An Introduction to Wavelets, 1st ed.; Academic Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Daubechies, I. The Wavelet Transform, Time-Frequency Localization and Signal Analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Tchamitchian, P.; Torresani, B. Ridge and skeleton extraction from the wavelet transform. In Proceedings of the CBMS-NSF Conference ‘Wavelets and Their Applications’, Lowell, MA, USA, 5–9 November 1990. [Google Scholar]
- Arnold, M. Effect of moisture on the bending properties of thermally modified beech and spruce. J. Mater. Sci. 2010, 45, 669–680. [Google Scholar] [CrossRef]
- Özgenç, Ö.; Durmaz, S.; Boyaci, I.H.; Eksi-Kocak, H. Determination of chemical changes in heat-treated wood using ATR-FTIR and FT Raman spectrometry. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2017, 171, 395–400. [Google Scholar] [CrossRef] [PubMed]
- Hosseinaei, O.; Wang, S.; Enayati, A.A.; Rials, T.G. Effects of hemicellulose extraction on properties of wood flour and wood-plastic composites. Compos. Part A 2012, 43, 686–694. [Google Scholar] [CrossRef]
- Obataya, E. Effects of natural and artificial ageing on the physical and acoustic properties of wood in musical instruments. J. Cult. Heritage 2017, 27, S63–S69. [Google Scholar] [CrossRef]
- Nop, P.; Tippner, J. Influence of dimensions of wooden samples for determination of acoustic parameters and sound timbre. Appl. Acoust. 2022, 196, 108895. [Google Scholar] [CrossRef]
- Longo, R.; Laux, D.; Pagano, S.; Delaunay, T.; Le Clézio, E.; Arnould, O. Elastic characterization of wood by Resonant Ultrasound Spectroscopy (RUS): A comprehensive study. Wood Sci. Technol. 2018, 52, 383–402. [Google Scholar] [CrossRef]
- Liu, M.; Lyu, S.; Cai, L.; Lei, Y.; Peng, L.; Yan, L.; Lyu, J. Acoustic and viscoelastic properties of string instrument fretboards made of radiata pine by densification and impregnation with furfuryl alcohol resin. Eur. J. Wood Wood Prod. 2024, 82, 285–297. [Google Scholar] [CrossRef]







| TM | RH | |||
|---|---|---|---|---|
| 20% | 44% | 76% | 88% | |
| A (untreated) | 7.2 | 9.9 | 13.3 | 19.1 |
| B (modified 180 °C) | 5.0 | 6.6 | 10.7 | 16.2 |
| C (modified 200 °C) | 4.0 | 5.7 | 8.8 | 11.8 |
| D (modified 230 °C) | 3.8 | 5.7 | 8.5 | 10.5 |
| TM | VM | LR Vibration Plane | LT Vibration Plane | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RH | RH | ||||||||
| 20% | 44% | 76% | 88% | 20% | 44% | 76% | 88% | ||
| A | 1 | 0.0057 | 0.0050 | 0.0063 | 0.0065 | 0.0048 | 0.0050 | 0.0056 | 0.0060 |
| (20.6) | (15.8) | (19.1) | (15.5) | (18.4) | (33.1) | (13.2) | (9.6) | ||
| 2746 | 2673 | 2686 | 2678 | 2746 | 2698 | 2658 | 2530 | ||
| (3) | (4.2) | (3.8) | (2.4) | (3.1) | (3) | (2.1) | (2.9) | ||
| 2 | 0.0064 | 0.0056 | 0.0078 | 0.0080 | 0.0076 | 0.0070 | 0.0080 | 0.0082 | |
| (8.2) | (37.4) | (6.8) | (6.4) | (19.5) | (24.9) | (12.9) | (15.5) | ||
| 5838 | 5770 | 5833 | 5566 | 5908 | 5793 | 5618 | 5361 | ||
| (3.4) | (3.6) | (1.7) | (1.7) | (1.4) | (1.6) | (1) | (1.2) | ||
| 3 | 0.0070 | 0.0074 | 0.0088 | 0.0094 | 0.0081 | 0.0080 | 0.0096 | 0.0097 | |
| (12.2) | (13.9) | (15.8) | (12) | (7.8) | (15.2) | (5.6) | (12.5) | ||
| 9039 | 9041 | 9038 | 8495 | 9275 | 9060 | 8617 | 8291 | ||
| (4) | (3.1) | (4.6) | (1.3) | (1.4) | (1.2) | (1.8) | (0.7) | ||
| B | 1 | 0.0057 | 0.0058 | 0.0067 | 0.0067 | 0.0047 | 0.0052 | 0.0055 | 0.0059 |
| (26) | (29.3) | (25.8) | (32) | (17.7) | (19) | (13.4) | (13.6) | ||
| 2693 | 2793 | 2643 | 2526 | 2665 | 2790 | 2680 | 2531 | ||
| (6.4) | (1) | (2.2) | (4.6) | (5.4) | (1.8) | (2.6) | (4.2) | ||
| 2 | 0.0072 | 0.0068 | 0.0072 | 0.0080 | 0.0072 | 0.0060 | 0.0077 | 0.0090 | |
| (10.6) | (9.5) | (12.3) | (9.2) | (17.7) | (19.6) | (10.7) | (13.8) | ||
| 5853 | 6052 | 5875 | 5567 | 5959 | 5985 | 5760 | 5459 | ||
| (3.9) | (1.8) | (1.1) | (2) | (2.8) | (1.9) | (1) | (2.7) | ||
| 3 | 0.0075 | 0.0085 | 0.0094 | 0.0088 | 0.0088 | 0.0086 | 0.0083 | 0.0096 | |
| (14) | (9.5) | (13.1) | (17.7) | (12.9) | (12) | (19.2) | (8.9) | ||
| 9258 | 9466 | 9249 | 8848 | 9479 | 9322 | 8979 | 8730 | ||
| (6.3) | (2.7) | (4.2) | (3.6) | (6) | (3.3) | (2.2) | (6.1) | ||
| C | 1 | 0.0054 | 0.0047 | 0.0058 | 0.0070 | 0.0049 | 0.0050 | 0.0058 | 0.0062 |
| (19.8) | (16.4) | (16.2) | (24.7) | (9.3) | (15.2) | (22.8) | (18.3) | ||
| 2769 | 2782 | 2716 | 2593 | 2813 | 2783 | 2700 | 2600 | ||
| (2.3) | (1.7) | (2.2) | (3.3) | (1.7) | (2.3) | (1.8) | (2.1) | ||
| 2 | 0.0075 | 0.0074 | 0.0081 | 0.0078 | 0.0076 | 0.0074 | 0.0077 | 0.0086 | |
| (9.7) | (18.5) | (11.1) | (9.3) | (12.8) | (24.5) | (9.8) | (11.9) | ||
| 6121 | 6076 | 5843 | 5639 | 6077 | 6000 | 5800 | 5563 | ||
| (2.3) | (1.4) | (2.3) | (2.2) | (1) | (2.3) | (1) | (1.7) | ||
| 3 | 0.0094 | 0.0086 | 0.0085 | 0.0091 | 0.0089 | 0.0089 | 0.0092 | 0.0094 | |
| (15.3) | (14.2) | (13.9) | (12.4) | (13.7) | (14.7) | (9) | (14) | ||
| 9573 | 9536 | 9154 | 8882 | 9499 | 9320 | 9051 | 8757 | ||
| (4) | (3) | (3.8) | (4.3) | (3) | (2.9) | (2.9) | (3.4) | ||
| D | 1 | 0.0059 | 0.0061 | 0.0068 | 0.0064 | 0.0055 | 0.0054 | 0.0064 | 0.0064 |
| (25.8) | (24.4) | (14.4) | (20.1) | (29.8) | (16.2) | (16.2) | (23.5) | ||
| 2764 | 2765 | 2682 | 2635 | 2757 | 2757 | 2688 | 2644 | ||
| (3.5) | (1.6) | (2.5) | (3.9) | (3) | (2.3) | (3) | (2) | ||
| 2 | 0.0075 | 0.0069 | 0.0079 | 0.0078 | 0.0091 | 0.0078 | 0.0087 | 0.0086 | |
| (21.5) | (20.6) | (11.2) | (10.9) | (19) | (10.8) | (6) | (18.3) | ||
| 5996 | 5983 | 5905 | 5733 | 5900 | 5937 | 5880 | 5651 | ||
| (4.2) | (2.2) | (2.7) | (2) | (4.5) | (0.9) | (1.2) | (1.2) | ||
| 3 | 0.0094 | 0.0087 | 0.0098 | 0.0095 | 0.0086 | 0.0098 | 0.0094 | 0.0098 | |
| (14.7) | (10.3) | (19.1) | (15.3) | (18.5) | (18.1) | (13.5) | (13.2) | ||
| 9302 | 9352 | 9436 | 9044 | 8989 | 9253 | 9412 | 8773 | ||
| (6.3) | (1.5) | (3.9) | (3.5) | (7.3) | (1.1) | (4.2) | (2.2) | ||
| Source | Type III Sum of Squares | df | Mean Square | F | Sig. |
|---|---|---|---|---|---|
| Corrected Model | 0.002 | 95 | 2.04 × 10−5 | 14.15 | 0.000 |
| Intercept | 0.048 | 1 | 0.048 | 33672.45 | 0.000 |
| TM | 5.91 × 10−5 | 3 | 1.97 × 10−5 | 13.69 | 0.000 |
| VD | 2.49 × 10−6 | 1 | 2.49 × 10−6 | 1.73 | 0.189 |
| RH | 0.000 | 3 | 6.15 × 10−5 | 42.76 | 0.000 |
| VM | 0.001 | 2 | 0.001 | 497.91 | 0.000 |
| TM × VD | 6.93 × 10−6 | 3 | 2.31 × 10−6 | 1.60 | 0.187 |
| TM × RH | 2.99 × 10−5 | 9 | 3.32 × 10−6 | 2.30 | 0.015 |
| TM × VM | 9.24 × 10−6 | 6 | 1.54 × 10−6 | 1.07 | 0.379 |
| VD × RH | 3.64 × 10−6 | 3 | 1.21 × 10−6 | 0.84 | 0.470 |
| VD × VM | 4.41 × 10−5 | 2 | 2.20 × 10−5 | 15.31 | 0.000 |
| RH × VM | 1.35 × 10−5 | 6 | 2.25 × 10−6 | 1.56 | 0.155 |
| TM × VD × RH | 1.09 × 10−5 | 9 | 1.22 × 10−6 | 0.84 | 0.575 |
| TM × VD × VM | 1.25 × 10−5 | 6 | 2.08 × 10−6 | 1.44 | 0.195 |
| TM × RH × VM | 3.33 × 10−5 | 18 | 1.85 × 10−6 | 1.29 | 0.189 |
| VD × RH × VM | 4.09 × 10−6 | 6 | 6.82 × 10−7 | 0.47 | 0.828 |
| TM × VD × RH × VM | 3.43 × 10−5 | 18 | 1.91 × 10−6 | 1.32 | 0.164 |
| Error | 0.001 | 801 | 1.44 × 10−6 | ||
| Total | 0.053 | 897 | |||
| Corrected Total | 0.003 | 896 |
| TM | VM | LR Vibration Plane | LT Vibration Plane | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RH | RH | ||||||||
| 20% | 44% | 76% | 88% | 20% | 44% | 76% | 88% | ||
| A | 1 | abcdefghi | abcd | cdefghijklmno | fghijklmnopqr | ab | abcd | abcdefgh | abcdefghijkl |
| 2 | defghijklmnop | abcdefghi | pqrstvwxyzABCD | stvwxyzABCDEFG | nopqrstvwxyzAB | ijklmnopqrstvw | stvwxyzABCDEF | vwxyzABCDEFGHI | |
| 3 | ijklmnopqrstvw | lmnopqrstvwxyz | ABCDEFGHIJ | GHIJ | stvwxyzABCDEFGH | stvwxyzABCDE | IJ | J | |
| B | 1 | abcdefghi | abcdefghijk | ghijklmnopqrs | ghijklmnopqrs | a | abcdef | abcdefgh | abcdefghijk |
| 2 | klmnopqrstvwxy | ghijklmnopqrst | jklmnopqrstvwx | stvwxyzABCDEF | jklmnopqrstvwx | abcdefghijkl | opqrstvwxyzABC | CDEFGHIJ | |
| 3 | nopqrstvwxyzAB | xyzABCDEFGHIJ | GHIJ | zABCDEFGHIJ | zABCDEFGHIJ | zABCDEFGHIJ | wxyzABCDEFGHI | IJ | |
| C | 1 | abcdefg | ab | abcdefghijk | ijklmnopqrstvw | abc | abcde | abcdefghij | cdefghijklmn |
| 2 | nopqrstvwxyzAB | lmnopqrstvwxyz | tvwxyzABCDEFGH | rstvwxyzABCD | nopqrstvwxyzAB | lmnopqrstvwxyz | opqrstvwxyzABC | yzABCDEFGHIJ | |
| 3 | FGHIJ | yzABCDEFGHIJ | xyzABCDEFGHIJ | DEFGHIJ | ABCDEFGHIJ | BCDEFGHIJ | EFGHIJ | GHIJ | |
| D | 1 | abcdefghijk | bcdefghijklm | ghijklmnopqrst | efghijklmnopq | abcdefgh | abcdefg | efghijklmnopq | efghijklmnopq |
| 2 | mnopqrstvwxyzA | hijklmnopqrstv | rstvwxyzABCDE | rstvwxyzABCD | DEFGHIJ | qrstvwxyzABCD | zABCDEFGHIJ | zABCDEFGHIJ | |
| 3 | GHIJ | zABCDEFGHIJ | J | HIJ | yzABCDEFGHIJ | J | HIJ | J | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Merhar, M.; Moutou Pitti, R. The Influence of Thermal Modification, Moisture Content, Frequency, and Vibration Direction Plane on the Damping of Spruce Wood (Picea abies) as Determined by the Wavelet Transform Method. Forests 2025, 16, 1055. https://doi.org/10.3390/f16071055
Merhar M, Moutou Pitti R. The Influence of Thermal Modification, Moisture Content, Frequency, and Vibration Direction Plane on the Damping of Spruce Wood (Picea abies) as Determined by the Wavelet Transform Method. Forests. 2025; 16(7):1055. https://doi.org/10.3390/f16071055
Chicago/Turabian StyleMerhar, Miran, and Rostand Moutou Pitti. 2025. "The Influence of Thermal Modification, Moisture Content, Frequency, and Vibration Direction Plane on the Damping of Spruce Wood (Picea abies) as Determined by the Wavelet Transform Method" Forests 16, no. 7: 1055. https://doi.org/10.3390/f16071055
APA StyleMerhar, M., & Moutou Pitti, R. (2025). The Influence of Thermal Modification, Moisture Content, Frequency, and Vibration Direction Plane on the Damping of Spruce Wood (Picea abies) as Determined by the Wavelet Transform Method. Forests, 16(7), 1055. https://doi.org/10.3390/f16071055






