Abstract
Trees play a vital role in urban environments by mitigating heat islands, floods, and pollution, while promoting public health and well-being. Acoustic tomography is an effective tool for assessing tree integrity, but its high-cost limits widespread use. To reduce costs, this study evaluated the use of ultrasonic tomography with standardized velocity thresholds (VTs) for detecting cavities and decay in trunks. A total of 38 discs from 21 trees species were analyzed using different VTs (35%, 40%, 45%, and 50%). The results showed that thresholds of 35% Vmax for cavity detection and 50% Vmax for cavity with decay detection can be adopted for tomographic image assessments of trees, regardless of species. Using the same velocity thresholds regardless of species enables the practical application of the technology, with average accuracy losses (below 5%) that are quite reasonable considering the variability of the material under inspection. These findings support the broader use of technology in tree failure risk assessments.
1. Introduction
Trees are fundamental elements in urban environments, contributing in multiple ways by reducing heat islands [1], mitigating floods [2], and lowering pollution levels, while also promoting public health and well-being [3,4,5]. However, being large living organisms, trees can cause severe accidents if they fall, potentially damaging infrastructure and endangering people [6,7,8,9].
One of the primary strategies to prevent tree failure is regular inspection aimed at detecting signs of decay. These inspections can range from visual assessments to advanced techniques involving equipment of varying levels of technological sophistication [9,10,11,12].
Among these techniques, acoustic tomography is one of the most widely applied as it enables the internal condition of the trunk to be imaged, allowing inferences about the presence and location of decay [9]. Acoustic tomography can use either stress waves or ultrasonic waves, with stress waves being more common in commercial equipment [13,14,15]. However, the main drawback of commercial tomography systems is their high cost, which limits their use by municipalities with constrained budgets and small service providers. As a result, research has been directed towards simplified technologies that aim to provide reliable results without compromising accuracy [16,17].
It is important to note that, like any technology, tomography is an inference tool and not an exact diagnostic method [18]. Even commercial tomographs are subject to interference that can affect their ability to accurately detect defects [19,20,21]. The literature reports issues such as defect merging when they are closely spaced [22], inaccuracies in representing irregular defects [16,21,23], and the enlargement of defects in the presence of cracks [24,25]. Improvements to these systems often require access to design details which are typically unavailable in commercial devices due to proprietary technology. Advances can also be made through the development of new algorithms, including the application of machine learning techniques [21].
To guide technological improvements, objective evaluation metrics are essential. In imaging studies, evaluations often rely on visual comparisons between tomographic and real cross-sectional images of tree trunks [19,26,27,28,29]. However, this approach does not allow for objective validation. The confusion matrix is a metric used to assess the performance of classification models and can also be applied to compare tomographic images with ground-truth images [15,16,17,25,30].
For homogeneous, isotropic materials with low variability—such as metals—it is possible to use fixed reference values for wave propagation velocity to assess material integrity [31,32,33]. Deviations from this reference may indicate defects. In wood, however, a fixed velocity reference is less viable due to variability between species, within species, and even within the same tree, both longitudinally and radially [34,35,36,37]. One way to work around this is to use the wood sample itself as a reference. In studies conducted by our research group the maximum velocity (Vmax) observed in the measurement grid is used as a reference to evaluate internal variation within the cross-section [16,17].
In previous research [17] applying this methodology to a single species (Cenostigma pluviosum (DC.) Gagnon & G.P.Lewis) it was found that the most accurate tomographic images for cavity detection were obtained when using velocity thresholds (VTs) of up to 40% of Vmax. For zones containing both cavities and associated decay the optimal threshold was up to 45% of Vmax.
Building on the methodology proposed and applied to a single species [17], this study aimed to determine, for different tree species, the velocity thresholds that yield the highest accuracy in identifying cavities and biodeterioration. The feasibility of standardizing velocity thresholds regardless of species was assessed by quantifying the loss of accuracy.
2. Materials and Methods
2.1. Experimental Design
The research followed the experimental design outlined in Figure 1.

Figure 1.
Experimental design.
2.2. Sampling
The sample set consisted of 38 discs obtained from the trunks of 21 tree species, including 19 sound discs and 19 defective discs (Table 1). All the discs were approximately 200 mm thick. The trees were all located on the campus of the State University of Campinas (UNICAMP) in the city of Campinas, Brazil, at coordinates 22°49′38″ S, 47°04′04″ W. The trees were cut down not only due to phytosanitary conditions but also for other reasons, such as construction works, installation of urban equipment, and hazardous surroundings, among others.

Table 1.
List of species with respective basic densities and details of sound and defective discs.
2.3. Methodology
2.3.1. Tests
The perimeter (P) of the discs was measured to determine the number of measurement points in the diffraction mesh (Figure 2). The number of measurement points (n) was calculated using Equation (1), as proposed by [16]. Based on Equation (1) the number of points in the diffraction mesh ranged from 8 to 12 (Table 2). It is important to emphasize that, according to [16], the number of points must be even to ensure radial paths, and the minimum number of points to be used is 8.
n = 5 P
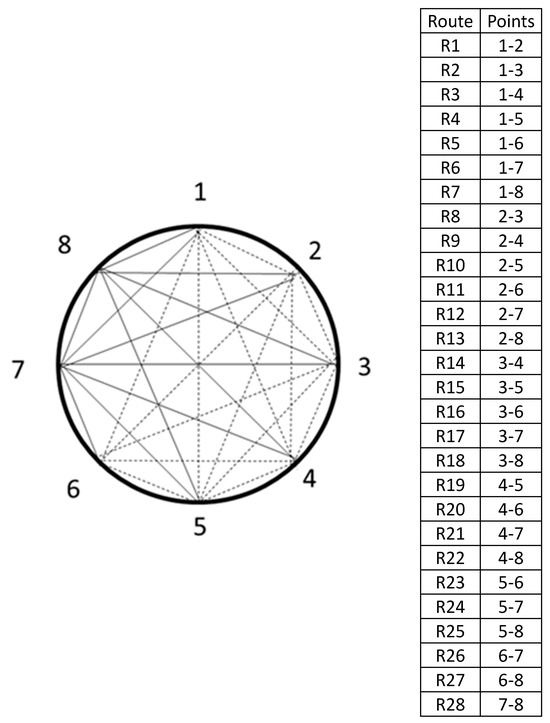
Figure 2.
Example of diffraction mesh with 8 measurement points and 28 theoretical wave propagations routes.

Table 2.
Data of the discs by species.
Measurements were taken at only one height of the disc, just below the surface (approximately 20 mm), meaning the analysis was conducted in a 2D manner. Although this methodology allows for the generation of 3D images through measurements at multiple heights, this was not performed in the present study. The objective was to evaluate the correspondence between the tomographic image and the actual defects observed on the surface near the measurement plane.
2.3.2. Tomographic Images
To generate tomographic images, a software developed by the research group (GPEND) called ImageWood (version 3.1, Campinas, Brazil) was used. To process the data, the programme requires two input spreadsheets, one containing the coordinates of the measurement points in the diffraction mesh, and the other containing the coordinates of the initial and final points of the theoretical wave propagation paths, along with the corresponding wave propagation times for each path. Based on these spreadsheets, the software calculates the wave velocities along the theoretical paths and estimates velocities outside these paths using data interpolation, following the model proposed by [45].
To construct the images, it is necessary to insert velocity threshold (VTs) ranges associated with specific colours. Since there are no absolute velocity thresholds that reliably indicate sound wood, the VTs intervals were defined as a percentage of the maximum velocity (Vmax) obtained for each disc itself. In this study, only two VTs intervals were used: the lower interval was associated with red and the higher interval with yellow.
Considering that the aim of this study was to determine the VTs interval that provides the best accuracy for inferring cavities or cavities associated with decay, images were generated using different VTs intervals based on the ranges proposed by previous research [17]—up to 40% Vmax for cavity detection and up to 45% Vmax for cavities associated with decay. To identify the best range, four images were produced for each disc using VTs intervals of up to 35%, 40%, 45%, and 50% of Vmax, resulting in a total of 152 images (38 discs × 4 images each).
2.3.3. Confusion Matrix
For such evaluations it is necessary to define the comparison region (internal points), construct a reference model of the actual defect based on the real image of the disc (model), and compare it with the defect representation generated by tomography (roi). The process involves pixel-wise comparison within the internal points between the “model” and the “roi” using the methodology and Python script proposed by [25]. Several metrics can be derived from this comparison depending on the analysis goal. The most common metrics are accuracy, precision, sensitivity, and Fscore. These metrics are calculated based on true and false positives and negatives. For example, in a binary classification—defective (e.g., cavity) vs. sound wood—if the image correctly identifies a cavity, it is a true positive (TP), if it identifies a cavity where there is none it is a false positive (FP), correctly identifying sound wood is a true negative (TN), and missing a cavity is a false negative (FN). The metrics are defined as follows:
In this study a confusion matrix was used as a method to assess how accurately the tomographic images represented the actual condition of each disc, using accuracy (Equation (2)) as the performance metric.
In this context, the target defects were cavities or cavities associated with decay. Thus, pixels representing these defects were considered positive, while pixels corresponding to sound wood were considered negative.
Before applying the confusion matrix to compare the images, a series of preprocessing steps were necessary, as described in the following subsections.
Scale Adjustment
To ensure that the confusion matrix could be properly applied, all images had to be scaled to the same pixel dimensions. This adjustment was performed using the open-source software ImageJ (version 1.54f; National Institutes of Health, Bethesda, MD, USA.
Model, ROI, and Internal Points Parameters
To compare the pixels between the real disc images and the tomographic images, each disc face was polished using sandpapers of different grits. The polished faces were then photographed and regions with cavities and decay were outlined in the images.
For each disc a region of interest was defined for pixel comparison, referred to as “internal-points” (Figure 3a). From the real image of the disc (Figure 3b), the target defect region was extracted and referred to as the “model” (Figure 3c), representing the actual defect to be inferred. From each tomographic image (Figure 3d), the corresponding inferred defect region was extracted and referred to as the “roi” (Figure 3e).

Figure 3.
Example of parameters used in the confusion matrix. Real image of the disc (a), defined comparison area: “internal-points” (b), model of the target defect: “model” (c), tomographic image (d), and inferred defect region from the tomographic image: “roi” (e).
Accuracy Calculation
After preparing the images and defining the confusion matrix parameters (internal-points, model, and roi), automated image comparisons and accuracy calculations (Equation (1)) were performed using a script proposed by the authors of [25].
Evaluation of Results
Accuracy results were analyzed for each species, considering the different wood conditions (sound, cavity, and cavity associated with decay). The goal was to assess the feasibility of adopting a single VTs interval regardless of species, as well as to quantify the potential accuracy loss if such a unified interval were used.
3. Results
The discs included in the study sample exhibited naturally occurring defects and were not selected based on specific characteristics. Their inclusion was determined by the opportunity for tree removal, rather than by prior knowledge of internal conditions. The discs were taken from trunk sections where deterioration was more likely as the aim of this study was to evaluate tomographic image quality rather than to assess differences related to sampling location. As a result, 19 of them showed no visible defects (Figure 4a), and among those that did, only 2 presented isolated cavities (Figure 4b) surrounded by relatively sound wood. Most defective discs exhibited a mix of deteriorated zones and cavities (Figure 4c). This condition made the analysis more challenging, but it reflects a real situation commonly found in urban trees, thus representing a relevant and meaningful result.
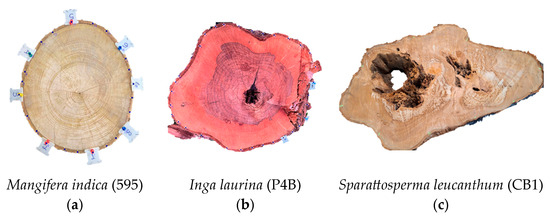
Figure 4.
Example of a disc with no visible decay (a), a disc with a relatively well-defined cavity zone within a relative sound or insipient decayed area (b), and a disc with a cavity blended with the decayed zone (c).
As described in the methodology, tomographic image accuracies were obtained with the objective of inferring cavities and cavities associated with decay. The images were generated using four different VTs intervals, always based on the maximum velocity obtained from the measurement paths on each disc. The accuracy results, obtained using the confusion matrix, are presented in Table 3 for the inference of cavities and in Table 4 for the inference of cavities associated with decay.

Table 3.
Accuracy of tomographic images in the inference of cavities, obtained with different velocity thresholds based on the maximum velocity (Vmax) in the disc.

Table 4.
Accuracy of tomographic images in the inference of cavities + decay, obtained with different velocity thresholds based on the maximum velocity (Vmax) in the disc.
4. Discussion
For 100% of the discs with no visible defects, it was observed that for all species (10 species presenting this condition) and for all studied percentages of maximum velocity (35%, 40%, 45%, and 50%) the tomographic image always displayed a single colour (yellow). Thus, the red colour—representative of zones with cavities and/or deterioration—did not appear in the image, indicating that the condition of the disc was accurately represented (Example in Figure 5). For the confusion matrix, since there was only a true negative (TN) condition, accuracy was 100% (Table 3 and Table 4). Given that this behaviour was repeated for 19 discs from 10 different species, we conclude that the methodology is adequate for inferring intact wood conditions without generating false positives.
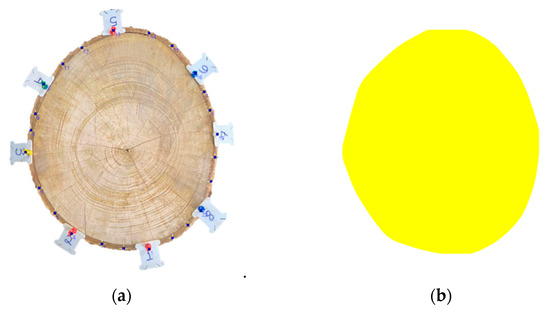
Figure 5.
Example of a tomographic image (b) generated from a disc with no visible defect (clean wood) (a). Species: Mangifera indica (595).
The two discs, both from the genus Inga, which presented isolated cavities (IP4B and 657B) were the ones with the highest accuracies in cavity detection, 95% and 94%, respectively, and both achieved with a VTs interval of 35% Vmax (Table 3). For the species Cenostigma pluviosum, the best accuracy was with a 40% Vmax interval [9]. However, it is noteworthy that with 40% Vmax the accuracies were also high (>90%), with a small decrease of 2.6% compared to 35% Vmax. Increasing the percentage of Vmax used as a reference to infer cavities results in more false positives as the range of VR assumed to indicate cavities is expanded. Thus, if there is any degree of decay around the cavity that lowers the velocity that region may be interpreted as a cavity in the image, increasing its size (Figure 6). On the other hand, for Cenostigma pluviosum using 35% Vmax instead of 40% could lead to more false negatives, reducing the cavity’s size in the image.
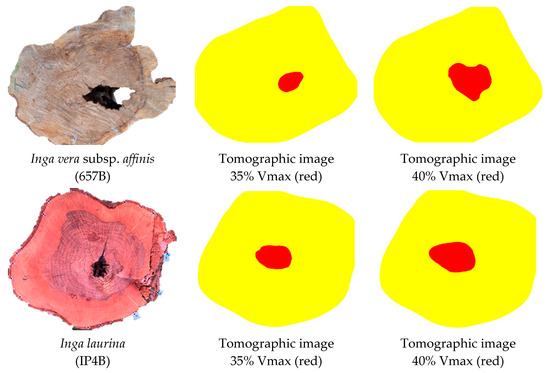
Figure 6.
Discs from the Inga species with their respective tomographic images constructed using velocity threshold (VTs) intervals of 35% and 40% of the maximum velocity (Vmax) in the disc for cavity identification (red zone).
For discs with a mixed condition of cavities and decay (most of the sample), the average of the best accuracies in cavity detection was 84.3%. The VTs intervals with the best accuracies ranged between up to 35% Vmax (78% of discs) and up to 40% Vmax (22% of discs) across species. The best accuracy for Cenostigma pluviosum was 40% Vmax [17]. However, considering all species studied in the present research, accuracy variation between the two VTs intervals (35% and 40% Vmax) was small. Therefore, adopting the interval with the highest number of discs showing the best accuracy (up to 35% Vmax) results in an average accuracy of 84%, only 0.36% lower. Using the interval found by [17] (up to 40% Vmax) for all species would yield an average accuracy of 79.6%, a loss of 4.7%. This indicates that it is possible to adopt a single VTs interval for all species without significant loss of accuracy in images for cavity detection, with 35% Vmax being the most suitable.
When the process involves inferring zones with cavities associated with decay the complexity increases, making it harder to accurately represent these areas using tomography [17,26]. In this case, the average of the best accuracies drops from 84.3% (cavity detection) to 68% (cavities with decay). Furthermore, the best VTs interval is spread across all tested intervals, with 16% of discs in each, except for the 50% Vmax interval which accounted for 53% of discs. The variation in accuracy among VTs intervals is greater than for cavity-only inference (Table 4). However, for the last two intervals (45% and 50% Vmax) these differences are smaller. Therefore, adopting the VTs interval with the highest number of best results (up to 50% Vmax) leads to an average accuracy of 65%, a loss of 4.6%. Previous research obtained that the best accuracy for Cenostigma pluviosum was 45% Vmax [17]. Using this same interval for the present dataset results in an average accuracy of 64%, a 6% loss. Hence, just as with cavity inference, adopting a single VTs interval is feasible for constructing images to infer areas affected by cavities associated with decay.
Considering the 20 species included in the sample and the 35% Vmax VTs interval, the lowest accuracy for cavity detection was 71%, obtained only for the Gymnosperm (Araucaria angustifolia, disc 652PS) and for Ligustrum lucidum (Table 3). However, for this same species (Araucaria angustifolia), the second disc (652PI) reached an accuracy of 88%, indicating that detection performance seems unrelated to species or family. For these two discs accuracies for detecting zones with cavities and decay were similar at 56% and 54%, respectively (Table 4). A more detailed inspection reveals that disc 652PS has three separate cavities and cracks formed along growth rings, encircling the disc. Disc 652PI has two adjacent cavities and one isolated, located in the heartwood. It is important to note that cracks or cavities may not be interpreted as cavities if they do not extend fully through the cross-sectional plane being analyzed, meaning they are either shallow or located deeper within the disc without sufficient interaction with the propagation paths of the ultrasonic waves. As a result, such defects may not produce significant velocity reductions and can be missed in the tomographic image. Therefore, depending on the inspection point relative to the defect depth, the ultrasonic wave may or may not reach it, affecting velocity reduction and thus detection. This results in a discrepancy between the “roi” in the tomographic image and the “model” identified in the actual image (Figure 7).
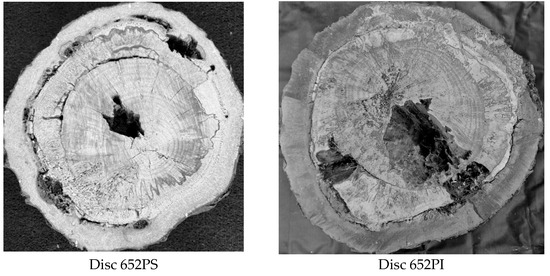
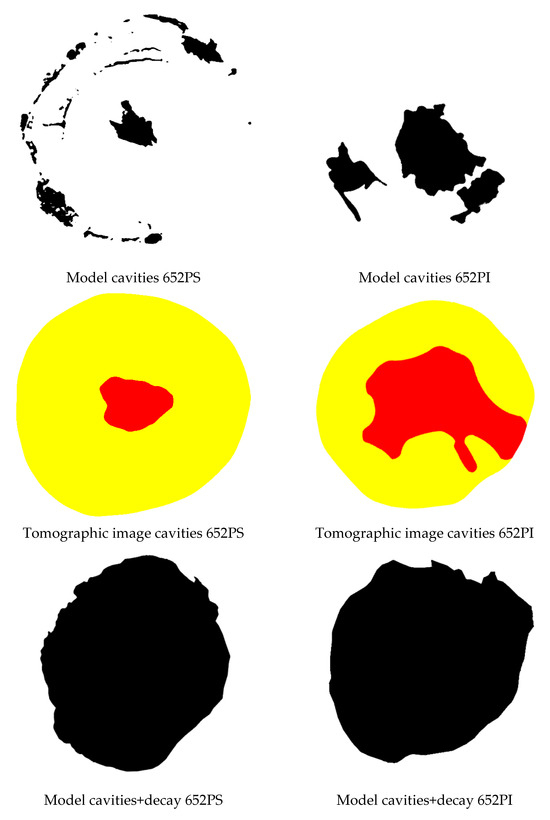
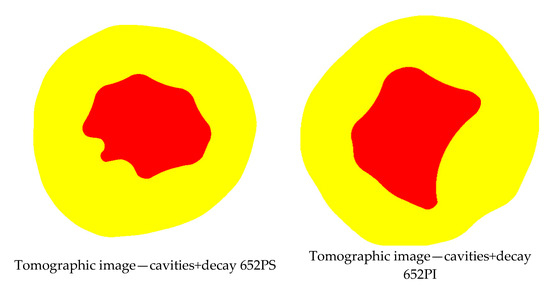
Figure 7.
Images of the cross-sections of the two Araucaria angustifolia discs with their respective models of cavities and decay and generated tomographic images.
Regarding decay, both discs were considered almost entirely affected, as reflected in the “model” for both. However, the tomographic image minimized the deteriorated area, showing it only in the sapwood (Figure 7).
Disc 666 from Jacaranda mimosifolia had the lowest accuracy (44%) for detecting cavities associated with decay (Table 4). Closer examination reveals that this disc has no cavities but was considered completely biodeteriorated in the “model” (Figure 8). However, the deterioration was more advanced only in the central region of the disc and was not detected by tomography in the outer areas, where deterioration was still in its early stages (Figure 8). This conclusion is based on visual inspection of the cross-sectional surface. No additional tests (e.g., localized density measurements or microscopic analysis) were conducted to confirm the internal extent of deterioration, posing a limitation of the current study.

Figure 8.
Image of the cross-section of the Jacaranda mimosifolia disc with its respective decay model and generated tomographic image.
The size of the defect is one of the most influential factors in the results obtained through acoustic tomography in wood [46,47]. Large cavities surrounded by sound wood are easier to detect using this technique, as demonstrated in this study by the examples of the Inga species (discs IP4B and 657B) which showed the highest accuracies (95% and 94%) in cavity detection. In the case of this research, even when surrounded by biodeteriorated wood, as in the species Sparattosperma leucanthum (disc CB1), accuracies of 85% for cavity inference (Table 2) and 78% for inference of cavities associated with decay (Table 4) were obtained using the VTs intervals of 35% Vmax and 50% Vmax, respectively, adopted for all species in tomographic image construction. Within this research sample, this disc had the highest proportion of cavities (Figure 9).
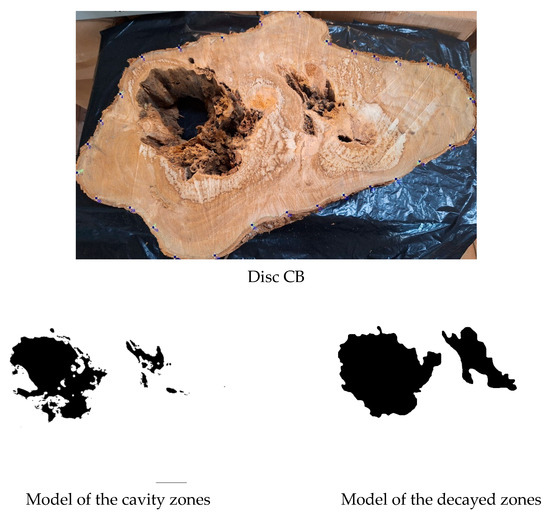
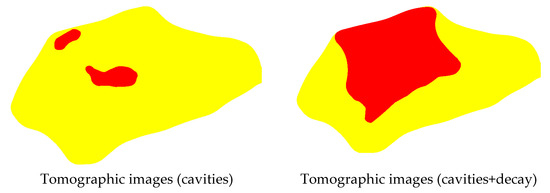
Figure 9.
Image of the Sparattosperma leucanthum disc face with its respective decayed model and generated tomographic image.
Although the dimensions and positioning are not exact, in general, when visually analyzing the images (Examples in Figure 10) it is possible to confirm—regardless of species and defect type—the feasibility of inferring zones with cavities and decay using the methodology and VTs intervals adopted in this study.
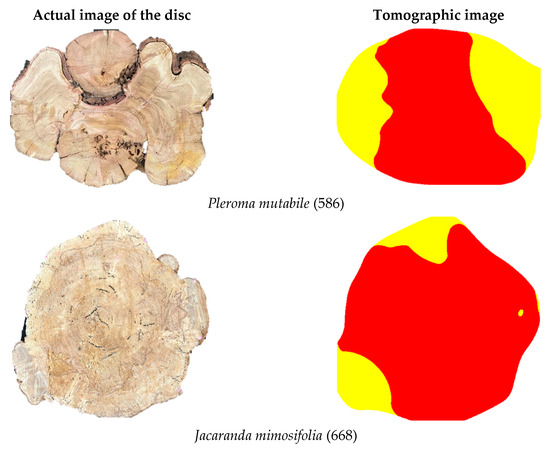
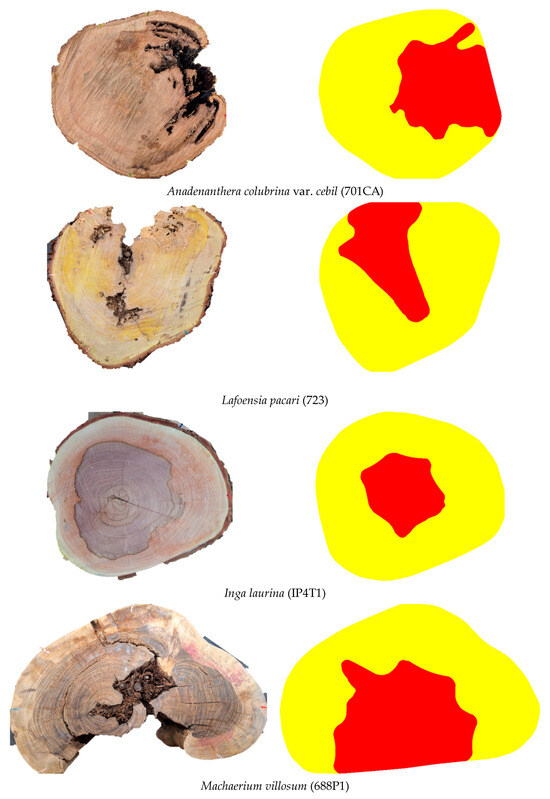

Figure 10.
Visual comparison between the disc condition and tomographic images showing zones with cavities + decay for some of the different discs included in the study sample.
By separately using VTs intervals to build images representative of cavities and of decay it is also possible to isolate these defects within the same image (example in the figures of Figure 11). However, this procedure was not the aim of the present study, especially considering the binary nature of the confusion matrix analysis.
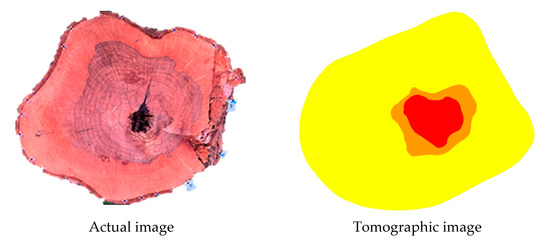
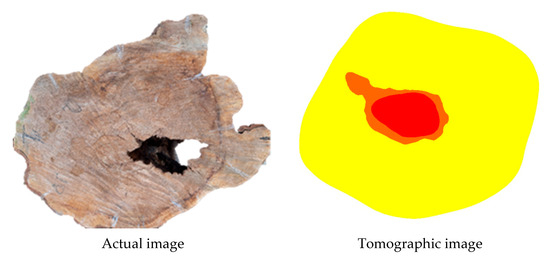
Figure 11.
Example of images produced with two colours showing the inference of zones with cavities and with decay. Legend: red = cavity; orange = cavity + decay.
Danielli [47] proposed a classification of apparent wood density into the following three categories: low density (less than 550 kg/m3), medium density (551–720 kg/m3), and high density (greater than 721 kg/m3). Using this classification, among the 19 discs that contained decay with or without cavities, only 1 disc was classified as low density (5.3%), 12 were classified as medium density (63.2%), and 6 as high density (31.5%), as can be seen in Table 1.
An ANOVA statistical analysis indicated that, statistically, the density class of the species did not affect the maximum accuracy (dependent variable), as can be seen in Figure 12. Numerically, the average maximum accuracy was higher for the high-density class (70.2%) than for the medium-density class (67.5%). Density class 1 (low) could not be included in the statistical analysis due to insufficient sample size, but numerically it showed the lowest accuracy (49%).
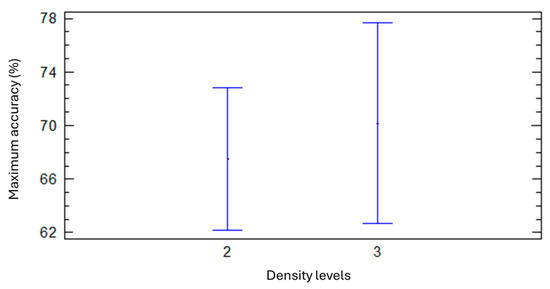
Figure 12.
Mean and confidence interval of accuracy percentages for two density levels (2 = medium and 3 = high).
When considering the VTs interval (in % Vmax) there was also no influence from the density class. The maximum accuracy values were obtained with threshold velocities between approximately 40% and 50% of the maximum velocity, as can be seen in Figure 13.
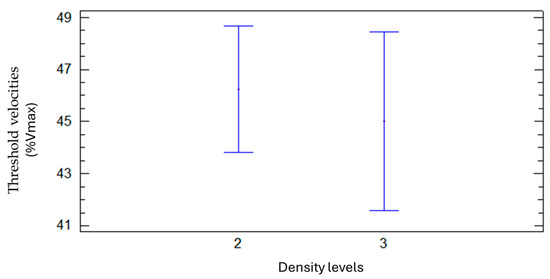
Figure 13.
Mean and confidence interval of threshold velocity percentages (relative to Vmax) for two density levels (2 = medium and 3 = high).
5. Conclusions
- When the trunk is clean or with early stage decay the tomographic image generated using the proposed methodology accurately reflects this condition, showing no signs of deterioration regardless of the velocity thresholds interval adopted (35% to 50% of the maximum velocity). In this case the accuracy was 100%.
- For discs with isolated cavities (surrounded by clear wood or wood with early stage decay) the velocity thresholds intervals up to 35% Vmax show accuracy greater than 94%.
- For discs with cavities associated with decay the velocity thresholds intervals up to 35% Vmax can be adopted, independent of the species, to infer the cavity zone with good accuracy (84% on average). To infer the decayed zone the velocity threshold intervals up to 50%, also independent of the species, allow moderate accuracy (65% on average).
Considering practical applications in field assessments of standing trees, where the internal condition is unknown and there is no reference image available, the results of this study suggest that velocity thresholds of up to 35% of Vmax can be used for cavity detection and up to 50% of Vmax for detecting cavities associated with decay. These thresholds demonstrated acceptable accuracy across different species and can serve as standardized reference values for broader use in urban tree risk assessments.
6. Patents
The necessary documentation for the patent application of the image generation software (ImageWood) is being prepared.
Author Contributions
Conceptualization and methodology, R.G. and S.S.A.P.; investigation, L.T.V.; formal analysis: L.T.V. and S.S.A.P.; data curation, L.T.V. and R.G.; writing—original draft preparation, R.G.; writing—review and editing, R.G., S.S.A.P. and L.T.V.; supervision, R.G.; project administration, R.G.; funding acquisition, R.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by FAPESP (São Paulo Research Foundation) grant number 2023/03111-0 and CAPES (Coordination for the Improvement of Higher Education) finance code 001 (scholarship).
Data Availability Statement
The data supporting reported results can be found, including links to publicly archived datasets generated during the study, at the University repository (available after the paper is approved).
Acknowledgments
The authors would like to thank the Environmental Division of University of Campinas (Unicamp) for providing the material (trees) used in this study; the Research Group on Non-Destructive Testing (GPEND) for their support during the testing procedures; and the School of Agricultural Engineering (FEAGRI) for providing the infrastructure.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sankar Cheela, V.R.; Michele, J.; Wahidul, B.; Prabir, S. Combating Urban Heat Island Effect—A Review of Reflective Pavements and Tree Shading Strategies. Buildings 2021, 11, 93. [Google Scholar] [CrossRef]
- Liu, N.; Zhang, F. Urban green spaces and flood disaster management: Toward sustainable urban design. Front. Public Health 2025, 13, 1583978. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, T.; Biswas, T.; Campbell, L.S.; Franklin, B.; Parker, S.S.; Tukman, M. Feasibility of afforestation as an equitable nature-based solution in urban areas. Sustain. Cities Soc. 2022, 81, 103826. [Google Scholar] [CrossRef]
- Jones, B.A. Planting urban trees to improve quality of life? The life satisfaction impacts of urban afforestation. For. Policy Econ. 2021, 125, 102408. [Google Scholar] [CrossRef]
- Wolf, K.L.; Lam, S.T.; McKeen, J.K.; Richardson, G.R.A.; van den Bosch, M.; Bardekjian, A.C. Urban Trees and Human Health: A Scoping Review. Int. J. Environ. Res. 2020, 17, 4371. [Google Scholar] [CrossRef]
- Srivanit, M.; Kaewkhow, S. A machine learning-based protocol to support visual tree assessment and risk of failure classification on a university campus. Urban For. Urban Green. 2024, 99, 128420. [Google Scholar] [CrossRef]
- Hui, K.K.W.; Wong, M.S.; Kwok, C.Y.T.; Li, H.; Abbas, S.; Nichol, J.E. Unveiling falling urban trees before and during Typhoon Higos (2020): Empirical case study of potential structural failure using tilt sensor. Forests 2022, 13, 359. [Google Scholar] [CrossRef]
- Judice, A.; Gordon, J.; Abrams, J.; Irwin, K. Community perceptions of tree risk and management. Land 2021, 10, 1096. [Google Scholar] [CrossRef]
- Soge, A.O.; Popoola, O.I.; Adetoyinbo, A.A. Detection of wood decay and cavities in living trees: A review. Can. J. For. Res. 2021, 51, 937–947. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Li, Z.; Wen, J.; Tan, X. A review of research on tree risk assessment methods. Forests 2022, 13, 1556. [Google Scholar] [CrossRef]
- Coelho-Duarte, A.P.; Daniluk-Mosquera, G.; Gravina, V.; Vallejos-Barra, Ó.; Ponce-Donoso, M. Tree risk assessment: Component analysis of six visual methods applied in an urban park, Montevideo, Uruguay. Urban For. Urban Green. 2021, 59, 127005. [Google Scholar] [CrossRef]
- Klein, R.W.; Koeser, A.K.; Hauer, R.J.; Hansen, G.; Escobedo, F.J. Risk assessment and risk perception of trees: A review of literature relating to arboriculture and urban forestry. Arboric. Urban For. 2019, 45, 26–38. [Google Scholar] [CrossRef]
- Nicolotti, G.; Socco, L.V.; Martinis, R.; Godio, A.; Sambuelli, L. Application and comparison of three tomographic techniques for the detection of decay in trees. J. Arboric. 2003, 29, 66–78. [Google Scholar] [CrossRef]
- Wang, X.; Allison, R.B. Decay detection in red oak trees using a combination of visual inspection, acoustic testing, and resistance microdrilling. Arboric. Urban For. 2008, 34, 1–4. [Google Scholar] [CrossRef]
- Wang, X.; Wiedenbeck, J.; Liang, S. Acoustic tomography for decay detection in black cherry trees. Wood Fiber Sci. 2009, 41, 127–137. [Google Scholar]
- Palma, S.S.A.; Gonçalves, R. Tomographic images of tree trunks generated using ultrasound and post-processed images: Influence of the number of measurement points. BioResources 2022, 17, 6638–6655. [Google Scholar] [CrossRef]
- Palma, S.S.A.; Reis, M.N.; Gonçalves, R. Tomographic Images Generated from Measurements in Standing Trees Using Ultrasound and Postprocessed Images: Methodological Proposals for Cutting Velocity, Interpolation Algorithm and Confusion Matrix Metrics Focusing on Image Quality. Forests 2022, 13, 1935. [Google Scholar] [CrossRef]
- Wang, X.; Divos, F.; Pilon, C.; Brashaw, B.K.; Ross, R.J.; Pellerin, R.F. Assessment of Decay in Standing Timber Using Stress Wave Timing Nondestructive Evaluation Tools; USDA FS Forest Products Laboratory General Technical Report FPL-GTR-147; US Department of Agriculture Forest Service: Washington, DC, USA, 2004.
- Burcham, D.C.; Brazee, N.J.; Marra, R.E.; Kane, B. Geometry matters for sonic tomography of trees. Trees 2023, 37, 837–848. [Google Scholar] [CrossRef]
- Wei, X.; Xu, S.; Sun, L.; Tian, C.; Du, C. Propagation velocity model and two-dimensional defect imaging of stress wave in Larch (Larix gmelinii) wood. Bioresources 2021, 16, 6799–6813. [Google Scholar] [CrossRef]
- Yıldızcan, E.N.; Ari, M.E.; Tunga, B.; Gelir, A.; Kurul, F.; As, N.; Dündar, T. Machine learning based tomographic image reconstruction technique to detect hollows in wood. Wood Sci. Technol. 2024, 58, 1491–1516. [Google Scholar] [CrossRef]
- Ostrovský, R.; Kobza, M.; Gažo, J. Extensively damaged trees tested with acoustic tomography considering tree stability in urban greenery. Trees 2017, 31, 1015–1023. [Google Scholar] [CrossRef]
- Vieira-dos-Santos-Ataide, G.C.; dos-Santos-Ataide, D.H.; Cerqueira-Martins, B.; Monteiro-de-Carvalho, A.; de-Figueiredo-Latorraca, J.V. Historic urban trees: Assessing the trunk’s internal integrity. Bosque 2023, 44, 481–491. [Google Scholar] [CrossRef]
- Feng, H.; Li, G.; Fu, S.; Wang, X. Tomographic image reconstruction using an interpolation method for tree decay detection. BioResources 2014, 9, 3248–3263. [Google Scholar] [CrossRef]
- Strobel, J.R.A.; Carvalho, M.A.G.; Gonçalves, R.; Pedroso, C.B.; Reis, M.N.; Martins, P. Quantitative image analysis of acoustic tomography in woods. Eur. J. Wood Wood Prod. 2018, 76, 1379–1389. [Google Scholar] [CrossRef]
- Espinosa, L.; Prieto, F.; Brancheriau, L.; Lasaygues, P. Quantitative parametric imaging by ultrasound computed tomography of trees under anisotropic conditions: Numerical case study. Ultrasonics 2020, 102, 106060. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Li, G.; Jiao, Z.; Wang, X. Reliability of acoustic tomography and ground-penetrating radar for tree decay detection. Appl. Plant Sci. 2018, 6, e01187. [Google Scholar] [CrossRef]
- Dudkiewicz, M.; Durlak, W. Sonic Tomograph as a tool supporting the sustainable management of historical greenery of the UMCS Botanical Garden in Lublin. Sustainability 2021, 13, 9451. [Google Scholar] [CrossRef]
- Michajlová, K.; Gejdoš, M.; Gergeľ, T.; Gretsch, D. Evaluation of the quality of standing trees using an Arbotom acoustic stress tomograph. For. J. 2025, 71, 65–72. [Google Scholar] [CrossRef]
- Du, X.; Li, J.; Feng, H.; Chen, S. Image reconstruction of internal defects in wood based on segmented propagation rays of stress waves. Appl. Sci. 2018, 8, 1778. [Google Scholar] [CrossRef]
- Kralovec, C.; Schagerl, M. Review of structural health monitoring methods regarding a multi-sensor approach for damage assessment of metal and composite structures. Sensors 2020, 20, 826. [Google Scholar] [CrossRef]
- Marcantonio, V.; Monarca, D.; Colantoni, A.; Cecchini, M. Ultrasonic waves for materials evaluation in fatigue, thermal and corrosion damage: A review. Mech. Syst. Signal Process. 2019, 120, 32–42. [Google Scholar] [CrossRef]
- Honarvar, F.; Varvani-Farahani, A. A review of ultrasonic testing applications in additive manufacturing: Defect evaluation, material characterization, and process control. Ultrasonics 2020, 108, 106227. [Google Scholar] [CrossRef] [PubMed]
- Bucur, V. Acoustics of Wood, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2025; 917p. [Google Scholar]
- Bucur, V. A review on acoustics of wood as a tool for quality assessment. Forests 2023, 14, 1545. [Google Scholar] [CrossRef]
- Espinosa, L.; Prieto, F.; Brancheriau, L.; Lasaygues, P. Effect of wood anisotropy in ultrasonic wave propagation: A ray-tracing approach. Ultrasonics 2019, 91, 242–251. [Google Scholar] [CrossRef]
- Perlin, L.P.; de Andrade Pinto, R.C.; do Valle, Â. Ultrasonic tomography in wood with anisotropy consideration. Constr. Build. Mater. 2019, 229, 116958. [Google Scholar] [CrossRef]
- Lorenzi, H. Árvores Brasileiras: Manual de Identificação e Cultivo de Plantas Arbóreas Nativas do Brasil, 6th ed.; Plantarum: Nova Odessa, Brazil, 2014; Volume 1, p. 384. [Google Scholar]
- Silva, H.F.; Ribeiro, S.C.; Botelho, S.A.; Faria, R.A.V.B.; Teixeira, M.B.R.; Mello, J.M. Estimativa do estoque de carbono por métodos indiretos em área de restauração florestal em Minas Gerais. Sci. For. 2015, 43, 943–953. [Google Scholar] [CrossRef]
- Vale, A.; Sarmento, T.R.; Almeida, A.N. Caracterização e uso de madeiras de galhos de árvores provenientes da arborização de Brasília, DF. Ciênc. Florest. 2005, 15, 33–42. [Google Scholar] [CrossRef]
- Britez, R.M.; Borgo, M.; Tiepolo, G.; Ferretti, A.; Calmon, M.; Higa, R.C.V. Estoque e Incremento de Carbono em Florestas e Povoamentos de Espécies Arbóreas com Ênfase na Floresta Atlântica do Sul do Brasil; Embrapa Florestas: Colombo, Brazil, 2006; ISBN 85-89281-07-8. [Google Scholar]
- Restor. Biodiversity—Trees. Restor. Available online: https://restor.eco/pt/platform/sites/13831d32-d1c0-40f7-abe4-ed23d3d273f7/biodiversity/trees/ (accessed on 23 May 2025).
- Gonçalves, M.T.T. Contribuição para o Estudo da Usinagem de Madeiras. Master’s Dissertation, Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, Brazil, 1990. [Google Scholar] [CrossRef]
- Suryawanshi, M.; Patel, A.; Kale, T.; Patil, P. Carbon sequestration potential of tree species in the environment of North Maharashtra University Campus, Jalgaon (MS), India. Biosci. Discov. 2014, 5, 175–179. [Google Scholar]
- Du, X.; Li, S.; Li, G.; Feng, H.; Chen, S. Stress wave tomography of wood internal defects using ellipse-based spatial interpolation and velocity compensation. BioResources 2015, 10, 3948–3962. [Google Scholar] [CrossRef]
- Schubert, S.; Gsell, D.; Dual, J.; Motavalli, M.; Niemz, P. Acoustic wood tomography on trees and the challenge of wood heterogeneity. Holzforschung 2009, 63, 107–112. [Google Scholar] [CrossRef]
- Danielli, D. Densidade da Madeira e Potencial Dendrocronológico de Espéceis Nativas da Floresta Ombrófila Mista (Wood Density and Dendrochronological Potential of Native Species from Mixed Ombrophilous Forest). Master’s Dissertation, State University of Santa Catarina, Florianópolis, Brazil, 2017; p. 115. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).