Formulation and Numerical Verification of a New Rheological Model for Creep Behavior of Tropical Wood Species Based on Modified Variable-Order Fractional Element
Abstract
1. Introduction
2. Materials and Methods
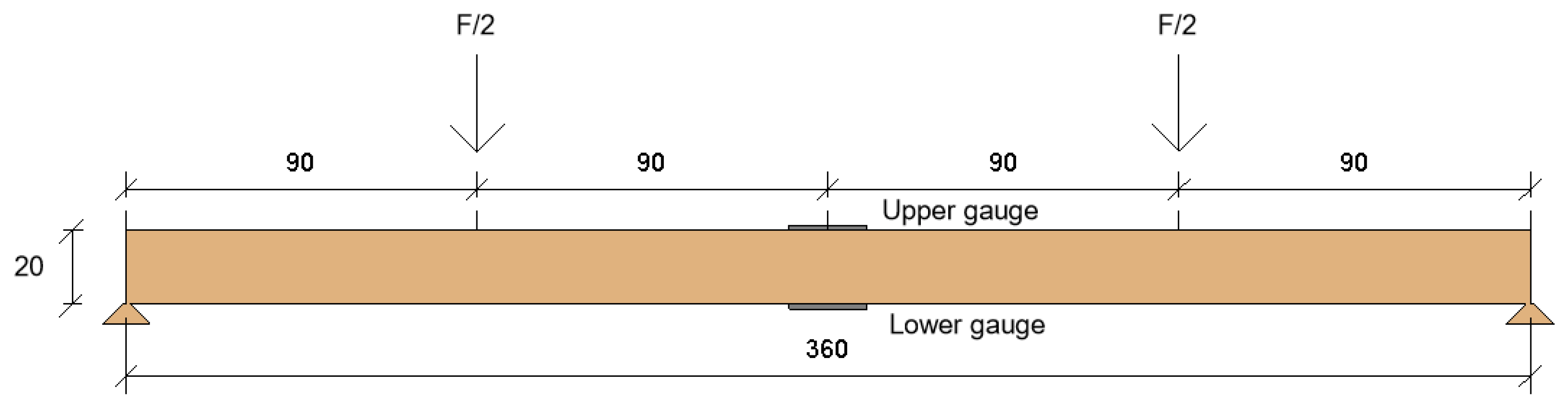
2.1. Materials and Experimental Setup
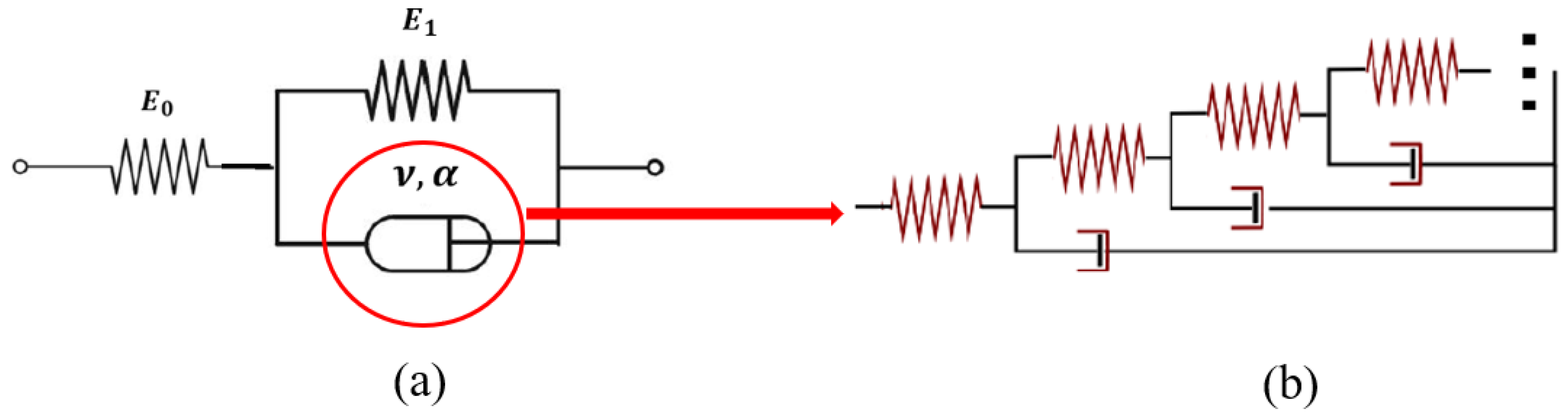
2.2. Description of Models
2.2.1. Constant-Order Fractional Rheological Model
2.2.2. Variable-Order Fractional Rheological Model
- If , , the behavior of the material depends only on the characteristics of the material at the present time: this is the elastic behavior;
- If , , the behavior will depend on infinitely neighboring instants; this is the viscous behavior [53].
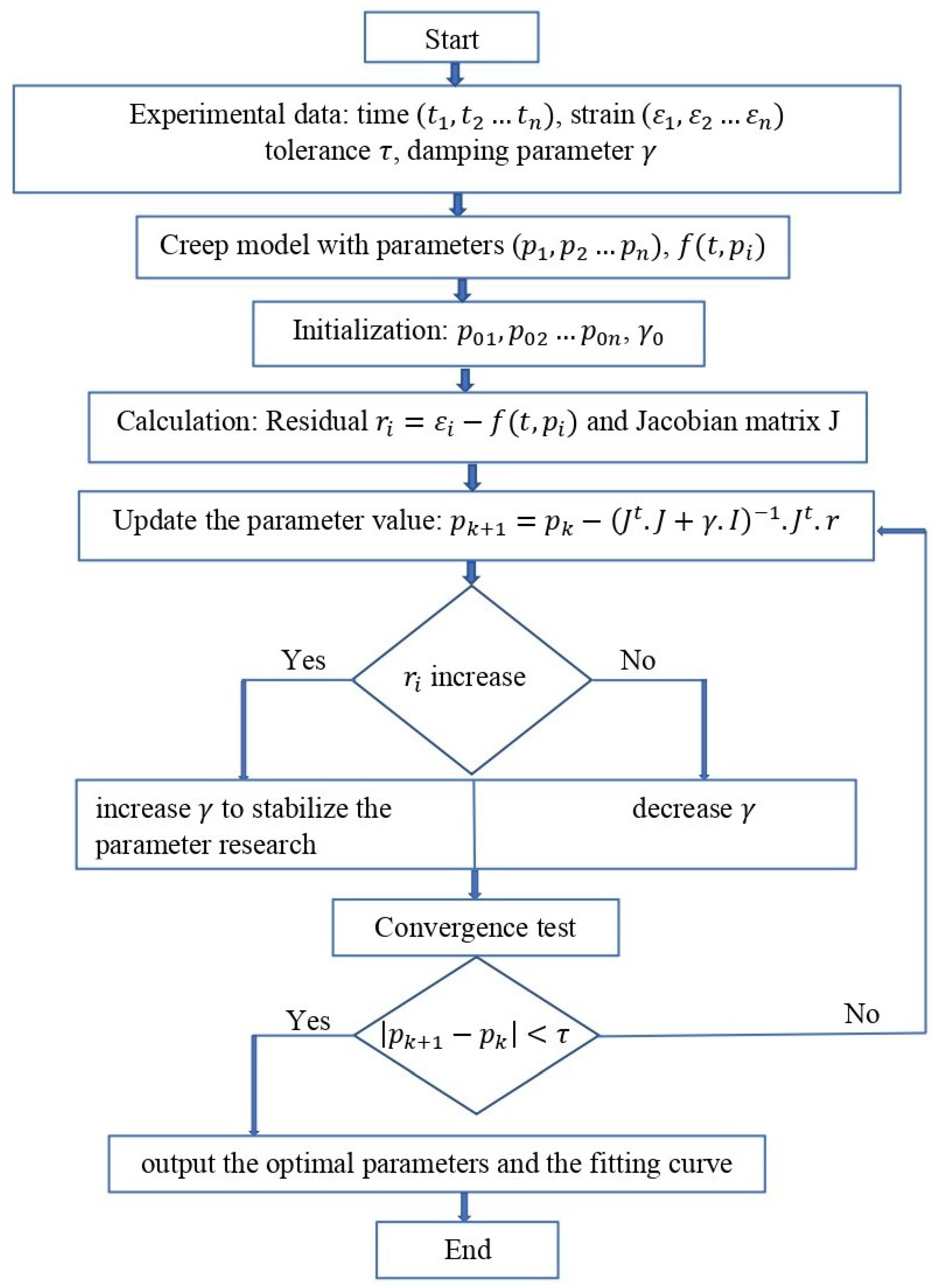
2.3. Method for Determining Creep Parameters
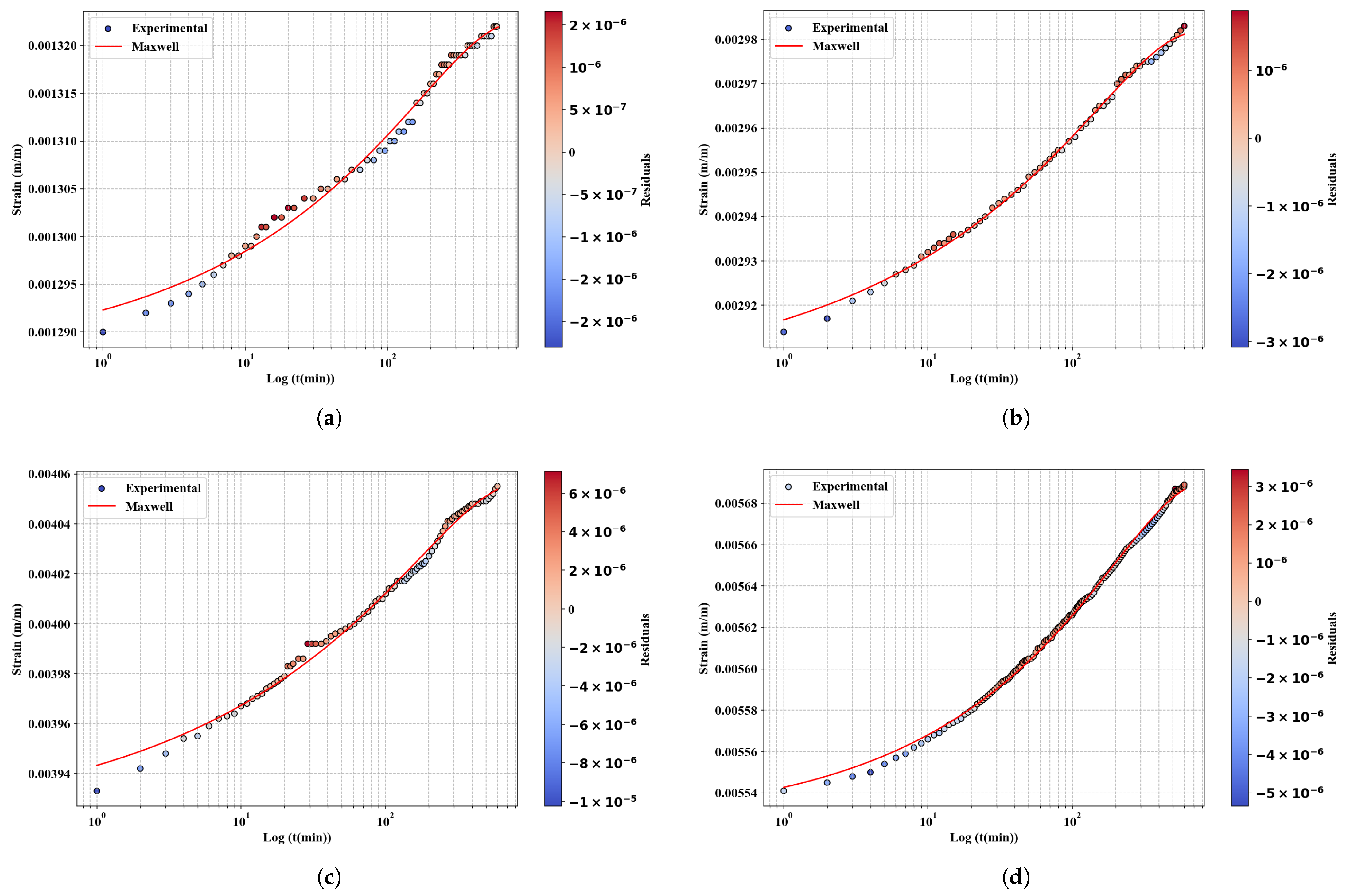
3. Results and Discussion
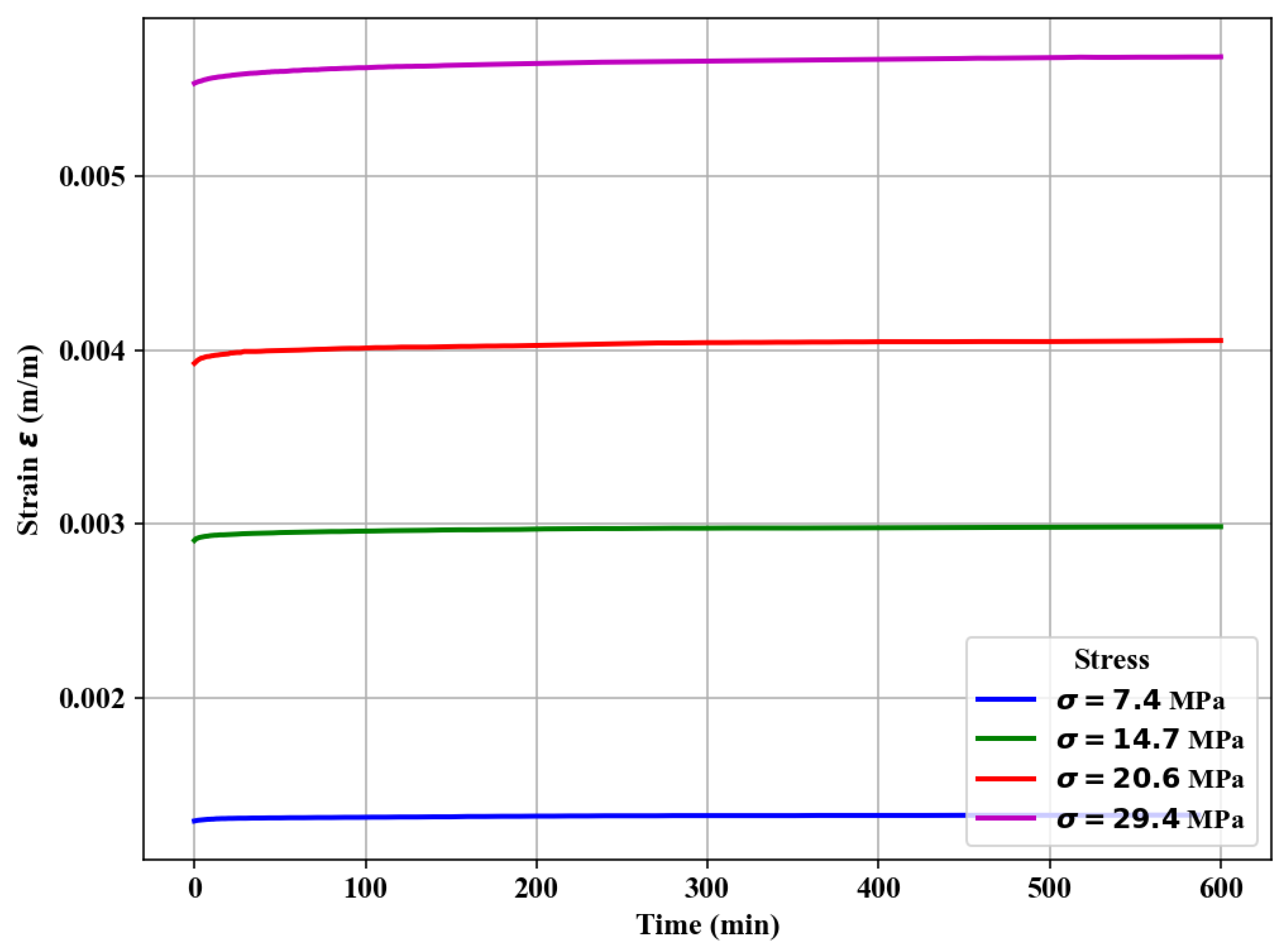
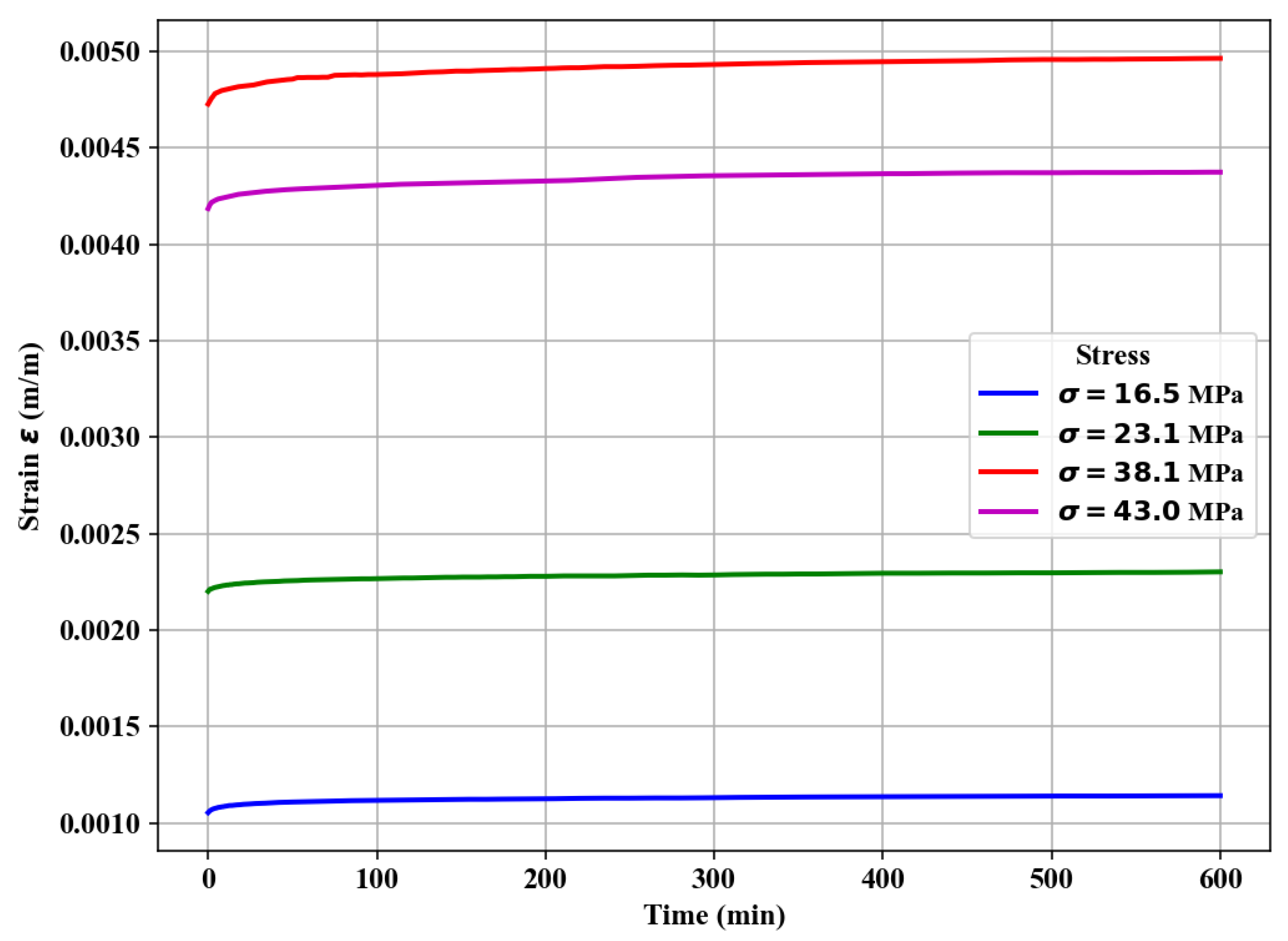
3.1. Prediction of Creep Using the Variable-Order Maxwell Fractional Model
3.2. Comparison Between the Constant-Order Fractional Model and the Variable-Order Fractional Model
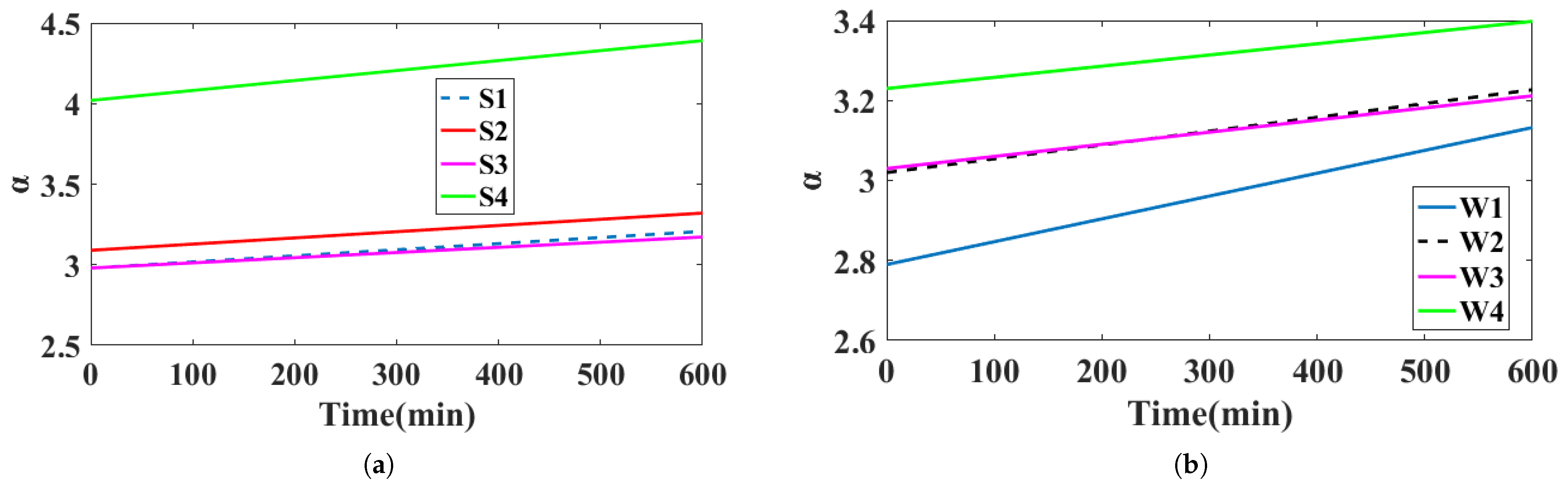
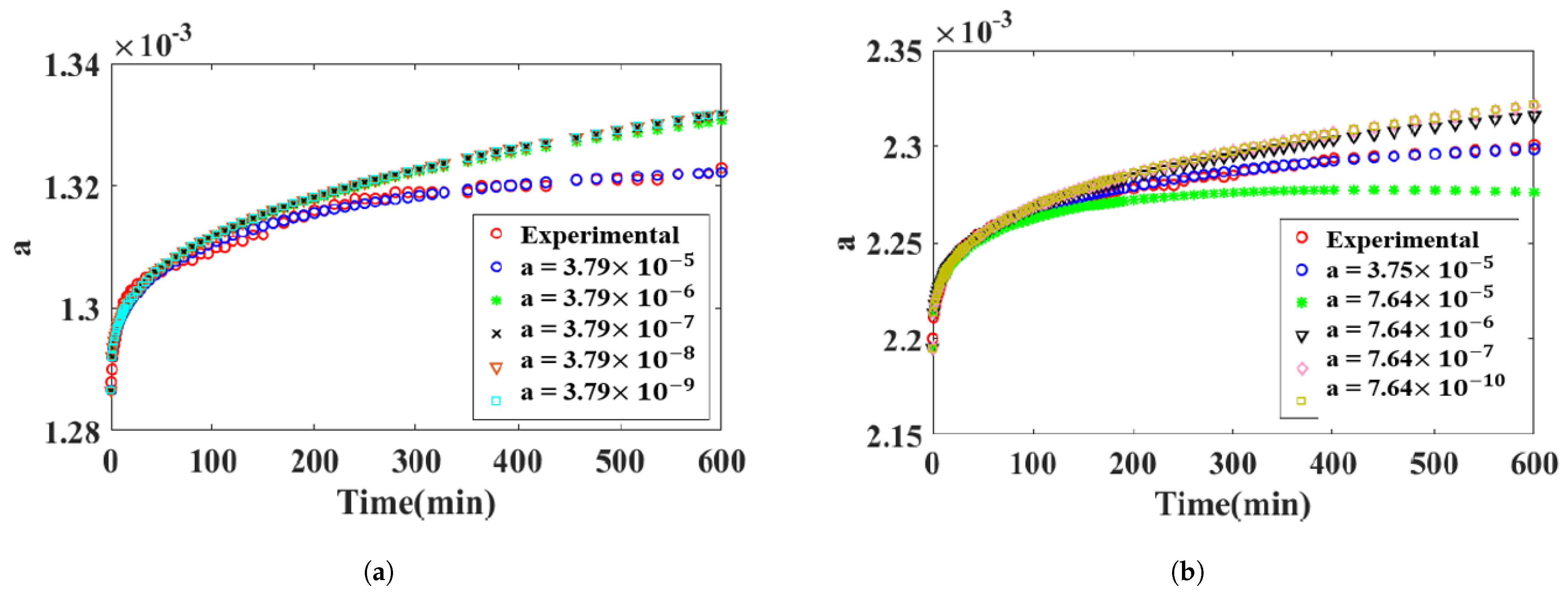
3.3. Analysis of the Sensitivity of Parameters a and b on the Creep Mechanism
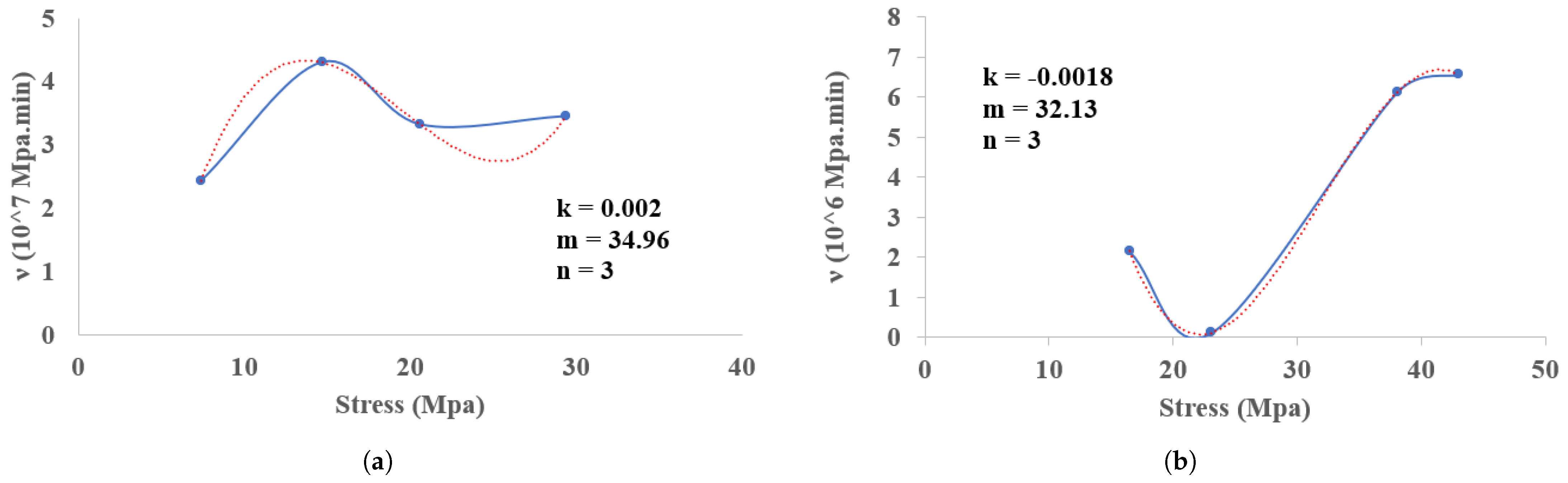
4. Proposal of Modified Model That Includes Spring–Pot with Stress-Dependent Changes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Residual Curves
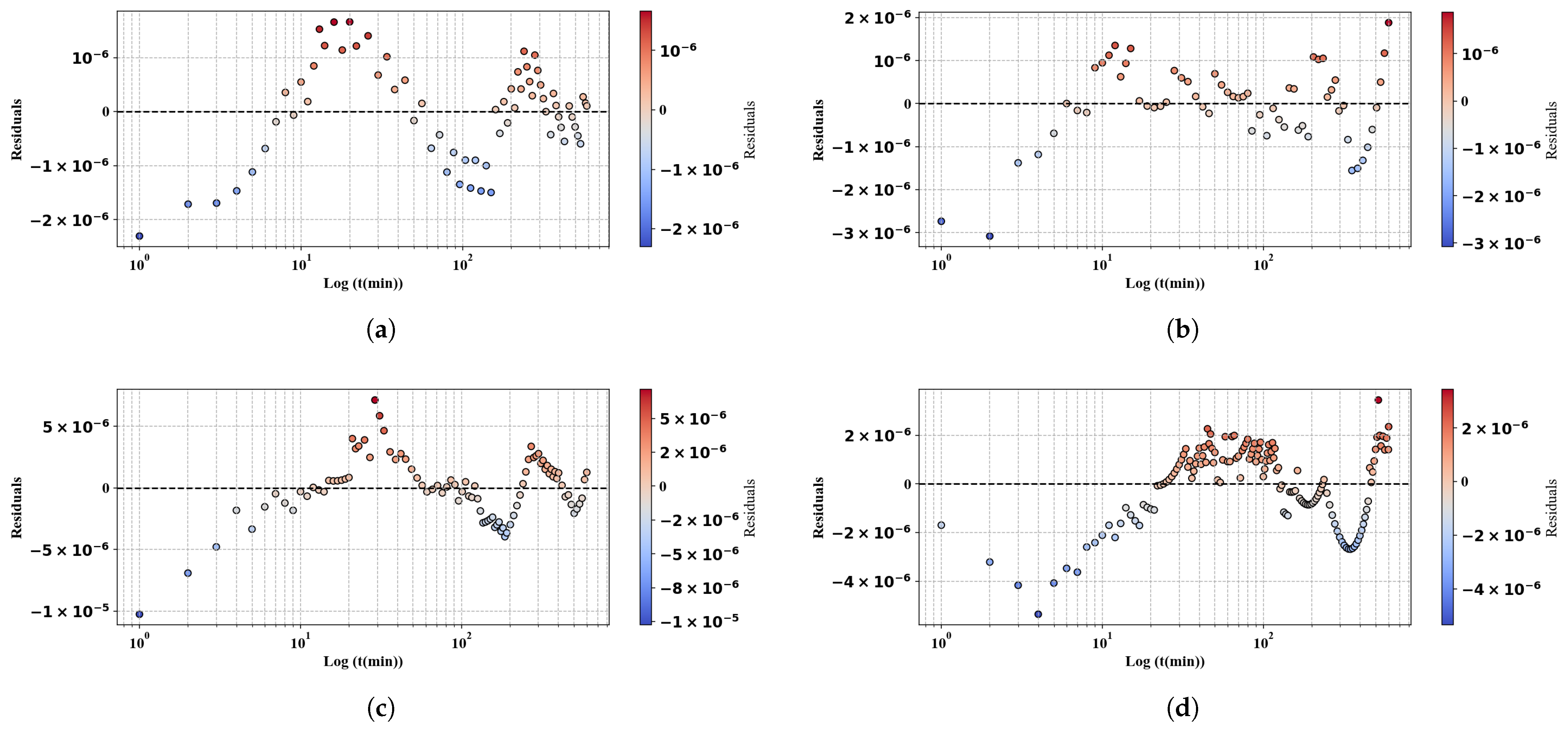
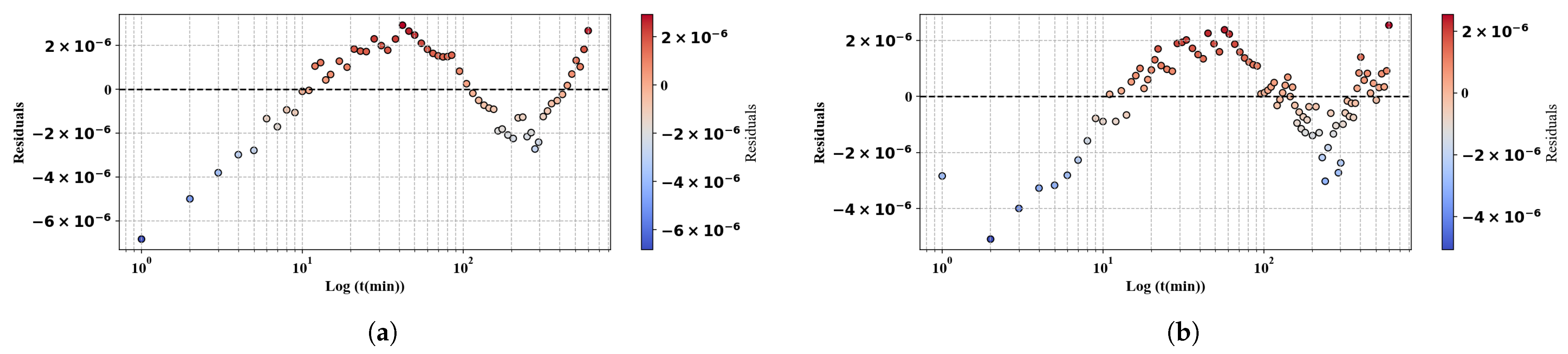
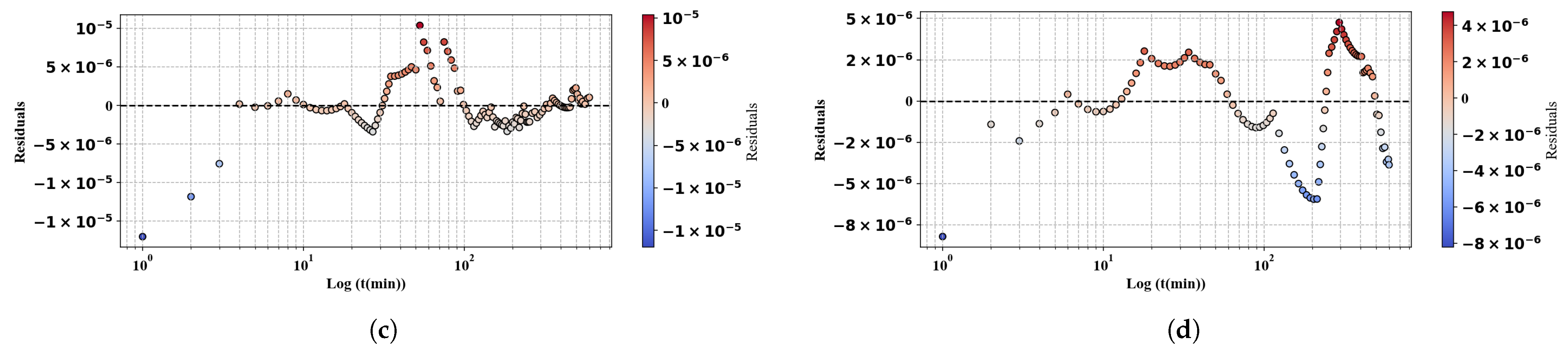
References
- Huang, C.; Chui, Y.; Gong, M.; Chana, F. Mechanical behaviour of wood compressed in radial direction: Part II. Influence of temperature and moisture content. J. Bioresour. Bioprod. 2020, 5, 266–275. [Google Scholar] [CrossRef]
- Gao, S.; Tao, X.; Wang, X.; Wang, L. Theoretical modeling of the effects of temperature and moisture content on the acoustic velocity of Pinus resinosa wood. J. For. Res. 2018, 29, 541–548. [Google Scholar] [CrossRef]
- Chiniforush, A.; Valipour, H.; Akbarnezhad, A. Water vapor diffusivity of engineered wood: Effect of temperature and moisture content. Constr. Build. Mater. 2019, 224, 1040–1055. [Google Scholar] [CrossRef]
- Tajvidi, M.; Falk, R.H.; Hermanson, J.C. Analysis of cantilever-beam bending stress relaxation properties of thin wood composites. Bioresources 2005, 97, 1995–2004. [Google Scholar]
- Hunt, J.F.; Zhang, H.; Huang, Y. Time-temperature superposition principle applied to a kenaf-fiber/high-density polyethylene composite. J. Appl. Polym. Sci. 2015, 10, 3131–3145. [Google Scholar]
- Asyraf, M.R.M.; Ishak, M.R.; Sapuan, S.M.; Yidris, N.; Ilyas, R.A. Woods and composites cantilever beam: A comprehensive review of experimental and numerical creep methodologies. J. Mater. Res. Technol. 2020, 9, 6759–6776. [Google Scholar] [CrossRef]
- Chowdhury, M.A.; Alam, M.M.; Rahman, M.M.; Islam, M.A. Model-based study of creep and recovery of a glassy polymer. Adv. Polym. Technol. 2022, 2022, 8032690. [Google Scholar] [CrossRef]
- Zhao, L.; Wei, Y.; Zhang, G.W.; Xi, F. Short-term creep properties and creep model of wood-plastic composites. Political Compass 2022, 43, 924–933. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, P.Y.; Jiang, Z.H. The creep behavior of wood-polymer composites. Adv. Mater. Res. 2013, 815, 632–638. [Google Scholar]
- Georgiopoulos, P.; Kontou, E.; Christopoulos, A. Short-term creep behavior of a biodegradable polymer reinforced with wood-fibers. Compos. Part B Eng. 2015, 80, 134–144. [Google Scholar] [CrossRef]
- Bouafif, H.; Koubaa, A.; Perré, P.; Cloutier, A. Creep behaviour of HDPE/wood particle composites. Int. J. Microstruct. Mater. Prop. 2013, 8, 225–238. [Google Scholar] [CrossRef]
- Asyraf, M.R.M.; Ishak, M.R.; Sapuan, S.M.; Yidris, N. Comparison of constant and long-term creep behaviors between balau wood and glass fiber reinforced polymer composite for cross-arm application. Fibers Polym. 2021, 22, 793–803. [Google Scholar] [CrossRef]
- Xi, F.; Zhao, L.; Wei, Y.; Yi, J.; Zhao, K. Effect of temperature on the bending and creep properties of wood plastic composites. Polym. Compos. 2023, 44, 4612–4622. [Google Scholar] [CrossRef]
- Ma, Y.R.; Li, X.J.; Deng, B.; Luo, Y.S. Basic study on creep properties of eucalyptus wood. Adv. Mater. Res. 2014, 911, 232–237. [Google Scholar]
- Lagana, M.K.; Babiak, M. Creep parameters of spruce wood in high temperature environment. Maderas Cienc. Tecnol. 2008, 10, 19–24. [Google Scholar]
- Dong, C.; Zhang, S.; Wang, J.; Chui, Y.H. Constant bending creep properties of furfurylated poplar wood. Constr. Build. Mater. 2021, 269, 121–308. [Google Scholar] [CrossRef]
- Pot, G.; Toussaint, E.; Coutand, C.; Le Cam, J.B. Experimental study of the viscoelastic properties of green poplar wood during maturation. J. Mater. Sci. 2013, 48, 6065–6073. [Google Scholar] [CrossRef]
- Yildirim, N.; Shaler, S.; West, W.; Gajic, E.; Edgar, R. The usability of Burger body model on determination of oriented strand boards’ creep behavior. Adv. Compos. Lett. 2020, 29, 263–336. [Google Scholar] [CrossRef]
- Saadallah, Y.; Flilissa, S.; Hamadouche, B. Viscoelastic creep in bending of olive wood (Olea europaea L.). J. Indian Acad. Wood Sci. 2024, 21, 58–64. [Google Scholar] [CrossRef]
- Shimazaki, K.; Ando, K. Analysis of shear creep properties of wood via modified Burger models and off-axis compression test method. Wood Sci. Technol. 2024, 58, 1473–1490. [Google Scholar] [CrossRef]
- Vidal-Sallé, E.; Chassagne, P. Constitutive equations for orthotropic nonlinear viscoelastic behaviour using a generalized Maxwell model: Application to wood material. Mech. Time-Depend. Mater. 2007, 11, 127–142. [Google Scholar] [CrossRef]
- Dubois, F.; Husson, J.M.; Sauvat, N.; Manfoumbi, N. Modeling of the viscoelastic mechano-sorptive behavior in wood. Mech. Time-Depend. Mater. 2012, 16, 439–460. [Google Scholar] [CrossRef]
- Kazemi, A.; Baghani, M.; Shahsavari, H.; Abrinia, K. A viscoelastic-viscoplastic constitutive model for high-temperature response of an advanced steel verified by biaxial measurement experiments. Eur. J. Mech.-A/Solids 2023, 97, 104–821. [Google Scholar] [CrossRef]
- Songsong, S. Study on the creep behavior of recombinant bamboo based on a modified generalized Kelvin model. Wood Sci. Technol. 2022, 56, 589–601. [Google Scholar] [CrossRef]
- Wang, P.; Cai, W.; Zhang, Y.; Wang, Z. A fractional rheological model for loading-dependent rheological behavior of polymers. Mech. Time-Depend. Mater. 2023, 28, 1543–1554. [Google Scholar] [CrossRef]
- Yang, X.-J.; Gao, F.; Srivastava, H.M. New rheological models within local fractional derivative. Rom. Rep. Phys. 2007, 69, 113. [Google Scholar]
- Su, X.; Xu, W.; Chen, W.; Yang, H. Fractional creep and relaxation models of viscoelastic materials via a non-Newtonian time-varying viscosity: Physical interpretation. Mech. Mater. 2020, 140, 103–222. [Google Scholar] [CrossRef]
- Bonfanti, A.; Kaplan, J.L.; Charras, G.; Kabla, A. Fractional viscoelastic models for power-law materials. Soft Matter 2020, 16, 6002–6020. [Google Scholar] [CrossRef]
- Nguedjio, L.C.; Mabekou Takam, J.S.; Moutou Pitti, R.; Blaysat, B.; Zemtchou, F.; Mezatio, A.K.; Talla, P.K. Modeling the nonlinear creep behavior of Entandrophragma cylindricum wood by a fractional derivative model. Mech. Time-Depend. Mater. 2024, 28, 303–319. [Google Scholar] [CrossRef]
- Atchounga, P.K.; Njankouo, J.M.; Foadieng, E.; Talla, P.K. Investigation of nonlinear creep behaviour of Millettia laurentii wood through Zener fractional rheological model. Int. J. Mech. Sci. 2021, 2, 1–7. [Google Scholar]
- Emmanuel, F.; Christian Martial, F.W.; Ulrich Gael, A.T.; Kisito, T.P.; Medard, F. Mechanical behavior of Pericopsis elata relative to age during growth. Adv. Mater. Sci. Eng. 2021, 2021, 4374181. [Google Scholar] [CrossRef]
- Nguedjio, L.C.; Mabekou Takam, J.S.; Moutou Pitti, R.; Blaysat, B.; Sauvat, N.; Gril, J.; Zemtchou, F.; Talla, P.K. Analyzing creep-recovery behavior of tropical Entandrophragma cylindricum wood: Traditional and fractional modeling methods. Int. J. Solids Struct. 2025, 306, 113–122. [Google Scholar] [CrossRef]
- Long, J.; Xiao, R.; Chen, W. Fractional viscoelastic models with non-singular kernels. Mech. Mater. 2018, 127, 55–64. [Google Scholar] [CrossRef]
- Fang, Z.W.; Sun, H.W.; Wang, H. A fast method for variable-order Caputo fractional derivative with applications to time-fractional diffusion equations. Comput. Math. Appl. 2020, 80, 1443–1458. [Google Scholar] [CrossRef]
- Sun, H.; Chang, A.; Zhang, Y.; Chen, W. A review on variable-order fractional differential equations: Mathematical foundations, physical models, numerical methods and applications. Fract. Calc. Appl. Anal. 2019, 22, 27–59. [Google Scholar] [CrossRef]
- Xiang, G.; Yin, D.; Meng, R.; Lu, S. Creep model for natural fiber polymer composites (NFPCs) based on variable order fractional derivatives: Simulation and parameter study. J. Appl. Polym. Sci. 2020, 24, 48–96. [Google Scholar] [CrossRef]
- Xiang, G.; Yin, D.; Meng, R.; Cao, C. Predictive model for stress relaxation behavior of glassy polymers based on variable-order fractional calculus. Polym. Adv. Technol. 2021, 32, 703–713. [Google Scholar] [CrossRef]
- Yuxiao, K.; Shuhua, M.; Yonghong, Z. Variable order fractional grey model and its application. Appl. Math. Model. 2021, 97, 619–635. [Google Scholar] [CrossRef]
- Zhou, F.X.; Wang, L.Y.; Liu, Z.Y.; Zhao, W.C. A viscoelastic-viscoplastic mechanical model of time-dependent materials based on variable-order fractional derivative. Mech. Time-Depend. Mater. 2022, 26, 699–717. [Google Scholar] [CrossRef]
- Meng, R.; Yin, D.; Drapaca, C.S. A variable order fractional constitutive model of the viscoelastic behavior of polymers. Int. J. Non-Linear Mech. 2019, 113, 171–177. [Google Scholar] [CrossRef]
- CIRAD. Tropix: Physical and Mechanical Properties of Tropical Entandrophragma cylindricum Wood; CIRAD: Montpellier, France, 2024; Available online: https://tropix.cirad.fr (accessed on 10 May 2025).
- Njankouo, J.M.; Atchounga, P.; Foadieng, E.; Talla, P.K. Investigation of physical, mechanical properties and long-term creep behavior of Millettia laurentii wood (ww). Appl. Eng. 2020, 4, 27–34. [Google Scholar]
- Talla Fotsing, G.B.; Foadieng, E.; Fogué, M.; Talla, P.K. Triaxial variation of the modulus of elasticity in the thermo-elastic range of six tropical wood species. Wood Mater. Sci. Eng. 2023, 18, 120–129. [Google Scholar]
- NF B 51-008; Wood–Static Bending–Determination of Ultimate Strength in Static Bending Using Small Clear Specimens. AFNOR: Paris, France, 1987.
- BS EN 408:1995; British Standard: Timber Structures–Structural Timber and Glued Laminated Timber–Determination of Some Physical and Mechanical Properties. AFNOR: Paris, France, 1995.
- Krasnobrizha, A. Modeling Hysteresis Mechanisms of Woven Composites Using a Collaborative Elasto-Plastic Damageable Model with Fractional Derivatives. Ph.D. Thesis, Ecole Centrale de Nantes, Nantes, France, 2015. [Google Scholar]
- Krasnobrizha, A.; Rozycki, P.; Cosson, P.; Gornet, L. Modeling hysteresis mechanisms of woven composites using a collaborative elasto-plastic damageable fractional derivative model. Mater. Technol. 2016, 104, 407. [Google Scholar] [CrossRef]
- Hamza, M. Existence and Uniqueness of the Solution of an Infinite-Time Impulsive Fractional Differential Equation in Banach Space; Université Badji Mokhtar: Annaba, Algeria, 2015. [Google Scholar]
- Khalouta, A. Solving Linear and Nonlinear Partial Differential Equations Using Analytical Approaches: Extension to Cases of Fractional Order PDEs; Ferhat Abbas Setif 1 University: Sétif, Algeria, 2019. [Google Scholar]
- Stankiewicz, A. Fractional Maxwell model of viscoelastic biological materials. BIO Web Conf. 2018, 10, 20–32. [Google Scholar] [CrossRef]
- Xu, Y.; Cheng, M.; Huang, R.; Yu, J. The General Kelvin Model and Poynting Model Based on the General Fractional Calculus. IOP Conf. Ser. Earth Environ. Sci. 2019, 252, 022151. [Google Scholar] [CrossRef]
- Songsong, S.; Maosong, W. Evaluation of the applicability of different viscoelasticity constitutive models in bamboo scrimber short-term tensile creep property research. Sci. Eng. Compos. Mater. 2021, 28, 363–371. [Google Scholar] [CrossRef]
- Di Paola, M.; Alotta, G.; Burlon, A.; Failla, G. A novel approach to nonlinear variable-order fractional viscoelasticity. Philos. Trans. R. Soc. A Math. Phys. Sci. 2020, 378, 20190296. [Google Scholar] [CrossRef]
- Di Paola, M.; Alotta, G.; Burlon, A.; Failla, G. Nonlinear Dynamics. Nonlinear Dyn. 2002, 29, 57. [Google Scholar]
- Kawada, Y.; Yajima, T.; Nagahama, H. Fractional-order derivative and time-dependent viscoelastic behaviour of rocks and minerals. Acta Geophys. 2013, 61, 1690–1702. [Google Scholar] [CrossRef]
- Meng, R.; Yin, D.; Zhou, C.; Wu, H. Fractional description of time-dependent mechanical property evolution in materials with strain softening behavior. Appl. Math. Model. 2016, 40, 398–406. [Google Scholar] [CrossRef]
- Giusti, A.; Colombaro, I.; Garra, R.; Garrappa, R.; Mentrelli, A. On variable-order fractional linear viscoelasticity. Fract. Calc. Appl. Anal. 2024, 27, 1564–1578. [Google Scholar] [CrossRef]
- Sun, H.G.; Chen, W.; Wei, H.; Chen, Y.Q.; Mentrelli, A. A comparative study of constant-order; variable-order fractional models in characterizing memory property of systems. Eur. Phys. J. Spec. Top. 2011, 193, 185–192. [Google Scholar] [CrossRef]
- Gavin, H.P. The Levenberg-Marquardt Algorithm for Nonlinear Least Squares Curve-Fitting Problems. Duke Univ. Dep. Civ. Environ. Eng. 2019, 3, 1–23. [Google Scholar]
- Moučka, R.; Sedlačík, M.; Pátíková, Z. Fractional viscoelastic models of porcine skin and its gelatin-based surrogates. Mech. Mater. 2023, 177, 104–559. [Google Scholar] [CrossRef]
- Zhang, X.; Cen, J.; Zhang, Y.; Han, S.; Gu, K.; Yu, Y.; Hou, J. Comparative Study of Numerical Simulation on Short-Term Creep Behavior of Steam-Pretreated White Oak (Quercus alba L.) Wood. Forest 2024, 15, 2166. [Google Scholar] [CrossRef]
- Xu, S.; Cao, Y.; Cao, X.; Yang, P.; Liu, X.; Tang, R.; Yan, Y.; Wu, Q. The Observation of Creep Strain Distribution in Laminated Veneer Lumber Subjected to Different Loading Regimes. Forest 2024, 15, 179. [Google Scholar] [CrossRef]
- Xing, D.; Wang, X.; Wang, S. Temperature-Dependent Creep Behavior and Quasi-constant Mechanical Properties of Heat-Treated Wood. Forest 2021, 12, 968. [Google Scholar]
- Zhou, H.W.; Wang, C.P.; Mishnaevsky, L., Jr.; Duan, Z.Q.; Ding, J.Y. A fractional derivative approach to full creep regions in salt rock. Mech.-Time-Depend. Mater. 2013, 17, 413–425. [Google Scholar] [CrossRef]




| (MPa) | ( MPa) | a () | b () | ||
|---|---|---|---|---|---|
| 7.4 | 5.73 | 2.43 | 3.79 | 3.26 | 0.9876 |
| 14.7 | 5.07 | 4.30 | 3.85 | 3.09 | 0.9925 |
| 20.6 | 5.25 | 3.32 | 3.21 | 2.98 | 0.9894 |
| 29.4 | 5.32 | 3.45 | 6.18 | 4.02 | 0.9928 |
| (MPa) | (104 MPa) | (106 MPa·min) | a () | b () | |
|---|---|---|---|---|---|
| 16.5 | 1.578 | 2.14 | 5.71 | 2.79 | 0.9916 |
| 23.1 | 1.055 | 0.11 | 3.45 | 3.02 | 0.9952 |
| 38.1 | 0.807 | 6.13 | 3.03 | 3.03 | 0.9892 |
| 43.0 | 1.028 | 6.56 | 2.80 | 3.23 | 0.9837 |
| Models | Fractional Zener Constant Order [29,30] | Factional Maxwell Variable Order |
|---|---|---|
| Number of parameters to be determined numerically | 4 | 4 |
| Number of rheological elements | 3 | 2 |
| Precision (Sapele) | [0.9600–0.9718] | [0.9876–0.9928] |
| Precision (Wenge) | [0.9570–0.9860] | [0.9837–0.9952] |
| Sobol Index | First Order (S1) | Total (ST) | Second Order (S2) |
|---|---|---|---|
| a | 0.99 | 0.99 | |
| b |
| (MPa) | ( MPa) | m ( MPa) | a | b | |
|---|---|---|---|---|---|
| 7.4 | 5.73 | 2.00 | 34.96 | 3.79 | 3.26 |
| 14.7 | 5.07 | 2.00 | 34.96 | 3.85 | 3.09 |
| 20.6 | 5.25 | 2.00 | 34.96 | 3.21 | 2.98 |
| 29.4 | 5.32 | 2.00 | 34.96 | 6.18 | 4.02 |
| (MPa) | ( MPa) | m ( MPa) | a | b | |
|---|---|---|---|---|---|
| 16.5 | 1.578 | 18.00 | 32.13 | 5.71 | 2.79 |
| 23.1 | 1.055 | 18.00 | 32.13 | 3.45 | 3.02 |
| 38.1 | 0.807 | 18.00 | 32.13 | 3.03 | 3.03 |
| 43.0 | 1.028 | 18.00 | 32.13 | 2.80 | 3.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguedjio, L.C.; Mabekou Takam, J.S.; Blaysat, B.; Talla, P.K.; Moutou Pitti, R. Formulation and Numerical Verification of a New Rheological Model for Creep Behavior of Tropical Wood Species Based on Modified Variable-Order Fractional Element. Forests 2025, 16, 824. https://doi.org/10.3390/f16050824
Nguedjio LC, Mabekou Takam JS, Blaysat B, Talla PK, Moutou Pitti R. Formulation and Numerical Verification of a New Rheological Model for Creep Behavior of Tropical Wood Species Based on Modified Variable-Order Fractional Element. Forests. 2025; 16(5):824. https://doi.org/10.3390/f16050824
Chicago/Turabian StyleNguedjio, Loic Chrislin, Jeanne Sandrine Mabekou Takam, Benoit Blaysat, Pierre Kisito Talla, and Rostand Moutou Pitti. 2025. "Formulation and Numerical Verification of a New Rheological Model for Creep Behavior of Tropical Wood Species Based on Modified Variable-Order Fractional Element" Forests 16, no. 5: 824. https://doi.org/10.3390/f16050824
APA StyleNguedjio, L. C., Mabekou Takam, J. S., Blaysat, B., Talla, P. K., & Moutou Pitti, R. (2025). Formulation and Numerical Verification of a New Rheological Model for Creep Behavior of Tropical Wood Species Based on Modified Variable-Order Fractional Element. Forests, 16(5), 824. https://doi.org/10.3390/f16050824






