Enhancing Airborne Laser Scanning-Based Growing Stock Volume Models with Climate and Site-Specific Information
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Research Data
2.2.1. Forest Inventory (Ground Data)
2.2.2. ALS Data Processing
2.2.3. Climate Data Processing
2.2.4. Site Types and Soil Moisture
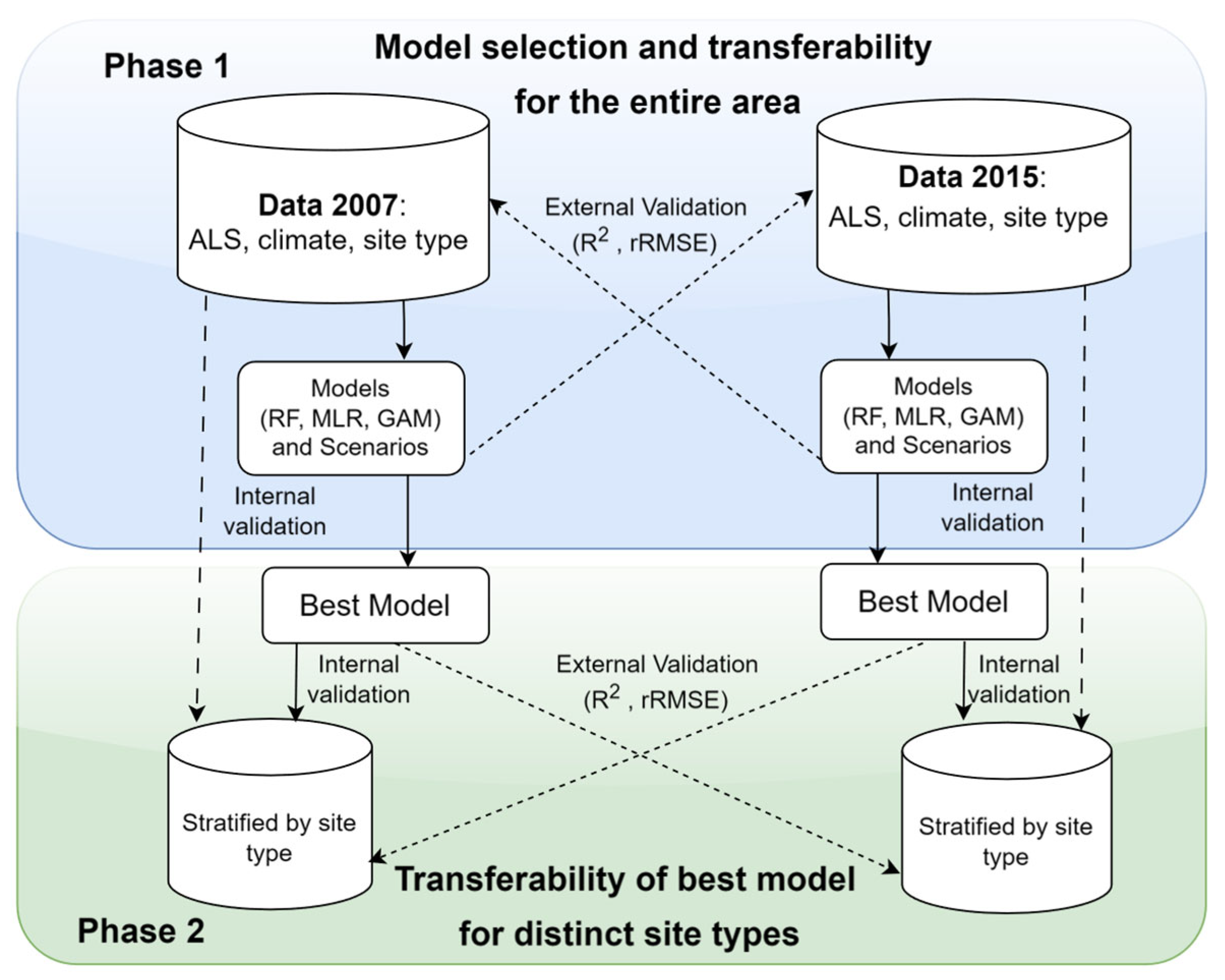
2.3. Methods
2.3.1. Correlation and Variable Selection
2.3.2. Modelling and Prediction
2.3.3. Model Validation and Selection
3. Results
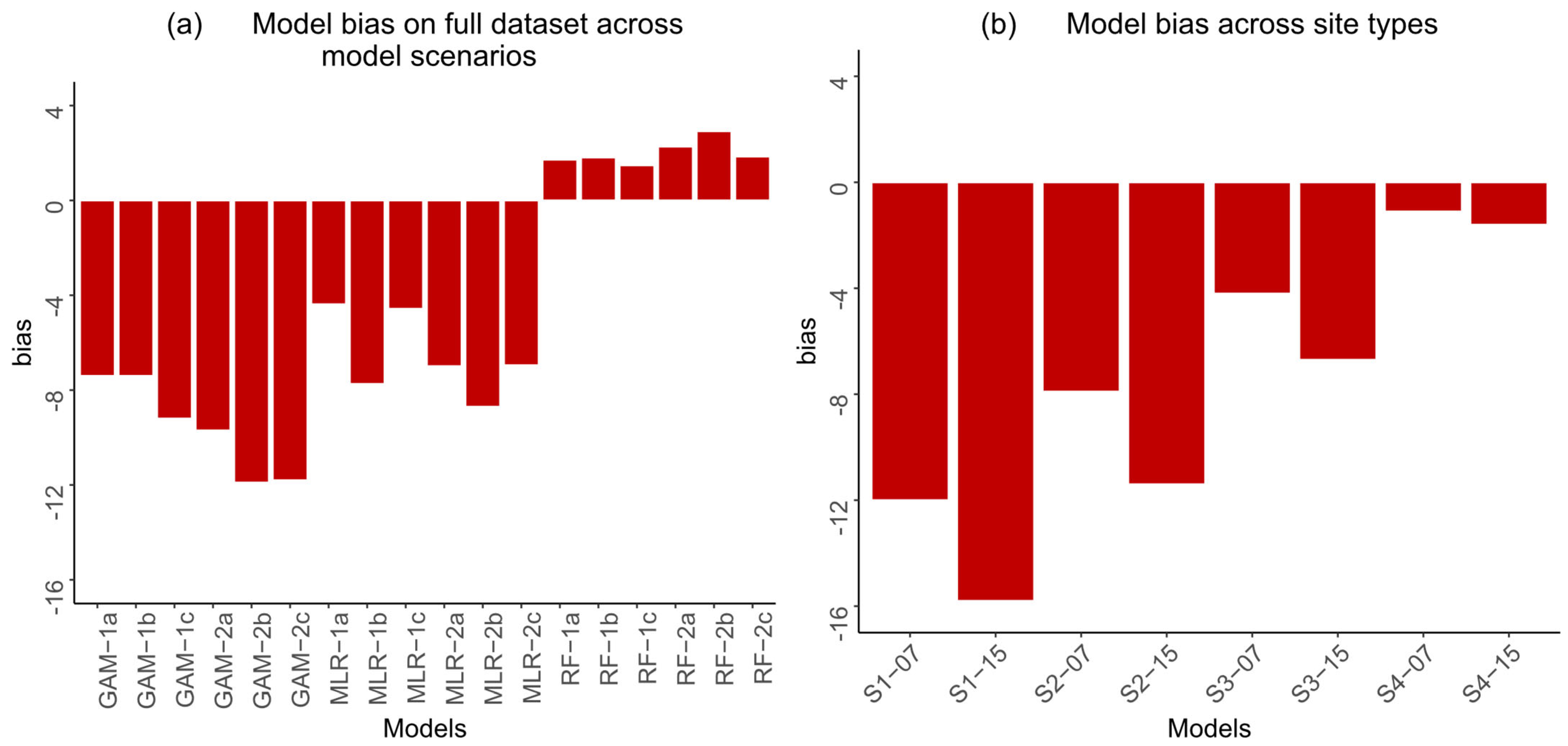
3.1. Model Performance
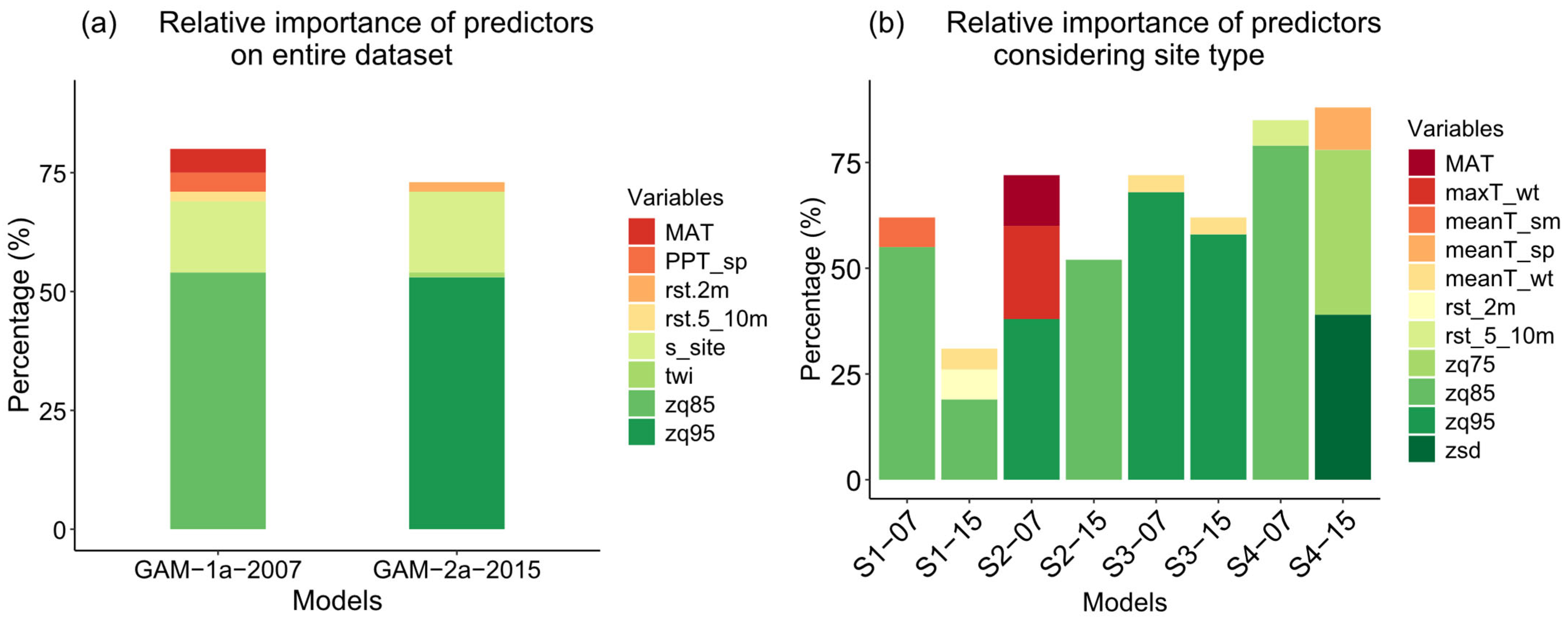
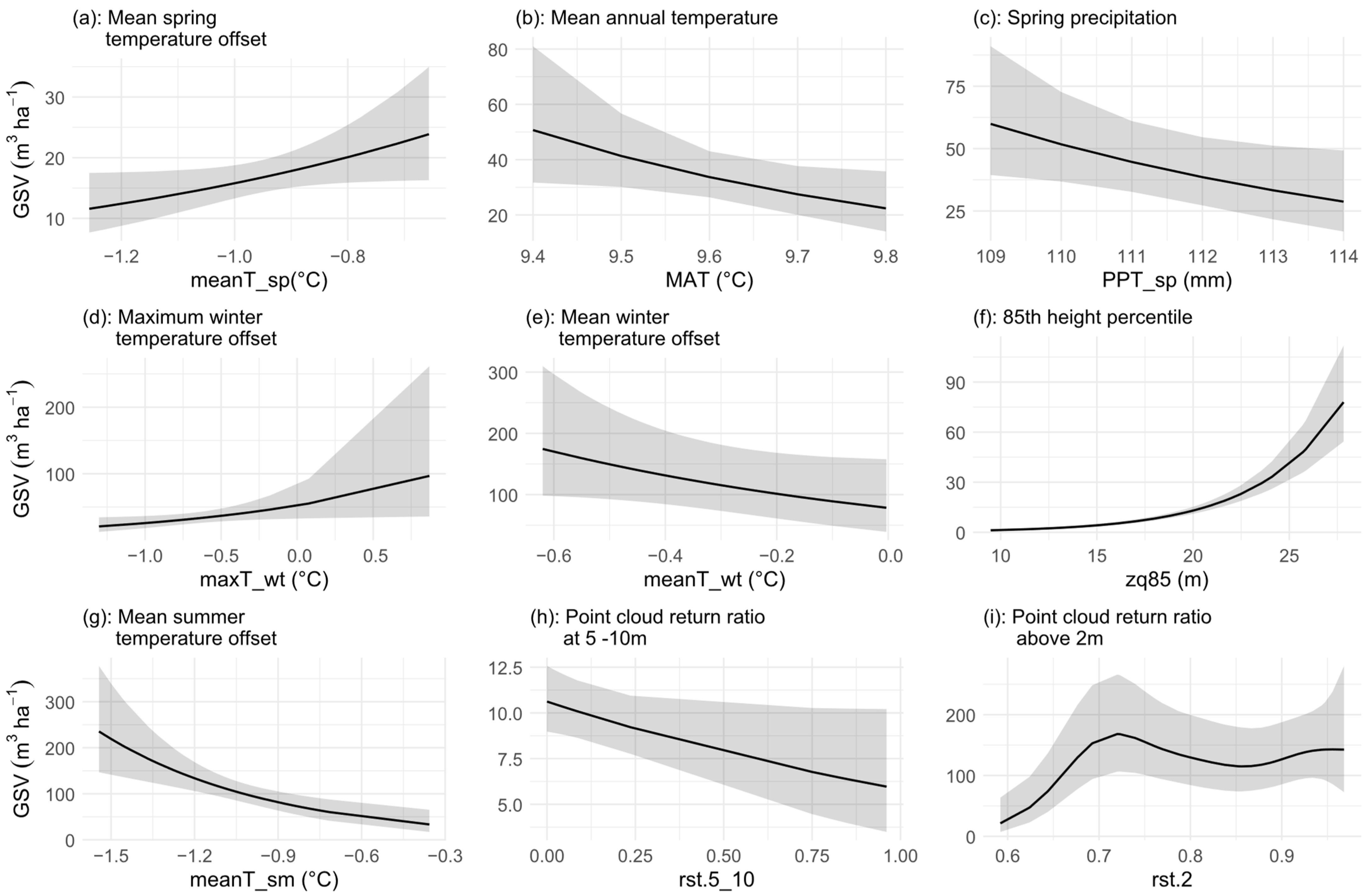
3.2. Variable Importance and Interaction
3.3. Model Transferability
4. Discussion
4.1. Model Performance and Selection
4.2. Model Validation and Transferability
4.3. Variable Importance
4.4. Limitations and Future Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krejza, J.; Světlík, J.; Bednář, P. Allometric Relationship and Biomass Expansion Factors (BEFs) for above- and below-Ground Biomass Prediction and Stem Volume Estimation for Ash (Fraxinus excelsior L.) and Oak (Quercus robur L.). Trees Struct. Funct. 2017, 31, 1303–1316. [Google Scholar] [CrossRef]
- Kurz, W.A.; Dymond, C.C.; White, T.M.; Stinson, G.; Shaw, C.H.; Rampley, G.J.; Smyth, C.; Simpson, B.N.; Neilson, E.T.; Trofymow, J.A.; et al. CBM-CFS3: A Model of Carbon-Dynamics in Forestry and Land-Use Change Implementing IPCC Standards. Ecol. Model. 2009, 220, 480–504. [Google Scholar] [CrossRef]
- Anderson-Teixeira, K.J.; Herrmann, V.; Rollinson, C.R.; Gonzalez, B.; Gonzalez-Akre, E.B.; Pederson, N.; Alexander, M.R.; Allen, C.D.; Alfaro-Sánchez, R.; Awada, T.; et al. Joint Effects of Climate, Tree Size, and Year on Annual Tree Growth Derived from Tree-Ring Records of Ten Globally Distributed Forests. Glob. Change Biol. 2022, 28, 245–266. [Google Scholar] [CrossRef] [PubMed]
- Cienciala, E.; Russ, R.; Šantrůčková, H.; Altman, J.; Kopáček, J.; Hůnová, I.; Štěpánek, P.; Oulehle, F.; Tumajer, J.; Ståhl, G. Discerning Environmental Factors Affecting Current Tree Growth in Central Europe. Sci. Total Environ. 2016, 573, 541–554. [Google Scholar] [CrossRef]
- Larson, J.; Vigren, C.; Wallerman, J.; Ågren, A.M.; Appiah Mensah, A.; Laudon, H. Tree Growth Potential and Its Relationship with Soil Moisture Conditions across a Heterogeneous Boreal Forest Landscape. Sci. Rep. 2024, 14, 10611. [Google Scholar] [CrossRef]
- Pretzsch, H.; Biber, P.; Schütze, G.; Uhl, E.; Rötzer, T. Forest Stand Growth Dynamics in Central Europe Have Accelerated since 1870. Nat. Commun. 2014, 5, 4967. [Google Scholar] [CrossRef]
- Schut, A.G.T.; Wardell-Johnson, G.W.; Yates, C.J.; Keppel, G.; Baran, I.; Franklin, S.E.; Hopper, S.D.; Van Niel, K.P.; Mucina, L.; Byrne, M. Rapid Characterisation of Vegetation Structure to Predict Refugia and Climate Change Impacts across a Global Biodiversity Hotspot. PLoS ONE 2014, 9, e82778. [Google Scholar] [CrossRef]
- Unterholzner, L.; Stolz, J.; van der Maaten-Theunissen, M.; Liepe, K.; van der Maaten, E. Site Conditions Rather than Provenance Drive Tree Growth, Climate Sensitivity and Drought Responses in European Beech in Germany. For. Ecol. Manag. 2024, 572, 122308. [Google Scholar] [CrossRef]
- Gril, E.; Laslier, M.; Gallet-Moron, E.; Durrieu, S.; Spicher, F.; Le Roux, V.; Brasseur, B.; Haesen, S.; Van Meerbeek, K.; Decocq, G.; et al. Using Airborne LiDAR to Map Forest Microclimate Temperature Buffering or Amplification. Remote Sens. Environ. 2023, 298, 113820. [Google Scholar] [CrossRef]
- Zellweger, F.; De Frenne, P.; Lenoir, J.; Vangansbeke, P.; Verheyen, K.; Bernhardt-Römermann, M.; Baeten, L.; Hédl, R.; Berki, I.; Brunet, J.; et al. Forest Microclimate Dynamics Drive Plant Responses to Warming. Science (1979) 2020, 368, 772–775. [Google Scholar] [CrossRef]
- Beland, M.; Parker, G.; Sparrow, B.; Harding, D.; Chasmer, L.; Phinn, S.; Antonarakis, A.; Strahler, A. On Promoting the Use of Lidar Systems in Forest Ecosystem Research. For. Ecol. Manag. 2019, 450, 117484. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar Remote Sensing for Ecosystem Studies. Bioscience 2002, 52, 19–30. [Google Scholar] [CrossRef]
- Bouvier, M.; Durrieu, S.; Fournier, R.A.; Renaud, J.P. Generalizing Predictive Models of Forest Inventory Attributes Using an Area-Based Approach with Airborne LiDAR Data. Remote Sens. Environ. 2015, 156, 322–334. [Google Scholar] [CrossRef]
- Marinelli, D.; Paris, C.; Bruzzone, L. A Novel Approach to 3-D Change Detection in Multitemporal LiDAR Data Acquired in Forest Areas. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3030–3046. [Google Scholar] [CrossRef]
- Zhao, K.; Suarez, J.C.; Garcia, M.; Hu, T.; Wang, C.; Londo, A. Utility of Multitemporal Lidar for Forest and Carbon Monitoring: Tree Growth, Biomass Dynamics, and Carbon Flux. Remote Sens. Environ. 2018, 204, 883–897. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Kaartinen, H.; Maltamo, M.; Hyyppä, H. Obtaining Plotwise Mean Height and Volume Growth in Boreal Forests Using Multi-Temporal Laser Surveys and Various Change Detection Techniques. Int. J. Remote Sens. 2008, 29, 1367–1386. [Google Scholar] [CrossRef]
- Moudrý, V.; Cord, A.F.; Gábor, L.; Laurin, G.V.; Barták, V.; Gdulová, K.; Malavasi, M.; Rocchini, D.; Stereńczak, K.; Prošek, J.; et al. Vegetation Structure Derived from Airborne Laser Scanning to Assess Species Distribution and Habitat Suitability: The Way Forward. Divers. Distrib. 2023, 29, 39–50. [Google Scholar] [CrossRef]
- Knapp, N.; Fischer, R.; Cazcarra-Bes, V.; Huth, A. Structure Metrics to Generalize Biomass Estimation from Lidar across Forest Types from Different Continents. Remote Sens. Environ. 2020, 237, 111597. [Google Scholar] [CrossRef]
- Hauglin, M.; Rahlf, J.; Schumacher, J.; Astrup, R.; Breidenbach, J. Large Scale Mapping of Forest Attributes Using Heterogeneous Sets of Airborne Laser Scanning and National Forest Inventory Data. For. Ecosyst. 2021, 8, 65. [Google Scholar] [CrossRef]
- Ma, Q.; Su, Y.; Tao, S.; Guo, Q. Quantifying Individual Tree Growth and Tree Competition Using Bi-Temporal Airborne Laser Scanning Data: A Case Study in the Sierra Nevada Mountains, California. Int. J. Digit. Earth 2018, 11, 485–503. [Google Scholar] [CrossRef]
- Knapp, N.; Fischer, R.; Huth, A. Linking Lidar and Forest Modeling to Assess Biomass Estimation across Scales and Disturbance States. Remote Sens. Environ. 2018, 205, 199–209. [Google Scholar] [CrossRef]
- Parkitna, K.; Krok, G.; Miścicki, S.; Ukalski, K.; Lisańczuk, M.; Mitelsztedt, K.; Magnussen, S.; Markiewicz, A.; Stereńczak, K. Modelling Growing Stock Volume of Forest Stands with Various ALS Area-Based Approaches. Forestry 2021, 94, 630–650. [Google Scholar] [CrossRef]
- Tompalski, P.; Coops, N.C.; White, J.C.; Goodbody, T.R.H.; Hennigar, C.R.; Wulder, M.A.; Socha, J.; Woods, M.E. Estimating Changes in Forest Attributes and Enhancing Growth Projections: A Review of Existing Approaches and Future Directions Using Airborne 3D Point Cloud Data. Curr. For. Rep. 2021, 7, 1–24. [Google Scholar] [CrossRef]
- White, J.; Wulder, M.; Varhola, A.; Vastaranta, M.; Coops, N.; Cook, B.D.; Pitt, D.; Woods, M. A Best Practices Guide for Generating Forest Inventory Attributes from Airborne Laser Scanning Data Using an Area-Based Approach; Natural Resources Canada: Victoria, BC, Canada, 2013. [Google Scholar]
- Penner, M.; Pitt, D.G.; Woods, M.E. Parametric vs. Nonparametric LiDAR Models for Operational Forest Inventory in Boreal Ontario. Can. J. Remote Sens. 2013, 39, 426–443. [Google Scholar] [CrossRef]
- Bollandsås, O.M.; Ene, L.T.; Gobakken, T.; Næsset, E. Estimation of Biomass Change in Montane Forests in Norway along a 1200 Km Latitudinal Gradient Using Airborne Laser Scanning: A Comparison of Direct and Indirect Prediction of Change under a Model-Based Inferential Approach. Scand. J. For. Res. 2018, 33, 155–165. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Innes, J.L.; Sheppard, S.R.J.; Fu, L.; Ruan, H.; She, G. Estimation of Forest Biomass Dynamics in Subtropical Forests Using Multi-Temporal Airborne LiDAR Data. Remote Sens. Environ. 2016, 178, 158–171. [Google Scholar] [CrossRef]
- Dalponte, M.; Jucker, T.; Liu, S.; Frizzera, L.; Gianelle, D. Characterizing Forest Carbon Dynamics Using Multi-Temporal Lidar Data. Remote Sens. Environ. 2019, 224, 412–420. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T.; Bollandsås, O.M. Indirect and Direct Estimation of Forest Biomass Change Using Forest Inventory and Airborne Laser Scanning Data. Remote Sens. Environ. 2015, 164, 36–42. [Google Scholar] [CrossRef]
- Tompalski, P.; Rakofsky, J.; Coops, N.C.; White, J.C.; Graham, A.N.V.; Rosychuk, K. Challenges of Multi-Temporal and Multi-Sensor Forest Growth Analyses in a Highly Disturbed Boreal Mixedwood Forests. Remote Sens. 2019, 11, 2102. [Google Scholar] [CrossRef]
- Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Queinnec, M.; Luther, J.E.; Bolton, D.K.; White, J.C.; Wulder, M.A.; van Lier, O.R.; Hermosilla, T. Modelling Lidar-Derived Estimates of Forest Attributes over Space and Time: A Review of Approaches and Future Trends. Remote Sens. Environ. 2021, 260, 112477. [Google Scholar] [CrossRef]
- Hawryło, P.; Francini, S.; Chirici, G.; Giannetti, F.; Parkitna, K.; Krok, G.; Mitelsztedt, K.; Lisańczuk, M.; Stereńczak, K.; Ciesielski, M.; et al. The Use of Remotely Sensed Data and Polish NFI Plots for Prediction of Growing Stock Volume Using Different Predictive Methods. Remote Sens. 2020, 12, 3331. [Google Scholar] [CrossRef]
- Wu, Y.; Mao, Z.; Guo, L.; Li, C.; Deng, L. Forest Volume Estimation Method Based on Allometric Growth Model and Multisource Remote Sensing Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 8900–8912. [Google Scholar] [CrossRef]
- Eastburn, J.F.; Campbell, M.J.; Dennison, P.E.; Anderegg, W.R.; Barrett, K.J.; Fekety, P.A.; Flake, S.W.; Huffman, D.W.; Kannenberg, S.A.; Kerr, K.L.; et al. Ecological and Climatic Transferability of Airborne Lidar-Driven Aboveground Biomass Models in Piñon-Juniper Woodlands. GISci. Remote Sens. 2024, 61, 2363577. [Google Scholar] [CrossRef]
- Hlásny, T.; Trombik, J.; Bošeľa, M.; Merganič, J.; Marušák, R.; Šebeň, V.; Štěpánek, P.; Kubišta, J.; Trnka, M. Climatic Drivers of Forest Productivity in Central Europe. Agric. For. Meteorol. 2017, 234–235, 258–273. [Google Scholar] [CrossRef]
- Charru, M.; Seynave, I.; Hervé, J.C.; Bertrand, R.; Bontemps, J.D. Recent Growth Changes in Western European Forests Are Driven by Climate Warming and Structured across Tree Species Climatic Habitats. Ann. For. Sci. 2017, 74, 33. [Google Scholar] [CrossRef]
- Haesen, S.; Lembrechts, J.J.; De Frenne, P.; Lenoir, J.; Aalto, J.; Ashcroft, M.B.; Kopecký, M.; Luoto, M.; Maclean, I.; Nijs, I.; et al. ForestTemp—Sub-Canopy Microclimate Temperatures of European Forests. Glob. Change Biol. 2021, 27, 6307–6319. [Google Scholar] [CrossRef]
- Haesen, S.; Lenoir, J.; Gril, E.; De Frenne, P.; Lembrechts, J.J.; Kopecký, M.; Macek, M.; Man, M.; Wild, J.; Van Meerbeek, K. Microclimate Reveals the True Thermal Niche of Forest Plant Species. Ecol. Lett. 2023, 26, 2043–2055. [Google Scholar] [CrossRef]
- Yates, K.L.; Bouchet, P.J.; Caley, M.J.; Mengersen, K.; Randin, C.F.; Parnell, S.; Fielding, A.H.; Bamford, A.J.; Ban, S.; Barbosa, A.M.; et al. Outstanding Challenges in the Transferability of Ecological Models. Trends Ecol. Evol. 2018, 33, 790–802. [Google Scholar] [CrossRef]
- Moreno-Arzate, C.N.; Martínez-Meyer, E. A Retrospective Approach for Evaluating Ecological Niche Modeling Transferability over Time: The Case of Mexican Endemic Rodents. PeerJ 2024, 12, e18414. [Google Scholar] [CrossRef]
- Stereńczak, K.; Lisańczuk, M.; Parkitna, K.; Mitelsztedt, K.; Mroczek, P.; Miścicki, S. The Influence of Number and Size of Sample Plots on Modelling Growing Stock Volume Based on Airborne Laser Scanning. Drewno 2018, 61, 5–22. [Google Scholar] [CrossRef]
- Bruchwald, A.; Rymer-Dudzinska, T.; Dudek, A.; Michalak, K.; Wróblewski, L.; Zasada, M. Wzory Empiryczne Do Okreslania Wysokosci i Piersnicowej Liczby Kształtu Grubizny Drzewa (Empirical Formulae for Defining Height and Dbh Shape FIgure of Thick Wood). Sylwan 2000, 144, 5–14. (In Polish) [Google Scholar]
- Bruchwald, A.; Miscicki, S.; Dmyterko, E.; Sterenczak, K. Ocena Dokładnosci Obreębowej Metody Inwentaryzacji Lasu Opartej Nalosowaniu Warstwowym (Assessment of the Accuracy of the Forest District Inventory Method Based on the Stratified Sampling). Sylwan 2017, 161, 909–916. (In Polish) [Google Scholar]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote Sensing Technologies for Enhancing Forest Inventories: A Review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Sparks, A.M.; Smith, A.M.S. Accuracy of a LiDAR-Based Individual Tree Detection and Attribute Measurement Algorithm Developed to Inform Forest Products Supply Chain and Resource Management. Forests 2021, 13, 3. [Google Scholar] [CrossRef]
- Strunk, J.L.; McGaughey, R.J. Stand Validation of Lidar Forest Inventory Modeling for a Managed Southern Pine Forest. Can. J. For. Res. 2023, 53, 71–89. [Google Scholar] [CrossRef]
- Roussel, J.R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Meador, A.S.; Bourdon, J.F.; de Boissieu, F.; Achim, A. LidR: An R Package for Analysis of Airborne Laser Scanning (ALS) Data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Böhner, J.; Selige, T. Spatial prediction of soil attributes using terrain analysis and climate regionalisation. Göttinger Geographische Abhandlungen 2006, 115, 13–28. [Google Scholar]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model. Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Marchi, M.; Castellanos-Acuña, D.; Hamann, A.; Wang, T.; Ray, D.; Menzel, A. ClimateEU, Scale-Free Climate Normals, Historical Time Series, and Future Projections for Europe. Sci. Data 2020, 7, 428. [Google Scholar] [CrossRef]
- Breiman, L. Random Forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wood, S.N. Generalized Additive Models: An Introduction with R, Second Edition, 2nd ed.; Chapman and Hall/CRC: New York, NY, USA, 2017; ISBN 9781315370279. [Google Scholar]
- Zuur, A.F.; Ieno, E.N.; Walker, N.; Saveliev, A.A.; Smith, G.M. Mixed Effects Models and Extensions in Ecology with R; Springer: New York, NY, USA, 2009; ISBN 978-0-387-87457-9. [Google Scholar]
- Wright, M.N.; Ziegler, A. Ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models, 1st ed.; Routledge: New York, NY, USA, 2017; ISBN 9780203753781. [Google Scholar]
- Araujo, M.; Pearson, R.; Thuiller, W.; Erhard, M. Validation of Species-Climate Impact Models under Climate Change. Glob. Change Biol. 2005, 11, 1504–1513. [Google Scholar] [CrossRef]
- Dobrowski, S.Z.; Thorne, J.H.; Greenberg, J.A.; Safford, H.D.; Mynsberge, A.R.; Crimmins, S.M.; Swanson, A.K. Modeling Plant Ranges over 75 Years of Climate Change in California, USA: Temporal Transferability and Species Traits. Ecol. Monogr. 2011, 81, 241–257. [Google Scholar] [CrossRef]
- García, M.; Riaño, D.; Chuvieco, E.; Danson, F.M. Estimating Biomass Carbon Stocks for a Mediterranean Forest in Central Spain Using LiDAR Height and Intensity Data. Remote Sens. Environ. 2010, 114, 816–830. [Google Scholar] [CrossRef]



| Plot Summary | Minimum | Maximum | Mean | Standard Deviation |
|---|---|---|---|---|
| 2005 (# trees = 763) | ||||
| Mean height [m] | 5 | 40 | 22.11 | 6.5 |
| Mean DBH [cm] | 7.5 | 75.7 | 26.51 | 12.15 |
| GSV [m3/ha] | 0.4 | 513.8 | 54.63 | 82.67 |
| 2007 * | ||||
| Mean tree height [m] | 6.3 | 40.77 | 22.77 | 6.43 |
| Mean DBH [cm] | 8.32 | 76.58 | 27.7 | 12.07 |
| GSV [m3/ha] | 0.56 | 539.72 | 60.01 | 86.06 |
| 2015 (# trees = 763) | ||||
| Mean tree height [m] | 11.5 | 44.1 | 25.3 | 5.89 |
| Mean DBH [cm] | 10.7 | 80.12 | 29.56 | 12.65 |
| GSV [m3/ha] | 1.2 | 643.4 | 82.67 | 100.68 |
| ALS1 (2007), t1 | ALS2 (2015), t2 | |
|---|---|---|
| Scanner | TopoSys GmbH FALCON II | Riegl LMSQ680i |
| Flight height | 700 m | 550 m |
| Data recording | May 2007 | August 2015 |
| Scanning angle | ±7.1° | 60° |
| Scan frequency | 83 kHz | 360 kHz |
| Average point density | 7 points/m2 | 10 points/m2 |
| Area covered | 90.68 km2 | 225.65 km2 |
| Season | Leaf on | Leaf on |
| Site Code | Description | Soil Characteristics |
|---|---|---|
| S1 | Pine-dominated | Sandy soils |
| S2 | Broadleaf (oak, ash, maple, and birch) | Rich fertile soils |
| S3 | Mixed broadleaf (oak, ash, and maple) | Soils of varying fertility |
| S4 | Alder and willow-dominated | Wet-to-water-logged soils |
| Metrics | Abbreviation | Scale | Description and Application |
|---|---|---|---|
| Height | Local | ||
| Percentiles [m] | zq85, zq95 | Vertical distribution of vegetation structure | |
| Standard | zmean, zsd | Mean height and height standard deviation, respectively | |
| a Canopy return height density | Local | Canopy development, density, and stratification | |
| rst. mean | Proportion of echoes above the mean tree height | ||
| rst.2m | Proportion of echoes above 2 m | ||
| rst.5m | Proportion of echoes above 5 m | ||
| rst.5_10m | Proportion of echoes at the 5th to 10th m height interval | ||
| rst.11_15m | Proportion of echoes at the 11th to 15th m height interval | ||
| rst.16_20m | Proportion of echoes at the 16th to 20th m height interval | ||
| Site factor | Local | Variability in soil moisture, freshness, and vegetation type | |
| s_site | Site type | ||
| Twi | Topographic wetness index | ||
| Climate | Annual, seasonal, or local variability in temperature and precipitation | ||
| [°C] | MAT | Global | Mean annual temperature |
| [mm] | PPT_sp | Global | Spring precipitation |
| [°C] | TD | TD | Temperature difference between the mean of the warmest month and the mean of the coldest month |
| [°C] | meanT_wt | Regional | Mean winter temperature offset |
| [°C] | minT_wt | Regional | Minimum winter temperature offset |
| [°C] | meanT_sm | Regional | Mean summer temperature offset |
| [°C] | meanT_sp | Regional | Mean spring temperature offset |
| Relative root mean square error | (3) | |
| Bias | (4) | |
| Coefficient of determination | (5) | |
| p-value | (6) |
| Model | Structure | AIC | p-Value |
|---|---|---|---|
| MLR-1a | log(gsv.2007) ~ zq85 + rst.5 + rst.5-10m+ MAT + PPT_sp + s_site | 372.2 | |
| MLR-1b | log(gsv.2007) ~ zq85 + rst.5 + rst.5_10m | 380.5 | 0.027 * |
| MLR-1c | log(gsv.2007) ~ zq85 + r.st.5m + s_site | 374.1 | 0.001 ** |
| MLR-2a | log(gsv.2015) ~ zq95 + rst.2m + TD + s_site | 366.3 | |
| MLR-2b | log(gsv.2015) ~ zq95 + rst.2m | 371.7 | 0.09 |
| MLR-2c | log(gsv.2015) ~ zq95 + rst.2m + s_site | 369.2 | 0.005 ** |
| GAM-1a | log(gsv.2007) ~ s(zq85) + rst.5_10m + MAT * PPT_sp + s_site | 363.3 | |
| GAM-1b | log(gsv.2007) ~ zq95 + rst.5 + rst.5_10m + ti(rst.16_20, zq50) | 372.3 | 0.002 ** |
| GAM-1c | log(gsv.2007) ~ s(zq95) + r.st5_10 + r.st.16_20m + s_site | 369.3 | 0.02 * |
| GAM-2a | log(gsv.2015) ~ s(zq95,) + s_site + te(twi, rst.2m) + s(meanT_wt, k = 15) | 338.8 | |
| GAM-2b | log(gsv.2015) ~ s(zq95) + s(rst.2m) | 369.9 | 0.008 ** |
| GAM-2c | log(gsv.2015) ~ s(zq95) + s_site | 365.0 | 0.006 ** |
| Site-Type Model Transfer | Number of Plots | R-Squared (Internal) | R-Squared (External) | rRMSE (Internal) | rRMSE (External) |
|---|---|---|---|---|---|
| S1_07 to S1_15 | 44 | 0.58 | 0.46 | 0.50 | 0.65 |
| S1_15 to S1_07 | 44 | 0.56 | 0.38 | 0.40 | 0.85 |
| S2_07 to S2_15 | 24 | 0.68 | 0.65 | 0.64 | 0.99 |
| S2_15 to S2_07 | 24 | 0.50 | 0.46 | 0.69 | 0.82 |
| S3_07 to S3_15 | 75 | 0.65 | 0.58 | 0.62 | 0.77 |
| S3_15 to S3_07 | 75 | 0.58 | 0.60 | 0.59 | 0.76 |
| S4_07_to_S415 | 37 | 0.72 | 0.85 | 0.57 | 0.67 |
| S4_15 to S4_07 | 37 | 0.80 | 0.70 | 0.57 | 0.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tangwa, E.; Tracz, W.; Erfanifard, Y.; Mielcarek, M.; Stereńczak, K. Enhancing Airborne Laser Scanning-Based Growing Stock Volume Models with Climate and Site-Specific Information. Forests 2025, 16, 815. https://doi.org/10.3390/f16050815
Tangwa E, Tracz W, Erfanifard Y, Mielcarek M, Stereńczak K. Enhancing Airborne Laser Scanning-Based Growing Stock Volume Models with Climate and Site-Specific Information. Forests. 2025; 16(5):815. https://doi.org/10.3390/f16050815
Chicago/Turabian StyleTangwa, Elvis, Wiktor Tracz, Yousef Erfanifard, Miłosz Mielcarek, and Krzysztof Stereńczak. 2025. "Enhancing Airborne Laser Scanning-Based Growing Stock Volume Models with Climate and Site-Specific Information" Forests 16, no. 5: 815. https://doi.org/10.3390/f16050815
APA StyleTangwa, E., Tracz, W., Erfanifard, Y., Mielcarek, M., & Stereńczak, K. (2025). Enhancing Airborne Laser Scanning-Based Growing Stock Volume Models with Climate and Site-Specific Information. Forests, 16(5), 815. https://doi.org/10.3390/f16050815









