Next Article in Journal
Reconstructing Hydroclimatic Variability (1657 AD) Using Tree-Ring Time Series and Observed and Gridded Precipitation Data in Central Greece
Previous Article in Journal
Advancements in Monitoring Tree Phenology Under Global Change: A Comprehensive Review
Previous Article in Special Issue
Engineered Bamboo Building Materials: Types, Production, and Applications
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 16
Issue 5
10.3390/f16050772
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

How the Scots Pine and Beech Aging Process Affects Wood

by
Tomasz Jelonek
1,
Katarzyna Klimek
1,
Bartłomiej Naskrent
1,*,
Arkadiusz Tomczak
1,
Marcin Jakubowski
1,
Robert Kuźmiński
2,
Tomasz Szwed
1,
Joanna Kopaczyk
1,
Daniel Grabowski
1 and
Jarosław Szaban
1
1
Department of Forest Utilization, Faculty of Forestry and Wood Technology, Poznan University of Life Sciences, Wojska Polskiego 71A, 60-625 Poznan, Poland
2
Department of Forest Entomology and Pathology, Faculty of Forestry and Wood Technology, Poznan University of Life Sciences, Wojska Polskiego 71C, 60-625 Poznan, Poland
*
Author to whom correspondence should be addressed.
Forests 2025, 16(5), 772; https://doi.org/10.3390/f16050772
Submission received: 10 March 2025 / Revised: 13 April 2025 / Accepted: 28 April 2025 / Published: 30 April 2025
(This article belongs to the Special Issue Novelties in Wood Engineering and Forestry—2nd Edition)
Browse Figures
Versions Notes

Abstract

:
This study investigates the effects of aging trees on wood properties, which are caused by climate change, the withdrawal of coniferous species from Central Europe, and the increased crown sweep in old beech stands. The research was carried out in old tree stands with a high proportion of Scots pine (Pinus sylvestris L.) and beech (Fagus sylvatica L.) species. The collected material was from five tree pine stands aged between 151 and 182 and three beech stands between the ages of 165 and 184. The samples were subjected to an analysis of wood properties such as density and modulus of elasticity. The results and findings of this study indicate that the Scots pine currently reaches the optimal wood tissue quality at around 80 years of age, which is approximately 20 years earlier than the species’ anticipated cutting age. However, the beech, which reaches maturity at about 120–140 years, reaches the maximal quality of wood tissue already at the age of 80–90 years. Above the age of 110, the quality of beech wood (density and modulus of elasticity) decreases. Moreover, it is necessary to emphasize that the radial trend of wood density does not coincide with the trend of the modulus of elasticity. Additionally, it is found that wood density is not a perfect representation of its mechanical qualities; it can, however, be regarded as a measure of the technical quality of wood tissue. The results indicate that the pine and the beech that grow on the European Plain mature faster and reach technical quality earlier than just a couple of decades before.

1. Introduction

The cambial growth of trees is a complicated process. It involves a number of biophysical and biochemical processes that occur on both a cellular and tissue level. The complexity of the processes is related to the formation of wood as well as the common occurrence of tree tissue biomodifications hinders the possibility to study and understand all of these dependencies and correlations in detail [1]. Among the reasons behind this are the individual differences related to growth pace, which naturally decreases with age, leading to a decline in a tree stand’s productivity [2]. Hence, the changes related to the physiological and biomechanical functioning of trees can be depicted as an age function. One of the elements of these changes is the aging process, which can be described as a decreased productivity and quality of the tree tissue [3,4]. Brutovská et al. [5] presented an interesting theory that considers tree aging as an internally regulated and controlled process. Moreover, the theory refers both to individual trees as well as the entire populations. This, however, is likely to lead to a number of widespread consequences and outcomes. Kollman [6] studied the aging process of trees and the manner in which it impacts wood properties. However, he focused only on carefully selected wood properties.
Currently, forestry is tackling a number of issues, one of which is climate change. Vacek [7,8] and Zaidler et al. [9] indicated that the changes constitute a significant threat to forest ecosystems. According to Cukor et al. [10] and Zaidler et al. [9], forest ecosystems are able to ameliorate the impact of climate change with carbon capture and storage in the process of photosynthesis. It is particularly significant to preserve the stability of forest ecosystems and, at the same time, preserve the continuity of forest production. Naturally, this is particularly crucial for the forest industry. Borecki et al. [11] revealed that climate change contributes to the deteriorating health of tree stands. The most endangered tree stands are those from the older age class. Previous climate models [12] have revealed that the frequency of droughts will increase, with prolonged duration. At the same time, air temperature will increase as well. These factors accelerate the process of self-thinning and shifting the natural distribution of tree species [13,14,15], which is significant for the economy. The most endangered species due to climate change and prolonged periods of drought is the Norway spruce.
One of the most important forest-forming species in Europe is the Scots pine (Pinus silvestris L.), particularly for economic and ecological reasons [16,17]. This species covers about 58.9% of the forest area in Poland [18]. The Scots pine grows mainly on dry and sandy ground [17,19] which means it is able to adjust to difficult habitats. Unfortunately, the levels of groundwater are decreasing due to drought in many areas in Europe [19,20,21], which means that water becomes inaccessible for tree root systems. The higher air temperature and water deficit weaken the trees and make them susceptible to illnesses, pests, and insects [22,23,24]. Among the most dangerous pests threatening the mortality of the Scots pine is the bark beetle (Ips acuminatus L.) [17]. Another one is the hemiparasitic species such as the mistletoe [25].
Despite the number of threats and stresses, the pine constitutes the core of tree stands, i.e., creates most tree stands in Central Europe and Eurasia. One of the main aims of the contemporary forest industry is the production of wood of the highest quality. Hence, it is particularly significant to establish the most suitable cutting age for each species to obtain the highest quality wood. As far as the selection of a cutting age for the pine is concerned, the conditions that affect tree growth play a critical role. In the case of trees growing in habitats characteristic of the pine, the cutting age is 100 years [26]. In the post-farmlands, the cutting age should be reduced to 60 years [4]. The density of trees is one of their most crucial physical properties, as it has an impact on mechanical properties. The variations in wood density can even be observed between the individuals within the same species, as well as in axial and radial variability within one trunk [27]. In the cross-section, the wood density increases in the direction from the pith to girth. However, wood density decreases in the direction from the butt end to the top end in the longitudinal section [28]. Tomczak et al. [29] revealed that the conventional density of young wood for the pine was on average 392 kg/m3, while for mature wood, it was 415 kg/m3. Wąsik et al. [30], who studied the wood properties of 260 pines of “Tabórz” Scots pines, obtained high values. They observed a mean wood density of 487 kg/m3. Pine wood is characterized by a high modulus of elasticity. According to Gurau et al. [31], the modulus of elasticity for pine wood was about 11.7 GPa, while in the study by Lindström et al. [32], it was between 8.6 and 17.6 GPa. However, in Meier’s study [33], the mean value of the modulus of elasticity was 10.08 GPa.
Another species that can ameliorate the effects of climate change and pine thinning is the European beech [8,34]. The European beech (Fagus sylvatica L.) is one of the most significant and common deciduous tree species in Europe. The share of the beech in some countries of Central Europe reaches between 6% [35] and 10% [36]. Beech tree stands constitute about 6.4% of the entire forest area in Poland [18]. As the range of the beech increases, the interest among scholars in beech wood increases as well [37,38]. Although beech wood is mainly used for the production of energy, the European Green Deal (European Commission) assumes that beech wood can be used in the building and construction industry, as well as in the furniture industry, i.e., for plywood production [38].
Beech wood is a raw material of great variability. The differences in built and properties occur not only between trees of different origins and between individual trees but also within one single tree [39]. The physical and mechanical properties of beech wood are significant [40]. A shorter fiber length, in comparison to coniferous trees, is the reason why beech wood is not used in the production of cellulose and paper [41]. The mean density of beech wood is about 720 kg/m3 at 12% moisture content. Beech wood density decreases along the radius of the stem (from the pith to the girth area) and with the height of the tree [40,42,43]. Its wood is hard, cleavable, and mechanically resistant, but with low durability [44].
Using beech wood as a building material in construction is still not popular, and it only contributes to a small extent in comparison with spruce. The reason behind this is that spruce wood is easier to work with and has lower density. However, the development of technologies such as cross-laminated timber (CLT) [45,46,47,48], glued laminated timber (GLT) [49,50,51,52] and laminated veneer lumber (LVL) [53,54,55,56,57] will contribute to the increased popularity of beech wood in building and construction. Moreover, the necessity to substitute spruce wood with other species in the future is the reason why research on beech wood gains is of significance. This refers both to modifications [58,59] and beech wood properties [60,61,62].
The aim of this study is to determine how the aging process of trees impacts the variability of selected physical and mechanical properties of pine and beech wood. Using the variability as a basis allows us to determine an approximate age at which a tree reaches the highest quality of tree tissue. It is assumed that the tree age impacts the physical and mechanical properties of wood. Preserving the wood longer on the stem beyond the optimal cutting age (for each species) results in deteriorated physical and mechanical properties of wood both for the pine and the beech. Determining the optimal cutting age is related to measurable outcomes for the economy. It is established that the cutting age of the species important for the economy should be reduced to an age before they lose their resistance to biotic and abiotic factors.

2. Materials and Methods

This study was carried out in Poland, between 2020 and 2022, at three locations which were spread across five research areas (plots) (Figure 1). The mature (overmature) spruce tree stands between the ages of 151 and 184 were chosen for our study (Table 1).
The process of choosing the model trees was based on environmental and dendrometric methods. For this purpose, in each tree stand, a research plot was developed, which allowed for the trees to be measured at DBH, and then we classified them following Kraft’s classes [63]. In the next step, the main tree stand was divided into three degrees (I, II, and III based on Kraft’s classes) using thickness and the dendrological method as the basis [64]. Based on thickness and width, an average tree was chosen from each class. Three model trees from each area were chosen. Five research plots were used to study a total of fifteen model trees.
Each sample, which was a 70 cm block, was taken from each model tree. The sample was collected between 1.0 m and 1.7 m above the ground (Figure 1), which is in compliance with ISO 13910:2014 [65] standards. For the laboratory testing, the material (i.e., matching blocks) was cut to size, which allowed us to study the mechanical properties and wood density of wet wood (30% moisture content, i.e., maximal saturation of fibers) and dry wood (maximum 4% moisture content, i.e., minimal saturation of fibers).

2.1. Wood Properties of Scots Pine and Beech

This study examined the radial variability of wood’s modulus of elasticity (E) in two extreme moisture content states, that is, dry wood with max. 4% saturation and wet wood (wood above the saturation point of cell membranes, i.e., above 30%). Additionally, the conventional density of wood was ascertained (Q). The mechanical wood properties were studied using a universal testing machine TiraTESt (Poland, Łódź) with the MatestService software2013. Matest-Service software and a universal testing machine, TiraTESt, were used to investigate the mechanical wood properties.

2.2. Wood Density of Scots Pine and Beech

The density was determined using a stereometric method, in compliance with ISO 13061-2:2014 [66] standards.
Basic density was calculated using the following formula:
Q = m 0 V m a x       [ k g m 3 ]
where
  • Q—basic density;
  • m0—mass of dry wood [kg];
  • Vmax—the volume of wet wood in the state of maximum moisture content [m3].

2.3. Modulus of Elasticity of Wood in Bending

The modulus of elasticity in bending (E), resilience to bending, and destructive bending strength were measured in accordance with PN-EN 380:1998 [67] and PN-EN 408:2004 [68] standards. After the bending test using ASTM D 143-94: 2000 [69] standard, the potential damage was analyzed as follows:
E = P i − P 1 × l 3 4 f i − f 1 × b × h 3     M P a
where
  • E—modulus of elasticity;
  • Pi—load of a given range [N];
  • P1—preload [N];
  • l—support spacing [mm];
  • b—width of the sample [mm];
  • h—height of the sample [mm];
  • fi—deflection value of the load of a given range [mm];
  • f1—deflection value forced by preload [mm].

2.4. Desorption Enhancement

Another factor that was examined was the desorption enhancement of wood at the modulus of elasticity, which is the difference between the modulus of elasticity (E) for dry and wet wood (WSDE = E0% − E30% [MPa]).

2.5. Statistical Analyses

The statistical analysis was performed using over 2000 samples. Initially, the goal of the mathematical and statistical analyses was to determine the distinguishable characteristics of comparable sets of variables and select the appropriate tests. First, any possible discrepancies between the populations and their distributions were confirmed using the Shapiro–Wilk test. A parametric HSD test was employed when the distribution was close to the normal distribution. In the case of non-normal distribution, a non-parametric test (the Kruskal–Wallis test) was used. The terms mean, median, decile range, standard deviation, and coefficient of variation were used to characterize the elements under study. To determine the links between the variables, the correlation coefficient was computed. A 95% confidence interval and a statistical significance of p < 0.05 were used for the statistical analyses. The STATISTICAS 14 set was used for the statistical analyses.

3. Results

This study examined the radial distribution of variables of the researched spruce wood properties and attributes throughout all plots in all locations. The main aim of the experiment was to observe the patterns of changing wood properties resulting from aging. The variability of the properties under study was equivalent to that of the full set of data, and the distribution of the properties under study was not always normal. These factors had a substantial impact on the distribution of the variables under study.

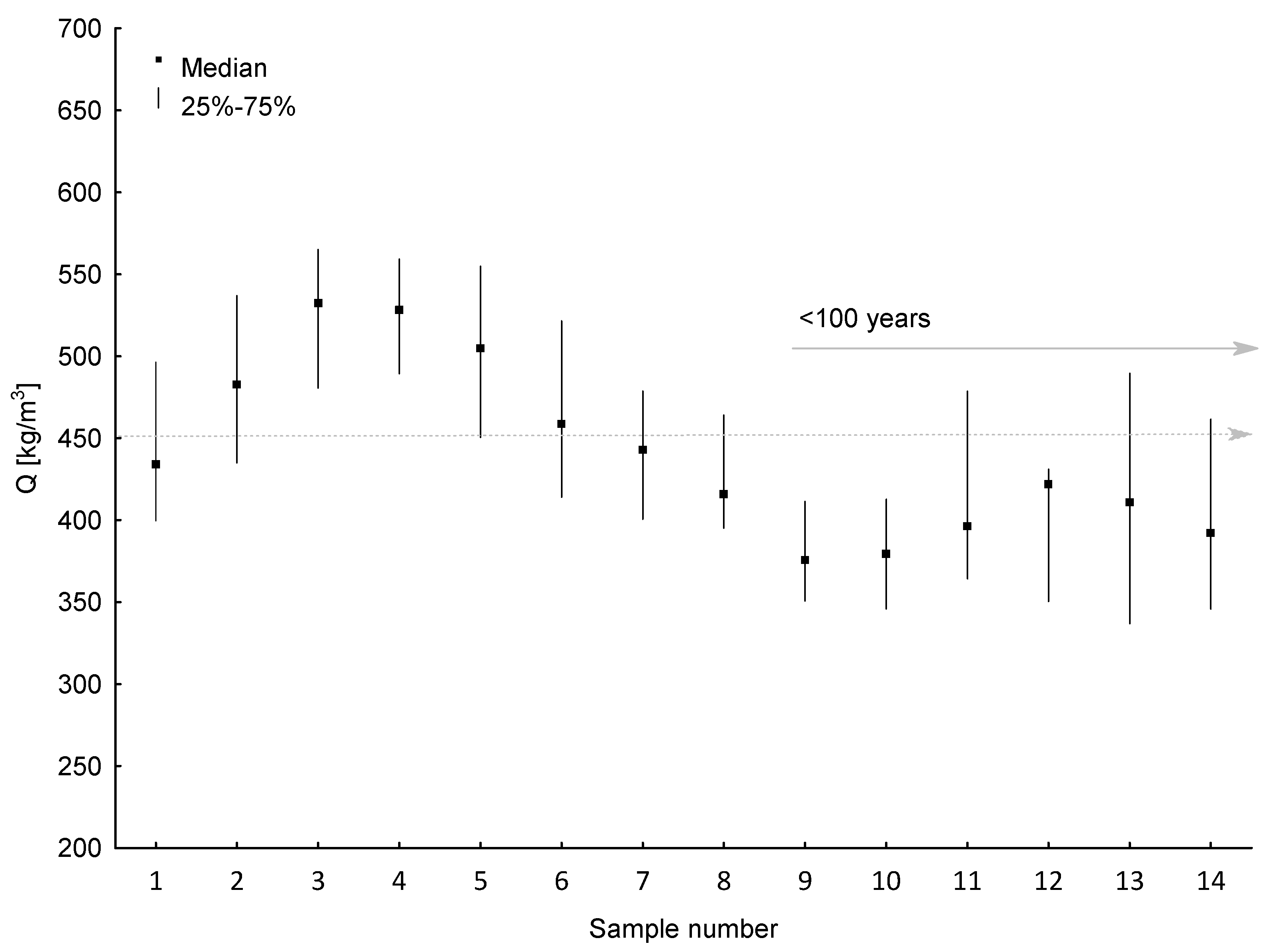
3.1. Wood Density of Beech Wood

The wood density of beech wood had a normal distribution (Shapiro–Wilk W = 0.99337, p = 0.35838), and its mean value was 653 kg/m3. The variability of the wood property reached 8.1%, and the established confidence interval of 95% certainty led us to the conclusion that the mean density of the studied beech wood was between 646 kg/m3 and 659 kg/m3 (Table 2).
An analysis of wood density variability was conducted in order to describe the influence of age on the variability of tree tissue; the analysis was performed starting with the pith in the direction of the girth. In the case of the radial variability of density for all the studied trees, a decrease in wood density along the radius was observed up to the age of 80, and the second significant decrease occurred above the age of 120–130 (Figure 2). The high values for beech wood were observed near the pith, and these values were maintained in the radial distribution until the age of 80.

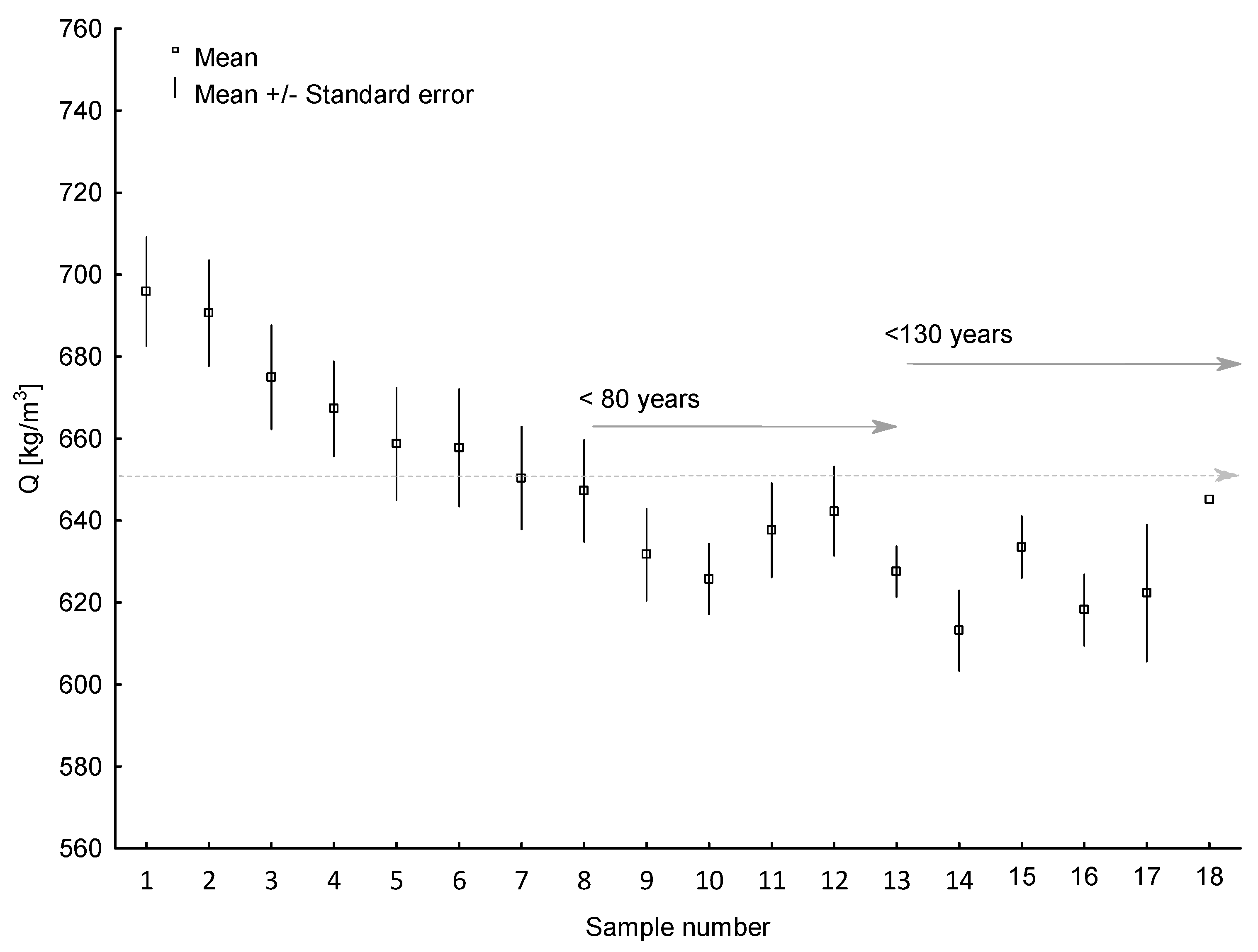
3.2. Wood Density of Scots Pine Wood

The wood density of Scots pine wood did not have a normal distribution (Shapiro–Wilk p = 0.00241), and its mean was 488 kg/m3. The variability of wood properties reached 14.7%, and the established confidence interval of 95% certainty led us to the conclusion that the mean density of the studied Scots pine was between 485 kg/m3 and 497 kg/m3 (Table 3).
The radial variability of wood density for Scots pine (Figure 3) is presented below. The trend indicates an increase in the values of wood density up to the age of 50–60. Once the pine is above the age of 80, a gradual decrease in wood density below the median is observed. This result is significant as it indicates that the aging process of the pine begins at the age of 80 when the technical quality of wood decreases. At the same time, it is possible to assume that each individual tree optimizes the characteristics and properties of the tissue to suit its mechanical and physiological functions. The reduced density above a certain age is a natural phenomenon and does not necessarily correspond with its mechanical properties.

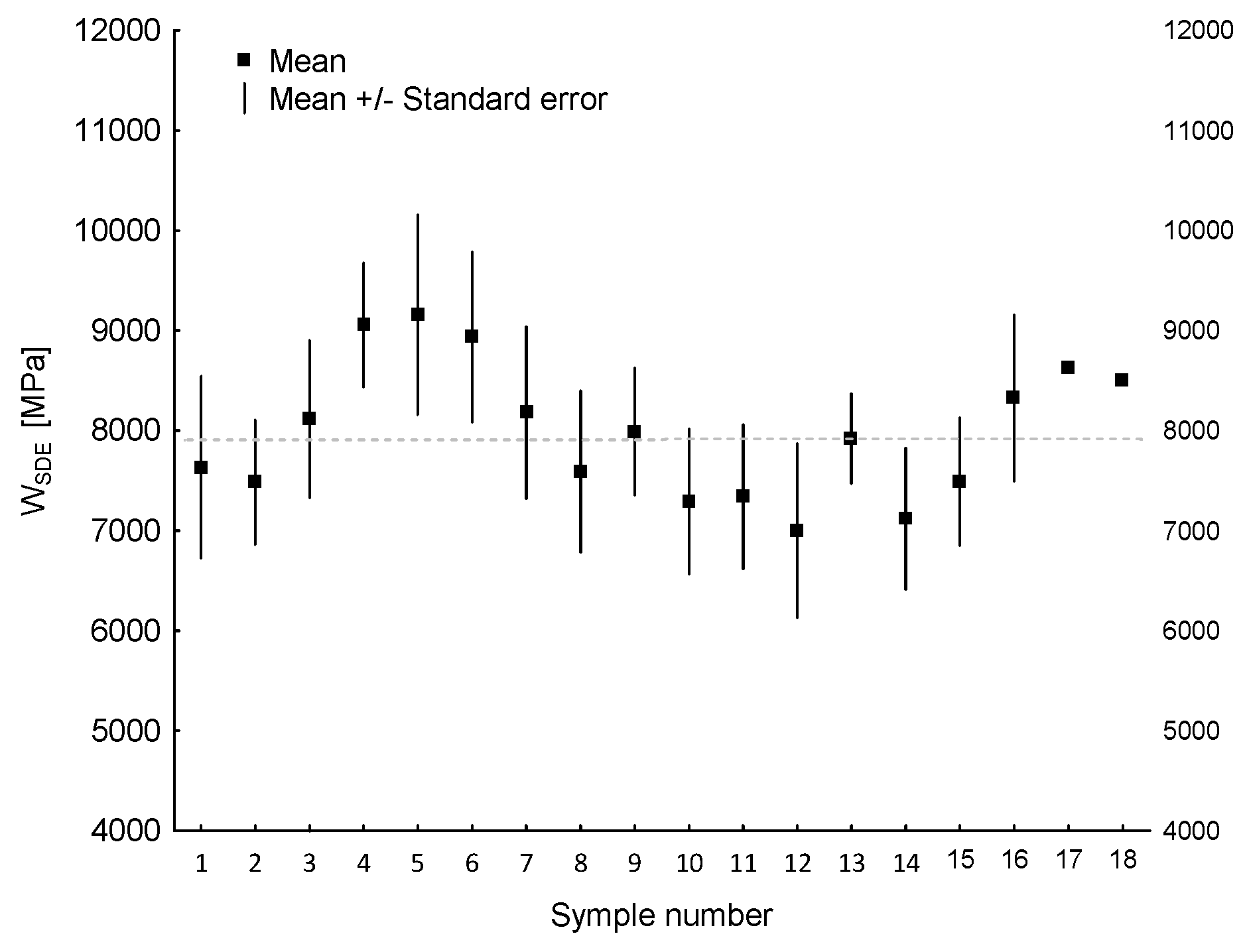
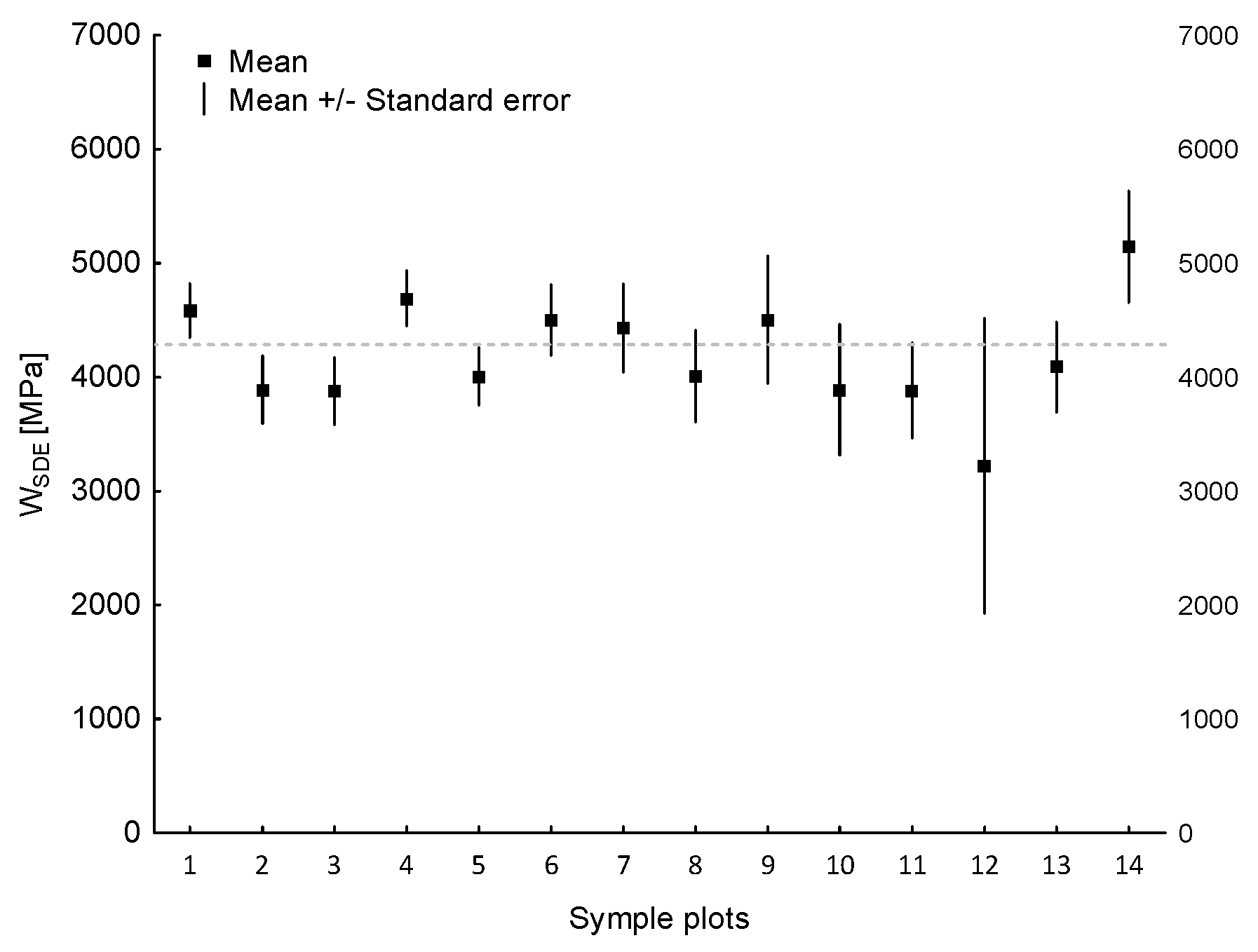
3.3. Modulus of Elasticity of Beech Wood in Bending

Modulus of elasticity is a mechanical property that reflects the technical quality of wood because it takes into account both resistance to bending and elongation along the fibers.
The distribution of the modulus of elasticity of wet wood (wood with maximal moisture content) and dry wood was similar to a normal distribution (E0% = Shapiro–Wilk p = 0.05257; E30% = Shapiro–Wilk p = 0.04659).
The mean value for the modulus of elasticity in the static bending of wet wood (E30%) was 8926 MPa, and that of dry wood (E0%) was 16,842 MPa. It can be assumed with 95% certainty that the modulus of elasticity for wet wood was between 8614 MPa and 9237 MPa, whereas the modulus of elasticity for dry wood was between 16,377 MPa and 17,307 MPa, which means it is within the range characteristic of this species (Table 4).
Similarly to density, the radial distribution of the modulus of elasticity for beech was analyzed as well. Regarding the modulus of elasticity in static bending for both dry wood (E0%) and wet wood (E30%), the values were lower in the near-pith zone (samples 1–3 for E0% and samples 1–5 for E30%) (Figure 4 and Figure 5). There was an increase in the modulus of elasticity, reaching values above the mean, in the middle zone of the radius for dry wood. While in the near-girth zone, starting with sample 14, the modulus of elasticity decreased and reached values below the mean. The only exception was sample 16, whose E0% value was close to the mean (Figure 4).
The radial variability of the modulus of elasticity for wet wood (E30%) is distributed slightly differently. In this case, the modulus of elasticity reached the values above the mean for samples 6 to 15. Only in the near-girth zones (samples 16–18), that is, the trees above the age of 150, did the modulus of elasticity drop below the mean for the sample (Figure 5).
A significant decrease in the modulus of elasticity was observed in young beech wood and in those past the cutting age, i.e., when they were above the ages of 140–150 (Figure 4 and Figure 5). This indicates that tree age impacts the formation of the mechanical properties of wood.
Moreover, the relationships between density and the moduli of elasticity were studied as well. The correlation between wood density and the modulus of elasticity of wet wood (E30%) was 0.205 (p ≥ 0.05), which was not statistically significant. The correlation between density and the modulus of elasticity of dry wood (E0%), albeit slightly higher, i.e., 0.228 (p ≥ 0.05), was also not statistically significant.

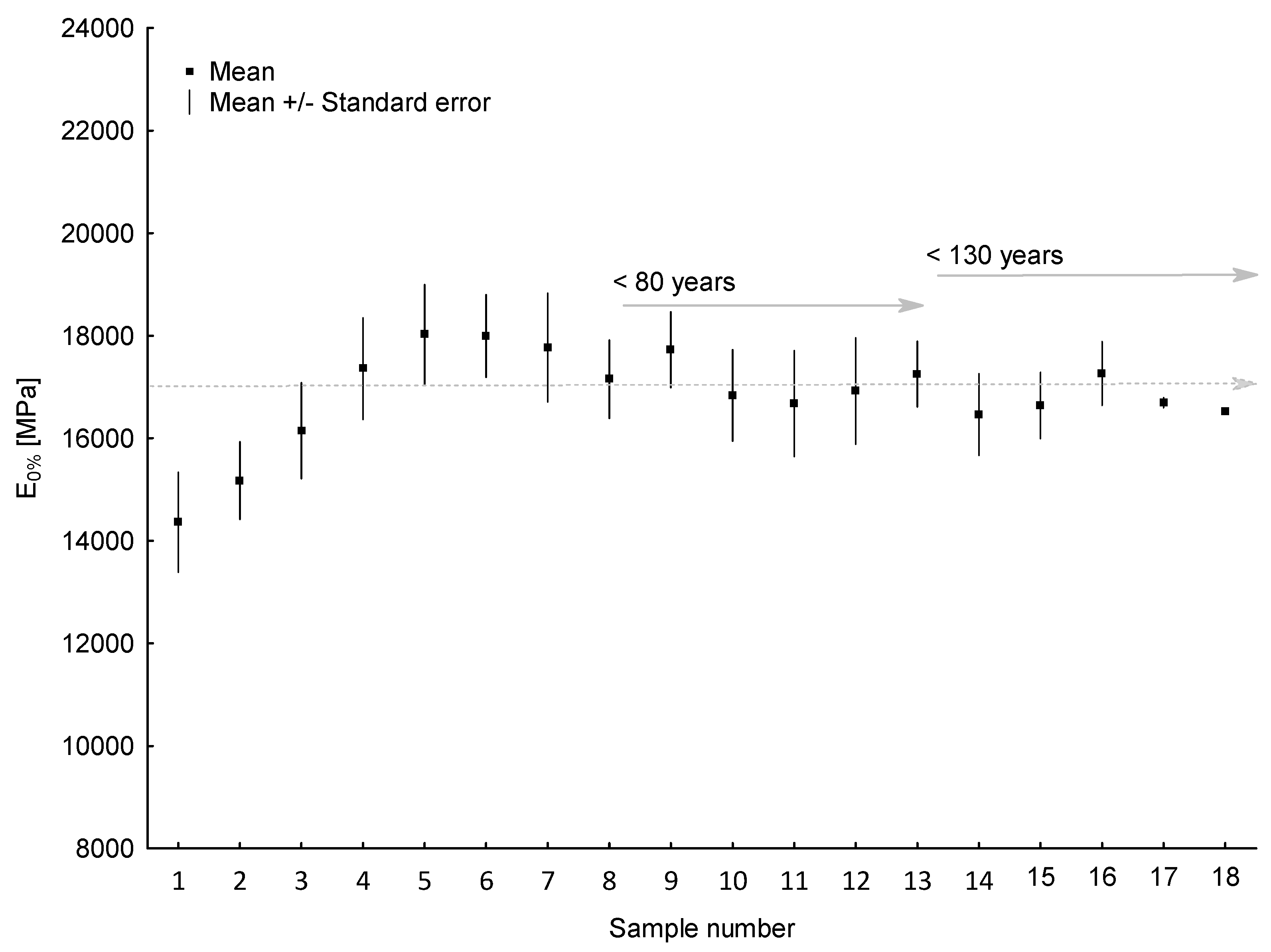
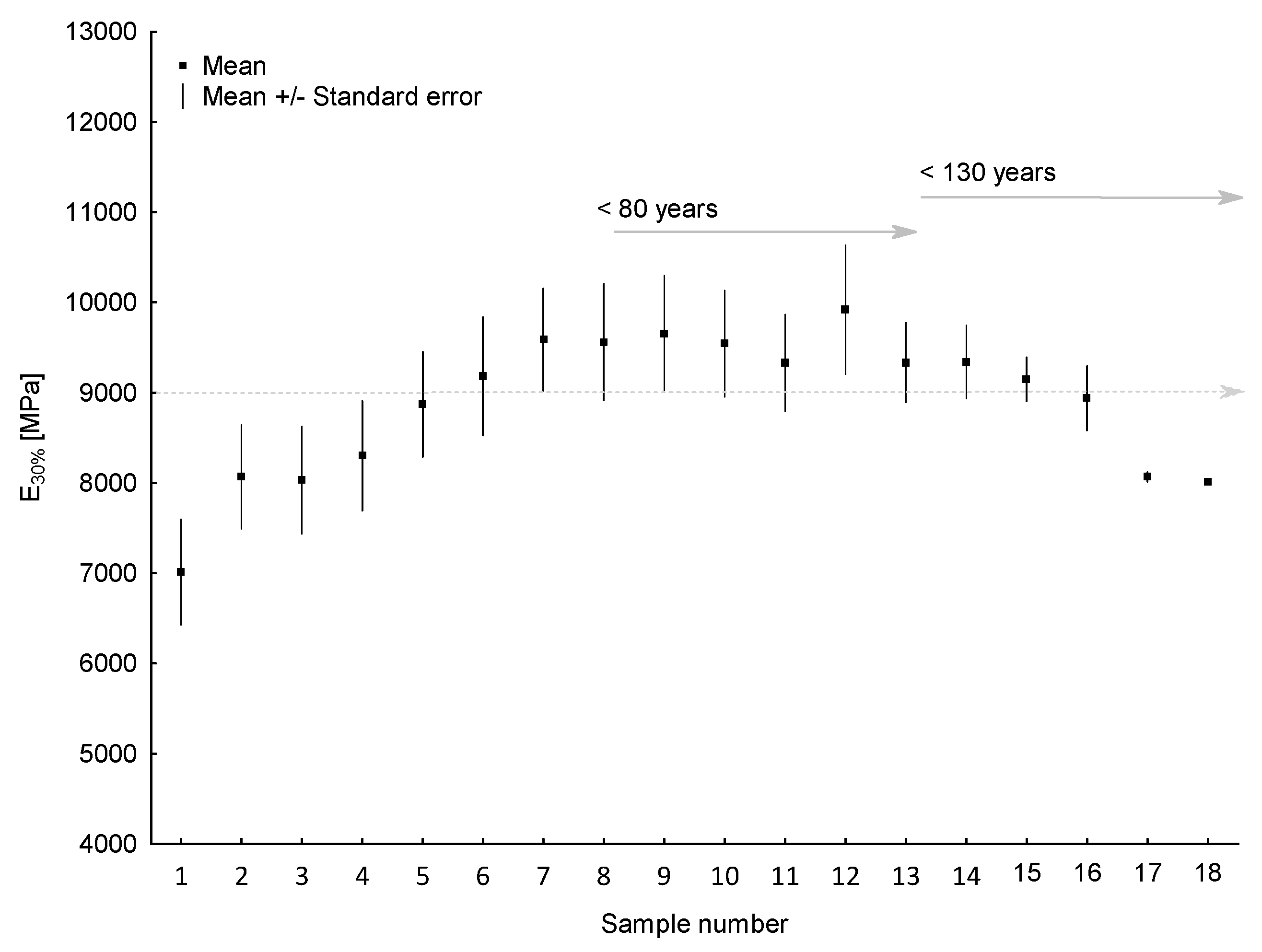
3.4. Modulus of Elasticity of Scots Pine Wood in Bending

The modulus of elasticity of wet wood and dry wood showed a distribution similar to normal (E30% = Shapiro–Wilk p = 0.32737; E0% = Shapiro–Wilk p = 0.05131).
The mean value for the modulus of elasticity in the static bending of wet wood (E30%) was 54134 MPa, and that of dry wood (E0%) was 9447 MPa.
It can be assumed with 95% certainty that the modulus of elasticity of wet wood was between 5254 MPa and 5571 MPa, whereas the modulus of elasticity of dry wood was between 9133 MPa and 9762 MPa. The standard deviation for the modulus of elasticity of wet wood was 1650 MPa, and that of dry wood was 3273 MPa (Table 5).
Another analyzed aspect was the radial variability for the modulus of elasticity of pine wood (Figure 6 and Figure 7). The lower values for the modulus (E30% and E0%), those below the mean, were observed in samples 1 and 2 (young wood) and beyond sample 8 (those past the cutting age of the tree, about 90-year-old trees). The area between samples 3 and 8 was characterized by values higher than the mean, which means the wood is of the highest technical quality (Figure 6 and Figure 7). The formation of the mechanical wood properties of pine wood determined by the modulus of elasticity is influenced by the ontogenetic development of trees. The Scots pine wood reaches technical maturity in Poland much faster than it was previously assumed.
It is worth emphasizing the fact that both the modulus of elasticity of dry wood E0% and wet wood E30%, show a similar trend, which indicates a similar distribution of desorption enhancement over the lifespan of a tree. This issue is discussed in detail below.
The relationship between wood density and the modulus of elasticity was determined as well. The correlation between wood density and the modulus of elasticity of wet wood (E30%) was 0.677 (p ≥ 0.05), which was statistically significant. The values for the modulus of elasticity of dry wood (E0%) were slightly lower: 0.460 (p ≥ 0.05).

4. Discussion

The key element when studying the impact of tree age on the quality of wood is to conduct a radial variability analysis of its properties and select suitable materials for the study. The opportunity to carry out studies on old pine and beech forests is of special academic and practical value. Firstly, there is a decreasing number of pine forests above 100 years of age and beech forests older than 140 years on the European Plain. Secondly, research methods that are harmful to these species involve samples collected from the lower parts of the stem, which are most valuable. Such methods, however, decrease the quality of the remaining part of the stem. Our study focused on the wood derived from old tree stands, which is of high quality. The results adequately describe the variability of important wood properties such as density and the modulus of elasticity, which are spread over the entire course of a tree’s life.
The aging process of the tree tissue lasts from the moment the first cells divide and differentiate until the moment of the tree’s physiological death or its felling. There is an abundance of research that describes the physical and mechanical properties of wood. However, what is missing is research that allows us to comprehend and determine the relationship between the variability of wood properties and the natural aging process of trees. Interestingly, the studies focusing on wood quality and the variability of wood properties are widely recognized and described in the literature [26,70,71,72,73,74,75,76,77,78]. The listed articles, both directly and indirectly, show that as the tree ages, the structure of the wood changes as well, including the wood properties. Trees optimize their form and structure adequately to match their function (physiological and mechanical) and simultaneously achieve optimal structure [79].
According to Fujimoto’s study [80], as trees age, their wood becomes more ordered, and aging is an irreversible process from the standpoint of the variety of wood qualities. The results of his study clearly define the natural variability of wood properties against the ontogenesis of trees. Moreover, that article provides guidelines concerning the future of sustainable forest management and the optimal exploitation of forest resources.
This study attempts to address the issue of the manner in which the aging process of trees affects the technical quality of wood by focusing on its properties: wood density (Q) and modulus of elasticity (E). These are the two most frequently studied and described wood properties, which adequately reflect its technical quality and thus affect wood quality. In the case of density, the results for both the pine and the beech are within the ranges provided by previous studies on this topic [35,40,81,82,83,84,85]. Moreover, the mean values of the modulus of elasticity of the pine and the beech are also within the ranges provided by previous studies on this topic [38,86,87,88,89].
Pine wood properties indicate varied values for the axial and radial directions [90]. However, it is still believed that the constant increase in density and mechanical properties occurs in the radial direction, i.e., from the pith to the girth [91].
The results presented by [83] show that pine wood density increases rapidly from the pith to approximately rings 20–30, before stabilizing, which partially corresponds with the results that were obtained in our study. In this study, we observed that pine wood density increased from the pith until the age of 40, and afterward, it started to decrease gradually. At the age of 80, the value of wood density dropped below the median, and until its death, it remained at a relatively low level, similar to the modulus of elasticity. In the period 80–182 years, it was possible to observe a slight increase in pine wood density at the age of about 130 years. This was also the case with the radial variability of the modulus of elasticity; hence, a statistically significant correlation between density and the modulus of elasticity was observed in pine wood.
This unusual variability of wood density in the near-girth zone of old pine tree trunks may be influenced by not only natural processes related to aging but also climate change. The results of the study conducted on three pine species presented by [92] prove that climate change significantly influences the structure of trees. The amount of precipitation is the main factor that affects the radial increment, the width of annual rings, and the wood density of the analyzed trees.
However, another study on the variability of beech wood density showed that the increase in the cambial age causes an increase in the mean wood density [93]. Klement et al. [85] claimed that beech wood density increases in the direction from the cambium to the pith. It is also worth emphasizing that their study was conducted on trees below the age of 90, which is much lower than that in our study. The results of this study indicate that there was a visible drop in wood density below the mean for the entire radius, and there were clear fluctuations in density with three peaks for the beech over the age of 80. The first peak appeared around 100 years, the second around 140, and the third around 180. This means that there are cyclic disruptions caused by the aging process itself; however, this is likely the result of numerous overlapping factors and issues, including water stress caused by climate change, as confirmed in previous studies [94,95,96]. Similar conclusions were reached by Bréda [97], who studied the correlation between the width of annual rings and the age of trees and wood density.
Van der Maaten et al. [98] studied the beech in Germany and revealed that water availability is critical for wood formation, and climate change impacts the wood density of the species and not just in the late vegetative season. Their results support the hypothesis of the impact of climate change and the reduced groundwater levels on the disruptions in the radial course of variable features and the properties of wood. The fluctuations of the studied wood properties in the near-girth zone were observed in both the beech and the pine, i.e., in old trees, which are more susceptible to stress.
Furthermore, in the case of the beech, there was no correlation between the radial trend of wood density and the modulus of elasticity. However, a clear increase was observed in the modulus of elasticity of the beech in the direction from the pith to the girth for trees aged 40–50 years for dry wood (E0%) and 70–80 years for wet wood (E30%). In other words, wood density is not a good predictor of the technical quality of beech wood.
The modulus of elasticity was deliberately determined for two extreme levels of wood moisture content (dry wood and wet wood, wood with maximal moisture content) in order to also determine the range of desorption enhancement of wood for the modulus of elasticity (Figure 8 and Figure 9). This is an easy, universal, but underestimated indicator of the technical quality of wood.
The submicroscopic structure of the tree is what causes desorption amplification [99,100]. This phenomenon can be linked to the chemical makeup of wood, specifically the proportion and shape of hemicellulose and hydrophilic cellulose in the tissue. Moreover, this phenomenon is strongly influenced by the proportion of crystalline to amorphous cellulose. Crystalline cellulose is inaccessible to water, but amorphic cellulose is extremely hygroscopic.
According to ASTLEY et al. [101], the ratio and the form of hydrophilic cellulose and hemicellulose in wood tissue impact its strength, and the higher the ratio of crystalline cellulose, the stronger the tracheid cell wall becomes. Hence, the increase in desorption enhancement can indicate the greater ratio of the amorphic form of cellulose to that of crystalline.
The radial variability of desorption enhancement (Figure 8 and Figure 9) indicates a significant role of primary and secondary bindings as far as strength is concerned for beech and pine wood. Both in the case of desorption enhancement for the beech (Figure 8) and the pine (Figure 9), it was observed that the value of the grith zone of the trunk increased. At the same time, the radial variability of desorption enhancement for the pine was noticeably lower than that for the beech, which points to a higher radial homogeneity (stability) of pine wood in comparison to beech wood.
On the basis of the results, it is possible to assume that the aging process also refers to the chemical composition of tree tissue, and its course is easier to observe in the beech than in the pine. In addition, as trees age, they form wood whose cell walls have lower levels of crystalline cellulose.
Tree aging is directly linked to the mechanical and hydraulic properties of the anatomical elements of the tree tissue, as described by Mencuccini et al. [79], Schniewind [102], and Sperry et al. [103]. These elements are optimized during the growth, development, and aging process of trees. As a result of these external and internal factors, numerous modifications occur that facilitate a compromise between the mechanical and hydraulic properties of wood. These modifications function as a survival strategy for the trees, and they are an inalienable element of their ontogenetic transformations.

5. Conclusions

Due to the complexity of the interactions, it is difficult or impossible to precisely determine the influence of a single factor on shaping the properties of wood. The presented results prove that the process also concerns the properties of tree tissue and most likely involves all levels of wood structures. At the same time, desorption enhancement is a good indicator of its course and adequately describes the variability of the technical quality of wood.
The presented results prompt reflection on the necessity to verify the principles of forest management in terms of the redetermination of the optimal felling age for pine and beech stands. Taking into account the technical quality of the wood raw material, it can be estimated that the general felling age of the pine is about 80 years, and in the case of the beech, it is about 110 years.

Author Contributions

Conceptualization, T.J. and K.K.; methodology, T.J., A.T. and K.K.; software, T.J.; formal analysis, T.J. and K.K.; investigation, T.J., K.K., B.N., M.J. and R.K.; writing—original draft preparation, T.J., K.K., B.N., A.T., J.K. and J.S.; writing—review and editing, M.J., R.K., J.K., T.S., D.G. and J.S.; visualization, T.J., K.K., T.S. and D.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Dataset available on request from the authors.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Savidge, R.A.; Barnett, J.R.; Napier, R. (Eds.) Cell and Molecular Biology of Wood Formation; BIOS Scientific: Oxford, UK, 2000. [Google Scholar]
  2. Zaehle, S. Effect of height on tree hydraulic conductance incompletely compensated by xylem tapering. Funct. Ecol. 2005, 19, 359–364. [Google Scholar] [CrossRef]
  3. Jelonek, T.; Pazdrowski, W.; Tomczak, A.; Grzywiński, W. Biomechanical stability of pines growing on former farmland in northern Poland. Wood Res. 2012, 57, 31–44. [Google Scholar]
  4. Jelonek, T. Biomechaniczna Stabilność Drzew a Wybrane Właściwości Fizyczne, Mechaniczne i Strukturalne Ksylemu Sosny Zwyczajnej (Pinus sylvestris L.) Wyrosłej w Warunkach Gruntów Porolnych i Leśnych; Rozprawy naukowe 455; Wydawnictwo Uniwersytetu Przyrodniczego: Poznań, Poland, 2013. [Google Scholar]
  5. Brutovská, E.; Sámelová, A.; Dušička, J.; Mičieta, K. Ageing of trees: Application of general ageing theories. Ageing Res. Rev. 2013, 12, 855–866. [Google Scholar] [CrossRef]
  6. Kollmann, F.F.P.; Wilfred, A.C.J. Principles of Wood Science and Technology: Solid Wood; Springer: Berlin/Heidelberg, Germany, 1968. [Google Scholar]
  7. Vacek, Z.; Prokůpková, A.; Vacek, S.; Cukor, J.; Bílek, L.; Gallo, J.; Bulušek, D. Silviculture as a tool to support stability and diversity of forests under climate change: Study from Krkonoše Mountains. Cent. Eur. For. J. 2020, 66, 116–129. [Google Scholar] [CrossRef]
  8. Vacek, Z.; Vacek, S.; Cukor, J. European forests under global climate change: Review of tree growth processes, crises and management strategies. J. Environ. Manag. 2023, 332, 117353. [Google Scholar] [CrossRef] [PubMed]
  9. Zeidler, A.; Borůvka, V.; Brabec, P.; Tomczak, K.; Bedřich, J.; Vacek, Z.; Cukor, J.; Vacek, S. The possibility of using non-native spruces for Norway Spruce wood replacement—A case study from the Czech Republic. Forests 2024, 15, 255. [Google Scholar] [CrossRef]
  10. Cukor, J.; Vacek, Z.; Vacek, S.; Linda, R.; Podrázský, V. Biomass productivity, forest stability, carbon balance, and soil transformation of agricultural land afforestation: A case study of suitability of native tree species in the submontane zone in Czechia. CATENA 2022, 210, 105893. [Google Scholar] [CrossRef]
  11. Borecki, T.; Orzechowski, M.; Stępień, E.; Wójcik, R. Expected impact of climate change on forest ecosystems and its consequences in forest management planning. Sylwan 2017, 161, 531–538. [Google Scholar]
  12. IPCC. Climate Change and Land: An IPCC Special Report on Climate Change, Desertification, Land Degradation, Sustainable Land Management, Food Security, and Greenhouse Gas Fluxes in Terrestrial; IPCC: Geneva, Switzerland, 2019. [Google Scholar]
  13. Netherer, S.; Schopf, A. Potential effects of climate change on insect herbivores in European forests—General aspects and the pine processionary moth as specific example. For. Ecol. Manag. 2010, 259, 831–838. [Google Scholar] [CrossRef]
  14. Brzeziecki, B.; Keczyński, A.; Zajączkowski, J.; Drozdowski, S.; Gawron, L.; Buraczyk, W.; Bielak, K.; Szeligowski, H.; Dzwonkowski, M. Threatened tree species of the Białowieża National Park (the Strict Reserve). Sylwan 2012, 156, 252–261. [Google Scholar]
  15. Drozdowski, S.; Brzeziecki, B.; Żybura, H.; Żybura, B.; Gawron, L.; Buraczyk, W.; Zajączkowski, J.; Bolibok, L.; Szeligowski, H.; Bielak, K.; et al. Long–term dynamics of old–growth stands in the managed part of the Białowieża Forest: Increasing and declining tree species. Sylwan 2012, 156, 663–671. [Google Scholar]
  16. Wójkiewicz, B.; Cavers, S.; Wachowiak, W. Current approaches and perspectives in population genetics of Scots pine (Pinus sylvestris L.). For. Sci. 2016, 62, 343–354. [Google Scholar] [CrossRef]
  17. Brichta, J.; Vacek, S.; Vacek, Z.; Cukor, J.; Mikeska, M.; Bílek, L.; Šimůnek, V.; Gallo, J.; Brabec, P. Importance and Potential of Scots Pine (Pinus sylvestris L.) in 21 St Century. Cent. Eur. For. J. 2023, 69, 3–20. [Google Scholar]
  18. Statistical Office in Białystok. Statistical Yearbook of Forestry 2024; Statistical Office in Białystok: Białystok, Poland, 2024; p. 39. [Google Scholar]
  19. Vacek, S.; Vacek, Z.; Bílek, L.; Simon, J.; Remeš, J.; Hůnová, I.; Král, J.; Putalova, T.; Mikeska, M. Structure, regeneration and growth of Scots pine (Pinus sylvestris L.) stands with respect to changing climate and environmental pollution. Silva Fenn. 2016, 50, 1564. [Google Scholar] [CrossRef]
  20. Gao, Y.; Markkanen, T.; Aurela, M.; Mammarella, I.; Thum, T.; Tsuruta, A.; Yang, H.; Aalto, T. Response of water use efficiency to summer drought in a boreal Scots pine forest in Finland. Biogeosciences 2017, 14, 44094422. [Google Scholar] [CrossRef]
  21. Buras, A.; Schunk, C.; Zeiträg, C.; Herrmann, C.; Kaiser, L.; Lemme, H.; Menzel, A. Are Scots pine forest edges particularly prone to drought-induced mortality? Environ. Res. Let. 2018, 13, 025001. [Google Scholar] [CrossRef]
  22. Allen, C.D.; Breshears, D.D.; McDowell, N.G. On underestimation of global vulnerability to tree mortality and forest die-off from hotter drought in the Anthropocene. Ecosphere 2015, 6, 129. [Google Scholar] [CrossRef]
  23. Kharuk, V.I.; Im, S.T.; Dvinskaya, M.L. Decline of spruce (Picea abies) in forests of Belarus. Russ. J. Ecol. 2016, 47, 241–248. [Google Scholar] [CrossRef]
  24. Haberstroh, S.; Werner, C.; Grün, M.; Kreuzwieser, J.; Seifert, T.; Schindler, D.; Christen, A. Central European 2018 hot drought shifts scots pine forest to its tipping point. Plant Biol. 2022, 7, 1186–1197. [Google Scholar] [CrossRef]
  25. Mutlu, S.; Osma, E.; Ilhan, V.; Turkoglu, H.I.; Atici, O. Mistletoe (Viscum album) reduces the growth of the Scots pine by accumulating essential nutrient elements in its structure as a trap. Trees 2016, 30, 815–824. [Google Scholar] [CrossRef]
  26. Jelonek, T.; Tomczak, A.; Jakubowski, M.; Grzywiński, W.; Pazdrowski, W.; Remlein, A.; Jurkiewicz, E. An analysis of the quality and value of timber in pine tree stands representing selected ecotypes of this species in Poland. Ann. WULS SGGW For. Wood Technol. 2016, 95, 20–28. [Google Scholar]
  27. Tomczak, A.; Pazdrowski, W.; Jelonek, T.; Grzywiński, W. Jakość drewna sosny zwyczajnej (Pinus sylvestris L.). Część I. Charakterystyka wybranych cech i właściwości drewna wpływających na jego jakość. Sylwan 2009, 153, 363–372. [Google Scholar]
  28. Repola, J. Models for vertical wood density of Scots pine, Norway spruce and birch stems, and their application to determine average wood density. Silva Fenn. 2006, 40, 673–685. [Google Scholar] [CrossRef]
  29. Tomczak, A.; Jelonek, T.; Zoń, L. Porównanie wybranych właściwości fizycznych drewna młodocianego i dojrzałego sosny zwyczajnej (Pinus sylvestris L.) z drzewostanów rębnych. Sylwan 2010, 154, 809–817. [Google Scholar]
  30. Wąsik, R.; Michalec, K.; Barszcz, A.; Mudryk, K. Variability of selected macrostructure features, density and compression strength along the grain of “taborz” scots pine wood (Pinus sylvestris L.). Wood 2020, 63, 205. [Google Scholar] [CrossRef]
  31. Gurau, L.; Cioncia, M.; Mansfield-Williams, H.; Sawyer, G.; Zeleniuc, O. Comparison of the mechanical properties of branch and stem wood for three species. Wood Fiber Sci. 2008, 40, 647–656. [Google Scholar]
  32. Lindström, H.; Reale, M.; Grekin, M. Using non-destructive testing to assess modulus of elasticity of Pinus sylvestris trees. Scand. J. For. Res. 2009, 24, 247–257. [Google Scholar] [CrossRef]
  33. Meier, E. WOOD! Identifying and Using Hundreds of Woods Worldwide; The Wood Database: Auckland, New Zealand, 2021. [Google Scholar]
  34. Hanewinkel, M.; Cullmann, D.A.; Schelhaas, M.J.; Nabuurs, G.J.; Zimmermann, N.E. Climate Change May Cause Severe Loss in the Economic Value of European Forest Land. Nat. Clim. Change 2013, 3, 203–207. [Google Scholar] [CrossRef]
  35. Gryc, V.; Vavrčík, H.; Gomola, Š. Selected properties of European beech (Fagus sylvatica L.). J. For. Sci. 2008, 54, 418–425. [Google Scholar] [CrossRef]
  36. BMLFUW. Holzeinschlagsmeldung Über Das Kalenderjahr 2020; BMLFUW: Vienna, Austria, 2021. [Google Scholar]
  37. Vrška, T.; Adam, D.; Hort, L.; Kolař, T. European beech (Fagus sylvatica L.) and silver fir (Abies alba Mill.) rotation in the Carpathians—A development cycle or a linear trend induced by man? For. Ecol. Manag. 2009, 258, 347–356. [Google Scholar]
  38. Pramreiter, M.; Grabner, M. The Utilization of European Beech Wood (Fagus sylvatica L.) in Europe. Forests 2023, 14, 1419. [Google Scholar] [CrossRef]
  39. Dudiak, M. Density of beech (Fagus sylvatica L.) wood through a cross-section of the trunk. Acta Facultatis Xylologiae Zvolen 2023, 65, 5–11. [Google Scholar]
  40. Wagenführ, R. Holzatlas; Fachbuchverlag: Lepzig, Germany, 2000; pp. 361–362. [Google Scholar]
  41. Geoffrey, D. Wood and Fibre Morphology. In Pulp and Paper Chemistry and Technology; De Gruyter: Stockholm, Sweden, 2009; Volume 1, p. 320. [Google Scholar]
  42. Bectaş, I.; Güller, C.; Baştürk, M.A. Principal mechanical properties of eastern beech wood (Fagus orientalis Lipsky) naturally grown in Andirin Northeastern Mediterranean Region of Turkey. Turk. J. Agric. For. 2002, 26, 147–154. [Google Scholar]
  43. Mišíková, O. The hardness and density of beech wood from necrotic wounds and opposite wood. In Proceedings of the 5th International Symposium Wood Structure of Properties ’06, Sliač-Sielnica, Slovakia, 3–6 September 2006; Arbora Publishers: Zvolen, Slovakia, 2006; pp. 309–311. [Google Scholar]
  44. Tarasiuk, S.; Jednoralski, G. Zmienność, jakość hodowlana i właściwości fizyczno–mechaniczne drewna trzech pochodzeń buka. Sylwan 2005, 3, 42–49. [Google Scholar]
  45. Aicher, S.; Hirsch, M.; Christian, Z. Hybrid cross-laminated timber plates with beech wood cross-layers. Constr. Build. Mater. 2016, 124, 1007–1018. [Google Scholar] [CrossRef]
  46. Brunetti, M.; Nocetti, M.; Pizzo, B.; Negro, F.; Aminti, G.; Burato, P.; Cremonini, C.; Zanuttini, R. Comparison of different bonding parameters in the production of beech and combined beech-spruce CLT by standard and optimized tests methods. Constr. Build. Mater. 2020, 265, 120168. [Google Scholar] [CrossRef]
  47. Hematabadi, H.; Madhoushi, M.; Khazaeian, A.; Ebrahimi, G. Structural performance of hybrid poplar-beech cross-laminated-timber (CLT). J. Build. Eng. 2021, 44, 102959. [Google Scholar] [CrossRef]
  48. Sciomenta, M.; Spera, L.; Bedon, C.; Rinaldi, V.; Fragiacomo, M.; Romagnoli, M. Mechanical characterization of novel homogeneous beech and hybrid beech-corsican pine thin cross-laminated timber panels. Constr. Build. Mater. 2021, 271, 121589. [Google Scholar] [CrossRef]
  49. Aicher, S.; Ohnesorge, D. Shear strength of glued laminated timber made from european beech timber. Eur. J. Wood Wood Prod. 2011, 69, 143–154. [Google Scholar] [CrossRef]
  50. Brandner, R.; Flatscher, G.; Ringhofer, A.; Schickhofer, G.; Thiel, A. cross laminated timber (CLT): Overview and development. Eur. J. Wood Wood Prod. 2016, 74, 331–351. [Google Scholar] [CrossRef]
  51. Ehrhart, T.; Steiger, R.; Lehmann, M.; Frangi, A. European beech (Fagus sylvatica L.) glued laminated timber: Lamination strength grading, production and mechanical properties. Eur. J. Wood Wood Prod. 2020, 78, 971–984. [Google Scholar] [CrossRef]
  52. Jauk, G.; Nöstler, M.; Fingerlos, B.; Zeman, R.; Gruber, B.; Pfeffer, C. BSP-Special 2021; Holzkurier: Vienna, Austria, 2021. [Google Scholar]
  53. Stepinac, M.; Rajčić, V.; Hunger, F.; van de Kuilen, J.W.G. Glued-in rods in beech laminated veneer lumber. Eur. J. Wood Wood Prod. 2016, 74, 463–466. [Google Scholar] [CrossRef]
  54. Benthien, J.T.; Riegler, M.; Engehausen, N.; Nopens, M. Specific dimensional change behavior of laminated beech veneer lumber (baubuche) in terms of moisture absorption and desorption. Fibers 2020, 8, 47. [Google Scholar] [CrossRef]
  55. Grönquist, P.; Weibel, G.; Leyder, C.; Frangi, A. Calibration of electrical resistance to moisture content for beech laminated veneer lumber “BauBuche S” and “BauBuche Q”. Forests 2021, 12, 635. [Google Scholar] [CrossRef]
  56. Zimmermann, M.; Raßbach, H. A study of the deformation behaviour of veneers resulting from water storage (A methodological approach for determining the swelling characteristic using the example of European beech veneer). Eur. J. Wood Wood Prod. 2018, 76, 1677–1683. [Google Scholar] [CrossRef]
  57. Fabbri, A.; Minghini, F.; Tullini, N. Monotonic and cyclic pull-pull tests on dowel-nut connector in laminated veneer lumber made of European beech wood. Constr. Build. Mater. 2022, 359, 129461. [Google Scholar] [CrossRef]
  58. Kubík, P.; Šebek, F.; Krejčí, P.; Brabec, M.; Tippner, J.; Dvořáček, O.; Lechowicz, D.; Frybort, S. Linear woodcutting of European beech: Experiments and computations. Wood Sci. Technol. 2023, 57, 51–74. [Google Scholar] [CrossRef]
  59. Rohumaa, A.; Viguier, J.; Girardon, S.; Krebs, M.; Denaud, L. Lathe check development and properties: Effect of log soaking temperature, compression rate, cutting radius and cutting speed during peeling process of European Beech (Fagus sylvatica L.) veneer. Eur. J. Wood Wood Prod. 2018, 76, 1653–1661. [Google Scholar] [CrossRef]
  60. Hering, S.; Keunecke, D.; Niemz, P. Moisture-dependent orthotropic elasticity of beech wood. Wood Sci. Technol. 2012, 46, 927–938. [Google Scholar] [CrossRef]
  61. Hering, S.; Niemz, P. Moisture-dependent, viscoelastic creep of European Beech wood in longitudinal direction. Eur. J. Wood Wood Prod. 2012, 70, 667–670. [Google Scholar] [CrossRef]
  62. Ozyhar, T.; Hering, S.; Niemz, P. Moisture-dependent elastic and strength anisotropy of European Beech wood in tension. J. Mater. Sci. 2012, 47, 6141–6150. [Google Scholar] [CrossRef]
  63. Kraft, G. Beiträge zur Lehre von den Durchforstungen, Schlagstellungen und Lichtungshieben; Klindworth: Hannover, Germany, 1884; pp. 85–130. [Google Scholar]
  64. Van Laar, A.; Akça, A. Forest Mensuration; Springer: Dordrecht, The Netherlands, 2007; pp. 95–147. [Google Scholar]
  65. ISO 13910:2014; Timber Structures. Strength Graded Timber. Test Methods for Structural Properties. International Organization for Standardization: Geneva, Switzerland, 2014.
  66. ISO 13061-2:2014; Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens. Part 2: Determination of Density for Physical and Mechanical Tests. International Organization for Standardization: Geneva, Switzerland, 2014.
  67. PN-EN 380:1998; Timber Structures—Test Methods—General Principles for Static Load Testing. European Committee for Standardization: Brussels, Belgium, 1998.
  68. PN-EN 408:2004; Konstrukcje Drewniane—Drewno Konstrukcyjne Lite i Klejone Warstwowo—Oznaczanie Niektórych Właściwości Fizycznych i Mechanicznych. Polski Komitet Normalizacyjny: Warsaw, Poland, 2004.
  69. ASTM D143-94; Standard Test Methods for Small Clear Specimens of Timber. ASTM International: West Conshohocken, PA, USA, 2000.
  70. Jeronimidis, G.; Barnett, J.R. (Eds.) Wood Quality and Its Biological Basis; Sheffield Biological Sciences Series, Wood Quality and Its Biological Basis; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
  71. Rowell, R.M. Handbook of Wood Chemistry and Wood Composites, 1st ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar] [CrossRef]
  72. Record, S.J. The Mechanical Properties of Wood. Including a Discussion of the Factors Affecting the Mechanical Properties, and Methods of Timber Testing; Hardpress Publications: Madrid, Spain, 2022. [Google Scholar]
  73. Mäkelä, H. Wood properties of Scots pine (Pinus sylvestris) and Norway spruce (Picea abies) in relation to age, site, and genetic factors. Scand. J. For. Res. 2000. [Google Scholar]
  74. Verma, S.K.; Kuroda, T. Wood properties of Beech (Fagus sylvatica L.) and their suitability for various applications. Wood Sci. Technol. 2008, 42, 391–404. [Google Scholar]
  75. U.S. Forest Service. Wood Quality of Beech and Pine Trees from the Northeastern United States; U.S. Forest Service Research Paper; U.S. Forest Service: Amboy, WA, USA, 1999.
  76. Zobel, B.J.; Van Buijtenen, J.P. Wood Variation: Its Causes and Control; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
  77. Kiseleva, A.V.; Snegireva, S.N.; Platonov, A.D. Formation of pine wood density depending on the parameters of annual ring and latitudinal zoning. In Proceedings of the October 2021 IOP Conference Series Earth and Environmental Science, Voronezh, Russia, 9–10 September 2021; Volume 875, p. 012035. [Google Scholar] [CrossRef]
  78. Plomion, C.; Leprovost, G.; Stokes, A. Wood formation in trees. Plant Physiol. 2001, 127, 1513–1523. [Google Scholar] [CrossRef]
  79. Mencuccini, M.; Grace, J.; Fioravanti, M. Biomechanical and hydraulic determinants of tree structure in Scots pine: Anatomical characteristics. Tree Physiol. 1997, 17, 105–113. [Google Scholar] [CrossRef]
  80. Fujimoto, T. Evaluation of the age dependent variation of wood properties based on the eigenvalue distribution of near infrared spectra. Chem. Int. Lab. Syst. 2022, 225, 104576. [Google Scholar] [CrossRef]
  81. Konofalska, E.; Kozakiewicz, P.; Buraczyk, W.; Szeligowski, H.; Lachowicz, H. The technical quality of the wood of Scots pine (Pinus sylvestris L.) of diverse genetic origin. Forests 2021, 12, 619. [Google Scholar] [CrossRef]
  82. Witkowska, J.; Lachowicz, H. Variability of conventional wood density of Scots pine (Pinus sylvestris L.) depending on the selected factors. Sylwan 2013, 157, 336–347. [Google Scholar]
  83. Auty, D.; Achim, A.; Macdonald, E.; Cameron, A.D.; Gardiner, B.A. Models for predicting wood density variation in Scots pine. For. Int. J. For. Res. 2014, 87, 449–458. [Google Scholar] [CrossRef]
  84. Frühwald, A.; Ressel, J.B.; Bernasconi, A. Hochwertiges Brettschnichtholz aus Buchenholz; Abschulssbericht: Hamburg, Germany, 2003; p. 181. [Google Scholar]
  85. Klement, I.; Vilkovský, P.; Vilkovská, T. Change in selected mechanical properties of beech wood at the contact drying. Materials 2022, 15, 7433. [Google Scholar] [CrossRef]
  86. Gustafsson, S.-I. The Strength Properties of Swedish Oak and Beech. Drewno. Pr. Nauk. Donies. Komunik. 2010, 53, 183. [Google Scholar]
  87. Wood Handbook: Wood as an Engineering Material; Centennial edition; General Technical Report FPL; GTR-190; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010; Chapter 5; pp. 5.1–5.46.
  88. Wood Handbook: Wood as an Engineering Material; United States Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010.
  89. Wood Handbook, Wood as an Engineering Material; USDA Forest Products Lab: Madison, WI, USA, 1999.
  90. Pearson, R.G.; Gilmore, R.C. Effect of fast growth on the mechanical properties of loblolly pine. For. Prod. J. 1980, 30, 47–54. [Google Scholar]
  91. Machado, J.; Cruz, H. Within stem variation of maritime pine timber mechanical. Eur. J. Wood Wood Prod. 2005, 63, 154–159. [Google Scholar] [CrossRef]
  92. Olivar, J.; Rathgeber, C.; Bravo, F. Climate change, tree-ring width and wood density of pines in mediterranean environments. IAWA J. 2015, 36, 257–269. [Google Scholar] [CrossRef]
  93. Diaconu, D.; Wassenberg, M.; Spiecker, H. Variability of European beech wood density as influenced by interactions between tree-ring growth and aspect. For. Ecosyst. 2016, 3, 6. [Google Scholar] [CrossRef]
  94. Teskey, R.O.; Hinckley, T.M. Moisture: Effects of Water Stress on Trees. In Stress Physiology and Forest Productivity; Hennessey, T.C., Dougherty, P.M., Kossuth, S.V., Johnson, J.D., Eds.; Springer: Dordrecht, The Netherlands, 1986. [Google Scholar] [CrossRef]
  95. Polle, A.; Chen, S.L.; Eckert, C.; Harfouche, A. Engineering Drought resistance in forest trees. Front. Plant Sci. 2019, 8, 1875. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
  96. Barigah, T.S.; Charrier, O.; Douris, M.; Bonhomme, M.; Herbette, S.; Améglio, T.; Fichot, R.; Brignolas, F.; Cochard, H. Water stress-induced xylem hydraulic failure is a causal factor of tree mortality in beech and poplar. Ann Bot. 2013, 112, 1431–1437. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
  97. Bréda, N. Modelling variability of wood density in beech as affected by ring age, radial growth and climate. Trees—Struct. Funct. 2004, 18, 264–276. [Google Scholar]
  98. van der Maaten, E.; van der Maaten-Theunissen, M.; Spiecker, H. Temporally resolved intra-annual wood density variations in European beech (Fagus sylvatica L.) as affected by climate and aspect. Ann. For. Res. 2012, 55, 113–124. [Google Scholar]
  99. Hématy, K.; Höfte, H. Cellulose and cell elongation. The expanding cell. Plant. Cell Monogr. 2007, 6, 33–56. [Google Scholar]
  100. Krauss, A. Ultrastrukturalne uwarunkowania wybranych właściwości mechanicznych drewna sosny i świerku. Rozpr. Nauk. UP Pozn. 2010, 406, 1–115. [Google Scholar]
  101. Astley, R.J.; Harrington, J.J.; Stol, K.A. Mechanical Modelling of Wood Microstructure, an Engineering approach. IPENZ Trans. 1997, 24, 1. [Google Scholar]
  102. Schniewind, A.P. Horizontal specifi c gravity variation in tree stems in relations to their support function. For. Sci. 1962, 8, 111–118. [Google Scholar]
  103. Sperry, J.S.; Hacke, U.G.; Pittermann, J. Size and function in conifer tracheids and angiosperm vessels. Am. J. Bot. 2006, 93, 1490–1500. [Google Scholar] [CrossRef]
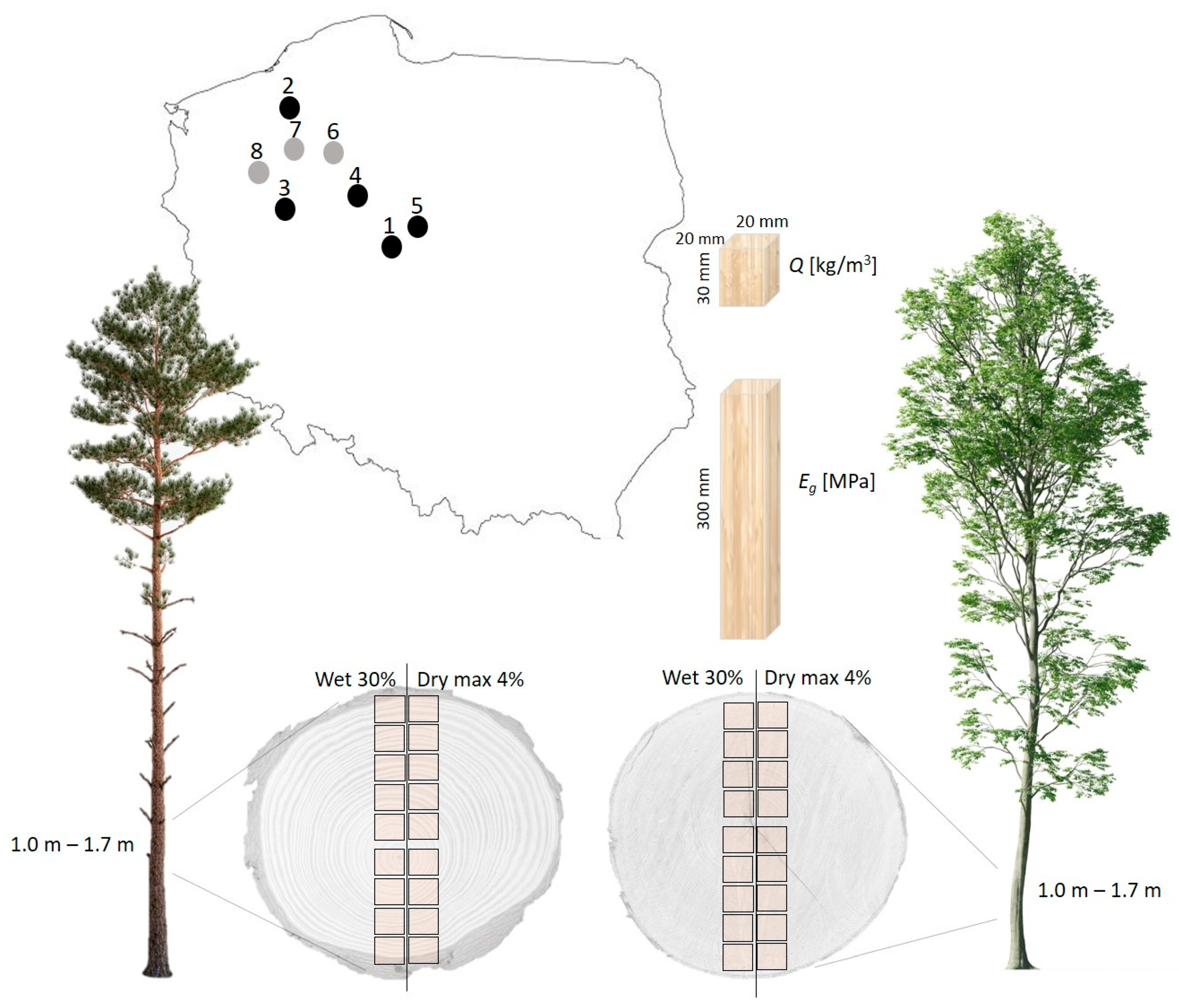
Forests 16 00772 g001
Figure 1. Location of research areas and sample collection from sample trees.
Figure 1. Location of research areas and sample collection from sample trees.
Forests 16 00772 g001
Forests 16 00772 g002
Figure 2. Radial variability of beech wood density.
Figure 2. Radial variability of beech wood density.
Forests 16 00772 g002
Forests 16 00772 g003
Figure 3. Radial variability of Scots pine’s wood density.
Figure 3. Radial variability of Scots pine’s wood density.
Forests 16 00772 g003
Forests 16 00772 g004
Figure 4. Radial variability of modulus of elasticity of beech wood (E0%).
Figure 4. Radial variability of modulus of elasticity of beech wood (E0%).
Forests 16 00772 g004
Forests 16 00772 g005
Figure 5. Radial variability of modulus of beech wood (E30%).
Figure 5. Radial variability of modulus of beech wood (E30%).
Forests 16 00772 g005
Forests 16 00772 g006
Figure 6. Radial variability of modulus of elasticity of Scots pine wood (E0%).
Figure 6. Radial variability of modulus of elasticity of Scots pine wood (E0%).
Forests 16 00772 g006
Forests 16 00772 g007
Figure 7. Radial variability of modulus of elasticity of Scots pine wood (E30%).
Figure 7. Radial variability of modulus of elasticity of Scots pine wood (E30%).
Forests 16 00772 g007
Forests 16 00772 g008
Figure 8. Desorption enhancement of modulus of elasticity (WSDE) for beech wood.
Figure 8. Desorption enhancement of modulus of elasticity (WSDE) for beech wood.
Forests 16 00772 g008
Forests 16 00772 g009
Figure 9. Desorption enhancement of modulus of elasticity (WSDE) for pine wood.
Figure 9. Desorption enhancement of modulus of elasticity (WSDE) for pine wood.
Forests 16 00772 g009
Table 1. Location and tree information.
Table 1. Location and tree information.
PlotTree NumberHeight [m]DBH [cm]Average Age of SamplesClass of the StandGPS
(WGS-84)
1/S131.051.5182IIN: 52.5770, E: 18.1748
230.250.0
328.848.5
2/S129.250.5156IIN: 54.2320, E: 16.8884
228.548.5
327.046.0
3/S129.449.5162IIN: 52.4989, E: 15.9889
228.248.5
326.847.0
4/S130.552.5167IIN: 52.5358, E: 17.1044
229.250.5
327.548.5
5/S132.049.5151IIN: 52.6228, E: 17.5698
231.248.5
329.647.0
6/B132.566.5170IIN: 53.3108, E: 17.1767
231.264.0
329.062.5
7/B130.659.5184IIN: 53.99078, E: 16.8472
229.558.0
327.856.6
8/B135.072.0165IIN: 53.4181, E:16.1911
233.870.5
332.168.0
Table 2. Statistical characteristics of conventional density of beech wood.
Table 2. Statistical characteristics of conventional density of beech wood.
Q [kg/m3]
MeanConfidenceStandard DeviationMinimumMaximum
−95%95%
Total652.71646.04659.3852.67524.28792.5
Table 3. Statistical characteristics of the conventional density of Scots pine wood.
Table 3. Statistical characteristics of the conventional density of Scots pine wood.
Q [kg/m3]
MeanConfidenceStandard DeviationMinimumMaximumQ 25MedianQ 75
−95%95%
Total491.41485.8497.0372.28319.33884.81434.16487.66542.02
Table 4. Statistical characteristics of modulus of elasticity of beech wood.
Table 4. Statistical characteristics of modulus of elasticity of beech wood.
Modulus of ElasticityE [MPa]
MeanConfidenceStandard DeviationMinimumMaximum
−95%95%
E0%16,84216,37717,3073663415026,133
E30%8926861492372460290315,728
Table 5. Statistical characteristics of modulus of elasticity of Scots pine wood.
Table 5. Statistical characteristics of modulus of elasticity of Scots pine wood.
Modulus of ElasticityE [MPa]
MeanConfidenceStandard
Deviation		MinimumMaximum
−95%95%
E0%9447.379132.689762.063273.151770.3716,278.11
E30%5412.775254.215571.391649.51859.449033.94
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Jelonek, T.; Klimek, K.; Naskrent, B.; Tomczak, A.; Jakubowski, M.; Kuźmiński, R.; Szwed, T.; Kopaczyk, J.; Grabowski, D.; Szaban, J. How the Scots Pine and Beech Aging Process Affects Wood. Forests 2025, 16, 772. https://doi.org/10.3390/f16050772

AMA Style

Jelonek T, Klimek K, Naskrent B, Tomczak A, Jakubowski M, Kuźmiński R, Szwed T, Kopaczyk J, Grabowski D, Szaban J. How the Scots Pine and Beech Aging Process Affects Wood. Forests. 2025; 16(5):772. https://doi.org/10.3390/f16050772

Chicago/Turabian Style

Jelonek, Tomasz, Katarzyna Klimek, Bartłomiej Naskrent, Arkadiusz Tomczak, Marcin Jakubowski, Robert Kuźmiński, Tomasz Szwed, Joanna Kopaczyk, Daniel Grabowski, and Jarosław Szaban. 2025. "How the Scots Pine and Beech Aging Process Affects Wood" Forests 16, no. 5: 772. https://doi.org/10.3390/f16050772

APA Style

Jelonek, T., Klimek, K., Naskrent, B., Tomczak, A., Jakubowski, M., Kuźmiński, R., Szwed, T., Kopaczyk, J., Grabowski, D., & Szaban, J. (2025). How the Scots Pine and Beech Aging Process Affects Wood. Forests, 16(5), 772. https://doi.org/10.3390/f16050772

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop