Next Article in Journal
The Application of Dendrochemistry to Assess Recent Changes in Environmental Chemistry of Urban Areas
Previous Article in Journal
Human and Machine Reliability in Postural Assessment of Forest Operations by OWAS Method: Level of Agreement and Time Resources
Previous Article in Special Issue
Growth Responses of European Beech (Fagus sylvatica L.) and Oriental Beech (Fagus orientalis Lipsky) Along an Elevation Gradient Under Global Climate Change
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 16
Issue 5
10.3390/f16050760
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Standardized Framework to Estimate Drought-Induced Vulnerability and Its Temporal Variation in Woody Plants Based on Growth

by
Antonio Gazol
1,*,
Elisa Tamudo-Minguez
1,
Cristina Valeriano
1,
Ester González de Andrés
1,
Michele Colangelo
2 and
Jesús Julio Camarero
1
1
Instituto Pirenaico de Ecología (IPE-CSIC), Avda. Montañana 1005, 50192 Zaragoza, Spain
2
Scuola di Scienze Agrarie, Forestali, Alimentari e Ambientali, Università della Basilicata, Viale dell’Ateneo Lucano 10, 85100 Potenza, Italy
*
Author to whom correspondence should be addressed.
Forests 2025, 16(5), 760; https://doi.org/10.3390/f16050760
Submission received: 28 March 2025 / Revised: 21 April 2025 / Accepted: 24 April 2025 / Published: 29 April 2025
(This article belongs to the Special Issue Tree Growth and Physiological Properties Under Ongoing Global Climate Change: 2nd Edition)
Browse Figures
Review Reports Versions Notes

Abstract

:
Forests and scrubland comprise a large proportion of terrestrial ecosystems and, due to the long lifespan of trees and shrubs, their capacity to grow and store carbon as lasting woody tissues is particularly sensitive to warming-enhanced drought occurrence. Climate change may trigger a transition from forests to scrubland in many drylands during the coming decades due to the higher resilience of shrubs. However, we lack standardized frameworks to compare the response to drought of woody plants. We present a framework and develop an index to estimate the drought-induced vulnerability (DrVi) of trees and shrubs based on the radial growth trajectory and the response of growth variability to a drought index. We used tree-ring width series of three tree (Pinus halepensis Mill., Juniperus thurifera L., and Acer monspessulanum L.) and three shrub (Juniperus oxycedrus L., Pistacia lentiscus L., and Ephedra nebrodensis Tineo ex Guss.) species from semi-arid areas to test this framework. We compared the DrVi values between species and populations and explored their temporal changes. Across species, the strongest DrVi values were found in declining P. halepensis stands and J. oxycedrus from the same site, while the lowest DrVi values were found in A. monspessulanum, P. lentiscus, and E. nebrodensis. Across populations, J. oxycedrus presented higher vulnerability in one of the dry sites. The P. halepensis declining stand showed a steady increase in DrVi value after the 1980s as the climate shifted toward warmer and drier conditions. We conclude that the DrVi allows comparing species and populations using a standardized general framework.

1. Introduction

The Earth is warming at a rate not seen before, potentially increasing the occurrence of extreme climate events such as droughts and heat waves [1,2]. Such an aridification trend is negatively affecting the functioning of ecosystems and, ultimately, human well-being [3]. Forests and scrubland, i.e., woody plant communities, account for an important proportion of the Earth’s land surface [4] and they are vulnerable to climate change threats [5,6], particularly in drylands such as most of the Mediterranean basin [7]. In this climate change hotspot, increases in temperature and atmospheric evaporative demand since the early 1980s have triggered the occurrence of more severe droughts [8]. This situation will worsen in the future, as a precipitation decrease is forecasted in the region [9], and the occurrences of drought-induced forest dieback and mortality events can trigger structural and compositional shifts from forests to scrubland [10]. Knowledge of how Mediterranean forests and scrubland respond to drought is important to advance the understanding of their vulnerability to climate change [11,12]. However, we lack knowledge on the response of shrubs to drought and a standardized framework to compare drought-induced vulnerability.
Trees and shrubs form annual growth rings that potentially register changes in climate variability, representing a valuable natural archive to track their past and current performance [13]. In addition, growth trajectories can reflect changes in vitality and productivity [14,15], although they are strongly influenced by tree ontogeny and phenological adjustments [16,17], as well as by stand density and competition [14]. In a climate change context, understanding how species, populations, and individuals vary in their growth responses to drought occurrence has become an important research challenge (e.g., [15,18,19,20,21,22]).
In terms of growth, gymnosperms present stronger and more pervasive drought impacts than angiosperms [23] and smaller trees seem to be less vulnerable to drought [24,25]. Under the same regional climate constraints, it is expected that drought-vulnerable species will present more negative growth trajectories and stronger relationships between growth variability and drought indices than drought-tolerant species (e.g., [19,26]). When comparing populations between regions, it is expected that those exposed to drier or hasher conditions will be more coupled to drought impacts [27,28] and be less resilient to drought [29]. The closer the population is to the driest border of the species distribution range, the higher its drought vulnerability will be, but this is not always the case [20]. Comparing the growth trajectories and responses to climate of trees and shrubs under the same environmental constraints and across climatic gradients can help to assess their drought vulnerability [22,26].
Increases in drought–growth coupling, overall loss of resilience, and negative growth trajectories can be considered early warning signals of forest dieback [30,31,32,33]. However, we still lack standardized frameworks that can serve to evaluate and compare the drought-induced vulnerability of trees and shrubs between species and populations. Growth resilience indices have been widely used because of their versatility and easy interpretation, and they have been complemented to offer a framework to study growth resilience [18,21]. However, vulnerability is a more complex concept that includes not only sensitivity but also exposure and the capacity to cope with it [34]. Recent analyses have revealed that resilience indices strongly depend on the relationship between growth variability and drought [35], which can be seen as a measure of sensitivity. Additionally, the loss in resilience capacity through time might be strongly linked to the existence of negative growth trajectories, which are also important to understand forest dieback and growth decline [15,33]. Thus, pervasive growth reductions can be indicative of a reduction in the capacity of trees to cope with drought due to an overall reduction in overall tree conductive area and vitality. Both growth–climate coupling and growth trajectories change through time [36], which is something that needs to be accounted for when interpreting their patterns. A standardized framework to evaluate drought-induced vulnerability is important to identify forests and scrubland prone to drought-induced dieback [37,38] and to elucidate which species or populations will be the winners and losers in a drier and warmer climate [26].
The growth trajectories and growth responses to climate of shrubs and small trees has been less studied that that of trees [39,40,41]. The ecological significance of this growth form is particularly important in dry regions such as the Mediterranean basin [42]. In some of these regions, shrubs are expected to play a fundamental role [12] and they can replace trees after drought- or fire-induced disturbances [10]. The comparison of growth patterns in shrubs and coexisting trees is challenging and poses substantial difficulties, but it is of primal importance if we want to infer whom, when, and why are more vulnerable to climate change [43,44].
In this study, we propose a framework to study drought-induced vulnerability between tree and shrub species and populations based on the growth trajectories using the basal area increment (BAI) and the relationship between growth variability (ring-width index; RWI) and a drought index (Standardized Precipitation Evapotranspiration Index). In addition, we present a new index, the drought-induced vulnerability index (DrVi), which standardizes and combines these metrics (Figure 1).

2. Materials and Methods

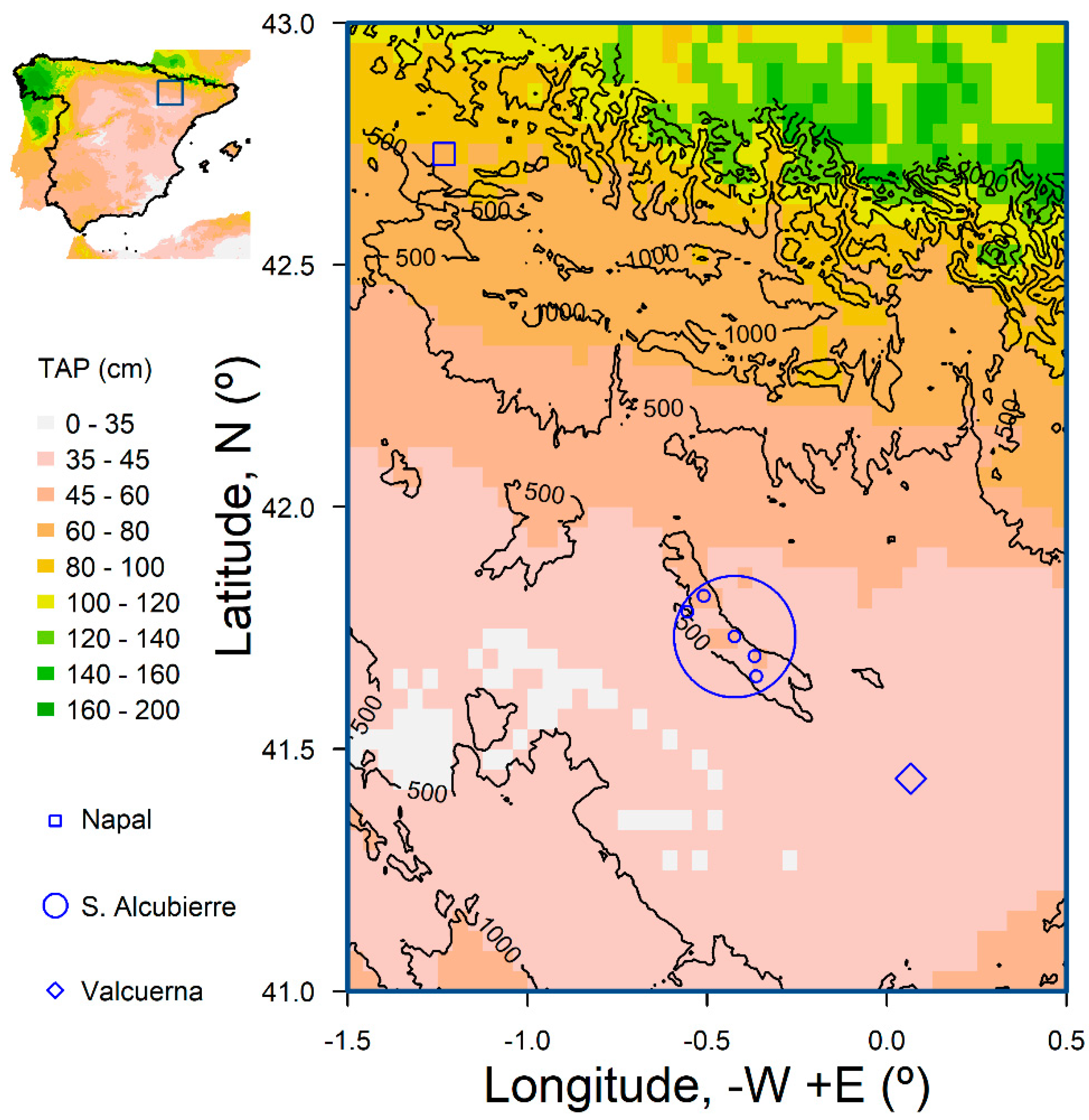
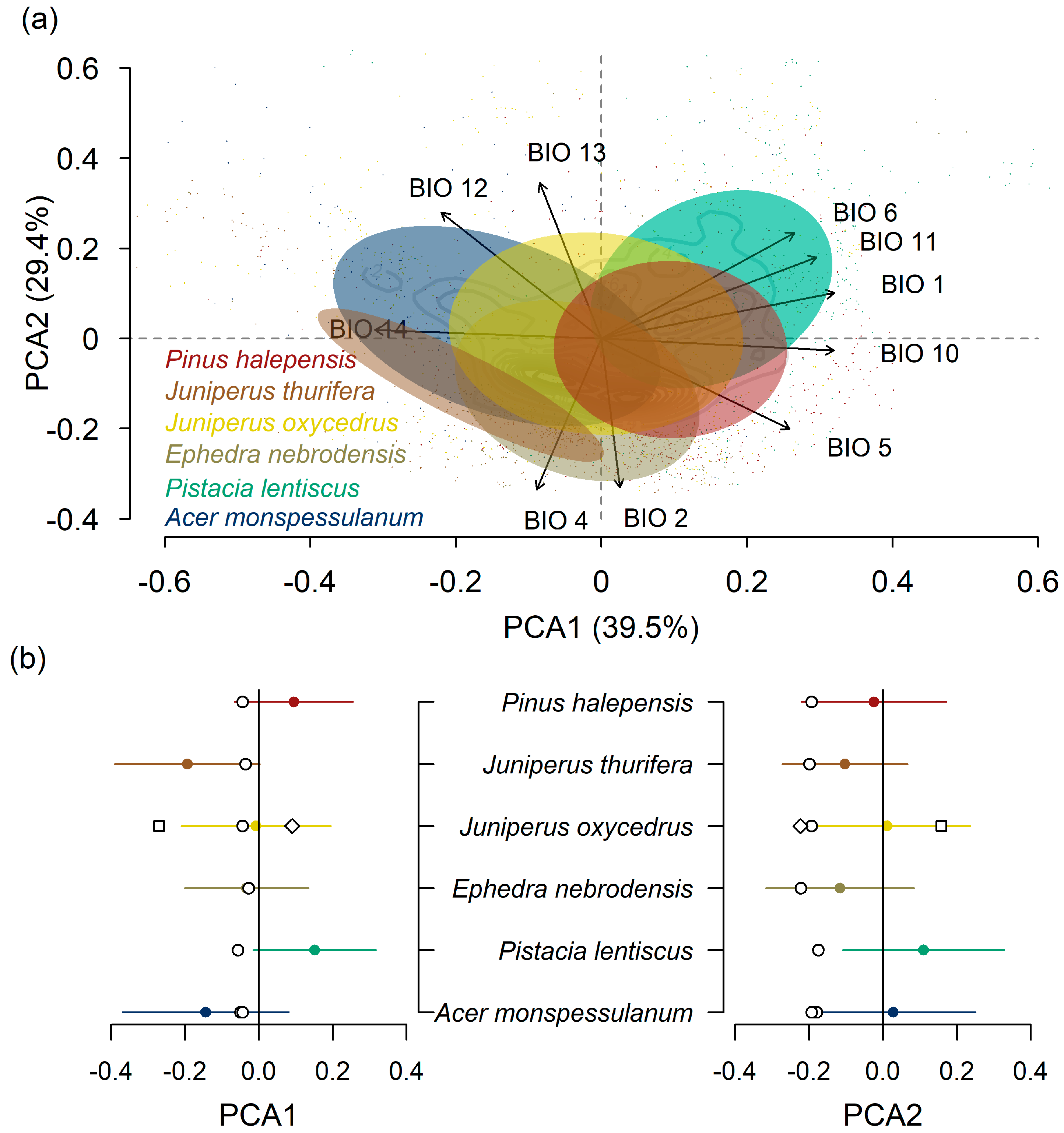
2.1. Study Sites and Species

Most sampled sites were located in “Sierra de Alcubierre”, a small mountain chain located in the semi-arid region in the middle of the Ebro Basin, Northeastern Spain (Figure 2). This range was defined by the famous Spanish politician and geographer Pascual Madoz [45] as “undoubtedly, the driest mountain in Spain”. The vegetation is dominated by gymnosperm shrubs from the genus juniper and angiosperm shrubs such as Pistacia lentiscus L., Rhamnus lycioides L., and Quercus coccifera L. The dominant trees are Aleppo pine (Pinus halepensis Mill.), Spanish juniper (Juniperus thurifera L.), and holm oak (Quercus rotundifolia Lam.) in wet sites. However, this mountainous massif situated in the middle of dry steppes offers refuge (e.g., N- and W-oriented slopes near valley bottoms) for species inhabiting wet-cool sites such as Quercus faginea Lam. or Acer monspessulanum L. [46].
We used dendrochronology to measure annual growth rings and reconstruct growth patterns of nine populations of Mediterranean tree (Pinus halepensis, Juniperus thurifera, and Acer monspessulanum) and shrub species (Juniperus oxycedrus L., Pistacia lentiscus, and Ephedra nebrodensis Tineo ex Guss.). At one of the sites (Sierra de Alcubierre), all of the species were sampled, and we compared their drought-induced vulnerability. For one of the species (J. oxycedrus), we considered three populations along a climatic gradient (Figure 2 and Figure S1), and we compared their drought-induced vulnerability. In Sierra de Alcubierre, we expect greater vulnerability for the trees P. halepensis and J. thurifera because large conifers are less resilient to drought [25] and shrubs are expected to be more drought tolerant than trees [40]. In the case of J. oxycedrus populations, we expect higher vulnerability in the population from the driest site since those populations exposed to drier conditions are expected to present stronger correlations between growth and drought [27,28,44] and to be less resilient to drought [29].
We sampled single populations of E. nebrodensis, J. oxycedrus, J. thurifera, P. lentiscus, and P. halepensis and two populations of A. monspessulanum. Additionally, we included two additional populations of J. oxycedrus sampled in wetter (Napal, Navarra; [47]) and drier sites (Valcuerna Valley, Huesca; [44]). The Napal site (42.712° N, 1.205° W, 694 m a.s.l.) is characterized by milder climate conditions due to oceanic influence, while the Valcuerna site (41.436° N, 0.072° W, 200 m a.s.l.) is characterized by a semi-arid climate.
We selected between 16 and 30 mature individuals of the species studied at the selected sites (Table 1). For J. thurifera and P. halepensis, two increment cores were taken at breast height (1.3 m) using a Pressler increment borer (Haglöf, Långsele, Sweden). In the case of shrubs, basal sections were taken from the thickest stem using a hand saw. Species and populations were selected because they come from different climate conditions and cover ample ecological gradients (Figure 2 and Figure S1).
Forests 16 00760 g002
Figure 2. The locations of the study sites and populations in Northeastern Spain. The colors represent total annual precipitation (TAP in cm) according to WorldClim [48]. The blue symbols show the locations of the study sites (blue) and populations within the Sierra de Alcubierre site (small dots within the circle). The contour lines indicate the elevation lines (in meters above sea level).
Figure 2. The locations of the study sites and populations in Northeastern Spain. The colors represent total annual precipitation (TAP in cm) according to WorldClim [48]. The blue symbols show the locations of the study sites (blue) and populations within the Sierra de Alcubierre site (small dots within the circle). The contour lines indicate the elevation lines (in meters above sea level).
Forests 16 00760 g002

2.2. Dendrochronological Methods

The collected cores and stem sections were air-dried in the laboratory. After that, we used sandpapers of different grains to polish the samples until the annual rings were visible. Finally, the samples were scanned at a resolution of 2400 dpi using an Epson Expression 10,000XL scanner (Epson, Suwa, Japan). Images were processed using CooRecorder and CDendro v.9.8.1 software [49]. Samples were visually cross-dated identifying ring borders, and ring widths were measured to the nearest 0.001 mm. The software COFECHA v.6.06 was used to assess the validity of the visual cross-dating [50]. This was done by calculating correlations between the resulting chronology for each species and site and the individual ring-width series of the measured individuals.
To estimate growth trajectories, the ring-width series were converted into basal area increments (BAI, cm2 year−1), assuming a circular outline of stems. It has been suggested that BAI is a more reliable proxy of tree growth than ring width because it removes the variation in radial growth attributable to increasing circumference while preserving long- and short-term changes in growth [51]. We used the following formula:
BAI = π (R2t − R2t−1)
where R is the radius of the tree and t is the year of tree ring formation.
To estimate growth variability, the measured ring-width series were standardized fitting a spline with a 50% frequency cutoff at a frequency equal to 25 years for all individual series. Temporal autocorrelation was eliminated by fitting autoregressive models to obtain residual ring-width series (RWI). Residual site chronologies were calculated using the Tukey bi-weight robust mean for each species at the site where it was sampled. The quality and reliability of the site chronologies was estimated by calculating the mean correlation among indexed ring-width series (rbar) and expressed population signal (EPS) for each species at each site [52,53]. The rbar was used to reflect the shared variability between individual series, and the EPS accounted for the number of series and reflected to what extent the chronology reflected a common signal.
We calculated the resilience indices proposed by Lloret et al. [18], which were further modified [21] to compare them with the proposed drought-induced vulnerability index. We considered the resistance (Rt), recovery (Rc), and resilience (Rs) indices, as well as the recovery period and the relative growth reduction. These indices were calculated for the years 2005 and 2012 because they were identified as abnormally dry years with strong impacts on forest productivity and tree growth across Spain [54].
All analyses were carried out using R software v.4.4.3 [55]. The chronologies were built using R package dplR [56]. The resilience indices were calculated using the pointRes package in R [57,58].

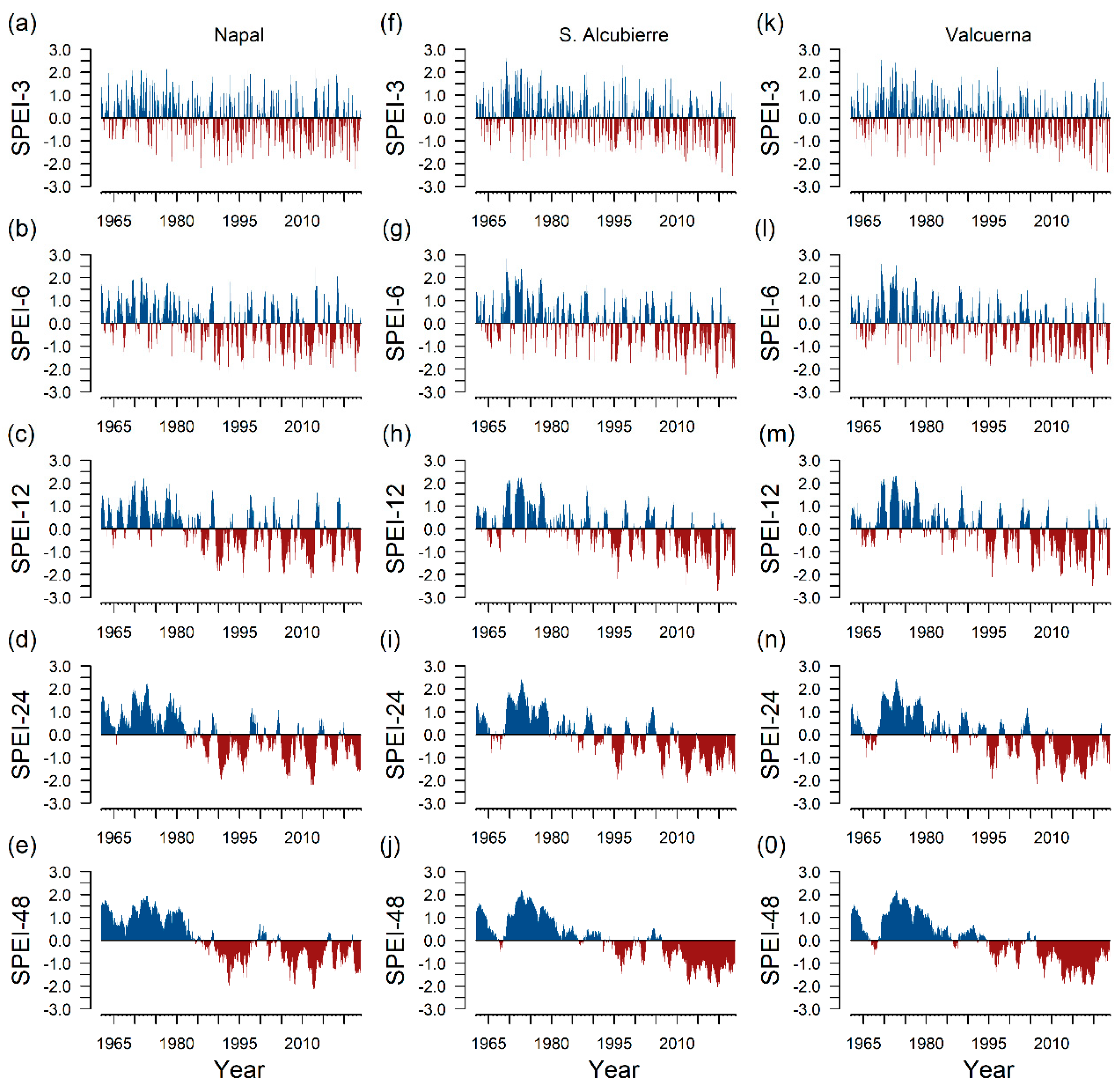
2.3. Climate Data and Drought Index

To assess drought severity, we used the Standardized Precipitation Evapotranspiration Index [59], which was calculated based on precipitation and potential evapotranspiration data from the Terraclimate dataset with a ~4 km spatial resolution [60]. The SPEI is a multi-scalar drought index with negative and positive values corresponding to dry and wet conditions, respectively [59]. We calculated monthly SPEI data from the period 1962–2024 at scales of 1 to 48 months using the R package SPEI [61]. SPEI patterns were similar between sites and presented a trend toward drier conditions after the 1980s and particularly during the 21st century (Figure 3), probably due to changes in temperature (Figure S1).
To represent the bioclimatic niche of each species in Spain, their distributions were obtained from the Anthos project (www.anthos.es, accessed on 5 February 2025) and the average climate conditions (19 bioclimatic variables) were obtained for each site during the period 1970–2000 from the WorldClim database (www.worldclim.org, accessed on 5 February 2025). Anthos is a Spanish plant information system that provides distribution maps of species based on the “Flora Iberica” catalog. WorldClim bioclimatic variables are derived from monthly temperature and precipitation records in the period 1970–2000 and provide information on climate annual trends, seasonality, and extremes [48]. For the selected species, we downloaded their occurrence from Anthos and extracted the bioclimatic variables associated with those locations. In addition, we also extracted the bioclimatic variables for the sampled populations (Table S1 and Figure S2).

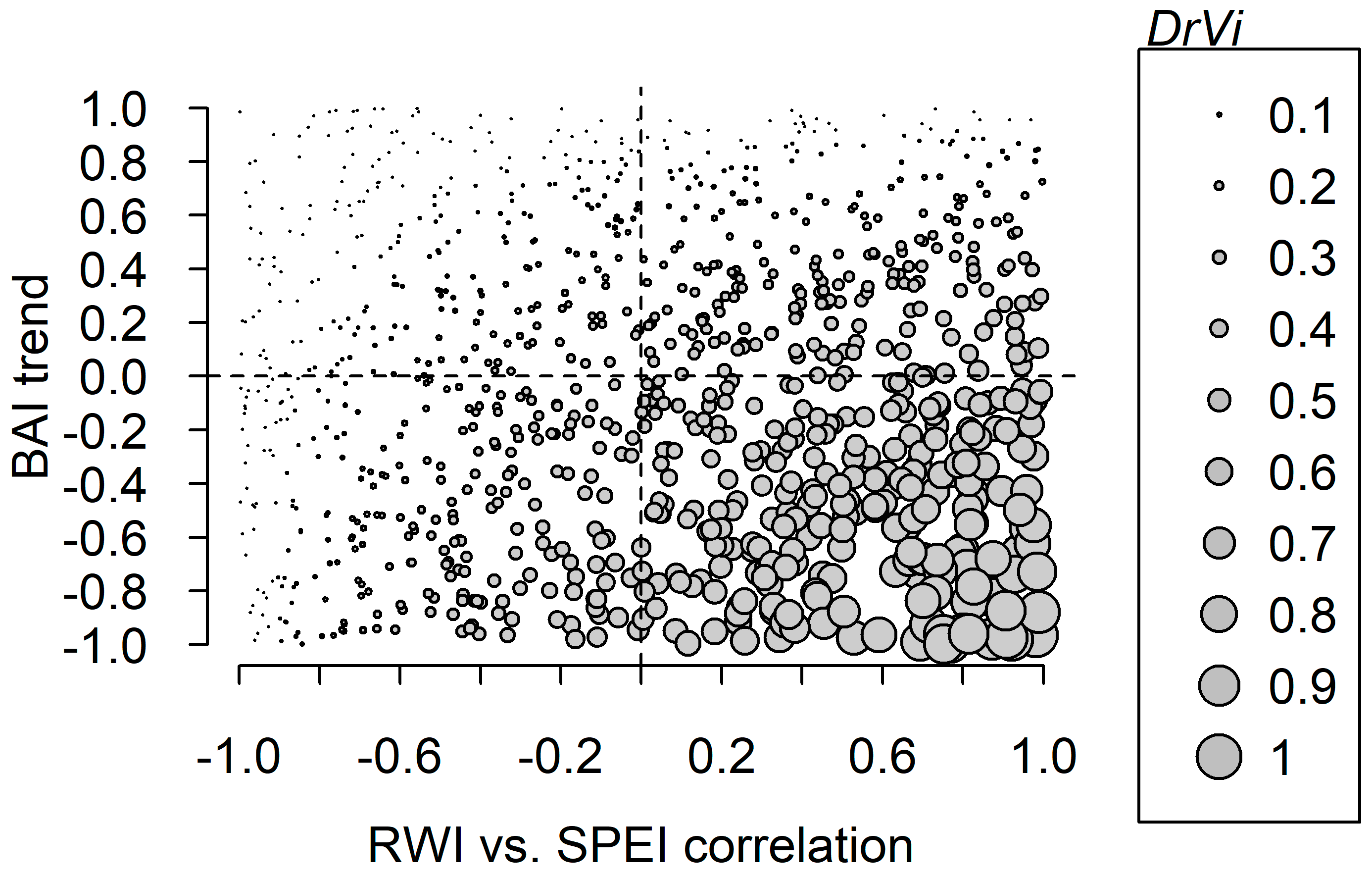
2.4. Statistical Analysis

To assess whether the study species varied in their bioclimatic niche, we performed a principal component analysis (PCA, [62]) followed by PERMANOVA with 999 permutations [63]. We used the values of the 19 bioclimatic variables extracted for the location of each species. In addition, we evaluated the location of each sampled population in accordance with the first (PCA1) and second (PCA2) principal components. Specifically, we calculated the mean and standard deviation (SD) of PC1 and PCA2 for each species and compared whether the value for the sampled populations fell within the SD for the species. In doing so, we could represent the bioclimatic niche of each species in Spain and the relative position at the sites in which each population was sampled.
To study the relationship between growth variability and drought severity (SPEI), we calculated Pearson correlation coefficients between the residual site chronologies of each species and the SPEI. Correlations were obtained for each month of the year, from September of the previous year of growth (t − 1) to September of the current year (t). The significance associated with the correlation coefficients (p < 0.05) was calculated using a permutation test. In our case, we used 1000 permutations to establish the significance of each correlation coefficient. Analyses were performed at scales from 1 to 48 months during the period 1962–2020 using 25-year moving windows. Thus, we studied how the RWI vs. SPEI correlations varied in time (25-year moving window) within the study period (1962–2020). For each moving window, we selected the maximum correlation between the growth variability and the SPEI drought index. These calculations were done using the treeclim package in R [64].
To study growth trajectories, we used linear models in which the BAI for the period 1962–2020 was the response variable and the calendar year was the explanatory variable. Calendar year was standardized prior to the analyses so that the slope of the relationship varied between −1 and 1. As done for the RWI vs. SPEI correlation, analyses were done using 25-year moving windows to evaluate temporal variations in growth trajectories.
We propose a framework to study the drought-induced vulnerability of species and populations in a harmonized approach based on their growth trajectories and the correlation between growth variability and a drought index (Figure 1). Prior to this, the variables were re-scaled so that they operated in a space between 0 and 1, in which zero represents the most positive growth trajectory and the most negative SPEI–growth coupling, respectively. Giving that the standardized BAI trend and the RWI vs. SPEI correlation varied between −1 and 1, they were transformed as follows:
BAI trend scaled = 1 − (BAI trend + 1)/2
RWI vs. SPEI correlation scaled = (RWI vs. SPEI + 1)/2
We calculated the drought-induced vulnerability index (DrVi) as the product of the BAI trend scaled and the RWI vs. SPEI correlation scaled. Therefore, the proposed index varied between 0 and 1, with high values representing negative growth trajectories and strong climate–drought coupling (Figure 1). As done for the growth trajectories (BAI trend scaled) and the relationship between growth variability and the drought index (RWI. Vs. SPEI correlation scaled), the DrVi was calculated for the period 1962–2020 using 25-year moving windows.

3. Results

We found differences in the bioclimatic niche between the species studied (Figure 4a), which were significant according to PERMANOVA (F = 303, df = 7815; R2 = 0.16; p < 0.001). PCA1 was mainly related to temperature-related bioclimatic variables such as mean annual temperature (BIO 1), mean temperature of the wettest and driest quarter (BIO 10, 11), and maximum temperature of the warmest and coldest months (BIO 5, 6). Species like P. lentiscus and P. halepensis tended to have positive PCA1 values while A. monspessulanum and J. thurifera presented negative values. PCA2 separated sites with elevated temperature range and seasonality (BIO 2, 4) from sites with high precipitation (BIO 12, 13). Species like E. nebrodensis and J. thurifera had lower PCA2 scores than species like A. monspessulanum and P. lentiscus (Figure 4a).
Regarding the studied sites, Sierra de Alcubierre presented low values of PCA1 for P. halepensis and P. lentiscus, average values for J. oxycedrus and E. nebrodensis, and relatively high values for A. monspessulanum and J. thurifera (Figure 4b). Most species presented low PCA2 values, particularly in the case of P. halepensis, J. oxycedrus, P. lentiscus, and A. monspessulanum. This means that, in Sierra de Alcubierre, all species were found in relatively dry and highly seasonal sites (low PC2 scores) and in warm sites in the case of J. thurifera and A. monspessulanum (high PC1 scores). In the case of J. oxycedrus populations, Napal was colder and wetter than Alcubierre and particularly Valcuerna (Figure 4b).
Radial growth varied between populations and species (Table 2 and Figure 5). The individuals from the J. thurifera population in Sierra de Alcubierre were the oldest and presented the widest rings, while the J. oxycedrus population from Valcuerna grew the least (Table 2). We found that the mean ring-width series (chronologies) of the species were reliable in most of the cases. In general, they presented higher rbar and EPS values for trees (P. halepensis, J. thurifera) than for shrubs, with the exception of J. oxycedrus in Valcuerna (Table 2). In the case of shrubs, higher rbar values and EPS values were found in drier sites (J. oxycedrus in Valcuerna). Most species presented a positive growth trend in the study period, with the exception of P. halepensis in Sierra de Alcubierre (Figure 5 and Table 3). However, the 25-year moving window analyses revealed that the mean BAI trend decreased from the beginning (1962–1987) to the end of the study period (1995–2020), with the exception of A. monspessulanum and P. halepensis in Sierra de Alcubierre and J. oxycedrus in Valcuerna (Figure 5 and Table 3).
The response of growth to drought varied between species and populations (Figure 6). All species responded positively to the SPEI at varying time scales (from 1 to 48 months) during the growing season (from May to August) but with substantial differences. The strongest correlations between RWI and SPEI were found for P. halepensis and J. thurifera in Sierra de Alcubierre (Table 3), which also were the species responding to longer time scales (Figure 6). We found variations in the RWI–SPEI correlation between 25-year periods with A. monspessulanum and J. thurifera in Sierra de Alcubierre and J. oxycedrus in Napal and Valcuerna, presenting a positive trend (Table 3). Thus, these populations were more impacted by drought now (1995–2020) than in the past (1962–1987).
We found that the drought-induced vulnerability index (DrVi) reflected the differences between species and populations and pointed to P. halepensis in Sierra de Alcubierre as the most vulnerable population in terms of growth (Figure 7). This was due to an overall negative BAI trend during the study period and a strong relationship between RWI and SPEI. However, the temporal variations in DrVi value through the period 1962–2020 displayed different trajectories depending on the populations considered. In Sierra de Alcubierre, a strong increase in the P. halepensis DrVi value was observed during the 1980s, while other species like J. thurifera, J. oxycedrus, and A. monspessulanum increased their DrVi values early in the 21st century (Figure 7). By the end of the study period, the lowest DrVi values were observed for P. lentiscus and E. nebrodensis, and also for one of the A. monspessulanum populations. Regarding the comparison of J. oxycedrus along a precipitation gradient, we found a higher increase in DrVi value for J. oxycedrus from Sierra de Alcubierre and constant and relatively low vulnerabilities of Napal and Valcuerna (Figure 7c). The DrVi value was strongly determined by the BAI trend and it was also negatively related to the resistance and resilience indices and positively to the recovery period and growth reductions in the 2005 and 2012 droughts (Figure S3). The DrVi value was not related to the average position of the species in the bioclimatic space.

4. Discussion

The results presented here indicate that tree and shrub populations vary in their drought-induced vulnerability, as reflected by changes in growth trajectories and responses to the drought index. Moreover, we show that this vulnerability is not stationary, pointing to the importance of considering evolving temporal windows to evaluate it [36]. The framework presented here describing a new drought vulnerability index allows the comparison of populations and species in a standardized bioclimatic space so as to identify those areas and populations that are vulnerable to climate change [11,12]. Regarding the comparison between species coexisting in the same site (Sierra de Alcubierre), we found partial evidence that growth of trees is more vulnerable to drought than that of shrubs, larger species are more vulnerable [24,25], and gymnosperms tend to be more vulnerable than angiosperms in terms of growth [23], particularly in this region [44]. We compared species that occupy different bioclimatic niches, but the drought vulnerability was not higher for those populations that find their dry or warm limit in Sierra de Alcubierre, as expected [14,27,29]. In fact, we found differences in drought-induced vulnerability between similar A. monspessulanum populations, which was not in accordance with our expectations but aligned with other studies [20]. Regarding the comparison of J. oxycedrus populations along a precipitation gradient, we found lower vulnerabilities in the wettest and driest populations, partially contradicting our hypothesis. Our results align with previous studies suggesting that local and microsite conditions can play an important role and can hinder general patterns in drought-induced vulnerability in some situations [20].
At the Sierra de Alcubierre site, we studied two gymnosperm trees (P. halepensis and J. thurifera) that are adapted to drought [65] but that vary in their bioclimatic niche, as demonstrated in our analyses (Figure 4). The growth of these species is known to respond to climate variability by substantially reducing their growth in dry years [66,67], and in the case of P. halepensis, its growth strongly depends on the precipitation during the previous autumn and winter [68]. However, J. thurifera is more adapted to continental climate conditions than P. halepensis (Figure 4). We found that the two species strongly responded to the SPEI during the study period but their growth trajectories differed (Figure 5). In particular, P. halepensis presented a declining trend in response to a climate shift in the early 1980s (Figure 3), while J. thurifera only started to decline after severe droughts occurred in the early 21st century. Junipers are drought-resistant species [69], but recent studies indicate that they may be also vulnerable to increases in the occurrence of severe hotter droughts [44]. In fact, our results indicate that the growth of J. thurifera has decreased in vigor and has become more drought limited during the last years (Table 3). The delayed increase in the vulnerability index of J. thurifera could be due to the location of the sampled population in valley bottoms [67], which might facilitate the access to deep water sources in comparison to the P. halepensis population. Collectively, our results confirm that these gymnosperm trees are becoming more vulnerable to drought as the climate warms (Figure 7), but a better understanding of how these and other coexisting species access deep water sources can be important to better interpret the obtained results [70].
As far as we know, this is the first dendrochronological assessment of the small tree A. monspessulanum (Table 2 and Figure 5). Studies have found that other maple species have dendrochronological potential and are drought tolerant [22]. Our results partially concur with this view because we found a low drought-induced vulnerability of one of the populations studied. However, the other population showed a relatively high increase in drought vulnerability after the severe droughts occurring in the early 21st century (Figure 5 and Figure 7). In fact, we found differences in the growth response to climate of the two populations sampled (Figure 6), pointing to the importance of microsite conditions in determining tree growth in harsh environments [28]. Interestingly, the population of A. monspessulanum displaying an increase in DrVi value coexists with the P. halepensis and J. oxycedrus populations that also show temporal increases in DrVi values (Figure 7). This suggests that this site is particularly vulnerable to recent increases in drought occurrence, as indicated by ongoing processes of P. halepensis crown dieback (Figure S4), in contraposition with the other A. monspessulanun population sampled near formerly cultivated fields. However, a proper comparison of the sites will require a more detailed screening of their topographic and soil conditions.
We included in this study three species of shrubs (Juniperus oxycedrus, Pistacia lentiscus, and Ephedra nebrodensis) that have been previously used in dendrochronological studies [41,44,47]. As expected, we found that their radial growth was sensitive to drought (Figure 6) and that they were, in general, less vulnerable to drought than trees, which points to the importance of size in determining drought vulnerability [71]. In particular, E. nebrodensis (gymnosperm) and P. lentiscus (angiosperm) showed relatively low values of DrVi and no clear increasing trends. The multi-stemmed nature of these shrubs and their low stature can benefit their recovery after drought occurrence [40]. However, we found marked increases in the DrVi values of J. oxycedrus in Sierra de Alcubierre, a pattern that requires further attention since it could represent an early warning signal of impending dieback. As said before, microsite conditions can be behind the increases in drought vulnerability of the three species studied in this site (Figure 7). However, it is also true that shrubby junipers have a superficial root system that makes them vulnerable to the occurrence of drought early in the growing season or to prolonged droughts [44]. The question that remains open is why the driest J. oxycedrus population found in Valcuerna (Figure 7) showed no increase in DrVi value despite this population presenting lower growth rates among those sampled (Table 2). This suggests that it might be well adapted to drought occurrence. In any case, a better understanding of how these coexisting species respond to drought and access soil water and nutrients is key to advancing our understanding of their drought-induced vulnerability.
Finally, several remarks can be presented on the proposed framework to study drought-induced vulnerability (Figure 1). We found that our index correlated well with other widely used indices of growth resilience [18,21], which reinforces its validity (Figure S3). However, some caveats should be considered in further applications of the index. First, it relies on growth trajectories, which are important to understand changes in vigor [14] and responses to climate change [19] but also depend on ontogeny and phenology [16,17]. This can be partially overcome by using moving temporal windows, but it also requires the consideration of the age of the studied populations or species when comparing their drought-induced vulnerability. Second, growth variability and its response to climate (and drought) is not static [36], which also needs to be considered and accounted for. Along this reasoning, we opted for the use of the maximum correlation between the growth variability and the SPEI drought index across multiple seasons (from previous to current September) and scales (from 1 to 48 months). This selection clearly displaces the potential scores of the species to the right side of the graph (Figure 7a). Optionally, the mean correlation value can be selected instead of the maximum value, but similar results were obtained in our case. Connected to this, the difference between the potential (Figure 1) and the realized space (Figure 7) in our proposed framework is unclear, which might depend on the species considered and the temporal resolution. For example, the variation in the growth trajectory is much clearer than the variation in the growth response to SPEI (comparing vertical and horizontal segments in Figure 7). This is probably because we worked with a system that is chronically drought-limited by definition. Finally, it is important to note that the drought-induced vulnerability index reflects temporary growth reductions and enhanced drought sensitivity but cannot be directly translated into permanent decline or tree dieback since postponed growth and growth plasticity can reflect the capacity to tolerate drought. An application of this framework to wider datasets across different biomes and considering healthy as well as declining stands can help to better define the realized zone of drought-induced vulnerability and its significance.

5. Conclusions

The drought-induced vulnerability index (DrVi) proved to be valid to represent changes in growth trajectories and the response of growth variability to drought between coexisting species and across populations. We found pieces of evidence indicating that the growth of trees was more vulnerable to drought than the growth of shrubs in Sierra de Alcubierre. Moreover, our results indicated that growth trajectories and the response of growth variability to drought are not stationary, pointing to the importance of considering varying temporal windows. The framework proposed here aligns with previous efforts to quantify the vulnerability of woody plants to climate change by using radial growth records (e.g., [15,18,19,21,22]) and can help to identify climate change winners and losers [22,26] and potential changes in woodland communities [10]. However, further applications of the standardized framework proposed here are required to better delimit how DrVi varies between species and populations.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/f16050760/s1, Figure S1. Mean maximum temperature and precipitation (1958–2023) at each site; Figure S2. The representation of the distribution of the studied species and sites according to MAT and TAP; Figure S3. The correlation between the average drought-induced vulnerability index (DrVi) and other variables; Figure S4. General view of one of the sites sampled in Sierra de Alcubierre; Table S1. The loadings of the bioclimatic variables in the first and second axes of the PCA (Figure 4).

Author Contributions

Conceptualization, A.G. and J.J.C.; methodology, A.G.; software, A.G.; validation, C.V., E.T.-M., and E.G.d.A.; formal analysis, A.G.; investigation, A.G.; resources, A.G. and J.J.C.; data curation, E.T.-M., C.V., and M.C.; writing—original draft preparation, A.G.; writing—review and editing, A.G., E.G.d.A., and J.J.C. All authors have read and agreed to the published version of the manuscript.

Funding

A. Gazol was supported by the “Ramón y Cajal” Program of the Spanish MICINN under grant RyC2020-030647-I and by CSIC under grant PIE-20223AT003. This research was funded by the Spanish Science and Innovation Ministry (projects PID2021-123675OB-C43 and TED2021-129770B-C21).

Data Availability Statement

Data will be made available upon reasonable request.

Acknowledgments

We appreciate the help of Emerita Gazol and Abel Serrano-Yuste during the field campaigns.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. AghaKouchak, A.; Chiang, F.; Huning, L.S.; Love, C.A.; Mallakpour, I.; Mazdiyasni, O.; Moftakhari, H.; Papalexiou, S.M.; Ragno, E.; Sadegh, M. Climate extremes and compound hazards in a warming world. Annu. Rev. Earth Planet. Sci. 2020, 48, 519–548. [Google Scholar] [CrossRef]
  2. Arias, P.A.; Bellouin, N.; Coppola, E.; Jones, R.G.; Krinner, G.; Marotzke, J.; Naik, V.; Palmer, M.D.; Plattner, G.-K.; Rogelj, J.; et al. Technical Summary. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 33–144. [Google Scholar]
  3. Pecl, G.T.; Araújo, M.B.; Bell, J.D.; Blanchard, J.; Bonebrake, T.C.; Chen, I.-C.; Clark, T.D.; Colwell, R.K.; Danielsen, F.; Evengård, B.; et al. Biodiversity redistribution under climate change: Impacts on ecosystems and human well-being. Science 2017, 355, eaai9214. [Google Scholar] [CrossRef] [PubMed]
  4. Friedl, M.A.; Woodcock, C.E.; Olofsson, P.; Zhu, Z.; Loveland, T.; Stanimirova, R.; Arevalo, P.; Bullock, E.; Hu, K.-T.; Zhang, Y.; et al. Medium spatial resolution mapping of global land cover and land cover change across multiple decades from Landsat. Front. Remote Sens. 2022, 3, 894571. [Google Scholar] [CrossRef]
  5. Allen, C.D.; Breshears, D.D.; McDowell, N.G. On underestimation of global vulnerability to tree mortality and forest die-off from hotter drought in the Anthropocene. Ecosphere 2015, 6, 129. [Google Scholar] [CrossRef]
  6. Hammond, W.M.; Williams, A.P.; Abatzoglou, J.T.; Adams, H.D.; Klein, T.; López, R.; Sáenz-Romero, C.; Hartmann, H.; Breshears, D.D.; Allen, C.D. Global field observations of tree die-off reveal hotter-drought fingerprint for Earth’s forests. Nat. Commun. 2022, 13, 1761. [Google Scholar] [CrossRef] [PubMed]
  7. Hidalgo-Triana, N.; Solakis, A.; Casimiro-Soriguer, F.; Choe, H.; Navarro, T.; Pérez-Latorre, A.V.; Thorne, J.H. The high climate vulnerability of western Mediterranean forests. Sci. Total Environ. 2023, 895, 164983. [Google Scholar] [CrossRef]
  8. Vicente-Serrano, S.M.; Peña-Angulo, D.; Beguería, S.; Domínguez-Castro, F.; Tomás-Burguera, M.; Noguera, I.; Gimeno-Sotelo, L.; El Kenawy, A. Global drought trends and future projections. Phil Trans. R. Soc. A 2022, 380, 20210285. [Google Scholar] [CrossRef]
  9. Tuel, A.; Eltahir, E.A. Why is the Mediterranean a climate change hot spot? J. Clim. 2020, 33, 5829–5843. [Google Scholar] [CrossRef]
  10. Batllori, E.; Lloret, F.; Aakala, T.; Anderegg, W.R.L.; Aynekulu, E.; Bendixsen, D.P.; Bentouati, A.; Bigler, C.; Burk, C.J.; Camarero, J.J.; et al. Forest and woodland replacement patterns following drought-related mortality. Proc. Natl. Acad. Sci. USA 2020, 117, 29720–29729. [Google Scholar] [CrossRef] [PubMed]
  11. Doblas-Miranda, E.; Martínez-Vilalta, J.; Lloret, F.; Álvarez, A.; Ávila, A.; Bonet, F.J.; Brotons, L.; Castro, J.; Curiel Yuste, J.; Díaz, M.; et al. Reassessing global change research priorities in mediterranean terrestrial ecosystems: How far have we come and where do we go from here? Glob. Ecol. Biogeogr. 2015, 24, 25–43. [Google Scholar] [CrossRef]
  12. Peñuelas, J.; Sardans, J. Global change and forest disturbances in the Mediterranean basin: Breakthroughs, knowledge gaps, and recommendations. Forests 2021, 12, 603. [Google Scholar] [CrossRef]
  13. Fritts, H.C. Tree Rings and Climate; Academic Press: London, UK, 1976. [Google Scholar]
  14. Jump, A.S.; Hunt, J.M.; Penuelas, J. Rapid climate change-related growth decline at the southern range edge of Fagus sylvatica. Glob. Change Biol. 2006, 12, 2163–2174. [Google Scholar] [CrossRef]
  15. Denisa, S.; Róbert, S.; Patrik, K.; Pavel, Ď.; Milan, S.; Peter, J.; Stanislav, K. Divergent growth responses of healthy and declining spruce trees to climatic stress: A case study from the Western carpathians. Dendrochronologia 2022, 76, 126023. [Google Scholar] [CrossRef]
  16. Bowman, D.M.; Brienen, R.J.; Gloor, E.; Phillips, O.L.; Prior, L.D. Detecting trends in tree growth: Not so simple. Trends Plant Sci. 2013, 18, 11–17. [Google Scholar] [CrossRef]
  17. Delpierre, N.; Berveiller, D.; Granda, E.; Dufrêne, E. Wood phenology, not carbon input, controls the interannual variability of wood growth in a temperate oak forest. New Phytol. 2015, 210, 459–470. [Google Scholar] [CrossRef]
  18. Lloret, F.; Keeling, E.G.; Sala, A. Components of tree resilience: Effects of successive low-growth episodes in old ponderosa pine forests. Oikos 2011, 120, 1909–1920. [Google Scholar] [CrossRef]
  19. Eilmann, B.; Rigling, A. Tree-growth analyses to estimate tree species’ drought tolerance. Tree Physiol. 2012, 32, 178–187. [Google Scholar] [CrossRef]
  20. Vilà-Cabrera, A.; Jump, A.S. Greater growth stability of trees in marginal habitats suggests a patchy pattern of population loss and retention in response to increased drought at the rear edge. Ecol. Lett. 2019, 22, 1439–1448. [Google Scholar] [CrossRef] [PubMed]
  21. Schwarz, J.; Skiadaresis, G.; Kohler, M.; Kunz, J.; Schnabel, F.; Vitali, V.; Bauhus, J. Quantifying growth responses of trees to drought—A critique of commonly used resilience indices and recommendations for future studies. Curr. Rep. 2020, 6, 185–200. [Google Scholar] [CrossRef]
  22. Schmucker, J.; Uhl, E.; Schmied, G.; Pretzsch, H. Growth and drought reaction of European hornbeam, European white elm, field maple and wild service tree. Trees 2023, 37, 1515–1536. [Google Scholar] [CrossRef]
  23. Anderegg, W.R.L.; Schwalm, C.R.; Biondi, F.; Camarero, J.J.; Koch, G.W.; Litvak, M.; Ogle, K.; Shaw, J.D.; Shevliakova, E.; Williams, A.P.; et al. Pervasive drought legacies in forest ecosystems and their implications for carbon cycle models. Science 2015, 349, 528–532. [Google Scholar] [CrossRef] [PubMed]
  24. Fernández-de-Uña, L.; Martínez-Vilalta, J.; Poyatos, R.; Mencuccini, M.; McDowell, N.G. The role of height-driven constraints and compensations on tree vulnerability to drought. New Phytol. 2023, 239, 2083–2098. [Google Scholar] [CrossRef]
  25. Camarero, J.J.; Pizarro, M.; Gernandt, D.S.; Gazol, A. Smaller conifers are more resilient to drought. Agric. For. Meteorol. 2024, 350, 109993. [Google Scholar] [CrossRef]
  26. Kasper, J.; Leuschner, C.; Walentowski, H.; Petritan, A.M.; Weigel, R. Winners and losers of climate warming: Declining growth in Fagus and Tilia vs. stable growth in three Quercus species in the natural beech–oak forest ecotone (western Romania). For. Ecol. Manag. 2022, 506, 119892. [Google Scholar] [CrossRef]
  27. Su, J.; Gou, X.; HilleRisLambers, J.; Deng, Y.; Fan, H.; Zheng, W.; Zhang, R.; Manzanedo, R.D. Increasing climate sensitivity of subtropical conifers along an aridity gradient. For. Ecol. Manag. 2021, 482, 118841. [Google Scholar] [CrossRef]
  28. Weigel, R.; Bat-Enerel, B.; Dulamsuren, C.; Muffler, L.; Weithmann, G.; Leuschner, C. Summer drought exposure, stand structure, and soil properties jointly control the growth of European beech along a steep precipitation gradient in northern Germany. Glob. Change Biol. 2023, 29, 763–779. [Google Scholar] [CrossRef]
  29. Serra-Maluquer, X.; Mencuccini, M.; Martínez-Vilalta, J. Changes in tree resistance, recovery and resilience across three successive extreme droughts in the northeast Iberian Peninsula. Oecologia 2018, 187, 343–354. [Google Scholar] [CrossRef]
  30. Camarero, J.J.; Gazol, A.; Sangüesa-Barreda, G.; Oliva, J.; Vicente-Serrano, S.M. To die or not to die: Early warnings of tree dieback in response to a severe drought. J. Ecol. 2015, 103, 44–57. [Google Scholar] [CrossRef]
  31. Cailleret, M.; Jansen, S.; Robert, E.M.R.; Desoto, L.; Aakala, T.; Antos, J.A.; Beikircher, B.; Bigler, C.; Bugmann, H.; Caccianiga, M.; et al. A synthesis of radial growth patterns preceding tree mortality. Glob. Change Biol. 2017, 23, 1675–1690. [Google Scholar] [CrossRef]
  32. DeSoto, L.; Cailleret, M.; Sterck, F.; Jansen, S.; Kramer, K.; Robert, E.M.R.; Aakala, T.; Amoroso, M.M.; Bigler, C.; Camarero, J.J.; et al. Low growth resilience to drought is related to future mortality risk in trees. Nat. Commun. 2020, 11, 545. [Google Scholar] [CrossRef]
  33. Cabon, A.; DeRose, R.J.; Shaw, J.D.; Anderegg, W.R.L. Declining tree growth resilience mediates subsequent forest mortality in the US Mountain West. Glob. Change Biol. 2023, 29, 4826–4841. [Google Scholar] [CrossRef] [PubMed]
  34. Foden, W.B.; Young, B.E.; Akçakaya, H.R.; Garcia, R.A.; Hoffmann, A.A.; Stein, B.A.; Thomas, C.D.; Wheatley, C.J.; Bickford, D.; Carr, J.A.; et al. Climate change vulnerability assessment of species. WIREs Clim. Change 2019, 10, e551. [Google Scholar] [CrossRef]
  35. Serra-Maluquer, X.; Gazol, A.; Anderegg, W.R.L.; Martínez-Vilalta, J.; Mencuccini, M.; Camarero, J.J. Wood density and hydraulic traits influence species’ growth response to drought across biomes. Glob. Change Biol. 2022, 28, 3871–3882. [Google Scholar] [CrossRef]
  36. Wilmking, M.; Van Der Maaten-Theunissen, M.; Van Der Maaten, E.; Scharnweber, T.; Buras, A.; Biermann, C.; Gurskaya, M.; Hallinger, M.; Lange, J.; Shetti, R.; et al. Global assessment of relationships between climate and tree growth. Glob. Change Biol. 2020, 26, 3212–3220. [Google Scholar] [CrossRef]
  37. Roshani Sajjad, H.; Kumar, P.; Masroor, M.; Rahaman, M.H.; Rehman, S.; Ahmed, R.; Sahana, M. Forest vulnerability to climate change: A review for future research framework. Forests 2022, 13, 917. [Google Scholar] [CrossRef]
  38. Martinez del Castillo, E.; Zang, C.S.; Buras, A.; Hacket-Pain, A.; Esper, J.; Serrano-Notivoli, R.; Hartl, C.; Weigel, R.; Klesse, S.; de Dios, V.R.; et al. Climate-change-driven growth decline of European beech forests. Commun. Biol. 2022, 5, 163. [Google Scholar] [CrossRef]
  39. Montserrat-Martí, G.; Palacio, S.; Milla, R.; Giménez-Benavides, L. Meristem growth, phenology, and architecture in chamaephytes of the Iberian Peninsula: Insights into a largely neglected life form. Folia Geobot. 2011, 46, 117–136. [Google Scholar] [CrossRef]
  40. Götmark, F.; Götmark, E.; Jensen, A.M. Why be a shrub? A basic model and hypotheses for the adaptive values of a common growth form. Front. Plant Sci. 2016, 7, 1095. [Google Scholar] [CrossRef] [PubMed]
  41. Camarero, J.J.; Valeriano, C.; Gazol, A.; Colangelo, M.; Sanchez-Salguero, R. Climate differently impacts the growth of coexisting trees and shrubs under semi-arid Mediterranean conditions. Forests 2021, 12, 381. [Google Scholar] [CrossRef]
  42. Lombardo, E.; Bancheva, S.; Domina, G.; Venturella, G. Distribution, ecological role and symbioses of selected shrubby species in the Mediterranean Basin: A review. Plant Biosyst. 2020, 154, 438–454. [Google Scholar] [CrossRef]
  43. Gazol, A.; Camarero, J.J. Mediterranean dwarf shrubs and coexisting trees present different radial-growth synchronies and responses to climate. Plant Ecol. 2012, 213, 1687–1698. [Google Scholar] [CrossRef]
  44. Tamudo, E.; Gazol, A.; Valeriano, C.; González, E.; Colangelo, M.; Camarero, J.J. Similar climate–growth relationships but divergent drought resilience strategies in coexisting Mediterranean shrubs. J. Ecol. 2024, 112, 1804–1817. [Google Scholar] [CrossRef]
  45. Madoz, P. Diccionario Geográfico-Estadístico-Histórico de España y sus Posesiones de Ultramar; Imprenta del Diccionario: Madrid, Spain, 1849; Volume 1. [Google Scholar]
  46. Molero Briones, J.; Sáez, L.; Villar, L. Interés florístico y geobotánico de la Sierra de Alcubierre (Monegros, Aragón). Acta Bot. Barcinonense 1998, 45, 363–390. [Google Scholar]
  47. Valeriano, C.; Gutiérrez, E.; Colangelo, M.; Gazol, A.; Sánchez-Salguero, R.; Tumajer, J.; Shishov, V.; Bonet, J.A.; de Aragón, J.M.; Ibáñez, R.; et al. Seasonal precipitation and continentality drive bimodal growth in Mediterranean forests. Dendrochronologia 2023, 78, 126057. [Google Scholar] [CrossRef]
  48. Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
  49. Larsson, L.A.; Larsson, P.O. CDendro and CooRecorder, v. 9.8.1; Cybis Elektronik and Data AB: Saltsjöbaden, Sweden, 2022.
  50. Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree-Ring Bull. 1983, 43, 51–67. [Google Scholar]
  51. Biondi, F.; Qeadan, F. A theory-driven approach to tree-ring standardization: Defining the biological trend from expected basal area increment. Tree-Ring Res. 2008, 64, 81–96. [Google Scholar] [CrossRef]
  52. Briffa, K.R.; Jones, P.D. Basic Chronology Statistics and Assessment. In Methods of Dendrochronology; Cook, E.R., Kairiukstis, L.A., Eds.; Kluwer: Dordrecht, The Netherlands, 1990; pp. 137–152. [Google Scholar]
  53. Wigley, T.M.; Briffa, K.R.; Jones, P.D. On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J. Appl. Meteorol. Climatol. 1984, 23, 201–213. [Google Scholar] [CrossRef]
  54. Tejedor, E.; Saz, M.A.; Esper, J.; Cuadrat, J.M.; De Luis, M. Summer drought reconstruction in northeastern Spain inferred from a tree ring latewood network since 1734. Geophys. Res. Lett. 2017, 44, 8492–8500. [Google Scholar] [CrossRef]
  55. R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2025. [Google Scholar]
  56. Bunn, A.G. A dendrochronology program library in R (dplR). Dendrochronologia 2008, 26, 115–124. [Google Scholar] [CrossRef]
  57. Van der Maaten-Theunissen, M.; van der Maaten, E.; Bouriaud, O. pointRes: An R package to analyze pointer years and components of resilience. Dendrochronologia 2015, 35, 34–38. [Google Scholar] [CrossRef]
  58. Van der Maaten-Theunissen, M.; Trouillier, M.; Schwarz, J.; Skiadaresism, G.; Thurm, A.A.; van der Maaten, E. pointRes 2.0: New functions to describe tree resilience. Dendrochronologia 2021, 70, 125899. [Google Scholar] [CrossRef]
  59. Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
  60. Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.Z.; Hegewisch, K.C. Terraclimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958–2015. Sci. Data 2018, 5, 170191. [Google Scholar] [CrossRef]
  61. Beguería, S.; Vicente-Serrano, S.M. SPEI: Calculation of the Standardized Precipitation-Evapotranspiration Index. R Package Version 1.8.1. 2021. Available online: https://CRAN.R-project.org/package=SPEI (accessed on 5 February 2025).
  62. Legendre, P.; Legendre, L. Numerical Ecology, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
  63. McArdle, B.H.; Anderson, M.J. Fitting multivariate models to community data: A comment on distance-based redundancy analysis. Ecology 2001, 82, 290–297. [Google Scholar] [CrossRef]
  64. Zang, C.; Biondi, F. treeclim: An R package for the numerical calibration of proxy-climate relationships. Ecography 2015, 38, 431–436. [Google Scholar] [CrossRef]
  65. Camarero, J.J.; Olano, J.M.; Parras, A. Plastic bimodal xylogenesis in conifers from continental Mediterranean climates. New Phytol. 2010, 185, 471–480. [Google Scholar] [CrossRef]
  66. Gazol, A.; Ribas, M.; Gutiérrez, E.; Camarero, J.J. Aleppo pine forests from across Spain show drought-induced growth decline and partial recovery. Agric. For. Meteorol. 2017, 232, 186–194. [Google Scholar] [CrossRef]
  67. Camarero, J.J.; Gazol, A.; Valeriano, C.; Pizarro, M.; González de Andrés, E. Topoclimatic modulation of growth and production of intra-annual density fluctuations in Juniperus thurifera. Dendrochronologia 2023, 82, 126145. [Google Scholar] [CrossRef]
  68. Pasho, E.; Camarero, J.J.; Vicente-Serrano, S.M. Climatic impacts and drought control of radial growth and seasonal wood formation in Pinus halepensis. Trees 2012, 26, 1875–1886. [Google Scholar] [CrossRef]
  69. Willson, C.J.; Manos, P.S.; Jackson, R.B. Hydraulic traits are influenced by phylogenetic history in the drought-resistant, invasive genus Juniperus (Cupressaceae). Am. J. Bot. 2008, 95, 299–314. [Google Scholar] [CrossRef] [PubMed]
  70. Illuminati, A.; Querejeta, J.I.; Pías, B.; Escudero, A.; Matesanz, S. Coordination between water uptake depth and the leaf economic spectrum in a Mediterranean shrubland. J. Ecol. 2022, 110, 1844–1856. [Google Scholar] [CrossRef]
  71. Fajardo, A.; McIntire, E.J.; Olson, M.E. When short stature is an asset in trees. Trends Ecol. Evol. 2019, 34, 193–199. [Google Scholar] [CrossRef] [PubMed]
Forests 16 00760 g001
Figure 1. Proposed framework to study drought-induced vulnerability. The product of the standardized growth trajectory (basal area increment, BAI trend) and growth response to the drought index (RWI vs. SPEI correlation) has a maximum value of 1 when the drought-induced vulnerability (DrVi) of the studied population is maximum. Grey points represent 999 random values of BAI trends and RWI vs. SPEI correlations with their size proportional to the DrVi value.
Figure 1. Proposed framework to study drought-induced vulnerability. The product of the standardized growth trajectory (basal area increment, BAI trend) and growth response to the drought index (RWI vs. SPEI correlation) has a maximum value of 1 when the drought-induced vulnerability (DrVi) of the studied population is maximum. Grey points represent 999 random values of BAI trends and RWI vs. SPEI correlations with their size proportional to the DrVi value.
Forests 16 00760 g001
Forests 16 00760 g003
Figure 3. The Standardized Precipitation Evapotranspiration Index (SPEI; [59]) for the studied sites. The SPEI was calculated at scales of 3, 6, 12, 24, and 48 months for the period 1962–2023 in the studied sites: Napal (plots a–e), Sierra de Alcubierre (plots f–j), and Valcuerna (plots k–o). Blue colors indicate positive SPEI values (wet conditions) and brown colors indicate negative SPEI values (dry conditions). The index was calculated using the SPEI package in R [61] and the Terraclimate dataset [60].
Figure 3. The Standardized Precipitation Evapotranspiration Index (SPEI; [59]) for the studied sites. The SPEI was calculated at scales of 3, 6, 12, 24, and 48 months for the period 1962–2023 in the studied sites: Napal (plots a–e), Sierra de Alcubierre (plots f–j), and Valcuerna (plots k–o). Blue colors indicate positive SPEI values (wet conditions) and brown colors indicate negative SPEI values (dry conditions). The index was calculated using the SPEI package in R [61] and the Terraclimate dataset [60].
Forests 16 00760 g003
Forests 16 00760 g004
Figure 4. The bioclimatic space occupied for the study tree and shrub species considered and the relative locations of the populations studied. In (a), the bioclimatic space occupied for each species is represented according to the WorldClim [48] data and the distribution data from the Anthos project (www.anthos.es, accessed on 5 February 2025). The dots represent the occurrences of each species, and the ellipses represent the distribution of each species. Several bioclimate variables out of the 19 considered (those more related with the axes) are represented (see Table S1). In (b), the mean and standard deviation of each species in the PCA1 and PCA2 axes are shown. The black dots indicate the populations sampled for each species in Napal (squares), Sierra de Alcubierre (circles), and Valcuerna (diamonds).
Figure 4. The bioclimatic space occupied for the study tree and shrub species considered and the relative locations of the populations studied. In (a), the bioclimatic space occupied for each species is represented according to the WorldClim [48] data and the distribution data from the Anthos project (www.anthos.es, accessed on 5 February 2025). The dots represent the occurrences of each species, and the ellipses represent the distribution of each species. Several bioclimate variables out of the 19 considered (those more related with the axes) are represented (see Table S1). In (b), the mean and standard deviation of each species in the PCA1 and PCA2 axes are shown. The black dots indicate the populations sampled for each species in Napal (squares), Sierra de Alcubierre (circles), and Valcuerna (diamonds).
Forests 16 00760 g004
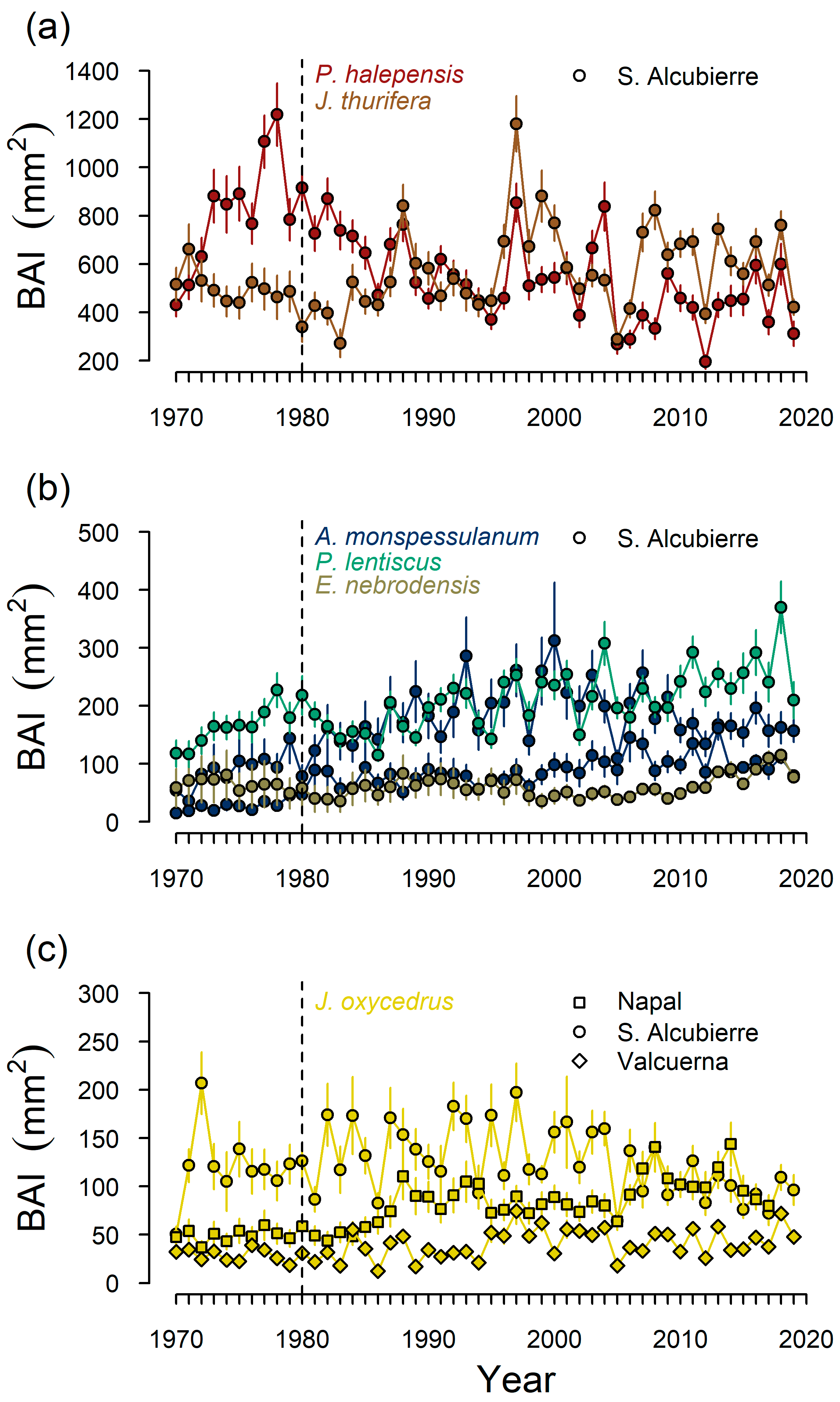
Forests 16 00760 g005
Figure 5. The basal area increments (BAI) of Pinus halepensis Mill. and Juniperus thurifera L. (a); Acer monspessulanum L., Pistacia lentiscus L. and Ephedra nebrodensis Tineo ex Guss. (b) in Sierra de Alcubierre; and Juniperus oxycedrus L. across all study populations (c). The vertical dashed lines indicate the year 1980, which coincides with a climatic shift (see Figure 2). Values are means ± SD.
Figure 5. The basal area increments (BAI) of Pinus halepensis Mill. and Juniperus thurifera L. (a); Acer monspessulanum L., Pistacia lentiscus L. and Ephedra nebrodensis Tineo ex Guss. (b) in Sierra de Alcubierre; and Juniperus oxycedrus L. across all study populations (c). The vertical dashed lines indicate the year 1980, which coincides with a climatic shift (see Figure 2). Values are means ± SD.
Forests 16 00760 g005
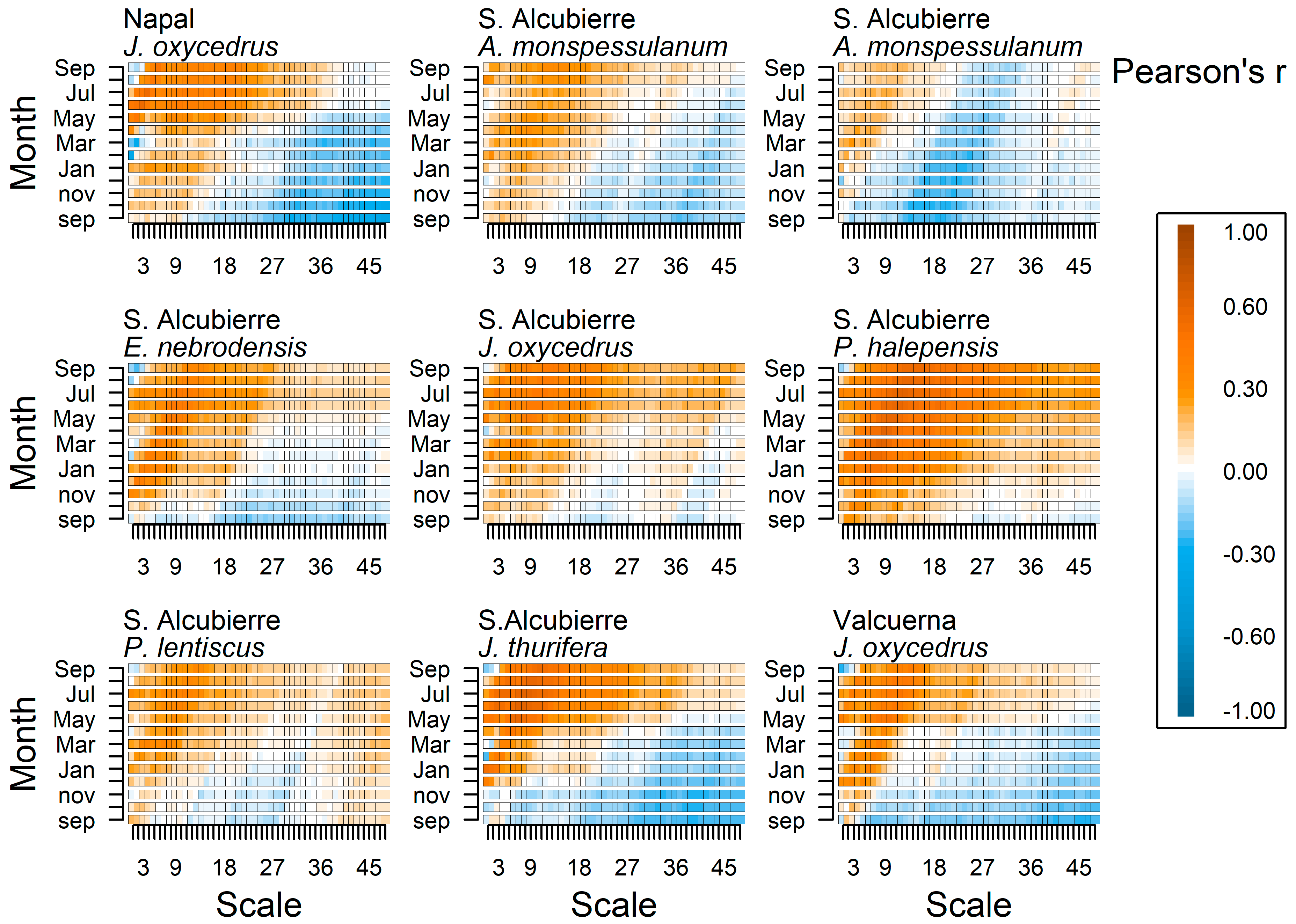
Forests 16 00760 g006
Figure 6. Relationship between growth indices and drought across species and populations. The average Pearson correlation coefficients (r) between RWI and SPEI in 25-year moving windows for the period 1962–2020 are shown. For each month (previous September to current September, y-axis; lower case letters correspond to the year before ring formation) and scale (1 to 48 months, x-axis), the values show the average correlation. Brown values indicate positive relationships and blue colors indicate negative relationships.
Figure 6. Relationship between growth indices and drought across species and populations. The average Pearson correlation coefficients (r) between RWI and SPEI in 25-year moving windows for the period 1962–2020 are shown. For each month (previous September to current September, y-axis; lower case letters correspond to the year before ring formation) and scale (1 to 48 months, x-axis), the values show the average correlation. Brown values indicate positive relationships and blue colors indicate negative relationships.
Forests 16 00760 g006
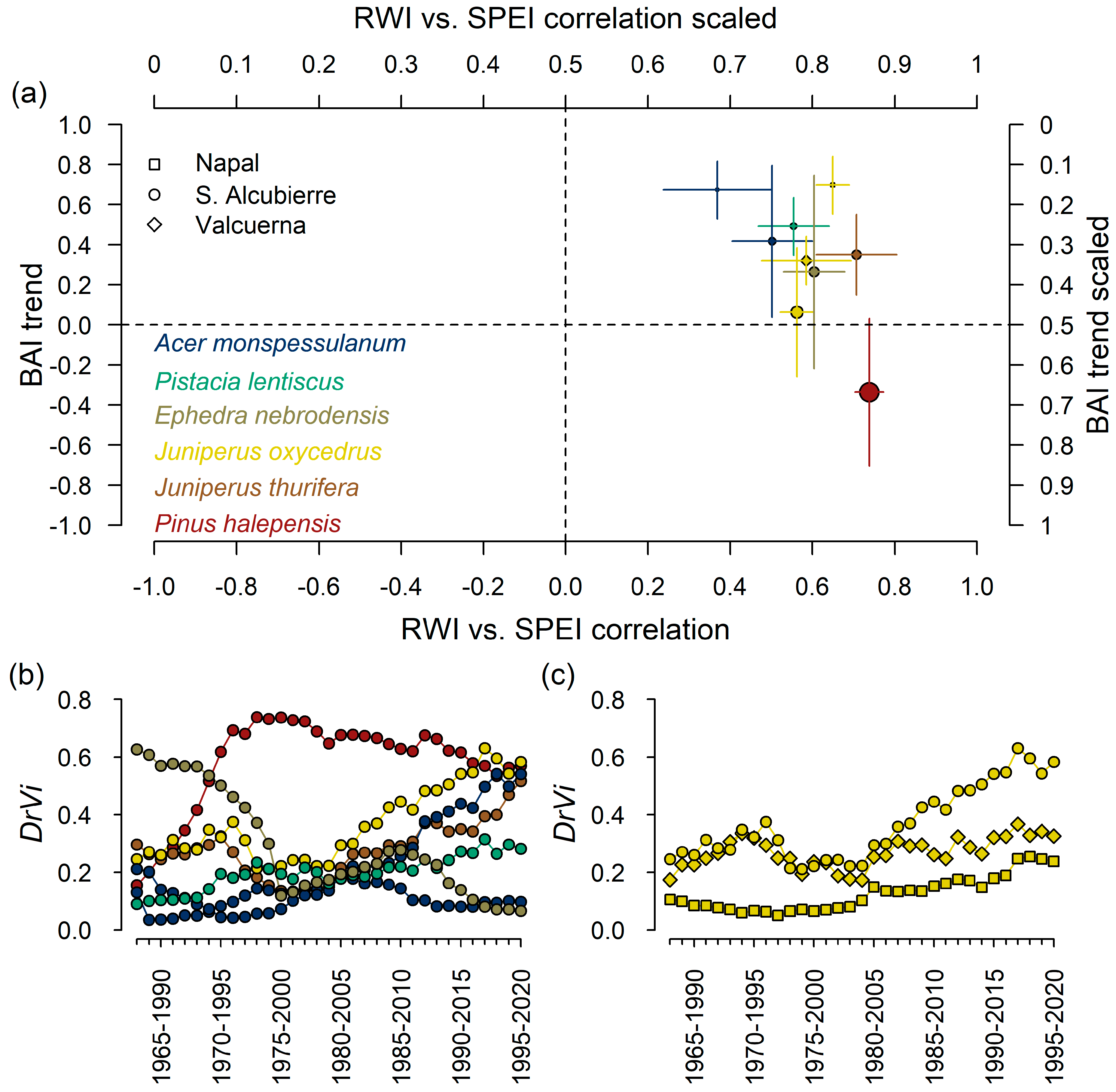
Forests 16 00760 g007
Figure 7. The variations in growth trajectory, growth–drought coupling, and the vulnerability index between populations and species. In (a), each population is represented according to the average BAI trend and maximum RWI–SPEI correlation in the period 1962–2020. Dots represent averages, with the size proportional to the drought-induced vulnerability index. The segments represent the standard deviations for the means in the BAI trend and RWI–SPEI correlation. In (b), the temporal variation in DrVi value is shown considering 25-year moving windows for the period 1962–2020 in Sierra de Alcubierre. In (c), the temporal variation in DrVi value is presented for the period 1965–2020 and the J. oxycedrus populations studied in Napal, Sierra de Alcubierre, and Valcuerna. Each species and population are represented with a different color and symbol, respectively.
Figure 7. The variations in growth trajectory, growth–drought coupling, and the vulnerability index between populations and species. In (a), each population is represented according to the average BAI trend and maximum RWI–SPEI correlation in the period 1962–2020. Dots represent averages, with the size proportional to the drought-induced vulnerability index. The segments represent the standard deviations for the means in the BAI trend and RWI–SPEI correlation. In (b), the temporal variation in DrVi value is shown considering 25-year moving windows for the period 1962–2020 in Sierra de Alcubierre. In (c), the temporal variation in DrVi value is presented for the period 1965–2020 and the J. oxycedrus populations studied in Napal, Sierra de Alcubierre, and Valcuerna. Each species and population are represented with a different color and symbol, respectively.
Forests 16 00760 g007
Table 1. Tree and shrub populations studied. The study sites, the coordinates of the sampling sites, the names of the species (angiosperms in bold), and the codes of the populations are shown.
Table 1. Tree and shrub populations studied. The study sites, the coordinates of the sampling sites, the names of the species (angiosperms in bold), and the codes of the populations are shown.
SiteLatitude (°) NLongitude (°) − W/+ ESpeciesCode
Sierra de Alcubierre41.8165−0.5088Acer monspessulanum L.ALAM
41.6920−0.3677Acer monspessulanum L.LAAM
41.6499−0.3635Ephedra nebrodensis Tineo ex Guss.LAEP
41.6920−0.3677Juniperus oxycedrus L.LAJO
41.6920−0.3677Pinus halepensis Mill.LAPH
41.7327−0.4237Pistacia lentiscus L.LAPL
41.7828−0.5544Juniperus thurifera L.PEJT
Napal42.7290−1.2312Juniperus oxycedrus L.NAJO
Valcuerna41.43870.0675Juniperus oxycedrus L.VAJO
Table 2. Dendrochronological characteristics of the populations studied. For each population (code), the timespan covered by the chronology, the mean ring width and its SD, the number of measured series and individuals, the first-order autocorrelation (AR1) with its SD, the rbar values, and the EPS values for the chronologies in the period 1990–2020 are shown.
Table 2. Dendrochronological characteristics of the populations studied. For each population (code), the timespan covered by the chronology, the mean ring width and its SD, the number of measured series and individuals, the first-order autocorrelation (AR1) with its SD, the rbar values, and the EPS values for the chronologies in the period 1990–2020 are shown.
CodeSiteSpeciesTimespanRing Width/SD (mm)No. Series/No. IndividualsAR1/SDrbarEPS
ALAMSierra de AlcubierreAcer monspessulanum L.1960–20230.852 ± 0.54422/110.360 ± 0.250.1930.724
LAAM Acer monspessulanum L.1926–20230.681 ± 0.44332/160.310 ± 0.2320.1770.751
LAEP Ephedra nebrodensis Tineo ex Guss.1936–20200.762 ± 0.41840/200.295 ± 0.2450.3130.732
LAJO Juniperus oxycedrus L.1880–20230.461 ± 0.39932/170.276 ± 0.2590.1630.768
LAPH Pinus halepensis Mill.1862–20230.838 ± 0.63641/210.373 ± 0.2310.6020.969
LAPL Pistacia lentiscus L.1936–20230.797 ± 0.45430/150.216 ± 0.2480.2350.821
NAJO Juniperus thurifera L.1849–20191.087 ± 0.79331/160.365 ± 0.2570.1500.739
PEJTNapalJuniperus oxycedrus L.1878–20170.589 ± 0.43687/460.383 ± 0.1670.5130.974
VAJOValcuernaJuniperus oxycedrus L.1914–20220.328 ± 0.21330/150.246 ± 0.1910.3240.878
Bold indicates angiosperm species.
Table 3. Relationships between growth, drought, and growth trajectory in each population. The average maximum correlation coefficient between the RWI and the SPEI at different scales (mean ± SE) is shown for 25-year moving windows in the period 1962–2020. The trend shows the presence of a significant (* p < 0.05) linear trend in the maximum correlation coefficient. The BAI trend for 25-year moving windows in the period 1962–2020 is shown together with its temporal trend (significant; * p < 0.05).
Table 3. Relationships between growth, drought, and growth trajectory in each population. The average maximum correlation coefficient between the RWI and the SPEI at different scales (mean ± SE) is shown for 25-year moving windows in the period 1962–2020. The trend shows the presence of a significant (* p < 0.05) linear trend in the maximum correlation coefficient. The BAI trend for 25-year moving windows in the period 1962–2020 is shown together with its temporal trend (significant; * p < 0.05).
CodeSiteSpeciesRWI–SPEI CorrelationTrend in the Max. RWI–SPEI CorrelationBAI Mean TrendTrend in the BAI Mean Trend
ALAMSierra de AlcubierreAcer monspessulanum L.0.500 ± 0.0170.751 *0.417 ± 0.066−0.846 *
LAAM Acer monspessulanum L.0.371 ± 0.0230.3420.673 ± 0.025−0.163
LAEP Ephedra nebrodensis Tineo ex Guss.0.604 ± 0.0120.1550.264 ± 0.0840.876 *
LAJO Juniperus oxycedrus L.0.559 ± 0.0070.1610.063 ± 0.056−0.828 *
LAPH Pinus halepensis Mill.0.738 ± 0.006−0.003−0.336 ± 0.064−0.476 *
LAPL Pistacia lentiscus L.0.553 ± 0.0160.2490.491 ± 0.025−0.845 *
NAJO Juniperus thurifera L.0.651 ± 0.0070.382 *0.697 ± 0.025−0.866 *
PEJTNapalJuniperus oxycedrus L.0.707 ± 0.0180.911 *0.350 ± 0.035−0.439 *
VAJOValcuernaJuniperus oxycedrus L.0.588 ± 0.0190.927 *0.321 ± 0.021−0.204
Bold indicates angiosperm species.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Gazol, A.; Tamudo-Minguez, E.; Valeriano, C.; González de Andrés, E.; Colangelo, M.; Camarero, J.J. A Standardized Framework to Estimate Drought-Induced Vulnerability and Its Temporal Variation in Woody Plants Based on Growth. Forests 2025, 16, 760. https://doi.org/10.3390/f16050760

AMA Style

Gazol A, Tamudo-Minguez E, Valeriano C, González de Andrés E, Colangelo M, Camarero JJ. A Standardized Framework to Estimate Drought-Induced Vulnerability and Its Temporal Variation in Woody Plants Based on Growth. Forests. 2025; 16(5):760. https://doi.org/10.3390/f16050760

Chicago/Turabian Style

Gazol, Antonio, Elisa Tamudo-Minguez, Cristina Valeriano, Ester González de Andrés, Michele Colangelo, and Jesús Julio Camarero. 2025. "A Standardized Framework to Estimate Drought-Induced Vulnerability and Its Temporal Variation in Woody Plants Based on Growth" Forests 16, no. 5: 760. https://doi.org/10.3390/f16050760

APA Style

Gazol, A., Tamudo-Minguez, E., Valeriano, C., González de Andrés, E., Colangelo, M., & Camarero, J. J. (2025). A Standardized Framework to Estimate Drought-Induced Vulnerability and Its Temporal Variation in Woody Plants Based on Growth. Forests, 16(5), 760. https://doi.org/10.3390/f16050760

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop