Intelligence Approach-Driven Bidirectional Analysis Framework for Efficiency Measurement and Resource Optimization of Forest Carbon Sink in China
Abstract
1. Introduction
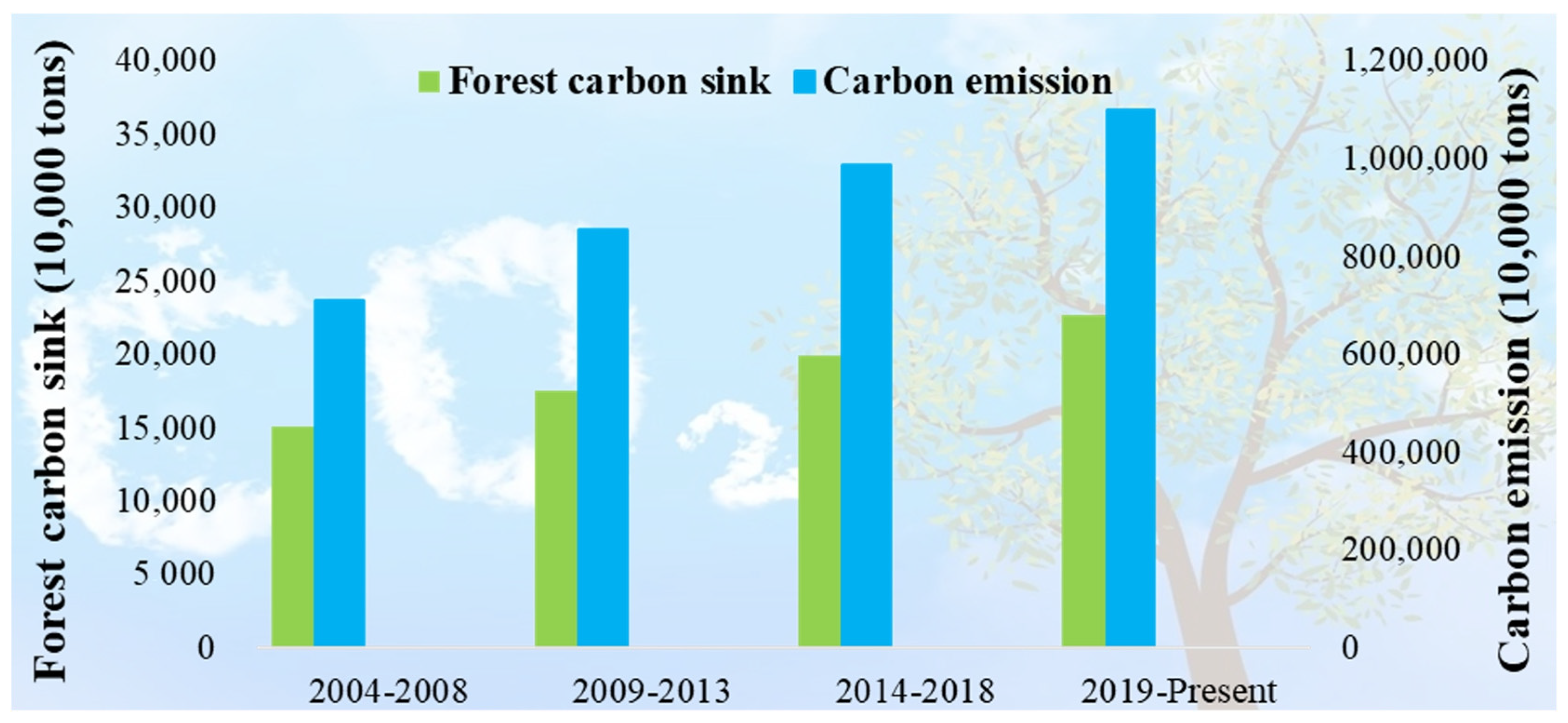
1.1. Background and Motivation
1.2. Literature Review
- (1)
- A deficiency in existing studies is the absence of a systematic assessment and analysis of FCSE using an integrated static and dynamic approach. Many studies measure FCSE solely from a static perspective or examine the main factors influencing it from a dynamic perspective.
- (2)
- An examination of current Inverse DEA research indicates that most studies are confined to theoretical exploration. There is scant research on the practical application of Inverse DEA and few studies investigating the optimization of FCS resource allocations.
- (3)
- There remains an absence of comprehensive research on the sustainable development of FCS. The development of an innovative framework for optimizing the allocation of FCS resources has yet to be developed. Long-term research is deficient in feedback. There is a gap in the research regarding how FCSE feedback can be used to inform improvements and how to achieve sustainable development.
- (1)
- By integrating the Super SBM and MI methods for a systematic spatial–temporal analysis of FCSE, encompassing both dynamic and static elements, and examining the main factors influencing FCSE progress.
- (2)
- By introducing the Inverse DEA model to the study of FCSE, the FCS resource allocation optimization is studied through Inverse DEA to solve the policy feasibility of increasing FCS.
- (3)
- In this study, the analysis framework consisting of four subsystems is constructed innovatively to further study the FCSE problem and the FCS resource allocation optimization problem. The optimal values of future input factors are measured, which will be a practical reference for formulating future forestry policies.
1.3. Objectives and Contributions
- (1)
- This study innovatively constructs an analytical framework incorporating four sub-models. This study adopts an innovative methodology for assessing FCSE by integrating the Super-SBM with the MI model. Methodologically, this innovation provides a novel perspective and a comprehensive toolkit for analyzing FCSE. Utilizing this approach enables the study to precisely identify variations and trends in FCSE, thereby providing scientific insights for policy development.
- (2)
- The study utilizes a comprehensive approach to reveal regional disparities. It extends its analysis to the provincial level, offering an exhaustive assessment of FCSE across 30 Chinese provinces. Comparative analysis of FCSE across provinces highlights significant regional disparities, offering valuable insights for policymaking and resource optimization.
- (3)
- This study guides resource optimization and has a wide range of applications. This study proposes the optimal values of future input indicators for provinces with low FCSE using the Inverse DEA model. This innovative approach not only helps to optimize resource allocation and enhance the FCSE, but also provides specific directions for improvement and implementation strategies for relevant provinces.
- (4)
- The study contributes evidence to inform policy development. The findings provide a scientific basis for governmental entities to formulate and implement policies related to FCS. Through assessments and analyses of FCSE across various provinces, this study identifies the main factors impacting FCSE, and potential areas for enhancement, and offers targeted policy recommendations to policymakers, addressing the sustainability of FCSE.
2. Materials and Methods
2.1. Selection of Indicators
2.2. Methodology for Calculating Forest Carbon Sink
2.3. Data Sources and Data Processing
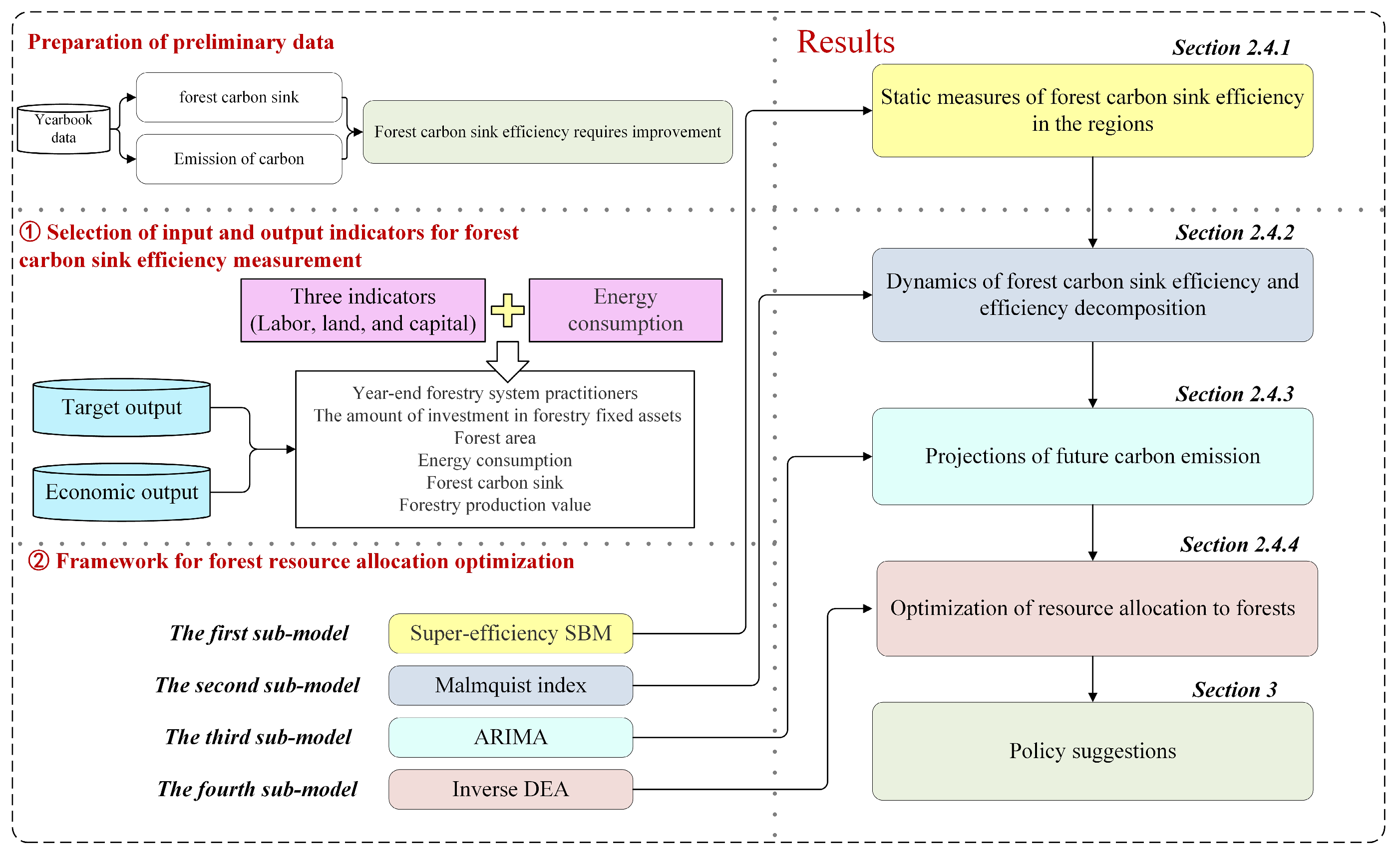
2.4. Models for Measuring Forest Carbon Sink Efficiency and Optimizing Resource Allocation
2.4.1. Forest Carbon Sink Efficiency Static Measurements (The First Sub-Model)
2.4.2. Forest Carbon Sink Efficiency Dynamic Analysis (The Second Sub-Model)
2.4.3. Projections of Carbon Sink Targets (The Third Sub-Model)
2.4.4. Measurement of Future Factor Values of Forest Inputs (The Fourth Sub-Model)
3. Results and Discussion
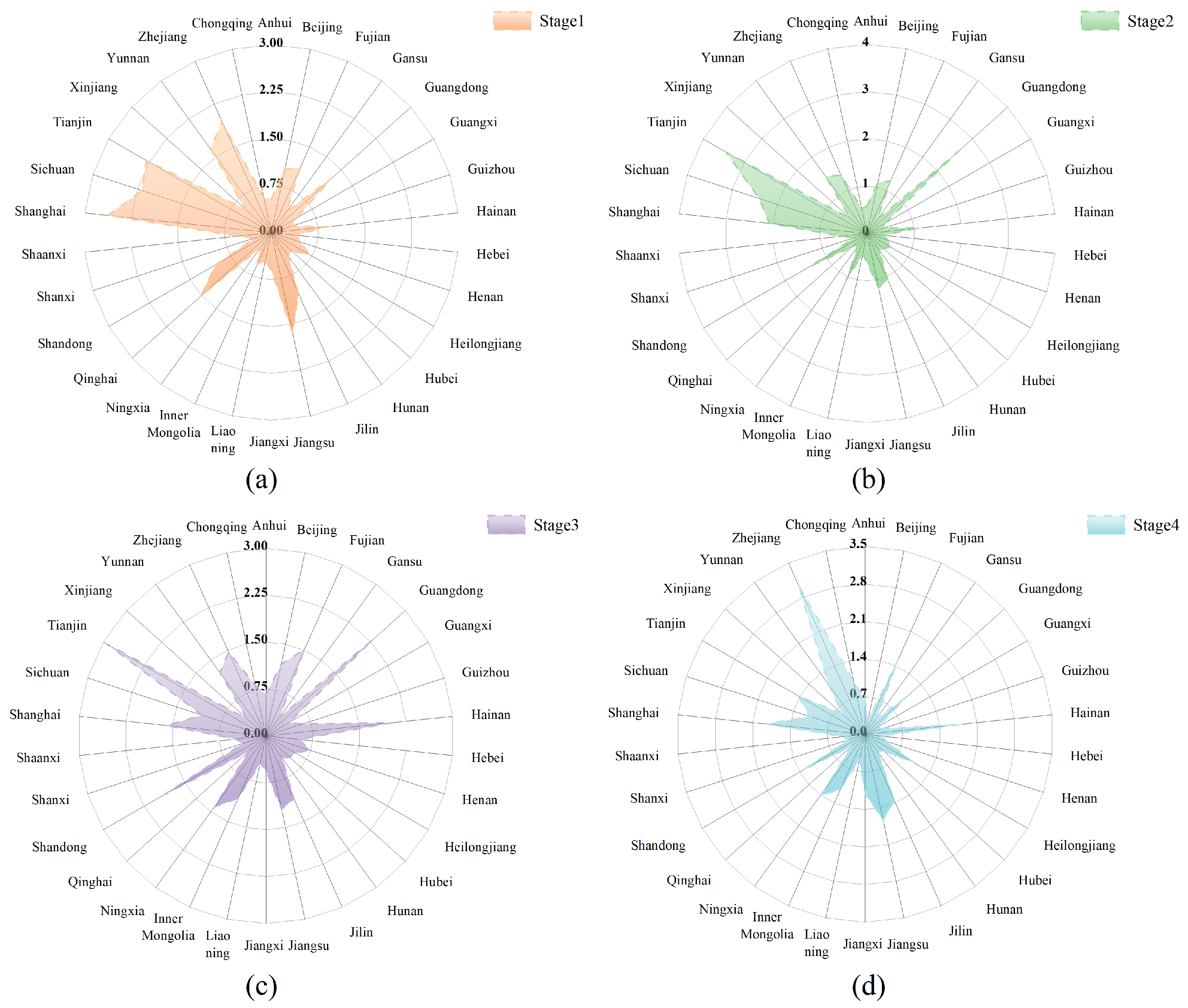
3.1. Static Changes in Forest Carbon Sink Efficiency (The First Sub-Model)
3.2. Dynamic Changes in Forest Carbon Sink Efficiency (The Second Sub-Model)
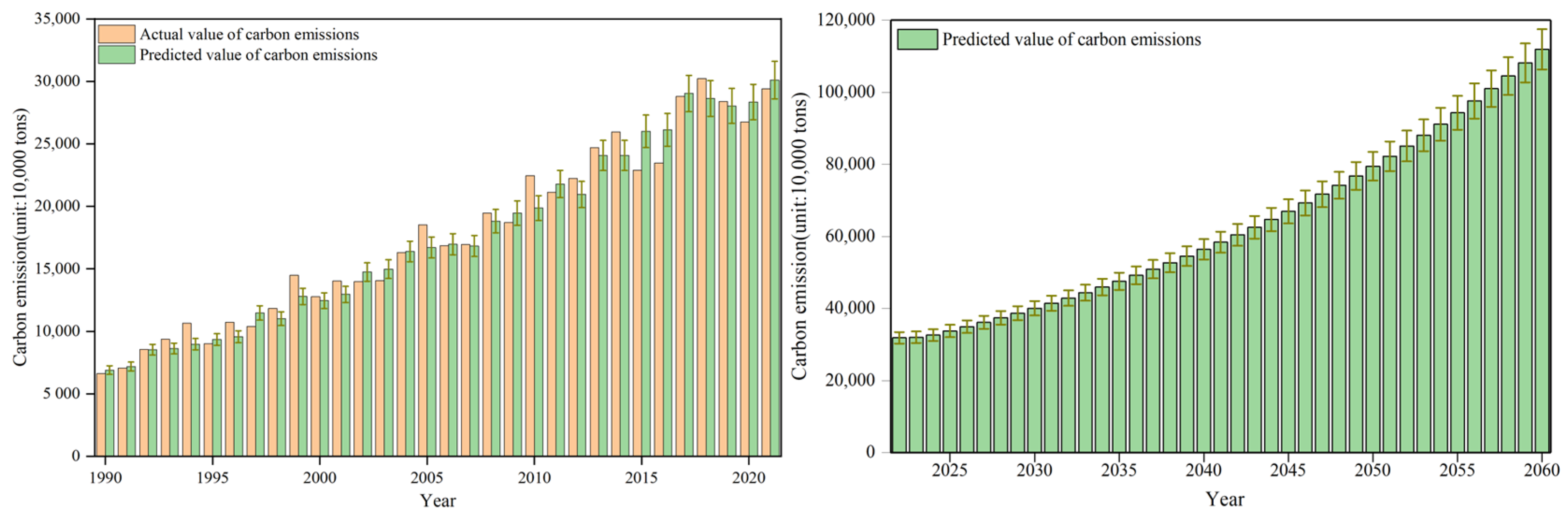
3.3. Forest Carbon Sink Autoregressive Integrated Moving Average Forecasts (The Third Sub-Model)
3.4. Resource Allocation Optimization of Forest Carbon Sink (The Fourth Sub-Model)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARIMA | Autoregressive Integrated Moving Average |
| ARMA | Autoregressive Moving Average |
| BCC | Banker–Charnes–Cooper |
| CCR | Charnes–Cooper–Rhodes |
| CCUS | Carbon Capture Utilization and Storage |
| CRS | Constant Return to Scale |
| DEA | Data Envelopment Analysis |
| DMUs | Decision-Making Units |
| EC | Efficiency Change |
| FCS | Forest Carbon Sink |
| FCSE | Forest Carbon Sink Efficiency |
| MI | Malmquist Index |
| SBM | Slacks-Based Measure |
| SFA | Stochastic Frontier Analysis |
| Super SBM | Super-efficiency SBM |
| TC | Technological change |
| TFP | Total Factor Productivity |
References
- Johnson, N.C.; Xie, S.-P.; Kosaka, Y.; Li, X. Increasing occurrence of cold and warm extremes during the recent global warming slowdown. Nat. Commun. 2018, 9, 1724. [Google Scholar] [CrossRef] [PubMed]
- Hoehne, N.; Gidden, M.J.; den Elzen, M.; Hans, F.; Fyson, C.; Geiges, A.; Jeffery, M.L.; Gonzales-Zuniga, S.; Mooldijk, S.; Hare, W.; et al. Wave of net zero emission targets opens window to meeting the Paris Agreement. Nat. Clim. Change 2021, 11, 820–822. [Google Scholar] [CrossRef]
- Makkonen, M.; Huttunen, S.; Primmer, E.; Repo, A.; Hilden, M. Policy coherence in climate change mitigation: An ecosystem service approach to forests as carbon sinks and bioenergy sources. For. Policy Econ. 2015, 50, 153–162. [Google Scholar] [CrossRef]
- Sporcic, M.; Landekic, M.; Lovric, M.; Martinic, I. Planning and Decision Making Models in Forestry. Croat. J. For. Eng. 2011, 32, 443–456. [Google Scholar]
- Zhao, N.; Wang, K.; Yuan, Y. Toward the carbon neutrality: Forest carbon sinks and its spatial spillover effect in China. Ecol. Econ. 2023, 209, 107837. [Google Scholar] [CrossRef]
- Salman, M.; Long, X.; Wang, G.; Zha, D. Paris climate agreement and global environmental efficiency: New evidence from fuzzy regression discontinuity design. Energy Policy 2022, 168, 113128. [Google Scholar] [CrossRef]
- Jiang, K.; Ashworth, P.; Zhang, S.; Liang, X.; Sun, Y.; Angus, D. China’s carbon capture, utilization and storage (CCUS) policy: A critical review. Renew. Sustain. Energy Rev. 2020, 119, 109601. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, L.; Wang, W.; Ma, W. Assessment of carbon emission and carbon sink capacity of China’s marine fishery under carbon neutrality target. J. Mar. Sci. Eng. 2022, 10, 1179. [Google Scholar] [CrossRef]
- Li, L.; Hao, T.; Chi, T. Evaluation on China’s forestry resources efficiency based on big data. J. Clean. Prod. 2017, 142, 513–523. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Yang, G.-l. A survey and analysis of the first 40 years of scholarly literature in DEA: 1978–2016. Socio-Econ. Plan. Sci. 2018, 61, 4–8. [Google Scholar] [CrossRef]
- Wang, Y.; Chao, X.; Ku, Y.; Ren, Q.; Wu, P. A DEA-based model for grouped internal carbon pricing: An analysis of a large coal producer. Environ. Impact Assess. Rev. 2024, 104, 107358. [Google Scholar] [CrossRef]
- Omrani, H.; Emrouznejad, A.; Teplova, T.; Amini, M. Efficiency evaluation of electricity distribution companies: Integrating data envelopment analysis and machine learning for a holistic analysis. Eng. Appl. Artif. Intell. 2024, 133, 108636. [Google Scholar] [CrossRef]
- Xu, W.; Bai, J.; Bao, Q. An empirical study on the extremely influential factors of technical efficiency of forestry production in Inner Mongolia: Based on stochastic frontier production function. For. Econ. 2017, 12, 89–94. [Google Scholar] [CrossRef]
- Strange, N.; Bogetoft, P.; Aalmo, G.O.; Talbot, B.; Holt, A.H.; Astrup, R. Applications of DEA and SFA in benchmarking studies in forestry: State-of-the-art and future directions. Int. J. For. Eng. 2021, 32, 87–96. [Google Scholar] [CrossRef]
- Chen, X.; Liu, X.; Wu, Q.; Deveci, M.; Martinez, L. Measuring technological innovation efficiency using interval type-2 fuzzy super-efficiency slack-based measure approach. Eng. Appl. Artif. Intell. 2022, 116, 105405. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, T.; Zhang, X. Environmental assessment and investment strategies of provincial industrial sector in China—Analysis based on DEA model. Environ. Impact Assess. Rev. 2016, 60, 156–168. [Google Scholar] [CrossRef]
- Zhang, J.; Ouyang, Y.; Ballesteros-Perez, P.; Li, H.; Philbin, S.P.; Li, Z.; Skitmore, M. Understanding the impact of environmental regulations on green technology innovation efficiency in the construction industry. Sustain. Cities Soc. 2021, 65, 102647. [Google Scholar] [CrossRef]
- Li, W.; Ji, Z.; Dong, F. Global renewable energy power generation efficiency evaluation and influencing factors analysis. Sustain. Prod. Consum. 2022, 33, 438–453. [Google Scholar] [CrossRef]
- Meng, F.; Su, B.; Thomson, E.; Zhou, D.; Zhou, P. Measuring China’s regional energy and carbon emission efficiency with DEA models: A survey. Appl. Energy 2016, 183, 1–21. [Google Scholar] [CrossRef]
- Sharifishourabi, M.; Dincer, I.; Mohany, A. Advancing energy transition with novel biomass-solar based multigeneration energy system using hydrogen and storage options for sustainable cities. Sustain. Cities Soc. 2024, 108, 105457. [Google Scholar] [CrossRef]
- Chen, Y.; Bouferguene, A.; Shen, Y.; Al-Hussein, M. Assessing accessibility-based service effectiveness (ABSEV) and social equity for urban bus transit: A sustainability perspective. Sustain. Cities Soc. 2019, 44, 499–510. [Google Scholar] [CrossRef]
- He, F.; Zhang, Q.; Lei, J.; Fu, W.; Xu, X. Energy efficiency and productivity change of China’s iron and steel industry: Accounting for undesirable outputs. Energy Policy 2013, 54, 204–213. [Google Scholar] [CrossRef]
- Fan, M.; Shao, S.; Yang, L. Combining global Malmquist-Luenberger index and generalized method of moments to investigate industrial total factor CO2 emission performance: A case of Shanghai (China). Energy Policy 2015, 79, 189–201. [Google Scholar] [CrossRef]
- Gan, L.; Wan, X.; Ma, Y.; Lev, B. Efficiency evaluation for urban industrial metabolism through the methodologies of emergy analysis and dynamic network stochastic block model. Sustain. Cities Soc. 2023, 90, 104396. [Google Scholar] [CrossRef]
- Mosbah, E.; Zaibet, L.; Dharmapala, P.S. A new methodology to measure efficiencies of inputs (outputs) of decision making units in Data Envelopment Analysis with application to agriculture. Socio-Econ. Plan. Sci. 2020, 72, 100857. [Google Scholar] [CrossRef]
- Mardani, A.; Zavadskas, E.K.; Streimikiene, D.; Jusoh, A.; Khoshnoudi, M. A comprehensive review of data envelopment analysis (DEA) approach in energy efficiency. Renew. Sustain. Energy Rev. 2017, 70, 1298–1322. [Google Scholar] [CrossRef]
- Mohebali, S.; Maghsoudy, S.; Ardejani, F.D. Application of data envelopment analysis in environmental impact assessment of a coal washing plant: A new sustainable approach. Environ. Impact Assess. Rev. 2020, 83, 106389. [Google Scholar] [CrossRef]
- Pan, Y.; Song, Y.; Zhang, C.C.; Zhu, Q.; Wu, J. Semiconductor industry’s transformation path under circular economy: Evidence from micro-level efficiency evaluation. Comput. Ind. Eng. 2024, 189, 109934. [Google Scholar] [CrossRef]
- Wang, H.; Du, S.; Zhong, Y.; Liu, S.; Xu, T.; Zhao, Y.; He, W.; Xue, H.; He, Y.; Gao, X.; et al. Unveiling the impact mechanism of urban resilience on carbon dioxide emissions of the Pearl River Delta urban agglomeration in China. Environ. Impact Assess. Rev. 2024, 105, 107422. [Google Scholar] [CrossRef]
- Wei, J.; Shen, M. Analysis of the Efficiency of Forest Carbon Sinks and Its Influencing Factors-Evidence from China. Sustainability 2022, 14, 11155. [Google Scholar] [CrossRef]
- Lin, B.; Ge, J. Carbon sinks and output of China’s forestry sector: An ecological economic development perspective. Sci. Total Environ. 2019, 655, 1169–1180. [Google Scholar] [CrossRef] [PubMed]
- Vilkov, A.; Tian, G. Efficiency Evaluation of Forest Carbon Sinks: A Case Study of Russia. Forests 2024, 15, 649. [Google Scholar] [CrossRef]
- Chen, X.; Liu, X.; Gong, Z.; Xie, J. Three-stage super-efficiency DEA models based on the cooperative game and its application on the R&D green innovation of the Chinese high-tech industry. Comput. Ind. Eng. 2021, 156, 107234. [Google Scholar] [CrossRef]
- Cheng, Z.; He, J.; Liu, Y.; Zhang, Q.; Deng, Y. Exploring the spatial structure and impact factors of water use efficiency in China. Environ. Impact Assess. Rev. 2023, 103, 107258. [Google Scholar] [CrossRef]
- Zhang, R.; Ying, W.; Wu, K.; Sun, H. The impact of innovative human capital agglomeration on urban green development efficiency: Based on panel data of 278 Cities in China. Sustain. Cities Soc. 2024, 111, 105566. [Google Scholar] [CrossRef]
- Yang, Z.; Zhan, J.; Wang, C.; Liu, W.; Wang, H.; Bai, C. Spatial spillover effects of conversion of new and old driving forces on high-quality development: Evidence from 283 cities in China. Sustain. Cities Soc. 2024, 108, 105487. [Google Scholar] [CrossRef]
- Yin, S.; Gong, Z.; Gu, L.; Deng, Y.; Niu, Y. Driving forces of the efficiency of forest carbon sequestration production: Spatial panel data from the national forest inventory in China. J. Clean. Prod. 2022, 330, 129776. [Google Scholar] [CrossRef]
- Liu, X.; Huang, J.; Zhou, H.; Sun, J.; Wang, Q.; Cheng, X. Dynamic Analysis of Provincial Forest Carbon Storage Efficiency in China Based on DEA Malmquist Index. Forests 2023, 14, 1629. [Google Scholar] [CrossRef]
- Yang, H.; Wang, X.; Bin, P. Agriculture carbon-emission reduction and changing factors behind agricultural eco-efficiency growth in China. J. Clean. Prod. 2022, 334, 130193. [Google Scholar] [CrossRef]
- Shen, N.; Liao, H.; Deng, R.; Wang, Q. Different types of environmental regulations and the heterogeneous influence on the environmental total factor productivity: Empirical analysis of China’s industry. J. Clean. Prod. 2019, 211, 171–184. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Amin, G.R.; Ghiyasi, M.; Michali, M. A review of inverse data envelopment analysis: Origins, development and future directions. Ima J. Manag. Math. 2023, 34, 421–440. [Google Scholar] [CrossRef]
- He, X.; Chen, L.; Huang, Y. A Study of Forest Carbon Sink Increment from the Perspective of Efficiency Evaluation Based on an Inverse DEA Model. Forests 2022, 13, 1563. [Google Scholar] [CrossRef]
- Lu, J.; Li, M.; Shen, Z. A new inverse DEA model with frontier changes for analyzing the achievement path of CO2 emissions target of China in 2030. J. Clean. Prod. 2022, 375, 134014. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Yang, G.-l.; Amin, G.R. A novel inverse DEA model with application to allocate the CO2 emissions quota to different regions in Chinese manufacturing industries. J. Oper. Res. Soc. 2019, 70, 1079–1090. [Google Scholar] [CrossRef]
- Wang, J.; Shi, K.; Hu, M. Measurement of Forest Carbon Sink Efficiency and Its Influencing Factors Empirical Evidence from China. Forests 2022, 13, 1909. [Google Scholar] [CrossRef]
- Chen, H.; Ma, Z.; Xiao, H.; Li, J.; Chen, W. The Impact of Digital Economy Empowerment on Green Total Factor Productivity in Forestry. Forests 2023, 14, 1729. [Google Scholar] [CrossRef]
- Xu, C.; Wang, B.; Chen, J. Forest carbon sink in China: Linked drivers and long short-term memory network-based prediction. J. Clean. Prod. 2022, 359, 132085. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Golany, B.; Seiford, L.; Stutz, J. Foundations of data envelopment analysis for Pareto-Koopmans efficient empirical production functions. J. Econom. 1985, 30, 91–107. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Du, J.; Liang, L.; Zhu, J. A slacks-based measure of super-efficiency in data envelopment analysis: A comment. Eur. J. Oper. Res. 2010, 204, 694–697. [Google Scholar] [CrossRef]
- Caves, D.W.; Christensen, L.R.; Diewert, W.E. The economic theory of index numbers and the measurement of input, output, and productivity. Econom. J. Econom. Soc. 1982, 50, 1393–1414. [Google Scholar] [CrossRef]
- Yunus, K.; Thiringer, T.; Chen, P. ARIMA-based frequency-decomposed modeling of wind speed time series. IEEE Trans. Power Syst. 2015, 31, 2546–2556. [Google Scholar] [CrossRef]
- Li, G.; Lu, J.; Chen, K.; Yang, H. A new hybrid prediction model of COVID-19 daily new case data. Eng. Appl. Artif. Intell. 2023, 125, 106692. [Google Scholar] [CrossRef] [PubMed]
- Shao, P.; Wang, H.; Long, G.; Liao, J.; Gan, F.; Xu, B.; Hu, K.; Teng, Y. A novel multi-step ahead prediction method for landslide displacement based on autoregressive integrated moving average and intelligent algorithm. Eng. Appl. Artif. Intell. 2024, 137, 109107. [Google Scholar] [CrossRef]
- Gao, F.; Shao, X. Electricity consumption prediction based on a dynamic decomposition-denoising-ensemble approach. Eng. Appl. Artif. Intell. 2024, 133, 108521. [Google Scholar] [CrossRef]
- Lertworasirikul, S.; Charnsethikul, P.; Fang, S.-C. Inverse data envelopment analysis model to preserve relative efficiency values: The case of variable returns to scale. Comput. Ind. Eng. 2011, 61, 1017–1023. [Google Scholar] [CrossRef]
- Ghiyasi, M.; Soltanifar, M.; Sharafi, H. A novel inverse DEA-R model with application in hospital efficiency. Socio-Econ. Plan. Sci. 2022, 84, 101427. [Google Scholar] [CrossRef]



| Forest Carbon Sink Efficiency Indicators | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Practitioners of the forestry system at the end of the year | √ | √ | √ | √ | √ | √ |
| Completion of fixed investment in forestry | √ | √ | √ | |||
| Forest area | √ | √ | √ | √ | √ | |
| Energy consumption | √ | |||||
| Forestry investment completion | √ | √ | √ | |||
| Afforestation area | √ |
| System | Subsystem | Ind icators | Unit | |
|---|---|---|---|---|
| Input | Labor input | Year-end forestry system practitioners | Number of state-owned economic units | People |
| Collective economic units | People | |||
| Other economic units | People | |||
| Capital investment | The amount of investment in forestry fixed assets | Investment in fixed assets in forestry | 10,000 a | |
| Forest industry fixed asset investment | 10,000 a | |||
| Land input | Forest area | Forest area | 10,000 ha | |
| Energy consumption | Energy consumption | Energy consumption | 10,000 tons | |
| Output | FCS | FCS | FCS | Megaton |
| Forestry production value | Forestry production value | Forestry production value | 10,000 a |
| Parameter | Value |
|---|---|
| BCEF (The biomass expansion factor) | 1.35 |
| D (The basic density of wood) | 0.441 |
| R (The ratio of below-ground biomass to above-ground biomass) | 0.404 |
| RDW (The dead-to-live ratio of dry weight of dead wood to live biomass) | 0.1727 |
| CF (The carbon fraction of dry matter) | 0.47 |
| Predictive Models | Advantages and Disadvantages Analysis | |
|---|---|---|
| Advantages | Disadvantages | |
| ARIMA | Simple structure, only time series data needed. | Requires stationary data, limited in capturing nonlinear relationships, sensitive to parameter selection. |
| Long Short-Term Memory | Handles long sequences, captures long-term dependencies, suitable for complex nonlinear problems. | Complex structure, high training costs, prone to overfitting, especially with small samples. |
| Stochastic Impacts by Regression on Population, Affluence, and Technology | Integrates various socio-economic factors, offers flexible and comprehensive carbon emission forecasts. | Requires substantial data input, sensitive to parameter selection and model configuration. |
| Grey Prediction Model | Provides reasonable forecasts when data is scarce, straightforward model construction. | Predictive accuracy is constrained, may fail to provide precise forecasts for complex systems. |
| Bayesian Optimization Support Vector Machine | Efficiently discovers optimal solutions in high-dimensional parameter spaces, enhancing prediction accuracy. | Entails potentially onerous computational demands, necessitates robust prior knowledge. |
| Region | Stage 1 | Stage 2 | Stage 3 | Stage 4 | Average |
|---|---|---|---|---|---|
| Anhui | 0.5333 | 0.5855 | 0.6578 | 0.6449 | 0.6054 |
| Beijing | 1.0377 | 1.1079 | 1.1746 | 0.2658 | 0.8965 |
| Fujian | 1.1283 | 1.2166 | 1.5137 | 1.5231 | 1.3454 |
| Gansu | 0.4131 | 0.3619 | 0.3704 | 0.3683 | 0.3784 |
| Guangdong | 1.3169 | 2.5852 | 2.3071 | 1.0177 | 1.8067 |
| Guangxi | 0.4598 | 0.4371 | 0.4252 | 0.3021 | 0.4061 |
| Guizhou | 0.3407 | 0.4072 | 0.6226 | 0.3298 | 0.4251 |
| Hainan | 0.8816 | 1.1175 | 2.0371 | 1.8042 | 1.4601 |
| Hebei | 0.4020 | 0.3439 | 0.5364 | 0.3059 | 0.3970 |
| Henan | 0.4954 | 0.4801 | 0.7446 | 0.4346 | 0.5387 |
| Heilongjiang | 0.6999 | 0.5667 | 0.5439 | 1.0649 | 0.7188 |
| Hubei | 0.4432 | 0.4710 | 0.5122 | 0.4672 | 0.4734 |
| Hunan | 0.4549 | 0.4451 | 0.4339 | 0.4215 | 0.4388 |
| Jilin | 1.0652 | 1.0753 | 1.1029 | 1.3516 | 1.1487 |
| Jiangsu | 1.6421 | 1.1754 | 1.1964 | 1.6308 | 1.4112 |
| Jiangxi | 0.5980 | 0.6143 | 0.5537 | 1.1013 | 0.7168 |
| Liaoning | 0.4711 | 0.4542 | 0.4402 | 0.4664 | 0.4580 |
| Inner Mongolia | 0.5586 | 1.0800 | 1.0905 | 1.1279 | 0.9643 |
| Ningxia | 0.2972 | 0.3371 | 1.4076 | 1.4060 | 0.8620 |
| Qinghai | 1.5197 | 0.4189 | 0.3690 | 0.3336 | 0.6603 |
| Shandong | 1.0283 | 1.4132 | 1.8714 | 1.3499 | 1.4157 |
| Shanxi | 0.2724 | 0.2718 | 0.3806 | 0.3325 | 0.3143 |
| Shaanxi | 0.5382 | 0.5509 | 0.4837 | 0.4054 | 0.4946 |
| Shanghai | 2.6294 | 2.0805 | 1.6029 | 1.8648 | 2.0444 |
| Sichuan | 2.1772 | 2.4009 | 1.0743 | 1.0764 | 1.6822 |
| Tianjin | 2.3033 | 3.4508 | 2.9372 | 1.4411 | 2.5331 |
| Xinjiang | 0.5530 | 0.4856 | 0.4066 | 0.5709 | 0.5040 |
| Yunnan | 1.6523 | 1.4940 | 1.2520 | 1.1521 | 1.3876 |
| Zhejiang | 1.9336 | 1.3565 | 1.4735 | 3.0542 | 1.9545 |
| Chongqing | 0.5718 | 0.5409 | 0.8246 | 1.0048 | 0.7355 |
| Average | 0.9473 | 0.9775 | 1.0116 | 0.9540 | 0.9726 |
| Variable | Coefficient | Std.Error | t-Statistic | Prob. |
|---|---|---|---|---|
| AR (1) | 1.034845 | 0.006899 | 150.0030 | 0.0000 |
| MA (1) | −0.847588 | 0.127717 | −6.636429 | 0.0000 |
| MA (2) | −0.354779 | 0.196677 | −1.803868 | 0.0824 |
| MA (3) | 0.743020 | 0.122086 | 6.086012 | 0.0000 |
| R-squared | 0.964478 | Akaike info criterion | 17.42131 | |
| Adjusted R-squared | 0.960531 | Schwarz criterion | 17.60634 | |
| Hannan–Quinn criterion | 17.48162 | |||
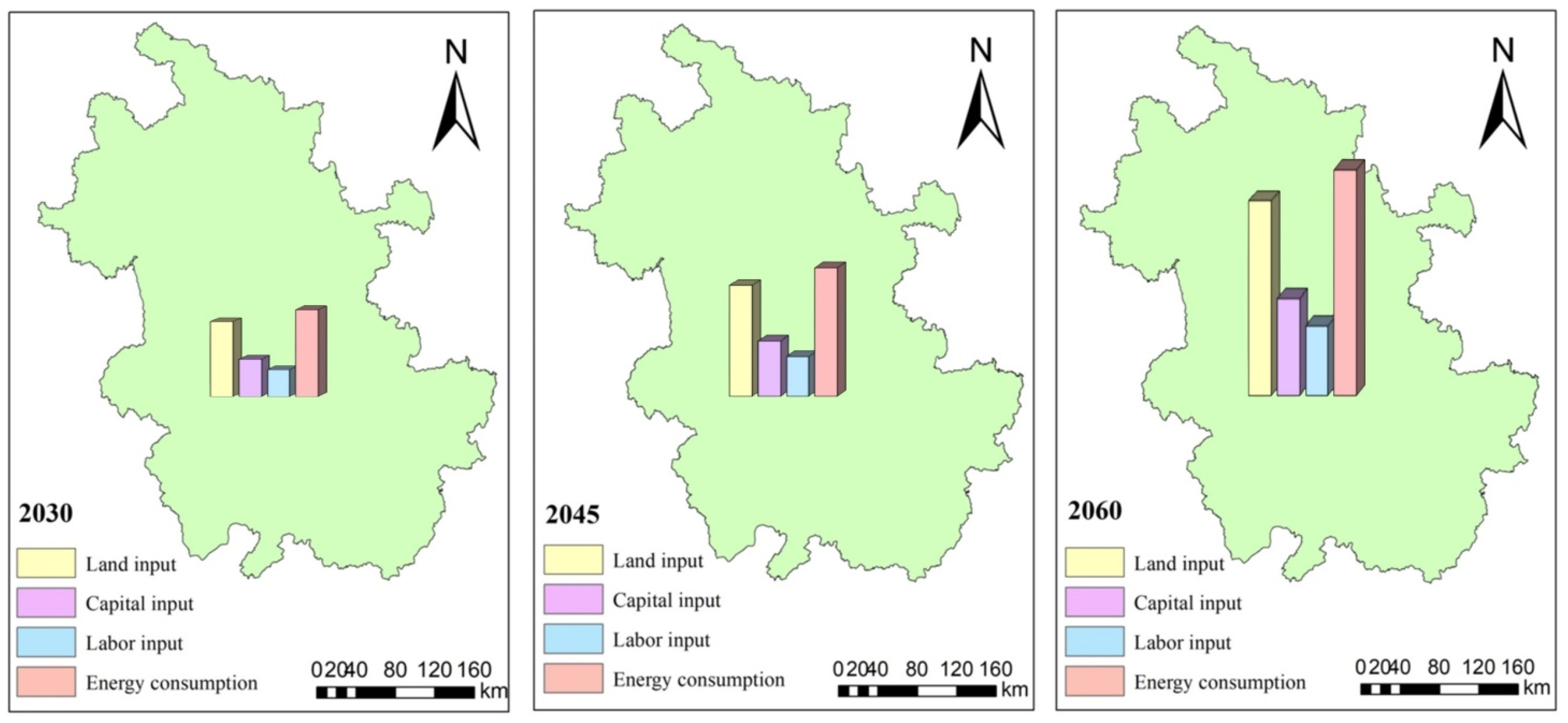
| Year | Forest Area | The Amount of Fixed Investment in Forestry | The Year-End Forestry System Practitioners | Energy Consumption |
|---|---|---|---|---|
| 2030 | 613.850868 | 306,959.5456 | 21,923.83597 | 7,127,768.39 |
| 2045 | 952.981633 | 476,543.7735 | 34,035.97534 | 11,065,606.83 |
| 2060 | 1592.99633 | 796,586.6872 | 56,894.25893 | 18,497,178.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Ran, J.; Ren, J.; Wang, Y.; Xu, Z.; Liu, D.; Yang, C. Intelligence Approach-Driven Bidirectional Analysis Framework for Efficiency Measurement and Resource Optimization of Forest Carbon Sink in China. Forests 2025, 16, 656. https://doi.org/10.3390/f16040656
Zhou J, Ran J, Ren J, Wang Y, Xu Z, Liu D, Yang C. Intelligence Approach-Driven Bidirectional Analysis Framework for Efficiency Measurement and Resource Optimization of Forest Carbon Sink in China. Forests. 2025; 16(4):656. https://doi.org/10.3390/f16040656
Chicago/Turabian StyleZhou, Jianli, Jia Ran, Jiayi Ren, Yaqi Wang, Zihan Xu, Dandan Liu, and Cheng Yang. 2025. "Intelligence Approach-Driven Bidirectional Analysis Framework for Efficiency Measurement and Resource Optimization of Forest Carbon Sink in China" Forests 16, no. 4: 656. https://doi.org/10.3390/f16040656
APA StyleZhou, J., Ran, J., Ren, J., Wang, Y., Xu, Z., Liu, D., & Yang, C. (2025). Intelligence Approach-Driven Bidirectional Analysis Framework for Efficiency Measurement and Resource Optimization of Forest Carbon Sink in China. Forests, 16(4), 656. https://doi.org/10.3390/f16040656







