Hyperspectral Remote Sensing Estimation and Spatial Scale Effect of Leaf Area Index in Moso Bamboo (Phyllostachys pubescens) Forests Under the Stress of Pantana phyllostachysae Chao
Abstract
1. Introduction
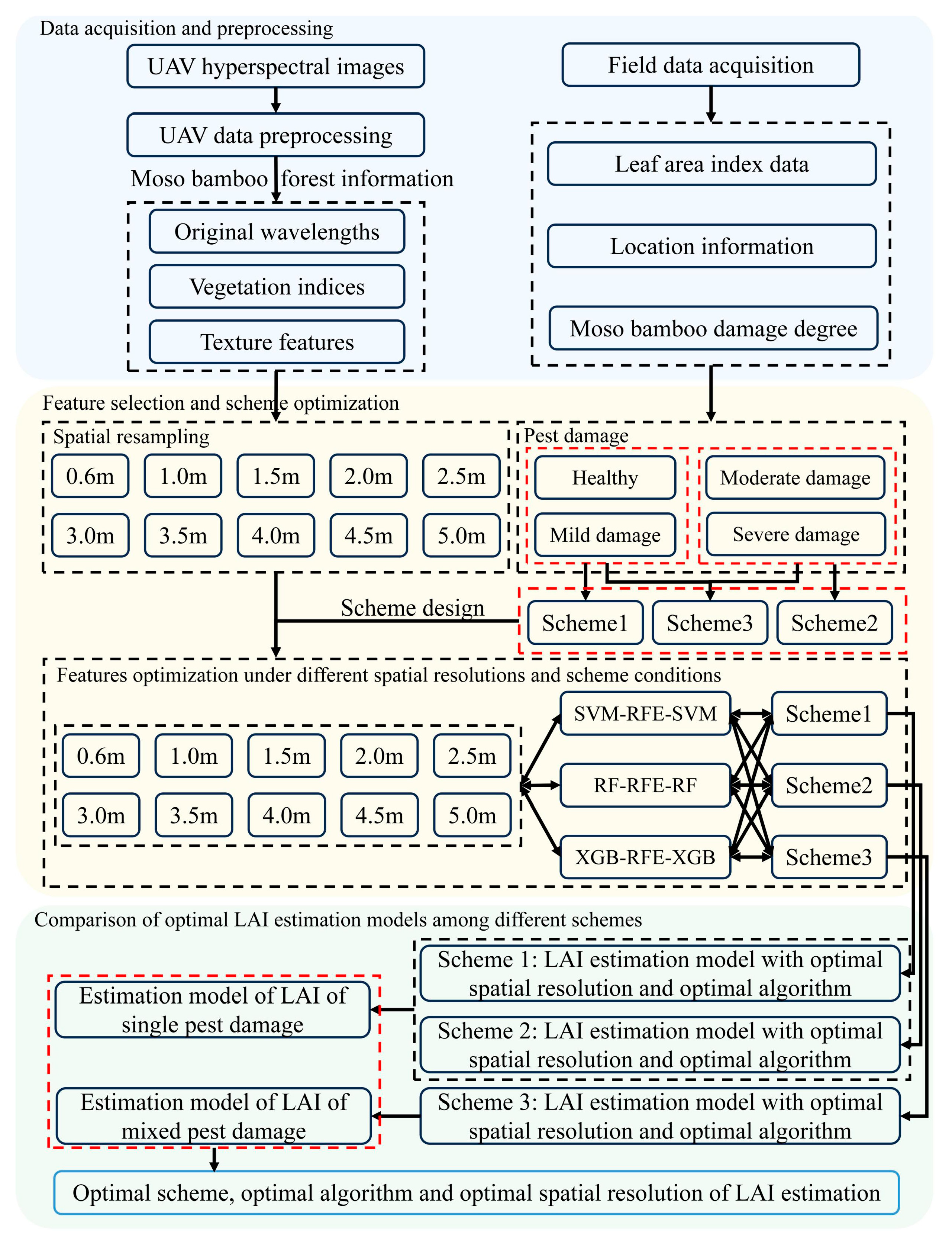
2. Materials and Methods
2.1. Study Area
2.2. Datasets and Preprocessing
2.2.1. Field Measured Point Data
2.2.2. Hyperspectral Image Acquisition and Processing of Moso Bamboo Forest Information
- (1)
- Multi-resolution remote sensing images: Considering the size of the bamboo canopy, a spatial scale that is too small may not cover the entire canopy, whereas one that is too large may include other objects. Therefore, a spatial scale interval of 0.5 m was chosen for resampling the hyperspectral data. The range of 0.6 to 5.0 m effectively addresses these concerns. Thus, in this study, the acquired 0.3 × 0.3 m UAV hyperspectral images were resampled into ten low spatial resolution images with resolutions of 0.6 m, 1 m, 1.5 m, 2 m, 2.5 m, 3 m, 3.5 m, 4 m, 4.5 m, and 5 m to investigate the effects of images with different spatial resolutions on LAI inversion. The resampling process utilized bilinear interpolation, calculating the value of each pixel by averaging the values of surrounding pixels.
- (2)
- Red edge parameter: This parameter serves as an indicator of plant health and is commonly used for detecting diseases and insect infestations in forests. The red edge index calculation formula selected for this study is provided in the following table (Table 2).
- (3)
- Spectral indices: There are numerous types of vegetation indices, and the infestation of P. phyllostachysae in bamboo stands exhibits a strong correlation with leaf water content and chlorophyll levels. Based on a review of previous studies, we selected the following vegetation indices to characterize the infestation (Table 2).
- (4)
- Texture features: Texture features are another category of indicators considered in remote sensing models, as they can reveal the spatial relationships between pixels and between individual pixels and the entire image. However, due to the large number of spectral bands in hyperspectral imagery, extracting texture features directly from the original hyperspectral bands is impractical and requires a significant amount of work. Therefore, dimensionality reduction is necessary. In this study, principal component analysis (PCA) was performed on raw hyperspectral images using ENVI 5.3 software to achieve dimensionality reduction. Following PCA processing, texture feature was extracted by calculating eight GLCM (Gray-Level Co-occurrence Matrix) parameters from the first principal component through the analytical modules of ENVI. The extracted texture features included mean, variance, homogeneity, contrast, dissimilarity, entropy, second moment, and correlation. The calculation formulas for the texture features selected are presented in Table 3.
- (5)
- Feature and model selection and optimization: Using SVM, RF, and XGBoost combined with the RFE algorithm, corresponding features were selected, and LAI estimation models were established for each scheme.
- (6)
- Model comparison across different schemes: By comparing the performance of the three schemes under different algorithms and spatial resolutions, the optimal estimation model for each scheme was selected. Additionally, the differences between the single pest level LAI estimation models (built from Scheme 1 and Scheme 2) and the mixed pest level LAI estimation model (built from Scheme 3) were analyzed.
2.3. Methods
2.3.1. Support Vector Machine
2.3.2. Random Forest
2.3.3. Extreme Gradient Boosting
2.3.4. Recursive Feature Elimination
2.3.5. Coefficient of Variation
3. Results
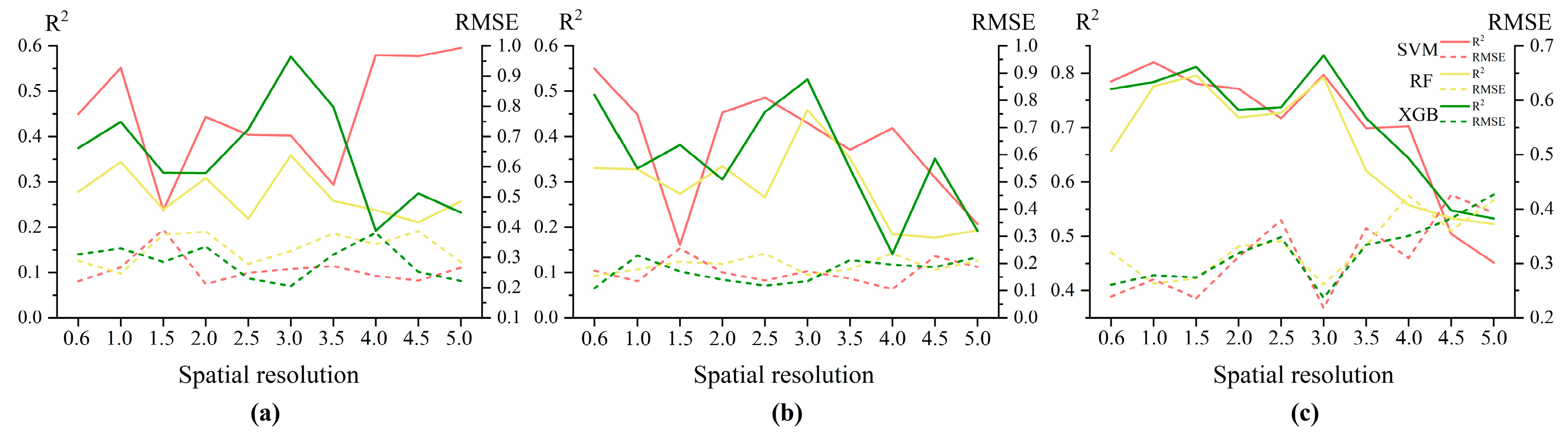
3.1. Comparison of Different Spatial Resolution Estimation Models
3.1.1. Comparison of Different Spatial Resolution Estimation Models Based on SVM Regression Algorithm
3.1.2. Comparison of Different Spatial Resolution Estimation Models Based on RF Regression Algorithm
3.1.3. Comparison of Different Spatial Resolution Estimation Models Based on XGBoost Regression Algorithm
3.1.4. Comparison of Different Algorithms Under the Optimal Spatial Resolution Estimation Model
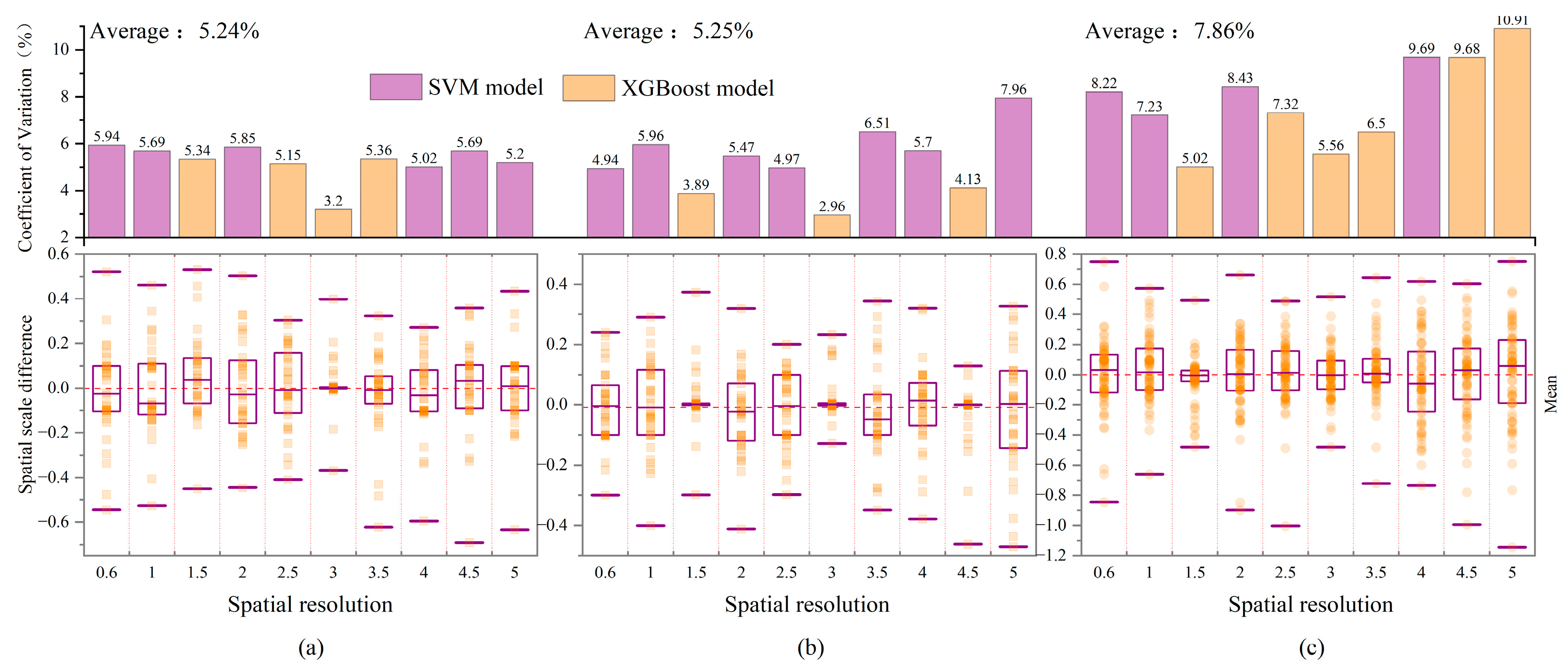
3.2. Spatial Scale Effect Difference of Leaf Area Index Under Different Schemes
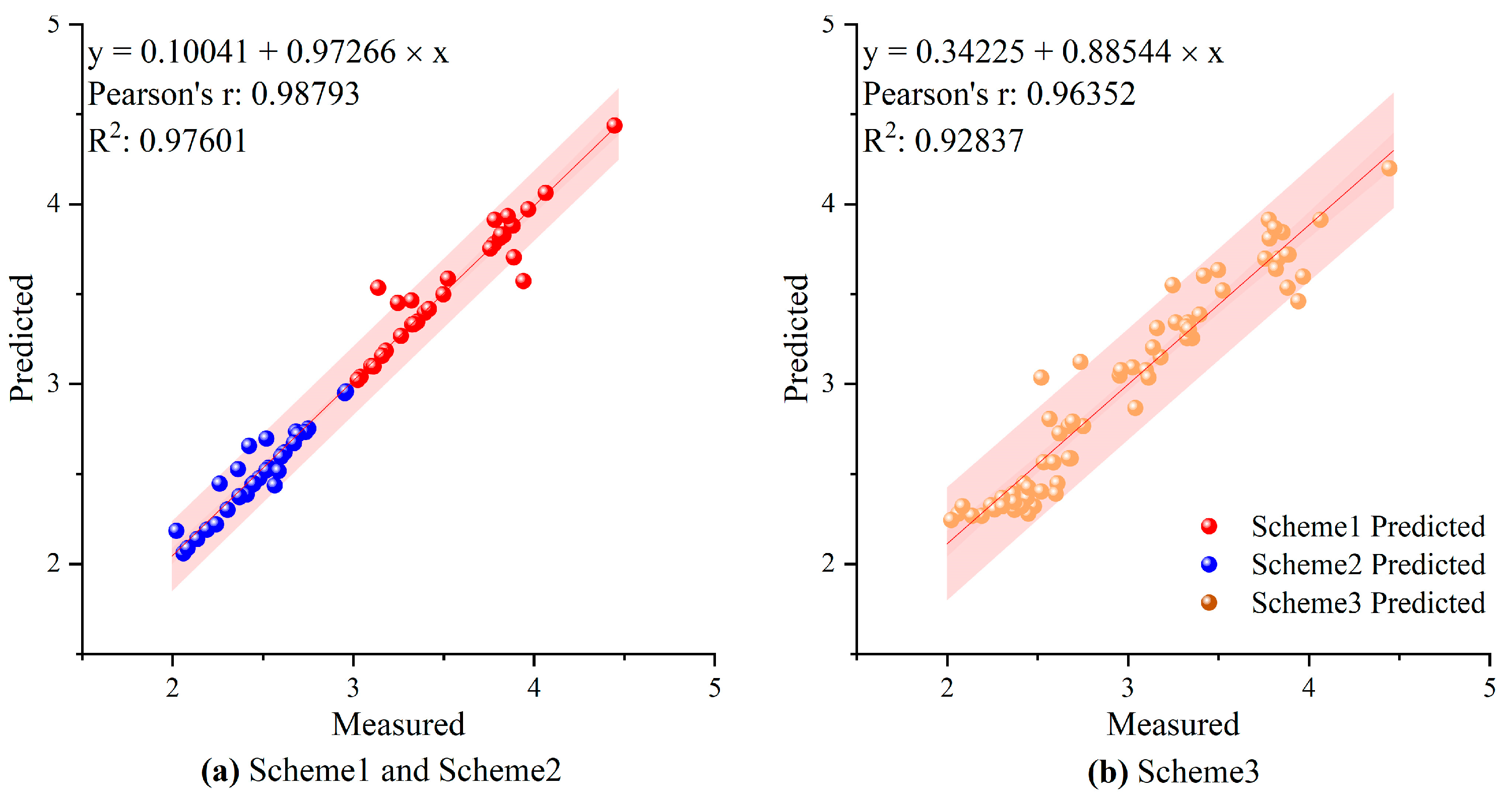
3.3. Remote Sensing Inversion of Leaf Area Index Using the Optimal Spatial Resolution and Algorithm
3.4. Comparison of Leaf Area Index Models Between Single Pest Damage Levels and Mixed Pest Damage Levels
4. Discussion
4.1. Effect of Bamboo Forest On-Year and Off-Year Phenomenon on Leaf Area Index
4.2. Applicability of Mixed Pest Damage Leaf Area Index Model and Single Pest Damage Model
4.3. Influencing Factors of Spatial Scale Efficiency of Leaf Area Index
5. Conclusions
- (1)
- By comparing the performance of LAI estimation models and analyzing spatial scale effects across different spatial resolutions, the combination of the XGBoost algorithm and a 3 m spatial resolution was identified as the optimal choice for the three schemes.
- (2)
- The coefficient of variation method further confirmed the XGBoost algorithm’s excellent LAI inversion capability and the accuracy of the 3 m spatial resolution for LAI estimation.
- (3)
- All three schemes show good inversion performance. Compared with the mixed pest-level LAI model, the single pest-level LAI model has higher estimation accuracy and a clear advantage in homogeneous pest-level regions of Moso bamboo forests.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Watson, D.J. Comparative physiological studies on the growth of field crops: I. Variation in net assimilation rate and leaf area between species and varieties, and within and between years. Ann. Bot. Bot. 1947, 11, 41–76. [Google Scholar]
- Wang, X.Q.; Ma, L.Y.; Jia, Z.K.; Xu, C.Y. Research and application advances in leaf area index (LAl). Chin. J. Ecol. 2005, 5, 537–541. [Google Scholar]
- Wu, W.B.; Hong, T.S.; Wang, X.P.; Peng, W.X.; Li, Z.; Zhang, W.Z. Advance in ground-based LAl measurement methods. J. Huazhong Agric. Univ. 2007, 2, 270–275. [Google Scholar]
- Yan, G.J.; Hu, R.H.; Luo, J.H.; Weiss, M.; Jiang, H.L.; Mu, X.H.; Xie, D.H.; Zhang, W.M. Review of indirect optical measurements of leaf area index: Recent advances, challenges, and perspectives. Agric. For. Meteorol. 2019, 265, 390–411. [Google Scholar]
- Ziliani, M.G.; Altaf, M.U.; Aragon, B.; Houborg, R.; Franz, T.E.; Lu, Y.; Sheffield, J.; Hoteit, I.; McCabe, M.F. Early season prediction of within-field crop yield variability by assimilating CubeSat data into a crop model. Agric. For. Meteorol. 2022, 313, 108736. [Google Scholar]
- Liu, S.B.; Jin, X.L.; Nie, C.W.; Wang, S.Y.; Yu, X.; Cheng, M.H.; Shao, M.C.; Wang, Z.X.; Tuohuti, N.; Bai, Y.; et al. Estimating leaf area index using unmanned aerial vehicle data: Shallow vs. deep machine learning algorithms. Plant Physiol. 2021, 187, 1551–1576. [Google Scholar]
- Huang, H.; Huang, J.; Wu, Y.; Zhuo, W.; Song, J.; Li, X.; Li, L.; Su, W.; Ma, H.; Liang, S. The improved winter wheat yield estimation by assimilating GLASS LAI Into a crop growth model with the proposed Bayesian Posterior-based ensemble kalman filter. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4401818. [Google Scholar]
- Wang, Y.L.; Wang, J.; Cui, T. Inversion of leaf area index of Silage Corn based on PROSAIL model. Trans. Chin. Soc. Agric. Eng. 2024, 55, 205–213. [Google Scholar]
- Chen, S.D.; Chen, Y.G.; Xu, X.J.; Liu, J.Y.; Guo, J.Z.; Hu, S.Y.; Lan, Y.B. Monitoring of corn leaf area index based on multispectral remote sensing of UAV. J. South China Agric. Univ. 2024, 45, 608–617. [Google Scholar]
- Li, C.H.; Li, B.Y.; Mao, Z.W.; Li, L.F.; Yu, K.Y.; Liu, J.; Zhong, Q.L. Canopy hyperspectral modeling of leaf area index at different expansion stages of Phyllostachys edulis into cunninghamia lanceolata forest. Spectrosc. Spectr. Anal. 2024, 44, 2365–2371. [Google Scholar]
- Bao, G.D.; Liu, T.; Zhang, Z.H.; Ren, Z.B.; Zhai, C.; Ding, M.M.; Jiang, X.F. Remote sensing inversion of effective leaf area index of four coniferous forest types and their spatial distribution rule in changbai mountain. Sci. Silvae Sin. 2024, 60, 127–138. [Google Scholar]
- Gu, C.Y.; Du, H.Q.; Zhou, G.M.; Han, N.; Xu, X.J.; Zhao, X.; Sun, X.Y. Retrieval of leaf area index of moso bamboo forest with Landsat Thematic Mapper image based on PROSAIL canopy radiative transfer model. J. Appl. Ecol. 2013, 24, 2248–2256. [Google Scholar]
- Yue, J.B.; Yang, H.; Yang, G.J.; Fu, Y.Y.; Wang, H.; Zhou, C.Q. Estimating vertically growing crop above-ground biomass based on UAV remote sensing. Comput. Electron. Agric. 2023, 205, 107627. [Google Scholar]
- Zhang, J.J.; Cheng, T.; Guo, W.; Xu, X.; Qiao, H.B.; Xie, Y.M.; Ma, X.M. Leaf area index estimation model for UAV image hyperspectral data based on wavelength variable selection and machine learning methods. Plant Methods 2021, 17, 49. [Google Scholar] [PubMed]
- Zhang, Y.; Yang, Y.; Zhang, Q.; Duan, R.; Liu, J.; Qin, Y.; Wang, X. Toward multi-stage phenotyping of soybean with multimodal UAV sensor data: A comparison of machine learning approaches for leaf area index estimation. Remote Sens. 2023, 15, 7. [Google Scholar]
- Xu, Z.H.; He, A.Q.; Zhang, Y.W.; Hao, Z.B.; Li, Y.F.; Xiang, S.Y.; Li, B.; Chen, L.Y.; Yu, H.; Shen, W.L.; et al. Retrieving chlorophyll content and equivalent water thickness of Moso bamboo (Phyllostachys pubescens) forests under Pantana phyllostachysae Chao-induced stress from Sentinel-2A/B images in a multiple LUTs-based PROSAIL framework. For. Ecosyst. 2023, 10, 100108. [Google Scholar]
- Xu, Z.H.; Zhang, C.F.; Xiang, S.Y.; Chen, L.Y.; Yu, X.E.; Li, H.T.; Li, Z.L.; Guo, X.Y.; Zhang, H.F.; Huang, X.Y.; et al. A hybrid method of PROSAIL RTM for the retrieval canopy LAI and chlorophyll content of Moso bamboo (Phyllostachys pubescens) forests from sentinel-2 MSI data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 3125–3143. [Google Scholar]
- Liu, X.Z.; Wu, L.; Chen, L.J.; Ma, Y.F.; Li, T.; Wu, T.T. LAI inversion and growth evaluation of winter wheat using semi-empirical and semi-mechanistic modeling. Trans. Chin. Soc. Agric. Eng. 2024, 40, 162–170. [Google Scholar]
- Zhang, Y.Y.; Han, X.; Yang, J. Estimation of leaf area index over heterogeneous regions using the vegetation type information and PROSAIL model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 5405–5415. [Google Scholar]
- Li, H.; Liu, G.H.; Liu, Q.S.; Chen, Z.X.; Huang, C. Retrieval of winter wheat leaf area index from Chinese GF-1 satellite data using the PROSAIL model. Sensors 2018, 18, 1120. [Google Scholar] [CrossRef]
- Hasan, U.; Sawut, M.; Chen, S. Estimating the leaf area index of winter wheat based on unmanned aerial vehicle RGB-image parameters. Sustainability 2019, 11, 1120. [Google Scholar] [CrossRef]
- Fang, H.; Man, W.D.; Liu, M.Y.; Zhang, Y.B.; Chen, X.T.; Li, X.; He, J.N.; Tian, D. Leaf area index inversion of Spartina alterniflora using UAV hyperspectral data based on multiple optimized machine learning algorithms. Remote Sens. 2023, 15, 4465. [Google Scholar] [CrossRef]
- Wang, Q.; Lu, X.H.; Zhang, H.N.; Yang, B.C.; Gong, R.X.; Zhang, J.; Jin, Z.N.; Xie, R.X.; Xia, J.W.; Zhao, J.M. Comparison of machine learning methods for estimating leaf area index and aboveground biomass of Cinnamomum camphora based on UAV multispectral remote sensing data. Forests 2023, 14, 1688. [Google Scholar] [CrossRef]
- Liu, Z.; Jin, G.; Zhou, M. Evaluation and correction of optically derived leaf area index in different temperate forests. Iforest-Biogeosci. For. 2016, 9, 55–62. [Google Scholar] [CrossRef]
- Liu, Z.; Jin, G. Improving accuracy of optical methods in estimating leaf area index through empirical regression models in multiple forest types. Trees-Struct. Funct. 2016, 30, 2101–2115. [Google Scholar] [CrossRef]
- Fu, B.L.; Sun, J.; Li, Y.Y.; Zuo, P.P.; Deng, T.F.; He, H.C.; Fan, D.L.; Gao, E.T. Mangrove LAI estimation based on remote sensing images and machine learning algorithms. Trans. Chin. Soc. Agric. Eng. 2022, 38, 218–228. [Google Scholar]
- Kamal, M.; Phinn, S.; Johansen, K. Assessment of multi-resolution image data for mangrove leaf area index mapping. Remote Sens. Environ. 2016, 176, 242–254. [Google Scholar] [CrossRef]
- Revill, A.; Florence, A.; MacArthur, A.; Hoad, S.; Rees, R.; Williams, M. Quantifying uncertainty and bridging the scaling gap in the retrieval of leaf area index by coupling sentinel-2 and UAV observations. Remote Sens. 2020, 12, 1843. [Google Scholar] [CrossRef]
- Williams, M.; Bell, R.; Spadavecchia, L.; Street, L.E.; Van Wijk, M.T. Upscaling leaf area index in an Arctic landscape through multiscale observations. Glob. Change Biol. 2008, 14, 1517–1530. [Google Scholar]
- Fan, W.J.; Gai, Y.Y.; Xu, X.R.; Yan, B.Y. The spatial scaling effect of the discrete-canopy effective leaf area index retrieved by remote sensing. Sci. China-Earth Sci. 2013, 56, 1548–1554. [Google Scholar] [CrossRef]
- Wu, L.; Liu, X.N.; Zheng, X.P.; Qin, Q.M.; Ren, H.Z.; Sun, Y.J. Spatial scaling transformation modeling based on fractal theory for the leaf area index retrieved from remote sensing imagery. J. Appl. Remote Sens. 2015, 9, 096015. [Google Scholar]
- He, A.Q.; Xu, Z.H.; Zhang, H.B.; Zhou, X.; Li, G.T.; Zhang, H.F.; Li, B.; Li, Y.F.; Guo, X.Y.; Li, Z.L.; et al. Simulation of Pantana phyllostachysae Chao hazard spread in Moso bamboo (Phyllostachys pubescens) forests based on XGBoost-CA model. IEEE Trans. Geosci. Remote Sens. 2025, 63, 4401616. [Google Scholar]
- Li, Y.F.; Xu, Z.H.; Hao, Z.B.; Yao, X.; Zhang, Q.; Huang, X.Y.; Li, B.; He, A.Q.; Li, Z.L.; Guo, X.Y. A comparative study of the performances of joint RFE with machine learning algorithms for extracting Moso bamboo (Phyllostachys pubescens) forest based on UAV hyperspectral images. Geocarto Int. 2023, 38, 2207550. [Google Scholar]
- He, A.Q.; Xu, Z.H.; Li, Y.F.; Li, B.; Huang, X.Y.; Zhang, H.F.; Guo, X.Y.; Li, Z.L. Monitoring Moso bamboo (Phyllostachys pubescens) forests damage caused by Pantana phyllostachysae Chao considering phenological differences between on-year and off-year using UAV hyperspectral images. Geo-Spat. Inf. Sci. 2025, 1–19. [Google Scholar] [CrossRef]
- LY/T 2011-2012; General Principles of Investigates on Main Forestry Pest. Standards Press of China: Beijing, China, 2012.
- Xie, Z.L.; Chen, Y.L.; Lu, D.S.; Li, G.Y.; Chen, E.X. Classification of land cover, forest, and tree species classes with ZiYuan-3 multispectral and stereo data. Remote Sens. 2019, 11, 164. [Google Scholar] [CrossRef]
- Rhodes, J.S.; Cutler, A.; Moon, K.R. Geometry- and Accuracy-Preserving Random Forest Proximities. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10947–10959. [Google Scholar]
- Shen, Y.D.; Liao, Z.W.; Tian, Y.C.; Tao, J.; Luo, J.X.; Wang, J.L.; Zhang, Q. Knowledge Assisted Differential Evolution Extreme Gradient Boost algorithm for estimating mangrove aboveground biomass. Appl. Soft Comput. 2025, 172, 112838. [Google Scholar] [CrossRef]
- Jeon, H.; Oh, S. Hybrid-recursive feature elimination for efficient feature selection. Appl. Sci. 2020, 10, 3211. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, G.; Zhu, J.; Ni, J. Scale-dependent spatial variation of species abundance and richness in two mixed evergreen-deciduous broad-leaved karst forests, Southwest China. Acta Ecol. Sin. 2012, 32, 5663–5672. [Google Scholar]
- Li, Y.H.; Lin, Z.Q.; Zhu, T.F.; Huang, Z.M.; Guo, X.; Su, J. Expression pattern of insect resistance related gene PhSPL17 in Phyllostachys heterocycle during on-and off-year. J. Fujian Agric. For. Univ. (Nat. Sci. Ed.) 2019, 48, 597–604. [Google Scholar]

| Parameter Name | Parameter Value |
|---|---|
| Spectral region | 400–1000 nm |
| Spectral resolution | 2.1 nm |
| Spectral sampling rate | 1.07 nm/5 nm |
| Carrying platform | RT650/DJI M600 Pro |
| Camera lens | 18.5 mm, 23 mm |
| Spectral channel number | 300 |
| Spatial resolution | 30 cm |
| Spectral Indices | Calculation Formula |
|---|---|
| Carotenoid Reflectance Index, CRI | |
| Enhanced Vegetation Index, EVI2 | |
| Gitelson-Merzlyak Index, GMI | |
| Modified Red Edge Normalized Vegetation Index 705, mNDVI705 | |
| Modified Red Edge Simple Ratio Index 705, mSR705 | |
| Normalized Difference Vegetation Index, NDVI | |
| Normalized Difference Vegetation Index 831, NDVI831 | |
| Red Edge Normalized Difference Vegetation Index 705, NDVI705 | |
| Normalized Pigment Chlorophyll Index, NPCI | |
| Photochemical Reflectance Index, PRI | |
| Red Edge Difference Vegetation Index, REDVI | |
| Red Edge Normalized Difference Vegetation Index, RENDVI | |
| Red Edge Ratio Index, RERVI | |
| Ratio Vegetation Index, RVI | |
| Soil-Adjusted Vegetation Index, SAVI | |
| Structure Insensitive Pigment Index, SIPI | |
| Simple Ratio Pigment Index, SRPI | |
| Transformed Chlorophyll Uptake Rate Index, TCARI | |
| Vogelmann Red Edge Index 1, VOG1 | |
| Vogelmann Red Edge Index 2, VOG2 | |
| Vogelmann Red Edge Index 3, VOG3 | |
| Water Band Index, WBI | |
| Chlorophyll Absorption Ratio Index, CARI | |
| RE Band Chlorophyll Index, CIrededge |
| Texture Features | Calculation Formula |
|---|---|
| Mean | |
| Variance | |
| Homogeneity | |
| Contrast | |
| Dissimilarity | |
| Entropy | |
| Second Moment | |
| Correlation |
| Spatial Resolution | Scheme 1 | Scheme 2 | Scheme 3 | |||
|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| 0.6 m | 0.4494 | 0.2211 | 0.5499 | 0.1731 | 0.7843 | 0.2391 |
| 1 m | 0.5514 | 0.2671 | 0.4481 | 0.1347 | 0.8201 | 0.2706 |
| 1.5 m | 0.2373 | 0.3926 | 0.1607 | 0.2553 | 0.7801 | 0.2359 |
| 2 m | 0.4434 | 0.2116 | 0.4529 | 0.1671 | 0.7712 | 0.3119 |
| 2.5 m | 0.4036 | 0.2487 | 0.4859 | 0.1373 | 0.7169 | 0.3797 |
| 3 m | 0.4023 | 0.2619 | 0.4297 | 0.1712 | 0.7969 | 0.2178 |
| 3.5 m | 0.2937 | 0.2711 | 0.3708 | 0.1439 | 0.6985 | 0.3648 |
| 4 m | 0.5801 | 0.2388 | 0.4185 | 0.1056 | 0.7024 | 0.3098 |
| 4.5 m | 0.5774 | 0.2231 | 0.3091 | 0.2268 | 0.5043 | 0.4263 |
| 5 m | 0.5957 | 0.2656 | 0.2068 | 0.1873 | 0.4515 | 0.3925 |
| Spatial Resolution | Scheme 1 | Scheme 2 | Scheme 3 | |||
|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| 0.6 m | 0.2781 | 0.2891 | 0.3306 | 0.1543 | 0.6564 | 0.3207 |
| 1 m | 0.3441 | 0.2465 | 0.3277 | 0.1777 | 0.7756 | 0.2628 |
| 1.5 m | 0.2391 | 0.3756 | 0.2736 | 0.2065 | 0.7954 | 0.2727 |
| 2 m | 0.3085 | 0.3853 | 0.3345 | 0.1986 | 0.7183 | 0.3309 |
| 2.5 m | 0.2188 | 0.2776 | 0.2662 | 0.2363 | 0.7269 | 0.3416 |
| 3 m | 0.3585 | 0.3216 | 0.4586 | 0.1581 | 0.7923 | 0.2617 |
| 3.5 m | 0.2579 | 0.3788 | 0.3525 | 0.1783 | 0.6203 | 0.3334 |
| 4 m | 0.2375 | 0.3435 | 0.1842 | 0.2364 | 0.5574 | 0.4251 |
| 4.5 m | 0.2109 | 0.3869 | 0.1769 | 0.1761 | 0.5331 | 0.3601 |
| 5 m | 0.2569 | 0.2841 | 0.1933 | 0.2101 | 0.5221 | 0.4162 |
| Spatial Resolution | Scheme 1 | Scheme 2 | Scheme 3 | |||
|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| 0.6 m | 0.3746 | 0.3104 | 0.4923 | 0.1086 | 0.7708 | 0.2608 |
| 1 m | 0.4323 | 0.3297 | 0.3295 | 0.2297 | 0.7835 | 0.2782 |
| 1.5 m | 0.3199 | 0.2851 | 0.3815 | 0.1702 | 0.8113 | 0.2741 |
| 2 m | 0.3194 | 0.3358 | 0.3053 | 0.1404 | 0.7321 | 0.3189 |
| 2.5 m | 0.4159 | 0.2302 | 0.4541 | 0.1186 | 0.7371 | 0.3484 |
| 3 m | 0.5764 | 0.2048 | 0.5261 | 0.1346 | 0.8326 | 0.2366 |
| 3.5 m | 0.4654 | 0.3097 | 0.3294 | 0.2125 | 0.7172 | 0.3344 |
| 4 m | 0.1922 | 0.3811 | 0.1412 | 0.1957 | 0.6434 | 0.3506 |
| 4.5 m | 0.2745 | 0.252 | 0.3512 | 0.1864 | 0.5476 | 0.3827 |
| 5 m | 0.2324 | 0.2218 | 0.1918 | 0.2229 | 0.5328 | 0.4268 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Xu, Z.; Li, Y.; Sun, L.; Zhang, H.; Zhang, C.; Yang, Y.; Guo, X.; Li, Z.; Guan, F. Hyperspectral Remote Sensing Estimation and Spatial Scale Effect of Leaf Area Index in Moso Bamboo (Phyllostachys pubescens) Forests Under the Stress of Pantana phyllostachysae Chao. Forests 2025, 16, 575. https://doi.org/10.3390/f16040575
Li H, Xu Z, Li Y, Sun L, Zhang H, Zhang C, Yang Y, Guo X, Li Z, Guan F. Hyperspectral Remote Sensing Estimation and Spatial Scale Effect of Leaf Area Index in Moso Bamboo (Phyllostachys pubescens) Forests Under the Stress of Pantana phyllostachysae Chao. Forests. 2025; 16(4):575. https://doi.org/10.3390/f16040575
Chicago/Turabian StyleLi, Haitao, Zhanghua Xu, Yifan Li, Lei Sun, Huafeng Zhang, Chaofei Zhang, Yuanyao Yang, Xiaoyu Guo, Zenglu Li, and Fengying Guan. 2025. "Hyperspectral Remote Sensing Estimation and Spatial Scale Effect of Leaf Area Index in Moso Bamboo (Phyllostachys pubescens) Forests Under the Stress of Pantana phyllostachysae Chao" Forests 16, no. 4: 575. https://doi.org/10.3390/f16040575
APA StyleLi, H., Xu, Z., Li, Y., Sun, L., Zhang, H., Zhang, C., Yang, Y., Guo, X., Li, Z., & Guan, F. (2025). Hyperspectral Remote Sensing Estimation and Spatial Scale Effect of Leaf Area Index in Moso Bamboo (Phyllostachys pubescens) Forests Under the Stress of Pantana phyllostachysae Chao. Forests, 16(4), 575. https://doi.org/10.3390/f16040575







